|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.
Paper's Title:
Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Inequalities for Functions of Selfadjoint Operators on Hilbert Spaces:
a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
College of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning inequalities for continuous functions of selfadjoint operators on complex Hilbert spaces. It is intended for use by both researchers in various fields of Linear Operator Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Trace Inequalities for Operators in Hilbert Spaces: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
School of Engineering
& Science
Victoria University,
PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
In this paper we survey some recent trace inequalities for operators in Hilbert spaces that are connected to Schwarz's, Buzano's and Kato's inequalities and the reverses of Schwarz inequality known in the literature as Cassels' inequality and Shisha-Mond's inequality. Applications for some functionals that are naturally associated to some of these inequalities and for functions of operators defined by power series are given. Further, various trace inequalities for convex functions are presented including refinements of Jensen inequality and several reverses of Jensen's inequality. Hermite-Hadamard type inequalities and the trace version of Slater's inequality are given. Some Lipschitz type inequalities are also surveyed. Examples for fundamental functions such as the power, logarithmic, resolvent and exponential functions are provided as well.
Paper's Title:
On Some Relations Among the Solutions of the Linear Volterra Integral Equations
Author(s):
Ismet Ozdemir and Faruk Temizer
Inönü Üniversitesi Eğitim Fakültesi,
44280-Malatya,
Turkey
Abstract:
The sufficient conditions for y1(x)≤ y2(x) were given in [1] such that ym(x)=fm(x)+∫ax Km(x, t)ym(t)dt,(m=1,2) and x∈ [a, b]. Some properties such as positivity, boundedness and monotonicity of the solution of the linear Volterra integral equation of the form f(t)=1-∫0tK(t-τ)f(τ)dτ=1-K*f, (0≤ t<∞) were obtained, without solving this equation, in [3,4,5,6]. Also, the boundaries for functions f', f'',..., f(n),(n ∈ N) defined on the infinite interval [0, ∞) were found in [7,8].
In this work, for the given equation f(t)=1-K* f and n≥ 2, it is derived that there exist the functions L2, L3,..., Ln which can be obtained by means of K and some inequalities among the functions f, h2, h3,..., hi for i=2, 3,...., n are satisfied on the infinite interval [0, ∞), where hi is the solution of the equation hi(t)=1-Li* hi and n is a natural number.
Paper's Title:
On the Sendov Conjecture for a Root Close to the Unit Circle
Author(s):
Indraneel G. Kasmalkar
Department of Mathematics,
University of California,
Berkeley, CA 94720
United States of America
E-mail: indraneelk@berkeley.edu
Abstract:
On Sendov's conjecture, T. Chijiwa quantifies the idea stated by V. Vâjâitu and A. Zaharescu (and M. J. Miller independently), namely that if a polynomial with all roots inside the closed unit disk has a root sufficiently close to the unit circle then there is a critical point at a distance of at most one from that root. Chijiwa provides an estimate of exponential order for the required 'closeness' of the root to the unit circle so that such a critical point may exist. In this paper, we will improve this estimate to polynomial order by making major modifications and strengthening inequalities in Chijiwa's proof.
Paper's Title:
Two Geometric Constants Related to Isosceles Orthogonality on Banach Space
Author(s):
Huayou Xie, Qi Liu and Yongjin Li
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P. R. China.
E-mail: xiehy33@mail2.sysu.edu.cn
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P. R. China.
E-mail: liuq325@mail2.sysu.edu.cn
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P. R. China.
E-mail: stslyj@mail.sysu.edu.cn
Abstract:
In this paper, we introduce new geometric constant C(X,ai,bi,ci,2) to measure the difference between isosceles orthogonality and special Carlsson orthogonalities. At the same time, we also present the geometric constant C(X,ai,bi,ci), which is a generalization of the rectangular constant proposed by Joly. According to the inequality on isosceles orthogonality, we give the boundary characterization of these geometric constants. Then the relationship between these geometric constants and uniformly non-square property can also be discussed. Furthermore, we show that there is a close relationship between these geometric constants and some important geometric constants.
Paper's Title:
Hyperbolic Barycentric Coordinates
Author(s):
Abraham A. Ungar
Department of Mathematics, North Dakota State University,
Fargo, ND 58105,
USA
Abraham.Ungar@ndsu.edu
URL: http://math.ndsu.nodak.edu/faculty/ungar/
Abstract:
A powerful and novel way to study Einstein's special theory of relativity and its underlying geometry, the hyperbolic geometry of Bolyai and Lobachevsky, by analogies with classical mechanics and its underlying Euclidean geometry is demonstrated. The demonstration sets the stage for the extension of the notion of barycentric coordinates in Euclidean geometry, first conceived by Möbius in 1827, into hyperbolic geometry. As an example for the application of hyperbolic barycentric coordinates, the hyperbolic midpoint of any hyperbolic segment, and the centroid and orthocenter of any hyperbolic triangle are determined.
Paper's Title:
Generalized Von Neumann-Jordan Constant for Morrey Spaces and Small Morrey Spaces
Author(s):
H. Rahman and H. Gunawan
Department of Mathematics,
Islamic State University Maulana Malik Ibrahim Malang,
Jalan Gajayana No.50,
Indonesia.
E-mail: hairur@mat.uin-malang.ac.id
Analysis and Geometry Group,
Faculty of Mathematics and Natural Sciences,
Bandung Institute of Technology, Bandung 40132,
Indonesia.
E-mail: hgunawan@math.itb.ac.id
URL:
http://personal.fmipa.itb.ac.id/hgunawan/
Abstract:
In this paper we calculate some geometric constants for Morrey spaces and small Morrey spaces, namely generalized Von Neumann-Jordan constant, modified Von Neumann-Jordan constants, and Zbaganu constant. All these constants measure the uniformly nonsquareness of the spaces. We obtain that their values are the same as the value of Von Neumann-Jordan constant for Morrey spaces and small Morrey spaces.
Paper's Title:
Existence, Global Regularity and Uniqueness of Solutions of the Navier-Stokes Equations in Space Dimension 3 when the Initial Data are Regular
Author(s):
Moulay D. Tidriri
Email: mtctyasa@gmail.com
Abstract:
The existence, regularity, and uniqueness of global solutions of the Navier-Stokes
equations in
are given for when the initial velocity
for all integers q ≥ 0 and div u0
= 0.
Paper's Title:
A general theory of decision making
Author(s):
Frank Hansen
Department of Economics,
University of Copenhagen,
Studiestraede 6, DK-1455 Copenhagen K
Denmark
Frank.Hansen@econ.ku.dk
URL: http://www.econ.ku.dk/okofh
Abstract:
We formulate a general theory of decision making based on a lattice of observable events, and we exhibit
a large class of representations called the general model. Some of the representations are equivalent to
the so called standard model in which observable events are modelled by
an algebra of measurable subsets of a state space, while others are not compatible with such a description.
We show that the general model collapses to the standard model, if and only if an additional axiom
is satisfied. We argue that this axiom is not very
natural and thus assert that the standard model may not be general enough to model all relevant
phenomena in economics. Using the general model we are
(as opposed to Schmeidler [16]) able to rationalize Ellsberg's paradox
without the introduction of non-additive measures.
Paper's Title:
Iterative Approximation of Common Fixed Points of a Finite Family of Asymptotically Hemi-contractive Type Mappings
Author(s):
Jui-Chi Huang
Center for General Education,
Northern Taiwan Institute of Science and Technology,
Peito, Taipei,
Taiwan, 11202, R.O.C.
juichi@ntist.edu.tw
Abstract:
In this paper, we prove that the sequence of
the modified Ishikawa-Xu,
Ishikawa-Liu, Mann-Xu and Mann-Liu iterative types of a finite family of
asymptotically hemi-contractive type mappings converges strongly to a common
fixed point of the family in a real p-uniformly convex Banach space with
p>1. Our results improve and extend some recent results.
Paper's Title:
Optimization and Approximation for Polyhedra in Separable Hilbert Spaces
Author(s):
Paolo d'Alessandro
Department of Mathematics,
Third University of Rome,
Italy.
E-mail: pdalex45@gmail.com
Abstract:
This paper studies infinite dimensional polyhedra, covering the case in which range spaces of operators defining inequality systems are not closed. A rangespace method of linear programming is generalized to infinite dimensions and finite dimensional methods of approximation are introduced.
Paper's Title:
Uniqueness Problems for Difference Polynomials Sharing a Non-Zero Polynomial of Certain Degree With Finite Weight
Author(s):
V. Priyanka, S. Rajeshwari and V. Husna
Department of Mathematics,
School of Engineering,
Presidency University,
Bangalore-560064,
India.
E-mail:
priyapriyankaram1994@gmail.com
rajeshwaripreetham@gmail.com
husnav43@gmail.com
Abstract:
In this paper, we prove a result on the value distribution of difference polynomials sharing higher order derivatives of meromorphic functions which improves some earlier results. At the same time, we also prove possible uniqueness relation of entire functions when the difference polynomial generated by them sharing a non zero polynomial of certain degree. The result obtained in the paper will improve and generalize a number of recent results in a compact and convenient way.
Paper's Title:
New Reverses of Schwarz, Triangle and Bessel Inequalities in Inner Product Spaces
Author(s):
S. S. Dragomir
School of Computer Science and Mathematics, Victoria
University of Technology, PO BOX
14428, MCMC 8001, VICTORIA, AUSTRALIA.
sever.dragomir@vu.edu.au
URL:
http://rgmia.vu.edu.au/SSDragomirWeb.html
Abstract:
New reverses of the Schwarz, triangle and Bessel inequalities in inner product spaces are pointed out. These results complement the recent ones obtained by the author in the earlier paper [13]. Further, they are employed to establish new Grüss type inequalities. Finally, some natural integral inequalities are stated as well.
Paper's Title:
Expected Utility with Subjective Events
Author(s):
Jacob Gyntelberg and Frank Hansen
Bank for International Settlements,
Basel,
Switzerland
Tohoku University, Institute for International Education,
Sendai,
Japan
Abstract:
We provide a new theory of expected utility with subjective events modeled by a lattice of projections. This approach allows us to capture the notion of a ``small world'' as a context dependent or local state space embedded into a subjective set of events, the ``grand world''. For each situation the decision makers' subjective ``small world'' reflects the events perceived to be relevant for the act under consideration. The subjective set of events need not be representable by a classical state space. Maintaining preference axioms similar in spirit to the classical axioms, we obtain an expected utility representation which is consistent across local state spaces and separates subjective probability and utility. An added benefit is that this alternative expected utility representation allows for an intuitive distinction between risk and uncertainty.
Paper's Title:
Polyanalytic Functions on Subsets of Z[i]
Author(s):
Abtin Daghighi
Linköping University,
SE-581 83,
Sweden.
E-mail: abtindaghighi@gmail.com
Abstract:
For positive integers q we consider the kernel of the powers Lq where L is one of three kinds of discrete analogues of the Cauchy-Riemann operator. The first two kinds are well-studied, but the third kind less so. We give motivations for further study of the third kind especially since its symmetry makes it more appealing for the cases q≥ 2.
From an algebraic perspective it makes sense that the chosen multiplication on the kernels is compatible with the choice of pseudo-powers. We propose such multiplications together with associated pseudo-powers. We develop a proof-tool in terms of certain sets of uniqueness.
Paper's Title:
Inequalities for the Area Balance of Functions of Bounded Variation
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
We introduce the area balance function associated to a Lebesgue
integrable function f:[a,b] →C by
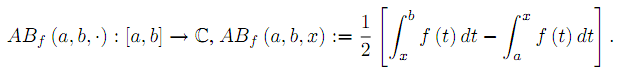
Several sharp bounds for functions of bounded variation are provided. Applications for Lipschitzian and convex functions are also given.
Paper's Title:
On Stan Ulam and his Mathematics
Author(s):
Krzysztof Ciesielski and Themistocles M. Rassias
Mathematics Institute, Jagiellonian University,
Abstract:
In this note we give a glimpse of the curriculum vitae of Stan Ulam, his personality and some of the mathematics he was involved in.
Paper's Title:
Good and Special Weakly Picard Operators for the Stancu Operators with Modified Coefficients
Author(s):
Loredana-Florentina Galea and Alexandru-Mihai Bica
The Agora University of Oradea,
Piata Tineretului no. 8,
410526, Oradea,
Romania
University of Oradea,
Str. Universitatii No. 1,
410087, Oradea,
Romania
loredana.galea@univagora.ro
smbica@yahoo.com
abica@uoradea.ro
Abstract:
In this paper some properties of good and special weakly Picard operators for the Stancu operators with modified coefficients are obtained. In the study of the sequence of iterates of these operators, we obtain the property of dual monotone iteration.
Paper's Title:
Some Moduli and Inequalities Related to Birkhoff Orthogonality in Banach Spaces
Author(s):
Dandan Du and Yongjin Li
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P.R. China.
E-mail: dudd5@mail2.sysu.edu.cn
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P.R. China.
E-mail: stslyj@mail.sysu.edu.cn
Abstract:
In this paper, we shall consider two new constants δB(X) and ρB(X), which are the modulus of convexity and the modulus of smoothness related to Birkhoff orthogonality, respectively. The connections between these two constants and other well-known constants are established by some equalities and inequalities. Meanwhile, we obtain two characterizations of Hilbert spaces in terms of these two constants, study the relationships between the constants δB(X), ρB(X) and the fixed point property for nonexpansive mappings. Furthermore, we also give a characterization of the Radon plane with affine regular hexagonal unit sphere.
Paper's Title:
Inequalities for
the
Author(s):
S. S. Dragomir
School of Engineering and Science
Victoria University, PO 14428
Melbourne City MC,
Victoria 8001,
Australia
sever.dragomir@vu.edu.au
URL: http://www.staff.vu.edu.au/RGMIA/dragomir/
Abstract:
Some recent inequalities for the Čebyšev functional of two functions of selfadjoint linear operators in Hilbert spaces, under suitable assumptions for the involved functions and operators, are surveyed.
Paper's Title:
Applications of Relations and Relators in the
Extensions of Stability Theorems for Homogeneous and Additive Functions
Author(s):
Árpád Száz
Institute of Mathematics, University of Debrecen,
H-4010 Debrecen,
Pf. 12,
Hungary
szaz@math.klte.hu
Abstract:
By working out an appropriate technique of relations and relators and extending the ideas of the direct methods of Z. Gajda and R. Ger, we prove some generalizations of the stability theorems of D. H. Hyers, T. Aoki, Th. M. Rassias and P. Găvruţă in terms of the existence and unicity of 2-homogeneous and additive approximate selections of generalized subadditive relations of semigroups to vector relator spaces. Thus, we obtain generalizations not only of the selection theorems of Z. Gajda and R. Ger, but also those of the present author.
Paper's Title:
On Interpolation of L2 functions
Author(s):
Anis Rezgui
Department of Mathematics,
Faculty of Sciences,
Taibah University, Al Madina Al Munawara,
KSA.
Mathematics Department,
INSAT,
University of Carthage, Tunis,
Tunisia
E-mail: anis.rezguii@gmail.com
Abstract:
In this paper we are interested in polynomial interpolation of irregular functions namely those elements of L2(R,μ) for μ a given probability measure. This is of course doesn't make any sense unless for L2 functions that, at least, admit a continuous version. To characterize those functions we have, first, constructed, in an abstract fashion, a chain of Sobolev like subspaces of a given Hilbert space H0. Then we have proved that the chain of Sobolev like subspaces controls the existence of a continuous version for L2 functions and gives a pointwise polynomial approximation with a quite accurate error estimation.
Paper's Title:
Construction of a Frame Multiresolution Analysis on Locally Compact Abelian Groups
Author(s):
R. Kumar and Satyapriya
Department of Mathematics,
Kirori Mal College,
University of Delhi,
Delhi,
India.
E-mail: rajkmc@gmail.com
Department of Mathematics,
University of Delhi,
Delhi,
India.
E-mail: kmc.satyapriya@gmail.com
Abstract:
The frame multiresolution analysis (FMRA) on locally compact Abelian groups has been studied and the results concerning classical MRA have been worked upon to obtain new results. All the necessary conditions, which need to be imposed on the scaling function φ to construct a wavelet frame via FMRA, have been summed up. This process of construction of FMRA has aptly been illustrated by sufficient examples.
Paper's Title:
Commutator For Singular Operators On Variable Exponent Sequence Spaces And Their Corresponding Ergodic Version
Author(s):
A.M. Alphonse and S.S.S. Anupindi
Department of Mathematics,
Birla Institute of Technology And Science- Pilani,
Hyderabad Campus, Jawahar Nagar, Kapra Mandal,
District.-Medchal-500 078, Telangana,
India.
E-mail:
alphonse@hyderabad.bits-pilani.ac.in
p20180442@hyderabad.bits-pilani.ac.in
URL:
https://www.bits-pilani.ac.in/hyderabad/a-michael-alphonse
https://www.bits-pilani.ac.in/research_scholars/sri-sakti-swarup-anupindi
Abstract:
In this paper, we prove strong type inequality for maximal commutator of singular operator on weighted lp spaces. Using these results we prove strong type inequality for the maximal commutator of singular operator on variable exponent sequence spaces. Using Calderon-Coifman-Weiss transference principle we prove strong type inequality for maximal ergodic commutator of singular operator on a probability space equipped with measure preserving transformation U.
Paper's Title:
Merit Functions and Error Bounds for Mixed Quasivariational Inequalities
Author(s):
Muhammad Aslam Noor
Mathematics Department, COMSATS Institute of Information Technology,
Islamabad, Pakistan
noormaslam@hotmail.com
Abstract:
It is well known that the mixed
quasivariational inequalities are equivalent to the fixed point
problems. We use this equivalent alternative formulation to
construct some merit functions for mixed quasivariational inequalities
and obtain error bounds under some conditions. Since mixed
quasivariational inequalities
include the classical variational inequalities and the complementarity
problems as special cases, our results continue to hold for these
problems.
Paper's Title:
Existence of Bounded Solutions for a Class of
Strongly Nonlinear Elliptic Equations in Orlicz-Sobolev Spaces
Author(s):
Abdelmoujib Benkirane and Ahmed Youssfi
Department of Mathematics and Informatics, Faculty of Sciences
Dhar El Mahraz
University Sidi Mohammed Ben Abdallah
PB 1796 Fez-Atlas, Fez
Morocco
a.benkirane@menara.ma
ahmed.youssfi@caramail.com
Abstract:
We prove, in the setting of Orlicz-Sobolev spaces, the existence of
bounded solutions for some strongly nonlinear elliptic equations
with operator of the principal part having degenerate coercivity and
lower order terms not satisfying the sign condition. The data have a
suitable summability and no Δ2-condition is needed for the
considered N-functions.
Paper's Title:
On an Extension of Hilbert’s Integral Inequality with Some Parameters
Author(s):
Bicheng Yang
Department of
Mathematics, Guangdong Education College, Guangzhou, Guangdong 510303, People’s
Republic of China.
bcyang@pub.guangzhou.gd.cn
URL:
http://www1.gdei.edu.cn/yangbicheng/index.html
Abstract:
In this paper, by introducing some parameters and estimating the
weight function, we give an extension of Hilbert’s integral inequality with a
best constant factor. As applications, we consider the equivalent form and some
particular results.
Paper's Title:
Uniqueness of Meromorphic Functions and
Weighted Sharing
Author(s):
Indrajit Lahiri and Rupa Pal
Department of Mathematics, University of
Kalyani, West Bengal 741235, India
indr9431@dataone.in
Jhargram Raj College,
Jhargram, Midnapur(W),
West Bengal 721507,
India
rupa.a.pal@gmail.com
Abstract:
With the help of the notion of weighted sharing of values, we prove a result on uniqueness of meromorphic functions and as a consequence we improve a result of P. Li
Paper's Title:
Unital Compact Homomorphisms Between Extended Analytic Uniform Algebras
Author(s):
D. Alimohammadi and M. Mayghani
Department of Mathematics,
Faculty of Science, Arak University,
PO Box 38156-8-8349, Arak,
Iran.
Abstract:
Let X and K be compact plane sets with K⊆X. We denote by A(X,K) and A(X) the algebras of all continuous complex-valued functions on X which are analytic on int(K) and int(X), respectively. It is known that A(X,K) and A(X) are natural uniform algebras on X. A(X) and A(X,K) are called analytic uniform algebra and extended analytic uniform algebra on X, respectively. In this paper we study unital homomorphisms between extended analytic uniform algebras and investigate necessary and sufficient conditions for which these homomorphisms to be compact. We also determine the spectrum of unital compact endomorphisms of extended analytic uniform algebras.
Paper's Title:
Differential Equations for Indicatrices, Spacelike and Timelike Curves
Author(s):
Sameer, Pradeep Kumar Pandey
Department of Mathematics,
Jaypee University of Information Technology,
Solan, Himachal Pradesh,
India.
E-mail: sksameer08@gmail.com,
pandeypkdelhi@gmail.com
Abstract:
Motivated by the recent work of Deshmukh et al. [20], in this paper we show that Tangent, Binormal, and Principal Normal indicatrices do not form non-trivial differential equations. Finally, we obtain the 4th-order differential equations for spacelike and timelike curves.
Paper's Title:
The Voronovskaja Type Theorem for the Stancu Bivariate
Operators
Author(s):
Ovidiu T. Pop
National College "Mihai Eminescu",
5 Mihai Eminescu Street,
Satu Mare 440014, Romania
Vest University "Vasile Goldis" of
Arad, Branch of Satu Mare,
26 Mihai Viteazul Street
Satu Mare 440030, Romania
ovidiutiberiu@yahoo.com
Abstract:
In this paper, the Voronovskaja type theorem for the Stancu
bivariate operators is established. As particular cases, we shall
obtain the Voronovskaja type theorem for the Bernstein and Schurer
operators.
Paper's Title:
Construction of Lyapunov Functionals In Functional Differential Equations With Applications To Exponential Stability In Volterra Integro-differential Equations
Author(s):
Youssef N. Raffoul
Department of Mathematics, University of Dayton,
Dayton OH 45469-2316,
USA
youssef.raffoul@notes.udayton.edu
URL:http://academic.udayton.edu/YoussefRaffoul
Abstract:
Non-negative definite Lyapunov functionals are employed to obtain
sufficient conditions that guarantee the exponential asymptotic
stability and uniform exponential asymptotic stability of the zero
solution of nonlinear functional differential systems. The theory
is applied to Volterra integro-differential equations in the form
of proposition examples.
Paper's Title:
Mass Transportation Approach For Parabolic P-Biharmonic Equations
Author(s):
A. Soglo, K. W. Houedanou, J. Adetola
Institut de Mathematiques et de Sciences
Physiques (IMSP)
Universite d'Abomey-Calavi,
Rep. of Benin
E-mail: ambroiso.soglo@gmail.com
Departement de Mathematiques
Faculte des Sciences et Techniques (FAST)
Universite d'Abomey-Calavi,
Rep. of Benin
E-mail: khouedanou@yahoo.fr
Universite Nationale des Sciences, Technologie, Ingenierie et
Mathematiques (UNSTIM,
Abomey,
Rep. of Benin
E-mail: adetolajamal58@yahoo.com
Abstract:
In this paper, we propose a mass transportation method to solving a parabolic p-biharmonic equations, which generalized the Cahn-Hilliard (CH) equations in RN, N∈N*. By using a time-step optimal approximation in the appropriate Wasserstein space, we define an approximate weak solution which converges to the exact solution of the problem. We also show that the solution under certain conditions may be unique. Therefore, we study the asymptotic behavior of the solution of the parabolic p-biharmonic problem.
Paper's Title:
Multivalued Hemiequilibrium Problems
Author(s):
Muhammad Aslam Noor
Mathematics Department,
COMSATS Institute of Information Technology,
Sector H-8/1, Islamabad,
Pakistan.
noormaslam@hotmail.com
Abstract:
In this paper, we introduce and study a new class of equilibrium problems, known
as multivalued hemiequilibrium problems. The auxiliary principle technique is used to suggest
and analyze some new classes of iterative algorithms for solving multivalued hemiequilibrium
problems. The convergence of the proposed methods either requires partially relaxed strongly
monotonicity or pseudomonotonicity. As special cases, we obtain a number of known and new
results for solving various classes of equilibrium and variational inequality problems. Since
multivalued hemiequilibrium problems include hemiequilibrium, hemivariational inequalities,
variational inequalities and complementarity problems as specials cases, our results still hold for
these problems.
Paper's Title:
On Perturbed Reflection Coefficients
Author(s):
J. L. Díaz-Barrero and J. J. Egozcue
Applied Mathematics III,
Universidad Politécnica de Cataluńa,
Barcelona, Spain
jose.luis.diaz@upc.edu
juan.jose.egozcue@upc.edu
Abstract:
Many control and signal processing applications require testing
stability of polynomials. Classical tests for locating zeros of
polynomials are recursive, but they must be stopped whenever the so
called "singular polynomials" appear. These ``singular cases'' are
often avoided by perturbing the "singular polynomial".
Perturbation techniques although always successful are not proven to
be well-founded. Our aim is to give a mathematical foundation to a
perturbation method in order to overcome "singular cases" when
using Levinson recursion as a testing method. The non-singular
polynomials are proven to be dense in the set of all polynomials
respect the L˛-norm on the unit circle . The proof is
constructive and can be used algorithmically.
Paper's Title:
Real Interpolation Methods and Quasilogarithmic Operators
Author(s):
Ming Fan
School of Industrial Technology and Management,
Dalarna University, 781 88 Borlänge, Sweden
fmi@du.se
URL: http://users.du.se/~fmi
Abstract:
The purpose of this paper is to deal with nonlinear quasilogarithmic operators, which possesses the uniformly bounded commutator property on various interpolation spaces in the sense of Brudnyi-Krugljak associated with the quasi-power parameter spaces. The duality, and the domain and range spaces of these operators are under consideration. Some known inequalities for the Lebesgue integration spaces and the trace classes are carried over to the non-commutative symmetric spaces of measurable operators affiliated with a semi-finite von Neumann algebra.
Paper's Title:
Weak solutions of non coercive stochastic Navier-Stokes equations in R2
Author(s):
Wilhelm Stannat and Satoshi Yokoyama
Technische Universität Berlin,
Strasse des 17. Juni 136, 10623 Berlin,
Germany.
Graduate School of Mathematical Sciences,
The University of Tokyo,
Komaba, Tokyo 153-8914,
Japan.
E-mail: stannat@math.tu-berlin.de
E-mail: satoshi2@ms.u-tokyo.ac.jp
Abstract:
We prove existence of weak solutions of stochastic Navier-Stokes equations in R2 which do not satisfy the coercivity condition. The equations are formally derived from the critical point of some variational problem defined on the space of volume preserving diffeomorphisms in R2. Since the domain of our equation is unbounded, it is more difficult to get tightness of approximating sequences of solutions in comparison with the case of a bounded domain. Our approach is based on uniform a priori estimates on the enstrophy of weak solutions of the stochastic 2D-Navier-Stokes equations with periodic boundary conditions, where the periodicity is growing to infinity combined with a suitable spatial cutoff-technique.
Paper's Title:
Examples of Fractals Satisfying the Quasihyperbolic Boundary Condition
Author(s):
Petteri Harjulehto and Riku Klén
Department of Mathematics and Statistics,
FI-20014 University of Turku,
Finland
E-mail: petteri.harjulehto@utu.fi
E-mail: riku.klen@utu.fi
Abstract:
In this paper we give explicit examples of bounded domains that satisfy the quasihyperbolic boundary condition and calculate the values for the constants. These domains are also John domains and we calculate John constants as well. The authors do not know any other paper where exact values of parameters has been estimated.
Paper's Title:
Generalized Composition Operators On Besov Spaces
Author(s):
Vishal Sharma, Sanjay Kumar and Stanzin Dolkar
Department of Mathematics,
Central University of Jammu,
Jammu and Kashmir,
India.
E-mail: sharmavishal911@gmail.com
Department of Mathematics,
Central University of Jammu,
Jammu and Kashmir,
India.
E-mail: sanjaykmath@gmail.com
Department of Mathematics,
Central University of Jammu,
Jammu and Kashmir,
India.
E-mail: stanzin.math@cujammu.ac.in
Abstract:
In this paper, we characterize boundedness, compactness and find the essential norm estimates for generalized composition operators between Besov spaces and Sp spaces.
Paper's Title:
On a Generalized Biharmonic Equation in Plane Polars with Applications to Functionally Graded Materials
Author(s):
Ciro D'Apice
Department of Information Engineering and Applied Mathematics (DIIMA),
University of Salerno, 84084 Fisciano (SA),
Salerno, Italy.
dapice@diima.unisa.it
Abstract:
In this paper we consider a generalized biharmonic
equation modelling a two-dimensional inhomogeneous
elastic state in the curvilinear rectangle 
where 
denote plane polar
coordinates. Such an arch--like region is maintained in equilibrium under
self--equilibrated traction applied on the edge 
while the other three
edges 
and 
are traction free. Our
aim is to derive some explicit spatial exponential decay bounds for the
specific Airy stress function and its derivatives. Two types of smoothly
varying inhomogeneity are considered: (i) the elastic moduli vary
smoothly with the polar angle, (ii) they vary smoothly
with the polar distance. Such types of smoothly varying inhomogeneous elastic
materials provide a model for technological important functionally graded
materials. The results of the present paper prove how the spatial decay rate
varies with the constitutive profile.
Paper's Title:
Growth and Products of Subharmonic Functions in the Unit Ball
Author(s):
R. Supper
Université de Strasbourg,
UFR de Mathématique et Informatique, URA CNRS 001,
7 rue René Descartes,
F--67 084 Strasbourg Cedex,
France
raphaele.supper@math.unistra.fr
Abstract:
The purpose of this paper is to link information on the application u→gu with some growth conditions on the functions u and g subharmonic in the unit ball of RN. Two kinds of growth are considered: the Bloch--type growth and growth conditions expressed through integrals involving involutions of the unit ball.
Paper's Title:
Generalized k-distance-balanced Graphs
Author(s):
Amir Hosseini and Mehdi Alaeiyan
Department of mathematics, Karaj Branch,
Islamic Azad university, Karaj,
Iran.
E-mail: amir.hosseini@kiau.ac.ir,
hosseini.sam.52@gmail.com
Department of Mathematics,
Iran University of Science and Technology, Tehran,
Iran.
E-mail: alaeiyan@iust.ac.ir
Abstract:
A nonempty graph Γ is called generalized k-distance-balanced, whenever every edge ab has the following property: the number of vertices closer to a than to b, k, times of vertices closer to b than to a, or conversely, k∈ N .In this paper we determine some families of graphs that have this property, as well as to prove some other result regarding these graphs.
Paper's Title:
Maximal Singular Operators On Variable Exponent Sequence Spaces and Their Corresponding Ergodic Version
Author(s):
Sri Sakti Swarup Anupindi and Michael A. Alphonse
Department of Mathematics, Birla Institute
of Technology And Science- Pilani,
Hyderabad Campus, Jawahar Nagar, Kapra Mandal,
District.-Medchal-500 078 Telangana,
India.
E-mail:
p20180442@hyderabad.bits-pilani.ac.in
alphonse@hyderabad.bits-pilani.ac.in
URL:
https://www.bits-pilani.ac.in/hyderabad/a-michael-alphonse
https://www.bits-pilani.ac.in/research_scholars/sri-sakti-swarup-anupindi
Abstract:
In this paper, we prove strong and weak type inequalities of singular operators on weighted lwp(Z)$. Using these results, we prove strong type and weak type inequalities of the maximal singular operator of Calderon-Zygmund type on variable exponent sequence spaces lp(·)(Z). Using the Calderon-Coifman-Weiss transference principle, we prove strong type, weak type inequalities of the maximal ergodic singular operator on Lwp(X,B,μ) spaces, where (X,B,μ) is a probability space equipped with measure preserving transformation U.
Paper's Title:
Viability
Theory And Differential Lanchester Type Models For Combat.
Differential Systems.
Author(s):
G. Isac and A. Gosselin
Department Of
Mathematics, Royal Military College Of Canada,
P.O. Box 17000, Stn Forces, Kingston,
Ontario, Canada K7k 7b4
isac-g@rmc.ca
gosselin-a@rmc.ca
URL:
http://www.rmc.ca/academic/math_cs/isac/index_e.html
URL:
http://www.rmc.ca/academic/math_cs/gosselin/index_e.html
Abstract:
In 1914, F.W. Lanchester proposed several mathematical models based on differential equations to describe combat situations [34]. Since then, his work has been extensively modified to represent a variety of competitions including entire wars. Differential Lanchester type models have been studied from many angles by many authors in hundreds of papers and reports. Lanchester type models are used in the planning of optimal strategies, supply and tactics. In this paper, we will show how these models can be studied from a viability theory stand point. We will introduce the notion of winning cone and show that it is a viable cone for these models. In the last part of our paper we will use the viability theory of differential equations to study Lanchester type models from the optimal theory point of view.
Paper's Title:
A Simple New Proof of Fan-Taussky-Todd Inequalities
Author(s):
Zhi-Hua Zhang and Zhen-Gang Xiao
Zixing Educational Research Section,
Chenzhou City, Hunan 423400, P. R. China.
Zhi-hua Zhang
Url: http://www.hnzxslzx.com/zzhweb/
Department Of Mathematics, Hunan Institute Of Science And Technology,
Yueyang City, Hunan 423400, P. R. China.
Zhen-gang Xiao
Abstract:
In this paper we present simple new proofs of the inequalities:
which holds for all real numbers a0 = 0, a1, · · · , an, an+1 = 0 and the coefficients
2(1 - cos(π/(n + 1))) and 2(1 + cos(π/(n + 1))) are the best possible; and
which holds for all real numbers a0 = 0, a1, · · · , an and the coefficients
2(1-cos(π/(2n + 1))) and 2(1 + cos(π/(2n + 1))) are the best possible.
Paper's Title:
General Oscillations for Some Third Order Differential Systems with Nonlinear Acceleration Term
Author(s):
Awar Simon Ukpera
Department of Mathematics,
Obafemi Awolowo University,
Ile-Ife,
Nigeria.
aukpera@oauife.edu.ng
Abstract:
We generate some general nonuniform hypotheses for third order differential systems
of the form X''' +F(t,X'' )+BX'+CX = P(t), in which B and C are not
necessarily
constant matrices. Some results requiring sharp conditions on this system have recently been
published by the author in
[5]. This work however examines more closely crucial properties
associated with the generalised nature of the nonlinear acceleration term F, which were largely
overlooked in the earlier paper.
Paper's Title:
Analysis of the Flow Field in Stenosed Bifurcated Arteries Through a Mathematical Model
Author(s):
S. Chakravarty and S. Sen
Department of Mathematics, Visva-Bharati University,
Santiniketan 731235,
India
santabrata2004@yahoo.co.in
Abstract:
The present study is dealt with an appropriate mathematical model
of the arotic bifurcation in the presence of constrictions using which
the physiological flow field is analized. The geometry of the bifurcated
arterial segment having constrictions in both the parent and its daughter
arterial lumen frequently occurring in the diseased arteries causing
malfunction of the cardiovascular system , is formed mathematically
with the introduction of appropriate curvatures at the lateral junctions
and the flow divider. The flowing blood contained in the stenosed
bifurcated artery is treated to be Newtonian and the flow is considered
to be two dimensional. The motion of the arterial wall and its effect
on local fluid mechanics is not ruled out from the present pursuit.
The flow analysis applies the time-dependent, two-dimensional incompressible
nonlinear Navier-Stokes equations for Newtonian fluid. The flow field
can be obtained primarily following the radial coordinate transformation
and using the appropriate boundary conditions and finally adopting
a suitable finite difference scheme numerically. The influences of
the arterial wall distensibility and the presence of stenosis on the
flow field, the flow rate and the wall shear stresses are quantified
in order to indicate the susceptibility to atherosclerotic lesions
and thereby to validate the applicability of the present theoretical
model.
Paper's Title:
Positive Periodic Solutions for
Second-Order Differential Equations with Generalized Neutral Operator
Author(s):
Wing-Sum Cheung, Jingli Ren and Weiwei Han
Department of Mathematics,
The University of Hong Kong
Pokfulam
Road,
Hong Kong
Department of Mathematics, Zhengzhou University
Zhengzhou 450001,
P.R. China
wscheung@hkucc.hku.hk
renjl@zzu.edu.cn
Abstract:
By some analysis of the neutral operator
and an application of the fixed-point
index theorem, we obtain sufficient conditions for the existence,
multiplicity and nonexistence of periodic solutions to a second-order
differential equation with the prescribed neutral operator, which improve
and extend some recent results of Lu-Ge, Wu-Wang, and Zhang. An example is
given to illustrate our results. Moreover, the analysis of the generalized
neutral operator will be helpful for other types of differential equations.
Paper's Title:
Ellipses of Minimal Area and of Minimal Eccentricity Circumscribed About a Convex Quadrilateral
Author(s):
Alan Horwitz
Penn State University,
25 Yearsley Mill Rd.,
Media, PA 19063,
U.S.A
alh4@psu.edu
Abstract:
First, we fill in key gaps in Steiner's nice characterization of
the most nearly circular ellipse which passes through the vertices of a convex
quadrilateral,
. Steiner proved that there is only one pair of conjugate
directions, M1 and M2, that belong to all ellipses of circumscription.
Then he proves that if there is an ellipse, E, whose equal
conjugate diameters possess the directional constants M1 and M2,
then E must be an ellipse of circumscription which has minimal eccentricity.
However, Steiner does not show the existence or uniqueness of such an ellipse.
We prove that there is a unique ellipse of minimal eccentricity which passes
through the vertices of
. We also show that there exists an ellipse which passes through the vertices of
and whose
equal conjugate diameters
possess the directional constants M1 and M2. We also show
that there exists a unique ellipse of minimal area which passes through the
vertices of
. Finally, we call a convex quadrilateral,
, bielliptic if the unique
inscribed and circumscribed ellipses of minimal eccentricity have the same
eccentricity. This generalizes the notion of bicentric quadrilaterals. In
particular, we show the existence of a bielliptic convex quadrilateral which is
not bicentric.
Paper's Title:
Shape Diagrams for 2D Compact Sets - Part I: Analytic
Convex Sets.
Author(s):
S. Rivollier, J. Debayle and J.-C. Pinoli
Ecole Nationale Supérieure des Mines de Saint-Etienne,
CIS - LPMG, UMR CNRS 5148, 158 cours Fauriel,
42023 Saint-Etienne Cedex 2, France.
rivollier@emse.fr;
debayle@emse.fr; pinoli@emse.fr
Abstract:
Shape diagrams are representations in the Euclidean plane introduced to study 3-dimensional and 2-dimensional compact convex sets. Such a set is represented by a point within a shape diagram whose coordinates are morphometrical functionals defined as normalized ratios of geometrical functionals. Classically, the geometrical functionals are the area, the perimeter, the radii of the inscribed and circumscribed circles, and the minimum and maximum Feret diameters. They allow thirty-one shape diagrams to be built. Most of these shape diagrams can also been applied to more general compact sets than compact convex sets. Starting from these six classical geometrical functionals, a detailed comparative study has been performed in order to analyze the representation relevance and discrimination power of these thirty-one shape diagrams. The purpose of this paper is to present the first part of this study, by focusing on analytic compact convex sets. A set will be called analytic if its boundary is piecewise defined by explicit functions in such a way that the six geometrical functionals can be straightforwardly calculated. The second and third part of the comparative study are published in two following papers [19.20]. They are focused on analytic simply connected sets and convexity discrimination for analytic and discretized simply connected sets, respectively.
Paper's Title:
Hardy Type Inequalities via Convexity - The Journey so Far
Author(s):
James A.
Oguntuase and Lars-Erik Persson
Department of Mathematics,
University of Agriculture,
P. M. B. 2240, Abeokuta, Nigeria.
Department of
Mathematics, Luleĺ University of Technology,
SE-971 87, Luleĺ , Sweden.
oguntuase@yahoo.com,
larserik@sm.luth.se .
Abstract:
It is nowadays well-known that Hardy's inequality (like many other inequalities) follows directly from Jensen's inequality. Most of the development of Hardy type inequalities has not used this simple fact, which obviously was unknown by Hardy himself and many others. Here we report on some results obtained in this way mostly after 2002 by mainly using this fundamental idea.
Paper's Title:
Attempts to Define a Baum--Connes Map Via Localization of Categories for Inverse Semigroups
Author(s):
Bernhard Burgstaller
Departamento de Matematica,
Universidade Federal de Santa Catarina,
CEP 88.040-900 Florianopolis-SC,
Brasil.
E-mail:
bernhardburgstaller@yahoo.de
URL:
http://mathematik.work/bernhardburgstaller/index.html
Abstract:
An induction functor in inverse semigroup equivariant KK-theory is considered, and together with %a restriction functors certain results similar to those known from the Mackey machinery are shown. It is also verified that for any so-called E-continuous inverse semigroup its equivariant KK-theory satisfies the universal property and is a triangulated category.
Paper's Title:
A Caratheodory's Approximate Solutions of Stochastic Differential Equations Under the Hölder Condition
Author(s):
Bo-Kyeong Kim and Young-Ho Kim
Department of Mathematics,
Changwon National University,
Changwon, Gyeongsangnam-do 51140,
Korea.
E-mail: claire9576@naver.com
yhkim@changwon.ac.kr
Abstract:
In this paper, based on the theorem of the uniqueness of the solution of the stochastic differential equation, the convergence possibility of the Caratheodory's approximate solution was studied by approximating the unique solution. To obtain this convergence theorem, we used a Hölder condition and a weakened linear growth condition. Furthermore, The auxiliary theorems for the existence and continuity of the Caratheodory's approximate solution were investigated as a prerequisite.
Paper's Title:
The successive approximations method and error estimation in terms of at most the first derivative for delay ordinary differential equations
Author(s):
Alexandru Mihai Bica
Department of Mathematics,
University of Oradea,
Str. Armatei Romane no.5,
410087, Oradea,
Romania
smbica@yahoo.com
abica@uoradea.ro
Abstract:
We present here a numerical method for first order delay ordinary differential
equations, which use the Banach's fixed point theorem, the sequence of
successive approximations and the trapezoidal quadrature rule. The error
estimation of the method uses a recent result of P. Cerone and S.S. Dragomir
about the remainder of the trapezoidal quadrature rule for Lipchitzian
functions and for functions with continuous first derivative.
Paper's Title:
Local and Global Existence and Uniqueness Results for Second and Higher Order Impulsive Functional Differential Equations with Infinite Delay
Author(s):
Johnny Henderson and Abdelghani Ouahab
Department of Mathematics, Baylor University,
Waco, Texas 76798-7328
USA.
Johnny_Henderson@baylor.edu
Laboratoire de Mathématiques, Université de Sidi Bel Abbés
BP 89, 22000 Sidi Bel Abbées,
Algérie.
ouahab@univ-sba.dz
Abstract:
In this paper, we discuss the local and global existence and
uniqueness results for second and higher order impulsive functional
differential equations with infinite delay. We shall rely on a
nonlinear alternative of Leray-Schauder. For the global existence
and uniqueness we apply a recent Frigon and Granas nonlinear
alternative of Leray-Schauder type in Fréchet spaces.
Paper's Title:
Long Correlations Applied to the Study of Agricultural Indices in Comparison with the S&P500 index
Author(s):
M. C. Mariani, J. Libbin, M.P. Beccar Varela,
V. Kumar Mani, C. Erickson, D.J. Valles Rosales
Department of Mathematical Sciences,
Science Hall 236, New Mexico State University,
Las Cruces, NM 88003-8001,
USA.
mmariani@nmsu.edu
Abstract:
Long-time correlations in agricultural indices are studied and their behavior is compared to the well-established S&P500 index. Hurst exponent and Detrended Fluctuation Analysis (DFA) techniques are used in this analysis. We detected long-correlations in the agricultural indices and briefly discussed some features specific in comparison to the S&P500 index.
Paper's Title:
Finite and Infinite Order
Solutions of a Class of Higher Order Linear Differential Equations
Author(s):
Saada Hamouda
Department of Mathematics,
Laboratory of Pure and Applied Mathematics,
University of Mostaganem, B. P 227 Mostaganem,
ALGERIA
hamouda_saada@yahoo.fr
Abstract:
In this paper, we investigate the growth of solutions of higher order linear differential equations where most of the coefficients have the same order and type with each other.
Paper's Title:
On Generalization of Hardy-type Inequalities
Author(s):
K. Rauf, S. Ponnusamy and J. O. Omolehin
Department of Mathematics,
University of Ilorin, Ilorin,
Nigeria
krauf@unilorin.edu.ng
Department of Mathematics,
Indian Institute of Technology Madras,
Chennai- 600 036,
India
samy@iitm.ac.in
Department of Mathematics,
University of Ilorin, Ilorin,
Nigeria
omolehin_joseph@yahoo.com
Abstract:
This paper is devoted to some new generalization of Hardy-type integral inequalities and the reversed forms. The study is to determine conditions on which the generalized inequalities hold using some known hypothesis. Improvement of some inequalities are also presented.
Paper's Title:
Existence Results for Second Order Impulsive Functional Differential Equations with Infinite Delay
Author(s):
M. Lakrib, A. Oumansour and K. Yadi
Laboratoire de Mathématiques, Université Djillali
Liabées, B.P. 89 Sidi Bel Abbčs 22000, Algérie
mlakrib@univ-sba.dz
oumansour@univ-sba.dz
Laboratoire de Mathématiques, Université Abou Bekr
Belkaid, B.P. 119 Tlemcen 13000, Algérie
k_yadi@mail.univ-tlemcen.dz
Abstract:
In this paper we study the existence of solutions for second order impulsive functional differential equations with infinite delay. To obtain our results, we apply fixed point methods.
Paper's Title:
Traub-Potra-Type Method for Set-Valued Maps
Author(s):
Ioannis K. Argyros and Saďd Hilout
Cameron University,
Department of Mathematics Sciences,
Lawton, OK 73505,
USA
URL: http://www.cameron.edu/~ioannisa/
Poitiers University,
Laboratoire de Mathematiques et Applications,
Bd. Pierre et Marie Curie, Teleport 2, B.P. 30179,
86962 Futuroscope Chasseneuil Cedex,
France
said.hilout@math.univ-poitiers.fr
http://www-math.univ-poitiers.fr/~hilout/
Abstract:
We introduce a new iterative method for approximating a locally unique solution of variational inclusions in Banach spaces by using generalized divided differences of the first order. This method extends a method considered by Traub (in the scalar case) and by Potra (in the Banach spaces case) for solving nonlinear equations to variational inclusions. An existence-convergence theorem and a radius of convergence are given under some conditions on divided differences operator and Lipschitz-like continuity property of set-valued mappings. The R-order of the method is equal to the unique positive root of a certain cubic equation, which is $1.839..., and as such it compares favorably to related methods such as the Secant method which is only of order $1.618....
Paper's Title:
On a Problem on Periodic Functions
Author(s):
Adel A. Abdelkarim
Mathematics Department, Faculty of
Science,
Jerash Private University, Jerash,
Jordan.
E-mail:
adelafifo_afifo@yahoo.com
Abstract:
Given a continuous periodic real function f with n translates f1 ,..., fn , where fi(x)=f(x+ai), i=1,...,n. We solve a problem by Erdos and Chang and show that there are rational numbers r,s such that f(r)≥ fi(r), f(s)≤ fi(s), i=1,...,n. No restrictions on the constants or any further restriction on the function f are necessary as was imposed earlier.
Paper's Title:
Existence and Regularity of Minima of an Integral Functional in Unbounded Domain
Author(s):
L. Aharouch, J. Bennouna and A. Bouajaja
King Khalid University
Faculty of Arts and Science Mha'l Asir
Saudi Arabia.
E-mail: laharouch@gmail.com
Université Sidi Mohammed Ben Abdellah
Faculté des Sciences Dhar-Mahraz
B.P 1796 Atlas Fčs,
Maroc.
Email: jbennouna@hotmail.com
E-mail: kadabouajaja@hotmail.com
Abstract:
We prove the existence and the regularity of minima for a functional defined on a suitable Sobolev space.
Paper's Title:
Optimization Techniques on Affine Differential Manifolds
Author(s):
Ali S Rasheed, Faik Mayah and Ahmed A H AL-Jumaili
Ministry of Higher Education and
Scientific Research,
Iraq.
E-mail: ahmedhashem@gmail.com
Department of Physics, College of
Sciences,
University of Wasit,
Iraq.
E-mail: faik.mayah@gmail.com
Abstract:
In addition to solid ground of Riemannian manifolds fundamentals, this article interviews some popular optimization methods on Riemannian manifolds. Several optimization problems can be better stated on manifolds rather than Euclidean space, such as interior point methods, which in turns based on self-concordant functions (logarithmic barrier functions). Optimization schemes like the steepest descent scheme, the Newton scheme, and others can be extended to Riemannian manifolds. This paper introduces some Riemannian and non-Riemannian schemes on manifolds.
Paper's Title:
Nonlinear System of Mixed Ordered Variational Inclusions Involving XOR Operation
Author(s):
Iqbal Ahmad, Abdullah and Syed Shakaib Irfan
Department of Mechanical Engineering,
College of Engineering, Qassim University
Buraidah 51452, Al-Qassim,
Saudi Arabia.
E-mail: iqbal@qec.edu.sa,
i.ahmad@qu.edu.sa
Zakir Husain Delhi College,
University of Delhi,
JLN Marg, New Delhi- 110 002,
India.
E-mail: abdullahdu@qec.edu.sa
Department of Mathematics,
Aligarh Muslim University, Aligarh,
India.
E-mail: shakaibirfan@gmail.com
Abstract:
In this work, we introduce and solve an NSMOVI frameworks system involving XOR operation with the help of a proposed iterative algorithm in real ordered positive Hilbert spaces. We discuss the existence of a solution of a considered system of inclusions involving XOR operation by applying the resolvent operator technique with XOR operation and also study the strong convergence of the sequences generated by the considered algorithm. Further, we give a numerical example in support of our considered problem which gives the grantee that all the proposed conditions of our main result are fulfilled.
Paper's Title:
Long Time Behavior for a Viscoelastic Problem with a Positive Definite Kernel
Author(s):
Nasser-eddine Tatar
King Fahd
University of Petroleum and Mineral, Department of Mathematical Sciences,
Dhahran, 31261 Saudi Arabia
tatarn@kfupm.edu.sa
Abstract:
We study the asymptotic behavior of solutions for an integro-differential problem which arises in the theory of viscoelasticity. It is proved that solutions go to rest in an exponential manner under new assumptions on the relaxation function in the memory term. In particular, we consider a new family of kernels which are not necessarily decreasing.
Paper's Title:
A New Hardy-Hilbert's Type Inequality for Double Series and its Applications
Author(s):
Mingzhe Gao
Department of Mathematics and Computer Science, Normal College Jishou University,
Jishou Hunan, 416000,
People's Republic of China
mingzhegao1940@yahoo.com.cn
Abstract:
In this paper, it is shown that a new Hardy-Hilbert’s type
inequality for double series can be established by introducing a parameter 
and the weight function of the form 
where c is Euler
constant and 
And
the coefficient 
and 
appear simultaneously in the coefficient and the weight
function when 
In particular, for
case 
some new Hilbert’s
type inequalities are obtained. As applications, some extensions of Hardy-Littlewood’s inequality are given.
Paper's Title:
Existence of Large Solutions to Non-Monotone Semilinear Elliptic Equations
Author(s):
Alan V. Lair, Zachary J. Proano, and Aihua W. Wood
Air Force Institute of Technology
2950 Hobson Way, AFIT/ENC
Wright-Patterson Air Force Base, OH, 45433-7765,
USA.
Aihua.Wood@afit.edu
URL: www.afit.edu
Abstract:
We study the existence of large solutions of the semilinear elliptic equation Δu=p(x)f(u) where f is not monotonic. We prove existence, on bounded and unbounded domains, under the assumption that f is Lipschitz continuous, f(0) = 0, f(s) > 0 for s > 0 and there exists a nonnegative, nondecreasing Hölder continuous function g and a constant M such that g(s) ≤ f(s) ≤ Mg(s) for large s. The nonnegative function p is allowed to be zero on much of the domain.
Paper's Title:
On the Asymptotic Behavior of Solutions of Third Order Nonlinear Differential Equations
Author(s):
Ivan Mojsej and Alena Tartaľová
Institute of Mathematics,
Faculty of Science, P. J. Šafárik University,
Jesenná 5, 041 54 Košice,
Slovak Republic
ivan.mojsej@upjs.sk
Department of Applied Mathematics and Business Informatics,
Faculty of Economics,
Technical University,
Nemcovej 32, 040 01 Košice,
Slovak Republic
alena.tartalova@tuke.sk
Abstract:
This paper is concerned with the asymptotic behavior of solutions of nonlinear differential equations of the
third order with quasiderivatives. Mainly, we present the necessary and sufficient conditions for the existence
of nonoscillatory solutions with specified asymptotic behavior as Paper's Title:
On Singular Numbers of Hankel Matrices of Markov Functions Author(s):
Vasily A. Prokhorov Department of Mathematics and Statistics, Abstract:
Let
E ⊂ (01,1) be a compact set and let
μ be a positive Borel measure with support
supp μ=E. Let
In the case when E=[a,b]⊂
(-1,1) and μ satisfies the
condition dμ/dx>0 a.e. on E, we investigate asymptotic behavior of
singular numbers σkn,n of the Hankel
matrix Dn, where kn/n→θ∈[0,1]
as n→∞. Moreover, we obtain
asymptotics of the Kolmogorov, Gelfand and linear k-widths, k=kn,
of the unit ball An,2 of Pn∩L2(Γ)
in the space L2(μ,E),
where Γ={z:|z|=1} and Pn is the class of all
polynomials of the degree at most n. Paper's Title:
Existence of Optimal Parameters for Damped Sine-Gordon Equation with Variable Diffusion Coefficient and Neumann Boundary Conditions Author(s):
N. Thapa Department of Mathematical Sciences, Abstract:
The parameter identification problem for sine-Gordon equation is of a major interests among mathematicians and scientists.\ In this work we the consider sine-Gordon equation with variable diffusion coefficient and Neumann boundary data. We show the existence and uniqueness of weak solution for sine-Gordon equation. Then we show that the weak solution continuously depends on parameters. Finally we show the existence of optimal set of parameters. Paper's Title:
Estimation for Bounded Solutions of Some Nonlinear Integral Inequalities with Delay in Several Variables Author(s):
Smakdji Mohamed Elhadi, Denche Mouhamed and Khellaf Hassane Department of Mathematics Abstract:
In this paper, some new nonlinear retarded integral inequalities of Gronwall-Bellman type for functions of two and n-independents variables are
investigated. The derived results can be applied in the study of differential-integral equations with time delay. An example is given to illustrate the application of our results. Paper's Title:
Multivalued Equilibrium Problems with Trifunction Author(s):
Muhammad Aslam Noor
Etisalat College of Engineering, P.O. Box 980, Sharjah, United Arab Emirates Abstract:
In this paper, we use the auxiliary principle technique to
suggest some new classes of iterative algorithms for solving multivalued
equilibrium problems with trifunction. The convergence of the proposed methods
either requires partially relaxed strongly monotonicity or pseudomonotonicity.
As special cases, we obtain a number of known and new results for solving
various classes of equilibrium and variational inequality problems. Since
multivalued equilibrium problems with trifunction include equilibrium,
variational inequality and complementarity problems as specials cases, our
results continue to hold for these problems. Paper's Title:
Existence of solutions for Neutral Stochastic Functional Differential Systems with Infinite Delay in Abstract Space
Author(s):
P. Balasubramaniam, A. V. A. Kumar and S. K. Ntouyas
Department of Mathematics, Gandhigram Rural Institute,
Department of Mathematics, Gandhigram Rural Institute,
Department of Mathematics, University of Ioannina, Abstract:
In this paper we prove existence results for semilinear stochastic neutral functional differential systems with unbounded delay in abstract space. Our theory makes use of analytic semigroups and fractional power of closed operators and Sadovskii fixed point theorem. Paper's Title:
Product Formulas Involving Gauss Hypergeometric Functions
Author(s):
Edward Neuman
Department of Mathematics, Mailcode 4408, Abstract:
New formulas for a product of two Gauss hypergeometric functions are derived.
Applications to special functions, with emphasis on Jacobi polynomials, Jacobi functions, and Bessel functions of the first kind, are included.
Most of the results are obtained with the aid of the double Dirichlet average of a univariate function.
Paper's Title:
On an Elliptic Over-Determined Problem in
Dimension Two Author(s):
Lakhdar Ragoub Abstract:
We extend the method of Weinberger for a
non-linear over-determined elliptic problem Paper's Title:
Some Operator Order Inequalities for Continuous Functions of Selfadjoint Operators in Hilbert Spaces Author(s):
S. S. Dragomir1,2 and
Charles E. M. Pearce3 1Mathematics, School of Engineering & Science, 2School of Computational & Applied Mathematics,
sever.dragomir@vu.edu.au 3School
of Mathematical Sciences, Abstract:
Various bounds in the operator order for the following operator transform
Paper's Title:
Analysis of a Dynamic Elasto-viscoplastic Frictionless Antiplan Contact Problem with Normal Compliance Author(s):
A. Ourahmoun1, B. Bouderah2, T. Serrar3 1,2Applied Mathematics
Laboratory, 3Applied Mathematics
Laboratory, Abstract:
We consider a mathematical model which describes the dynamic evolution of a
thermo elasto viscoplastic contact problem between a body and a rigid
foundation. The mechanical and thermal properties of the obstacle coating
material near its surface. A variational formulation of this dynamic contact
phenomenon is derived in the context of general models of thermo elasto
viscoplastic materials. The displacements and temperatures of the bodies in
contact are governed by the coupled system consisting of a variational
inequality and a parabolic differential equation. The proof is based on a
classical existence and uniqueness result on parabolic
inequalities,differential equations and fixed point arguments. Paper's Title:
Lie Group Theoretic Approach of One-Dimensional Black-Scholes Equation Author(s):
P. L. Zondi and M. B. Matadi Department of Mathematical sciences, Abstract:
This study discusses the Lie Symmetry Analysis of Black-Scholes equation via a modified local one-parameter transformations. It can be argued that the transformation of the Black-Scholes equation is firstly obtained by means of riskless rate. Thereafter, the corresponding determining equations to the reduced equation are found. Furthermore, new symmetries of the Black-Scholes equation are constructed and lead to invariant solutions. Paper's Title:
Timelike Surfaces with a Common Line of Curvature in Minkowski 3-Space Author(s):
M.K. Saad, A.Z. Ansari, M. Akram and F. Alharbi Department of Mathematics , Abstract:
In this paper, we analyze the problem of constructing a timelike surface family from a given non-null curve line of curvature. Using
the Frenet frame of the non-null curve in Minkowski space E13 we express the family of surfaces as a linear combination of the
components of this frame, and derive the necessary and sufficient conditions for the coefficients to satisfy both the line of curvature and the isoparametric requirements. In addition, a necessary and sufficient condition for the given non-null curve to satisfy the line of curvature and
the geodesic requirements is investigated. The extension to timelike surfaces of revolution is also outlined. Meanwhile, some representative non-null curves are chosen to construct the corresponding timelike surfaces which possessing these curves as lines of curvature. Results presented in this paper have applications in geometric
modeling and the manufacturing of products. In addition, some computational examples are given and plotted. Paper's Title:
Constraint Qualifications for Multiobjective Programming Problems on Hadamard Manifolds Author(s):
Arnav Ghosh, Balendu Bhooshan Upadhyay and I.M. Stancu-Minasian Department of Mathematics, Department of Mathematics, "Gheorghe Mihoc-Caius Iacob" Institute of
Mathematical Statistics and Applied Mathematics of the Romanian Academy, Abstract:
The study of optimization methods on manifolds has emerged as an immensely significant topic in mathematics due its ubiquitous applicability as well as various computational advantages associated with it. Motivated by this fact, the present article is devoted to the study of a class of constrained multiobjective programming problems (MOPP) in the framework of Hadamard manifolds. We present the generalized Guignard constraint qualification (GGCQ) in the framework of Hadamard manifolds for (MOPP). Employing (GGCQ), we derive Karush-Kuhn-Tucker type necessary optimality criteria for (MOPP). Moreover, we present several other constraint qualifications (CQs) on Hadamard manifolds, namely, Abadie's CQ, generalized Abadie's CQ, Cottle-type CQ, Slater-type CQ, linear CQ, linear objective CQ and Mangasarian-Fromovitz CQ. Further, we establish various relations between these constraint qualifications. In particular, we show that these constraint qualifications, in turn, become sufficient conditions ensuring that (GGCQ) is satisfied. Paper's Title:
On the Ulam Stability for Euler-Lagrange Type Quadratic Functional Equations
Author(s):
Matina John Rassias and John Michael Rassias Statistics and Modelling Science, Abstract:
In 1940 (and 1968) S. M. Ulam proposed the well-known Ulam stability problem.
In 1941 D.H. Hyers solved the Hyers-Ulam problem for linear mappings. In 1951 D. G. Bourgin
has been the second author treating the Ulam problem for additive mappings. In 1978 according
to P.M. Gruber this kind of stability problems is of particular interest in probability theory and in
the case of functional equations of different types. In 1982-2004 we established the Hyers-Ulam
stability for the Ulam problem for different mappings. In 1992-2000 J.M. Rassias investigated
the Ulam stability for Euler-Lagrange mappings. In this article we solve the Ulam problem
for Euler-Lagrange type quadratic functional equations. These stability results can be applied
in mathematical statistics, stochastic analysis, algebra, geometry, as well as in psychology and
sociology.
Paper's Title:
Iterated Order of Fast Growth Solutions of Linear Differential Equations
Author(s):
Benharrat Belaďdi
Department of Mathematics Abstract:
In this paper, we investigate the growth of solutions of the differential
equation
f(k) + Ak-1 (z) f(k-1) +...+ A1 (z) f' + A0 (z) f= F (z),
where
Ao (z), ..., Ak-1 (z)
and
F (z) Paper's Title:
Strongly Nonlinear Variational Parabolic Problems in Weighted Sobolev Spaces Author(s):
L. Aharouch, E. Azroul and M. Rhoudaf
Dép. Math. Faculté des Sciences Dhar-Mahraz Abstract:
In this paper , we study the existence of a weak solutions for the
initial-boundary value problems of the strongly nonlinear degenerated parabolic
equation,
where
A is a Leray-lions operator acted from
Lp(0,T,W01,p(Ώ,w)) into its dual. g(x,t,u,∇ u)
is a nonlinear term with critical growth condition with respect to ∇ u
and no growth with respect to u.
The source term f is assumed to belong to Lp'(0,T,W-1,p'(Ώ,w*)). Paper's Title:
On some Strongly Nonlinear Elliptic Problems
in Lą-data with a Nonlinearity Having a Constant Sign in Orlicz
Spaces via Penalization Methods
Author(s):
E. Azroul, A. Benkirane and M.
Rhoudaf Dep. Math., Faculté des Sciences
Dhar-Mahraz, Abstract:
This paper is concerned with the existence result of the
unilateral problem associated to the equations of the type
Paper's Title:
On a Hilbert-type Inequality with the Polygamma Function Author(s):
Bing He and Bicheng Yang
Department of Mathematics, Guangdong Education College, Abstract:
By applying the method of weight function and the technique of real analysis, a Hilbert-type inequality with a best constant factor is established, where the best constant factor is made of the polygamma function. Furthermore, the inverse form is given. Paper's Title:
A Note On The Global Behavior Of A Nonlinear System of Difference Equations Author(s):
Norman H. Josephy, Mihaela Predescu and Samuel W. Woolford
Department of Mathematical Sciences,
mpredescu@bentley.edu Abstract:
This paper deals with the global asymptotic stability character of solutions of a discrete time deterministic model proposed by Wikan and Eide in Bulletin of Mathematical Biology, 66, 2004, 1685-1704. A stochastic extension of this model is proposed and discussed. Computer simulations suggest that the dynamics of the stochastic model includes a mixture of the dynamics observed in the deterministic model.
Paper's Title:
Asymptotic Analysis of Positive Decreasing Solutions of a Class of Systems of Second Order Nonlinear Differential Equations in the Framework of Regular Variation Author(s):
Jaroslav Jaroš, Kusano Takaŝi, Tomoyuki Tanigawa Department of Mathematical Analysis and
Numerical Mathematics, E-mail:
ksntksjm4@gmail.com Professor Emeritus at: Hiroshima
University, E-mail:
jaros@fmph.uniba.sk Department of Mathematics, Faculty of
Education, E-mail:
tanigawa@educ.kumamoto-u.ac.jp Abstract:
The system of nonlinear differential equations Paper's Title:
Strong
Convergence Theorems for a Common Zero of an Infinite Family of Gamma-Inverse
Strongly Monotone Maps with Applications Author(s):
Charles Ejike Chidume, Ogonnaya Michael Romanus, and Ukamaka Victoria Nnyaba African University of Science and
Technology, Abuja, Abstract:
Let E be a uniformly convex and uniformly smooth real Banach space with
dual space E* and let Ak:E→E*,
k=1, 2, 3 , ... Paper's Title:
Kinematic Model for Magnetic Null-points in 2 Dimensions Author(s):
Ali Khalaf Hussain Al-Hachami Department of Mathematics,
Abstract:
The adjacent configurations of two-dimensional magnetic null point centers are analyzed by an immediate examination about the null. The configurations are classified as either potential or non-potential. By then the non-potential cases are subdivided into three cases depending upon whether the component of current is less than, equal to or greater than a threshold current. In addition the essential structure of reconnection in 2D is examined. It unfolds that the manner by which the magnetic flux is rebuilt. In this paper, we center on the ramifications of kinematic arrangements; that is, we fathom just Maxwell's conditions and a resistive Ohm's law. Paper's Title:
Residual-Based A Posteriori Error Estimates For A Conforming Mixed Finite Element Discretization of the Monge-Ampere Equation Author(s):
J. Adetola, K. W. Houedanou and B. Ahounou Institut de Mathematiques et de Sciences
Physiques (IMSP), Departement de Mathematiques, Departement de Mathematiques, Abstract:
In this paper we develop a new a posteriori error analysis
for the Monge-Ampere equation approximated by conforming finite element method
on isotropic meshes in R2. The approach utilizes a slight variant of the
mixed discretization proposed by Gerard Awanou and
Hengguang Li in [4].
The a posteriori error estimate is based on a suitable evaluation on the residual of the finite element
solution. It is proven that the a posteriori error estimate provided in this paper is both reliable and efficient. Paper's Title:
The Effect of Harvesting Activities on Prey-Predator Fishery Model with Holling type II in Toxicant Aquatic Ecosystem Author(s):
Moh Nurul Huda, Fidia Deny Tisna Amijaya, Ika Purnamasari Department of Mathematics, Faculty of
Mathematics and Natural Science, Abstract:
This paper discussed prey-predator fishery models, in particular by analysing the effects of toxic substances on aquatic ecosystems. It is assumed in this model, that the prey population is plankton and the predator population is fish.\ Interaction between the two populations uses the Holling type II function. The existence of local and global critical points of the system are shown and their stability properties are analysed. Furthermore, Bionomic equilibrium and optimal control of harvesting are discussed. Finally, numerical simulations have been carried out to show in the interpretation of results. Paper's Title:
A Self-adaptive Subgradient Extragradient Algorithm for Variational Inequality Problems and Fixed Point Problems in Banach Spaces Author(s):
F. U. Ogbuisi School of Mathematics, Statistics and
Computer Science, Department of Mathematics, Abstract:
In this paper, we propose and analyze a type of subgradient extragradient algorithm for the approximation of a solution of variational inequality problem which is also a common fixed point of an infinite family of relatively nonexpansive mappings in 2-uniformly convex Banach spaces which are uniformly smooth. By using the generalized projection operator, we prove a strong convergence theorem which does not require the prior knowledge of the Lipschitz constant of cost operator. We further applied our result to constrained convex minimization problem, convex feasibility problem and infinite family of equilibrium problems. Our results improve and complement related results in 2-uniformly convex and uniformly smooth Banach spaces and Hilbert spaces. Paper's Title:
Coexisting Attractors and Bubbling Route to Chaos in Modified Coupled Duffing Oscillators Author(s):
B. Deruni1, A. S. Hacinliyan1,2, E. Kandiran3, A. C. Keles2, S. Kaouache4, M.-S. Abdelouahab4, N.-E. Hamri4 1Department
of Physics, 2Department
of Information Systems and Technologies, 3Department
of Software Development, 4Laboratory
of Mathematics and their interactions, E-mail:
berc890@gmail.com Abstract:
In this article dynamical behavior of coupled Duffing oscillators is analyzed under a small modification. The oscillators have cubic damping instead of linear one. Although single duffing oscillator has complex dynamics, coupled duffing systems possess a much more complex structure. The dynamical behavior of the system is investigated both numerically and analytically. Numerical results indicate that the system has double scroll attractor with suitable parameter values. On the other hand, bifurcation diagrams illustrate rich behavior of the system, and it is seen that, system enters into chaos with different routes. Beside classical bifurcations, bubbling route to chaos is observed for suitable parameter settings. On the other hand, Multistability of the system is indicated with the coexisting attractors, such that under same parameter setting the system shows different periodic and chaotic attractors. Moreover, chaotic synchronization of coupled oscillators is illustrated in final section. Paper's Title:
Semivectorial Bilevel Optimization on Affine-Finsler-Metric Manifolds Author(s):
Faik Mayah1, Ali S Rasheed2 and Naseif J. Al- Jawari3 1Department of Physics, 3Dept.
of Mathematics, Abstract:
A Finsler manifold is a differential manifold together with a Finsler metric, in this paper we construct a new class of Finsler metric affine
manifolds on bilevel semivectorial with optimization problems. The first steps for this purpose involve the study of bilevel optimization on affine manifolds. The bilevel programming problem can
be viewed as a static version of the noncooperative, two-person game which was introduced in the context of unbalanced economic markets.
Bilevel optimization is a special kind of optimization where one problem is embedded within another. Paper's Title:
An Algorithm to Compute Gaussian-Type Quadrature Formulae Author(s):
Allal Guessab Laboratoire de Mathématiques Appliquées, Abstract:
It is well-known that for sufficiently smooth integrands on an interval, numerical integration
can be performed stably and efficiently via the classical (polynomial) Gauss quadrature
formulae. However, for many other sets of integrands these quadrature formulae do not perform
well. A very natural way of avoiding this problem is to include a wide class among arbitrary
functions (not necessary polynomials) to be integrated exactly. The spline functions are natural
candidates for such problems. In this paper, after studying Gaussian type quadrature formulae
which are exact for spline functions and which contain boundary terms involving derivatives at
both end points, we present a fast algorithm for computing their nodes and weights. It is also
shown, taking advantage of the close connection with ordinary Gauss quadrature formula, that
the latter are computed, via eigenvalues and eigenvectors of real symmetric tridiagonal matrices.
Hence a new class of quadrature formulae can then be computed directly by standard software
for ordinary Gauss quadrature formula. Comparative results with classical Gauss quadrature
formulae are given to illustrate the numerical performance of the approach.
Paper's Title:
On the Optimal Buckling Loads of Clamped Columns
Author(s):
Samir Karaa
Department of Mathematics and Statistics
URL: http://ajmaa.org/EditorsU/SKaraa.php Abstract:
We consider the problem of determining the optimal shape of a clamped column of given length and volume, without minimum cross section constraints.
We prove that the necessary condition of optimality derived by
Olhoff
and Rasmussen is sufficient when 0<
12: Paper Source
PDF document
University of South Alabama,
Mobile, Alabama 36688-0002,
USA.
E-mail: prokhoro@southalabama.edu
URL:
http://www.southalabama.edu/mathstat/people/prokhorov.shtml 
12: Paper Source
PDF document
Cameron University,
2800 West Gore Blvd,
73505 Lawton, Oklahoma,
USA.
E-mail: nthapa@cameron.edu
URL: http://www.cameron.edu/~nthapa/
12: Paper Source
PDF document
University of Frčres Mentouri
PO Box 25000, Ain Elbay,
Constantine,
Algeria.
E-mail: khellafhassane@umc.edu.dz
11: Paper Source
PDF document
noor@ece.ac.ae
11: Paper Source
PDF document
Deemed University, Gandhigram - 624 302,
Tamil Nadu, India.
pbalgri@rediffmail.com
Deemed University, Gandhigram - 624 302,
Tamil Nadu, India.
nnddww@tom.com
451 10 Ioannina,
Greece.
sntouyas@cc.uoi.gr
URL: http://www.math.uoi.gr/~sntouyas
11: Paper Source
PDF document
Southern Illinois University,
1245 Lincoln Drive,
Carbondale, IL 62901,
USA.
edneuman@math.siu.edu
URL: http://www.math.siu.edu/neuman/personal.html
11: Paper Source
PDF document
Department of Mathematics and Information of Tiyadhechnology
AL Yamamah University
P.O. Box 45 180, Riyadh 11 512
Saudi Arabia.
in R2.
We prove that the domain in consideration is a ball. The
tool of this investigation are maximum principles and P-functions.
11: Paper Source
PDF document
Victoria University,
PO Box 14428,
Melbourne City, MC 8001,
Australia.
University of
the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
URL: http://rgmia.org/dragomir
The University of Adelaide,
Adelaide,
Australia
where A is a selfadjoint operator in the Hilbert space H with the
spectrum Sp( A) ⊆ [ m,M]
and f:[m,M] -> C is a continuous function on [m,M]
are given. Applications for the power and logarithmic functions are provided as
well.
11: Paper Source
PDF document
M'sila University, 28000,
Algeria.
E-mail: ourahmounabbes@yahoo.fr
Setif 1 University, 19000,
Algeria.
11: Paper Source
PDF document
Faculty of Sciences & Agriculture, University of Zululand,
P Bag X1001, Kwa-Dlangezwa 3886,
South Africa.
E-mail: matadim@unizulu.ac.za
zondip@unizulu.ac.za
11: Paper Source
PDF document
Faculty of Science,
Islamic University of Madinah,
KSA
11: Paper Source
PDF document
Indian Institute of Technology Patna,
Patna,
India.
E-mail: arnav_2021ma09@iitp.ac.in
Indian Institute of Technology Patna,
Patna,
India.
E-mail: bhooshan@iitp.ac.in
Bucharest,
Romania.
E-mail: stancu_minasian@yahoo.com
10: Paper Source
PDF document
University of Strathclyde,
Livingstone Tower,
26 Richmond Str,
Glasgow, Uk, G1 1xh
Pedagogical Department, E. E., National and Capodistrian University of Athens,
Section of Mathematics and Informatics,
4, Agamemnonos Str, Aghia Paraskevi,
Athens 15342, Greece
10: Paper Source
PDF document
Laboratory of Pure and Applied Mathematics
University of Mostaganem
B. P. 227 Mostaganem,
ALGERIA.
belaidi@univ-mosta.dz
0
are entire functions. Some estimates are given for the iterated order of solutions of the above quation when one of the coefficients As is being dominant in the sense that it has larger growth than Aj (j≠s) and F.
10: Paper Source
PDF document
B.P 1796 Atlas Fés,
Maroc.
rhoudaf_mohamed@yahoo.fr
∂u
+A(u)+g(x,t,u,∇ u)=f
∂t
10: Paper Source
PDF document
B.P 1796 Atlas Fčs,
Maroc
Departement of Mathematics,
Faculty of Sciences and Techniques of Tangier,
B.P. 416, Tangier,
Morocco.
rhoudaf_mohamed@yahoo.fr
in Orlicz spaces, without
assuming the sign condition in the nonlinearity g. The source term f belongs to Lą(Ώ).
10: Paper Source
PDF document
Department of Mathematics, Guangdong Education College,
Guangzhou, 510303,
China.
Guangzhou, 510303,
China.
10: Paper Source
PDF document
Bentley University,
Waltham, MA 02452,
U.S.A.
njosephy@bentley.edu
swoolford@bentley.edu
10: Paper Source
PDF document
Faculty of Mathematics, Physics and Informatics,
Comenius Universiy, 842 48 Bratislava,
Slovakia.
Department of Mathematics, Faculty of Science,
Higashi-Hiroshima 739-8526,
Japan.
Kumamoto University, Kumamoto 860-8555,
Japan.
is under consideration, where αi
and βi are positive constants and
pi(t) and qi(t) are continuous regularly varying functions
on [a,∞). Two kinds of criteria are established for
the existence of strongly decreasing regularly varying solutions with negative
indices of (A) with precise asymptotic behavior at infinity. Fixed point
techniques and basic theory of regular variation are utilized for this purpose.
10: Paper Source
PDF document
Nigeria.
E-mail: cchidume@aust.edu.ng
E-mail: romanusogonnaya@gmail.com
E-mail: nnyabavictoriau@gmail.com
be a family of inverse strongly monotone maps such that ∩∞k=1
Ak-1(0)≠∅.
A new iterative algorithm is constructed and proved to converge strongly to a
common zero of the family.
As a consequence of this result, a strong convergence theorem for approximating
a common J-fixed point for an infinite family of
gamma-strictly J-pseudocontractive maps is proved. These results are new and
improve recent results obtained for these classes of nonlinear maps.
Furthermore, the technique of proof is of independent interest.
10: Paper Source
PDF document
College of Education For Pure Sciences,
Wasit University,
Iraq.
E-mail: alhachamia@uowasit.edu.iq
10: Paper Source
PDF document
Universite d'Abomey-Calavi
E-mail: adetolajamal58@yahoo.com
Faculte des Sciences et Techniques (FAST),
Universite d'Abomey-Calavi
E-mail: khouedanou@yahoo.fr
Faculte des Sciences et Techniques (FAST),
Universite d'Abomey-Calavi
E-mail: bahounou@yahoo.fr
10: Paper Source
PDF document
Mulawarman University,
Samarinda, East Kalimantan,75123
Indonesia.
E-mail: muh.nurulhuda@fmipa.unmul.ac.id
fidiadta@fmipa.unmul.ac.id
ika.purnamasari@fmipa.unmul.ac.id
10: Paper Source
PDF document
University of KwaZulu-Natal, Durban,
South Africa.
University of Nigeria, Nsukka,
Nigeria.
E-mail: ferdinard.ogbuisi@unn.edu.ng
fudochukwu@yahoo.com
10: Paper Source
PDF document
University of Yeditepe,
Turkey.
University of Yeditepe,
Turkey
University of Yeditepe,
Turkey.
University Center of Abdelhafid Boussouf,
Mila 43000,
Algeria.
ahacinliyan@yeditepe.edu.tr
engin.kandiran@yeditepe.edu.tr
cihan.keles@yeditepe.edu.tr
s.kaouache@centr-univ-mila.dz
medsalah3@yahoo.fr
n.hamri@centre-univ-mila.dz
10: Paper Source
PDF document
College of Sciences,
University of Wasit,
Iraq.
E-mail: faik.mayah@gmail.com
2Ministry of Higher Education and Scientific Research,
Iraq.
E-mail: ali.math2018@yahoo.com
ahmedhashem@gmail.com
College of Science,
Mustansiriyah University, Baghdad,
Iraq.
E-mail: nsaif642014@yahoo.com
9: Paper Source
PDF document
that Integrate Polynomials and Some Spline Functions Exactly
Université de Pau, 64000, Pau,
France.
allal.guessab@univ-pau.fr
URL: http://www.univ-pau.fr/~aguessab/
9: Paper Source
PDF document
Sultan Qaboos University, P.O. Box 36, Alkhod 123
Muscat, Sultanate of Oman
skaraa@squ.edu.om
Paper's Title:
Normalized Truncated Levy models applied to the study of Financial Markets
Author(s):
M. C. Mariani, K. Martin, D. W. Dombrowski and D. Martinez
Department of Mathematical Sciences and Department of Finance,
New Mexico State University, P.O. Box 30001
Department 3MB Las Cruces, New Mexico 88003-8001
USA.
mmariani@nmsu.edu
kjmartin@nmsu.edu
Abstract:
This work is devoted to the study of the statistical properties of financial instruments from developed markets. We performed a new analysis of the behavior of companies corresponding to the DJIA index, and of the index itself, by using a normalized Truncated Levy walk model. We conclude that the Truncated Levy distribution describes perfectly the evolution of the companies and of the index near a crash.
Paper's Title:
Generalized Efficient Solutions to One Class of Vector Optimization Problems in Banach Space
Author(s):
Peter I. Kogut, Rosanna Manzo, and Igor V. Nechay
Department of Differential Equations,
Dnipropetrovsk National University,
Naukova str., 13,
49050 Dnipropetrovsk,
Ukraine
p.kogut@i.ua
Dipartimento di Ingegneria
Dell’informazione e Matematica Applicata,
Universitŕ di Salerno,
Via
Ponte
Don Melillo,
84084 Fisciano
(Sa),
Italy
manzo@diima.unisa.it
Department of Technical Cybernetics,
Dnipropetrovsk Technical University,
Acad. Lazarjan str., 2,
49010
Dnipropetrovsk,
Ukraine
i.nechay@i.ua
Abstract:
In this paper, we study vector optimization problems in Banach spaces for essentially nonlinear operator equations with additional control and state constraints. We assume that an objective mapping possesses a weakened property of lower semicontinuity and make no assumptions on the interior of the ordering cone. Using the penalization approach we derive both sufficient and necessary conditions for the existence of efficient solutions of the above problems. We also prove the existence of the so-called generalized efficient solutions via the scalarization of some penalized vector optimization problem.
Paper's Title:
Shape Diagrams for 2D Compact Sets - Part II: Analytic
Simply Connected Sets.
Author(s):
S. Rivollier, J. Debayle and J.-C. Pinoli
Ecole Nationale Supérieure des Mines de Saint-Etienne,
CIS - LPMG, UMR CNRS 5148, 158 cours Fauriel,
42023 Saint-Etienne Cedex 2, France.
rivollier@emse.fr;
debayle@emse.fr; pinoli@emse.fr
Abstract:
Shape diagrams are representations in the Euclidean plane introduced to study 3-dimensional and 2-dimensional compact convex sets. However, they can also been applied to more general compact sets than compact convex sets. A compact set is represented by a point within a shape diagram whose coordinates are morphometrical functionals defined as normalized ratios of geometrical functionals. Classically, the geometrical functionals are the area, the perimeter, the radii of the inscribed and circumscribed circles, and the minimum and maximum Feret diameters. They allow twenty-two shape diagrams to be built. Starting from these six classical geometrical functionals, a detailed comparative study has been performed in order to analyze the representation relevance and discrimination power of these twenty-two shape diagrams. The first part of this study is published in a previous paper 16. It focused on analytic compact convex sets. A set will be called analytic if its boundary is piecewise defined by explicit functions in such a way that the six geometrical functionals can be straightforwardly calculated. The purpose of this paper is to present the second part, by focusing on analytic simply connected compact sets. The third part of the comparative study is published in a following paper 17. It is focused on convexity discrimination for analytic and discretized simply connected compact sets.
Paper's Title:
Some Inequalities for Gramian Normal Operators and for Gramian Self-Adjoint Operators in Pseudo-Hilbert Spaces
Author(s):
Loredana Ciurdariu
Department of Mathematics,"Politehnica" University of Timisoara,
P-ta. Victoriei, No.2, 300006-Timisoara,
ROMANIA
cloredana43@yahoo.com.
Abstract:
Several inequalities for gramian normal operators and for gramian self-adjoint operators in pseudo-Hilbert spaces are presented.
Paper's Title:
Numerical Solution of A System of Singularly Perturbed Convection-Diffusion Boundary-Value Problems Using Mesh Equidistribution Technique
Author(s):
Pratibhamoy Das and Srinivasan Natesan
Department of Mathematics,
Indian Institute of Technology Guwahati,
Guwahati - 781 039,
India.
pratibhamoy@gmail.com
natesan@iitg.ernet.in
URL:
http://www.iitg.ernet.in/natesan/
Abstract:
In this article, we consider a system of singularly perturbed weakly coupled convection-diffusion equations having diffusion parameters of different magnitudes. These small parameters give rise to boundary layers. An upwind finite difference scheme on adaptively generated mesh is used to obtain a suitable monitor function that gives first-order convergence which is robust with respect to the diffusion parameters. We present the results of numerical experiments for linear and semilinear system of differential equations to support the effectiveness of our preferred monitor function obtained from theoretical analysis.
Paper's Title:
On Eigenvalues and Boundary Curvature of the C*-algebra Numerical Rang
Author(s):
M. T. Heydari
Department of Mathematics,
College of Sciences,
Yasouj University,
Yasouj, 75914-74831,
Iran.
E-mail: heydari@yu.ac.ir
Abstract:
Let A be a C*-algebra with unit 1 and a∈A be a nilpotent. By Donoghue's Theorem, all corner points of its numerical range V(a) belong to the spectrum σ(a). It is therefore natural to expect that, more generally, the distance from a point p on the boundary ∂ V(a) of V(a) to σ(a) should be in some sense bounded by the radius of curvature of ∂ V(a) at p.
Paper's Title:
Introducing the Dorfmanian: A Powerful Tool for the Calculus Of Variations
Author(s):
Olivier de La Grandville
Department of Management Science and Engineering,
Stanford University,
475 Via Ortega, Stanford, CA 94305,
U. S. A.
E-mail: odelagrandville@gmail.com
Abstract:
We show how a modified Hamiltonian proposed by Robert Dorfman [1] to give intuitive sense
to the Pontryagin maximum principle can be extended to easily obtain all
high-order equations of the calculus of variations. This new concept is
particularly efficient to determine the differential equations leading to
the extremals of functionals defined by n-uple integrals, while a
traditional approach would require -- in some cases repeatedly -- an
extension of Green's theorem to n-space.
Our paper is dedicated to the memory of Robert Dorfman (1916 - 2002).
Paper's Title:
A Multivalued Version of the
Radon-Nikodym Theorem, via the Single-valued Gould Integral
Author(s):
Domenico Candeloro1, Anca Croitoru2, Alina Gavriluţ2, Anna Rita Sambucini1
1Dept. of Mathematics and Computer
Sciences,
University of Perugia,
1, Via Vanvitelli -- 06123, Perugia,
Italy.
E-mail: domenico.candeloro@unipg.it,
anna.sambucini@unipg.it
2Faculty of Mathematics,
Al. I. Cuza University,
700506 Iaşi,
Romania.
E-mail: croitoru@uaic.ro,
gavrilut@uaic.ro
Abstract:
In this paper we consider a Gould type integral of real functions with respect to a compact and convex valued not necessarily additive measure. In particular we will introduce the concept of integrable multimeasure and, thanks to this notion, we will establish an exact Radon-Nikodym theorem relative to a fuzzy multisubmeasure which is new also in the finite dimensional case. Some results concerning the Gould integral are also obtained.
Paper's Title:
Global Analysis on Riemannian Manifolds
Author(s):
Louis Omenyi and Michael Uchenna
Department of Mathematics, Computer
Science, Statistics and Informatics,
Alex Ekwueme Federal University, Ndufu-Alike,
Nigeria.
E-mail: omenyi.louis@funai.edu.ng,
michael.uchenna@funai.edu.ng
URL: http://www.funai.edu.ng
Abstract:
In this paper, an exposition of the central concept of global analysis on a Riemannan manifold is given. We extend the theory of smooth vector fields from open subsets of Euclidean space to Riemannan manifolds. Specifically, we prove that a Riemannian manifold admits a unique solution for a system of ordinary differential equations generated by the flow of smooth tangent vectors. The idea of partial differential equations on Riemannian manifold is highlighted on the unit sphere.
Paper's Title:
Generalised Models for Torsional Spine Reconnection
Author(s):
Ali Khalaf Hussain Al-Hachami
Department of Mathematics,
College of Education For Pure Sciences,
Wasit University,
Iraq.
E-mail: alhachamia@uowasit.edu.iq
Abstract:
Three-dimensional (3D) null points are available in wealth in the solar corona, and the equivalent is probably going to be valid in other astrophysical situations. On-going outcomes from sun oriented perceptions and from reproductions propose that reconnection at such 3D nulls may assume a significant job in the coronal dynamics. The properties of the torsional spine method of magnetic reconnection at 3D nulls are researched. Kinematic model are created, which incorporate the term ηJ that is spatially localised around the null, stretching out along the spine of the null. The null point is to research the impact of shifting the level of asymmetry of the null point magnetic field on the subsequent reconnection process where past examinations constantly considered a non-nonexclusive radially symmetric null. Specifically we analyse the rate of reconnection of magnetic flux at the spine of null point. Logical arrangements are determined for the enduring kinematic equation, and contrasted and the after effects of torsional spine reconnection models when the current is restricted in which the Maxwell conditions are illuminated. The geometry of the current layers inside which torsional spine reconnection happen is autonomous on the symmetry of the magnetic field. Torsional spine reconnection happens in a thin cylinder around the spine, with circular cross-segment when the fan eigenvalues are extraordinary. The short axis of the circle being along the solid field bearing. Just as it was discovered that the fundamental structure of the method of attractive reconnection considered is unaffected by changing the magnetic field symmetry, that is, the plasma flow is discovered rotational around the spine of null point. The spatiotemporal pinnacle current, and the pinnacle reconnection rate achieved, are found not to rely upon the level of asymmetry.
Paper's Title:
ψ(m,q)-Isometric Mappings on Metric Spaces
Author(s):
Sid Ahmed Ould Beinane, Sidi Hamidou Jah and Sid Ahmed Ould Ahmed Mahmoud
Mathematical Analysis and Applications,
Mathematics Department, College of Science,
Jouf University,
Sakaka P.O.Box 2014,
Saudi Arabia.
E-mail: beinane06@gmail.com
Department of Mathematics, College of
Science Qassim University,
P.O. Box 6640, Buraydah 51452,
Saudi Arabia.
E-mail: jahsiidi@yahoo.fr
Mathematical Analysis and Applications,
Mathematics Department, College of Science, Jouf University,
Sakaka P.O.Box 2014,
Saudi Arabia.
E-mail: sidahmed@ju.edu.sa,
sidahmed.sidha@gmail.com
Abstract:
The concept of (m,p)-isometric operators on Banach space was extended to
(m,q)-isometric mappings on general metric spaces in [6].
This paper is devoted to define the concept of
ψ(m, q)-isometric, which is the
extension of A(m, p)-isometric operators on Banach spaces introduced in [10].
Let T,ψ: (E,d) -> (E, d) be two mappings.
For some positive integer m and q ∈ (0,∞).
T is said to be an ψ(m,q)-isometry,
if for all y,z ∈ E,
Paper's Title:
Pointwise Convergence of Fourier-type Series with Exponential Weights
Author(s):
Hee Sun Jung and Ryozi Sakai
Department of Mathematics Education,
Sungkyunkwan University,
Seoul 110-745,
Republic of Korea.
E-mail: hsun90@skku.edu
Department of Mathematics,
Meijo University, Nagoya 468-8502,
Japan.
E-mail: ryozi@hm.aitai.ne.jp
Abstract:
Let R = ( - ∞,∞), and let Q∈C1(R):R→[0,∞) be an even function. We consider the exponential weights w(x)=e-Q(x), x∈R. In this paper we obtain a pointwise convergence theorem for the Fourier-type series with respect to the orthonormal polynomials {pn(w2;x)}.
Paper's Title:
Uniqueness of Meromorphic Functions that Share Three Values
Author(s):
Abhijit Banerjee
Department of Mathematics
Kalyani Government Engineering College
West Bengal 741235
India.
abanerjee_kal@yahoo.co.in
abanerjee@mail15.com
abanerjee_kal@rediffmail.com
Abstract:
In the paper dealing with the uniqueness problem of meromorphic functions we prove five theorems one of which will improve a result given by Lahiri \cite{5} and the remaining will supplement some previous results.
Paper's Title:
A Sum Form Functional Equation and Its Relevance in Information Theory
Author(s):
Prem Nath and Dhiraj Kumar Singh
Department of Mathematics
University of Delhi
Delhi - 110007
India
pnathmaths@gmail.com
dksingh@maths.du.ac.in
Abstract:
The general solutions of a sum form functional equation containing four unknown mappings have been investigated. The importance of these solutions in relation to various entropies in information theory has been emphasised.
Paper's Title:
On
the Convergence in Law of Iterates of Random-Valued Functions
Author(s):
Karol Baron
Uniwersytet
Śląski, Instytut MatematykiAbstract:
Given a probability space (Ω,
A, P) a separable and complete metric space X with the
σ-algebra B of all
its Borel subsets and a B
A -measurable f : X
*
Ω
→ X we consider its iterates fn, n
N,
defined on X
*
ΩN by f1(x,ω) = f(x,ω1) and
fn+1(x,ω)=f(fn(x,ω),ωn+1),
provide a simple criterion for the convergence in law of
fn(x,·))
n
N, to a random variable independent of
x
X , and apply
this criterion to linear functional equations in a single variable.
Paper's Title:
Asymptotic Inequalities for the Maximum Modulus of the Derivative of a Polynomial
Author(s):
Clément Frappier
Département de Mathématiques et de Génie industriel École Polytechnique de
Montréal,
C.P.~6079, succ. Centre-ville Montréal (Québec),
H3C 3A7, CANADA
Abstract:
Let
be an algebraic polynomial of degree
≤n, and let ∥p∥= max {|p(z)|:|z| = 1}.
We study the asymptotic behavior of the best possible constant φn,k (R), for
k = 0 and k=1, in the inequality ∥p'(Rz)∥ + φn,k (R) |ak|
≤ nRn-1 ∥p∥, R → ∞.
Paper's Title:
Approximation of an AQCQ-Functional Equation and its Applications
Author(s):
Choonkil Park and Jung Rye Lee
Department of Mathematics,
Research Institute for Natural Sciences,
Hanyang University, Seoul 133-791,
Korea;
Department of Mathematics,
Daejin University,
Kyeonggi 487-711,
Korea
baak@hanyang.ac.kr
jrlee@daejin.ac.kr
Abstract:
This paper is a survey on the generalized Hyers-Ulam stability of an AQCQ-functional equation in several spaces. Its content is divided into the following sections:
1. Introduction and preliminaries.
2. Generalized Hyers-Ulam stability of an AQCQ-functional equation in Banach spaces: direct method.
3. Generalized Hyers-Ulam stability of an AQCQ-functional equation in Banach spaces: fixed point method.
4. Generalized Hyers-Ulam stability of an AQCQ-functional equation in random Banach spaces: direct method.
5. Generalized Hyers-Ulam stability of an AQCQ-functional equation in random Banach spaces: fixed point method.
6. Generalized Hyers-Ulam stability of an AQCQ-functional equation in non-Archi-medean Banach spaces: direct method.
7. Generalized Hyers-Ulam stability of an AQCQ-functional equation in non-Archi-medean Banach spaces: fixed point method.
Paper's Title:
Some Functional Inequalities for the Geometric Operator Mean
Author(s):
Mustapha Raissouli
Taibah University, Faculty of Sciences,
Department of Mathematics,
Al Madinah Al Munawwarah, P.O.Box 30097,
Kingdom of Saudi Arabia.
Abstract:
In this paper, we give some new inequalities of functional type for the power geometric operator mean involving several arguments.
Paper's Title:
A Dynamic Contact Problem for an Electro Viscoelastic Body
Author(s):
Denche M. and Ait Kaki L.
Laboratoire Equations Differentielles,
Departement de Mathematiques,
Universite Constantine 1,
Algeria.
Ecole Normale Superieure,
Departement des Sciences Exactes et Informatique,
Plateau Mansourah, Constantine.
Algeria.
E-mail:
m.denche@umc.edu.dz
leilaitkaki@yahoo.fr
Abstract:
We consider a dynamic problem which describes a contact between a piezoelectric body and a conductive foundation. The frictionless contact is modelled with the normal compliance, the electric conditions are supposed almost perfect. We prove the existence of a unique weak solution for almost perfect electric contact.
Paper's Title:
Iterative Approximation of Zeros of Accretive Type Maps, with Applications
Author(s):
Charles Ejike Chidume, Chinedu Godwin Ezea, and Emmanuel Ezzaka Otubo
African University of Science and
Technology, Abuja,
Nigeria.
E-mail: cchidume@aust.edu.ng
E-mail: chinedu.ezea@gmail.com
E-mail: mrzzaka@yahoo.com
Department of Mathematics,
Nnamdi Azikiwe University,
Awka,
Nigeria
E-mail: chinedu.ezea@gmail.com
Ebonyi State University,
Abakaliki,
Nigeria
E-mail: mrzzaka@yahoo.com
Abstract:
Let E be a reflexive real Banach space with uniformly Gâteaux differentiable norm. Let J:E→ E* be the normalized duality map on E and let A:E*→ E be a map such that AJ is an accretive and uniformly continuous map. Suppose that (AJ)-1(0) in nonempty. Then, an iterative sequence is constructed and proved to converge strongly to some u* in (AJ)-1(0). Application of our theorem in the case that E is a real Hilbert space yields a sequence which converges strongly to a zero of A. Finally, non-trivial examples of maps A for which AJ is accretive are presented..
Paper's Title:
A New Interpretation of the Number e
Author(s):
Olivier de La Grandville
Faculty of Economics, Goethe University,
Frankfurt, Theodor-Adorno Platz 4,
60323 Frankfurt am Main,
Germany.
E-mail:
odelagrandville@gmail.com
Abstract:
We show that e is the amount that 1 becomes when it is invested during an arbitrary time span of length T, at any continuously compounded interest rates as long as their average is equal to 1/T . A purely mathematical interpretation of e is the amount a unit quantity becomes after any duration T when the average of its instantaneous growth rates is 1/T. This property can be shown to remain valid if T tends to infinity as long as the integral of the growth rates converges to unity.
Paper's Title:
Analysis of a Frictional Contact Problem for Viscoelastic Piezoelectric Materials
Author(s):
Meziane Said Ameur, Tedjani Hadj Ammar and Laid Maiza
Departement of Mathematics,
El Oued University,
P.O. Box 789, 39000 El Oued,
Algeria.
E-mail:
said-ameur-meziane@univ-eloued.dz
Departement of Mathematics,
El Oued University,
P.O. Box 789, 39000 El Oued,
Algeria.
E-mail:
hadjammar-tedjani@univ-eloued.dz
Department of Mathematics,
Kasdi Merbah University,
30000 Ouargla,
Algeria.
E-mail: maiza.laid@univ-ouargla.dz
Abstract:
In this paper, we consider a mathematical model that describes the quasi-static process of contact between two thermo-electro-viscoelastic bodies with damage and adhesion. The damage of the materials caused by elastic deformations. The contact is frictional and modeled with a normal compliance condition involving adhesion effect of contact surfaces. Evolution of the bonding field is described by a first order differential equation. We derive variational formulation for the model and prove an existence and uniqueness result of the weak solution. The proof is based on arguments of evolutionary variational inequalities, parabolic inequalities, differential equations, and fixed point theorem.
Paper's Title:
Sharp Inequalities Between Hölder and Stolarsky Means of Two Positive Numbers
Author(s):
M. Bustos Gonzalez and A. I. Stan
The University of Iowa,
Department of Mathematics,
14 MacLean Hall,
Iowa City, Iowa,
USA.
E-mail:
margarita-bustosgonzalez@uiowa.edu
The Ohio State University at Marion,
Department of Mathematics,
1465 Mount Vernon Avenue,
Marion, Ohio,
USA.
E-mail: stan.7@osu.edu
Abstract:
Given any index of the Stolarsky means, we find the greatest and least indexes of the H\"older means, such that for any two positive numbers, the Stolarsky mean with the given index is bounded from below and above by the Hölder means with those indexes, of the two positive numbers. Finally, we present a geometric application of this inequality involving the Fermat-Torricelli point of a triangle.
Paper's Title:
An Integration Technique for Evaluating Quadratic Harmonic Sums
Author(s):
J. M. Campbell and K.-W. Chen
Department of Mathematics and Statistics,
York University, 4700 Keele St, Toronto,
ON M3J 1P3,
Canada.
E-mail: jmaxwellcampbell@gmail.com
Department of Mathematics, University of Taipei,
No. 1, Ai-Guo West Road,
Taipei 10048, Taiwan.
E-mail: kwchen@uTaipei.edu.tw
URL:
https://math.utaipei.edu.tw/p/412-1082-22.php
Abstract:
The modified Abel lemma on summation by parts has been applied in many ways recently to determine closed-form evaluations for infinite series involving generalized harmonic numbers with an upper parameter of two. We build upon such results using an integration technique that we apply to ``convert'' a given evaluation for such a series into an evaluation for a corresponding series involving squared harmonic numbers.
Paper's Title:
Optimal Conditions using Multi-valued G-Presic type Mapping
Author(s):
Deb Sarkar, Ramakant Bhardwaj, Vandana Rathore, and Pulak Konar
Department of Mathematics, Amity
University, Kadampukur, 24PGS(N), Kolkata, West Bengal, 700135,
India.
E-mail: debsarkar1996@gmail.com
Department of Mathematics, Amity
University, Kadampukur, 24PGS(N), Kolkata, West Bengal, 700135,
India.
E-mail: drrkbhardwaj100@gmail.com
School of Engineering and Technology,
Jagran Lakecity University, Bhopal, MP-462044,
India.
E-mail: drvandana@jlu.edu.in
Department of Mathematics,
VIT University, Chennai, Tamil Nadu-600127,
India.
E-mail: pulakkonar@gmail.com
Abstract:
In the present paper, some best proximity results have been presented using the concept of G-Presic type multi-valued mapping. These results are the extensions of Presic's theorem in the non-self mapping. A suitable example has also been given. Here, some applications are presented in θ-chainable space and ordered metric space.
Paper's Title:
Some Nonlinear Gronwall-Bellman Type Retarded Integral Inequalities with Power and Their Applications
Author(s):
Ammar Boudeliou
Department of Mathematics, University of Constantine 1
Brothers Mentouri,
BP, 325, Ain El Bey Street, 25017,
Algeria.
E-mail: ammar_boudeliou@umc.edu.dz
Abstract:
In this paper, we investigate a certain class of nonlinear Gronwall-Bellman type integral inequalities with power in more general cases involving retarded term and more general nonlinearities. Our results generalize some known integral inequalities and other results obtained very recently. The inequalities given here can be used to estimate the bound on the solutions of retarded integral equation of Volterra type and integro-differential equations (IDE) with power. Two examples are given to show the validity of our established theorems.
Paper's Title:
General Extension of Hardy-Hilbert's Inequality (I)
Author(s):
W. T. Sulaiman
College of Computer Science and Mathematics, University of Mosul,
Iraq.
waadsulaiman@hotmail.com
Abstract:
A generalization for Hardy-Hilbert's inequality that extends the recent
results of Yang and Debnath
[6], is given.
Paper's Title:
Boundary Value Problems for Fractional Diffusion-Wave equation
Author(s):
Varsha Daftardar-Gejji and Hossein Jafari
Department of Mathematics, University of Pune,
Ganeshkhind, Pune - 411007,
INDIA.
vsgejji@math.unipune.ernet.in
jafari_h@math.com
Abstract:
Non homogeneous fractional diffusion-wave equation has been solved under linear/nonlinear boundary conditions. As the order of time derivative changes from
0 to 2, the process changes from slow diffusion to classical diffusion to mixed diffusion-wave behaviour.
Numerical examples presented here confirm this inference. Orthogonality of eigenfunctions in case of fractional Stürm-Liouville problem has been established
Paper's Title:
Equilibria and Periodic Solutions of Projected Dynamical Systems on Sets with Corners
Author(s):
Matthew D. Johnston and Monica-Gabriela Cojocaru
Department of Applied Mathematics, University of Waterloo,
Ontario, Canada
mdjohnst@math.uwaterloo.ca
Department of Mathematics & Statistics, University of
Guelph,
Ontario, Canada
mcojocar@uoguelph.ca
Abstract:
Projected dynamical systems theory represents a bridge between the
static worlds of variational inequalities and equilibrium
problems, and the dynamic world of ordinary differential
equations. A projected dynamical system (PDS) is given by the flow
of a projected differential equation, an ordinary differential
equation whose trajectories are restricted to a constraint set
K. Projected differential equations are defined by discontinuous
vector fields and so standard differential equations theory cannot
apply. The formal study of PDS began in the 90's, although some
results existed in the literature since the 70's. In this paper we
present a novel result regarding existence of equilibria and
periodic cycles of a finite dimensional PDS on constraint sets
K, whose points satisfy a corner condition. The novelty is due
to proving existence of boundary equilibria without using a
variational inequality approach or monotonicity type conditions.
Paper's Title:
Contact With Adhesion between a Deformable Body and a Foundation
Author(s):
B. Teniou and M. Sofonea
Laboratoire de Mathematiques Appliquées et Modélisation,
Université Mentouri, Constantine 25000,
Algeria
tenioubou2@yahoo.fr
Laboratoire de Mathématiques et Physiques pour les Systémes,
Univesité de Perpignan,
France.
sofonea@univ-perp.fr
Abstract:
The aim of this work is study a dynamic contact problem between a
deformable body and a foundation where the deformations are supposed
to be small. The contact is with adhesion and normal compliance. The
behavior of this body is modeled by a nonlinear
elastic-visco-plastic law. The evolution of bonding field is
described by a nonlinear differential equation. We derive a
variational formulation of the contact problem and we prove the
existence and uniqueness of its solution. The proof is based on the
construction of three intermediate problems and then we construct a
contraction mapping whose unique fixed point will be the weak
solution of the mechanical problem.
Paper's Title:
Integer Sums of Powers of Trigonometric Functions (MOD p), for prime p
Author(s):
G. J. Tee
Department of Mathematics, University of Auckland,
Auckland,
New Zealand
tee@math.auckland.ac.nz
Abstract:
Many multi--parameter families of congruences (mod p) are found for integer
sums of
qth powers of the trigonometric functions over various sets of equidistant
arguments, where
p is any prime factor of q. Those congruences provide sensitive
tests for the accuracy
of software for evaluating trigonometric functions to high precision.
Paper's Title:
Fractional Integral Operators and Olsen Inequalities on
Non-Homogeneous Spaces
Author(s):
Idha Sihwaningrum, Herry P. Suryawan, Hendra Gunawan
Analysis and Geometry Group,
Faculty of Mathematics and Natural Sciences,
Bandung Institute of Technology, Bandung 40132,
Indonesia
hgunawan@math.itb.ac.id
URL:
http://personal.fmipa.itb.ac.id/hgunawan/
Abstract:
We prove the boundedness of the fractional integral operator Iα on generalized Morrey spaces of non-homogeneous type. In addition, we also present Olsen-type inequalities for a multiplication operator involving Iα. Our proof uses a result of García-Cuerva and Martell [3].
Paper's Title:
Some Remarks on a Result of Bougoffa
Author(s):
James A. Oguntuase, Lars-Erik Persson and Josip E. Pečarič
Department of
Mathematics,University of Agriculture,
P M B 2240, Abeokuta, Nigeria
Department of Mathematics,
Luleĺ University of Technology,
SE-971 87, Luleĺ , Sweden
Faculty of Textile Technology, University of Zagreb,
Pierottijeva 6, 10000 Zagreb, Croatia
oguntuase@yahoo.com,
larserik@sm.luth.se,
pecaric@hazu.hr.
Abstract:
Some new generalizations of the result of
L. Bougoffa [J. Inequal. Pure Appl. Math. 7 (2) (2006), Art. 60]
are derived and discussed.
Paper's Title:
L∞- Error Estimate of Schwarz Algorithm for Elliptic Quasi-Variational Inequalities Related to Impulse Control Problem
Author(s):
Saadi Samira and Mehri Allaoua
Lab. LANOS, Department of Mathematics,
University Badji Mokhtar Annaba,
P.O.Box 12, Annaba 23000,
Algeria.
Lab. LAIG, Department of Mathematics,
University May 8th 1945,
P.O.Box 401, Guelma 24000,
Algeria.
E-mail:
saadisamira69@yahoo.fr
allmehri@yahoo.fr
Abstract:
In this work, we study Schwarz method for a class of elliptic quasi-variational inequalities. The principal result of this investigation is to prove the error estimate in ∞-norm for two domains with overlapping nonmatching grids, using the geometrical convergence, and the uniform convergence of Cortey Dumont.
Paper's Title:
Some Grüss Type Inequalities in Inner Product Spaces
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir
Abstract:
Some inequalities in inner product spaces
that provide upper bounds for the quantities
and
,
where e,f ∈ H with
and x,y are vectors in H satisfying some appropriate assumptions are
given. Applications for discrete and integral inequalities are provided as
well.
Paper's Title:
On the Constant in a Transference Inequality for the Vector-valued Fourier Transform
Author(s):
Dion Gijswijt and Jan van Neerven
Delft University of Technology,
Faculty EEMCS/DIAM,
P.O. Box 5031,
2600 GA Delft,
The Netherlands.
URL:
http://aw.twi.tudelft.nl/~neerven/
URL:
http://homepage.tudelft.nl/64a8q/
E-mail:
J.M.A.M.vanNeerven@TUDelft.nl
E-mail: D.C.Gijswijt@TUDelft.nl
Abstract:
The standard proof of the equivalence of Fourier type on Rd and on the torus Td is usually stated in terms of an implicit constant, defined as the minimum of a sum of powers of sinc functions. In this note we compute this minimum explicitly.
Paper's Title:
Strong Convergence Theorem for a Common Fixed Point of an
Infinite Family of J-nonexpansive Maps with Applications
Author(s):
Charlse Ejike Chidume, Otubo Emmanuel Ezzaka and Chinedu Godwin Ezea
African University of Science and
Technology,
Abuja,
Nigeria.
E-mail:
cchidume@aust.edu.ng
Ebonyi State University,
Abakaliki,
Nigeria.
E-mail: mrzzaka@yahoo.com
Nnamdi Azikiwe University,
Awka,
Nigeria.
E-mail: chinedu.ezea@gmail.com
Abstract:
Let E be a uniformly convex and uniformly smooth real Banach space with dual space E*. Let {Ti}∞i=1 be a family of J-nonexpansive maps, where, for each i,~Ti maps E to 2E*. A new class of maps, J-nonexpansive maps from E to E*, an analogue of nonexpansive self maps of E, is introduced. Assuming that the set of common J-fixed points of {Ti}∞i=1 is nonempty, an iterative scheme is constructed and proved to converge strongly to a point x* in ∩∞n=1FJTi. This result is then applied, in the case that E is a real Hilbert space to obtain a strong convergence theorem for approximation of a common fixed point for an infinite family of nonexpansive maps, assuming existences. The theorem obtained is compared with some important results in the literature. Finally, the technique of proof is also of independent interest.
Paper's Title:
Stability of the D-Bar Reconstruction Method for Complex Conductivities
Author(s):
1S. El Kontar, 1T. El Arwadi, 1H. Chrayteh, 2J.-M. Sac-Épée
1Department of Mathematics and
Computer Science,
Faculty of Science, Beirut Arab University,
P.O. Box: 11-5020, Beirut,
Lebanon.
E-mail: srs915@student.bau.edu.lb
2Institut Élie Cartan de
Lorraine,
Université de Lorraine - Metz,
France.
Abstract:
In 2000, Francini solved the inverse conductivity problem for twice-differentiable conductivities and permittivities. This solution was considered to be the first approach using D-bar methods with complex conductivities. In 2012, based on Francini's work, Hamilton introduced a reconstruction method of the conductivity distribution with complex values. The method consists of six steps. A voltage potential is applied on the boundary. Solving a D-Bar equation gives the complex conductivity. In this paper, the stability of the D-Bar equation is studied via two approximations, texp and tB, for the scattering transform. The study is based on rewriting the reconstruction method in terms of continuous operators. The conductivity is considered to be non smooth.
Paper's Title:
Weakly Compact Composition Operators on Real Lipschitz Spaces of Complex-valued Functions on Compact Metric Spaces with Lipschitz Involutions
Author(s):
D. Alimohammadi and H. Alihoseini
Department of Mathematics,
Faculty of Science,
Arak University
P. O. Box,38156-8-8349,
Arak,
Iran.
E-mail: d-alimohammadi@araku.ac.ir
E-mail:
hr_alihoseini@yahoo.com
URL: http://www.araku.ac.ir
Abstract:
We first show that a bounded linear operator T on a real Banach space E is weakly compact if and only if the complex linear operator T on the complex Banach space EC is weakly compact, where EC is a suitable complexification of E and iT' is the complex linear operator on EC associated with T. Next we show that every weakly compact composition operator on real Lipschitz spaces of complex-valued functions on compact metric spaces with Lipschitz involutions is compact.
Paper's Title:
A Comparison Between Two Different Stochastic Epidemic Models with Respect to the Entropy
Author(s):
Farzad Fatehi and Tayebe Waezizadeh
Department of Mathematics,
University of Sussex,
Brighton BN1 9QH,
UK.
E-mail: f.fatehi@sussex.ac.uk
URL:
http://www.sussex.ac.uk/profiles/361251
Department of Pure Mathematics, Faculty
of Mathematics and Computer,
Shahid Bahonar University of Kerman,
Kerman 76169-14111,
Iran.
E-mail: waezizadeh@uk.ac.ir
URL:
http://academicstaff.uk.ac.ir/en/tavaezizadeh
Abstract:
In this paper at first a brief history of mathematical models is presented with the aim to clarify the reliability of stochastic models over deterministic models. Next, the necessary background about random variables and stochastic processes, especially Markov chains and the entropy are introduced. After that, entropy of SIR stochastic models is computed and it is proven that an epidemic will disappear after a long time. Entropy of a stochastic mathematical model determines the average uncertainty about the outcome of that random experiment. At the end, we introduce a chain binomial epidemic model and compute its entropy, which is then compared with the DTMC SIR epidemic model to show which one is nearer to reality.
Paper's Title:
A Method of the Study of the Cauchy Problem for~a~Singularly Perturbed Linear Inhomogeneous Differential Equation
Author(s):
E. E. Bukzhalev and A. V. Ovchinnikov
Faculty of Physics,
Moscow State University,
1 Leninskie Gory,
Moscow, 119991,
Russia
E-mail: bukzhalev@mail.ru
Russian Institute for Scientific and
Technical Information of the Russian Academy of Sciences,
20 Usievicha St., Moscow, 125190,
Russia
E-mail: ovchinnikov@viniti.ru
Abstract:
We construct a sequence that converges to a solution of the Cauchy problem for a singularly perturbed linear inhomogeneous differential equation of an arbitrary order. This sequence is also an asymptotic sequence in the following sense: the deviation (in the norm of the space of continuous functions) of its nth element from the solution of the problem is proportional to the (n+1)th power of the parameter of perturbation. This sequence can be used for justification of asymptotics obtained by the method of boundary functions.
Paper's Title:
Euler-Maclaurin Formulas for Functions of Bounded Variation
Author(s):
G. De Marco, M. De Zotti, C. Mariconda
Dipartimento di Matematica Tullio Levi-Civita,
Universita degli Studi di Padova
Via Trieste 63, Padova 35121,
Italy.
E-mail: carlo.mariconda@unipd.it
URL: http://www.math.unipd.it
Abstract:
The first-order Euler-Maclaurin formula relates the sum of the values of a smooth function on an interval of integers with its integral on the same interval on R. We formulate here the analogue for functions that are just of bounded variation.
Paper's Title:
Existence and Estimate of the Solution for the Approximate Stochastic Equation to the Viscous Barotropic Gas
Author(s):
R. Benseghir and A. Benchettah
LANOS Laboratory,
Badji Mokhtar University,
PO Box 12,
Annaba, Algeria.
E-mail:
benseghirrym@ymail.com,
abenchettah@hotmail.com
Abstract:
A stochastic equation of a viscous barotropic gas is considered. The application of Ito formula to a specific functional in an infinite dimensional space allows us to obtain an estimate which is useful to analyse the behavior of the solution. As it is difficult to exploit this estimate, we study an approximate problem. More precisely, we consider the equation of a barotropic viscous gas in Lagrangian coordinates and we add a diffusion of the density. An estimate of energy is obtained to analyse the behavior of the solution for this approximate problem and Galerkin method is used to prove the existence and uniqueness of the solution.
Paper's Title:
An Existence of the Solution to Neutral Stochastic Functional Differential Equations Under the Holder Condition
Author(s):
Young-Ho Kim
Department of Mathematics,
Changwon National University,
Changwon, Gyeongsangnam-do 51140,
Korea.
E-mail: iyhkim@changwon.ac.kr
Abstract:
In this paper, we show the existence and uniqueness of solution of the neutral stochastic functional differential equations under weakened H\"{o}lder condition, a weakened linear growth condition, and a contractive condition. Furthermore, in order to obtain the existence of a solution to the equation we used the Picard sequence.
Paper's Title:
Bounds on the Jensen Gap, and Implications for Mean-Concentrated Distributions
Author(s):
Xiang Gao, Meera Sitharam, Adrian E. Roitberg
Department of Chemistry, and Department
of Computer & Information Science & Engineering,
University of Florida,
Gainesville, FL 32611,
USA.
E-mail: qasdfgtyuiop@gmail.com
URL:
https://scholar.google.com/citations?user=t2nOdxQAAAAJ
Abstract:
This paper gives upper and lower bounds on the gap in Jensen's inequality, i.e., the difference between the expected value of a function of a random variable and the value of the function at the expected value of the random variable. The bounds depend only on growth properties of the function and specific moments of the random variable. The bounds are particularly useful for distributions that are concentrated around the mean, a commonly occurring scenario such as the average of i.i.d. samples and in statistical mechanics.
Paper's Title:
Fractional exp(-φ(ξ))- Expansion Method and its Application to Space--Time Nonlinear Fractional Equations
Author(s):
A. A. Moussa and L. A. Alhakim
Department of Management Information
System and Production Management,
College of Business and Economics, Qassim University,
P.O. BOX 6666, Buraidah: 51452,
Saudi Arabia.
E-mail: Alaamath81@gmail.com
URL:
https://scholar.google.com/citations?user=ccztZdsAAAAJ&hl=ar
Department of Management Information
System and Production Management,
College of Business and Economics, Qassim University,
P.O. BOX 6666, Buraidah: 51452,
Saudi Arabia.
E-mail: Lama2736@gmail.com
URL:
https://scholar.google.com/citations?user=OSiSh1AAAAAJ&hl=ar
Abstract:
In this paper, we mainly suggest a new method that depends on the fractional derivative proposed by Katugampola for solving nonlinear fractional partial differential equations. Using this method, we obtained numerous useful and surprising solutions for the space--time fractional nonlinear Whitham--Broer--Kaup equations and space--time fractional generalized nonlinear Hirota--Satsuma coupled KdV equations. The solutions obtained varied between hyperbolic, trigonometric, and rational functions, and we hope those interested in the real-life applications of the previous two equations will find this approach useful.
Paper's Title:
On the Oldest Problem in the Calculus of Variations: A New Message from Queen Dido
Author(s):
Olivier de La Grandville
Faculty of Economics,
Goethe University Frankfurt,
Theodore Adorno Platz 4, 60323 Frankfurt,
Germany.
E-mail: odelagrandville@gmail.com
Abstract:
We consider the problem of finding the optimal curve of given length linking two points in a plane such as it encloses a maximal area. We show that if the curve is not described by a single-valued function, its determination does not necessarily imply to work with a parametric representation of the curve. We show that a simpler approach is at hand -- and, who knows? -- this might well be the method Queen Dido used.
Paper's Title:
Topological Aspects of Discrete Switch Dynamical Systems
Author(s):
Faiz Imam and Sharan Gopal
Department of Mathematics,
BITS - Pilani, Hyderabad Campus,
India.
E-mail: mefaizy@gmail.com
Department of Mathematics,
BITS - Pilani, Hyderabad Campus,
India.
E-mail: sharanraghu@gmail.com
ABSTRACT NOT FOUND. WEBSITE ERROR
Abstract:
Paper's Title:
Finite Volume Approximation of a Class of 2D Elliptic Equations with Discontinuous and Highly Oscillating Coefficients
Author(s):
J. D. Bambi Pemba and B. Ondami
Université Marien Ngouabi
Factuté des Sciences et Techniques
BP 69 Brazzaville,
Congo.
E-mail: bondami@gmail.com
URL:
https://www.researchgate.net/profile/Bienvenu-Ondami
https://www.linkedin.com/in/bienvenu-ondami
Abstract:
In this paper, we are interested in the Finite Volume approximation of a second-order two-dimensional elliptic equation in heterogeneous porous medium with a periodic structure. The equation's coefficients are therefore discontinuous and highly oscillating. This class of problems has been extensively studied in the literature, where various methods proposed for determining the so-called homogenized problem. What we are particularly interested in is the direct numerical approximation of the problem, which has received little attention in the literature. We use the cell-centered finite volume approach for this purpose. Error estimates are established, and numerical simulations are conducted for both the isotropic and anisotropic media cases. The obtained solution is compared to the homogenized solution, and the results show that this approach provides an adequate approximation of the exact solution.
Paper's Title:
Positive Periodic Time-Scale Solutions for Functional Dynamic Equations
Author(s):
Douglas R. Anderson and Joan Hoffacker
Department of Mathematics and Computer Science
Concordia College
Moorhead, MN 56562 USA
andersod@cord.edu
URL: http://www.cord.edu/faculty/andersod/
Department of Mathematical Sciences
Clemson University
Clemson, SC 29634 USA
johoff@clemson.edu
URL: http://www.math.clemson.edu/facstaff/johoff.htm
Abstract:
Using Krasnoselskii's fixed point theorem, we establish the existence of positive periodic solutions
to two pairs of related nonautonomous functional delta dynamic equations on periodic time scales, and then extend the discussion to higher-dimensional equations. Two pairs of corresponding nabla equations
are also provided in an analogous manner.
Paper's Title:
Coincidences and Fixed Points of Hybrid Maps in Symmetric Spaces
Author(s):
S. L. Singh and Bhagwati Prasad
Vedic MRI, 21 Govind Nagar,
Department of Mathematics, Gurukula Kangri University,
Rishikesh 249201
India
vedicmri@gmail.com
Hardwar 249404,
India
Abstract:
The purpose of this paper is to obtain a new coincidence theorem for a
single-valued and two multivalued operators in symmetric spaces. We derive
fixed point theorems and discuss some special cases and applications.
Paper's Title:
On Pseudo Almost
Periodic Solutions to Some Neutral Functional-Differential
Equations
Author(s):
Toka Diagana and Eduardo Hernández
Department of Mathematics, Howard University
2441 6th Street NW,
Washington DC 20059,
USA.
tdiagana@howard.edu
Departamento de Matemática, I.C.M.C. Universidade de Săo Paulo,
Caixa Postal
668, 13560-970, Săo Carlos SP,
Brazil.
lalohm@icmc.sc.usp.br
Abstract:
This paper discusses the existence and uniqueness of pseudo almost periodic solutions to a class of partial neutral functional-differential equations. Under some suitable assumptions, existence and uniqueness results are obtained. An example is given to illustrate abstract results.
Paper's Title:
Shape Diagrams for 2D Compact Sets - Part III: Convexity
Discrimination for Analytic and Discretized Simply Connected Sets.
Author(s):
S. Rivollier, J. Debayle and J.-C. Pinoli
Ecole Nationale Supérieure des Mines de Saint-Etienne,
CIS - LPMG, UMR CNRS
5148,
158 cours Fauriel,
42023 Saint-Etienne Cedex 2, France.
rivollier@emse.fr;
debayle@emse.fr; pinoli@emse.fr
Abstract:
Shape diagrams are representations in the Euclidean plane introduced to study 3-dimensional and 2-dimensional compact convex sets. However, they can also been applied to more general compact sets than compact convex sets. A compact set is represented by a point within a shape diagram whose coordinates are morphometrical functionals defined as normalized ratios of geometrical functionals. Classically, the geometrical functionals are the area, the perimeter, the radii of the inscribed and circumscribed circles, and the minimum and maximum Feret diameters. They allow twenty-two shape diagrams to be built. Starting from these six classical geometrical functionals, a detailed comparative study has been performed in order to analyze the representation relevance and discrimination power of these twenty-two shape diagrams. The two first parts of this study are published in previous papers 8,9. They focus on analytic compact convex sets and analytic simply connected compact sets, respectively. The purpose of this paper is to present the third part, by focusing on the convexity discrimination for analytic and discretized simply connected compact sets..
Paper's Title:
Approximation of Common Fixed Points of a Finite Family of Asymptotically Demicontractive Mappings in Banach Spaces
Author(s):
Yuchao Tang, Yong Cai, Liqun Hu and Liwei Liu
Department of Mathematics, NanChang University,
Nanchang 330031, P.R. China
Department of Mathematics, Xi'an Jiaotong University,
Xi'an 710049, P.R.
China
Abstract:
By virtue of new analytic techniques, we analyze and
study
several strong convergence theorems for the approximation of
common fixed points of asymptotically demicontractive mappings
via the multistep iterative sequence with errors in Banach
spaces. Our results improve and extend the corresponding ones
announced by Osilike , Osilike and Aniagbosor, Igbokwe, Cho et
al., Moore and Nnoli, Hu and all the others.
Paper's Title:
A New Property of General Means of Order p with an Application to the Theory of Economic Growth
Author(s):
Olivier de La Grandville
Department of Management Science and Engineering,
Huang Engineering Center, Stanford University,
475 Via Ortega, Stanford, California 94305
U.S.A.
Abstract:
The purpose of this note is to demonstrate a new property of the
general mean of order p of m ordered positive numbers
.
If p < 0 and if
,
the elasticity of
with
respect to xm, defined by
,
tends towards zero, and therefore
.
This property is then applied to optimal growth theory.
Paper's Title:
Ulam Stability of Reciprocal Difference and Adjoint Functional Equations
Author(s):
K. Ravi, J. M. Rassias and B. V. Senthil Kumar
Department of Mathematics,
Sacred Heart College, Tirupattur - 635601,
India
Pedagogical Department E. E.,
Section of Mathematics and Informatics,
National and Capodistrian University of Athens,
4, Agamemnonos Str., Aghia Paraskevi,
Athens, Attikis 15342,
GREECE
Department of Mathematics,
C.Abdul Hakeem College of Engineering and
Technology, Melvisharam - 632 509, India
shckavi@yahoo.co.in
jrassias@primedu.uoa.gr
bvssree@yahoo.co.in
Abstract:
In this paper, the reciprocal difference functional equation (or RDF equation) and the reciprocal adjoint functional equation (or RAF equation) are introduced. Then the pertinent Ulam stability problem for these functional equations is solved, together with the extended Ulam (or Rassias) stability problem and the generalized Ulam (or Ulam-Gavruta-Rassias) stability problem for the same equations.
Paper's Title:
Schwarz Method
for Variational Inequalities Related to Ergodic Control Problems
Author(s):
S. Saadi, H. Mécheri
Department of Mathematics, Badji Mokhtar
University, Annaba 23000,
P.O.Box. 12, Annaba 23000, Algeria
Abstract:
In this paper, we study variational inequalities related to ergodic control problems studied by M. Boulbrachčne and H. Sissaoui [11], where the "discount factor" (i.e., the zero order term) is set to 0, we use an overlapping Schwarz method on nomatching grid which consists in decomposing the domain in two subdomains. For α ∈ ]0.1[ we provide the discretization on each subdomain converges in L∞ -norm.
Paper's Title:
Renormalized Solutions for Nonlinear Parabolic Equation with Lower Order Terms
Author(s):
A. Aberqi1, J. Bennouna1, M. Mekkour1 and H. Redwane2
1Université Sidi Mohammed Ben
Abdellah,
Département de Mathématiques,
Laboratoire LAMA, Faculté des Sciences Dhar-Mahrez,
B.P 1796 Atlas Fés,
Morocco.
2Faculté des Sciences
Juridiques, Economiques et Sociales,
Université Hassan 1, B.P. 784. Settat,
Morocco.
aberqiahmed@ya_hoo.fr
jbennouna@hotmail.com
mekkour.mounir@yahoo.fr
redwane_hicham@yahoo.fr
Abstract:
In this paper, we study the existence of renormalized solutions for the
nonlinear parabolic problem:
,where
the right side belongs to L1(Ω×(0,T))
and b(u) is unbounded function of u,
the term div(a(x,t,u,∇u)) is a Leray--Lions
operator and the function φ is a nonlinear lower order and satisfy only the
growth condition.
Paper's Title:
Some New Nonlinear Integro-Differential Inequalities of Gronwall-Bellman-Pachpatte Type
Author(s):
A. ABDELDAIM
Department of Mathematics and Computer
Sciences,
Faculty of Science,
Port Said University, Port Said,
EGYPT.
Department of Mathematics,
Faculty of Science and Humanities,
Shaqra University, Dawadmi,
SAUDI ARABIA.
E-mail:
ahassen@su.edu.sa
URL:
http://faculty.ksu.edu.sa/DRABDELDAIM/Pages/Home.aspx
Abstract:
In this paper we establish some new nonlinear integro-differential inequalities of Gronwall-Bellman-Pachpatte type for function of one independent variable. The purpose of this paper is to extend certain results which proved by Pachpatte in [On some fundamental integrodifferential and integral inequalities, An. Sti. Univ. Al. I. Cuza, Iasi, Vol.23 (1977), 77-86]. The inequalities obtained here can be used in the theory of some new classes of nonlinear integro-differential equations. Some applications are also given to illustrate the usefulness of our results.
Paper's Title:
Weak Type Inequalities for Some Operators on Generalized Morrey Spaces Over Metric Measure Spaces
Author(s):
Idha Sihwaningrum, Ari Wardayani, Hendra Gunawan
Faculty of Mathematics and Natural
Sciences,
Jenderal Soedirman University, Purwokerto 53122,
Indonesia.
E-mail: idha.sihwaningrum@unsoed.ac.id
ariwardayani@yahoo.co.id
Faculty of Mathematics and Natural
Sciences,
Bandung Institute of Technology, Bandung 40132,
Indonesia.
E-mail: hgunawan@math.itb.ac.id
URL:
http://personal.fmipa.itb.ac.id/hgunawan/
Abstract:
We discuss weak type inequalities for maximal and fractional integral operators on generalized Morrey spaces over metric measure spaces. Here the measure satisfies the so called growth condition. By taking into account the maximal operator, we obtain a Hedberg type inequality, which leads us to the weak type inequality for the fractional integral operator on the same spaces.
Paper's Title:
Some New Generalizations of Jensen's Inequality with Related Results and Applications
Author(s):
Steven G. From
Department of Mathematics
University of Nebraska at Omaha
Omaha, Nebraska 68182-0243.
E-mail: sfrom@unomaha.edu
Abstract:
In this paper, some new generalizations of Jensen's inequality are presented. In particular, upper and lower bounds for the Jensen gap are given and compared analytically and numerically to previously published bounds for both the discrete and continuous Jensen's inequality cases. The new bounds compare favorably to previously proposed bounds. A new method based on a series of locally linear interpolations is given and is the basis for most of the bounds given in this paper. The wide applicability of this method will be demonstrated. As by-products of this method, we shall obtain some new Hermite-Hadamard inequalities for functions which are 3-convex or 3-concave. The new method works to obtain bounds for the Jensen gap for non-convex functions as well, provided one or two derivatives of the nonlinear function are continuous. The mean residual life function of applied probability and reliability theory plays a prominent role in construction of bounds for the Jensen gap. We also present an exact integral representation for the Jensen gap in the continuous case. We briefly discuss some inequalities for other types of convexity, such as convexity in the geometric mean, and briefly discuss applications to reliability theory.
Paper's Title:
Presentation a mathematical model for bone metastases control by using tamoxifen
Author(s):
Maryam Nikbakht, Alireza Fakharzadeh Jahromi and Aghileh Heydari
Department of Mathematics,
Payame Noor University,
P.O.Box 19395-3697, Tehran,
Iran.
.E-mail:
maryam_nikbakht@pnu.ac.ir
Department of Mathematics,
Faculty of Basic Science,
Shiraz University of Technology.
E-mail:
a_fakharzadeh@sutech.ac.ir
Department of Mathematics,
Payame Noor University,
P.O.Box 19395-3697, Tehran,
Iran.
E-mail: a-heidari@pnu.ac.ir
Abstract:
Bone is a common site for metastases (secondary tumor) because of breast and prostate cancer. According to our evaluations the mathematical aspect of the effect of drug in bone metastases has not been studied yet. Hence, this paper suggested a new mathematical model for bone metastases control by using tamoxifen. The proposed model is a system of nonlinear partial differential equations. In this paper our purpose is to present a control model for bone metastases. At end by some numerical simulations, the proposed model is examined by using physician.
Paper's Title:
Relation Between The Set Of Non-decreasing Functions And The Set Of Convex Functions
Author(s):
Qefsere Doko Gjonbalaj and Luigj Gjoka
Department of Mathematics, Faculty of
Electrical and Computer Engineering,
University of Prishtina "Hasan Prishtina",
Prishtine 10000,
Kosova
E-mail:
qefsere.gjonbalaj@uni-pr.edu
Department of Engineering Mathematics,
Polytechnic University of Tirana, Tirana,
Albania.
E-mail: luigjgjoka@ymail.com
Abstract:
In this article we address the problem of integral presentation of a convex function. Let I be an interval in R. Here, using the Riemann or Lebesgue’s integration theory, we find the necessary and sufficient condition for a function f: I→ R to be convex in I.
Paper's Title:
Stability Analysis Epidemic Model of SIR Type (Susceptible, Infectious, Recovered) On The Spread Dynamic of Malaria in Ambon City
Author(s):
Alwi Smith
Education Faculty, Biology Education
Programme,
University of Pattimura,
Ir. M. Putuhena Street, Poka Ambon, Moluccas, 97233,
Indonesia.
E-mail: alwi.smith1963@gmail.com
Abstract:
This research discusses the spread of malaria in Ambon city through SIR (Susceptible, Infected, Recovered) model. This research analyzes the stability of equilibrium point on deterministic model and Basic Reproduction Ratio (R0). The result shows that the epidemic model has two equilibrium points. They are disease free equilibrium, [E0=[S,I,R]=[1,0,0]], and epidemic equilibrium, Ei=[S,I,R]= [5,497808;-3,680341;-0,818288]. The Basic Reproduction Ratio of malaria disease in Ambon city is 0,181891. This result implies that malaria disease in Ambon will not be an endemic, because malaria disease in Ambon city will be eradicated slowly over time.
Paper's Title:
Iterative Algorithm for Split Generalized Mixed Equilibrium Problem Involving Relaxed Monotone Mappings in Real Hilbert Spaces
Author(s):
1U.A. Osisiogu, F.L. Adum, and 2C. Izuchukwu
1Department of Mathematics and
Computer Science,
Ebonyi State University, Abakaliki,
Nigeria.
E-mail: uosisiogu@gmail.com,
adumson2@yahoo.com
2School of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: izuchukwuc@ukzn.ac.za,
izuchukwu_c@yahoo.com
Abstract:
The main purpose of this paper is to introduce a certain class of split generalized mixed equilibrium problem involving relaxed monotone mappings. To solve our proposed problem, we introduce an iterative algorithm and obtain its strong convergence to a solution of the split generalized mixed equilibrium problems in Hilbert spaces. As special cases of the proposed problem, we studied the proximal split feasibility problem and variational inclusion problem.
Paper's Title:
On Finding Integrating Factors and First Integrals for a Class of Higher Order Differential Equations
Author(s):
Mohammadkheer M. Al-Jararha
Department of Mathematics,
Yarmouk University,
Irbid, 21163,
Jordan.
E-mail: mohammad.ja@yu.edu.jo
Abstract:
If the $n-th$ order differential equation is not exact, under certain
conditions, an integrating factor exists which transforms the differential
equation into an exact one. Thus, the order of differential equation can be
reduced to the lower order. In this paper, we present a technique for finding
integrating factors of the following class of differential equations:
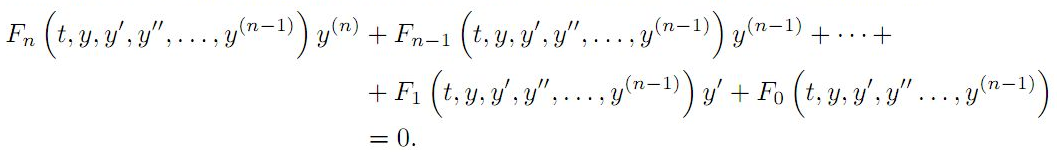
Here, the functions F0,F1,F2,
…,Fn are assumed to be continuous
functions with their first partial derivatives on some simply connected domain
Ω ⊂ Rn+1.
We also presented some demonstrative examples
Paper's Title:
Characterization of Caristi Type Mapping Through its Absolute Derivative
Author(s):
M. Muslikh1, A. Kilicman2,3, S. H. Sapar4 and N. Bacho5
1Department of Mathematics,
University of Brawijaya,
Malang 65143, East Java,
Indonesia.
E-mail: mslk@ub.ac.id
2Department of Mathematics,
Universiti Putra Malaysia,
43400 UPM, Serdang, Selangor,
Malaysia
E-mail: akilic@upm.edu.my
3Department of Electrical and Electronic Engineering,
Istanbul Gelisim University,
Avcilar, Istanbul,
Turkey
4Department of Mathematics,
Universiti Putra Malaysia,
43400 UPM, Serdang, Selangor,
Malaysia
E-mail: sitihas@upm.edu.my
5Department of Mathematics,
Universiti Putra Malaysia,
43400 UPM, Serdang, Selangor,
Malaysia
E-mail: norfifah@upm.edu.my
Abstract:
The purpose of this article to characterize the Caristi type mapping by the absolute derivative. The equivalences of the Caristi mapping with contraction mapping is discussed too. In addition, it was shown that the contraction mapping can be tested through its absolute derivative.
Paper's Title:
A Low Order Least-Squares Nonconforming Finite Element Method for Steady Magnetohydrodynamic Equations
Author(s):
Z. Yu, D. Shi and H. Zhu
College of Science,
Zhongyuan
University of Technology,
Zhengzhou 450007,
China.
E-mail:
5772@zut.edu.cn
School of Mathematics and Statistics,
Zhengzhou University,
Zhengzhou 450001,
China.
E-mail:
shi_dy@126.com
Mathematics Department,
University of Southern Mississippi,
Hattiesburg MS, 39406,
U.S.A
E-mail:
huiqing.zhu@usm.edu
Abstract:
A low order least-squares nonconforming finite element (NFE) method is proposed for magnetohydrodynamic equations with EQ1rot element and zero-order Raviart-Thomas element. Based on the above element's typical interpolations properties, the existence and uniqueness of the approximate solutions are proved and the optimal order error estimates for the corresponding variables are derived.
Paper's Title:
Extension of Factorization Theorems of Maurey to s-positively Homogeneous Operators
Author(s):
Abdelmoumen Tiaiba
Department of Physics,
University of M'sila,
Algeria.
E-mail: tiaiba05@yahoo.fr
Abstract:
In the present work, we prove that the class of s-positively homogeneous operators is a Banach space. As application, we give the generalization of some Maurey factorization theorems to T which is a s-positively homogeneous operator from X a Banach space into Lp. Where we establish necessary and sufficient conditions to proof that T factors through Lq. After this we give extend result of dual factorization theorem to same class of operators above.
Paper's Title:
Sweeping Surfaces with Darboux Frame in Euclidean 3-space E3
Author(s):
F. Mofarreh, R. Abdel-Baky and N. Alluhaibi
Mathematical Science Department, Faculty
of Science,
Princess Nourah bint Abdulrahman University
Riyadh 11546,
Saudi Arabia.
E-mail: fyalmofarrah@pnu.edu.sa
Department of Mathematics, Faculty of Science,
University of Assiut,
Assiut 71516,
Egypt.
E-mail: rbaky@live.com
Department of Mathematics Science and
Arts, College Rabigh Campus,
King Abdulaziz University
Jeddah,
Saudi Arabia.
E-mail: nallehaibi@kau.edu.sa
Abstract:
The curve on a regular surface has a moving frame and it is called Darboux frame. We introduce sweeping surfaces along the curve relating to the this frame and investigate their geometrical properties. Moreover, we obtain the necessary and sufficient conditions for these surfaces to be developable ruled surfaces. Finally, an example to illustrate the application of the results is introduced.
Paper's Title:
A Note on Schur's Lemma in Banach Function Spaces
Author(s):
R. E. Castillo, H. Rafeiro and E. M. Rojas
Universidad Nacional de Colombia,
Departamento de Matematicas, Bogota,
Colombia.
E-mail: recastillo@unal.edu.co
United Arab Emirates University,
Department of Mathematical Sciences, Al Ain,
United Arab Emirates.
E-mail: rafeiro@uaeu.ac.ae
Universidad Nacional de Colombia,
Departamento de Matematicas, Bogota,
Colombia.
E-mail: emrojass@unal.edu.co
Abstract:
In this small note, in a self contained presentation, we show the validity of Schur's type lemma in the framework of Banach function spaces.
Paper's Title:
On Some Nonlinear Retarded Integrodifferential Inequalities in Two and n Independent Variables and their Applications
Author(s):
Bitat Dalila and Khellaf Hassane
Department of Mathematics, Laboratory of
Applied Mathematics and Modeling,
University of Constantine,
PO Box 325, Ain El Bey Road, Constantine 25017,
Algeria.
E-mail: bitat.dalila@umc.edu.dz
khellafhassane@umc.edu.dz
URL: https://www.umc.edu.dz
Abstract:
In this paper, we establish some new nonlinear retarded integrodifferential inequalities in two and n independent variables. Some applications are given as illustration.
Paper's Title:
On the Equiform Geometry of the Involute-evolute Curve Couple in Hyperbolic and de Sitter Spaces
Author(s):
M. Khalifa Saad, H. S. Abdel-Aziz and A. A. Abdel-Salam
Department of Mathematics,
Faculty of Science,
Islamic University of Madinah,
KSA.
E-mail: mohammed.khalifa@iu.edu.sa
Department of Mathematics,
Faculty of Science,
Sohag University, Sohag,
EGYPT.
E-mail: habdelaziz2005@yahoo.com
Department of Mathematics,
Faculty of Science,
Sohag University, Sohag,
EGYPT.
E-mail: asem2e@yahoo.com
Abstract:
In this paper, we aim to investigate the equiform differential geometric properties of the involute-evolute curve couple with constant equiform curvatures in three-dimensional hyperbolic and de Sitter spaces. Also, we obtain some relations between the curvature functions of these curves and investigate some special curves with respect to their equiform curvatures. Finally, we defray two computational examples to support our main findings.
Paper's Title:
On Infinite Unions and Intersections of Sets in a Metric Space
Author(s):
Spiros Konstantogiannis
Ronin Institute,
Montclair, New Jersey,
United States.
E-mail:
spiros.konstantogiannis@ronininstitute.org
URL:
https://www.researchgate.net/profile/Spiros-Konstantogiannis
Abstract:
The aim of this paper is to examine infinite unions and intersections of sets in a general metric space, with a view to explaining when an infinite intersection of open sets is an open set and when an infinite union of closed sets is a closed set.
Paper's Title:
Inequalities Involving A∞ Weights by Extrapolations
Author(s):
Chunping Xie
Mathematics Department,
Milwaukee School of Engineering,
1025 N. Broadway,
Milwaukee, Wisconsin 53202,
U.S.A.
E-mail: xie@msoe.edu
URL:
https://www.msoe.edu/directory/profile/chunping.xie/
Abstract:
We generalize the extrapolation theorem from Ap weights to A∞ weights on the setting of weighted Morrey spaces by using the Rubio de Francia algorithm and ideas in a paper by D. Cruz-Uribe et al. First we have proved the classical Hardy-Littlewood maximal operator is bounded on the weighted Morrey spaces if the weight w(x) is in A∞ and then we have obtained inequalities involving the maximal operator, vector-valued maximal operator, the sharp maximal operator, and A∞ weights.
Paper's Title:
On the Oscillatory Behavior of Self Adjoint Fractional Extensible Beam Equations
Author(s):
S. Priyadharshini1, G.E. Chatzarakis2, S. L. Panetsos2 and V. Sadhasivam1
1Post
Graduate and Research Department of Mathematics,
Thiruvalluvar Government Arts College,
Rasipuram - 637 401, Namakkal Dt., Tamil Nadu,
India.
E-mail: s.priya25april@gmail.com,
ovsadha@gmail.com
2Department
of Electrical and Electronic Engineering Educators,
School of Pedagogical and Technological Education(ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
gea.xatz@aspete.gr,
spanetsos@aspete.gr
Abstract:
The main objective of this paper is to study the oscillatory behavior of the solutions of self adjoint fractional extensible beam equations by using integral average method. Some new sufficient conditions are established with various boundary conditions over a cylindrical domains. Examples illustrating the results are given.
Paper's Title:
Existence of Non-spurious Solutions to Discrete Boundary Value Problems
Author(s):
Irena Rachunkova and Christopher C. Tisdell
Department of Mathematics
School of Mathematics
Palacky University
771 46 Olomouc, Czech Republic.
rachunko@risc.upol.cz
URL: http://phoenix.inf.upol.cz/~rachunekl/mathair/matha-en.htm
The University of New South Wales
Sydney 2052, Australia.
cct@unsw.edu.au
URL: http://www.maths.unsw.edu.au/~cct
Abstract:
This paper investigates discrete boundary value problems (BVPs) involving second-order difference equations and two-point boundary conditions.
General theorems guaranteeing the existence and uniqueness of solutions to the discrete BVP are established. The methods involve a sufficient growth condition to yield an a priori bound on solutions to a certain family of discrete BVPs. The em a priori bounds on solutions to the discrete BVP do not depend on the step-size and thus there are no ``spurious'' solutions. It is shown that solutions of the discrete BVP will converge to solutions of ordinary differential equations.
Paper's Title:
A Different Proof for the non-Existence of Hilbert-Schmidt Hankel Operators with
Anti-Holomorphic Symbols on the Bergman Space
Author(s):
Georg Schneider
Universität Wien, Brünnerstr. 72 A-1210 Wien,
Austria.
georg.schneider@univie.ac.at
URL: http://www.univie.ac.at/bwl/cont/mitarbeiter/schneider.htm
Abstract:
We show that there are no (non-trivial) Hilbert-Schmidt Hankel
operators with anti-holomorphic symbols on the Bergman space of
the unit-ball B2(Bl) for l≥2. The result dates back to
[6]. However, we give a different proof. The methodology can
be easily applied to other more general settings. Especially, as
indicated in the section containing generalizations, the new
methodology allows to prove some robustness results for existing
ones.
Paper's Title:
A Nonlinear Proximal Alternating Directions Method for Structured Variational Inequalities
Author(s):
M. Li
Department of Management Science and Engineering, School of Economics and Management
Southeast University, Nanjing, 210096,
China.
liminnju@yahoo.com
Abstract:
In this paper, we present a nonlinear proximal alternating directions method (NPADM) for solving a class of structured variational inequalities (SVI). By choosing suitable Bregman functions, we generalize the proximal alternating directions method proposed by He, et al.. The convergence of the method is proved under quite mild assumptions and flexible parameter conditions.
Paper's Title:
Isoperimetric Inequalities for Dual Harmonic Quermassintegrals
Author(s):
Yuan Jun, Zao Lingzhi and Duan Xibo
School of Mathematics and Computer Science,
Nanjing Normal University, Nanjing, 210097,
China.
yuanjun_math@126.com
Department of Mathematics, Nanjing Xiaozhuang University,
Nanjing, 211171,
China.
lzhzhao@163.com
Department of Mathematics, Shandong Water Polytechnic,
Shandong, 276826,
China
dxb1111@sohu.com
Abstract:
In this paper, some isoperimetric inequalities for the dual harmonic
quermassintegrals are established.
Paper's Title:
Regular Variation on Time Scales and Dynamic Equations
Author(s):
Pavel Řehák
Institute of Mathematics, Academy of Sciences of the Czech Republic
Žižkova 22, CZ61662 Brno,
Czech Republic
rehak@math.muni.cz
URL:http://www.math.muni.cz/~rehak
Abstract:
The purpose of this paper is twofold. First, we want to initiate a study
of regular variation on time scales by introducing this concept in such a
way that it
unifies and extends well studied continuous and discrete cases.
Some basic properties of regularly varying functions on time scales will be
established as well.
Second, we give conditions under which certain solutions of linear second
order
dynamic equations are regularly varying.
Open problems and possible directions for a future research are discussed,
too.
Paper's Title:
Differentiability of
Distance Functions in p-Normed Spaces
Author(s):
M. S. Moslehian, A. Niknam, S. Shadkam Torbati
Department of Pure Mathematics,
Centre of Excellence in Analysis on Algebraic Structures (CEAAS),,
Ferdowsi University of Mashhad,
P. O. Box
1159, Mashhad,
Iran
moslehian@ferdowsi.um.ac.ir
niknam@math.um.ac.ir
shadkam.s@wali.um.ac.ir
Abstract:
The farthest point mapping in a p-normed space X is studied in virtue of the Gateaux derivative and the Frechet derivative. Let M be a closed bounded subset of X having the uniformly p-Gateaux differentiable norm. Under certain conditions, it is shown that every maximizing sequence is convergent, moreover, if M is a uniquely remotal set then the farthest point mapping is continuous and so M is singleton. In addition, a Hahn--Banach type theorem in $p$-normed spaces is proved.
Paper's Title:
On Some
Mapping Properties of M
Author(s):
Nihal Yilmaz Özgür
Balkesir University,
Faculty of Arts and Sciences, Department of Mathematics,
10145 Balkesir,
TURKEY
nihal@balikesir.edu.tr
URL: http://w3.balikesir.edu.tr/~nihal/
Abstract:
We consider spheres corresponding to any norm function on the complex plane and their images under the Möbius transformations. We see that the sphere preserving property is not an invariant characteristic property of Möbius transformations except in the Euclidean case.
Paper's Title:
Some Open Problems in Analysis
Author(s):
A.G. Ramm
Mathematics Department, Kansas State University,
Manhattan, KS 66506-2602,
USA
ramm@math.ksu.edu
URL: http://www.math.ksu.edu/~ramm
Abstract:
In this paper some open problems in analysis are formulated. These problems were formulated and discussed by the author at ICMAA6.
Paper's Title:
Nontrivial Solutions of Singular Superlinear Three-point
Boundary Value Problems at Resonance
Author(s):
Feng Wang, Fang Zhang
School of Mathematics and Physics,
Changzou University,
Changzhou, 213164,
China.
fengwang188@163.com
Abstract:
The singular superlinear second order three-point boundary value problems at resonance
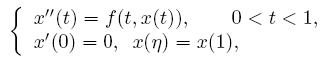
are considered under some conditions concerning the first eigenvalues corresponding to the relevant linear operators, where n ∈ (0,1) is a constant, f is allowed to be singular at both t=0 and t=1. The existence results of nontrivial solutions are given by means of the topological degree theory.
Paper's Title:
Sharp Lp Improving Results for Singular Measures on Cn+1
Author(s):
E. Ferreyra, M. Urciuolo
FaMAF-CIEM,
Universidad Nacional de Córdoba-Conicet,
Ciudad Universitaria, 5000 Córdoba,
Argentina
eferrey@famaf.unc.edu.ar
urciuolo@famaf.unc.edu.ar
Abstract:
For j=1,...,n, let Ωj be open sets of the complex plane and let φj be holomorphic functions on Ωj such that φj'' does not vanish identically on Ωj. We consider φ(z1,...,zn) =φ1(z1) +...+φn(zn). We characterize the pairs (p,q) such that the convolution operator with the surface measure supported on a compact subset of the graph of φ is p-q bounded.
Paper's Title:
Solving Fractional Transport Equation via Walsh Function
Author(s):
A. Kadem
L. M. F. N., Mathematics Department,
University of Setif,
Algeria
abdelouahak@yahoo.fr
Abstract:
In this paper we give a complete proof of A method for the solution of fractional transport equation in three-dimensional case by using Walsh function is presented. The main characteristic of this technique is that it reduces these problems to those of solving a system of algebraic equations, thus greatly simplifying the problem.
Paper's Title:
A Note on Mixed Norm Spaces of Analytic Functions
Author(s):
K. Avetisyan
Faculty of Physics, Yerevan State
University,
Alex Manoogian st. 1, Yerevan, 375025,
Armenia
avetkaren@ysu.am
Abstract:
A direct and elementary proof of an estimate of Littlewood is given together with an application concerning the sharpness and strictness of some inclusions in mixed norm spaces of analytic functions.
Paper's Title:
New Stochastic Calculus
Author(s):
Moawia Alghalith
Department of Economics,
University of the West Indies, St. Augustine,
Trinidad and Tobago.
E-mail:
malghalith@gmail.com
Abstract:
We present new stochastic differential equations, that are more general and simpler than the existing Ito-based stochastic differential equations. As an example, we apply our approach to the investment (portfolio) model.
Paper's Title:
Commutators of Hardy Type Operators
Author(s):
Chunping Xie
Department of Mathematics,
Milwaukee School of Engineering,
1025 N. Broadway,
Milwaukee, Wisconsin 53202,
USA.
E-mail:
xie@msoe.edu
URL:
http://www.msoe.edu/people/chunping.xie
Abstract:
The note deals with commutaors of the Hardy operator, Hardy type operators on Morrey spaces on R+. We have proved that the commutators generated by Hardy operator and Hardy type operators with a BMO function b are bounded on the Morrey spaces.
Paper's Title:
Bilinear Regular Operators on Quasi-Normed Functional Spaces
Author(s):
D. L. Fernandez and E. B. Silva
Universidade Estadual de Campinas -
Unicamp
Instituto de Matematica
Campinas - SP
Brazil.
E-mail: dicesar@ime.unicamp.br
Universidade Estadual de Maringa--UEM
Departamento de Matematica
Av.~Colombo 5790
Maringa - PR
Brazil.
E-mail: ebsilva@uem.br
Abstract:
Positive and regular bilinear operators on quasi-normed functional spaces are introduced and theorems characterizing compactness of these operators are proved. Relations between bilinear operators and their adjoints in normed functional spaces are also studied.
Paper's Title:
Applications of the Structure Theorem of (w1,w2)-Tempered
Ultradistributions
Author(s):
Hamed M. Obiedat and Lloyd E. Moyo
Department of Mathematics,
Hashemite University,
P.O.Box 150459, Zarqa13115,
Jordan.
E-mail: hobiedat@hu.edu.j
Department of Mathematics, Computer
Science & Statistics,
Henderson State University,
1100 Henderson Street, Arkadelphia, AR 71999,
USA.
E-mail: moyol@hsu.edu
Abstract:
Using a previously obtained structure theorem for (w1, w2)-tempered ultradistributions, we prove that these ultradistributions can be represented as initial values of solutions of the heat equation.
Paper's Title:
MSplit Equality for Monotone Inclusion Problem and Fixed Point Problem in
Real Banach Spaces
Author(s):
1,2Christian Chibueze Okeke, 3Abdumalik Usman Bello, 1Chinedu Izuchukwu, and 1Oluwatosin Temitope Mewomo
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: okekec@ukzn.ac.za
E-mail: izuchukwuc@ukzn.ac.za
E-mail: mewomoo@ukzn.ac.za
2DST-NRF
Center of Excellence in Mathematical and Statistical Sciences (CoE-Mass)
Johannesburg,
South Africa.
3Federal
University,
Dutsin-Ma, Katsina State,
Nigeria.
E-mail:
uabdulmalik@fudutsinma.edu.ng
Abstract:
In this paper a new iterative algorithm for approximating a common solution of split equality monotone inclusion problem and split equality fixed point problem is introduced. Using our algorithm, we state and prove a strong convergence theorem for approximating an element in the intersection of the set of solutions of a split equality monotone inclusion problem and the set of solutions of a split equality fixed point problem for right Bregman strongly nonexpansive mappings in the setting of p-uniformly convex Banach spaces which are also uniformly smooth. We also give some applications.
Paper's Title:
New Exact Taylor's Expansions without the Remainder: Application to Finance
Author(s):
Moawia Alghalith
Economics Dept.,
University of the West Indies,
St Augustine,
Trinidad and Tobago.
E-mail: malghalith@gmail.com
Abstract:
We present new exact Taylor's expansions with fixed coefficients and without the remainder. We apply the method to the portfolio model.
Corrigendum.
A corrigendum for this article has been published. To view the corrigendum,
please click
here.
Paper's Title:
Polynomial Dichotomy of C0-Quasi Semigroups in Banach Spaces
Author(s):
Sutrima1,2, Christiana Rini Indrati2, Lina Aryati2
1Department of Mathematics,
Universitas Sebelas Maret,
PO Box 57126, Surakarta,
Indonesia.
E-mail: sutrima@mipa.uns.ac.id
2Department of Mathematics,
Universitas Gadjah Mada,
PO Box 55281, Yogyakarta,
Indonesia.
E-mail: rinii@ugm.ac.id,
lina@ugm.ac.id
Abstract:
Stability of solutions of the problems is an important aspect for application purposes. Since its introduction by Datko [7], the concept of exponential stability has been developed in various types of stability by various approaches. The existing conditions use evolution operator, evolution semigroup, and quasi semigroup approach for the non-autonomous problems and a semigroup approach for the autonomous cases. However, the polynomial stability based on C0-quasi semigroups has not been discussed in the references. In this paper we propose a new stability for C0-quasi semigroups on Banach spaces i.e the polynomial stability and polynomial dichotomy. As the results, the sufficient and necessary conditions for the polynomial and uniform polynomial stability are established as well as the sufficiency for the polynomial dichotomy. The results are also confirmed by the examples.
Paper's Title:
A Generalization of Ostrowski's Inequality for Functions of Bounded
Variation via a Parameter
Author(s):
Seth Kermausuor
Department of Mathematics and Computer
Science,
Alabama State University,
Montgomery, AL 36101,
USA.
E-mail:
skermausour@alasu.edu
Abstract:
In this paper, we provide a generalization of the Ostrowski's inequality for functions of bounded variation for k points via a parameter λ∈[0,1]. As a by product, we consider some particular cases to obtained some interesting inequalities in these directions. Our results generalizes some of the results by Dragomir in [S. S. DRAGOMIR, The Ostrowski inequality for mappings of bounded variation, Bull. Austral. Math. Soc., 60 (1999), pp. 495--508.]
Paper's Title:
The Jacobson Density Theorem for Non-Commutative Ordered Banach
Algebras
Author(s):
Kelvin Muzundu
University of Zambia,
Deparment of Mathematics and Statistics,
P.O. Box 32379, Lusaka,
Zambia.
E-mail: kmzundu@gmail.com
Abstract:
The Jacobson density theorem for general non-commutative Banach algebras states as follows: Let π be a continuous, irreducible representation of a non-commutative Banach algebra A on a Banach space X. If x1,x2,...,xn are linearly independent in X and if y1,y2,...,yn are in X, then there exists an a∈ A such that π(a)xi=yi for i=1,2,...,n. By considering ordered Banach algebras A and ordered Banach spaces X, we shall establish an order-theoretic version of the Jacobson density theorem.
Paper's Title:
Simplicial (co)-homology of Band Semigroup
Author(s):
Yasser Farhat
Academic Support Department,
Abu Dhabi Polytechnic,
P.O. Box 111499, Abu Dhabi,
UAE.
E-mail: yasser.farhat@adpoly.ac.ae, farhat.yasser.1@gmail.com
Abstract:
We consider the Banach algebra l1(S), with convolution, where S is a band semigroup. We prove directly, without using the cyclic cohomology, that the simplicial cohomology groups Hn(l1(S), l1(S)*) vanish for all n≥1. This proceeds in three steps. In each step, we introduce a bounded linear map. By iteration in each step, we achieve our goal.
Paper's Title:
Operators On Frames
Author(s):
Javad Baradaran and Zahra Ghorbani
Department of Mathematics,
Jahrom University, P.B. 7413188941,
Jahrom,
Iran.
E-mail:
baradaran@jahromu.ac.ir
Department of Mathematics,
Jahrom University, P.B. 7413188941,
Jahrom,
Iran.
E-mail: ghorbani@jahromu.ac.ir
Abstract:
In this paper, we first show the conditions under which an operator on a Hilbert space H can be represented as sum of two unitary operators. Then, it is concluded that a Riesz basis for a Hilbert space H can be written as a sum of two orthonormal bases. Finally, the study proves that if A is a normal maximal partial isometry on a Hilbert space H and if {ek}∞k=1 is an orthonormal basis for H, then {Aek}∞k=1 is a 1-tight frame for H.
Paper's Title:
Double Difference of Composition Operator on Bloch Spaces
Author(s):
Rinchen Tundup
Department of Mathematics
University of Jammu
Jammu and Kashmir
India.
E-mail: joneytun123@gmail.com
Abstract:
In this paper we characterize the compactness of double difference of three non-compact composition operators on Bloch space induced by three holomorphic self maps on the unit disc.
Paper's Title:
Riemann-Stieltjes Integrals and Some Ostrowski Type Inequalities
Author(s):
W. G. Alshanti
Department of General Studies,
Jubail University College,
KSA.
E-mail: shantiw@ucj.edu.sa
Abstract:
In this article, we investigate new integral inequalities of Ostrowski's type of various functional aspects. For mapping's second derivative, we assume two cases, namely, L1 and L∞ spaces. Moreover, for first derivative, we investigate two different characteristics, namely, bounded variation and locally Lipchitz continuity. Applications to special means and composite quadrature rules are also carried out.
Paper's Title:
Numerical Solution of Certain Types of Fredholm-Volterra Integro-Fractional Differential Equations via Bernstein Polynomials
Author(s):
Alias B. Khalaf1, Azhaar H. Sallo2 and Shazad S. Ahmed3
1Department
of Mathematics, College of Science,
University of Duhok,
Kurdistan Region,
Iraq.
E-mail: aliasbkhalaf@uod.ac
2Department
of Mathematics, College of Science,
University of Duhok,
Kurdistan Region,
Iraq.
E-mail: azhaarsallo@uod.ac
3Department
of Mathematics, College of Science,
University of Sulaimani,
Kurdistan Region,
Iraq.
E-mail: shazad.ahmed@univsul.edu
Abstract:
In this article we obtain a numerical solution for a certain fractional order integro-differential equations of Fredholm-Volterra type, where the fractional derivative is defined in Caputo sense. The properties of Bernstein polynomials are applied in order to convert the fractional order integro-differential equations to the solution of algebraic equations. Some numerical examples are investigated to illustrate the method. Moreover, the results obtained by this method are compared with the exact solution and with the results of some existing methods as well.
Paper's Title:
SQIRV Model for Omicron Variant with Time Delay
Author(s):
S. Dickson, S. Padmasekaran, G. E. Chatzarakis and S. L. Panetsos
Mathematics, Periyar University, Periyar
Palkalai Nagar, Salem,
636011, Tamilnadu,
India.
E-mail:
dickson@periyaruniversity.ac.in,
padmasekarans@periyaruniversity.ac.in
Electrical and Electronic Engineering
Educators, School of
Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
spanetsos@aspete.gr
Abstract:
In order to examine the dynamics of the Omicron variant, this paper uses mathematical modelling and analysis of a SQIRV model, taking into account the delay in the conversion of susceptible individuals into infected individuals and infected individuals into recovered individuals. The pandemic was eventually controlled as a result of the massive delays. To assure the safety of the host population, this concept incorporates quarantine and the COVID-19 vaccine. Both local and global stability of the model are examined. It is found that the fundamental reproduction number affects both local and global stability conditions. Our findings show that asymptomatic cases caused by an affected population play an important role in increasing Omicron infection in the general population. The most recent data on the pandemic Omicron variant from Tamil Nadu, India, is verified.
Paper's Title:
Linear System of Singularly Perturbed Initial Value Problems with Robin Initial Conditions
Author(s):
S. Dinesh, G. E. Chatzarakis, S. L. Panetsos and S. Sivamani
Department of Mathematics,
Saranathan College of Engineering,
Tiruchirappalli-620012,
Tamil Nadu,
India.
Department of Electrical and Electronic
Engineering Educators,
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail:
geaxatz@otenet.gr,
dineshselvaraj24@gmail.com,
spanetsos@aspete.gr,
winmayi2012@gmail.com
Abstract:
On the interval (0,1], this paper considers an initial value problem for a system of n singularly perturbed differential equations with Robin initial conditions. On a piecewise uniform Shishkin mesh, a computational approach based on a classical finite difference scheme is proposed. This approach is shown to be first-order convergent in the maximum norm uniformly in the perturbation parameters. The theory is illustrated by a numerical example.
Paper's Title:
Using Direct and Fixed Point Technique of Cubic Functional Equation and its Hyers-Ulam Stability
Author(s):
Ramanuja Rao Kotti, Rajnesh Krishnan Mudaliar, Kaushal Neelam Devi, Shailendra Vikash Narayan
Fiji National University,
Department of Mathematics & Statistics,
P.O. Box 5529, Lautoka,
Fiji.
E-mail: ramanuja.kotti@fnu.ac.fj
URL: https://www.fnu.ac.fj
Abstract:
In this present work, we introduce a new type of finite dimensional cubic functional equation of the form
where Φ≥4 is an integer, and derive its general solution. The main purpose of this work is to investigate the Hyers-Ulam stability results for the above mentioned functional equation in Fuzzy Banach spaces by means of direct and fixed point methods.
Paper's Title:
A New Iterative Approximation of a Split Fixed Point Constraint Equilibrium Problem
Author(s):
Musa Adewale Olona1, Adhir Maharaj2 and Ojen Kumar Narain3
1School
of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 219095783@stu.ukzn.ac.za
2Department
of Mathematics,
Durban University of Technology, Durban,
South Africa.
E-mail: adhirm@dut.ac.za
3School
of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
The purpose of this paper is to introduce an iterative algorithm for approximating an element in the solution set of the common split feasibility problem for fixed points of demimetric mappings and equilibrium problem for monotone mapping in real Hilbert spaces. Motivated by self-adaptive step size method, we incorporate the inertial technique to accelerate the convergence of the proposed method and establish a strong convergence of the sequence generated by the proposed algorithm. Finally, we present a numerical example to illustrate the significant performance of our method. Our results extend and improve some existing results in the literature.
Paper's Title:
Fixed Point Theorems for a Finite Family of Asymptotically Nonexpansive Mappings
Author(s):
E. Prempeh
Department of Mathematics,
Kwame Nkrumah University of Science and Technology,
Kumasi, Ghana
edward_prempeh2000@yahoo.com
Abstract:
Let
be a real reflexive Banach space with a uniformly Gâteaux differentiable norm,
be a nonempty bounded closed convex subset of
i=1,2,...,r be a finite family of asymptotically nonexpansive mappings
such that for each
Let
be a nonempty set of common fixed points of
and define
. Let
be fixed and let
be such that
as
. We can prove that the sequence
satisfying the relation
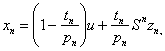
associated with
, converges strongly to a fixed point of
provided
possesses uniform normal structure. Furthermore we prove that the iterative process:
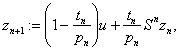
, converges strongly to a fixed point of
Paper's Title:
Positive Solutions of Evolution Operator Equations
Author(s):
Radu Precup
Department of Applied Mathematics,
Babes-Bolyai University,
Cluj, Romania
Abstract:
Existence and localization results are derived from Krasnoselskii’s compressionexpansion
fixed point theorem in cones, for operator equations in spaces of continuous functions
from a compact real interval to an abstract space. The main idea, first used in [12], is to handle
two equivalent operator forms of the equation, one of fixed point type giving the operator to
which Krasnoselskii’s theorem applies and an other one of coincidence type which is used to
localize a positive solution in a shell. An application is presented for a boundary value problem
associated to a fourth order partial differential equation on a rectangular domain.
Paper's Title:
Some Approximation for the linear combinations of modified Beta operators
Author(s):
Naokant Deo
Department of Applied Mathematics
Delhi College of Engineering
Bawana Road, Delhi - 110042,
India.
dr_naokant_deo@yahoo.com
Abstract:
In this paper, we propose a sequence of new positive linear operators βn to study the ordinary approximation of unbounded functions by using some properties of the Steklov means.
Paper's Title:
Weyl Transform Associated With Bessel and Laguerre Functions
Author(s):
E. Jebbari and M . Sifi
Department of Mathematics Faculty of Sciences of Tunis,
1060 Tunis,
Tunisia.
mohamed.sifi@fst.rnu.tn
Abstract:
We define and study the Wigner transform associated to Bessel and Laguerre transform and we prove an inversion formula for this transform. Next we consider a class of symbols which allows to define the Bessel-Laguerre Weyl transform. We establish a relation between the Wigner and Weyl transform. At last, we discuss criterion in term of symbols for the boundedness and compactness of the Bessel-Laguerre Weyl transform.
Paper's Title:
Comparison Results for Solutions of Time Scale Matrix Riccati
Equations and Inequalities
Author(s):
R. Hilscher
Department of Mathematical Analysis, Faculty of Science,
Masaryk University, Janáčkovo nám. 2a,
CZ-60200, Brno, Czech Republic.
hilscher@math.muni.cz
URL: http://www.math.muni.cz/~hilscher/
Abstract:
In this paper we derive comparison results for Hermitian solutions of time scale matrix Riccati
equations and Riccati inequalities. Such solutions arise from special conjoined bases
(X,U) of the corresponding time scale symplectic system via the Riccati quotient
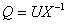. We also discuss properties of a unitary matrix solution 
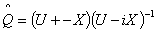of a certain
associated Riccati equation.
Paper's Title:
A Strengthened Hardy-Hilbert's Type Inequality
Author(s):
Weihong Wang and Bicheng Yang
Department of Mathematics, Guangdong Education Institute,
Guangzhou, Guangdong 520303,
People's Republic Of China
wwh@gdei.edu.cn
bcyang@pub.guangzhou.gd.cn
URL: http://www1.gdei.edu.cn/yangbicheng/index.html
Abstract:
By using the improved Euler-Maclaurin's summation formula and
estimating the weight coefficient, we give a new strengthened
version of the more accurate Hardy-Hilbert's type inequality. As
applications, a strengthened version of the equivalent form is
considered.
Paper's Title:
On the Generalized Inverse 
over Integral Domains
Author(s):
Yaoming Yu and Guorong Wang
College of Education, Shanghai Normal University
Shanghai 200234
People's Republic of China.
yuyaoming@online.sh.cn
grwang@shnu.edu.cn
Abstract:
In this paper, we study further the generalized inverse
of a matrix A over an integral domain. We give
firstly some necessary and sufficient conditions for the existence
of the generalized inverse , an explicit expression
for the elements of the generalized inverse and an
explicit expression for the generalized inverse ,
which reduces to the {1} inverse. Secondly, we verify that the
group inverse, the Drazin inverse, the Moore-Penrose inverse and the
weighted Moore-Penrose inverse are identical with the generalized
inverse 
for an appropriate matrix G,
respectively, and then we unify the conditions for the existence and
the expression for the elements of the weighted Moore-Penrose
inverse, the Moore-Penrose inverse, the Drazin inverse and the group
inverse over an integral domain. Thirdly, as a simple application,
we give the relation between some rank equation and the existence of
the generalized inverse , and a method to compute the
generalized inverse . Finally, we give an example of
evaluating the elements of without calculating
.
Paper's Title:
The Iterated Variational Method for the Eigenelements of a Class of Two-Point Boundary Value Problems
Author(s):
Muhammed I. Syam and Qasem M. Al-Mdallal
Department of Mathematical Sciences, College of Science, UAE University,
P. O. Box 17551, Al-Ain,
United Arab Emirates
Q.Almdallal@uaeu.ac.ae
M.Syam@uaeu.ac.ae
Abstract:
The iterated variational method is considered in the approximation
of eigenvalues and eigenfunctions for a class of two point boundary
value problems. The implementation of this method is easy and
competes well with other methods. Numerical examples are presented
to show the efficiency of the method proposed. Comparison with the
work of others is also illustrated.
Paper's Title:
On Interaction of Discontinuous Waves in a Gas with Dust Particles
Author(s):
J. Jena
Department of Mathematics, Netaji Subhas institute of technology,
Sector-3, Dwarka, New Delhi - 110 075,
India.
jjena67@rediffmail.com
jjena@nsit.ac.in
Abstract:
In this paper, the interaction of the strong shock with the weak discontinuity has been investigated for the system of partial differential equations describing one dimensional unsteady plane flow of an inviscid gas with large number of dust particles. The amplitudes of the reflected and transmitted waves after interaction of the weak discontinuity through a strong shock are evaluated by exploiting the results of general theory of wave interaction.
Paper's Title:
Ergodic Solenoidal Homology II:
Density of Ergodic Solenoids
Author(s):
Vicente Muńoz and Ricardo Pérez Marco
Instituto de Ciencias Matem
áticas CSIC-UAM-UC3M-UCM,Abstract:
A measured solenoid is a laminated space endowed with a tranversal measure invariant by holonomy. A measured solenoid immersed in a smooth manifold produces a closed current (known as a generalized Ruelle-Sullivan current). Uniquely ergodic solenoids are those for which there is a unique (up to scalars) transversal measure. It is known that for any smooth manifold, any real homology class is represented by a uniquely ergodic solenoid. In this paper, we prove that the currents associated to uniquely ergodic solenoids are dense in the space of closed currents, therefore proving the abundance of such objects.
Paper's Title:
An Improved Mesh Independence Principle for Solving Equations and their Discretizations using Newton's Method
Author(s):
Ioannis K. Argyros
Cameron university,
Department of Mathematics Sciences,
Lawton, OK 73505,
USA
iargyros@cameron.edu
Abstract:
We improve the mesh independence principle [1] which states that when Newton's method is applied to an equation on a Banach space as well as to their finite--dimensional discretization there is a difference of at most one between the number of steps required by the two processes to converge to within a given error tolerance. Here using a combination of Lipschitz and center Lipschitz continuity assumptions instead of just Lipschitz conditions we show that the minimum number of steps required can be at least as small as in earlier works. Some numerical examples are provided whereas our results compare favorably with earlier ones.
Paper's Title:
A Study of the Effect of Density Dependence in a Matrix Population Model
Author(s):
N. Carter and M. Predescu
Department of Mathematical Sciences,
Bentley University,
Waltham, MA 02452,
U.S.A.
ncarter@bentley.edu
mpredescu@bentley.edu
Abstract:
We study the behavior of solutions of a three dimensional discrete time nonlinear matrix population model. We prove results concerning the existence of equilibrium points, boundedness, permanence of solutions, and global stability in special cases of interest. Moreover, numerical simulations are used to compare the dynamics of two main forms of the density dependence function (rational and exponential).
Paper's Title:
Approximation of Derivatives in a Singularly Perturbed Second Order Ordinary Differential Equation with Discontinuous Terms Arising in Chemical Reactor Theory
Author(s):
R. Mythili Priyadharshini and N. Ramanujam
Department of Mathematics, Bharathidasan University,
Tiruchirappalli - 620 024, Tamilnadu, India.
matram2k3@yahoo.com
URL:
http://www.bdu.ac.in/depa/science/ramanujam.htm
Abstract:
In this paper, a singularly perturbed second order ordinary differential equation with a discontinuous convection coefficient arising in chemical reactor theory is considered. A robust-layer-resolving numerical method is suggested. An ε-uniform global error estimate for the numerical solution and also to the numerical derivative are established. Numerical results are provided to illustrate the theoretical results.
Paper's Title:
Trapping of Water Waves By Underwater Ridges
Author(s):
1A. M. Marin, 1R. D. Ortiz and 2J. A. Rodriguez-Ceballos.
1Facultad de Ciencias Exactas y Naturales
Universidad de Cartagena
Sede Piedra de Bolivar, Avenida del Consulado
Cartagena de Indias, Bolivar,
Colombia.
2Instituto Tecnológico de
Morelia Facultad de Ciencias Fisico Matematicas
Universidad Michoacana
Tecnológico
1500, Col. Lomas de Santiaguito Edificio Be ,
Ciudad Universitaria,
58120 Morelia, Michoacan,
Mexico.
amarinr@unicartagena.edu.co,
ortizo@unicartagena.edu.co.
URL: www.unicartagena.edu.co.
Abstract:
As is well-known, underwater ridges and
submerged horizontal cylinders can serve as waveguides for surface water waves.
For large values of the wavenumber in the direction of the ridge, there is only
one trapped wave (this was proved in Bonnet & Joly (1993, SIAM J. Appl. Math.
53, pp 1507-1550)).
We construct the asymptotics of these trapped waves and their frequencies at
high frequency by means of reducing the initial problem to a pair of boundary
integral equations and then by applying the method of Zhevandrov & Merzon (2003,
AMS Transl. (2) 208, pp 235-284), in order to solve
them.
Paper's Title:
Uniform Convergence of Schwarz Method for Noncoercive Variational Inequalities Simple Proof
Author(s):
M. Haiour and E. Hadidi.
Department of mathematics, LANOS Laboratory,
Faculty of the Sciences, University Badji Mokhtar,
P.O 23000 Annaba,
Algeria.
haiourm@yahoo.fr,
ehadidi71@yahoo.fr
Abstract:
In this paper we study noncoercive variational inequalities, using the Schwarz method. The main idea of this method consists in decomposing the domain in two subdomains. We give a simple proof for the main result concerning L∞ error estimates, using the Zhou geometrical convergence and the L∞ approximation given for finite element methods by Courty-Dumont.
Paper's Title:
Necessary and Sufficient Conditions for Cyclic Homogeneous Polynomial Inequalities of Degree Four in Real Variables
Author(s):
Vasile Cirtoaje and Yuanzhe Zhou
Department of Automatic Control and Computers
University of Ploiesti
Romania.
vcirtoaje@upg-ploiesti.ro.
High School Affiliated to Wuhan University, China
Abstract:
In this paper, we give two sets of necessary and sufficient conditions that the inequality f4(x,y,z) ≥ 0 holds for any real numbers x,y,z, where f4(x,y,z) is a cyclic homogeneous polynomial of degree four. In addition, all equality cases of this inequality are analysed. For the particular case in which f4(1,1,1)=0, we get the main result in [3]. Several applications are given to show the effectiveness of the proposed methods.
Paper's Title:
On an Autocorrection Phenomenon of the Eckhoff Interpolation
Author(s):
A. Poghosyan
Institute of Mathematics, National Academy
of Sciences,
24b Marshal Baghramian ave., Yerevan 0019,
Republic of Armenia
arnak@instmath.sci.am
Abstract:
The paper considers the Krylov-Lanczos and the Eckhoff interpolations of a function with a discontinuity at a known point. These interpolations are based on certain corrections associated with jumps in the first derivatives. In the Eckhoff interpolation, approximation of the exact jumps is accomplished by the solution of a system of linear equations. We show that in the regions where the 2-periodic extension of the interpolated function is smooth, the Eckhoff interpolation converges faster compared with the Krylov-Lanczos interpolation. This accelerated convergence is known as the autocorrection phenomenon. The paper presents a theoretical explanation of this phenomenon. Numerical experiments confirm theoretical estimates.
Paper's Title:
Szegö Limits and Haar Wavelet Basis
Author(s):
M. N. N. Namboodiri and S. Remadevi
Dept. of Mathematics, Cochin University
of Science and Technology,
Cochin-21, Kerala,
India.
Dept. of Mathematics, College of
Engineering,
Cherthala, Kerala,
India.
Abstract:
This paper deals with Szegö type limits for multiplication operators on L2 (R) with respect to Haar orthonormal basis. Similar studies have been carried out by Morrison for multiplication operators Tf using Walsh System and Legendre polynomials [14]. Unlike the Walsh and Fourier basis functions, the Haar basis functions are local in nature. It is observed that Szegö type limit exist for a class of multiplication operators Tf , f∈ L∞ (R) with respect to Haar (wavelet) system with appropriate ordering. More general classes of orderings of Haar system are identified for which the Szegö type limit exist for certain classes of multiplication operators. Some illustrative examples are also provided.
Paper's Title:
A One-Line Derivation of the Euler and Ostrogradski Equations
Author(s):
Olivier de La Grandville
Stanford University,
Department of Management Science and Engineering,
Stanford, CA 94305,
U. S. A
Abstract:
At the very heart of major results of classical physics, the Euler and Ostrogradski equations have apparently no intuitive interpretation. In this paper we show that this is not so. Relying on Euler's initial geometric approach, we show that they can be obtained through a direct reasoning that does not imply any calculation. The intuitive approach we suggest offers two benefits: it gives immediate significance to these fundamental second-order non-linear differential equations; and second, it allows to obtain a property of the calculus of variations that does not seem to have been uncovered until now: the Euler and Ostrogradski equations can be derived not necessarily by giving a variation to the optimal function -- as is always done; one could equally well start by giving a variation to their derivative(s).
Paper's Title:
On Convergence Theorems of an Implicit Iterative Process with Errors for a
Finite Family of Asymptotically quasi I-nonexpansive Mappings
Author(s):
Farrukh Mukhamedov and Mansoor Saburov
Department of Computational & Theoretical
Sciences,
Faculty of Sciences, International Islamic University Malaysia,
P.O. Box, 141, 25710, Kuantan,
Malaysia
Abstract:
In this paper we prove the weak and strong convergence of the implicit iterative process with errors to a common fixed point of a finite family {Tj}Ni=1 of asymptotically quasi Ij-nonexpansive mappings as well as a family of {Ij}Nj=1 of asymptotically quasi nonexpansive mappings in the framework of Banach spaces. The obtained results improve and generalize the corresponding results in the existing literature.
Paper's Title:
An Improvement of the Hermite-Hadamard Inequality for Functions Convex on the Coordinates
Author(s):
Milica Klaričić Bakula
Faculty of Science,
University of Split,
Teslina 12, 21000 Split.
Croatia
E-mail: milica@pmfst.hr
Abstract:
An improvement of the Hermite-Hadamard inequality for functions convex on the coordinates is given.
Paper's Title:
On A Conjecture of A Logarithmically Completely Monotonic Function
Author(s):
Valmir Krasniqi, Armend Sh. Shabani
Department of Mathematics,
University of Prishtina,
Republic of Kosova
E-mail:
vali.99@hotmail.com
armend_shabani@hotmail.com
Abstract:
In this short note we prove a conjecture, related to a logarithmically completely monotonic function, presented in [5]. Then, we extend by proving a more generalized theorem. At the end we pose an open problem on a logarithmically completely monotonic function involving q-Digamma function.
Paper's Title:
End-Point and Transversality Conditions in the Calculus of Variations: Derivations through Direct Reasoning
Author(s):
Olivier de La Grandville
Stanford University,
Department of Management Science and Engineering,
475 Via Ortega, Stanford, CA 94305,
U. S. A.
E-mail: ola@stanford.edu
Abstract:
We offer an intuitive explanation of the end-point and transversality conditions that complement the Euler equation in the calculus of variations. Our reasoning is based upon the fact that any variation given to an optimal function must entail a zero net gain to the functional, all consequences of implied changes in its derivative being fully taken into account.
Paper's Title:
Ap Functions and Maximal Operator
Author(s):
Chunping Xie
Department of Mathematics,
Milwaukee School of Engineering,
1025 N. Broadway,
Milwaukee, Wisconsin 53202,
U. S. A.
E-mail: xie@msoe.edu
URL: http://www.msoe.edu/people/chunping.xie
Abstract:
The relationship between Ap functions and Hardy-Littlewood maximal operator on Lp,λ(w), the weighted Morrey space, has been studied. Also the extropolation theorem of Lp,λ(w) has been considered.
Paper's Title:
Stability of an Almost Surjective epsilon-Isometry in The Dual of Real Banach Spaces
Author(s):
Minanur Rohman, Ratno Bagus Edy Wibowo, Marjono
Department of Mathematics, Faculty of
Mathematics and Natural Sciences,
Brawijaya University,
Jl. Veteran Malang 65145,
Indonesia.
E-mail:
miminanira@gmail.com
Department of Mathematics, Faculty of
Mathematics and Natural Sciences,
Brawijaya University,
Jl. Veteran Malang 65145,
Indonesia.
E-mail:
rbagus@ub.ac.id
Department of Mathematics, Faculty of
Mathematics and Natural Sciences,
Brawijaya University,
Jl. Veteran Malang 65145,
Indonesia.
E-mail:
marjono@ub.ac.id
Abstract:
In this paper, we study the stability of epsilon-isometry in the dual of real Banach spaces. We prove that the almost surjective epsilon-isometry mapping is stable in dual of each spaces. The proof uses Gâteaux differentiability space (GDS), weak-star exposed points, norm-attaining operator, and some studies about epsilon-isometry that have been done before.
Paper's Title:
Lower and Upper Bounds for the Point-Wise Directional Derivative of the Fenchel Duality Map
Author(s):
M. Raissouli1,2, M. Ramezani3
1Department
of Mathematics,
Science Faculty, Taibah University,
P.O. Box 30097, Zip Code 41477, Al Madinah Al Munawwarah,
Saudi Arabia.
2Department
of Mathematics,
Science Faculty, Moulay Ismail University, Meknes,
Morocco.
E-mail:
raissouli.mustapha@gmail.com
3Department
of Mathematics,
University of Bojnord, Bojnord,
Iran.
E-mail: m.ramezani@ub.ac.ir
Abstract:
In this paper, we introduce the point-wise directional derivative of the Fenchel duality map and we study its properties. The best lower and upper bounds of this point-wise directional derivative are also given. We explain how our functional results contain those related to the positive bounded linear operators.
Paper's Title:
Some New Inequalities of Hermite-Hadamard and Fejér Type for Certain Functions with Higher Convexity
Author(s):
Steven G. From
Department of Mathematics,
University of Nebraska at Omaha,
Omaha, Nebraska 68182-0243,
U.S.A.
E-mail: sfrom@unomaha.edu
Abstract:
In this paper, we present some new inequalities of Hermite-Hadamard or Fejér
type for certain functions satisfying some higher convexity conditions on one or
more derivatives.
An open problem is given also.
Some applications to the logarithmic mean are given.
Paper's Title:
Extreme Curvature of Polynomials and Level Sets
Author(s):
Stephanie P. Edwards, arah J. Jensen, Edward Niedermeyer, and Lindsay Willett
Department of Mathematics,
Hope College,
Holland, MI 49423,
U.S.A.
E-mail: sedwards@hope.edu
E-mail: tarahjaye@gmail.com
E-mail: eddie.niedermeyer@gmail.com
E-mail: willettlm1@gmail.com
WWW: http://math.hope.edu/sedwards/
Abstract:
Let f be a real polynomial of degree n. Determining the maximum number of zeros of kappa, the curvature of f, is an easy problem: since the zeros of kappa are the zeros of f'', the curvature of f is 0 at most n-2 times. A much more intriguing problem is to determine the maximum number of relative extreme values for the function kappa. Since kappa'=0 at each extreme point of kappa, we are interested in the maximum number of zeros of kappa'. In 2004, the first author and R. Gordon showed that if all the zeros of f'' are real, then f has at most n-1 points of extreme curvature. We use level curves and auxiliary functions to study the zeros of the derivatives of these functions. We provide a partial solution to this problem, showing that f has at most n-1 points of extreme curvature, given certain geometrical conditions. The conjecture that f has at most n-1 points of extreme curvature remains open.
Paper's Title:
Wavelet Frames in Higher Dimensional Sobolev Spaces
Author(s):
Raj Kumar, Manish Chauhan, and Reena
Department of Mathematics,
Kirori Mal College, University of Delhi,
New Delhi-110007,
India.
E-mail: rajkmc@gmail.com
Department of Mathematics,
University of Delhi,
New Delhi-110007,
India
E-mail: manish17102021@gmail.com
Department of Mathematics,
Hans Raj College, University of Delhi,
New Delhi-110007,
India
E-mail: reena.bhagwat29@gmail.com
Abstract:
In this paper, we present sufficient condition for the sequence
of vectors
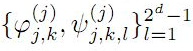to be a frame for Hs(Rd) are derived. Necessary and
sufficient conditions for the sequence of vectors
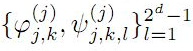to be tight wavelet frames in Hs(Rd) are obtained.
Further, as an application an example of tight wavelet frames for Hs(R2) as bivariate box spline over 3-direction are given.
Paper's Title:
Cubic Alternating Harmonic Number Sums
Author(s):
Anthony Sofo
Victoria University,
College of Engineering and Science,
Melbourne City,
Australia.
E-mail:
Anthony.Sofo@vu.edu.au
Abstract:
We develop new closed form representations of sums of cubic alternating harmonic numbers and reciprocal binomial coefficients. We also identify a new integral representation for the ζ (4) constant.
Paper's Title:
Numerical Approximation by the Method of Lines with Finite-volume Approach of a Solute Transport Equation in Periodic Heterogeneous Porous Medium
Author(s):
D. J. Bambi Pemba and B. Ondami
Université Marien Ngouabi,
Factuté des Sciences et Techniques,
BP 69, Brazzaville,
Congo.
E-mail: bondami@gmail.com
Abstract:
In this paper we are interested in the numerical approximation of a two-dimensional solute transport equation in heterogeneous porous media having periodic structures. It is a class of problems which has been the subject of various works in the literature, where different methods are proposed for the determination of the so-called homogenized problem. We are interested in this paper, in the direct resolution of the problem, and we use the method of lines with a finite volume approach to discretize this equation. This discretization leads to an ordinary differential equation (ODE) that we discretize by the Euler implicit scheme. Numerical experiments comparing the obtained solution and the homogenized problem solution are presented. They show that the precision and robustness of this method depend on the ratio between, the mesh size and the parameter involved in the periodic homogenization.
Paper's Title:
Existence and Approximation of Traveling Wavefronts for the Diffusive Mackey-Glass Equation
Author(s):
C. Ramirez-Carrasco and J. Molina-Garay
Facultad de Ciencias Basicas,
Universidad Catolica del Maule, Talca,
Chile
E-mail: carloshrc1989@gmail.com
molina@imca.edu.pe
Abstract:
In this paper, we consider the diffusive Mackey-Glass model with discrete delay. This equation describes the dynamics of the blood cell production. We investigate the existence of traveling wavefronts solutions connecting the two steady states of the model. We develop an alternative proof of the existence of such solutions and we also demonstrate the existence of traveling wavefronts moving at minimum speed. The proposed approach is based on the use technique of upper-lower solutions. Finally, through an iterative procedure, we show numerical simulations that approximate the traveling wavefronts, thus confirming our theoretical results.
Paper's Title:
Some Properties of Cosine Series with Coefficients from Class of General Monotone Sequences Order r
Author(s):
Corina Karim, Moch. Aruman Imron
Department of Mathematics,
Universitas Brawijaya,
Indonesia.
E-mail: co_mathub@ub.ac.id
maimr@ub.ac.id
Abstract:
The coefficient of sine series from general monotone class has been generalized by Bogdan Szal to the new class which is called class of general monotone order r. This coefficient class is more general than class of general monotone introduced by Tikhonov. By special case, we study properties of cosine series with coefficient of sine series from the class of general monotone order r.
Paper's Title:
Some Remarks On Quasinearly Subharmonic Functions
Author(s):
Mansour Kalantar
Universite Toulouse III-Paul Sabatier,
118 Route de Narbonne, 31062 Toulouse,
France.
E-mail:
mansour.kalantar@math.univ-toulouse.fr,
mankalantar12@yahoo.com
Abstract:
We prove some basic properties of quasi-nearly subharmonic functions and quasi-nearly subharmonic functions in the narrow sense.
Paper's Title:
Locally Bicomplex Convex Module and Their Applications
Author(s):
Stanzin Kunga and Aditi Sharma
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: stanzinkunga19@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: aditi.sharmaro@gmail.com
Abstract:
Let X be a locally BC convex module and L(X) be the family of all continuous bicomplex linear operators on X. In this paper, we study some concepts of D-valued seminorms on locally BC convex module. Further, we study the bicomplex version of Co and (Co,1) semigroup. The work of this paper is inspired by the work in [2] and [6].
Paper's Title:
Algorithms for Nonlinear Problems Involving Strictly Pseudocontractive Mappings
Author(s):
Mathew Olajiire Aibinu1, Surendra Colin Thakur2, Sibusiso Moyo3
1Institute for Systems Science
& KZN E-Skill CoLab,
Durban University of Technology,
Durban 4000,
South Africa.
1DSI-NRF
Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: moaibinu@yahoo.com
mathewa@dut.ac.za
2 KZN E-Skill CoLab,
Durban University of Technology,
Durban 4000,
South Africa.
E-mail: thakur@dut.ac.za
3Institute for Systems Science & Office of the DVC Research,
Innovation & Engagement Milena Court,
Durban University of Technology,
Durban 4000,
South Africa.
E-mail: dvcrie@dut.ac.za
Abstract:
The puzzles in approximating a fixed point of nonlinear problems involving the class of strictly pseudocontractive mappings are conquered in this paper through viscosity implicit rules. Using generalized contraction mappings, a new viscosity iterative algorithm which is implicit in nature is proposed and analysed in Banach spaces for the class of strictly pseudocontractive mappings. The computations and analysis which are used in the proposed scheme are easy to follow and this gives rooms for a broad application of the scheme. It is obtained that the proposed iterative algorithm converges strongly to a fixed point of a μ-strictly pseudocontractive mapping which also solves a variational inequality problem. The result is also shown to hold for finite family of strictly pseudocontractive mappings. A numerical example is given to show the skillfulness of the proposed scheme and its implementation.
Paper's Title:
A Regularity of the Weak Solution Gradient of the Dirichlet Problem for Divergent Form Elliptic Equations in Morrey Spaces
Author(s):
Nicky K. Tumalun and Philotheus E. A. Tuerah
Mathematics Department, Universitas Negeri Manado,
Tondano Selatan, Minahasa Regency,
Sulawesi Utara Province,
Indonesia.
E-mail: nickytumalun@unima.ac.id,
pheatuerah@unima.ac.id
Abstract:
In this paper we prove that the gradient of the weak solution of the Dirichlet problem for divergent form elliptic equations, with the known term belongs to the Morrey spaces, is the element of the weak Morrey spaces.
Paper's Title:
On General Class of Nonlinear Contractive Maps and their Performance Estimates
Author(s):
Olalekan Taofeek Wahab and Salaudeen Alaro Musa
Department of Mathematics and
Statistics
Kwara State University, Malete
P. M. B. 1530 Ilorin,
Nigeria.
E-mail: taofeek.wahab@kwasu.edu.ng
Abstract:
This paper considers two independent general class of nonlinear contractive maps to study the existence properties of nonlinear operators with prior degenerate. The existence properties are proved in the framework of approximate fixed points with the imposition of the general class of contractive conditions in metrical convex spaces without emphasis on completeness or compactness. For computational purposes, the performance estimates and the sensitivity dependence of these conditions are obtained for the Picard operator. Practical examples are also considered to justify the validity of the conditions. The results ensure no term is lost in the operators with prior degenerate and the conditions are strictly larger class when compare with others in the literature.
Paper's Title:
Oscillatory Behavior of Second-Order Non-Canonical
Retarded Difference Equations
Author(s):
G.E. Chatzarakis1, N. Indrajith2, E. Thandapani3 and K.S. Vidhyaa4
1Department
of Electrical and Electronic Engineering Educators,
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail: gea.xatz@aspete.gr,
geaxatz@otenet.gr
2Department
of Mathematics,
Presidency College, Chennai - 600 005,
India.
E-mail: indrajithna@gmail.com
3Ramanujan
Institute for Advanced Study in Mathematics,
University of Madras,
Chennai - 600 005,
India.
E-mail: ethandapani@yahoo.co.in
4
Department of Mathematics,Abstract:
Using monotonic properties of nonoscillatory solutions, we obtain new oscillatory criteria for the second-order non-canonical difference equation with retarded argument
Our oscillation results improve and extend the earlier ones. Examples illustrating the results are provided.
Paper's Title:
Bounds for the Extremal Eigenvalues of Positive Definite Matrices
Author(s):
Shivani Singh and Pravin Singh
Unisa, Department of Decision Sciences,
PO Box 392,
Pretoria,
0003,
South Africa.
E-mail: singhs2@unisa.ac.za
University of KwaZulu-Natal,
School of Mathematics Statistics and Computer Sciences
Private Bag X54001,
Durban,
4000,
South Africa.
E-mail: singhprook@gmail.com
Abstract:
We use a projection to achieve bounds for a vector function of the eigenvalues of a positive definite matrix. For various choices of the monotonic function we are able to obtain bounds for the extremal eigenvalues in terms of the traces of the matrix and its powers. These bounds are relatively simple to compute.
Paper's Title:
A Self Adaptive Method for Solving Split Bilevel Variational Inequalities Problem in Hilbert Spaces
Author(s):
Francis Akutsah1, Ojen Kumar Narain2, Funmilayo Abibat Kasali3 Olawale Kazeem Oyewole4 and Akindele Adebayo Mebawondu5
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 216040405@stu.ukzn.ac.za,
akutsah@gmail.com
2School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
3Mountain Top University,
Prayer City, Ogun State,
Nigeria.
E-mail: fkasali@mtu.edu.ng
4Technion-Israel
Institute of Technology.
E-mail: 217079141@stu.ukzn.ac.za,
oyewoleolawalekazeem@gmail.co
5School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
DST-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
Mountain Top University,
Prayer City, Ogun State,
Nigeria.
E-mail: dele@aims.ac.za
Abstract:
In this work, we study the split bilevel variational inequality problem in two real Hilbert spaces. We propose a new modified inertial projection and contraction method for solving the aforementioned problem when one of the operators is pseudomonotone and Lipschitz continuous while the other operator is α-strongly monotone. The use of the weakly sequential continuity condition on the Pseudomonotone operator is removed in this work. A Strong convergence theorem of the proposed method is proved under some mild conditions. In addition, some numerical experiments are presented to show the efficiency and implementation of our method in comparison with other methods in the literature in the framework of infinite dimensional Hilbert spaces. The results obtained in this paper extend, generalize and improve several.
Paper's Title:
Lozi Maps With Max Function and its Application
Author(s):
Abdellah Menasri
Higher National School of Forests,
Khenchela,
Algeria.
E-mail: abdellah.menasri70@gmail.com
Abstract:
In this paper, we study the Lozi map by replacing the piecewise linear term in the first equation by the function max (f(x,y);g(x,y)) such that f and g are two arbitrary functions in R2. This is a family model that allows us to study several new piecewise-smooth maps. We demonstrate that these models converge to a robust chaotic attractor and give some applications of these models in the real world.
Paper's Title:
Higher Order Accurate Compact Schemes for Time Dependent Linear and Nonlinear Convection-Diffusion Equations
Author(s):
S. Thomas, Gopika P.B. and S. K. Nadupuri
Department of Mathematics
National Institute of Technology Calicut
Kerala
673601
India.
E-mail:
sobinputhiyaveettil@gmail.com
pbgopika@gmail.com nsk@nitc.ac.in
Abstract:
The primary objective of this work is to study higher order compact finite difference schemes for finding the numerical solution of convection-diffusion equations which are widely used in engineering applications. The first part of this work is concerned with a higher order exponential scheme for solving unsteady one dimensional linear convection-diffusion equation. The scheme is set up with a fourth order compact exponential discretization for space and cubic $C^1$-spline collocation method for time. The scheme achieves fourth order accuracy in both temporal and spatial variables and is proved to be unconditionally stable. The second part explores the utility of a sixth order compact finite difference scheme in space and Huta's improved sixth order Runge-Kutta scheme in time combined to find the numerical solution of one dimensional nonlinear convection-diffusion equations. Numerical experiments are carried out with Burgers' equation to demonstrate the accuracy of the new scheme which is sixth order in both space and time. Also a sixth order in space predictor-corrector method is proposed. A comparative study is performed of the proposed schemes with existing predictor-corrector method. The investigation of computational order of convergence is presented.
Paper's Title:
Approximately Dual p-Approximate Schauder Frames
Author(s):
K. Mahesh Krishna and P. Sam Johnson
Stat-Math Unit, Indian Statistical
Institute, Bangalore Centre,
Karnataka 560 059
India.
Department of Mathematical and
Computational Sciences,
National Institute of Technology Karnataka (NITK),
Surathkal, Mangaluru 575 025,
India.
E-mail: kmaheshak@gmail.com
sam@nitk.edu.in
Abstract:
Approximately dual frame in Hilbert spaces was introduced by Christensen and Laugesen to overcome difficulties in constructing dual frames for a given Hilbert space frame. It becomes even more difficult in Banach spaces to construct duals. For this purpose, we introduce approximately dual frames for a class of approximate Schauder frames for Banach spaces and develop basic theory. Approximate dual for this subclass is completely characterized and its perturbation is also studied.
Paper's Title:
Growth and Approximation of Entire Solutions of Linear Partial Differential Equation in Terms of Bessel Polynomial Approximation Errors in Lp-norm, 1 ≤ p ≤ ∞
Author(s):
Devendra Kumar
Department of Mathematics, Faculty of
Sciences
Al-Baha University,
P.O.Box-7738 Alaqiq, Al-Baha-65799,
Saudi Arabia.
E-mail:
d_kumar001@rediffmail.com,
dsingh@bu.edu.sa
Abstract:
We deal with entire solutions of some special type linear homogeneous partial differential equations that are represented in convergent series of Bessel polynomials. We determine the growth orders and types of the solutions, in terms of Bessel polynomial approximation errors in both sup norm and Lp-norm, 1 ≤ p ≤ ∞.
Paper's Title:
Pseudomonotonicity and Quasimonotonicity
by Translations versus Monotonicity in Hilbert Spaces
Author(s):
George Isac and Dumitru Motreanu
Department of
Mathematics, Royal Military College of Canada, P.O. Box 17000 Stn Forces
Kingston, Ontario, Canada, K7k 7b4.
gisac@juno.com
Département de Mathématiques, Université de Perpignan, 66860
Perpignan, France.
motreanu@univ-perp.fr
Abstract:
Let 
be a Gâteaux differentiable mapping on
an open convex subset 
of a
Hilbert space
. If there exists a straight line 
such that 
is pseudomonotone for any 
then 
is monotone. Related results using a
regularity condition are given.
Paper's Title:
Integrability of Sine and Cosine Series Having Coefficients of a New Class
Author(s):
L. Leindler Bolyai Institute,
University of Szeged, Aradi Vértanúk Tere 1, H-6720 Szeged, Hungary
leindler@math.u-szeged.hu
Abstract:
Some integrability theorems or only their sufficient part are
generalized such that the coefficients of the sine and cosine series belong to a
new class of sequences being wider than the class of sequences of rest bounded
variation, which itself is a generalization of the monotone decreasing
sequences, but a subclass of the almost monotone decreasing sequences. It is
also verified that the new class of sequences and the class of almost monotone
decreasing sequences are not comparable.
Paper's Title:
Reverses of the Triangle Inequality in Inner Product Spaces
Author(s):
Sever S. Dragomir
School of Computer Science and Mathematics,
Victoria University Of Technology,
PO Box 14428, Mcmc 8001,
Victoria, Australia.
sever@csm.vu.edu.au
Url:
http://rgmia.vu.edu.au/SSDragomirWeb.html
Abstract:
Some new reverses for the generalised triangle inequality in inner product spaces are given. Applications in connection to the Schwarz inequality and for vector-valued integrals are provided as well.
Paper's Title:
Essential Random Fixed Point Set of Random Operators
Author(s):
Ismat Beg
Centre for Advanced Studies in Mathematics,
Lahore University of Management Sciences (LUMS),
54792-Lahore, PAKISTAN.
ibeg@lums.edu.pk
URL: http://web.lums.edu.pk/~ibeg
Abstract:
We obtain necessary and sufficient conditions for the existence of essential random fixed point of a random operator defined on a compact metric space. The structure of the set of essential random fixed points is also studied.
Paper's Title:
Logarithmically complete monotonicity properties for the gamma functions
Author(s):
Chao-Ping Chen and Feng Qi
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University,
Jiaozuo City, Henan 454010,
China.
chenchaoping@hpu.edu.cn
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University,
Jiaozuo City, Henan 454010,
China.
qifeng@hpu.edu.cn
fengqi618@member.ams.org
Abstract:
Some logarithmically completely monotonic functions involving the gamma functions are presented. As a consequence, some known results are proved and refined.
Paper's Title:
Inverse problems for parabolic equations
Author(s):
A. G. Ramm
Mathematics Department,
Kansas State University,
Manhattan, KS 66506-2602,
USA
ramm@math.ksu.edu
URL: http://www.math.ksu.edu/~ramm
Abstract:
Let 
in 
, where 
is a bounded domain with a smooth connected boundary 
, 
, 
is the delta-function. Assume that 
, 
on . Given the extra data 
, 
, can one find 
, 
and 
Here 
is some number. An answer to this question and a method for finding , and 
are given.
Paper's Title:
Solution of the Hyers-Ulam Stability Problem for Quadratic Type Functional Equations in Several Variables
Author(s):
John Michael Rassias
Pedagogical Department, E.E., National and Capodistrian University of Athens,
Section of Mathematics and Informatics,
4, Agamemnonos Str., Aghia Paraskevi,
Athens 15342,
Greece
jrassias@primedu.uoa.gr
URL: http://www.primedu.uoa.gr/~jrassias/
Abstract:
In 1940 (and 1968) S. M. Ulam proposed the well-known Ulam stability problem. In 1941 D. H. Hyers solved the Hyers-Ulam problem for linear mappings. In 1951 D. G. Bourgin has been the second author treating the Ulam problem for additive mappings. In 1978 according to P. M. Gruber this kind of stability problems is of particular interest in probability theory and in the case of functional equations of different types. In 1982-2004 we established the Hyers-Ulam stability for the Ulam problem for different mappings. In this article we solve the Hyers-Ulam problem for quadratic type functional equations in several variables. These stability results can be applied in stochastic analysis, financial and actuarial mathematics, as well as in psychology and sociology.
Paper's Title:
A New Family of Periodic Functions as Explicit Roots of a Class of Polynomial Equations
Author(s):
M. Artzrouni
Department of Mathematics, University of Pau
64013 Pau Cedex
Pau, France
marc.artzrouni@univ-pau.fr
URL: http://www.univ-pau.fr/~artzroun
Abstract:
For any positive integer n a new family of periodic functions in power series form and
of period n is used to solve in closed form a class of polynomial equations of order
n. The n roots are the values of the appropriate function from that family taken at
0, 1, ... , n-1.
Paper's Title:
Some Stability Results For Fixed Point Iteration Processes
Author(s):
M. O. Olatinwo, O. O. Owojori, and C. O. Imoru
Department of Mathematics, Obafemi Awolowo University,
Ile-Ife,
Nigeria.
polatinwo@oauife.edu.ng
walejori@oauife.edu.ng
cimoru@oauife.edu.ng
Abstract:
In this paper, we present some stability results for both the general Krasnoselskij and the Kirk's iteration processes. The method of Berinde \cite{VBE1} is employed but a more general contractive condition than those of Berinde \cite{VBE1}, Harder and Hicks \cite{HAM}, Rhoades \cite{RHO1} and Osilike \cite{OSI1} is considered.
Paper's Title:
Reconstruction of Discontinuities of Functions Given Noisy Data
Author(s):
Eric D. Mbakop
67A Beaver Park Rd,
Framingham, MA, 01702,
U. S. A.
ericsteve86@yahoo.fr
Abstract:
Suppose one is given noisy data of a discontinuous piecewise-smooth
function along with a bound on its second derivative. The locations
of the points of discontinuity of f and their jump sizes are not
assumed known, but are instead retrieved stably from the noisy data.
The novelty of this paper is a numerical method that allows one to
locate some of these points of discontinuity with an accuracy that
can be made arbitrarily small.
Paper's Title:
On the Numerical Solution for Deconvolution Problems with Noise
Author(s):
N. H. Sweilam
Cairo University, Faculty of Science, Mathematics Department,
Giza, Egypt.
n-sweilam@yahoo.com
Abstract:
In this paper three different stable methods for solving numerically deconvolution problems with noise are studied. The methods examined are the variational regularization method, the dynamical systems method, and the iterative regularized processes. Gravity surveying problem with noise is studied as a model problem. The results obtained by these methods are compared to the exact solution for the model problem. It is found that these three methods are highly stable methods and always converge to the solution even for large size models. The relative higher accuracy is obtained by using the iterative regularized processes.
Paper's Title:
Existence of Solutions for Third Order Nonlinear Boundary Value Problems
Author(s):
Yue Hu and Zuodong Yang
School of Mathematics and Computer Science, Nanjing Normal University, Jiangsu Nanjing 210097,
China.
huu3y2@163.com
College of Zhongbei, Nanjing Normal University, Jiangsu Nanjing 210046,
China.
zdyang_jin@263.net
yangzuodong@njnu.edu.cn
Abstract:
In this paper, the existence of solution for a class of third order quasilinear ordinary differential equations with nonlinear boundary value problems
(Φp(u"))'=f(t,u,u',u"), u(0)=A, u'(0)=B, R(u'(1),u"(1))=0
is established. The results are obtained by using upper and lower solution methods.
Paper's Title:
On Oscillation of
Second-Order Delay Dynamic Equations on Time Scales
Author(s):
S. H. Saker
Department of Mathematics, Faculty of Science,
Mansoura University, Mansoura, 35516,
Egypt.
shsaker@mans.edu.eg
Abstract:
Some new oscillation criteria for second-order linear delay dynamic equation
on a time scale T are established. Our results improve the
recent results for delay dynamic equations and in the special case when
T=R, the results include the oscillation results established by Hille [1948,
Trans. Amer. Math. Soc. 64 (1948), 234-252] and Erbe [Canad. Math. Bull. 16
(1973), 49-56.] for differential equations. When T=Z the
results include and improve some oscillation criteria for difference
equations. When T=hZ, h>0, T=qN and T=N2, i.e., for generalized second order delay difference equations our
results are essentially new and can be applied on different types of time
scales. An example is considered to illustrate the main results.
Paper's Title:
Existence Results for Perturbed Fractional Differential
Inclusions
Author(s):
Y.-K. Chang
Department of Mathematics,
Lanzhou Jiaotong University, Lanzhou, Gansu 730070, People's
Republic of China
lzchangyk@163.com
Abstract:
This paper is mainly concerned with the following fractional differential
inclusions with boundary condition
A sufficient condition is established for the existence of solutions of the
above problem by using a fixed point theorem for multivalued maps due to
Dhage. Our result is proved under the mixed generalized Lipschitz and
Carathéodory conditions.
Paper's Title:
Some Properties of the Solution of a Second Order Elliptic Abstract Differential Equation
Author(s):
A. Aibeche and K. Laidoune
Mathematics Department, Faculty of Sciences,
University Ferhat Abbas, Setif,
Route de Scipion, 19000,
Setif,
Algeria
aibeche@univ-setif.dz
Abstract:
In this paper we study a class of non regular boundary value
problems for elliptic differential-operator equation of second order with an
operator in boundary conditions. We give conditions which guarantee the
coerciveness of the solution of the considered problem, the completeness of
system of root vectors in Banach-valued functions spaces and we establish
the Abel basis property of this system in Hilbert spaces. Finally, we apply
this abstract results to a partial differential equation in cylindrical
domain.
Paper's Title:
On a Method of Proving the Hyers-Ulam Stability
of Functional Equations on Restricted Domains
Author(s):
Janusz Brzdęk
Department of Mathematics
Pedagogical University Podchor
Abstract:
We show that generalizations of some (classical) results on the Hyers-Ulam stability of functional equations, in several variables, can be very easily derived from a simple result on stability of a functional equation in single variable
Paper's Title:
Ulam Stability of Functional Equations
Author(s):
Stefan Czerwik and Krzysztof Król
Institute of Mathematics
Silesian University of Technology
Kaszubska 23,
44-100 Gliwice,
Poland
Stefan.Czerwik@polsl.pl
Krzysztof.Krol@polsl.pl
Abstract:
In this survey paper we present some of the main results on Ulam-Hyers-Rassias stability for important functional equations.
Paper's Title:
On the Generalized Stability and
Asymptotic Behavior of Quadratic Mappings
Author(s):
Hark-Mahn Kim, Sang-Baek Lee and Eunyoung Son
Department of Mathematics
Chungnam National University
Daejeon,
305-764,
Republic of Korea
hmkim@cnu.ac.kr
Abstract:
We extend the stability of quadratic mappings to the stability of general quadratic mappings with several variables, and then obtain an improved asymptotic property of quadratic mappings on restricted domains.
Paper's Title:
Fixed Points and Stability
of the Cauchy Functional Equation
Author(s):
Choonkil Park and Themistocles M. Rassias
Department of Mathematics, Hanyang University,
Seoul 133-791,
Republic of Korea
Department of Mathematics,
National Technical University of Athens,
Zografou Campus, 15780 Athens,
Greece
baak@hanyang.ac.kr
trassias@math.ntua.gr
Abstract:
Using fixed point methods, we prove the generalized Hyers-Ulam stability of homomorphisms in Banach algebras and of derivations on Banach algebras for the Cauchy functional equation.
Paper's Title:
The Riemann-Stieltjes Integral on Time Scales
Author(s):
D. Mozyrska, E. Pawłuszewicz, D. Torres
Faculty Of Computer Science,
Białystok University Of Technology,
15-351 Białystok,
Poland
d.mozyrska@pb.edu.pl
Department Of Mathematics,
University Of Aveiro,
3810-193 Aveiro,
Portugal
ewa@ua.pt
Department Of Mathematics,
University Of Aveiro,
3810-193 Aveiro,
Portugal
delfim@ua.pt
Abstract:
We study the process of integration on time scales in the sense of Riemann-Stieltjes. Analogues of the classical properties are proved for a generic time scale, and examples are given
Paper's Title:
Asymptotic Distribution of Products of Weighted Sums of Dependent
Random Variables
Author(s):
Y. Miao and J. F. Li
College
of Mathematics
and Information
Science,
Henan Normal
University
Henan,
China
yumiao728@yahoo.com.cn
College
of Mathematics
and Information
Science,
Henan Normal
University, 453007
Henan,
China.
junfen_li@yahoo.com.cn
Abstract:
In this paper we establish the asymptotic distribution of products of weighted sums of dependent positive random variable, which extends the results of Rempała and Wesołowski (2002).
Paper's Title:
Topological Aspects of Scalarization in Vector Optimization Problems.
Author(s):
Peter I. Kogut, Rosanna Manzo and Igor V. Nechay
Department of Differential Equations,
Dnipropetrovsk National University, Naukova
STR.,
13,
49010 Dnipropetrovsk,
Ukraine
p.kogut@i.ua
Universitŕ di Salerno,
Department of Technical Cybernetics,
Dipartimento di Ingegneria dell'Informazione e Matematica Applicata,
Via Ponte don Melillo, 84084 Fisciano (SA),
Italy
manzo@diima.unisa.it
Dnipropetrovsk Technical University,
Acad. Lazarjan
STR., 2,
49010 Dnipropetrovsk,
Ukraine
i.nechay@i.ua
Abstract:
In this paper, we study vector optimization problems in partially ordered Banach spaces. We suppose that the objective mapping possesses a weakened property of lower semicontinuity and make no assumptions on the interior of the ordering cone. We derive sufficient conditions for existence of efficient solutions of the above problems and discuss the role of topological properties of the objective space. We discuss the scalarization of vector optimization problems when the objective functions are vector-valued mappings with a weakened property of lower semicontinuity. We also prove the existence of the so-called generalized efficient solutions via the scalarization process. All principal notions and assertions are illustrated by numerous examples.
Paper's Title:
On the Degree of Approximation of Continuous Functions that Pertains to the Sequence-To-Sequence Transformation
Author(s):
Xhevat Z. Krasniqi
University of Prishtina,
Department of Mathematics and Computer Sciences,
5
Mother Teresa Avenue, Prishtinë, 10000,
Republic of Kosovo.
Abstract:
In this paper we prove analogous theorems like Leindler's 3 using the so-called A-transform of the B-transform of the partial sums of Fourier series. In addition, more than two such transforms are introduced and for them analogous results are showed as well.
Paper's Title:
Hyperbolic Models Arising in the Theory of Longitudinal Vibration of Elastic Bars
Author(s):
1I. Fedotov, 1J. Marais, 1,2M. Shatalov and 1H.M. Tenkam
1Department of Mathematics and Statistics,
Tshwane University
of
Technology
Private Bag X6680, Pretoria 0001
South Africa.
fedotovi@tut.ac.za,
julian.marais@gmail.com,
djouosseutenkamhm@tut.ac.za.
2Manufacturing and
Materials
Council of Scientific and Industrial
Research (CSIR)
P.O. Box 395, Pretoria, 0001
South Africa.
mshatlov@csir.co.za
Abstract:
In this paper a unified approach to the
derivation of families of one
dimensional hyperbolic differential equations and boundary conditions describing
the longitudinal vibration of elastic bars is outlined. The longitudinal and
lateral displacements are expressed in the form of a power series expansion in
the lateral coordinate. Equations of motion and boundary conditions are derived
using Hamilton's variational principle. Most of the well known models in this
field fall within the frames of the proposed theory, including the classical
model, and the more elaborated models proposed by by Rayleigh, Love, Bishop,
Mindlin, Herrmann and McNiven. The exact solution is presented for the
Mindlin-Herrmann case in terms of Green functions. Finally, deductions regarding
the accuracy of the models are made by comparison with the exact
Pochhammer-Chree solution for an isotropic cylinder.
Paper's Title:
Generalizing Polyhedra to Infinite Dimension
Author(s):
Paolo d'Alessandro
Department of Mathematics, Third University of Rome,
Lgo S.L. Murialdo 1, 00146 Rome, Italy.
URL:
http://www.mat.uniroma3.it/users/dalex/dalex.html.
Abstract:
This paper generalizes polyhedra to infinite dimensional Hilbert spaces as countable intersections of closed semispaces. Highlights are the structure theory that shows that a polyhedron is the sum of compact set (in a suitable topology) plus a closed pointed cone plus a closed subspace, giving the internal representation of polyhedra. In the final part the dual range space technique is extended to the solution of infinite dimensional LP problems.
Paper's Title:
Error Estimates for Approximations of the Laplace transform of Functions in Lp Spaces
Author(s):
Andrea Aglić Aljinović
Department of Applied Mathematics,
Faculty of Electrical Engineering and Computing,
University of Zagreb,
Unska 3, 10 000 Zagreb,
Croatia
Abstract:
In this paper error estimates of approximations in complex domain for the Laplace transform are given for functions which vanish beyond a finite domain and whose derivatives belongs to Lp spaces. New inequalities concerning the Laplace transform, as well as estimates of the difference between the two Laplace transforms are presented and used to obtain two associated numerical rules and error bounds of their remainders.
Paper's Title:
A-Normal Operators In Semi Hilbertian Spaces
Author(s):
A. Saddi
Department of Mathematics,
College of Education for Girls in Sarat Ebeidah 61914, Abha,
King Khalid University
Saudi Arabia
adel.saddi@fsg.rnu.tn
Abstract:
In this paper we study some properties and inequalities of A-normal operators in semi-Hilbertian spaces by employing some known results for vectors in inner product spaces. We generalize also most of the inequalities of (α,β)-normal operators discussed in Hilbert spaces [7].
Paper's Title:
On Opial's Inequality for Functions of n-Independent Variables
Author(s):
S. A. A. El-Marouf and S. A. AL-Oufi
Department of Mathematics,
Faculty of Science,
Minoufiya University,
Shebin El-Koom,
Egypt
Department of Mathematics,
Faculty of Science, Taibah University,
Madenahmonwarah,
Kingdom of Saudia Arabia
Abstract:
In this paper, we introduce Opial inequalities for functions of n-independent variables. Also, we discuss some different forms of Opial inequality containing functions of n independent variables and their partial derivatives with respect to independent variables.
Paper's Title:
Equivalence of the Nonsmooth Nonlinear Complementarity Problems to Unconstrained Minimization
Author(s):
M. A. Tawhid and J. L. Goffin
Department of Mathematics and Statistics,
School of Advanced Technologies and Mathematics,
Thompson Rivers University,
900 McGill Road, PO Box 3010, Kamloops, BC V2C 5N3
Canada
Alexandria University and Egypt Japan University of Science and Technology,
Alexandria-Egypt
mtawhid@tru.ca
Faculty of Management, McGill University,
1001 Sherbrooke Street West, Montreal, Quebec, H3A 1G5
Canada.
Jean-Louis.Goffin@McGill.ca
Abstract:
This paper deals with nonsmooth nonlinear complementarity problem, where the underlying functions are nonsmooth which admit the H-differentiability but not necessarily locally Lipschitzian or directionally differentiable. We consider a reformulation of the nonlinear complementarity problem as an unconstrained minimization problem. We describe H-differentials of the associated penalized Fischer-Burmeister and Kanzow and Kleinmichel merit functions. We show how, under appropriate P0, semimonotone (E0), P, positive definite, and strictly semimonotone (E) -conditions on an H-differential of f, finding local/global minimum of a merit function (or a `stationary point' of a merit function) leads to a solution of the given nonlinear complementarity problem. Our results not only give new results but also unify/extend various similar results proved for C1.
Paper's Title:
Fejér-type Inequalities
Author(s):
Nicuşor Minculete and Flavia-Corina Mitroi
"Dimitrie Cantemir" University,
107 Bisericii Române Street, Braşov, 500068,
România
minculeten@yahoo.com
University of Craiova, Department of Mathematics,
Street A. I. Cuza
13, Craiova, RO-200585,
Romania
fcmitroi@yahoo.com
Abstract:
The aim of this paper is to present some new Fejér-type results for convex functions. Improvements of Young's inequality (the arithmetic-geometric mean inequality) and other applications to special means are pointed as well.
Paper's Title:
Positive Solutions to a System of Boundary Value Problems for Higher-Dimensional Dynamic Equations on Time Scales
Author(s):
I. Y. Karaca
Department of Mathematics,
Ege University,
35100 Bornova, Izmir,
Turkey
URL:
http://ege.edu.tr
Abstract:
In this paper, we consider the system of boundary value problems for higher-dimensional dynamic equations on time scales. We establish criteria for the existence of at least one or two positive solutions. We shall also obtain criteria which lead to nonexistence of positive solutions. Examples applying our results are also given.
Paper's Title:
Multilinear Fractional Integral Operators on Herz Spaces
Author(s):
Yasuo Komori-Furuya
School of High Technology and Human Welfare,
Tokai University,
317 Nishino Numazu Shizuoka, 410-0395
Japan
Abstract:
We prove the boundedness of the multilinear fractional integral operators of Kenig and Stein type on Herz spaces. We also show that our results are optimal.
Paper's Title:
New Inequalities of Mill's Ratio and Application to The Inverse Q-function Approximation
Author(s):
Pingyi Fan
Department of Electronic Engineering,
Tsinghua University, Beijing,
China
Abstract:
In this paper, we investigate the Mill's ratio estimation problem and get two new inequalities. Compared to the well known results obtained by Gordon, they becomes tighter. Furthermore, we also discuss the inverse Q-function approximation problem and present some useful results on the inverse solution. Numerical results confirm the validness of our theoretical analysis. In addition, we also present a conjecture on the bounds of inverse solution on Q-function.
Paper's Title:
A Nonhomogeneous Subdiffusion Heat Equation
Author(s):
Joel-Arturo Rodriguez-Ceballos, Ana-Magnolia Marin, Ruben-Dario Ortiz
Instituto Tecnológico de Morelia,
Morelia, Michoacan,
Mexico
E-mail: joel@ifm.umich.mx
Universidad de Cartagena,
Campus San Pablo,
Cartagena de Indias, Bolivar,
Colombia
E-mail: amarinr@unicartagena.edu.co
E-mail: joel@ifm.umich.mx
Abstract:
In this paper we consider a nonhomogeneous subdiffusion heat equation of fractional order with Dirichlet boundary conditions.
Paper's Title:
On Some Constructive Method of Rational Approximation
Author(s):
Vasiliy A. Prokhorov
Department of Mathematics and Statistics
University of South Alabama
Mobile, Alabama 36688-0002,
USA.
E-mail:
prokhoro@southalabama.edu
URL:
http://www.southalabama.edu/mathstat/people/prokhorov.shtml
Abstract:
We study a constructive method of rational approximation of analytic functions based on ideas of the theory of Hankel operators. Some properties of the corresponding Hankel operator are investigated. We also consider questions related to the convergence of rational approximants. Analogues of Montessus de Ballore's and Gonchars's theorems on the convergence of rows of Padé approximants are proved.
Paper's Title:
Credibility Based Fuzzy Entropy Measure
Author(s):
G. Yari, M. Rahimi, B. Moomivand and P. Kumar
Department of Mathematics,
Iran University
of Science and Technology,
Tehran,
Iran.
E-mail:
Yari@iust.ac.ir
E-mail:
Mt_Rahimi@iust.ac.ir
URL:
http://www.iust.ac.ir/find.php?item=30.11101.20484.en
URL:
http://webpages.iust.ac.ir/mt_rahimi/en.html
Qarzol-hasaneh
Mehr Iran Bank, Tehran,
Iran.
E-mail:
B.moomivand@qmb.ir
Department of Mathematics and Statistics,
University of Northern British Columbia,
Prince George, BC,
Canada.
E-mail:
Pranesh.Kumar@unbc.ca
Abstract:
Fuzzy entropy is the entropy of a fuzzy variable, loosely representing the information of uncertainty. This paper, first examines both previous membership and credibility based entropy measures in fuzzy environment, and then suggests an extended credibility based measure which satisfies mostly in Du Luca and Termini axioms. Furthermore, using credibility and the proposed measure, the relative entropy is defined to measure uncertainty between fuzzy numbers. Finally we provide some properties of this Credibility based fuzzy entropy measure and to clarify, give some examples.
Paper's Title:
New Implicit Kirk-Type Schemes for General Class of Quasi-Contractive Operators in Generalized Convex Metric Spaces
Author(s):
K. Rauf, O. T. Wahab and A. Ali
Department of Mathematics,
University of Ilorin, Ilorin,
Nigeria.
E-mail: krauf@unilorin.edu.ng
Department of Statistics and Mathematical
Sciences,
Kwara State University, Malete,
Nigeria.
Department of Mathematics,
Mirpur University of Science and Technology, Mirpur,
Pakistan.
Abstract:
In this paper, we introduce some new implicit Kirk-type iterative schemes in generalized convex metric spaces in order to approximate fixed points for general class of quasi-contractive type operators. The strong convergence, T-stability, equivalency, data dependence and convergence rate of these results were explored. The iterative schemes are faster and better, in term of speed of convergence, than their corresponding results in the literature. These results also improve and generalize several existing iterative schemes in the literature and they provide analogues of the corresponding results of other spaces, namely: normed spaces, CAT(0) spaces and so on.
Paper's Title:
Existence of Positive Solutions for
Nonlinear Fractional Differential Equations
with Multi-point Boundary Conditions
Author(s):
N. Adjeroud
Khenchela University, Department of
Mathematics,
Khenchela, 40000,
Algeria.
E-mail: adjnac@gmail.com
Abstract:
This paper is devoted to the existence results of positive solutions for a nonlinear fractional differential equations with multi-point boundary conditions. By means of the Schauder fixed point theorem, some results on the existence are obtained.
Paper's Title:
Mapped Chebyshev Spectral Methods for Solving Second Kind Integral Equations on the Real Line
Author(s):
Ahmed Guechi and Azedine Rahmoune
Department of Mathematics, University of Bordj Bou Arréridj,
El Anasser, 34030, BBA,
Algeria.
E-mail: a.guechi2017@gmail.com
E-mail: a.rahmoune@univ-bba.dz
Abstract:
In this paper we investigate the utility of mappings to solve numerically an important class of integral equations on the real line. The main idea is to map the infinite interval to a finite one and use Chebyshev spectral-collocation method to solve the mapped integral equation in the finite interval. Numerical examples are presented to illustrate the accuracy of the method.
Paper's Title:
Local Boundedness of Weak Solutions for Singular Parabolic Systems of p-Laplacian Type
Author(s):
Corina Karim, Marjono
Department of Mathematics,
Universitas Brawijaya,
Indonesia.
E-mail: co_mathub@ub.ac.id,
marjono@ub.ac.id
Abstract:
We study the local boundedness of weak solutions for evolutional p-Laplacian systems in the singular case. The initial data is belonging to Lebesgue space L∞ (0,T;W(1,p) (Ω,Rn )). We use intrinsic scaling method to treat the boundedness of weak solutions. The main result is to make the local boundedness of weak solution for the systems well-worked in the intrinsic scaling.
Paper's Title:
A Note on Taylor Expansions Without the Differentiability Assumption
Author(s):
Moawia Alghalith
Economics Dept.,
University of the West Indies,
St Augustine,
Trinidad and Tobago.
E-mail: malghalith@gmail.com
Abstract:
We introduce new Taylor expansions when the function is not differentiable.
Retraction
This article has been retracted under the authority of the Editor on Chief on 1 April, 2021. The PDF file is no longer available, but can be obtained from the editorial office upon request.
Paper's Title:
Some Inequalities of the Hermite-Hadamard Type for k-Fractional Conformable Integrals
Author(s):
C.-J. Huang, G. Rahman, K. S. Nisar, A. Ghaffar and F. Qi
Department of Mathematics, Ganzhou Teachers College,
Ganzhou 341000, Jiangxi,
China.
E-mail:
hcj73jx@126.com ,
huangcj1973@qq.com
Department of Mathematics, Shaheed Benazir
Bhutto University,
Sheringal, Upper Dir, Khyber Pakhtoonkhwa,
Pakistan.
E-mail: gauhar55uom@gmail.com
Department of Mathematics, College of Arts
and Science at Wadi Aldawaser, 11991,
Prince Sattam Bin Abdulaziz University, Riyadh Region,
Kingdom of Saudi Arabia.
E-mail: n.sooppy@psau.edu.sa,
ksnisar1@gmail.com
Department of Mathematical Science,
Balochistan University of Information Technology,
Engineering and Management Sciences, Quetta,
Pakistan.
E-mail: abdulghaffar.jaffar@gmail.com
School of Mathematical Sciences, Tianjin
Polytechnic University,
Tianjin 300387,
China; Institute of Mathematics,
Henan Polytechnic University, Jiaozuo 454010, Henan,
China.
E-mail: qifeng618@gmail.com,
qifeng618@qq.com
Abstract:
In the paper, the authors deal with generalized k-fractional conformable integrals, establish some inequalities of the Hermite-Hadamard type for generalized k-fractional conformable integrals for convex functions, and generalize known inequalities of the Hermite-Hadamard type for conformable fractional integrals.
Paper's Title:
Formulation of Approximate Mathematical Model for Incoming Water to Some Dams on Tigris and Euphrates Rivers Using Spline Function
Author(s):
Nadia M. J. Ibrahem, Heba A. Abd Al-Razak, and Muna M. Mustafa
Mathematics Department,
College of Sciences for Women,
University of Baghdad, Baghdad,
Iraq.
E-mail:
Nadiamj_math@csw.uobaghdad.edu.iq
Abstract:
In this paper, we formulate three mathematical models using spline functions, such as linear, quadratic and cubic functions to approximate the mathematical model for incoming water to some dams. We will implement this model on dams of both rivers; dams on the Tigris are Mosul and Amara while dams on the Euphrates are Hadetha and Al-Hindya.
Paper's Title:
Weyl's theorem for class Q and k - quasi class Q Operators
Author(s):
S. Parvatham and D. Senthilkumar
Department of Mathematics and Humanities,
Sri Ramakrishna Institute of Technology, Coimbatore-10, Tamilnadu,
India.
E-mail: parvathasathish@gmail.com
Post Graduate and Research Department of
Mathematics,
Govt. Arts College, Coimbatore-641018, Tamilnadu,
India.
E-mail: senthilsenkumhari@gmail.com
Abstract:
In this paper, we give some properties of class Q operators. It is proved that every class Q operators satisfies Weyl's theorem under the condition that T2 is isometry. Also we proved that every k quasi class Q operators is Polaroid and the spectral mapping theorem holds for this class of operator. It will be proved that single valued extension property, Weyl and generalized Weyl's theorem holds for every k quasi class Q operators.
Paper's Title:
An Efficient Modification of Differential Transform Method for Solving Integral and Integro-differential Equations
Author(s):
S. Al-Ahmad, Ibrahim Mohammed Sulaiman*, and M. Mamat
Faculty of Informatics and Computing,
Universiti Sultan Zainal Abidin,
Terengganu, Besut Campus, 22200,
Malaysia.
E-mail: Alahmad.shadi@yahoo.com,
*sulaimanib@unisza.edu.my,
must@unisza.edu.my
Abstract:
In this paper, classes of integral and integro-differential equations are solved using a modified differential transform method. This proposed technique is based on differential transform method (DTM), Laplace transform (LT) procedure and Pad\'{e} approximants (PA). The proposed method which gives a good approximation for the true solution in a large region is referred to modified differential transform method (MDTM). An algorithm was developed to illustrate the flow of the proposed method. Some numerical problems are presented to check the applicability of the proposed scheme and the obtained results from the computations are compared with other existing methods to illustrates its efficiency. Numerical results have shown that the proposed MDTM method is promising compared to other existing methods for solving integral and integro-differential equations.
Paper's Title:
Antiderivatives and Integrals Involving Incomplete Beta Functions with Applications
Author(s):
R. AlAhmad1,2 and H. Almefleh1
Mathematics Department,
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: rami_thenat@yu.edu.jo
Faculty of Engineering,
Higher Colleges of Technology,
Ras Alkhaimah,
UAE.
Abstract:
In this paper, we prove that incomplete beta functions are antiderivatives of several products and powers of trigonometric functions, we give formulas for antiderivatives for products and powers of trigonometric functions in term of incomplete beta functions, and we evaluate integrals involving trigonometric functions using incomplete beta functions. Also, we extend some properties of the beta functions to the incomplete beta functions. As an application for the above results, we find the moments for certain probability distributions.
Paper's Title:
Hermite-Hadamard Type Inequalities for MN-Convex Functions
Author(s):
Sever S. Dragomir1,2
1Mathematics,
College of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
The present work endeavours to briefly present some of the fundamental results connected to the Hermite-Hadamard inequality for special classes of convex functions such as AG, AH, GA, GG, GH, HA, HG and HH -convex functions in which the author have been involved during the last five years. For simplicity, we call these classes of functions such as MN-convex functions, where M and N stand for any of the Arithmetic (A), Geometric (G) or Harmonic (H) weighted means of positive real numbers. The survey is intended for use by both researchers in various fields of Approximation Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
A New Relaxed b-metric Type and Fixed Point Results
Author(s):
P. Singh, V. Singh and Thokozani Cyprian Martin Jele
Department of Mathematics,
University of KwaZulu-Natal,
Private Bag X54001, Durban,
South Africa.
E-mail: singhp@ukzn.ac.za,
singhv@ukzn.ac.za,
thokozani.jele@nwu.ac.za
Abstract:
The purpose of this paper is to introduce a new relaxed α, β b-metric type by relaxing the triangle inequality. We investigate the effect that this generalization has on fixed point theorems.
Paper's Title:
Rational Expressions of Arithmetic and Geometric Means for the Sequence
npn ∈ N and the Geometric Progression
Author(s):
M. Kinegawa, S. Miyamoto and Y. Nishizawa
Faculty of Education, Saitama University,
Shimo-okubo 255, Sakura-ku, Saitama-city, Saitama,
Japan.
E-mail: m.kinegawa.645@ms.saitama-u.ac.jp
Faculty of Education, Saitama University,
Shimo-okubo 255, Sakura-ku, Saitama-city, Saitama,
Japan.
E-mail: s.miyamoto.245@ms.saitama-u.ac.jp
Faculty of Education, Saitama University,
Shimo-okubo 255, Sakura-ku, Saitama-city, Saitama,
Japan.
E-mail:
ynishizawa@mail.saitama-u.ac.jp
Abstract:
In this paper, we consider the arithmetic and geometric means for the sequence npn ∈ N and the geometric progression. We obtain the results associated with the rational expressions of the means.
Paper's Title:
Analysis of the Dynamic Response of the Soil-pile Behavioral Model Under Lateral Load
Author(s):
Ibrahima Mbaye, Mamadou Diop, Aliou Sonko and Malick Ba
University of Thies,
Department of Mathematics, Bp 967 Thies,
Senegal.
E-mail: imbaye@univ-thies.sn
mamadou.diop@univ-thies.sn
aliousonko59@gmail.com
mmalickba@hotmail.fr
URL: https://www.univ-thies.sn
Abstract:
This work aims to extend and improve our previous study on mathematical and numerical analysis of stationary Pasternak model. In this paper a dynamic response of Pasternak model is considered. On the one hand we establish the existence and uniqueness of the solution by using the Lax-Milgram theorem and the spectral theory thus the existence of a Hilbert basis is shown and the spectral decomposition of any solution of the problem can be established and on the other hand the finite element method is used to determinate the numerical results. Furthermore, the influence of soil parameters Gp and Kp on the displacement of the pious is studied numerically at any time tn.
Paper's Title:
Orthogonal Collocation on Finite Elements Using Quintic Hermite Basis
Author(s):
P. Singh, N. Parumasur and C. Bansilal
University of KwaZulu-Natal,
School of Mathematics Statistics and Computer Sciences,
Private Bag X54001,
Durban, 4000,
South Africa.
E-mail: singhprook@gmail.com
parumasurn1@ukzn.ac.za
christelle18@gmail.com
Abstract:
In this paper we consider the orthogonal collocation on finite elements (OCFE) method using quintic Hermite (second degree smooth) basis functions and use it to solve partial differential equations (PDEs). The method is particularly tailored to solve third order BVPS and PDEs and to handle their special solutions such as travelling waves and solitons, which typically is the case in the KdV equation. The use of quintic polynomials and collocation using Gauss points yields a stable high order superconvergent method. OCFE using quintic Hermite basis is optimal since it is computationally more efficient than collocation methods using (first degree smooth) piecewise-polynomials and more accurate than the (third degree smooth) B-splines basis. Various computational simulations are presented to demonstrate the computational efficiency and versatility of the OCFE method.
Paper's Title:
A New Relaxed Complex-valued b-metric Type and Fixed Point Results
Author(s):
P. Singh, V. Singh and T. C. M. Jele
Department of Mathematics, University of
KwaZulu-Natal,
Private Bag X54001, Durban,
South Africa.
E-mail: singhp@ukzn.ac.za
singhv@ukzn.ac.za
thokozani.jele@nwu.ac.za
Abstract:
In this paper, we study the existence and uniqueness of fixed point in complex valued b-metric spaces and introduce a new relaxed α, β Complex-valued b-metric type by relaxing the triangle inequality and determine whether the fixed point theorems are applicable in these spaces.
Paper's Title:
A New Method with Regularization for Solving Split Variational Inequality Problems in Real Hilbert Spaces
Author(s):
Francis Akutsah1 and Ojen Kumar Narain2
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 216040405@stu.ukzn.ac.za,
akutsah@gmail.com
2School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
In this paper, we introduce a new inertial extrapolation method with regularization for approximating solutions of split variational inequality problems in the frame work of real Hilbert spaces. We prove that the proposed method converges strongly to a minimum-norm solution of the problem without using the conventional two cases approach. In addition, we present some numerical experiments to show the efficiency and applicability of the proposed method. The results obtained in this paper extend, generalize and improve several results in this direction.
Paper's Title:
A Generalization of a Partial b-metric and Fixed Point Theorems
Author(s):
Pravin Singh and Virath Singh
Department of Mathematics, University of
KwaZulu-Natal,
Private Bag X54001, Durban,
South Africa.
E-mail: singhp@ukzn.ac.za
singhv@ukzn.ac.za
Abstract:
The purpose of this paper is to introduce the concept of a Partial α, β b-metric as a generalization of a partial b-metric and prove theorems for some contractive type mapping.
Paper's Title:
On Trigonometric Approximation of Continuous Functions by Deferred Matrix Means
Author(s):
Xhevat Zahir Krasniqi
Faculty of Education,
University of Prishtina "Hasan Prishtina",
Avenue "Mother Theresa " no. 5, Prishtinë
10000,
Republic of Kosovo.
E-mail: xhevat.krasniqi@uni-pr.edu
URL:
https://staff.uni-pr.edu/profile/xhevatkrasniqi
Abstract:
In this paper, for the first time, we introduce the deferred matrix means which contain the well-known generalized deferred Nörlund, deferred Nörlund, deferred Riesz, deferred Cesŕro means introduced earlier by others, and a new class of sequences (predominantly a wider class than the class of Head Bounded Variation Sequences). In addition, using the deferred matrix means of Fourier series of a continuous function, we determine the degree of approximation of such function via its modulus of continuity and a positive mediate function.
Paper's Title:
Improved Oscillation Criteria of Second-Order Advanced Non-canonical Difference Equation
Author(s):
G. E. Chatzarakis1, N. Indrajith2, S. L. Panetsos1, E. Thandapani3
1Department
of Electrical and Electronic Engineering Educators
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail: gea.xatz@aspete.gr,
geaxatz@otenet.gr
spanetsos@aspete.gr
2Department
of Mathematics,
Presidency College, Chennai - 600 005,
India.
E-mail: indrajithna@gmail.com
3Ramanujan
Institute for Advanced Study in Mathematics,
University of Madras Chennai - 600 005,
India.
E-mail: ethandapani@yahoo.co.in
Abstract:
Employing monotonic properties of nonoscillatory solutions, we derive some new oscillation criteria for the second-order advanced non-canonical difference equation
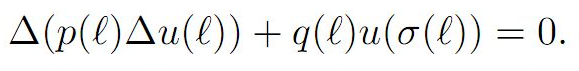
Our results extend and improve the earlier ones. The outcome is illustrated via some particular difference equations.
Paper's Title:
The Boundedness of Gradient Solutions of P-Laplacian Type
Author(s):
Corina Karim, Khoirunisa, Ratno Bagus Edy Wibowo
Department of Mathematics,
Universitas Brawijaya,
Veteran Street, Malang,
Indonesia.
E-mail: co_mathub@ub.ac.id
khrnisa@student.ub.ac.id
rbagus@ub.ac.id
Abstract:
In this paper, we give the boundedness of gradient solutions result for p-Laplacian systems only in the singular case. The Lebesgue space for initial data belong to guarantee the local boundedness of gradient solutions.
Paper's Title:
Additive Mappings on Semiprime Rings Functioning as Centralizers
Author(s):
Abu Zaid Ansari and Faiza Shujat
Department of Mathematics,
Faculty of Science,
Islamic University of Madinah, Madinah
K.S.A.
E-mail: ansari.abuzaid@gmail.com,
ansari.abuzaid@iu.edu.sa
Department of Mathematics,
Faculty of Science,
Taibah University, Madinah,
K.S.A.
E-mail: faiza.shujat@gmail.com,
fullahkhan@taibahu.edu.sa
Abstract:
The objective of this research is to prove that an additive mapping T:R → R is a centralizer on R if it satisfies any one of the following identities:
for all x ∈ R, where n ≥ 1 is a fixed integer and R is any suitably torsion free semiprime ring. Some results on involution "*" are also presented as consequences of the main theorems. In addition, we will take criticism in account with examples.
Paper's Title:
On the Class of Totally Polynomially Posinormal Operators
Author(s):
E. Shine Lal, T. Prasad, P. Ramya
Department of Mathematics,University
College,
Thiruvananthapuram, Kerala, 695034.
India.
E-mail: shinelal.e@gmail.com
Department of Mathematics,
University of Calicut,
Malapuram, Kerala 673635,
India.
E-mail: prasadvalapil@gmail.com
Department of Mathematics,
N.S.S College,
Nemmara, Kerala, 678508
India.
E-mail: ramyagcc@gmail.com
Abstract:
In this paper, we proved that if T ∈
B(H) is totally P-posinormal operator with
. Moreover, we study spectral continuity and range kernel orthogonality of these class of operators.
Paper's Title:
Numerical Study of a Mathematical Model of a Free-Surface Potential Flow
Author(s):
H. Serguine, F. Guechi and A. Gasmi
Department Of Mathematics, Faculty of Science,
Ferhat Abbas Universty,
19000, Setif,
Algeria.
E-mail: houria.serguine@univ-msila.dz
Department Of Mathematics, Faculty of Science,
Ferhat Abbas Universty,
19000, Setif,
Algeria.
E-mail: fairouz.chegaar@univ-setif.dz
Laboratory of Pure and Applied Mathematics, Faculty of Mathematics and
Computer Science,
Mohamed Boudiaf Universty,
28000, M'sila,
Algeria.
E-mail: abdelkader.gasmi@univ-msila.dz
Abstract:
In this work, the problem of a potential and two-dimensional flow with a free surface of an incompressible, irrotational and inviscid fluid of a jet in front an inclined wall is considered, where γ is the inclination angle with the horizontal. The shape of the free surface is presented by curves which are found numerically by the series truncation method. This technique is based on the conformal transformations, resulting with the surface tension effect T with the boundary conditions on the free surfaces given by Bernoulli's equation. The found results are dependant on parameters which are: the Weber's number α and the angle γ. For each Weber's number value, only one solution is specified and some shapes of free surfaces of the jet are illustrated.
Paper's Title:
Geometrical Properties of Subclass of Analytic Function with Odd Degree
Author(s):
K. Sivagami Sundari and B. Srutha Keerthi
Divison of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology, Chennai Campus, Chennai - 600 127,
India.
E-mail: sivagamisundari.2298@gmail.com
Divison of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology, Chennai Campus, Chennai - 600 127,
India.
E-mail: keerthivitmaths@gmail.com
Abstract:
The objective of the paper is to study the geometrical
properties of the class B(λ, t).
For which we have proved that the radius
is optimal ,(i.e)
the number
cannot be replaced by a larger one. Additionally, the graphs for various values of t and
λ are compared in order to study the sharpness of the coefficient bounds.
Paper's Title:
Generalized Triangular and Symmetric Splitting Method for Steady State Probability Vector of Stochastic Matrices
Author(s):
B. Harika, D. Rajaiah, L. P. RajKumar, Malla Reddy Perati
Department of Mathematics,
Kakatiya University
E-mail: hbolledla@gmail.com
Department of Mathematics,
Kakatiya Institute of Technology and Science
E-mail: dr.mh@kitsw.ac.in
Department of Mathematics,
Kakatiya University
E-mail: ladalla@gmail.com
Department of Mathematics,
Kakatiya University
E-mail: mperati@yahoo.com
Abstract:
To find the steady state probability vector of homogenous linear system π Q=0 of stochastic rate matrix Q, generalized triangular and symmetric (GTS) splitting method is presented. Convergence analysis and choice of parameters are given when the regularized matrix A=QT+ε I of the regularized linear system Ax=b is positive definite. Analysis shows that the iterative solution of GTS method converges unconditionally to the unique solution of the regularized linear system. From the numerical results, it is clear that the solution of proposed method converges rapidly when compared to the existing methods.
Paper's Title:
Inequalities Relating to the Gamma Function
Author(s):
Chao-Ping Chen and Feng Qi
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
chenchaoping@hpu.edu.cn
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
qifeng@hpu.edu.cn,
fengqi618@member.ams.org
Url:
http://rgmia.vu.edu.au/qi.html,
http://dami.hpu.edu.cn/qifeng.html
Abstract:
For 
, we have
.
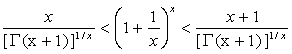For
,
,
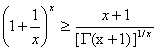And equality occurs for x=1.
Paper's Title:
An Application of Quasi Power Increasing Sequences
Author(s):
Hüseyín Bor
Department of Mathematics, Erciyes University, 38039 Kayseri,
Turkey
Url:
Http://math.erciyes.edu.tr/Hbor.htm
Abstract:
In this paper a result of Bor
[2] has been proved
under weaker conditions by using a -quasi power increasing sequence instead of
an almost increasing sequence.
Paper's Title:
Generalized Fuglede-Putnam Theorem and Orthogonality
Author(s):
A. Bachir and A. Sagres
Department of
Mathematics, Faculty of Science, King Khaled
University, Abha, P.O. Box 9004 Kingdom Saudi Arabia
bachir_ahmed@hotmail.com
sagres@hotmail.com
Abstract:
An asymmetric Fuglede-Putnam’s theorem for dominant operators
and
Paper's Title:
Ellipses of Maximal Area and of Minimal Eccentricity Inscribed in a Convex Quadrilateral
Author(s):
Alan Horwitz
Penn State University,
25 Yearsley Mill Rd., Media, Pa 19063
alh4@psu.edu
Url: www.math.psu.edu/horwitz
Abstract:
Let Đ be a convex quadrilateral in the plane and let M1 and M2 be the midpoints
of the diagonals of Đ. It is well–known that if E is an ellipse inscribed in Đ, then the center of
E must lie on Z, the open line segment connecting M1 and M2 . We use a theorem of Marden
relating the foci of an ellipse tangent to the lines thru the sides of a triangle and the zeros of a
partial fraction expansion to prove the converse: If P lies on Z, then there is a unique ellipse with
center P inscribed in Đ. This completely characterizes the locus of centers of ellipses inscribed
in Đ. We also show that there is a unique ellipse of maximal area inscribed in Đ. Finally, we
prove our most signifigant results: There is a unique ellipse of minimal eccentricity inscribed in
Đ.
Paper's Title:
Weak Solution for Hyperbolic Equations with a Non-Local Condition
Author(s):
Lazhar Bougoffa
King Khalid
University, Faculty of Science, Department of Mathematics,
P.O.Box 9004, Abha, Saudi Arabia
abogafah@kku.edu.sa
Abstract:
In this paper, we study hyperbolic equations with a non-local condition. We prove
the existence and uniqueness of weak solutions, using energy inequality and the density of the
range of the operator generated by the problem.
Paper's Title:
Refinement Inequalities Among Symmetric Divergence Measures
Author(s):
Inder Jeet Taneja
Departamento de Matemática,
Universidade Federal de Santa Catarina, 88.040-900
Florianópolis, Sc, Brazil
taneja@mtm.ufsc.br
URL: http://www.mtm.ufsc.br/~taneja
Abstract:
There are three classical divergence measures in the literature
on information theory and statistics, namely, Jeffryes-Kullback-Leiber’s
J-divergence, Sibson-Burbea-Rao’s Jensen- Shannon divegernce and
Taneja’s arithemtic - geometric mean divergence. These bear an
interesting relationship among each other and are based on logarithmic
expressions. The divergence measures like Hellinger discrimination,
symmetric χ2−divergence, and triangular discrimination
are not based on logarithmic expressions. These six divergence measures are
symmetric with respect to probability distributions. In this paper some
interesting inequalities among these symmetric divergence measures are studied.
Refinements of these inequalities are also given. Some inequalities due to
Dragomir et al. [6]
are also improved.
Paper's Title:
Note on the Rank of Birkhoff Interpolation
Author(s):
J. Rubió-Massegú
Applied Mathematics III, Universitat Politčcnica de Catalunya,
Colom 1, 08222, Terrassa,
Spain
josep.rubio@upc.edu
Abstract:
The relationship between a variant of the rank of a univariate
Birkhoff interpolation problem, called normal rank, and other
numbers of interest associated to the interpolation problem is
studied.
Paper's Title:
On Positive Entire Solutions of Second Order Quasilinear Elliptic Equations
Author(s):
Zuodong Yang and Honghui Yin
Institute of Mathematics, School of Mathematics and Computer Science,
Nanjing Normal University, Jiangsu Nanjing 210097,
China;
zdyang_jin@263.net
Department of Mathematics, Huaiyin Teachers College,
Jiangsu Huaian 223001,
China;
School of Mathematics and Computer Sciences,
Nanjing Normal University, Jiangsu Nanjing 210097,
China.
yin_hh@sina.com
Abstract:
In this paper, our main purpose is to establish the existence
theorem of positive entire solutions of second order quasilinear
elliptic equations under new conditions. The main results of the
present paper are new and extend the previously known results.
Paper's Title:
A Wallis Type Inequality and a Double Inequality for Probability Integral
Author(s):
Jian Cao, Da-Wei Niu and Feng Qi
School of Mathematics and Informatics,
Henan Polytechnic University, Jiaozuo City,
Henan Province, 454010,
China
21caojian@163.com
School of Mathematics and Informatics,
Henan Polytechnic University, Jiaozuo City,
Henan Province, 454010,
China
nnddww@tom.com
Research Institute of Mathematical Inequality Theory,
Henan Polytechnic University, Jiaozuo City,
Henan Province, 454010,
China
qifeng@hpu.edu.cn
fengqi618@member.ams.org
qifeng618@hotmail.com
qifeng618@msn.com
qifeng618@qq.com
URL: http://rgmia.vu.edu.au/qi.html
Abstract:
In this short note, a Wallis type inequality with the best upper and lower
bounds is established. As an application, a double inequality for the
probability integral is found.
Paper's Title:
Weighted Generalization of the Trapezoidal Rule via Fink Identity
Author(s):
S. Kovač, J. Pečarić and A. Vukelić
Faculty of Geotechnical Engineering, University of Zagreb,
Hallerova aleja 7, 42000 Varaždin,
Croatia.
sanja.kovac@gtfvz.hr
Faculty of Textile Technology, University of Zagreb,
Pierottijeva 6, 10000 Zagreb,
Croatia.
pecaric@hazu.hr
Faculty of Food Technology and Biotechnology, Mathematics department, University of Zagreb,
Pierottijeva 6, 10000 Zagreb,
Croatia.
avukelic@pbf.hr
Abstract:
The weighted Fink identity is given and used to obtain generalized
weighted trapezoidal formula for n-time differentiable functions.
Also, an error estimate is obtained for this formula.
Paper's Title:
A New Step Size Rule in Noor's Method for Solving General Variational Inequalities
Author(s):
Abdellah Bnouhachem
School of Management Science and Engineering, Nanjing University,
Nanjing, 210093
P.R. China.
babedallah@yahoo.com
Abstract:
In this paper, we propose a new step size rule in Noor's method
for solving general
variational inequalities. Under suitable conditions, we prove that the
new method is globally convergent. Preliminary numerical
experiments are included to illustrate the advantage and
efficiency of the proposed method.
Paper's Title:
Generalized Quasilinearization Method for the Forced Düffing Equation
Author(s):
Ramzi S. N. Alsaedi
Department of Mathematics, King Abdul Aziz University,
Jeddah P.O. Box 80203,
Saudi Arabia.
ramzialsaedi@yahoo.co.uk
Abstract:
A generalized quasilinearization method for the periodic
problem related to the forced D\"{u}ffing equation is developed and a
sequence of approximate solutions converging monotonically and quadratically
to the solution of the given problem is presented.
Paper's Title:
Two Classes of Completely Monotonic Functions Involving Gamma and Polygamma Functions
Author(s):
Bai-Ni Guo, Xiao-Ai Li and Feng Qi
School of Mathematics and Informatics,
Henan Polytechnic University,
Jiaozuo City, Henan Province, 454010,
China.
bai.ni.guo@gmail.com
College of Mathematics and Information Science,
Henan Normal University, Xinxiang City,
Henan Province, 453007,
China.
lxa.hnsd@163.com
Research Institute of Mathematical Inequality Theory, Abstract:
The function Paper's Title:
An Approximation of Jordan Decomposable Functions for a Lipschitz Function
Author(s):
Ibraheem Alolyan
Mathematics Department, Abstract:
The well known Jordan decomposition theorem gives the useful
characterization that any function of bounded variation can be
written as the difference of two increasing functions. Functions
which can be expressed in this way can be used to formulate an
exclusion test for the recent Cellular Exclusion Algorithms for
numerically computing all zero points or the global minima of
functions in a given cellular domain [2,8,9].
In this paper we give an algorithm to approximate such increasing
functions when only the values of the function of bounded variation
can be computed. For this purpose, we are led to introduce the idea
of ε-increasing functions.
It is shown that for any Lipschitz continuous function,
we can find two ε-increasing functions such that the Lipschitz function can be written as the difference of these
functions.
Paper's Title:
Generalized Stieltjes Transform and its Fractional Integrals for Integrable Boehmian Author(s):
Deshna Loonker and P. K. Banerji
Department Of Mathematics, Faculty Of Science, Abstract:
This paper investigates generalized Stieltjes transform for integrable Boehmian and further, generalized Stieltjes transform of fractional integrals are defined for integrable Boehmian.
Paper's Title:
Positive Solutions for Systems of Three-point Nonlinear Boundary Value Problems Author(s):
J. Henderson and S. K. Ntouyas
Department of Mathematics, Baylor University
Department of Mathematics, University of Ioannina Abstract:
Values of λ are determined for which there exist
positive solutions of the system of three-point boundary value problems,
u''(t)+ λa(t)f(v(t))=0, v''(t)+λb(t)g(u(t))=0,
for 0 < t <1, and
satisfying, u(0) = 0, u(1)=α u(η),
v(0) = 0, v(1)=α v(η). A Guo-Krasnosel'skii fixed
point theorem is applied. Paper's Title:
Some Generalized Difference Sequence Spaces Defined by Orlicz Functions
Author(s):
Ramzi S. N. Alsaedi and Ahmad H. A. Bataineh
Department of Mathematics, King Abdul Aziz University,
Department of Mathematics, Al al-Bayt University, Abstract:
In this paper, we define the sequence spaces: [V,M,p,u,Δ ],[V,M,p,u,Δ]0 and
[V,M,p,u,Δ]∞, where for any sequence x=(xn),
the difference sequence Δx is given by Δx=(Δxn)
Paper's Title:
Reverses of the CBS Integral Inequality in Hilbert Spaces and Related
Results
Author(s):
I. Brnetić, S. S. Dragomir, R. Hoxha and J. Pečarić
Department of Applied Mathematics, Faculty of Electrical
Engineering and Computing,
School of Computer Science & Mathematics, Victoria University
Faculty of Applied Technical Sciences, University of Prishtina,
Faculty of Textile Technology, University of Zagreb, Abstract:
There are many known reverses of the Cauchy-Bunyakovsky-Schwarz (CBS)
inequality in the literature. We obtain here a general integral inequality
comprising some of those results and also provide other related
inequalities. The discrete case, which is of interest in its own turn, is
also analysed. Paper's Title:
A Method for Solving Systems of Nonlinear Equations
Author(s):
J. Shokri
Department of Mathematics, Urmia University,
Abstract:
In this paper, we suggest and analyze a new two-step iterative
method for solving nonlinear equation systems using the combination
of midpoint quadrature rule and Trapezoidal quadrature rule. We
prove that this method has quadratic convergence. Several examples
are given to illustrate the efficiency of the proposed method.
Paper's Title:
A Double Inequality for Divided Differences and Some Identities of the Psi and Polygamma Functions Author(s):
B. N. Guo and F. Qi School of
Mathematics and Informatics, Henan Polytechnic University, Jiaozuo City, Henan
Province, 454010, China School of
Research Institute of Mathematical Inequality Theory, Henan Polytechnic University, Jiaozuo City, Henan Province, 454010, China Abstract:
In this short note, from the logarithmically completely monotonic property
of the function
Paper's Title:
Linearly Transformable Minimal Surfaces Author(s):
Harold R. Parks and Walter B. Woods
Department of Mathematics,
Oregon State University, Abstract:
We give a complete description of a nonplanar minimal surface
in R3 with the surprising property that the surface remains
minimal after mapping by a linear transformation
that dilates by three distinct factors in three
orthogonal directions. The surface is defined in closed form
using Jacobi elliptic functions.
Paper's Title:
Stability of Almost Multiplicative Functionals Author(s):
Norio Niwa, Hirokazu Oka, Takeshi Miura and Sin-Ei Takahasi
Henan Polytechnic University, Jiaozuo City,
Henan Province, 454010,
China
qifeng618@gmail.com
qifeng618@hotmail.com
qifeng618@qq.com
URLhttp://rgmia.vu.edu.au/qi.html
is logarithmically completely monotonic in (0,∞) if and only if c≥1
and its reciprocal is logarithmically completely monotonic in (0,∞) if and only if
c≤0. The function
is completely monotonic in (0,∞) if and only if c≥1 and its
negative is completely monotonic in (0,∞) if and only if c≤0.
2: Paper Source
PDF document
College of Science, King Saud University
P.O.Box: 2455, Riyadh 11451,
Saudi Arabia
ialolyan05@yahoo.com
2: Paper Source
PDF document
J. N. V. University Jodhpur,
342 005,
India
deshnap@yahoo.com
banerjipk@yahoo.com
2: Paper Source
PDF document
Waco, Texas
76798-7328 USA.
Johnny_Henderson@baylor.edu
URL: http://www3.baylor.edu/~Johnny_Henderson
451 10 Ioannina,
Greece.
sntouyas@cc.uoi.gr
URL: http://www.math.uoi.gr/~sntouyas
2: Paper Source
PDF document
Jeddah P.O.Box 80203,
Saudia Arabia
ramzialsaedi@yahoo.co.uk
Mafraq 25113,
Jordan
ahabf2003@yahoo.ca
= (xn-xn-1) . We also study some properties and theorems of
these spaces. These are generalizations of those defined and studied by
Savas and Savas and some others before.
2: Paper Source
PDF document
University of Zagreb, Unska 3, 10 000 Zagreb,
Croatia
andrea@zpm.fer.hr
Po Box 14428, Melbourne Vic 8001
Australia
sever.dragomir@vu.edu.au
URL:http://rgmia.vu.edu.au/dragomir
Mother
Theresa 5, 38 000 Prishtina
Kosova
razimhoxha@yahoo.com
Pierottijeva 6, 10000
Zagreb,
Croatia
pecaric@hazu.hr
2: Paper Source
PDF document
P. O. Box 165, Urmia,
Iran
j.shokri@urmia.ac.ir
2: Paper Source
PDF document
bai.ni.guo@gmail.com,
bai.ni.guo@hotmail.com
qifeng618@gmail.com,
qifeng618@hotmail.com,
qifeng618@qq.com
URL:http://qifeng618.spaces.live.com
, a double inequality for the divided differences and some identities of the psi and polygamma functions are presented.
2: Paper Source
PDF document
Corvallis, Oregon 97331--4605,
USA
parks@math.oregonstate.edu
URL: http://www.math.oregonstate.edu/people/view/parks/
2: Paper Source
PDF document
Faculty of Engineering, Osaka Electro-Communication University,
Neyagawa 572-8530,
Japan
Faculty of Engineering, Ibaraki University,
Hitachi 316-8511,
Japan
Department of Applied Mathematics and Physics, Graduate School of
Science and Engineering,
Yamagata University,
Yonezawa 992-8510
Japan
oka@mx.ibaraki.ac.jp
miura@yz.yamagata-u.ac.jp
sin-ei@emperor.yz.yamagata-u.ac.jp
Abstract:
Let
δ
and p be non-negative real numbers. Let
be the
real or complex number field and
a normed algebra
over . If a mapping
satisfies
then we show that
φ
is multiplicative or
for all 
If, in
addition,
φ
satisfies
for some p≠1, then by using Hyers-Ulam-Rassias
stability of additive Cauchy equation, we show that
φ
is a ring homomorphism or
for all
In other words,
φ
is a ring homomorphism, or an approximately zero
mapping. The results of this paper are inspired by Th.M. Rassias' stability
theorem.
Paper's Title:
A Coincidence Theorem for Two Kakutani Maps
Author(s):
Mircea Balaj
Department of Mathematics,
University of Oradea,
410087, Oradea,
Romania.
mbalaj@uoradea.ro
Abstract:
In this paper we prove the following theorem: Let X be a nonempty compact convex set in a locally convex Hausdorff topological vector space, D be the set of its extremal points and F,T: X―◦X two Kakutani maps; if for each nonempty finite subset A of D and for any x ∈ coA, F (x) ∩ coA ≠ Ř, then F and T have a coincidence point. The proof of this theorem is given first in the case when X is a simplex, then when X is a polytope and finally in the general case. Several reformulations of this result are given in the last part of the paper.
Paper's Title:
On a Class of Uniformly Convex Functions Defined by Convolution with Fixed Coefficient
Author(s):
T. N. Shanmugam, S. Sivasubramanian, and G. Murugusundaramoorthy
Department of Mathematics,
College of Engineering,
Anna University,
Chennai - 600 025,
India.
drtns2001@yahoo.com
Department of Mathematics,
University College of Engineering,
Tindivanam
Anna University-Chennai,
Saram-604 703,
India.
sivasaisastha@rediffmail.com
School of Sciences and Humanities,
VIT University, Vellore-632 014,
India.
gmsmoorthy@yahoo.com
Abstract:
We define a new subclass of uniformly convex functions with negative and fixed second coefficients defined by convolution. The main object of this paper is to obtain coefficient estimates distortion bounds, closure theorems and extreme points for functions belong to this new class . The results are generalized to families with fixed finitely many coefficients.
Paper's Title:
The Superstability of the Pexider Type Trigonometric Functional Equation
Author(s):
Gwang Hui Kim and Young Whan Lee
Department of Mathematics, Kangnam
University Yongin, Gyeonggi, 446-702, Korea.
ghkim@kangnam.ac.kr
Department of Computer and Information Security
Daejeon University, Daejeon 300-716, Korea.
ywlee@dju.ac.kr
Abstract:
The aim of this paper is to investigate the stability
problem for
the Pexider type (hyperbolic) trigonometric functional equation
f(x+y)+f(x+σy)=λg(x)h(y) under the conditions :
|f(x+y)+f(x+σy)- λg(x)h(y)|≤φ(x),
φ(y), and min {φ(x), φ (y)}.
As a consequence, we have generalized the results of stability for
the cosine(d'Alembert), sine, and the Wilson functional equations by J.
Baker, P. Găvruta, R. Badora and R. Ger, Pl.~Kannappan, and G.
H. Kim
Paper's Title:
On
the Inequality 
Author(s):
A. Coronel and F. Huancas
Departamento de Ciencias Básicas,
Facultad de Ciencias, Universidad del Bío-Bío, Casilla 447,
Campus Fernando May, Chillán, Chile.
acoronel@roble.fdo-may.ubiobio.cl
Departamento Académico de Matemática,
Facultad de Ciencias Físicas y Matemáticas,
Universidad Nacional Pedro Ruiz Gallo, Juan XIII s/n,
Lambayeque, Perú
Abstract:
In this paper we give a complete proof of
for all positive real numbers a, b and c. Furthermore, we present
another way to prove the statement for
Paper's Title:
Ellipses Inscribed in Parallelograms
Author(s):
A. Horwitz
Penn State University,
25 Yearsley Mill Rd.
Media, PA 19063
U. S. A.
alh4@psu.edu
Abstract:
We prove that there exists a unique ellipse of minimal eccentricity, EI, inscribed in a parallelogram, Đ. We also prove that the smallest nonnegative angle between equal conjugate diameters of $EI equals the smallest nonnegative angle between the diagonals of Đ. We also prove that if EM is the unique ellipse inscribed in a rectangle, R, which is tangent at the midpoints of the sides of R, then EM is the unique ellipse of minimal eccentricity, maximal area, and maximal arc length inscribed in R. Let Đ be any convex quadrilateral. In previous papers, the author proved that there is a unique ellipse of minimal eccentricity, EI, inscribed in Đ, and a unique ellipse, EO, of minimal eccentricity circumscribed about Đ. We defined Đ to be bielliptic if EI and EO have the same eccentricity. In this paper we show that a parallelogram, Đ, is bielliptic if and only if the square of the length of one of the diagonals of Đ equals twice the square of the length of one of the sides of Đ .
Paper's Title:
On the Boundedness of Hardy's Averaging Operators
Author(s):
Dah-Chin Luor
Department of Applied Mathematics,
I-Shou University, Dashu District,
Kaohsiung City 84001,
Taiwan, R.O.C.
dclour@isu.edu.tw
Abstract:
In this paper we establish scales of sufficient conditions for the boundedness of Hardy's averaging operators on weighted Lebesgue spaces. The estimations of the operator norms are also obtained. Included in particular are the Erdélyi-Kober operators.
Paper's Title:
Further Bounds for Two Mappings Related
to the Hermite-Hadamard Inequality
Author(s):
S. S. Dragomir1,2 and I. Gomm1
1Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428,
Melbourne City, MC 8001,
Australia.
2School of Computational & Applied Mathematics,
University of
the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
sever.dragomir@vu.edu.au
ian.gomm@vu.edu.au
URL: http://rgmia.org/dragomir
Abstract:
Some new results concerning two mappings associated to the celebrated Hermite-Hadamard integral inequality for twice differentiable functions with applications for special means are given.
Paper's Title:
C*-algebras Associated Noncommutative Circle and Their K-theory
Author(s):
Saleh Omran
Taif University,
Faculty of Science,
Taif,
KSA
South Valley University,
Faculty of Science,
Math. Dep.
Qena,
Egypt
Abstract:
In this article we investigate the universal C*-algebras associated to certain 1 - dimensional simplicial flag complexes which describe the noncommutative circle. We denote it by S1nc. We examine the K-theory of this algebra and the subalgebras S1nc/Ik, Ik . Where Ik, for each k, is the ideal in S1nc generated by all products of generators hs containing at least k+1 pairwise different generators. Moreover we prove that such algebra divided by the ideal I2 is commutative.
Paper's Title:
Some Applications of Fejér's Inequality for Convex Functions (I)
Author(s):
S.S. Dragomir1,2 and I. Gomm1
1Mathematics, School of
Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia.
URL: http://rgmia.org/dragomir
2School of Computational &
Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
Abstract:
Some applications of Fejér's inequality for convex functions are explored. Upper and lower bounds for the weighted integral
under various assumptions for f with applications to the trapezoidal quadrature rule are given. Some inequalities for special means are also provided
Paper's Title:
Some Properties of the Marshall-Olkin and Generalized Cuadras-Augé Families of Copulas
Author(s):
Edward Dobrowolski and Pranesh Kumar
Department of Mathematics and Statistics
University of Northern British Columbia
Prince George, BC,
Canada, V2N 4Z9
E-mail: Pranesh.Kumar@unbc.ca
Abstract:
We investigate some properties of the families of two parameter Marshall-Olkin and Generalized Cuadras-Augé copulas. Some new results are proved for copula parameters, dependence measure and mutual information. A numerical application is discussed.
Paper's Title:
Sufficient Conditions for Certain Types of Functions to be Parabolic Starlike
Author(s):
A. Gangadharan and S. Chinthamani
Department of Mathematics,
Easwari Engineering College,
Ramapuram, Chennai - 89,
India.
Research Scholar,
Anna University,
Chennai
E-mail: ganga.megalai@gmail.com
E-mail: chinvicky@rediffmail.com
Abstract:
In this paper sufficient conditions are determined for functions of
the form
and certain other types of functions to be parabolic starlike.
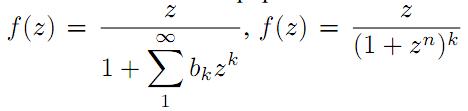
Paper's Title:
On the Biharmonic Equation with Nonlinear Boundary Integral Conditions
Author(s):
R. Hamdouche and H. Saker
L.M.A. Department of Mathematics, Faculty
of Sciences,
University of Badji Mokhtar,
P.O.Box 12. Annaba 23000,
Algeria.
E-mail: h_saker@yahoo.fr,
hmdch.rahma16@gmail.com
Abstract:
In the present work, we deal with the biharmonic problems in a bounded domain in the plane with the nonlinear boundary integral conditions. After applying the Boundary integral method, a system of nonlinear boundary integral equations is obtained. The result show that when the nonlinearity satisfies some conditions lead the existence and uniqueness of the solution.
Paper's Title:
On the Hyers-Ulam Stability of Homomorphisms and Lie Derivations
Author(s):
Javad Izadi and Bahmann Yousefi
Department of Mathematics, Payame Noor
University,
P.O. Box: 19395-3697, Tehran,
Iran.
E-mail: javadie2003@yahoo.com,
b_yousefi@pnu.ac.ir
Abstract:
Let A be a Lie Banach*-algebra. For each elements (a, b) and (c, d) in A2:= A * A, by definitions
(a, b) (c, d)= (ac, bd),
|(a, b)|= |a|+ |b|,
(a, b)*= (a*, b*),
A2 can be considered as a Banach*-algebra. This Banach*-algebra is called a Lie Banach*-algebra whenever it is equipped with the following definitions of Lie product:
for all a, b, c, d in A. Also, if A is a Lie Banach*-algebra, then D: A2→A2 satisfying
D ([ (a, b), (c, d)])= [ D (a, b), (c, d)]+ [(a, b), D (c, d)]
for all $a, b, c, d∈A, is a Lie derivation on A2. Furthermore, if A is a Lie Banach*-algebra, then D is called a Lie* derivation on A2 whenever D is a Lie derivation with D (a, b)*= D (a*, b*) for all a, b∈A. In this paper, we investigate the Hyers-Ulam stability of Lie Banach*-algebra homomorphisms and Lie* derivations on the Banach*-algebra A2.
Paper's Title:
Hyponormal and K-Quasi-Hyponormal Operators On Semi-Hilbertian Spaces
Author(s):
Ould Ahmed Mahmoud Sid Ahmed and Abdelkader Benali
Mathematics Department,
College of Science,
Aljouf University,
Aljouf 2014,
Saudi Arabia.
E-mail:
sididahmed@ju.edu.sa
Mathematics Department, Faculty of
Science,
Hassiba Benbouali, University of Chlef,
B.P. 151 Hay Essalem, Chlef 02000,
Algeria.
E-mail:
benali4848@gmail.com
Abstract:
Let H be a Hilbert space and let A be a positive bounded operator on H. The semi-inner product < u|v>A:=<Au|v>, u,v ∈ H induces a semi-norm || .||A on H. This makes H into a semi-Hilbertian space. In this paper we introduce the notions of hyponormalities and k-quasi-hyponormalities for operators on semi Hilbertian space (H,||.||A), based on the works that studied normal, isometry, unitary and partial isometries operators in these spaces. Also, we generalize some results which are already known for hyponormal and quasi-hyponormal operators. An operator T ∈ BA (H) is said to be (A, k)-quasi-hyponormal if
Paper's Title:
The boundedness of Bessel-Riesz operators on generalized Morrey spaces
Author(s):
Mochammad Idris, Hendra Gunawan and Eridani
Department of Mathematics,
Bandung Institute of Technology,
Bandung 40132,
Indonesia.
E-mail:
mochidris@students.itb.ac.id
Department of Mathematics,
Bandung Institute of Technology,
Bandung 40132,
Indonesia.
E-mail: hgunawan@math.itb.ac.id
URL:
http://personal.fmipa.itb.ac.id/hgunawan/
Department of Mathematics,
Airlangga University,
Surabaya 60115,
Indonesia.
E-mail: eridani.dinadewi@gmail.com
Abstract:
In this paper, we prove the boundedness of Bessel-Riesz operators on generalized Morrey spaces. The proof uses the usual dyadic decomposition, a Hedberg-type inequality for the operators, and the boundedness of Hardy-Littlewood maximal operator. Our results reveal that the norm of the operators is dominated by the norm of the kernels.
Paper's Title:
Robust Error Analysis of Solutions to Nonlinear Volterra Integral Equation in Lp Spaces
Author(s):
Hamid Baghani, Javad Farokhi-Ostad and Omid Baghani
Department of Mathematics, Faculty of
Mathematics,
University of Sistan and Baluchestan, P.O. Box 98135-674, Zahedan,
Iran.
E-mail:
h.baghani@gmail.com
Department of Mathematics, Faculty of
Basic Sciences,
Birjand University of Technology, Birjand,
Iran.
E-mail: j.farrokhi@birjandut.ac.ir
Department of Mathematics and Computer
Sciences,
Hakim Sabzevari University, P.O. Box 397, Sabzevar,
Iran.
E-mail:
o.baghani@gmail.com
Abstract:
In this paper, we propose a novel strategy for proving an important inequality for a contraction integral equations. The obtained inequality allows us to express our iterative algorithm using a "for loop" rather than a "while loop". The main tool used in this paper is the fixed point theorem in the Lebesgue space. Also, a numerical example shows the efficiency and the accuracy of the proposed scheme.
Paper's Title:
On The Rayleigh-Love Rod Accreting In Both Length And
Cross-Sectional Area: Forced And Damped Vibrations
Author(s):
M.L.G. Lekalakala1, M. Shatalov2, I. Fedotov3, S.V. Joubert4
1Department
of Mathematics, Vaal University of Technology, P.O. Box 1889, Secunda, 2302,
South Africa.
E-mail1:
glen@vut.ac.za
2,3,4Department of Mathematics and Statistics, Tshwane University of Technology, Pretoria, South Africa.
Abstract:
In this paper an elastic cylindrical rod that is subjected to forced and damped vibrations is considered. The rod is assumed to be isotropic. The applied external force of excitation is assumed to be harmonic, and the damping force is that of Kelvin-Voigt. The longitudinally vibrating rod is fixed at the left end and free at the other end. The rod is assumed to be accreting in length and cross-sectional area as it vibrates. The problem arising and the dynamics of the vibrating rod are described and investigated within the Rayleigh-Love theories of the rod. A partial differential equation describing the longitudinal displacement of the rod is formulated. The formulated partial differential equation, together with the corresponding boundary conditions as per the configuration of the rod, is solved numerically using the Galerkin-Kantorovich method. The frequency of vibration of the harmonic exciting force is kept constant in this investigation.
It is shown that in this periodically forced viscoelastic damped vibration, all the modes of vibration are subjected to the resonance behaviour within a proper time interval, depending on the length of the accreting rod.
Paper's Title:
The Dynamics of an Ebola Epidemic Model with Quarantine of Infectives
Author(s):
Eliab Horub Kweyunga
Department of Mathematics,
Kabale University,
P.O.Box 317, Kabale,
Uganda.
E-mail: hkweyunga@kab.ac.ug
Abstract:
The recurrent outbreaks of ebola in Africa present global health challenges. Ebola is a severe, very fatal disease with case fatality rates of up to 90%. In this paper, a theoretical deterministic model for ebola epidemic with quarantine of infectives is proposed and analyzed. The model exhibits two equilibria; the disease free and endemic equilibrium points. The basic reproduction number, R0, which is the main threshold, is obtained and the stability of the equilibrium points established. Using parameter values drawn from the 2014 West Africa ebola outbreak, a numerical simulation of the model is carried out. It is found that the dynamics of the model are completely determined by R0 and that a quarantine success rate of at least 70% is sufficient to contain the disease outbreak.
Paper's Title:
Integrating Factors and First Integrals of a Class of Third Order Differential Equations
Author(s):
Mohammadkheer Al-Jararha
Department of Mathematics,
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: mohammad.ja@yu.edu.jo
Abstract:
The principle of finding an integrating factor for a none exact differential equations is extended to a class of third order differential equations. If the third order equation is not exact, under certain conditions, an integrating factor exists which transforms it to an exact one. Hence, it can be reduced into a second order differential equation. In this paper, we give explicit forms for certain integrating factors of a class of the third order differential equations.
Paper's Title:
Closedness and Skew Self-Adjointness of Nadir's Operator
Author(s):
Mostefa Nadir and Abdellatif Smati
Department of Mathematics,
University of Msila 28000,
ALGERIA.
E-mail: mostefanadir@yahoo.fr
E-mail: smatilotfi@gmail.com
Abstract:
In this paper, we present some sufficient conditions which ensure the compactness, the normality, the positivity, the closedness and the skew self-adjointness of the unbounded Nadir's operator on a Hilbert space. We get also when the measurement of its adjointness is null and other related results are also established.
Paper's Title:
Fractional class of analytic functions Defined Using q-Differential Operator
Author(s):
K . R. Karthikeyan, Musthafa Ibrahim and S. Srinivasan
Department of Mathematics and
Statistics,
Caledonian College of Engineering, Muscat,
Sultanate of Oman.
E-mail: kr_karthikeyan1979@yahoo.com
College of Engineering,
University of Buraimi, Al Buraimi,
Sultanate of Oman.
E-mail: musthafa.ibrahim@gmail.com
Department of Mathematics, Presidency
College (Autonomous),
Chennai-600005, Tamilnadu,
India.
Abstract:
We define a q-differential fractional operator, which generalizes Salagean and Ruscheweyh differential operators. We introduce and study a new class of analytic functions involving q-differential fractional operator. We also determine the necessary and sufficient conditions for functions to be in the class. Further, we obtain the coefficient estimates, extreme points, growth and distortion bounds.
Paper's Title:
On Closed Range C*-modular Operators
Author(s):
Javad Farokhi-Ostad and Ali Reza Janfada
Department of Mathematics,
Faculty of Mathematics and Statistics Sciences,
University of Birjand, Birjand,
Iran.
E-mail: j.farokhi@birjand.ac.ir
ajanfada@birjand.ac.ir
Abstract:
In this paper, for the class of the modular operators on Hilbert C*-modules, we give the conditions to closedness of their ranges. Also, the equivalence conditions for the closedness of the range of the modular projections on Hilbert C*-modules are discussed. Moreover, the mixed reverse order law for the Moore-Penrose invertible modular operators are given.
Paper's Title:
Relations Between Differentiability And One-sided Differentiability
Author(s):
Q. D. Gjonbalaj, V. R. Hamiti and L. Gjoka
Department of Mathematics, Faculty of
Electrical and Computer Engineering,
University of Prishtina "Hasan Prishtina",
Prishtine 10000, Kosova.
E-mail: qefsere.gjonbalaj@uni-pr.edu
{Department of Mathematics, Faculty of
Electrical and Computer Engineering,
University of Prishtina "Hasan Prishtina",
Prishtine 10000, Kosova.
E-mail: valdete.rexhebeqaj@uni-pr.edu
Department of Mathematical Engineering,
Polytechnic University of Tirana, Tirana,
Albania
E-mail: luigjgjoka@ymail.com
Abstract:
In this paper, we attempt to approach to the problem of connection between differentiation and one-side differentiation in a more simple and explicit way than in existing math literature. By replacing the condition of differentiation with one-sided differentiation, more precisely with right-hand differentiation, we give the generalization of a theorem having to do with Lebesgue’s integration of derivative of a function. Next, based on this generalized result it is proven that if a continuous function has bounded right-hand derivative, then this function is almost everywhere differentiable, which implies that the set of points where the function is not differentiable has measure zero.
Paper's Title:
The Influence of Fluid Pressure in Macromechanical Cochlear Model
Author(s):
F. E. Aboulkhouatem1, F. Kouilily1, N. Achtaich1, N. Yousfi1 and M. El Khasmi2
1Department
of Mathematics and Computer Science, Faculty of Sciences
Ben M'sik, Hassan II University, Casablanca,
Morocco.
2Department
of Biology, Faculty of Sciences
Ben M'sik, Hassan II University, Casablanca,
Morocco.
E-mail:
fatiaboulkhouatem@gemail.com
URL: http://www.fsb.univh2c.ma/
Abstract:
An increase of pressure in the structure of cochlea may cause a hearing loss. In this paper, we established the relationship between the fluid pressure and the amplitude of displacement of Basilar Membrane to clarify the mechanisms of hearing loss caused by increasing of this pressure. So, a mathematical cochlear model was formulated using finite difference method in order to explain and demonstrate this malfunction in passive model. Numerical simulations may be considered as helpful tools which may extend and complete the understanding of a cochlea dysfunction.
Paper's Title:
Some Convergence Results for Jungck-Am Iterative Process In Hyperbolic Spaces
Author(s):
Akindele Adebayo Mebawondu and Oluwatosin Temitope Mewomo
School of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail:
216028272@stu.ukzn.ac.za,
mewomoo@ukzn.ac.za
Abstract:
In this paper, we introduce a new three steps iterative process called Jungck-AM iterative process and show that the proposed iterative process can be used to approximate fixed points of Jungck-contractive type mappings and Jungck-Suzuki type mappings. In addition, we establish some strong and Δ-convergence results for the approximation of fixed points of Jungck-Suzuki type mappings in the frame work of uniformly convex hyperbolic space. Furthermore, we show that the newly proposed iterative process has a better rate of convergence compare to the Jungck-Noor, Jungck-SP, Jungck-CR and some existing iterative processes in the literature. Finally, stability, data dependency results for Jungck-AM iterative process is established and we present an analytical proof and numerical examples to validate our claim.
Paper's Title:
Applications of Von Neumann Algebras to Rigidity Problems of (2-Step) Riemannian (Nil-)Manifolds
Author(s):
Atefeh Hasan-Zadeh and Hamid-Reza Fanai
DFouman Faculty of Engineering,
College of Engineering, University of Tehran,
Iran.
E-mail: hasanzadeh.a@ut.ac.ir
Department of Mathematical Sciences,
Sharif University of Technology,
Iran
E-mail: fanai@sharif.edu
Abstract:
In this paper, basic notions of von Neumann algebra and its direct analogues in the realm of groupoids and measure spaces have been considered. By recovering the action of a locally compact Lie group from a crossed product of a von Neumann algebra, other proof of one of a geometric propositions of O'Neil and an extension of it has been proposed. Also, using the advanced exploration of nilmanifolds in measure spaces and their corresponding automorphisms (Lie algebraic derivations) a different proof of an analytic theorem of Gordon and Mao has been attained. These two propositions are of the most important ones for rigidity problems of Riemannian manifolds especially 2-step nilmanifolds.
Paper's Title:
On Ruled Surfaces According to Quasi-Frame in Euclidean 3-Space
Author(s):
M. Khalifa Saad and R. A. Abdel-Baky
Department of Mathematics, Faculty of
Science,
Islamic University of Madinah,
KSA.
Department of Mathematics, Faculty of Science,
Sohag University, Sohag,
EGYPT.
E-mail:
mohamed_khalifa77@science.sohag.edu.eg,
mohammed.khalifa@iu.edu.sa
Department of Mathematics, Faculty of
Science,
Assiut University, Assiut,
EGYPT.
E-mail: rbaky@live.com
Abstract:
This paper aims to study the skew ruled surfaces by using the quasi-frame of Smarandache curves in the Euclidean 3-space. Also, we reveal the relationship between Serret-Frenet and quasi-frames and give a parametric representation of a directional ruled surface using the quasi-frame. Besides, some comparative examples are given and plotted which support our method and main results.
Paper's Title:
Solving Non-Autonomous Nonlinear Systems of Ordinary Differential Equations Using Multi-Stage Differential Transform Method
Author(s):
K. A. Ahmad, Z. Zainuddin, F. A. Abdullah
School of Mathematical Sciences
Universiti Sains Malaysia
11800 USM Penang
Malaysia.
E-mail: abumohmmadkh@hotmail.com
zarita@usm.my
farahaini@usm.my
Abstract:
Differential equations are basic tools to describe a wide variety of phenomena in nature such as, electrostatics, physics, chemistry, economics, etc. In this paper, a technique is developed to solve nonlinear and linear systems of ordinary differential equations based on the standard Differential Transform Method (DTM) and Multi-stage Differential Transform Method (MsDTM). Comparative numerical results that we are obtained by MsDTM and Runge-Kutta method are proposed. The numerical results showed that the MsDTM gives more accurate approximation as compared to the Runge-Kutta numerical method for the solutions of nonlinear and linear systems of ordinary differential equations
Paper's Title:
Optimal Control Analysis of HIV/AIDS Epidemic Model with an Antiretroviral Treatment
Author(s):
U. Habibah and R. A. Sari
Mathematics Department and Reseach Group
of Biomathematics,
Faculty of Mathematics and Natural Science,
Brawijaya University, Jl. Veteran Malang 65145,
Indonesia.
E-mail: ummu_habibah@ub.ac.id
Abstract:
A mathematical model of HIV/AIDS is governed by a system of ordinary differential equations in the presence of an antiretroviral treatment (ARV). The theory of optimal control is applied to an epidemic model of HIV/AIDS which an ARV is used as a control strategy in order to prevent the spread of HIV/AIDS. The optimality system is derived by applying the Pontryagin's Minimum Principle. We analyze the boundedness and positivity of solutions, and an existence of the optimal control. Numerical simulations are conducted to obtain numerical solution of the optimally system.
Paper's Title:
Inequalities of Gamma Function Appearing in Generalizing Probability Sampling Design
Author(s):
Mohammadkheer M. Al-Jararha And Jehad M. Al-Jararha
Department of Mathematics,
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: mohammad.ja@yu.edu.jo
Department of Statistics,
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: jehad@yu.edu.jo
Abstract:
In this paper, we investigate the complete monotonicity of some functions involving gamma function. Using the monotonic properties of these functions, we derived some inequalities involving gamma and beta functions. Such inequalities can be used to generalize different probability distribution functions. Also, they can be used to generalize some statistical designs, e.g., the probability proportional to the size without replacement design.
Paper's Title:
Existence of Solution of Differential and Riemann-Liouville Equation Via Fixed Point Approach in Complex Valued b-Metric Spaces
Author(s):
K. Afassinou, A. A. Mebawondu, H. A. Abass and O. K. Narain
Department of Science Access,
University of Zululand, KwaDlangezwa,
South Africa.
E-mail: komia@aims.ac.za
DST-NRF Centre of Excellence in
Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: dele@aims.ac.za
DST-NRF Centre of Excellence in
Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: hammedabass548@gmail.com
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
In this paper, we establish some fixed point and common fixed point results for a new type of generalized contractive mapping using the notion of C-class function in the framework of complex valued b-metric spaces. As an application, we establish the existence and uniqueness of a solution for Riemann-Liouville integral and ordinary differential equation in the framework of a complete complex valued b-metric spaces. The obtained results generalize and improve some fixed point results in the literature.
Paper's Title:
Introducing the Picard-S3 Iteration for Fixed Points
Author(s):
Pravin Singh, Virath Singh and Shivani Singh
University of KwaZulu-Natal,
School of Mathematics Statistics and Computer Sciences,
Private Bag X54001,
Durban, 4000
South Africa.
Unisa,
Department of Decision Sciences,
PO Box 392,
Pretoria, 0003
South Africa.
E-mail: singhprook@gmail.com
singhv@ukzn.ac.za
shivstarsingh@gmail.com
Abstract:
In this paper we introduce a three step iteration method and show that it can be used to approximate the fixed point of a weak contraction mapping. Furthermore, we prove that this scheme is equivalent to the Mann iterative scheme. A comparison is made with other three step iterative methods by examining the speed of convergence. Results are presented in tables to support our conclusion.
Paper's Title:
Preserver of Local Spectrum of Skew-product Operators
Author(s):
Rohollah Parvinianzadeh1,*, Meysam Asadipour2 and Jumakhan Pazhman3
1Department
of Mathematics,
College of Sciences,
University of Yasouj,
Yasouj, 75918-74934,
Iran.
E-mail: r.parvinian@yu.ac.ir
2Department
of Mathematics,
College of Sciences,
University of Yasouj,
Yasouj, 75918-74934,
Iran.
E-mail: Asadipour@yu.ac.ir
3Department
of Mathematics,
Ghor Institute of higher education,
Afghanistan.
E-mail: jumapazhman@gmail.com
Abstract:
Let H and K be infinite-dimensional complex Hilbert spaces, and B(H) (resp. B(K)) be the algebra of all bounded linear operators on H (resp. on K). For an operator T∈ B(H) and a vector h∈ H, let σT(h) denote the local spectrum of T at h. For two nonzero vectors h0∈ H and k0∈ K, we show that if two maps φ1 and φ2 from B(H) into B(K) satisfy
σφ1(T)φ2(S)*(k0)= σTS*(h0})
for all T, S ∈ B(H), and their range containing all operators of rank at most two, then there exist bijective linear maps P : H→ K and Q : K→ H such that φ1(T) = PTQ and φ2(T)* =Q-1T*P-1 for all T ∈ B(H). Also, we obtain some interesting results in this direction.
Paper's Title:
Application of Chebyshev Polynomials to Volterra-Fredholm Integral Equations
Author(s):
Aissa Lakhal, Mostefa Nadir and Mohamed Nasseh Nadir
Department of Mathematics,
Faculty of Mathematics and
Informatics,
University of Msila,
Algeria.
E-mail:
aissa.lakhal@univ-msila.dz
mostefa.nadir@univ-msila.dz
nadir.mohamednasseh@yahoo.com
URL: https://www.mostefanadir.com
Abstract:
The goal of this work is to examine the numerical solution of linear Volterra-Fredholm integral equations of the second kind using the first, second, third and fourth Chebyshev polynomials. Noting that, the approximate solution is given in the form of series which converges to the exact one. Numerical examples are compared with other methods, in order to prove the applicability and the efficiency of this technical.
Paper's Title:
On Statistically Φ-Convergence
Author(s):
Supama
Department of Mathematics,
Gadjah Mada
University,
Yogyakarta 55281,
Indonesia.
E-mail: supama@ugm.ac.id
Abstract:
The idea of statistical convergence was introduced by Antoni Zygmund in 1935. Based on in the idea of Zygmund, Henry Fast and Hugo Steinhaus independently introduced a concept of statistical convergence as a generalization of an ordinary convergence in the same year 1951. In this paper, by using the Orlicz function, we introduce a concept of statistical Φ-convergence, as a generalization of the statistical convergence. Further, we observe some basic properties and some topological properties of the statistical Φ-convergent sequences
Paper's Title:
A Unifying View of Some Banach Algebras
Author(s):
R. Kantrowitz
Mathematics & Statistics Department,
Hamilton College,
198 College Hill Road,
Clinton, NY 13323, USA.
E-mail: rkantrow@hamilton.edu
Abstract:
The purpose of this article is to shed light on a unifying framework for some normed algebras and, in particular, for some Banach algebras. The focus is on linear operators T between normed algebras X and Y and specified subalgebras A of Y. When the action of T on products in X satisfies a certain operative equation, the subspace T-1(A) is stable under the multiplication of X and is readily equipped with a family of canonical submultiplicative norms. It turns out that many familiar and important spaces are encompassed under this versatile perspective, and we offer a sampling of several such. In this sense, the article presents an alternative lens through which to view a host of normed algebras. Moreover, recognition that a normed linear space conforms to this general structure provides another avenue to confirming that it is at once stable under multiplication and also outfitted with an abundance of equivalent submultiplicative norms.
Paper's Title:
Semigroup of Linear Operator In Bicomplex Scalars
Author(s):
Stanzin Kunga, Amjad Ali and Aditi Sharma
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: stanzinkunga19@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail:
amjadladakhi687@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: aditi.sharmaro@gmail.com
Abstract:
In this paper, we have studied the generators of C0-semigroups of bicomplex linear operators on BC-Banach modules. This work is based on [5].
Paper's Title:
Results on Bounds of the Spectrum of Positive Definite Matrices by Projections
Author(s):
P. Singh, S. Singh, V. Singh
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
E-mail: singhp@ukzn.ac.za
University of South Africa, Department of
Decision Sciences,
PO Box 392, Pretoria, 0003,
South Africa.
E-mail: singhs2@unisa.ac.za
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
E-mail: singhv@ukzn.ac.za
Abstract:
In this paper, we develop further the theory of trace bounds and show that in some sense that the earlier bounds obtained by various authors on the spectrum of symmetric positive definite matrices are optimal. Our approach is by considering projection operators, from which several mathematical relationships may be derived. Also criteria for positive lower bounds are derived.
Paper's Title:
Some Ostrowski Type Inequalities for Two Cos-Integral Transforms of Absolutely Continuous Functions
Author(s):
S. S. Dragomir and G. Sorrentino
Mathematics, College Sport, Health and
Engineering,
Victoria University, PO Box 14428,
Melbourne City, MC 8001,
Australia.
DST-NRF Centre of Excellence in the
Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
E-mail: sever.dragomir@vu.edu.au
URL: http://rgmia.org/dragomir
Mathematics, First Year College,
Victoria University, PO Box 14428,
Melbourne City, MC 8001,
Australia.
Abstract:
For a Lebesgue integrable function f:[a,b] ⊂[0,π]→C
we consider the cos-integral transforms
and
We provide in this paper some upper bounds for the quantities
and
for
x ∈ [ a,b], in terms of the p-norms of the derivative
f ' for absolutely continuous functions f:[a,b] ⊂[0,π]→C.
Applications for approximating Steklov cos-average functions and Steklov
split cos-average functions are also provided.
Paper's Title:
Li-Yorke and Expansivity for Composition Operators on Lorentz Space
Author(s):
Rajat Singh and Romesh Kumar
Department of Mathematics,
University of Jammu,
Jammu 180006,
INDIA.
E-mail: rajat.singh.rs634@gmail.com
Department of Mathematics,
University of Jammu,
Jammu 180006,
INDIA.
E-mail: romeshmath@gmail.com
Abstract:
In this paper, we investigate Li-Yorke composition operators and some of its variations on Lorentz spaces. Further, we also study expansive composition operators on these spaces. The work of the paper is essentially based on the work in [3], [6], [8] and [15].
Paper's Title:
Jordan Canonical Form of Interval Matrices and Applications
Author(s):
S. Hema Surya, T. Nirmala and K. Ganesan
Department of Mathematics, College of
Engineering and Technology,
SRM Institute of Science and Technology,
Kattankulathur,
Chennai-603203,
India.
E-mail: nirmalat@srmist.edu.in
URL:
https://www.srmist.edu.in/faculty/dr-t-nirmala/
Abstract:
A square interval matrix over R can be converted to diagonal form if certain prerequisites are satisfied. However not all square matrices can be diagonalized. As a consequence, we strive the next simplest form to which it can be reduced while retaining important properties such as eigenvalues, rank, nullity, and so on. It turns out that any real interval matrix has a Jordan Canonical Form (JCF) over E if it has n interval eigenvalues in IR. We discuss in this paper a method for computing the Jordan canonical form of an interval matrix using a new pairing technique and a new type of interval arithmetic that will make classifying and analyzing interval matrices easier and more efficient. We conclude with a numerical example that supports the theory and application of predator-prey model.
Paper's Title:
Corrigendum for Differential Equations for Indicatrices, Spacelike and Timelike Curves
Author(s):
Sameer, Pradeep Kumar Pandey
Department of Mathematics,
Jaypee University of Information Technology,
Solan, Himachal Pradesh,
India.
E-mail: sksameer08@gmail.com,
pandeypkdelhi@gmail.com
ABSTRACT NOT FOUND. WEBSITE ERROR
Abstract:
Paper's Title:
Eigenvalue Bounds based on Projections
Author(s):
Pravin Singh, Shivani Singh, Virath Singh
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
University of South Africa,
Department of Decision Sciences, PO Box 392,
Pretoria,0003,
South Africa.
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
E-mail:
singhp@ukzn.ac.za,
singhs2@unisa.ac.za,
singhv@ukzn.ac.za
Abstract:
In this paper, we derive expressions for the bounds of the extremal eigenvalues of positive definite matrices. Our approach is to use a symmetric projection operator onto an n-2 dimensional subspace of the real space of n tuples. These bounds are based on traces of the matrix and its powers. They are relatively easy and inexpensive to compute.
Paper's Title:
On Automorphisms and Bi-derivations of Semiprime Rings
Author(s):
Abu Zaid Ansari, Faiza Shujat, Ahlam Fallatah
Department of Mathematics,
Faculty of Science,
Islamic University of Madinah, Madinah
K.S.A.
E-mail: ansari.abuzaid@gmail.com,
ansari.abuzaid@iu.edu.sa
Department of Mathematics
Faculty of Science
Taibah University, Madinah,
K.S.A.
E-mail: faiza.shujat@gmail.com,
fullahkhan@taibahu.edu.sa
Department of Mathematics
Faculty of Science
Taibah University, Madinah,
K.S.A.
E-mail: Afallatah@taibahu.edu.sa
Abstract:
In this article, our goal is to figure out a functional equation involving automorphisms and bi-derivations on certain semiprime ring. Also, we characterize the structure of automorphism, in case of prime rings.
Paper's Title:
A New Look at the Equations of the Calculus of Variations
Author(s):
Olivier de La Grandville
Faculty of Economics, Goethe University
Frankfurt,
Theodore Adorno Platz 4, 60323 Frankfurt,
Germany.
E-mail: odelagrandville@gmail.com
Abstract:
We first offer an entirely new way to derive the celebrated Euler equation of the calculus of variations. The advantage of this approach is two-fold. On the one hand, it entirely eschews the two hurdles encountered by Lagrange, which become challenging in the case of elaborate functionals: getting rid of the arbitrary character of the perturbation given to the optimal function, and demonstrating the fundamental lemma of the calculus of variations. On the other hand, it leads in a direct way to the remarkable discovery made by Robert Dorfman ( 1969) when he introduced a modified Hamiltonian, which we called a Dorfmanian (2018) to honor his memory. In turn, extending the Dorfmanian enables to obtain readily the fundamental equations of the calculus of variations for the optimization of high-order functionals, or multiple integrals.
Paper's Title:
Solving Strongly Nonlinear Fractional Fredholm Integral-Differential Equations in Caputo's Sense Using the SBA Method
Author(s):
Germain Kabore1, Bakari Abbo2, Ousseni So3 and Blaise Some1
1Laboratoire
d'Analyse Numerique, Informatique et de Biomathmathiques (L.N.I.BIO),
Universite Joseph Ki-Zerbo,
Burkina Faso.
E-mail: germainkabore982@gmail.com,
blaisesomeouaga1@gmail.com
2University
of N'Damena, Tchad.
E-mail: bakariabbo@yahoo.fr
3Laboratoire
d'Analyse Numerique, Informatique et de Biomathemathiques (L.N.I.BIO),
Ecole Normale Superieure,
Burkina Faso.
E-mail: sousseni@yahoo.fr
Abstract:
The work addressed in this article consists in constructing the exact solutions, where they exist, of fractional Fredholm-type integro-differential equations in the sense of Caputo. Our results are obtained using the SBA method. The simplification of the approach, the analysis of its convergence, and the generalization of this method to these types of highly nonlinear equations constitute our scientific contribution.
Paper's Title:
Analytical and Numerical Solutions of the Inhomogenous Wave Equation
Author(s):
T. Matsuura and S. Saitoh
Department of Mechanical Engineering, Faculty of Engineering,
Gunma University, Kiryu 376-8515, Japan
matsuura@me.gunma-u.ac.jp
Department of Mathematics, Faculty of Engineering,
Gunma University, Kiryu 376-8515, Japan
ssaitoh@math.sci.gunma-u.ac.jp
Abstract:
In this paper, by a new concept and method we give approximate
solutions of the inhomogenous wave equation on multidimensional spaces.
Numerical experiments are conducted as well.
Paper's Title:
Norm Estimates for the Difference between Bochner’s Integral and the Convex Combination of Function’s Values
Author(s):
P. Cerone, Y.J. Cho, S.S. Dragomir, J.K. Kim, and S.S. Kim
School of
Computer Science and Mathematics,
Victoria University of Technology,
Po Box 14428, Mcmc 8001, Victoria, Australia.
pietro.cerone@vu.edu.au
URL:
http://rgmia.vu.edu.au/cerone/index.html
Department of
Mathematics Education, College of Education,
Gyeongsang National University, Chinju 660-701, Korea
yjcho@nongae.gsnu.ac.kr
School of
Computer Science and Mathematics,
Victoria University of Technology,
Po Box 14428, Mcmc 8001, Victoria, Australia.
sever.dragomir@vu.edu.au
URL:
http://rgmia.vu.edu.au/SSDragomirWeb.html
Department of
Mathematics, Kyungnam University,
Masan,, Kyungnam 631-701, Korea
jongkyuk@kyungnam.ac.kr
Department of
Mathematics, Dongeui University,
Pusan 614-714, Korea
sskim@dongeui.ac.kr
Abstract:
Norm estimates are developed between the Bochner integral of a vector-valued function in Banach spaces having the Radon-Nikodym property and the convex combination of function values taken on a division of the interval [a, b].
Paper's Title:
Positive Solution For Discrete Three-Point Boundary Value
Problems
Author(s):
Wing-Sum Cheung And Jingli Ren
Department of Mathematics,
The University of Hong Kong,
Pokfulam, Hong Kong
wscheung@hku.hk
Institute of Systems Science,
Chinese Academy of Sciences,
Beijing 100080, P.R. China
renjl@mx.amss.ac.cn
Abstract:
This paper is concerned with the existence of positive solution to the discrete three-point boundary value problem
,
where
, and f is allowed to change sign. By constructing
available operators, we shall apply the method of lower solution and the method
of topology degree to obtain positive solution of the above problem for
on a suitable interval.
The associated Green’s function is first given.
Paper's Title:
Error estimates for aproximations of the Fourier transform of functions in Lp spaces
Author(s):
A. Aglic
Aljinovic and J. Pecaric Department of Applied Mathematics,
Faculty of Electrical Engineering and Computing,
University Of Zagreb, Unska 3, 10 000 Zagreb,
Croatia
andrea@zpm.fer.hr
Faculty of Textile Technology,
University of Zagreb, Pierottijeva 6, 10000 Zagreb,
Croatia
pecaric@hazu.hr
Abstract:
New inequalities concerning the Fourier transform are given. Estimates of the difference between two Fourier transforms and even bounds to the associated numerical quadrature formulae are provided as well.
Paper's Title:
New Proofs of the Grüss Inequality
Author(s):
A.Mc.D. Mercer
and Peter R.
Mercer
Dept. Mathematics and Statistics,
University of Guelph, Guelph, Ontario,
Canada.
amercer@reach.net
Dept. Mathematics,
S.U.N.Y. College at Buffalo, Buffalo, NY,
U.S.A.
mercerpr@math.buffalostate.edu
Abstract:
We present new proofs of the Grüss inequality in its original form and in its linear functional form.
Paper's Title:
Generalizations of two theorems on absolute summability methods
Author(s):
H.S. Özarslan and
H.N. Öğdük
Department of Mathematics,
Erciyes University, 38039 Kayseri,
Turkey
seyhan@erciyes.edu.tr
nogduk@erciyes.edu.tr
URL:
http://fef.erciyes.edu.tr/math/hikmet.htm
Abstract:
In this paper two theorems on 
summability methods, which generalize two theorems of Bor on 
summability methods, have been proved.
Paper's Title:
New Coincidence and Fixed Point Theorems for Strictly Contractive Hybrid Maps
Author(s):
S. L. Singh and Amal M. Hashim
21, Govind Nagar, Rishikesh 249201,
Ua, India
vedicmri@sancharnet.in
Dept. of Math., College of Science,
Univ. of Basarah,
Iraq.
Abstract:
The purpose of this paper is to study the (EA)-property and noncompatible maps
of a hybrid pair of single-valued and multivalued maps in fixed point considerations. Such maps
have the remarkable property that they need not be continuous at their common fixed points. We
use this property to obtain some coincidence and fixed point theorems for strictly contractive
hybrid maps without using their continuity and completeness or compactness of the space.
Paper's Title:
Quantitative Estimates for Positive Linear Operators Obtained by Means of Piecewise Linear Functions
Author(s):
Vasile Mihesan
Technical University of Cluj-Napoca,
Department of Mathematics,
Str. C. Daicoviciu 15,
Cluj-Napoca,
Romania
Vasile.Mihesan@math.utcluj.ro
Abstract:
In this paper we obtain estimates for the remainder in approximating continuous
functions by positive linear operators, using piecewise linear functions.
Paper's Title:
Classes of Meromorphic p-valent Parabolic Starlike Functions with Positive Coefficients
Author(s):
S. Sivaprasad Kumar, V. Ravichandran, and G. Murugusundaramoorthy
Department of Applied Mathematics
Delhi College of Engineering,
Delhi 110042, India
sivpk71@yahoo.com
School of Mathematical Sciences
Universiti Sains Malaysia
11800 USM Penang
Malaysia
vravi@cs.usm.my
URL: http://cs.usm.my/~vravi
Department of Mathematics
Vellore Institute of Technology (Deemed University)
Vellore 632 014, India
gmsmoorthy@yahoo.com
Abstract:
In the present paper, we consider two general subclasses of meromorphic p-valent starlike functions with positive coefficients and obtain a necessary and sufficient condition for functions to be in these classes. Also we obtain certain other related results as a consequences of our main results.
Paper's Title:
Boundedness for Vector-Valued Multilinear Singular Integral Operators on Triebel-Lizorkin Spaces
Author(s):
Liu Lanzhe
College of Mathematics
Changsha University of Science and Technology,
Changsha 410077,
P.R. of China.
lanzheliu@263.net
Abstract:
In this paper, the boundedness for some vector-valued multilinear operators associated to certain
fractional singular integral operators on Triebel-Lizorkin space are obtained. The operators include Calderón-Zygmund
singular integral operator and fractional integral operator.
Paper's Title:
A relation between nuclear cones and full nuclear cones
Author(s):
G. Isac and A. B. Nemeth
Department of Mathematics,
Royal Military College of Canada,
P. O. Box 17000 STN Forces Kingston, Ontario,
Canada K7K 7B4.
isac-g@rmc.ca
Faculty of Mathematics and Computer Science,
Babes-Bolyai University,
3400 Cluj-Napoca,
Romania.
nemab@math.ubbcluj.ro
Abstract:
The notion of nuclear cone in locally convex spaces corresponds to the notion of well based cone in normed spaces. Using the bipolar theorem from locally convex spaces it is proved that every closed nuclear cone is a full nuclear cone. Thus every closed nuclear cone can be associated to a mapping from a family of continuous seminorms in the space to the topological dual of the space. The relation with Pareto efficiency is discussed.
Paper's Title:
Parameter dependence of the solution of second order nonlinear ODE's via Perov's fixed point theorem
Author(s):
A. M. Bica, S. Muresan and G. Grebenisan
University of Oradea,
Str. Armatei Romane no.5, 410087,
Oradea, Romania.
smbica@yahoo.com
smuresan@uoradea.ro
grebe@uoradea.ro
Abstract:
Using the Perov's fixed point theorem, the smooth dependence by parameter of
the solution of a two point boundary value problem corresponding to nonlinear
second order ODE's is obtained.
Paper's Title:
Oscillations of First Order Linear Delay Difference Equations
Author(s):
G. E. Chatzarakis and I. P. Stavroulakis
Department of Mathematics, University of Ioannina,
451 10, Greece
ipstav@cc.uoi.gr
Abstract:
Consider the first order linear delay difference equation of
the form 
where
is
a sequence of nonnegative real numbers, k is a positive integer and 
denotes
the forward difference operator 
New
oscillation criteria are established when the well-known oscillation conditions
and
are
not satisfied. The results obtained essentially improve known results in the
literature.
Paper's Title:
A Reverse
of the Triangle Inequality in Inner Product Spaces and Applications for
Polynomials
Author(s):
I. Brnetić, S. S. Dragomir, R. Hoxha and J. Pečarić
Department of Applied Mathematics, Faculty of Electrical
Engineering and Computing,
University of Zagreb, Unska 3, 10 000 Zagreb,
Croatia
andrea@zpm.fer.hr
School of Computer Science & Mathematics, Victoria University
Po Box 14428, Melbourne Vic 8001
Australia
sever.dragomir@vu.edu.au
URL:http://rgmia.vu.edu.au/dragomir
Faculty of Applied Technical Sciences, University of Prishtina,
Mother
Theresa 5, 38 000 Prishtina
Kosova
razimhoxha@yahoo.com
Faculty of Textile Technology, University of Zagreb,
Pierottijeva 6, 10000
Zagreb,
Croatia
pecaric@hazu.hr
Abstract:
A reverse of the triangle inequality in inner product spaces related to the
celebrated Diaz-Metcalf inequality with applications for complex polynomials
is given.
Paper's Title:
On Vector Variational Inequality Problem in Terms of Bifunctions
Author(s):
C. S. Lalitha and Monika Mehta
Department of Mathematics, Rajdhani College,
Department of Mathematics, Satyawati College,
University of Delhi, Raja Garden,
Delhi 110015, India
cslalitha@rediffmail.com
University Of Delhi, Ashok Vihar,
Phase-III, Delhi 110052, India
mridul_in@yahoo.com
Abstract:
In this paper, we consider a generalized vector variational
inequality problem expressed in terms of a bifunction and establish
existence theorems for this problem by using the concepts of cone
convexity and cone strong quasiconvexity and employing the
celebrated Fan's Lemma. We also give two types of gap functions for this problem.
Paper's Title:
Algebraic Approach to the Fractional Derivatives
Author(s):
Kostadin Trenčevski and Živorad Tomovski
Institute of Mathematics,
St. Cyril and Methodius University,
P.O. Box 162, 1000 Skopje,
Macedonia
kostatre@iunona.pmf.ukim.edu.mk
Abstract:
In this paper we introduce an alternative definition of the fractional derivatives and also a characteristic class of so called ideal functions, which admit arbitrary fractional derivatives (also integrals). Further some ideal functions are found, which lead to representations of the Bernoulli and Euler numbers Bk and Ek for any real number k, via fractional derivatives of some functions at x=0.
Paper's Title:
A Stability of the G-type Functional Equation
Author(s):
Gwang Hui Kim
Department of Mathematics, Kangnam University
Suwon 449-702, Korea.
ghkim@kangnam.ac.kr
Abstract:
We will investigate the stability in the sense of G
Paper's Title:
Numerical Studies on Dynamical Systems Method for Solving Ill-posed Problems with Noise
Author(s):
N. H. Sweilam and A. M. Nagy
Mathematics Department, Faculty of Science,
Mathematics Department, Faculty of Science,
Cairo University,
Giza, Egypt.
n_sweilam@yahoo.com
Benha University,
Benha, Egypt.
abdelhameed_nagy@yahoo.com
Abstract:
In this paper, we apply the dynamical systems method proposed by
A. G. RAMM, and the the variational regularization method to
obtain numerical solution to some ill-posed problems with noise.
The results obtained are compared to exact solutions. It is found
that the dynamical systems method is preferable because it is
easier to apply, highly stable, robust, and it always converges to
the solution even for large size models.
Paper's Title:
Komatu Integral Transforms of Analytic Functions Subordinate to Convex Functions
Author(s):
T. N. Shanmugam and C. Ramachandran
Department of Mathematics, College of Engineering,
Anna University, Chennai-600 025, Tamilnadu,
India
shan@annauniv.edu
Department of Mathematics, College of Engineering,
Anna University, Chennai-600 025, Tamilnadu,
India
crjsp2004@yahoo.com
Abstract:
In this paper, we consider the class A of the functions f(z) of the form
which are analytic in an open disk
has some property. Certain inclusion and the closure properties like convolution with convex univalent function etc. are studied.
and study certain subclass of the class A, for which
Paper's Title:
Necessary and Sufficient Conditions for Uniform Convergence and Boundedness of a General Class of Sine Series
Author(s):
Laszlo Leindler
Bolyai Institute, University of Szeged,
Aradi Vértanúk tere 1,
H-6720 Szeged,
Hungary.
leindler@math.u-szeged.hu
Abstract:
For all we know theorems pertaining to sine series with coefficients from the
class γGBVS give only sufficient
conditions. Therefore we define a subclass of
Paper's Title:
On an Integral Inequality of the Hardy-Type
Author(s):
C. O. Imoru and A. G. Adeagbo-Sheikh
Department of Mathematics
Obafemi Awolowo University, Ile-Ife, Nigeria.
cimoru@oauife.edu.ng
asheikh@oauife.edu.ng
Abstract:
In this paper, we obtain an integral inequality which extends Shum's and Imoru's generalization of Hardy's Inequality. Our main tool is Imoru's adaptation of Jensen's Inequality for convex functions.
Paper's Title:
Oscillation and Boundedness of Solutions to First and Second Order Forced Dynamic Equations with Mixed Nonlinearities
Author(s):
Ravi P. Agarwal and Martin Bohner
Department of Mathematical Sciences, Florida Institute of Technology
Melbourne, FL 32901,
U.S.A.
bohner@mst.edu
URL:http://web.mst.edu/~bohner
Department of Economics and Finance, Missouri University of Science and Technology
Rolla, MO 65401,
U.S.A.
agarwal@fit.edu
Abstract:
Some oscillation and boundedness criteria for solutions to certain
first and second order forced dynamic equations
with mixed nonlinearities are established. The main tool in the proofs
is an inequality due to Hardy, Littlewood and Pólya.
The obtained results can be applied to differential equations,
difference equations and q-difference equations. The results
are illustrated with numerous examples.
Paper's Title:
The Invariant Subspace Problem for Linear Relations on Hilbert Spaces
Author(s):
Daniel Grixti-Cheng
Department of Mathematics and Statistics,
The University of Melbourne,
Melbourne, VIC, 3010
Australia.
D.Grixti@ms.unimelb.edu.au
Abstract:
We consider the invariant subspace problem for linear relations on Hilbert spaces with the aim of promoting interest in the problem as viewed from the theory of linear relations. We present an equivalence between the single valued and multivalued invariant subspace problems and give some new theorems pertaining to the invariant subspace problem for linear relations on a Hilbert space.
Paper's Title:
On Stable Numerical Differentiation
Author(s):
N. S. Hoang and A. G. Ramm
Mathematics Department, Kansas State University Abstract:
Based on a regularized Volterra equation, two different approaches for numerical differentiation are considered.
The first approach consists of solving a regularized Volterra equation while the second approach is based on solving a disretized version of the regularized Volterra equation.
Numerical experiments show that these methods are efficient and compete favorably with the variational regularization method for stable calculating the derivatives of noisy functions.
Paper's Title:
The Bernoulli Inequality in Uniformly
Complete f-algebras with Identity Author(s):
Adel Toumi and Mohamed Ali Toumi
Laboratoire de Physique des Liquides Critiques, Département de Physique, Faculté des Sciences de Bizerte,
7021, Zarzouna, Bizerte, TUNISIA
Département de Mathématiques, Faculté des Sciences de Bizerte, 7021, Zarzouna,
Bizerte, TUNISIA Abstract:
The main purpose of this paper is to establish with a constructive proof the
Bernoulli inequality: let A be a uniformly complete f-algebra
with e as unit element, let 1<p<∞, then (e+a)p≥e+pa for all a∈A+. As an
application we prove the Hölder
inequality for positive linear functionals on a uniformly complete f-algebra with identity by using the Minkowski inequality. Paper's Title:
Error Inequalities for Weighted Integration Formulae and Applications
Author(s):
Nenad Ujević and Ivan Lekić
Department of Mathematics Abstract:
Weighted integration formulae are derived. Error inequalities for the
weighted integration formulae are obtained. Applications to some special
functions are also given. Paper's Title:
The ε-Small Ball Drop Property
Author(s):
C. Donnini and A. Martellotti Dipartimento
di Statistica e Matematica per la Ricerca Economica,
{Dipartimento di Matematica e Informatica, Abstract:
We continue the investigation on classes of small sets in a
Banach space that give alternative formulations of the Drop
Property. The small sets here considered are the set having the
small ball property, and we show that for sets having non-empty
intrinsic core and whose affine hull contains a closed affine space
of infinite dimension the Drop Property can be equivalently
formulated in terms of the small ball property. Paper's Title:
Stability of a Mixed Additive, Quadratic and Cubic Functional Equation In Quasi-Banach Spaces
Author(s):
A. Najati and F. Moradlou
Department of Mathematics, Faculty of Sciences,
Faculty of Mathematical Sciences, Abstract:
In this paper we establish the general solution of a mixed additive,
quadratic and cubic functional equation and investigate the
Hyers--Ulam--Rassias stability of this equation in quasi-Banach
spaces. The concept of Hyers-Ulam-Rassias stability originated from
Th. M. Rassias' stability theorem that appeared in his paper: On the
stability of the linear mapping in Banach spaces, Proc. Amer. Math.
Soc. 72 (1978), 297--300. Paper's Title:
A Fixed Point Approach to
the Stability of the Equation Author(s):
Soon-Mo Jung
Mathematics Section, College of Science and Technology Abstract:
We will apply a fixed point method for proving the Hyers--Ulam stability of
the functional equation
Paper's Title:
Purely Unrectifiable Sets with Large Projections Author(s):
Harold R. Parks
Manhattan, KS 66506-2602,
U. S. A.
nguyenhs@math.ksu.edu
ramm@math.ksu.edu
URL:http://math.ksu.edu/~ramm
1: Paper Source
PDF document
Adel.Toumi@fst.rnu.tn
MohamedAli.Toumi@fsb.rnu.tn
1: Paper Source
PDF document
University of Split
Teslina 12/III, 21000 Split
CROATIA.
ujevic@pmfst.hr
ivalek@pmfst.hr
1: Paper Source
PDF document
Universitŕ degli Studi di Napoli "Parthenope",
Via Medina, 80133 Napoli,
Italy
chiara.donnini@uniarthenope.it
Universitŕ degli Studi di Perugia,
Via Pascoli - 06123 Perugia,
Italy.
amart@dipmat.unipg.it
URL:
www.dipmat.unipg.it/~amart/
1: Paper Source
PDF document
University of Mohaghegh Ardabili, Ardabil,
Iran
a.nejati@yahoo.com
University of Tabriz, Tabriz,
Iran
moradlou@tabrizu.ac.ir
1: Paper Source
PDF document
Hong-Ik
University, 339-701 Chochiwon
Republic of Korea.
smjung@hongik.ac.kr
.
1: Paper Source
PDF document
Department of Mathematics,
Oregon State University,
Corvallis, Oregon 97331--4605,
USA
parks@math.oregonstate.edu
URL: http://www.math.oregonstate.edu/people/view/parks/
Abstract:
For n≥2,
we give a construction of a compact
subset of 
that is dispersed enough that it is
purely unrectifiable, but that nonetheless
has an orthogonal projection that hits every
point of an (n-1)-dimensional unit cube.
Moreover, this subset has the additional
surprising property that
the orthogonal projection onto
any straight line in
is a set of positive
1-dimensional Hausdorff measure.
Paper's Title:
Hyers-Ulam-Rassias Stability
of a Generalized Jensen Functional Equation
Author(s):
A. Charifi, B. Bouikhalene, E. Elqorachi and A. Redouani
Department of
Mathematics, Faculty of Sciences,
Ibn Tofail University,
Kenitra, Morocco
charifi2000@yahoo.fr
bbouikhalene@yahoo.fr
Department of
Mathematics, Faculty of Sciences,
Ibn Zohr University,
Agadir, Morocco
elqorachi@hotmail.com
Redouani-ahmed@yahoo.fr
Abstract:
In this paper we obtain the Hyers-Ulam-Rassias stability for the generalized Jensen's functional equation in abelian group (G,+). Furthermore we discuss the case where G is amenable and we give a note on the Hyers-Ulam-stability of the K-spherical (n × n)-matrix functional equation.
Paper's Title:
Two Remarks on Commutators of Hardy Operator
Author(s):
Yasuo Komori-Furuya
School of High Technology for Human Welfare
Tokai University
317 Nishino Numazu, Shizuoka 410-0395 Japan
komori@wing.ncc.u-tokai.ac.jp
Abstract:
Fu and Lu showed that
the commutator of multiplication operator by b and
the n-dimensional Hardy operator
is bounded on Lp if b is in some CMO space.
We shall prove the converse of this theorem
and also prove that their result is optimal by giving a counterexample
Paper's Title:
Maximal Inequalities for Multidimensionally Indexed Demimartingales and the Hájek-Rényi Inequality for Associated Random Variables
Author(s):
Tasos C. Christofides and Milto Hadjikyriakou
Department of Mathematics and Statistics
University of Cyprus
P.O.Box 20537, Nicosia 1678, Cyprus
tasos@ucy.ac.cy
miltwh@gmail.com
Abstract:
Demimartingales and demisubmartingales introduced by
Newman and
Wright (1982) generalize the notion of martingales and
submartingales respectively. In this paper we define
multidimensionally indexed demimartingales and demisubmartingales
and prove a maximal inequality for this general class of random
variables. As a corollary we obtain a Hájek-Rényi inequality
for multidimensionally indexed associated random variables, the bound of which,
when reduced to the case of single index, is sharper than the bounds already
known in the literature.
Paper's Title:
The Best Upper Bound for Jensen's Inequality
Author(s):
Vasile Cirtoaje
Department of Automatic Control and Computers
University of Ploiesti
Romania.
Abstract:
In this paper we give the best upper bound for the weighted Jensen's discrete inequality applied to a convex function f defined on a closed interval I in the case when the bound depends on f, I and weights. In addition, we give a simpler expression of the upper bound, which is better than existing similar one.
Paper's Title:
A New Method for Comparing Closed Intervals
Author(s):
Ibraheem Alolyan
Department of Mathematics, College of Sciences,
King Saud University, P. O. Box 2455, Riyadh 11451,
Saudi Arabia
ialolyan@ksu.edu.sa
URL:http://faculty.ksu.edu.sa/ALolyan
Abstract:
The usual ordering ``≤" on R is a total ordering, that is, for any two real numbers in R, we can determine their order without difficulty. However, for any two closed intervals in R, there is not a natural ordering among the set of all closed intervals in R. Several methods have been developed to compare two intervals. In this paper, we define the μ-ordering which is a new method for ordering closed intervals.
Paper's Title:
An Lp Inequality for `Self-Reciprocal' Polynomials. II
Author(s):
M. A. Qazi
Department of Mathematics,
Tuskegee University,
Tuskegee, Alabama 36088
U.S.A.
Abstract:
The main result of this paper is a sharp integral mean inequality for the derivative of a `self-reciprocal' polynomial.
Paper's Title:
Bounds for Two Mappings Associated to
the Hermite-Hadamard Inequality
Author(s):
S. S. Dragomir1,2 and I. Gomm1
1Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428,
Melbourne City, MC 8001,
Australia.
2School of Computational & Applied Mathematics,
University of
the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
sever.dragomir@vu.edu.au
ian.gomm@vu.edu.au
URL: http://rgmia.org/dragomir
Abstract:
Some inequalities concerning two mappings associated to the celebrated Hermite-Hadamard integral inequality for convex function with applications for special means are given.
Paper's Title:
Some Inequalities Concerning Derivative and Maximum Modulus of Polynomials
Author(s):
N. K. Govil, A. Liman and W. M. Shah
Department of Mathematics & Statistics,
Auburn University, Auburn,
Alabama 36849-5310,
U.S.A
Department of Mathematics,
National Institute of Technology,
Srinagar, Kashmir,
India - 190006
Department of Mathematics,
Kashmir University,
Srinagar, Kashmir,
India - 190006
govilnk@auburn.edu
abliman22@yahoo.com
wmshah@rediffmail.com
Abstract:
In this paper, we prove some compact generalizations of some well-known Bernstein type inequalities concerning the maximum modulus of a polynomial and its derivative in terms of maximum modulus of a polynomial on the unit circle. Besides, an inequality for self-inversive polynomials has also been obtained, which in particular gives some known inequalities for this class of polynomials. All the inequalities obtained are sharp.
Paper's Title:
On the Three Variable Reciprocity Theorem and Its Applications
Author(s):
D. D. Somashekara and D. Mamta
Department of Studies in Mathematics,
University of Mysore,
Manasagangotri, Mysore-570 006
India
dsomashekara@yahoo.com
Department of Mathematics,
The National Institute of Engineering,
Mysore-570 008,
India
mathsmamta@yahoo.com
Abstract:
In this paper we show how the three variable reciprocity theorem can be easily derived from the well known two variable reciprocity theorem of Ramanujan by parameter augmentation. Further we derive some q-gamma, q-beta and eta-function identities from the three variable reciprocity theorem.
Paper's Title:
Harmonic Functions with Positive Real Part
Author(s):
Sďbel Yalçin
Uludag Universitesi,
Fen Edebiyat Fakultesi, Matematik Bolumu,
16059 Bursa,
Turkey
Abstract:
In this paper, the class of harmonic functions f=h+{g} with positive real part and normalized by f(ζ )=1, (|ζ|<1) is studied, where h and g are analytic in U={z:|z|<1}. Some properties of this class are searched. Sharp coefficient relations are given for functions in this class. On the other hand, the author make use of Alexander integral transforms of certain analytic functions (which are starlike with respect to f(ζ)) with a view to investigating the construction of sense preserving, univalent and close to convex harmonic functions.
Paper's Title:
Certain Coefficient Estimates for Bi-univalent Sakaguchi Type Functions
Author(s):
B. Srutha Keerthi, S. Chinthamani
Department of Applied Mathematics,
Sri Venkateswara College of Engineering,
Sriperumbudur, Chennai - 602105,
India
Abstract:
Estimates on the initial coefficients are obtained for normalized analytic functions f in the open unit disk with f and its inverse g = f-1 satisfying the conditions that zf'(z) / f(z) and zg'(z) / g(z) are both subordinate to a starlike univalent function whose range is symmetric with respect to the real axis. Several related classes of functions are also considered, and connections to earlier known results are made.
Paper's Title:
Properties of Certain Multivalent Functions Involving Ruscheweyh Derivatives
Author(s):
N-Eng Xu and Ding-Gong Yang
Department of Mathematics,
Changshu Institute of Technology,
Changshu, Jiangsu 215500,
China
Abstract:
Let Ap(p∈ N) be the class of functions
which are analytic
in the unit disk. By virtue of the Ruscheweyh derivatives we introduce the new
subclasses Cp(n,α,β,λ,μ) of Ap. Subordination relations, inclusion relations,
convolution properties and a sharp coefficient estimate are
obtained. We also give a sufficient condition for a function to be
in Cp(n,α,β,λ,μ)
Paper's Title:
Certain Compact Generalizations of Well-Known Polynomial Inequalities
Author(s):
N. A. Rather and Suhail Gulzar
Department of Mathematics,
University of Kashmir, Hazratbal Srinagar-190006,
India.
Abstract:
In this paper, certain sharp compact generalizations of well-known Bernstien-type inequalities for polynomials, from which a variety of interesting results follow as special cases, are obtained.
Paper's Title:
Uniform Continuity and k-Convexity
Author(s):
Adel Afif Abdelkarim
Mathematics Department, Faculty of Science,
J
erash University, Jerash
Jordan.
Abstract:
A closed arcwise-connected subset A of Rn is called k-convex if for each positive number a and for all elements x and y in A there is a positive number b such that if the norm of x-y is less than or equal to b then the length of the shortest curve l(x,y) in A is less than k times the norm of x-y plus a. We show that a union of two non disjoint closed finite convex subsets need not be k-convex. Let f(x) be a uniformly continuous functions on a finite number of closed subsets A_{1},...,A_{n} of R^{n} such that the union of A_{j},...,A_{n},j=1,...,n-1 is k-convex. We show that f is uniformly continuous on the union of the sets A_{i},i=1,...,n. We give counter examples if this condition is not satisfied. As a corollary we show that if f(x) is uniformly continuous on each of two closed convex sets A,B then f(x) is uniformly continuous on the union of A and B.
Paper's Title:
Application of Equivalence Method to Classify Monge-Ampčre Equations of Elliptic Type
Author(s):
Moheddine Imsatfia
E-mail: imsatfia@math.jussieu.fr
Abstract:
In this paper, we apply Cartan's equivalence method to give a local classification of Monge-Ampčre equations of elliptic type. Then we find a necessary and sufficient conditions such that a Monge-Ampčre equation is either contactomorphic to the Laplace equation or to an Euler-Lagrange equation.
Paper's Title:
On the Regularization of Hammerstein's type Operator Equations
Author(s):
E. Prempeh, I. Owusu-Mensah and K. Piesie-Frimpong
Department of Mathematics,
KNUST, Kumasi-
Ghana.
Department of Science Education,
University of Education,
Winneba
Department of Mathematics,
Presbyterian University College, Abetifi,
Ghana
E-mail: isaacowusumensah@gmail.com
E-mail: eprempeh.cos@knust.edu.gh
E-mail: piesie74@yahoo.com
Abstract:
We have studied Regularization of Hammerstein's Type Operator Equations in general Banach Spaces. In this paper, the results have been employed to establish regularized solutions to Hammerstein's type operator equations in Hilbert spaces by looking at three cases of regularization.
Paper's Title:
Ostrowski Type Fractional Integral Inequalities for Generalized (s,m,
Author(s):
Artion Kashuri and Rozana Liko
University of Vlora "Ismail Qemali",
Faculty of Technical Science,
Department of Mathematics, 9400,
Albania.
E-mail:
artionkashuri@gmail.com
E-mail: rozanaliko86@gmail.com
Abstract:
In the present paper, the notion of generalized (s,m,φ)-preinvex function is introduced and some new integral inequalities for the left hand side of Gauss-Jacobi type quadrature formula involving generalized (s,m,φ)-preinvex functions along with beta function are given. Moreover, some generalizations of Ostrowski type inequalities for generalized (s,m,φ)-preinvex functions via Riemann-Liouville fractional integrals are established.
Paper's Title:
Hermite-Hadamard Type Inequalities for k-Riemann Liouville Fractional Integrals Via Two Kinds of Convexity
Author(s):
R. Hussain1, A. Ali2, G. Gulshan3, A. Latif4 and K. Rauf5
1,2,3,4Department
of Mathematics,
Mirpur University of Science and Technology, Mirpur.
Pakistan.
E-mail1:
rashida12@gmail.com
E-mail2:
unigraz2009@yahoo.com
E-mail3:
ghazalagulshan@yahoo.com
E-mail4:
asialatif87@gmail.com
5Department
of Mathematics,
University of Ilorin, Ilorin,
Nigeria.
E-mail5:
krauf@unilorin.edu.ng
Abstract:
In this article, a fundamental integral identity including the first order derivative of a given function via k-Riemann-Liouville fractional integral is established. This is used to obtain further Hermite-Hadamard type inequalities involving left-sided and right-sided k-Riemann-Liouville fractional integrals for m-convex and (s,m)-convex functions respectively.
Paper's Title:
A Generalization of Viete's Infinite Product and New Mean Iterations
Author(s):
Ryo Nishimura
Department of Frontier Materials
Nagoya Institute of Technology
Gokiso-cho, Showa-ku, Nagoya
Aichi, 466-8555, Japan.
E-mail: rrnishimura@gmail.com
Abstract:
In this paper, we generalize Viéte's infinite product formula by use of Chebyshev polynomials. Furthermore, the infinite product formula for the lemniscate sine is also generalized. Finally, we obtain new mean iterations by use of these infinite product formulas.
Paper's Title:
A Note on Divergent Fourier Series and λ-Permutations
Author(s):
A. Castillo, J. Chavez and H. Kim
Tufts University,
Department of Mathematics,
Medford, MA 02155,
USA
E-mail: angel.castillo@tufts.edu
Texas Tech University,
Department of Mathematics and Statistics,
Lubbock, TX 79409,
USA
E-mail: josechavez5@my.unt.edu
University of Michigan-Dearborn,
Department of Mathematics and Statistics,
Dearborn, MI 48128,
USA.
E-mail: khyejin@umich.edu
Abstract:
We present a continuous function on [-π,π] whose Fourier series diverges and it cannot be rearranged to converge by a λ-permutation.
Paper's Title:
Generalized Weighted Trapezoid and Gr
Author(s):
Eze Raymond Nwaeze
Department of Mathematics,
Tuskegee University,
Tuskegee, AL 36088,
USA.
E-mail: enwaeze@mytu.tuskegee.edu
Abstract:
In this work, we obtain some new generalized weighted trapezoid and Grüss type inequalities on time scales for parameter functions. Our results give a broader generalization of the results due to Pachpatte in [14]. In addition, the continuous and discrete cases are also considered from which, other results are obtained.
Paper's Title:
A Note on Calderon Operator
Author(s):
Chunping Xie
Department of Mathematics,
Milwaukee School of Engineering,
1025 N. Broadway,
Milwaukee, Wisconsin 53202,
U. S. A.
E-mail: xie@msoe.edu
URL: http://www.msoe.edu/people/chunping.xie
Abstract:
We have shown that the Calderon operator is bounded on Morrey Spaces on R+. Also under certain conditions on the weight, the Hardy operator, the adjoint Hardy operator, and therefore the Caldern operator are bounded on the weighted Morrey spaces.
Paper's Title:
Euler Series Solutions for Linear Integral Equations
Author(s):
Mostefa Nadir and Mustapha Dilmi
Department of Mathematics,
University of Msila 28000,
ALGERIA.
E-mail: mostefanadir@yahoo.fr
E-mail: dilmiistapha@yahoo.fr
Abstract:
In this work, we seek the approximate solution of linear integral equations by truncation Euler series approximation. After substituting the Euler expansions for the given functions of the equation and the unknown one, the equation reduces to a linear system, the solution of this latter gives the Euler coefficients and thereafter the solution of the equation. The convergence and the error analysis of this method are discussed. Finally, we compare our numerical results by others.
Paper's Title:
Coefficient Estimates for Certain Subclasses of Bi-univalent Sakaguchi
Type Functions by using Faber Polynomial
Author(s):
P. Murugabharathi, B. Srutha Keerthi
Mathematics Division,
School of Advanced Sciences,
VIT Chennai, Vandaloor, Kelambakkam Road,
Chennai - 600 127, India.
E-mail: bharathi.muhi@gmail.com
E-mail: sruthilaya06@yahoo.co.in
Abstract:
In this work, considering a general subclass of bi-univalent Sakaguchi type functions, we determine estimates for the general Taylor-Maclaurin coefficients of the functions in these classes. For this purpose, we use the Faber polynomial expansions. In certain cases, our estimates improve some of those existing coefficient bounds.
Paper's Title:
Birkhoff-James orthogonality and Best Approximant in L1(X)
Author(s):
Mecheri Hacene and Rebiai Belgacem
Department of Mathematics and
Informatics,
LAMIS laboratory, University of Tebessa,
Algeria.
E-mail: mecherih2000@yahoo.fr
Department of Mathematics and
Informatics,
LAMIS laboratory, University of Tebessa,
Algeria.
E-mail: brebiai@gmail.com
Abstract:
Let X be a complex Banach space and let (X,ρ) be a positive measure space. The Birkhoff-James orthogonality is a generalization of Hilbert space orthogonality to Banach spaces. We use this notion of orthogonality to establish a new characterization of Birkhoff-James orthogonality of bounded linear operators in L1(X,ρ) also implies best approximation has been proved.
Paper's Title:
Invariant Subspaces Close to Almost Invariant Subspaces for Bounded Linear Operators
Author(s):
M. A. Farzaneh, A. Assadi and H. M. Mohammadinejad
Department of Mathematical and
Statistical Sciences,
University of Birjand,
PO Box 97175/615, Birjand,
Iran.
E-mail: farzaneh@birjand.ac.ir
Department of Mathematical and
Statistical Sciences,
University of Birjand,
PO Box 97175/615, Birjand,
Iran.
E-mail: assadi-aman@birjand.ac.ir
Department of Mathematical and
Statistical Sciences,
University of Birjand,
PO Box 97175/615, Birjand,
Iran.
E-mail: hmohammadin@birjand.ac.ir
Abstract:
In this paper, we consider some features of almost invariant subspace notion. At first, we restate the notion of almost invariant subspace and obtain some results. Then we try to achieve an invariant subspace completely close to an almost invariant subspace. Also, we introduce the notion of "almost equivalent subspaces" to simply the subject related to almost invariant subspaces and apply it.
Paper's Title:
The Conservativeness of Girsanov Transformed for Symmetric Jump-diffusion Process
Author(s):
Mila Kurniawaty and Marjono
Department of Mathematics,
Universitas Brawijaya,
Malang,
Indonesia.
E-mail: mila_n12@ub.ac.id,
marjono@ub.ac.id
Abstract:
We study about the Girsanov transformed for symmetric Markov processes with jumps associated with regular Dirichlet form. We prove the conservativeness of it by dividing the regular Dirichlet form into the "small jump" part and the "big jump" part.
Paper's Title:
A kind of Function Series and Its Applications
Author(s):
Yang Tianze
Mechanical Engineering,
Shandong University, Xinglongshan Campus,
Jinan, Shandong,
China.
E-mail: qdyangtianze@163.com
Abstract:
A kind of new function series is obtained in this paper. Their theorems and proofs are shown, and some applications are given. We give the expansion form of general integral and the series expansion form of function and the general expansion form of derivative. Using them in the mathematics,we get some unexpected result.
Paper's Title:
Hankel Operators on Copson's Spaces
Author(s):
Nicolae Popa
Institute of Mathematics of Romanian Academy,
P.O. BOX 1-764
RO-014700 Bucharest,
Romania.
E-mail: Nicolae.Popa@imar.ro, npopafoc@gmail.com
Abstract:
We give a characterization of boundedness of a Hankel matrix, generated by a pozitive decreasing sequence, acting on Copson's space cop(2).
Paper's Title:
On a New Class of Eulerian's Type Integrals Involving Generalized Hypergeometric Functions
Author(s):
Sungtae Jun, Insuk Kim and Arjun K. Rathie
General Education Institute,
Konkuk University, Chungju 380-701,
Republic of Korea.
Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Republic of Korea.
Department of Mathematics,
Vedant College of Engineering and Technology (Rajasthan Technical University),
Bundi-323021, Rajasthan,
India.
E-mail: sjun@kku.ac.kr, iki@wku.ac.kr, arjunkumarrathie@gmail.com
Abstract:
Very recently Masjed-Jamei and Koepf established interesting and useful generalizations of various classical summation theorems for the 2F1, 3F2, 4F3, 5F4 and 6F5 generalized hypergeometric series. The main aim of this paper is to establish eleven Eulerian's type integrals involving generalized hypergeometric functions by employing these theorems. Several special cases have also been given.
Paper's Title:
An Analytical Solution of Perturbed Fisher's Equation Using Homotopy Perturbation Method (HPM), Regular Perturbation Method (RPM) and Adomian Decomposition Method (ADM)
Author(s):
Moussa Bagayogo, Youssouf Minoungou, Youssouf Pare
Departement de Mathematique,
Universite Ouaga I Pr Joseph Ki-Zerbo,
Burkina Faso.
E-mail:
moussabagayogo94@gmail.com,
m.youl@yahoo.fr,
pareyoussouf@yahoo.fr.
Abstract:
In this paper, Homotopy Perturbation Method (HPM), Regular Pertubation Method (RPM) and Adomian decomposition Method (ADM) are applied to Fisher equation. Then, the solution yielding the given initial conditions is gained. Finally, the solutions obtained by each method are compared
Paper's Title:
Dynamical Analysis of HIV/AIDS Epidemic Model with Two Latent Stages, Vertical Transmission and Treatment
Author(s):
Nur Shofianah, Isnani Darti, Syaiful Anam
Mathematics Department,Faculty of
Mathematics and Natural Sciences.
University of Brawijaya,
Jl. Veteran, Malang 65145,
Indonesia.
E-mail:
nur_shofianah@ub.ac.id,
isnanidarti@ub.ac.id,
syaiful@ub.ac.id
Abstract:
We discuss about dynamical analysis of HIV/AIDS epidemic model with two latent stages, vertical transmission and treatment. In this model, the spreading of HIV occurs through both horizontal and vertical transmission. There is also treatment for individual who has been HIV infected. The latent stage is divided into slow and fast latent stage based on the immune condition which varies for each individual. Dynamical analysis result shows that the model has two equilibrium points: the disease-free equilibrium point and the endemic equilibrium point. The existence and global stability of equilibrium points depend on the basic reproduction number R0. When R0 <1, only the disease-free equilibrium point exists. If R0 >1, there are two equilibrium points, which are the disease-free equilibrium point and the endemic equilibrium point. Based on the result of stability analysis, the disease-free equilibrium point is globally asymptotically stable if R0 <1, while if R0 > 1 and p=q, the endemic equilibrium point will be globally asymptotically stable. In the end, we show some numerical simulations to support the analytical result.
Paper's Title:
Action of Differential Operators On Chirpsconstruct On L∞
Author(s):
Taoufik El Bouayachi and Naji Yebari
Laboratoire de Mathematiques et
applications,
Faculty of sciences and techniques, Tangier,
Morocco.
E-mail:
figo407@gmail.com,
yebarinaji@gmail.com
Abstract:
We will study in this work the action of differential operators on L∞ chirps and we will give a new definition of logarithmic chirp. Finally we will study the action of singular integral operators on chirps by wavelet characterization and Kernel method.
Paper's Title:
On an extension of Edwards's double integral with applications
Author(s):
I. Kim, S. Jun, Y. Vyas and A. K. Rathie
Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Republic of Korea.
General Education Institute,
Konkuk University,
Chungju 380-701,
Republic of Korea.
Department of Mathematics, School of
Engineering,
Sir Padampat Singhania University,
Bhatewar, Udaipur, 313601, Rajasthan State,
India.
Department of Mathematics,
Vedant College of Engineering and Technology,
(Rajasthan Technical University),
Bundi-323021, Rajasthan,
India.
E-mail: iki@wku.ac.kr
sjun@kku.ac.kr
yashoverdhan.vyas@spsu.ac.in
arjunkumarrathie@gmail.com
Abstract:
The aim of this note is to provide an extension of the well known and useful Edwards's double integral. As an application, new class of twelve double integrals involving hypergeometric function have been evaluated in terms of gamma function. The results are established with the help of classical summation theorems for the series 3F2 due to Watson, Dixon and Whipple. Several new and interesting integrals have also been obtained from our main findings.
Paper's Title:
Solving Two Point Boundary Value Problems by Modified Sumudu Transform Homotopy Perturbation Method
Author(s):
Asem AL Nemrat and Zarita Zainuddin
School of Mathematical Sciences,
Universiti Sains Malaysia,
11800 Penang,
Malaysia.
E-mail: alnemrata@yahoo.com
zarita@usm.my
Abstract:
This paper considers a combined form of the Sumudu transform with the modified homotopy perturbation method (MHPM) to find approximate and analytical solutions for nonlinear two point boundary value problems. This method is called the modified Sumudu transform homotopy perturbation method (MSTHPM). The suggested technique avoids the round-off errors and finds the solution without any restrictive assumptions or discretization. We will introduce an appropriate initial approximation and furthermore, the residual error will be canceled in some points of the interval (RECP). Only a first order approximation of MSTHPM will be required, as compared to STHPM, which needs more iterations for the same cases of study. After comparing figures between approximate, MSTHPM, STHPM and numerical solutions, it is found through the solutions we have obtained that they are highly accurate, indicating that the MSTHPM is very effective, simple and can be used to solve other types of nonlinear boundary value problems (BVPs).
Paper's Title:
The Concept of Convergence for 2-Dimensional Subspaces Sequence in Normed Spaces
Author(s):
M. Manuharawati, D. N. Yunianti, M. Jakfar
Mathematics Department, Universitas
Negeri Surabaya,
Jalan Ketintang Gedung C8,
Surabaya 60321,
Indonesia.
E-mail: manuharawati@unesa.ac.id,
dwiyunianti@unesa.ac.id,
muhammadjakfar@unesa.ac.id
Abstract:
In this paper, we present a concept of convergence of sequence, especially, of 2-dimensional subspaces of normed spaces. The properties of the concept are established. As consequences of our definition in an inner product space, we also obtain the continuity property of the angle between two 2-dimensional subspaces of inner product spaces.
Paper's Title:
Accuracy of Implicit DIMSIMs with Extrapolation
Author(s):
A. J. Kadhim, A. Gorgey, N. Arbin and N. Razali
Mathematics Department, Faculty of
Science and Mathematics,
Sultan Idris Education University,
35900 Tanjong Malim, Perak,
Malaysia
E-mail: annie_gorgey@fsmt.upsi.edu.my
Unit of Fundamental Engineering Studies,
Faculty of Engineering, Built Environment,
The National University of Malaysia,
43600 Bangi,
Malaysia.
Abstract:
The main aim of this article is to present recent results concerning diagonal implicit multistage integration methods (DIMSIMs) with extrapolation in solving stiff problems. Implicit methods with extrapolation have been proven to be very useful in solving problems with stiff components. There are many articles written on extrapolation of Runge-Kutta methods however fewer articles on extrapolation were written for general linear methods. Passive extrapolation is more stable than active extrapolation as proven in many literature when solving stiff problems by the Runge-Kutta methods. This article takes the first step by investigating the performance of passive extrapolation for DIMSIMs type-2 methods. In the variable stepsize and order codes, order-2 and order-3 DIMSIMs with extrapolation are investigated for Van der Pol and HIRES problems. Comparisons are made with ode23 solver and the numerical experiments showed that implicit DIMSIMs with extrapolation has greater accuracy than the method itself without extrapolation and ode23.
Paper's Title:
On The Degree of Approximation of Periodic Functions from Lipschitz and Those from Generalized Lipschitz Classes
Author(s):
Xhevat Z. Krasniqi
Faculty of Education,
University of Prishtina "Hasan Prishtina",
Avenue "Mother Theresa " no. 5, Prishtinë
10000,
Republic of Kosovo.
E-mail: xhevat.krasniqi@uni-pr.edu
Abstract:
In this paper we have introduced some new trigonometric polynomials. Using these polynomials, we have proved some theorems which determine the degree of approximation of periodic functions by a product of two special means of their Fourier series and the conjugate Fourier series. Many results proved previously by others are special case of ours.
Paper's Title:
On Subspace-Supercyclic Operators
Author(s):
Mansooreh Moosapoor
Assistant Professor,
Department of Mathematics,
Farhangian University, Tehran,
Iran.
E-mail: mosapor110@gmail.com
m.mosapour@cfu.ac.ir
Abstract:
In this paper, we prove that supercyclic operators are subspace-supercyclic and by this we give a positive answer to a question posed in ( L. Zhang, Z. H. Zhou, Notes about subspace-supercyclic operators, Ann. Funct. Anal., 6 (2015), pp. 60--68). We give examples of subspace-supercyclic operators that are not subspace-hypercyclic. We state that if T is an invertible supercyclic operator then Tn and T-n is subspace-supercyclic for any positive integer n. We give two subspace-supercyclicity criteria. Surprisingly, we show that subspace-supercyclic operators exist on finite-dimensional spaces.
Paper's Title:
Some Properties of (co)homology of Lie Algebra
Author(s):
Alaa Hassan Noreldeen Mohamed, Hegagi Mohamed Ali, Samar Aboquota
Department of Mathematics,
Faculty of
Science,
Aswan University, Aswan,
Egypt.
E-mail: ala2222000@yahoo.com
hegagi_math@aswu.edu.eg
scientist_samar@yahoo.com
Abstract:
Lie algebra is one of the important types of algebras. Here, we studied lie algebra and discussed its properties. Moreover, we define the Dihedral homology of lie algebra and prove some relations among Hochschild, Cyclic and Dihedral homology of lie algebra. Finally, we prove the Mayer-vetories
sequence on Dihedral homology of lie algebra and proved that
.
Paper's Title:
Hankel Functional Connected to Lemniscate of Bernoulli
Author(s):
K. Ramanuja Rao, Rajnesh Lal and Kaushal Singh
Fiji National University,
Department of Mathematics & Statistics,
P.O. Box 5529, Lautoka,
Fiji.
E-mail: ramanuja.kotti@fnu.ac.fj
rajnesh.lal@fnu.ac.fj
kaushal.singh@fnu.ac.fj
Abstract:
The aim of present paper is to derive a higher bound (HB) of 3rd order Hankel determinant for a collection of holomorphic mappings connected with exactly to the right side of the lemniscate of Bernoulli, whose polar coordinates form is r2 = 2cos2(2θ). The method carried in this paper is more refined than the method adopted by the authors (see [1]), who worked on this problem earlier.
Paper's Title:
Existence of Compositional Square Roots of Circle Maps
Author(s):
K. Ali Akbar and T. Mubeena
Department of Mathematics,
School of Physical Sciences,
Central University of Kerala,
Periya - 671320,
Kasaragod,
Kerala,
India.
E-mail: aliakbar.pkd@gmail.com,
aliakbar@cukerala.ac.in
Department of Mathematics,
School of Mathematics and Computational Sciences,
University of Calicut,
Thenhipalam-673635,
Malappuram,
Kerala,
India.
E-mail: mubeenatc@gmail.com,
mubeenatc@uoc.ac.in
Abstract:
In this paper, we discuss the existence of compositional square roots of circle maps. If f and g are two maps such that g ○ g = f, we say that g is a compositional square root of f.
Paper's Title:
A Review on Minimally Supported Frequency Wavelets
Author(s):
K Pallavi1, M C Lineesh1, A Noufal2
1
Department of Mathematics,2Department of Mathematics,
Cochin University of Science and Technology,
Kerala 682022,
India.
E-mail: noufal@cusat.ac.in
Abstract:
This paper provides a review on Minimally Supported Frequency (MSF) wavelets that includes the construction and characterization of MSF wavelets. The characterization of MSF wavelets induced from an MRA is discussed and the nature of the low-pass filter associated with it is explained. The concept of wavelet set and dimension function is introduced to study this class of wavelets. Along with MSF wavelets, s-elementary wavelets and unimodular wavelets are also considered due to the similarity in definitions. Examples and illustrations are provided for more clarity.
Paper's Title:
Conservativeness Criteria of Girsanov Transformation for Non-Symmetric Jump-diffusion
Author(s):
Mila Kurniawaty
DDepartment of Mathematics,
Universitas Brawijaya, Malang,
Indonesia.
E-mail: mila_n12@ub.ac.id
Abstract:
We develop the condition in our previous paper [The Conservativeness of Girsanov transformed for symmetric jump-diffusion process (2018)] in the framework of nonsymmetric Markov process with jumps associated with regular Dirichlet form. We prove the conservativeness of it by relation in duality of Girsanov transformed process and recurrent criteria of Dirichlet form.
Paper's Title:
A Fuzzy Soft Quotient Topology and Its Properties
Author(s):
Haripamyu, Riri Alfakhriati, Monika Rianti Helmi, Jenizon
Department of Mathematics and Data Science, Andalas University, Padang, Indonesia.
E-mail: haripamyu@sci.unand.ac.id
ririalfakhriati123@gmail.com
monikariantihelmi@sci.unand.ac.id
jenizon@gmail.com
Abstract:
This research is to construct a new topology on fuzzy soft set by using the concept of quotient topology. Then we study the concept of quotient map to define the fuzzy soft quotient map and provide some relevant properties of fuzzy soft quotient map. Furthermore, we give some examples related to fuzzy soft quotient topology and fuzzy soft quotient map to apply some properties of fuzzy soft quotient map.
Paper's Title:
Fekete-Szegö Inequality for Sakaguchi Type of functions in Petal Shaped Domain
Author(s):
E. K. Nithiyanandham and B. Srutha Keerthi
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: nithiyankrish@gmail.com
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com
Abstract:
In this paper, we estimate coefficient bounds,|a_2|,|a_3| and |a_4|, Fekete-Szegö inequality
and Toeplitz determinant
T2(2) and T3(1) for functions belonging to the following class
the function being holomorphic, we expand using Taylor series and obtain several corollaries and consequences for the main result.
Paper's Title:
Toeplitz Determinant for Sakaguchi Type Functions Under Petal Shaped Domain
Author(s):
B. Nandhini and B. Srutha Keerthi
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail:
nandhinibaskar1996@gmail.com
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com
Abstract:
We introduce a new general subclass GPt,ρ of Sakaguchi kind function on a Petal shaped domain. We obtain coefficients bounds and upper bounds for the Fekete-Szegö functional over the class. From these functions we obtain the bounds of first four coefficients, and then we have derived the Toeplitz determinant T2(2) and T3(1) whose diagonal entries are the coefficients of functions.
Paper's Title:
High Order Collocation Method for the Generalized Kuramoto-Sivashinsky Equation
Author(s):
Zanele Mkhize, Nabendra Parumasur and Pravin Singh
School of Mathematics, Statistics and
Computer Sciences,
University of KwaZulu-Natal,
Private Bag X 54001,
Durban 4000.
E-mail: mkhizez2@ukzn.ac.za
parumasurn1@ukzn.ac.za
singhp@ukzn.ac.za
URL: https://www.ukzn.ac.za
Abstract:
In this paper, we derive the heptic Hermite basis functions and use them as basis functions in the orthogonal collocation on finite elements (OCFE) method. We apply the method to solve the generalized Kuramoto-Sivashinsky equation. Various numerical simulations are presented to justify the computational efficiency of the proposed method.
Paper's Title:
Metric Functionals for the Hästö Metric
Author(s):
G. Bettencourt and S. Mendes
Departamento de Matemática,
Universidade da Beira Interior -
Covilhă Portugal,
Centro de Matemática e Aplicaçőes
Universidade da Beira Interior -
Covilhă Portugal.
E-mail: gastao@ubi.pt
ISCTE - University Institute of Lisbon - Lisbon Portugal,
Centro de Matemática e Aplicaçőes
Universidade da Beira Interior -
Covilhă Portugal.
E-mail: sergio.mendes@iscte-iul.pt
Abstract:
In 2002, new classes of weighted metrics on Rn were introduced by Peter Hästö. In this article we compute the metric functionals for such classes of metrics.
Paper's Title:
A Determinantal Representation of Core EP Inverse
Author(s):
Divya Shenoy Purushothama
Department of Mathematics,
Manipal Institute of Technology,
Manipal Academy of Higher Education,
Manipal -576104, Karnataka,
India.
E-mail: divya.shenoy@manipal.edu
URL:
https://manipal.edu/mit/department-faculty/faculty-list/divya-shenoy-p.html
Abstract:
The notion of Core EP inverse is introduced by Prasad in the article "Core - EP inverse" and proved its existence and uniqueness. Also, a formula for computing the Core EP inverse is obtained from particular linear combination of minors of a given matrix. Here a determinantal representation for Core EP inverse of a matrix A with the help of rank factorization of A is obtained.
Paper's Title:
Coefficient Bounds for Sakaguchi Kind of Functions Associated with Sine Function
Author(s):
Serap Bulut, H. Priya and B. Srutha Keerth
Kocaeli University,
Faculty of Aviation and Space Sciences,
Arslanbey Campus, 41285 Kartepe-Kocaeli,
Turkey.
E-mail: serap.bulut@kocaeli.edu.tr
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus, Chennai - 600 048,
India.
E-mail: priyaharikrishnan18@gmail.com,
priya.h2020@vitstudent.ac.in
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus, Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com,
sruthakeerthi.b@vit.ac.in
Abstract:
In this paper, we introduce a new general subclass of analytic functions with respect to symmetric points in the domain of sine function. We obtain sharp coefficient bounds and upper bounds for the Fekete-Szegö functional. Also we get sharp bounds for the logarithmic coefficients of functions belonging to this new class.
Paper's Title:
Two Further Methods for Deriving Four Results Contiguous to Kummer's Second Theorem
Author(s):
I. Kim and J. Kim
Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Korea.
E-mail: iki@wku.ac.kr
Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Korea.
E-mail: joohyung@wku.ac.kr
Abstract:
In the theory of generalized hypergeometric function, transformation and summation formulas play a key role. In particular, in one of the Kummer's transformation formulas, Kim, et al. in 2012, have obtained ten contiguous results in the form of a single result with the help of generalization of Gauss's second summation theorem obtained earlier by Lavoie, et al.. In this paper, we aim at presenting four of such results by the technique of contiguous function relations and integral method developed by MacRobert.
Paper's Title:
(p,q)-Lucas Polynomial and Their Applications to a Certain Family of Bi-univalent Functions Defined by Wanas Operator
Author(s):
M Musthafa Ibrahim, Saleem Ahmed
College of Engineering
University of Buraimi
Al Buraimi, P.O.Box 512,
Oman
E-mail: musthafa.i@uob.edu.om,
saleem.a@uob.edu.om
Abstract:
In this article, by making use of (p,q)-Lucas polynomials, we introduce and investigate a certain family of analytic and biunivalent functions associated with Wanas operator which defined in the open unit disk U. Also, the upper bounds for the initial Taylor-Maclaurin coefficients and the Fekete-Szegö inequality of functions belonging to this family are obtained.
Paper's Title:
Using an Euler Type Transform for Accelerating Convergence of Series
Author(s):
Nimete Sh. Berisha, Faton M. Berisha*, Murat Sadiku
Faculty of Economics, University of
Prishtina,
Agim Ramadani st., 10000 Pristina,
Kosovo.
E-mail: nimete.berisha@uni-pr.edu
URL:
https://staff.uni-pr.edu/profile/nimeteberisha
Faculty of Mathematics and Sciences,
University of Prishtina,
Mother Teresa st., 10000 Pristina,
Kosovo.
E-mail: faton.berisha@uni-pr.edu
URL:
https://staff.uni-pr.edu/profile/fatonberisha
Faculty of Business Administration,
South East European University,
Tetovo,
North Macedonia.
E-mail: m.sadiku@seeu.edu.mk
Abstract:
In the paper we give a property of an operator of generalised difference, defined earlier, linear on a set of sequences, and use it to establish Euler type transforms for alternating series. These transforms accelerate the convergence of series under the same conditions as the transforms of non-alternating series. We also give analysis of an algorithm for computing a partial sum of the transformed series by using a higher order operator of generalised difference, and prove a theorem stating its order of complexity.
Paper's Title:
Recursive Bounds for the Eigenvalues of Symmetric Positive Definite Matrices
Author(s):
Pravin Singh, Shivani Singh, Virath Singh
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
University of South Africa,
Department of Decision Sciences, PO Box 392,
Pretoria,0003,
South Africa.
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
E-mail:
singhp@ukzn.ac.za,
singhs2@unisa.ac.za,
singhv@ukzn.ac.za
Abstract:
In this paper, we bound the extremal eigenvalues of a positive definite real symmetric matrix by considering a part of the characteristic equation in the region of the smallest and largest eigenvalues. An expansion around these values leads to a sequence of monotonic functions, whose zeros coincide with the extremal zeros of associated polynomials. The latter is shown to yield bounds that are fairly accurate.
Paper's Title:
ℵ0 Algebra and its Novel Application in Edge Detection
Author(s):
G. E. Chatzarakis1, S. Dickson2, S. Padmasekaran2, S. L. Panetsos1, and J. Ravi3
1Electrical
and Electronic Engineering Educators,
School of Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
spanetsos@aspete.gr
2Mathematics,
Periyar University,
Periyar Palkalai Nagar, Salem, 636011, Tamilnadu,
India.
E-mail: dix.bern@gmail.com,
padmasekarans@periyaruniversity.ac.in
3Department
of Mathematics, Amity University,
Bengaluru, Karnataka,
India.
E-mail:
jravistat@gmail.com
Abstract:
In this paper a new type of ℵ0-algebra has been defined. With its help, the fuzzy cross subalgebra and the fuzzy η-relation on the ℵ0-algebra are introduced and their respective properties are derived. Moreover, the fuzzy cross ℵ0-ideal of the ℵ0-algebra is defined with some theorems and intuitionistic fuzzy ℵ0-ideals of the ℵ0-algebra are introduced. This fuzzy algebra concept is applied in image processing to detect edges. This ℵ0-algebra is a novelty in the field of research.
Paper's Title:
Some Inequalities for the Generalized Riesz Potential on the Generalized Morrey Spaces over Hypergroups
Author(s):
I. Sihwaningrum, Renny, Y. Dasril
Jenderal Soedirman University,
Indonesia.
E-mail: idha.sihwaningrum@unsoed.ac.id
renny@unsoed.ac.id
Universiti Tun Hussein Onn,
Malaysia.
E-mail:
yosza@uthm.edu.my
Abstract:
We present in this paper some inequalities for the generalized Riesz potential on the generalized Morrey spaces over commutative hypergroups. The results can be found by employing the maximal operator.
Paper's Title:
A Note on Evaluation of a New Class of Integrals Involving Generalized Hypergeometric Function
Author(s):
Madhav Prasad Poudel, Dongkyu Lim*, Narayan Prasad Pahari, Arjun K. Rathie
School of Engineering,
Pokhara University, Pokhara-30, Kaski,
Nepal.
E-mail: pdmadav@gmail.com
Department of Mathematics Education,
Andong National University, Andong 36729,
Republic of Korea.
E-mail: dklim@anu.ac.kr
Central Department of Mathematics,
Tribhuvan University, Kirtipur, Kathmandu,
Nepal.
E-mail: nppahari@gmail.com
Department of Mathematics,
Vedant College of Engineering & Technology (Rajasthan Technical University),
Village: Tulsi,
Jakhamund, Dist. Bundi, Rajasthan State,
India.
E-mail:
arjunkumarrathie@gmail.com
Abstract:
In the theory of hypergeometric and generalized hypergeometric series, classical summation theorems such as those of Gauss, Gauss second, Bailey and Kummer for the series
2F1; Watson, Dixon, Whipple and Saalshutz play a key role. Applications of the above mentioned summation theorems are well known for the series
3F2. In our present investigation, we aim to evaluate twenty five new class of integrals involving generalized hypergeometric function in the form of a single integral of the form:
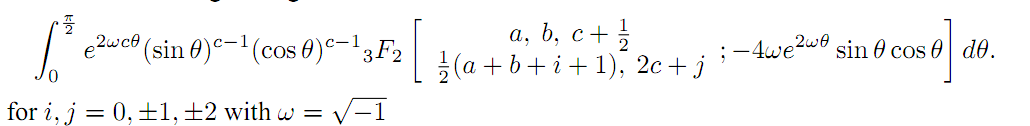
The results are established with the help of the generalizations of the classical Watson's summation theorem obtained earlier by Lavoie et al.. Fifty interesting integrals in the form of two integrals (twenty five each) have also been given as special cases of our main findings.
Paper's Title:
Automatic Continuity of Generalized Derivations in Certain *-Banach Algebras
Author(s):
M. Aboulekhlef, Y. Tidli and M. Belam
Laboratory of Applied Mathematics and
Information and Communication Technology Polydisciplinary
Faculty of Khouribga University of Sultan Moulay Slimane
Morocco.
E-mail:
aboulekhlef@gmail.com
y.tidli@gmail.com
m.belam@gmail.com
Abstract:
Consider the map φ of the Banach algebra Β in Β, if there exists a derivation δ of Β in Β so that for every x, y ∈ Β , φ(xy) =φ(x)y+xδ(y) . φ is called a generalized derivation of Β. In [9], Bresar introduced the concept of generalized derivations. We prove several results about the automatic continuity of generalized derivations on certain Banach algebras.
Search and serve lasted 1 second(s).