|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Some Convergence Results for Jungck-Am Iterative Process In Hyperbolic Spaces
Author(s):
Akindele Adebayo Mebawondu and Oluwatosin Temitope Mewomo
School of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail:
216028272@stu.ukzn.ac.za,
mewomoo@ukzn.ac.za
Abstract:
In this paper, we introduce a new three steps iterative process called Jungck-AM iterative process and show that the proposed iterative process can be used to approximate fixed points of Jungck-contractive type mappings and Jungck-Suzuki type mappings. In addition, we establish some strong and Δ-convergence results for the approximation of fixed points of Jungck-Suzuki type mappings in the frame work of uniformly convex hyperbolic space. Furthermore, we show that the newly proposed iterative process has a better rate of convergence compare to the Jungck-Noor, Jungck-SP, Jungck-CR and some existing iterative processes in the literature. Finally, stability, data dependency results for Jungck-AM iterative process is established and we present an analytical proof and numerical examples to validate our claim.
Paper's Title:
Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Asymptotic Behavior of Mixed Type Functional Equations
Author(s):
J. M. Rassias
Pedagogical Department, E.E., National and
Capodistrian University of Athens, Section of Mathematics And Informatics, 4, Agamemnonos
Str., Aghia Paraskevi, Athens 15342,Greece
jrassias@primedu.uoa.gr
URL:
http://www.primedu.uoa.gr/~jrassias/
Abstract:
In 1983 Skof [24] was the first author to solve the Ulam problem for additive mappings on a restricted domain. In 1998 Jung [14] investigated the Hyers-Ulam stability of additive and quadratic mappings on restricted domains. In this paper we improve the bounds and thus the results obtained by Jung [14], in 1998 and by the author [21], in 2002. Besides we establish new theorems about the Ulam stability of mixed type functional equations on restricted domains. Finally, we apply our recent results to the asymptotic behavior of functional equations of different types.
Paper's Title:
A Fixed Point Approach to
the Stability of the Equation
![]()
Author(s):
Soon-Mo Jung
Mathematics Section, College of Science and Technology
Hong-Ik
University, 339-701 Chochiwon
Republic of Korea.
smjung@hongik.ac.kr
Abstract:
We will apply a fixed point method for proving the Hyers--Ulam stability of
the functional equation
![]() .
.
Paper's Title:
Applications of Relations and Relators in the
Extensions of Stability Theorems for Homogeneous and Additive Functions
Author(s):
Árpád Száz
Institute of Mathematics, University of Debrecen,
H-4010 Debrecen,
Pf. 12,
Hungary
szaz@math.klte.hu
Abstract:
By working out an appropriate technique of relations and relators and extending the ideas of the direct methods of Z. Gajda and R. Ger, we prove some generalizations of the stability theorems of D. H. Hyers, T. Aoki, Th. M. Rassias and P. Găvruţă in terms of the existence and unicity of 2-homogeneous and additive approximate selections of generalized subadditive relations of semigroups to vector relator spaces. Thus, we obtain generalizations not only of the selection theorems of Z. Gajda and R. Ger, but also those of the present author.
Paper's Title:
Ulam Stability of Reciprocal Difference and Adjoint Functional Equations
Author(s):
K. Ravi, J. M. Rassias and B. V. Senthil Kumar
Department of Mathematics,
Sacred Heart College, Tirupattur - 635601,
India
Pedagogical Department E. E.,
Section of Mathematics and Informatics,
National and Capodistrian University of Athens,
4, Agamemnonos Str., Aghia Paraskevi,
Athens, Attikis 15342,
GREECE
Department of Mathematics,
C.Abdul Hakeem College of Engineering and
Technology, Melvisharam - 632 509, India
shckavi@yahoo.co.in
jrassias@primedu.uoa.gr
bvssree@yahoo.co.in
Abstract:
In this paper, the reciprocal difference functional equation (or RDF equation) and the reciprocal adjoint functional equation (or RAF equation) are introduced. Then the pertinent Ulam stability problem for these functional equations is solved, together with the extended Ulam (or Rassias) stability problem and the generalized Ulam (or Ulam-Gavruta-Rassias) stability problem for the same equations.
Paper's Title:
Approximation of an AQCQ-Functional Equation and its Applications
Author(s):
Choonkil Park and Jung Rye Lee
Department of Mathematics,
Research Institute for Natural Sciences,
Hanyang University, Seoul 133-791,
Korea;
Department of Mathematics,
Daejin University,
Kyeonggi 487-711,
Korea
baak@hanyang.ac.kr
jrlee@daejin.ac.kr
Abstract:
This paper is a survey on the generalized Hyers-Ulam stability of an AQCQ-functional equation in several spaces. Its content is divided into the following sections:
1. Introduction and preliminaries.
2. Generalized Hyers-Ulam stability of an AQCQ-functional equation in Banach spaces: direct method.
3. Generalized Hyers-Ulam stability of an AQCQ-functional equation in Banach spaces: fixed point method.
4. Generalized Hyers-Ulam stability of an AQCQ-functional equation in random Banach spaces: direct method.
5. Generalized Hyers-Ulam stability of an AQCQ-functional equation in random Banach spaces: fixed point method.
6. Generalized Hyers-Ulam stability of an AQCQ-functional equation in non-Archi-medean Banach spaces: direct method.
7. Generalized Hyers-Ulam stability of an AQCQ-functional equation in non-Archi-medean Banach spaces: fixed point method.
Paper's Title:
New Coincidence and Fixed Point Theorems for Strictly Contractive Hybrid Maps
Author(s):
S. L. Singh and Amal M. Hashim
21, Govind Nagar, Rishikesh 249201,
Ua, India
vedicmri@sancharnet.in
Dept. of Math., College of Science,
Univ. of Basarah,
Iraq.
Abstract:
The purpose of this paper is to study the (EA)-property and noncompatible maps
of a hybrid pair of single-valued and multivalued maps in fixed point considerations. Such maps
have the remarkable property that they need not be continuous at their common fixed points. We
use this property to obtain some coincidence and fixed point theorems for strictly contractive
hybrid maps without using their continuity and completeness or compactness of the space.
Paper's Title:
Analysis of the Flow Field in Stenosed Bifurcated Arteries Through a Mathematical Model
Author(s):
S. Chakravarty and S. Sen
Department of Mathematics, Visva-Bharati University,
Santiniketan 731235,
India
santabrata2004@yahoo.co.in
Abstract:
The present study is dealt with an appropriate mathematical model
of the arotic bifurcation in the presence of constrictions using which
the physiological flow field is analized. The geometry of the bifurcated
arterial segment having constrictions in both the parent and its daughter
arterial lumen frequently occurring in the diseased arteries causing
malfunction of the cardiovascular system , is formed mathematically
with the introduction of appropriate curvatures at the lateral junctions
and the flow divider. The flowing blood contained in the stenosed
bifurcated artery is treated to be Newtonian and the flow is considered
to be two dimensional. The motion of the arterial wall and its effect
on local fluid mechanics is not ruled out from the present pursuit.
The flow analysis applies the time-dependent, two-dimensional incompressible
nonlinear Navier-Stokes equations for Newtonian fluid. The flow field
can be obtained primarily following the radial coordinate transformation
and using the appropriate boundary conditions and finally adopting
a suitable finite difference scheme numerically. The influences of
the arterial wall distensibility and the presence of stenosis on the
flow field, the flow rate and the wall shear stresses are quantified
in order to indicate the susceptibility to atherosclerotic lesions
and thereby to validate the applicability of the present theoretical
model.
Paper's Title:
Ulam Stability of Functional Equations
Author(s):
Stefan Czerwik and Krzysztof Król
Institute of Mathematics
Silesian University of Technology
Kaszubska 23,
44-100 Gliwice,
Poland
Stefan.Czerwik@polsl.pl
Krzysztof.Krol@polsl.pl
Abstract:
In this survey paper we present some of the main results on Ulam-Hyers-Rassias stability for important functional equations.
Paper's Title:
Common Fixed Point Results for Banach Operator Pairs and Applications to Best Approximation
Author(s):
Hemant Kumar Nashine
Department of Mathematics,
Disha Institute of Management and Technology,
Satya Vihar, Vidhansabha - Chandrakhuri Marg (Baloda Bazar Road),
Mandir Hasaud,
Raipur - 492101(Chhattisgarh), India.
hemantnashine@rediffmail.com
nashine_09@rediffmail.com
Abstract:
The common fixed point results for Banach operator pair with generalized nonexpansive mappings in q-normed space have been obtained in the present work. As application, some more general best approximation results have also been determined without the assumption of linearity or affinity of mappings. These results unify and generalize various existing known results with the aid of more general class of noncommuting mappings.
Paper's Title:
Attempts to Define a Baum--Connes Map Via Localization of Categories for Inverse Semigroups
Author(s):
Bernhard Burgstaller
Departamento de Matematica,
Universidade Federal de Santa Catarina,
CEP 88.040-900 Florianopolis-SC,
Brasil.
E-mail:
bernhardburgstaller@yahoo.de
URL:
http://mathematik.work/bernhardburgstaller/index.html
Abstract:
An induction functor in inverse semigroup equivariant KK-theory is considered, and together with %a restriction functors certain results similar to those known from the Mackey machinery are shown. It is also verified that for any so-called E-continuous inverse semigroup its equivariant KK-theory satisfies the universal property and is a triangulated category.
Paper's Title:
Stability of a Mixed Additive, Quadratic and Cubic Functional Equation In Quasi-Banach Spaces
Author(s):
A. Najati and F. Moradlou
Department of Mathematics, Faculty of Sciences,
University of Mohaghegh Ardabili, Ardabil,
Iran
a.nejati@yahoo.com
Faculty of Mathematical Sciences,
University of Tabriz, Tabriz,
Iran
moradlou@tabrizu.ac.ir
Abstract:
In this paper we establish the general solution of a mixed additive,
quadratic and cubic functional equation and investigate the
Hyers--Ulam--Rassias stability of this equation in quasi-Banach
spaces. The concept of Hyers-Ulam-Rassias stability originated from
Th. M. Rassias' stability theorem that appeared in his paper: On the
stability of the linear mapping in Banach spaces, Proc. Amer. Math.
Soc. 72 (1978), 297--300.
Paper's Title:
Hyers-Ulam-Rassias Stability
of a Generalized Jensen Functional Equation
Author(s):
A. Charifi, B. Bouikhalene, E. Elqorachi and A. Redouani
Department of
Mathematics, Faculty of Sciences,
Ibn Tofail University,
Kenitra, Morocco
charifi2000@yahoo.fr
bbouikhalene@yahoo.fr
Department of
Mathematics, Faculty of Sciences,
Ibn Zohr University,
Agadir, Morocco
elqorachi@hotmail.com
Redouani-ahmed@yahoo.fr
Abstract:
In this paper we obtain the Hyers-Ulam-Rassias stability for the generalized Jensen's functional equation in abelian group (G,+). Furthermore we discuss the case where G is amenable and we give a note on the Hyers-Ulam-stability of the K-spherical (n × n)-matrix functional equation.
Paper's Title:
A Generalization of a Trace Inequality for Positive Definite Matrices
Author(s):
E. V. Belmega, M. Jungers, and S. Lasaulce
Université Paris-Sud Xi, SUPELEC,
Laboratoire Des Signaux Et Systčmes,
Gif-Sur-Yvette,
France.
belmega@lss.supelec.fr
http://veronica.belmega.lss.supelec.fr
CNRS, ENSEM, CRAN, Vandoeuvre,
France.
marc.jungers@cran.uhp-nancy.fr
http://perso.ensem.inpl-nancy.fr/Marc.Jungers/
CNRS, SUPELEC, Laboratoire des Signaux et
Systčmes,
Gif-Sur-Yvette,
France.
lasaulce@lss.supelec.fr
http://samson.lasaulce.lss.supelec.fr
Abstract:
In this note, we provide a generalization of the trace inequality derived in [Belmega].
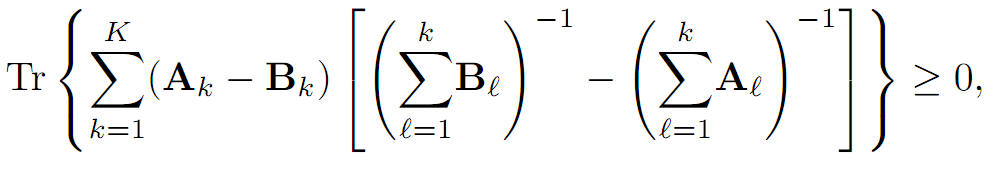
More precisely, we prove that for arbitrary K ≥ 1 where Tr(∙) denotes the matrix trace operator, A1, B1 are any positive definite matrices and Ak, Bk for all k∈{2,...,k}, are any positive semidefinite matrices.
Paper's Title:
On an extension of Edwards's double integral with applications
Author(s):
I. Kim, S. Jun, Y. Vyas and A. K. Rathie
Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Republic of Korea.
General Education Institute,
Konkuk University,
Chungju 380-701,
Republic of Korea.
Department of Mathematics, School of
Engineering,
Sir Padampat Singhania University,
Bhatewar, Udaipur, 313601, Rajasthan State,
India.
Department of Mathematics,
Vedant College of Engineering and Technology,
(Rajasthan Technical University),
Bundi-323021, Rajasthan,
India.
E-mail: iki@wku.ac.kr
sjun@kku.ac.kr
yashoverdhan.vyas@spsu.ac.in
arjunkumarrathie@gmail.com
Abstract:
The aim of this note is to provide an extension of the well known and useful Edwards's double integral. As an application, new class of twelve double integrals involving hypergeometric function have been evaluated in terms of gamma function. The results are established with the help of classical summation theorems for the series 3F2 due to Watson, Dixon and Whipple. Several new and interesting integrals have also been obtained from our main findings.
Paper's Title:
Existence of Solution of Differential and Riemann-Liouville Equation Via Fixed Point Approach in Complex Valued b-Metric Spaces
Author(s):
K. Afassinou, A. A. Mebawondu, H. A. Abass and O. K. Narain
Department of Science Access,
University of Zululand, KwaDlangezwa,
South Africa.
E-mail: komia@aims.ac.za
DST-NRF Centre of Excellence in
Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: dele@aims.ac.za
DST-NRF Centre of Excellence in
Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: hammedabass548@gmail.com
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
In this paper, we establish some fixed point and common fixed point results for a new type of generalized contractive mapping using the notion of C-class function in the framework of complex valued b-metric spaces. As an application, we establish the existence and uniqueness of a solution for Riemann-Liouville integral and ordinary differential equation in the framework of a complete complex valued b-metric spaces. The obtained results generalize and improve some fixed point results in the literature.
Paper's Title:
Pseudomonotonicity and Quasimonotonicity
by Translations versus Monotonicity in Hilbert Spaces
Author(s):
George Isac and Dumitru Motreanu
Department of
Mathematics, Royal Military College of Canada, P.O. Box 17000 Stn Forces
Kingston, Ontario, Canada, K7k 7b4.
gisac@juno.com
Département de Mathématiques, Université de Perpignan, 66860
Perpignan, France.
motreanu@univ-perp.fr
Abstract:
Let ![]() be a Gâteaux differentiable mapping on
an open convex subset
be a Gâteaux differentiable mapping on
an open convex subset ![]() of a
Hilbert space
of a
Hilbert space![]() . If there exists a straight line
. If there exists a straight line ![]() such that
such that ![]() is pseudomonotone for any
is pseudomonotone for any ![]() then
then ![]() is monotone. Related results using a
regularity condition are given.
is monotone. Related results using a
regularity condition are given.
Paper's Title:
Komatu Integral Transforms of Analytic Functions Subordinate to Convex Functions
Author(s):
T. N. Shanmugam and C. Ramachandran
Department of Mathematics, College of Engineering,
Anna University, Chennai-600 025, Tamilnadu,
India
shan@annauniv.edu
Department of Mathematics, College of Engineering,
Anna University, Chennai-600 025, Tamilnadu,
India
crjsp2004@yahoo.com
Abstract:
In this paper, we consider the class A of the functions f(z) of the form
which are analytic in an open disk
has some property. Certain inclusion and the closure properties like convolution with convex univalent function etc. are studied.

 and study certain subclass of the class A, for which
and study certain subclass of the class A, for which
Paper's Title:
On the Generalized Stability and
Asymptotic Behavior of Quadratic Mappings
Author(s):
Hark-Mahn Kim, Sang-Baek Lee and Eunyoung Son
Department of Mathematics
Chungnam National University
Daejeon,
305-764,
Republic of Korea
hmkim@cnu.ac.kr
Abstract:
We extend the stability of quadratic mappings to the stability of general quadratic mappings with several variables, and then obtain an improved asymptotic property of quadratic mappings on restricted domains.
Paper's Title:
Stability Problems for Generalized Additive Mappings and Euler-Lagrange Type Mappings
Author(s):
M. Todoroki, K. Kumahara, T. Miura and S.-E. Takahasi
The Open University of Japan,
Chiba, 261-8586,
Japan
tomamiyu3232@sky.sannet.ne.jp
kumahara@ouj.ac.jp
Yamagata University,
Yonezawa 992-8510,
Japan
miura@yz.yamagata-u.ac.jp
Toho University, Yamagata University,
Chiba, 273-0866,
Japan
sin_ei1@yahoo.co.jp
Abstract:
We introduce a generalized additivity of a mapping between Banach spaces and establish the Ulam type stability problem for a generalized additive mapping. The obtained results are somewhat different from the Ulam type stability result of Euler-Lagrange type mappings obtained by H. -M. Kim, K. -W. Jun and J. M. Rassias.
Paper's Title:
A Geometric Generalization of Busemann-Petty Problem
Author(s):
Liu Rong and Yuan Jun
Shanghai Zhangjiang Group Junior Middle School,
Huo Xiang Road, Shanghai, 201203,
China
Abstract:
The norm defined by Busemann's inequality establishes a class of star body - intersection body. This class of star body plays a key role in the solution of Busemann-Petty problem. In 2003, Giannapoulos [1] defined a norm for a new class of half-section. Based on this norm, we give a geometric generalization of Busemann-Petty problem, and get its answer as a result
Paper's Title:
Introducing the Dorfmanian: A Powerful Tool for the Calculus Of Variations
Author(s):
Olivier de La Grandville
Department of Management Science and Engineering,
Stanford University,
475 Via Ortega, Stanford, CA 94305,
U. S. A.
E-mail: odelagrandville@gmail.com
Abstract:
We show how a modified Hamiltonian proposed by Robert Dorfman [1] to give intuitive sense
to the Pontryagin maximum principle can be extended to easily obtain all
high-order equations of the calculus of variations. This new concept is
particularly efficient to determine the differential equations leading to
the extremals of functionals defined by n-uple integrals, while a
traditional approach would require -- in some cases repeatedly -- an
extension of Green's theorem to n-space.
Our paper is dedicated to the memory of Robert Dorfman (1916 - 2002).
Paper's Title:
Characterization of Caristi Type Mapping Through its Absolute Derivative
Author(s):
M. Muslikh1, A. Kilicman2,3, S. H. Sapar4 and N. Bacho5
1Department of Mathematics,
University of Brawijaya,
Malang 65143, East Java,
Indonesia.
E-mail: mslk@ub.ac.id
2Department of Mathematics,
Universiti Putra Malaysia,
43400 UPM, Serdang, Selangor,
Malaysia
E-mail: akilic@upm.edu.my
3Department of Electrical and Electronic Engineering,
Istanbul Gelisim University,
Avcilar, Istanbul,
Turkey
4Department of Mathematics,
Universiti Putra Malaysia,
43400 UPM, Serdang, Selangor,
Malaysia
E-mail: sitihas@upm.edu.my
5Department of Mathematics,
Universiti Putra Malaysia,
43400 UPM, Serdang, Selangor,
Malaysia
E-mail: norfifah@upm.edu.my
Abstract:
The purpose of this article to characterize the Caristi type mapping by the absolute derivative. The equivalences of the Caristi mapping with contraction mapping is discussed too. In addition, it was shown that the contraction mapping can be tested through its absolute derivative.
Paper's Title:
Sharp Inequalities Between Hölder and Stolarsky Means of Two Positive Numbers
Author(s):
M. Bustos Gonzalez and A. I. Stan
The University of Iowa,
Department of Mathematics,
14 MacLean Hall,
Iowa City, Iowa,
USA.
E-mail:
margarita-bustosgonzalez@uiowa.edu
The Ohio State University at Marion,
Department of Mathematics,
1465 Mount Vernon Avenue,
Marion, Ohio,
USA.
E-mail: stan.7@osu.edu
Abstract:
Given any index of the Stolarsky means, we find the greatest and least indexes of the H\"older means, such that for any two positive numbers, the Stolarsky mean with the given index is bounded from below and above by the Hölder means with those indexes, of the two positive numbers. Finally, we present a geometric application of this inequality involving the Fermat-Torricelli point of a triangle.
Paper's Title:
Pointwise Convergence of Fourier-type Series with Exponential Weights
Author(s):
Hee Sun Jung and Ryozi Sakai
Department of Mathematics Education,
Sungkyunkwan University,
Seoul 110-745,
Republic of Korea.
E-mail: hsun90@skku.edu
Department of Mathematics,
Meijo University, Nagoya 468-8502,
Japan.
E-mail: ryozi@hm.aitai.ne.jp
Abstract:
Let R = ( - ∞,∞), and let Q∈C1(R):R→[0,∞) be an even function. We consider the exponential weights w(x)=e-Q(x), x∈R. In this paper we obtain a pointwise convergence theorem for the Fourier-type series with respect to the orthonormal polynomials {pn(w2;x)}.
Paper's Title:
ℵ0 Algebra and its Novel Application in Edge Detection
Author(s):
G. E. Chatzarakis1, S. Dickson2, S. Padmasekaran2, S. L. Panetsos1, and J. Ravi3
1Electrical
and Electronic Engineering Educators,
School of Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
spanetsos@aspete.gr
2Mathematics,
Periyar University,
Periyar Palkalai Nagar, Salem, 636011, Tamilnadu,
India.
E-mail: dix.bern@gmail.com,
padmasekarans@periyaruniversity.ac.in
3Department
of Mathematics, Amity University,
Bengaluru, Karnataka,
India.
E-mail:
jravistat@gmail.com
Abstract:
In this paper a new type of ℵ0-algebra has been defined. With its help, the fuzzy cross subalgebra and the fuzzy η-relation on the ℵ0-algebra are introduced and their respective properties are derived. Moreover, the fuzzy cross ℵ0-ideal of the ℵ0-algebra is defined with some theorems and intuitionistic fuzzy ℵ0-ideals of the ℵ0-algebra are introduced. This fuzzy algebra concept is applied in image processing to detect edges. This ℵ0-algebra is a novelty in the field of research.
Paper's Title:
A Note on Evaluation of a New Class of Integrals Involving Generalized Hypergeometric Function
Author(s):
Madhav Prasad Poudel, Dongkyu Lim*, Narayan Prasad Pahari, Arjun K. Rathie
School of Engineering,
Pokhara University, Pokhara-30, Kaski,
Nepal.
E-mail: pdmadav@gmail.com
Department of Mathematics Education,
Andong National University, Andong 36729,
Republic of Korea.
E-mail: dklim@anu.ac.kr
Central Department of Mathematics,
Tribhuvan University, Kirtipur, Kathmandu,
Nepal.
E-mail: nppahari@gmail.com
Department of Mathematics,
Vedant College of Engineering & Technology (Rajasthan Technical University),
Village: Tulsi,
Jakhamund, Dist. Bundi, Rajasthan State,
India.
E-mail:
arjunkumarrathie@gmail.com
Abstract:
In the theory of hypergeometric and generalized hypergeometric series, classical summation theorems such as those of Gauss, Gauss second, Bailey and Kummer for the series
2F1; Watson, Dixon, Whipple and Saalshutz play a key role. Applications of the above mentioned summation theorems are well known for the series
3F2. In our present investigation, we aim to evaluate twenty five new class of integrals involving generalized hypergeometric function in the form of a single integral of the form:
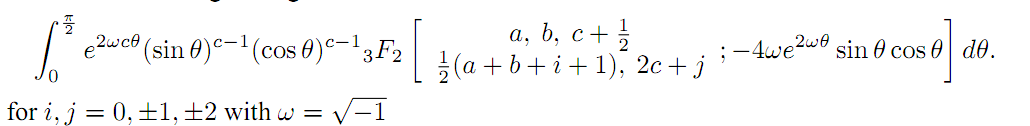
The results are established with the help of the generalizations of the classical Watson's summation theorem obtained earlier by Lavoie et al.. Fifty interesting integrals in the form of two integrals (twenty five each) have also been given as special cases of our main findings.
Paper's Title:
Fixed Point Theorems for a Finite Family of Asymptotically Nonexpansive Mappings
Author(s):
E. Prempeh
Department of Mathematics,
Kwame Nkrumah University of Science and Technology,
Kumasi, Ghana
edward_prempeh2000@yahoo.com
Abstract:
Let
![]() be a real reflexive Banach space with a uniformly Gâteaux differentiable norm,
be a real reflexive Banach space with a uniformly Gâteaux differentiable norm,
![]() be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of
![]() i=1,2,...,r be a finite family of asymptotically nonexpansive mappings
such that for each
i=1,2,...,r be a finite family of asymptotically nonexpansive mappings
such that for each
![]()
![]() Let
Let
![]() be a nonempty set of common fixed points of
be a nonempty set of common fixed points of
![]() and define
and define
![]()
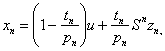
![]() associated with
associated with
![]() , converges strongly to a fixed point of
, converges strongly to a fixed point of
![]() provided
provided
![]() possesses uniform normal structure. Furthermore we prove that the iterative process:
possesses uniform normal structure. Furthermore we prove that the iterative process:
![]()
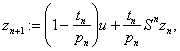
![]() , converges strongly to a fixed point of
, converges strongly to a fixed point of
![]()
Paper's Title:
Solution of the Hyers-Ulam Stability Problem for Quadratic Type Functional Equations in Several Variables
Author(s):
John Michael Rassias
Pedagogical Department, E.E., National and Capodistrian University of Athens,
Section of Mathematics and Informatics,
4, Agamemnonos Str., Aghia Paraskevi,
Athens 15342,
Greece
jrassias@primedu.uoa.gr
URL: http://www.primedu.uoa.gr/~jrassias/
Abstract:
In 1940 (and 1968) S. M. Ulam proposed the well-known Ulam stability problem. In 1941 D. H. Hyers solved the Hyers-Ulam problem for linear mappings. In 1951 D. G. Bourgin has been the second author treating the Ulam problem for additive mappings. In 1978 according to P. M. Gruber this kind of stability problems is of particular interest in probability theory and in the case of functional equations of different types. In 1982-2004 we established the Hyers-Ulam stability for the Ulam problem for different mappings. In this article we solve the Hyers-Ulam problem for quadratic type functional equations in several variables. These stability results can be applied in stochastic analysis, financial and actuarial mathematics, as well as in psychology and sociology.
Paper's Title:
A general common fixed point theorem for reciprocally continuous mappings satisfying an implicit relation
Author(s):
A. Djoudi and A. Aliouche
Faculty of Science, University of Annaba,
P.O. Box 23000, Annaba,
Algeria.
adjoudi@yahoo.com
Department of Mathematics, University of Larbi Ben M'Hidi,
Oum-El-Bouaghi 04000,
Algeria.
abdmath@hotmail.com
Abstract:
A general common fixed point theorem for compatible mappings satisfying an
implicit relation is obtained by replacing the continuity of one mapping
by the reciprocal continuity of two mappings.
Paper's Title:
A Stability of the G-type Functional Equation
Author(s):
Gwang Hui Kim
Department of Mathematics, Kangnam University
Suwon 449-702, Korea.
ghkim@kangnam.ac.kr
Abstract:
We will investigate the stability in the sense of G
Paper's Title:
Generalizations of Hermite-Hadamard's Inequalities for Log-Convex Functions
Author(s):
Ai-Jun Li
School of Mathematics and Informatics,
Henan Polytechnic University,
Jiaozuo City, Henan Province,
454010, China.
liaijun72@163.com
Abstract:
In this article, Hermite-Hadamard's inequalities are extended in
terms of the weighted power mean and log-convex
function. Several refinements, generalizations and related
inequalities are obtained.
Paper's Title:
On the Generalized Inverse  over Integral Domains
over Integral Domains
Author(s):
Yaoming Yu and Guorong Wang
College of Education, Shanghai Normal University
Shanghai 200234
People's Republic of China.
yuyaoming@online.sh.cn
grwang@shnu.edu.cn
Abstract:
In this paper, we study further the generalized inverse
 of a matrix A over an integral domain. We give
firstly some necessary and sufficient conditions for the existence
of the generalized inverse
of a matrix A over an integral domain. We give
firstly some necessary and sufficient conditions for the existence
of the generalized inverse  , an explicit expression
for the elements of the generalized inverse
, an explicit expression
for the elements of the generalized inverse  and an
explicit expression for the generalized inverse
and an
explicit expression for the generalized inverse  ,
which reduces to the {1} inverse. Secondly, we verify that the
group inverse, the Drazin inverse, the Moore-Penrose inverse and the
weighted Moore-Penrose inverse are identical with the generalized
inverse
,
which reduces to the {1} inverse. Secondly, we verify that the
group inverse, the Drazin inverse, the Moore-Penrose inverse and the
weighted Moore-Penrose inverse are identical with the generalized
inverse 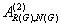 for an appropriate matrix G,
respectively, and then we unify the conditions for the existence and
the expression for the elements of the weighted Moore-Penrose
inverse, the Moore-Penrose inverse, the Drazin inverse and the group
inverse over an integral domain. Thirdly, as a simple application,
we give the relation between some rank equation and the existence of
the generalized inverse
for an appropriate matrix G,
respectively, and then we unify the conditions for the existence and
the expression for the elements of the weighted Moore-Penrose
inverse, the Moore-Penrose inverse, the Drazin inverse and the group
inverse over an integral domain. Thirdly, as a simple application,
we give the relation between some rank equation and the existence of
the generalized inverse  , and a method to compute the
generalized inverse
, and a method to compute the
generalized inverse  . Finally, we give an example of
evaluating the elements of
. Finally, we give an example of
evaluating the elements of  without calculating
without calculating
 .
.
Paper's Title:
A Subclass of Meromorphically Multivalent Functions with Applications to Generalized Hypergeometric Functions
Author(s):
M. K. Aouf
Mathematics Department,
Faculty of Science,
Mansoura University 35516,
Egypt
mkaouf127@yahoo.com
Abstract:
In this paper a new subclass of meromorphically multivalent functions, which
is defined by means of a Hadamard product (or convolution) involving some
suitably normalized meromorphically p-valent functions. The main object of
the present paper is to investigate the various important properties and
characteristics of this subclass of meromorphically multivalent functions.
We also derive many interesting results for the Hadamard products of
functions belonging to this subclass. Also we consider several applications
of our main results to generalized hypergeomtric functions.
Paper's Title:
Some Identities for Ramanujan - Göllnitz - Gordon Continued fraction
Author(s):
M. S. Mahadeva Naika, B. N. Dharmendra and S. Chandan Kumar
Department of Mathematics,
Bangalore University,
Central College Campus,
Bangalore-560 001,
INDIA
Department of Mathematics,
Maharani's Science College for Women,
J. L. B. Road, Mysore-570 001,
INDIA
Abstract:
In this paper, we obtain certain P--Q eta--function identities, using which we establish identities providing modular relations between Ramanujan-Göllnitz-Gordon continued fraction H(q) and H(q^n) for n= 2, 3, 4, 5, 7, 8, 9, 11, 13, 15, 17, 19, 23, 25, 29 and 55.
Paper's Title:
On a New Class of Eulerian's Type Integrals Involving Generalized Hypergeometric Functions
Author(s):
Sungtae Jun, Insuk Kim and Arjun K. Rathie
General Education Institute,
Konkuk University, Chungju 380-701,
Republic of Korea.
Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Republic of Korea.
Department of Mathematics,
Vedant College of Engineering and Technology (Rajasthan Technical University),
Bundi-323021, Rajasthan,
India.
E-mail: sjun@kku.ac.kr, iki@wku.ac.kr, arjunkumarrathie@gmail.com
Abstract:
Very recently Masjed-Jamei and Koepf established interesting and useful generalizations of various classical summation theorems for the 2F1, 3F2, 4F3, 5F4 and 6F5 generalized hypergeometric series. The main aim of this paper is to establish eleven Eulerian's type integrals involving generalized hypergeometric functions by employing these theorems. Several special cases have also been given.
Paper's Title:
Formulation of Approximate Mathematical Model for Incoming Water to Some Dams on Tigris and Euphrates Rivers Using Spline Function
Author(s):
Nadia M. J. Ibrahem, Heba A. Abd Al-Razak, and Muna M. Mustafa
Mathematics Department,
College of Sciences for Women,
University of Baghdad, Baghdad,
Iraq.
E-mail:
Nadiamj_math@csw.uobaghdad.edu.iq
Abstract:
In this paper, we formulate three mathematical models using spline functions, such as linear, quadratic and cubic functions to approximate the mathematical model for incoming water to some dams. We will implement this model on dams of both rivers; dams on the Tigris are Mosul and Amara while dams on the Euphrates are Hadetha and Al-Hindya.
Paper's Title:
On Euler's First Transformation Formula for k-hypergeometric Function
Author(s):
Sungtae Jun and Insuk Kim
General Education Institute,
Konkuk University, Chungju 380-701,
Republic of Korea.
E-mail: sjun@kku.ac.kr
Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Republic of Korea.
E-mail: iki@wku.ac.kr
Abstract:
Mubeen et al. obtained Kummer's first transformation for the k-hypergeometric function. The aim of this note is to provide the Euler-type first transformation for the k-hypergeometric function. As a limiting case, we recover the results of Mubeen et al. In addition to this, an alternate and easy derivation of Kummer's first transformation for the k-hypergeometric function is also given.
Paper's Title:
A Self Adaptive Method for Solving Split Bilevel Variational Inequalities Problem in Hilbert Spaces
Author(s):
Francis Akutsah1, Ojen Kumar Narain2, Funmilayo Abibat Kasali3 Olawale Kazeem Oyewole4 and Akindele Adebayo Mebawondu5
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 216040405@stu.ukzn.ac.za,
akutsah@gmail.com
2School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
3Mountain Top University,
Prayer City, Ogun State,
Nigeria.
E-mail: fkasali@mtu.edu.ng
4Technion-Israel
Institute of Technology.
E-mail: 217079141@stu.ukzn.ac.za,
oyewoleolawalekazeem@gmail.co
5School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
DST-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
Mountain Top University,
Prayer City, Ogun State,
Nigeria.
E-mail: dele@aims.ac.za
Abstract:
In this work, we study the split bilevel variational inequality problem in two real Hilbert spaces. We propose a new modified inertial projection and contraction method for solving the aforementioned problem when one of the operators is pseudomonotone and Lipschitz continuous while the other operator is α-strongly monotone. The use of the weakly sequential continuity condition on the Pseudomonotone operator is removed in this work. A Strong convergence theorem of the proposed method is proved under some mild conditions. In addition, some numerical experiments are presented to show the efficiency and implementation of our method in comparison with other methods in the literature in the framework of infinite dimensional Hilbert spaces. The results obtained in this paper extend, generalize and improve several.
Paper's Title:
A New Proof of Classical Watson's Summation Theorem for the Series 3F2(1)
Author(s):
Insuk Kim, Arjun K. Rathie
Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Korea.
E-mail: iki@wku.ac.kr
Department of Mathematics,
Vedant College of Engineering and Technology (Rajasthan Technical University),
Bundi, Rajasthan,
India.
E-mail:
arjunkumarrathie@gmail.com
Abstract:
The aim of this short research note is to provide a new proof of classical Watson's summation theorem for the series 3F2(1). The theorem is obtained by evaluating an infinite integral and making use of classical Gauss's first and second summation theorems for the series 2F1.
Paper's Title:
Integrability of Sine and Cosine Series Having Coefficients of a New Class
Author(s):
L. Leindler Bolyai Institute,
University of Szeged, Aradi Vértanúk Tere 1, H-6720 Szeged, Hungary
leindler@math.u-szeged.hu
Abstract:
Some integrability theorems or only their sufficient part are
generalized such that the coefficients of the sine and cosine series belong to a
new class of sequences being wider than the class of sequences of rest bounded
variation, which itself is a generalization of the monotone decreasing
sequences, but a subclass of the almost monotone decreasing sequences. It is
also verified that the new class of sequences and the class of almost monotone
decreasing sequences are not comparable.
Paper's Title:
Viability
Theory And Differential Lanchester Type Models For Combat.
Differential Systems.
Author(s):
G. Isac and A. Gosselin
Department Of
Mathematics, Royal Military College Of Canada,
P.O. Box 17000, Stn Forces, Kingston,
Ontario, Canada K7k 7b4
isac-g@rmc.ca
gosselin-a@rmc.ca
URL:
http://www.rmc.ca/academic/math_cs/isac/index_e.html
URL:
http://www.rmc.ca/academic/math_cs/gosselin/index_e.html
Abstract:
In 1914, F.W. Lanchester proposed several mathematical models based on differential equations to describe combat situations [34]. Since then, his work has been extensively modified to represent a variety of competitions including entire wars. Differential Lanchester type models have been studied from many angles by many authors in hundreds of papers and reports. Lanchester type models are used in the planning of optimal strategies, supply and tactics. In this paper, we will show how these models can be studied from a viability theory stand point. We will introduce the notion of winning cone and show that it is a viable cone for these models. In the last part of our paper we will use the viability theory of differential equations to study Lanchester type models from the optimal theory point of view.
Paper's Title:
On the Ulam Stability for Euler-Lagrange Type Quadratic Functional Equations
Author(s):
Matina John Rassias and John Michael Rassias
Statistics and Modelling Science,
University of Strathclyde,
Livingstone Tower,
26 Richmond Str,
Glasgow, Uk, G1 1xh
Pedagogical Department, E. E., National and Capodistrian University of Athens,
Section of Mathematics and Informatics,
4, Agamemnonos Str, Aghia Paraskevi,
Athens 15342, Greece
Abstract:
In 1940 (and 1968) S. M. Ulam proposed the well-known Ulam stability problem.
In 1941 D.H. Hyers solved the Hyers-Ulam problem for linear mappings. In 1951 D. G. Bourgin
has been the second author treating the Ulam problem for additive mappings. In 1978 according
to P.M. Gruber this kind of stability problems is of particular interest in probability theory and in
the case of functional equations of different types. In 1982-2004 we established the Hyers-Ulam
stability for the Ulam problem for different mappings. In 1992-2000 J.M. Rassias investigated
the Ulam stability for Euler-Lagrange mappings. In this article we solve the Ulam problem
for Euler-Lagrange type quadratic functional equations. These stability results can be applied
in mathematical statistics, stochastic analysis, algebra, geometry, as well as in psychology and
sociology.
Paper's Title:
Classes of Meromorphic p-valent Parabolic Starlike Functions with Positive Coefficients
Author(s):
S. Sivaprasad Kumar, V. Ravichandran, and G. Murugusundaramoorthy
Department of Applied Mathematics
Delhi College of Engineering,
Delhi 110042, India
sivpk71@yahoo.com
School of Mathematical Sciences
Universiti Sains Malaysia
11800 USM Penang
Malaysia
vravi@cs.usm.my
URL: http://cs.usm.my/~vravi
Department of Mathematics
Vellore Institute of Technology (Deemed University)
Vellore 632 014, India
gmsmoorthy@yahoo.com
Abstract:
In the present paper, we consider two general subclasses of meromorphic p-valent starlike functions with positive coefficients and obtain a necessary and sufficient condition for functions to be in these classes. Also we obtain certain other related results as a consequences of our main results.
Paper's Title:
Distortion Theorems for Certain Analytic Functions Involving the Coefficient Inequalities
Author(s):
Shigeyoshi Owa and Junichi Nishiwaki
Department of Mathematics, Kinki University,
Higashi-Osaka, Osaka 577-8502,
Japan
Abstract:
By virtue of the coefficient inequalities for certain
analytic functions ![]() in the open unit disk
in the open unit disk ![]() two subclasses
two subclasses ![]() and
and ![]() are introduced. The
object of the present paper is to discuss the distortion thorems
of functions
are introduced. The
object of the present paper is to discuss the distortion thorems
of functions ![]() belonging to the
classes
belonging to the
classes ![]()
![]() involving the
coefficient inequalities.
involving the
coefficient inequalities.
Paper's Title:
Coincidences and Fixed Points of Hybrid Maps in Symmetric Spaces
Author(s):
S. L. Singh and Bhagwati Prasad
Vedic MRI, 21 Govind Nagar,
Department of Mathematics, Gurukula Kangri University,
Rishikesh 249201
India
vedicmri@gmail.com
Hardwar 249404,
India
Abstract:
The purpose of this paper is to obtain a new coincidence theorem for a
single-valued and two multivalued operators in symmetric spaces. We derive
fixed point theorems and discuss some special cases and applications.
Paper's Title:
Product Formulas Involving Gauss Hypergeometric Functions
Author(s):
Edward Neuman
Department of Mathematics, Mailcode 4408,
Southern Illinois University,
1245 Lincoln Drive,
Carbondale, IL 62901,
USA.
edneuman@math.siu.edu
URL: http://www.math.siu.edu/neuman/personal.html
Abstract:
New formulas for a product of two Gauss hypergeometric functions are derived.
Applications to special functions, with emphasis on Jacobi polynomials, Jacobi functions, and Bessel functions of the first kind, are included.
Most of the results are obtained with the aid of the double Dirichlet average of a univariate function.
Paper's Title:
Isoperimetric Inequalities for Dual Harmonic Quermassintegrals
Author(s):
Yuan Jun, Zao Lingzhi and Duan Xibo
School of Mathematics and Computer Science,
Nanjing Normal University, Nanjing, 210097,
China.
yuanjun_math@126.com
Department of Mathematics, Nanjing Xiaozhuang University,
Nanjing, 211171,
China.
lzhzhao@163.com
Department of Mathematics, Shandong Water Polytechnic,
Shandong, 276826,
China
dxb1111@sohu.com
Abstract:
In this paper, some isoperimetric inequalities for the dual harmonic
quermassintegrals are established.
Paper's Title:
On Stan Ulam and his Mathematics
Author(s):
Krzysztof Ciesielski and Themistocles M. Rassias
Mathematics Institute, Jagiellonian University,
Abstract:
In this note we give a glimpse of the curriculum vitae of Stan Ulam, his personality and some of the mathematics he was involved in.
Paper's Title:
A One-Line Derivation of the Euler and Ostrogradski Equations
Author(s):
Olivier de La Grandville
Stanford University,
Department of Management Science and Engineering,
Stanford, CA 94305,
U. S. A
Abstract:
At the very heart of major results of classical physics, the Euler and Ostrogradski equations have apparently no intuitive interpretation. In this paper we show that this is not so. Relying on Euler's initial geometric approach, we show that they can be obtained through a direct reasoning that does not imply any calculation. The intuitive approach we suggest offers two benefits: it gives immediate significance to these fundamental second-order non-linear differential equations; and second, it allows to obtain a property of the calculus of variations that does not seem to have been uncovered until now: the Euler and Ostrogradski equations can be derived not necessarily by giving a variation to the optimal function -- as is always done; one could equally well start by giving a variation to their derivative(s).
Paper's Title:
On Convergence Theorems of an Implicit Iterative Process with Errors for a
Finite Family of Asymptotically quasi I-nonexpansive Mappings
Author(s):
Farrukh Mukhamedov and Mansoor Saburov
Department of Computational & Theoretical
Sciences,
Faculty of Sciences, International Islamic University Malaysia,
P.O. Box, 141, 25710, Kuantan,
Malaysia
Abstract:
In this paper we prove the weak and strong convergence of the implicit iterative process with errors to a common fixed point of a finite family {Tj}Ni=1 of asymptotically quasi Ij-nonexpansive mappings as well as a family of {Ij}Nj=1 of asymptotically quasi nonexpansive mappings in the framework of Banach spaces. The obtained results improve and generalize the corresponding results in the existing literature.
Paper's Title:
Certain Compact Generalizations of Well-Known Polynomial Inequalities
Author(s):
N. A. Rather and Suhail Gulzar
Department of Mathematics,
University of Kashmir, Hazratbal Srinagar-190006,
India.
Abstract:
In this paper, certain sharp compact generalizations of well-known Bernstien-type inequalities for polynomials, from which a variety of interesting results follow as special cases, are obtained.
Paper's Title:
Uniform Continuity and k-Convexity
Author(s):
Adel Afif Abdelkarim
Mathematics Department, Faculty of Science,
J
erash University, Jerash
Jordan.
Abstract:
A closed arcwise-connected subset A of Rn is called k-convex if for each positive number a and for all elements x and y in A there is a positive number b such that if the norm of x-y is less than or equal to b then the length of the shortest curve l(x,y) in A is less than k times the norm of x-y plus a. We show that a union of two non disjoint closed finite convex subsets need not be k-convex. Let f(x) be a uniformly continuous functions on a finite number of closed subsets A_{1},...,A_{n} of R^{n} such that the union of A_{j},...,A_{n},j=1,...,n-1 is k-convex. We show that f is uniformly continuous on the union of the sets A_{i},i=1,...,n. We give counter examples if this condition is not satisfied. As a corollary we show that if f(x) is uniformly continuous on each of two closed convex sets A,B then f(x) is uniformly continuous on the union of A and B.
Paper's Title:
Some Operator Order Inequalities for Continuous Functions of Selfadjoint Operators in Hilbert Spaces
Author(s):
S. S. Dragomir1,2 and Charles E. M. Pearce3
1Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428,
Melbourne City, MC 8001,
Australia.
2School of Computational & Applied Mathematics,
University of
the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
sever.dragomir@vu.edu.au
URL: http://rgmia.org/dragomir
3School
of Mathematical Sciences,
The University of Adelaide,
Adelaide,
Australia
Abstract:
Various bounds in the operator order for the following operator transform
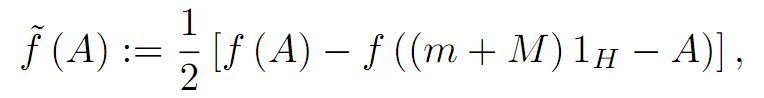
where A is a selfadjoint operator in the Hilbert space H with the
spectrum Sp( A) ⊆ [ m,M]
and f:[m,M] -> C is a continuous function on [m,M]
are given. Applications for the power and logarithmic functions are provided as
well.
Paper's Title:
On the Regularization of Hammerstein's type Operator Equations
Author(s):
E. Prempeh, I. Owusu-Mensah and K. Piesie-Frimpong
Department of Mathematics,
KNUST, Kumasi-
Ghana.
Department of Science Education,
University of Education,
Winneba
Department of Mathematics,
Presbyterian University College, Abetifi,
Ghana
E-mail: isaacowusumensah@gmail.com
E-mail: eprempeh.cos@knust.edu.gh
E-mail: piesie74@yahoo.com
Abstract:
We have studied Regularization of Hammerstein's Type Operator Equations in general Banach Spaces. In this paper, the results have been employed to establish regularized solutions to Hammerstein's type operator equations in Hilbert spaces by looking at three cases of regularization.
Paper's Title:
Hyponormal and K-Quasi-Hyponormal Operators On Semi-Hilbertian Spaces
Author(s):
Ould Ahmed Mahmoud Sid Ahmed and Abdelkader Benali
Mathematics Department,
College of Science,
Aljouf University,
Aljouf 2014,
Saudi Arabia.
E-mail:
sididahmed@ju.edu.sa
Mathematics Department, Faculty of
Science,
Hassiba Benbouali, University of Chlef,
B.P. 151 Hay Essalem, Chlef 02000,
Algeria.
E-mail:
benali4848@gmail.com
Abstract:
Let H be a Hilbert space and let A be a positive bounded operator on H. The semi-inner product < u|v>A:=<Au|v>, u,v ∈ H induces a semi-norm || .||A on H. This makes H into a semi-Hilbertian space. In this paper we introduce the notions of hyponormalities and k-quasi-hyponormalities for operators on semi Hilbertian space (H,||.||A), based on the works that studied normal, isometry, unitary and partial isometries operators in these spaces. Also, we generalize some results which are already known for hyponormal and quasi-hyponormal operators. An operator T ∈ BA (H) is said to be (A, k)-quasi-hyponormal if
![]()
Paper's Title:
The boundedness of Bessel-Riesz operators on generalized Morrey spaces
Author(s):
Mochammad Idris, Hendra Gunawan and Eridani
Department of Mathematics,
Bandung Institute of Technology,
Bandung 40132,
Indonesia.
E-mail:
mochidris@students.itb.ac.id
Department of Mathematics,
Bandung Institute of Technology,
Bandung 40132,
Indonesia.
E-mail: hgunawan@math.itb.ac.id
URL:
http://personal.fmipa.itb.ac.id/hgunawan/
Department of Mathematics,
Airlangga University,
Surabaya 60115,
Indonesia.
E-mail: eridani.dinadewi@gmail.com
Abstract:
In this paper, we prove the boundedness of Bessel-Riesz operators on generalized Morrey spaces. The proof uses the usual dyadic decomposition, a Hedberg-type inequality for the operators, and the boundedness of Hardy-Littlewood maximal operator. Our results reveal that the norm of the operators is dominated by the norm of the kernels.
Paper's Title:
On The Rayleigh-Love Rod Accreting In Both Length And
Cross-Sectional Area: Forced And Damped Vibrations
Author(s):
M.L.G. Lekalakala1, M. Shatalov2, I. Fedotov3, S.V. Joubert4
1Department
of Mathematics, Vaal University of Technology, P.O. Box 1889, Secunda, 2302,
South Africa.
E-mail1:
glen@vut.ac.za
2,3,4Department of Mathematics and Statistics, Tshwane University of Technology, Pretoria, South Africa.
Abstract:
In this paper an elastic cylindrical rod that is subjected to forced and damped vibrations is considered. The rod is assumed to be isotropic. The applied external force of excitation is assumed to be harmonic, and the damping force is that of Kelvin-Voigt. The longitudinally vibrating rod is fixed at the left end and free at the other end. The rod is assumed to be accreting in length and cross-sectional area as it vibrates. The problem arising and the dynamics of the vibrating rod are described and investigated within the Rayleigh-Love theories of the rod. A partial differential equation describing the longitudinal displacement of the rod is formulated. The formulated partial differential equation, together with the corresponding boundary conditions as per the configuration of the rod, is solved numerically using the Galerkin-Kantorovich method. The frequency of vibration of the harmonic exciting force is kept constant in this investigation.
It is shown that in this periodically forced viscoelastic damped vibration, all the modes of vibration are subjected to the resonance behaviour within a proper time interval, depending on the length of the accreting rod.
Paper's Title:
Iterative Approximation of Zeros of Accretive Type Maps, with Applications
Author(s):
Charles Ejike Chidume, Chinedu Godwin Ezea, and Emmanuel Ezzaka Otubo
African University of Science and
Technology, Abuja,
Nigeria.
E-mail: cchidume@aust.edu.ng
E-mail: chinedu.ezea@gmail.com
E-mail: mrzzaka@yahoo.com
Department of Mathematics,
Nnamdi Azikiwe University,
Awka,
Nigeria
E-mail: chinedu.ezea@gmail.com
Ebonyi State University,
Abakaliki,
Nigeria
E-mail: mrzzaka@yahoo.com
Abstract:
Let E be a reflexive real Banach space with uniformly Gâteaux differentiable norm. Let J:E→ E* be the normalized duality map on E and let A:E*→ E be a map such that AJ is an accretive and uniformly continuous map. Suppose that (AJ)-1(0) in nonempty. Then, an iterative sequence is constructed and proved to converge strongly to some u* in (AJ)-1(0). Application of our theorem in the case that E is a real Hilbert space yields a sequence which converges strongly to a zero of A. Finally, non-trivial examples of maps A for which AJ is accretive are presented..
Paper's Title:
Iterative Algorithm for Split Generalized Mixed Equilibrium Problem Involving Relaxed Monotone Mappings in Real Hilbert Spaces
Author(s):
1U.A. Osisiogu, F.L. Adum, and 2C. Izuchukwu
1Department of Mathematics and
Computer Science,
Ebonyi State University, Abakaliki,
Nigeria.
E-mail: uosisiogu@gmail.com,
adumson2@yahoo.com
2School of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: izuchukwuc@ukzn.ac.za,
izuchukwu_c@yahoo.com
Abstract:
The main purpose of this paper is to introduce a certain class of split generalized mixed equilibrium problem involving relaxed monotone mappings. To solve our proposed problem, we introduce an iterative algorithm and obtain its strong convergence to a solution of the split generalized mixed equilibrium problems in Hilbert spaces. As special cases of the proposed problem, we studied the proximal split feasibility problem and variational inclusion problem.
Paper's Title:
Solving Two Point Boundary Value Problems by Modified Sumudu Transform Homotopy Perturbation Method
Author(s):
Asem AL Nemrat and Zarita Zainuddin
School of Mathematical Sciences,
Universiti Sains Malaysia,
11800 Penang,
Malaysia.
E-mail: alnemrata@yahoo.com
zarita@usm.my
Abstract:
This paper considers a combined form of the Sumudu transform with the modified homotopy perturbation method (MHPM) to find approximate and analytical solutions for nonlinear two point boundary value problems. This method is called the modified Sumudu transform homotopy perturbation method (MSTHPM). The suggested technique avoids the round-off errors and finds the solution without any restrictive assumptions or discretization. We will introduce an appropriate initial approximation and furthermore, the residual error will be canceled in some points of the interval (RECP). Only a first order approximation of MSTHPM will be required, as compared to STHPM, which needs more iterations for the same cases of study. After comparing figures between approximate, MSTHPM, STHPM and numerical solutions, it is found through the solutions we have obtained that they are highly accurate, indicating that the MSTHPM is very effective, simple and can be used to solve other types of nonlinear boundary value problems (BVPs).
Paper's Title:
An Integration Technique for Evaluating Quadratic Harmonic Sums
Author(s):
J. M. Campbell and K.-W. Chen
Department of Mathematics and Statistics,
York University, 4700 Keele St, Toronto,
ON M3J 1P3,
Canada.
E-mail: jmaxwellcampbell@gmail.com
Department of Mathematics, University of Taipei,
No. 1, Ai-Guo West Road,
Taipei 10048, Taiwan.
E-mail: kwchen@uTaipei.edu.tw
URL:
https://math.utaipei.edu.tw/p/412-1082-22.php
Abstract:
The modified Abel lemma on summation by parts has been applied in many ways recently to determine closed-form evaluations for infinite series involving generalized harmonic numbers with an upper parameter of two. We build upon such results using an integration technique that we apply to ``convert'' a given evaluation for such a series into an evaluation for a corresponding series involving squared harmonic numbers.
Paper's Title:
Several New Closed-form Evaluations of the Generalized Hypergeometric Function with Argument 1/16
Author(s):
B. R. Srivatsa Kumar, Insuk Kim and Arjun K. Rathie
Department of Mathematics,
Manipal Institute of Technology,
Manipal Academy of Higher Education,
Manipal 576 104,
India.
E-mail: sri_vatsabr@yahoo.com
Department of Mathematics Education,
Wonkwang University,
Iksan, 54538,
Republic of Korea.
E-mail: iki@wku.ac.kr
Department of Mathematics,
Vedant College of Engineering and Technology,
Rajasthan Technical University,
Bundi, 323021, Rajasthan,
India.
E-mail: arjunkumarrathie@gmail.com
Abstract:
The main objective of this paper is to establish as many as thirty new closed-form evaluations of the generalized hypergeometric function q+1Fq(z) for q= 2, 3, 4. This is achieved by means of separating the generalized hypergeometric function q+1Fq(z) for q=1, 2, 3, 4, 5 into even and odd components together with the use of several known infinite series involving central binomial coefficients obtained earlier by Ji and Hei \& Ji and Zhang.
Paper's Title:
D-Iterative Method for Solving a Delay Differential Equation and a Two-Point Second-Order Boundary Value Problems in Banach Spaces
Author(s):
Francis Akutsah1, Akindele Adebayo Mebawondu2, Oluwatosin Babasola3, Paranjothi Pillay4 and Ojen Kumar Narain5
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 216040405@stu.ukzn.ac.za,
akutsah@gmail.com
2School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
DST-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
Mountain Top University,
Prayer City, Ogun State,
Nigeria.
E-mail: dele@aims.ac.za
3Department
of Mathematical Sciences,
University of Bath,
Claverton Down,
Bath, BA2 7AY
UK.
E-mail: ob377@bath.ac.uk
4School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: pillaypi@ukzn.ac.za
5School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
The purpose of this paper is to re-establish the convergence, stability and data dependence results established by [2] and [3] by removing the strong assumptions imposed on the sequences which were used to obtain their results. In addition, we introduced a modified approach using the D-iterative method to solve a two-point second-order boundary value problem, and also obtain the solution of a delay differential equations using the obtained results in this paper. The results presented in this paper do not only extend and improve the results obtained in [2, 3], it further extends and improve some existing results in the literature.
Paper's Title:
A Determinantal Representation of Core EP Inverse
Author(s):
Divya Shenoy Purushothama
Department of Mathematics,
Manipal Institute of Technology,
Manipal Academy of Higher Education,
Manipal -576104, Karnataka,
India.
E-mail: divya.shenoy@manipal.edu
URL:
https://manipal.edu/mit/department-faculty/faculty-list/divya-shenoy-p.html
Abstract:
The notion of Core EP inverse is introduced by Prasad in the article "Core - EP inverse" and proved its existence and uniqueness. Also, a formula for computing the Core EP inverse is obtained from particular linear combination of minors of a given matrix. Here a determinantal representation for Core EP inverse of a matrix A with the help of rank factorization of A is obtained.
Paper's Title:
Using Direct and Fixed Point Technique of Cubic Functional Equation and its Hyers-Ulam Stability
Author(s):
Ramanuja Rao Kotti, Rajnesh Krishnan Mudaliar, Kaushal Neelam Devi, Shailendra Vikash Narayan
Fiji National University,
Department of Mathematics & Statistics,
P.O. Box 5529, Lautoka,
Fiji.
E-mail: ramanuja.kotti@fnu.ac.fj
URL: https://www.fnu.ac.fj
Abstract:
In this present work, we introduce a new type of finite dimensional cubic functional equation of the form

where Φ≥4 is an integer, and derive its general solution. The main purpose of this work is to investigate the Hyers-Ulam stability results for the above mentioned functional equation in Fuzzy Banach spaces by means of direct and fixed point methods.
Paper's Title:
Finite Volume Approximation of a Class of 2D Elliptic Equations with Discontinuous and Highly Oscillating Coefficients
Author(s):
J. D. Bambi Pemba and B. Ondami
Université Marien Ngouabi
Factuté des Sciences et Techniques
BP 69 Brazzaville,
Congo.
E-mail: bondami@gmail.com
URL:
https://www.researchgate.net/profile/Bienvenu-Ondami
https://www.linkedin.com/in/bienvenu-ondami
Abstract:
In this paper, we are interested in the Finite Volume approximation of a second-order two-dimensional elliptic equation in heterogeneous porous medium with a periodic structure. The equation's coefficients are therefore discontinuous and highly oscillating. This class of problems has been extensively studied in the literature, where various methods proposed for determining the so-called homogenized problem. What we are particularly interested in is the direct numerical approximation of the problem, which has received little attention in the literature. We use the cell-centered finite volume approach for this purpose. Error estimates are established, and numerical simulations are conducted for both the isotropic and anisotropic media cases. The obtained solution is compared to the homogenized solution, and the results show that this approach provides an adequate approximation of the exact solution.
Paper's Title:
A New Look at the Equations of the Calculus of Variations
Author(s):
Olivier de La Grandville
Faculty of Economics, Goethe University
Frankfurt,
Theodore Adorno Platz 4, 60323 Frankfurt,
Germany.
E-mail: odelagrandville@gmail.com
Abstract:
We first offer an entirely new way to derive the celebrated Euler equation of the calculus of variations. The advantage of this approach is two-fold. On the one hand, it entirely eschews the two hurdles encountered by Lagrange, which become challenging in the case of elaborate functionals: getting rid of the arbitrary character of the perturbation given to the optimal function, and demonstrating the fundamental lemma of the calculus of variations. On the other hand, it leads in a direct way to the remarkable discovery made by Robert Dorfman ( 1969) when he introduced a modified Hamiltonian, which we called a Dorfmanian (2018) to honor his memory. In turn, extending the Dorfmanian enables to obtain readily the fundamental equations of the calculus of variations for the optimization of high-order functionals, or multiple integrals.
Paper's Title:
A New Iterative Approximation of a Split Fixed Point Constraint Equilibrium Problem
Author(s):
Musa Adewale Olona1, Adhir Maharaj2 and Ojen Kumar Narain3
1School
of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 219095783@stu.ukzn.ac.za
2Department
of Mathematics,
Durban University of Technology, Durban,
South Africa.
E-mail: adhirm@dut.ac.za
3School
of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
The purpose of this paper is to introduce an iterative algorithm for approximating an element in the solution set of the common split feasibility problem for fixed points of demimetric mappings and equilibrium problem for monotone mapping in real Hilbert spaces. Motivated by self-adaptive step size method, we incorporate the inertial technique to accelerate the convergence of the proposed method and establish a strong convergence of the sequence generated by the proposed algorithm. Finally, we present a numerical example to illustrate the significant performance of our method. Our results extend and improve some existing results in the literature.
Paper's Title:
Maximal Singular Operators On Variable Exponent Sequence Spaces and Their Corresponding Ergodic Version
Author(s):
Sri Sakti Swarup Anupindi and Michael A. Alphonse
Department of Mathematics, Birla Institute
of Technology And Science- Pilani,
Hyderabad Campus, Jawahar Nagar, Kapra Mandal,
District.-Medchal-500 078 Telangana,
India.
E-mail:
p20180442@hyderabad.bits-pilani.ac.in
alphonse@hyderabad.bits-pilani.ac.in
URL:
https://www.bits-pilani.ac.in/hyderabad/a-michael-alphonse
https://www.bits-pilani.ac.in/research_scholars/sri-sakti-swarup-anupindi
Abstract:
In this paper, we prove strong and weak type inequalities of singular operators on weighted lwp(Z)$. Using these results, we prove strong type and weak type inequalities of the maximal singular operator of Calderon-Zygmund type on variable exponent sequence spaces lp(·)(Z). Using the Calderon-Coifman-Weiss transference principle, we prove strong type, weak type inequalities of the maximal ergodic singular operator on Lwp(X,B,μ) spaces, where (X,B,μ) is a probability space equipped with measure preserving transformation U.
Paper's Title:
The Drazin-star and Star-Drazin Solutions to Quaternion Matrix Equations
Author(s):
Ivan I. Kyrchei, Dijana Mosić, Predrag Stanimirović
Pidstryhach Institute for Applied Problems
of Mechanics and Mathematics
of NAS of Ukraine, L'viv, 79060,
Ukraine.
E-mail:
ivankyrchei26@gmail.com
Faculty of Sciences and Mathematics,
University of Niš, P.O.
Box 224, 18000, Niš, Serbia.
E-mail: dijana@pmf.ni.ac.rs
Faculty of Sciences and Mathematics,
University of Niš, P.O.
Box 224, 18000, Niš, Serbia.
E-mail: pecko@pmf.ni.ac.rs
Abstract:
The notions of the Drazin-star and star-Drazin matrices are expanded to quaternion matrices in this paper. Their determinantal representations are developed in both cases in terms of noncommutative row-column determinants of quaternion matrices and for minors of appropriate complex matrices. We study all possible two-sided quaternion matrix equations with their one-sided partial cases whose uniquely determined solutions are based on the Drazin-star and star-Drazin matrices. Solutions of these equations are represented by Cramer's rules in both cases for quaternion and complex matrix equations. A numerical example is presented to illustrate our results.
Paper's Title:
Discrete-time Evolution and Stable Equilibria of Multi-compartment Dengue Tracker: Nonlinear Dynamics Modulated by Controlled Stochasticity
Author(s):
M. Bhaduri and M. Predescu
Department of Mathematical Sciences,
Bentley University,
Waltham, MA 02452,
U.S.A.
E-mail: mbhaduri@bentley.edu,
mpredescu@bentley.edu
Abstract:
We discuss the dynamics of solutions of a nonlinear discrete time model that will be useful in Dengue control. The proposed model may be utilized to analyze the dynamics of three variables (mosquito population, habitats and consciousness) across different parameters. Stochasticity has been introduced in realistic ways to highlight combinations of random parameters (on education and recollection) which limits the oscillatory recurrence of habitats and awareness. We propose optimal methods for implementing potential intervention strategies and offer interactive dashboards for vizualizing varied scenarios.
Paper's Title:
Inequalities Relating to the Gamma Function
Author(s):
Chao-Ping Chen and Feng Qi
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
chenchaoping@hpu.edu.cn
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
qifeng@hpu.edu.cn,
fengqi618@member.ams.org
Url:
http://rgmia.vu.edu.au/qi.html,
http://dami.hpu.edu.cn/qifeng.html
Abstract:
For ![]() , we have
, we have
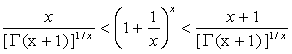 .
.
For![]() ,
,
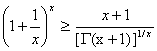 ,
,
And equality occurs for x=1.
Paper's Title:
Long Time Behavior for a Viscoelastic Problem with a Positive Definite Kernel
Author(s):
Nasser-eddine Tatar
King Fahd
University of Petroleum and Mineral, Department of Mathematical Sciences,
Dhahran, 31261 Saudi Arabia
tatarn@kfupm.edu.sa
Abstract:
We study the asymptotic behavior of solutions for an integro-differential problem which arises in the theory of viscoelasticity. It is proved that solutions go to rest in an exponential manner under new assumptions on the relaxation function in the memory term. In particular, we consider a new family of kernels which are not necessarily decreasing.
Paper's Title:
An Application of Quasi Power Increasing Sequences
Author(s):
Hüseyín Bor
Department of Mathematics, Erciyes University, 38039 Kayseri,
Turkey
Url:
Http://math.erciyes.edu.tr/Hbor.htm
Abstract:
In this paper a result of Bor
[2] has been proved
under weaker conditions by using a -quasi power increasing sequence instead of
an almost increasing sequence.
Paper's Title:
Analytical and Numerical Solutions of the Inhomogenous Wave Equation
Author(s):
T. Matsuura and S. Saitoh
Department of Mechanical Engineering, Faculty of Engineering,
Gunma University, Kiryu 376-8515, Japan
matsuura@me.gunma-u.ac.jp
Department of Mathematics, Faculty of Engineering,
Gunma University, Kiryu 376-8515, Japan
ssaitoh@math.sci.gunma-u.ac.jp
Abstract:
In this paper, by a new concept and method we give approximate
solutions of the inhomogenous wave equation on multidimensional spaces.
Numerical experiments are conducted as well.
Paper's Title:
Multivalued Equilibrium Problems with Trifunction
Author(s):
Muhammad Aslam Noor
Etisalat College of Engineering, P.O. Box 980, Sharjah, United Arab Emirates
noor@ece.ac.ae
Abstract:
In this paper, we use the auxiliary principle technique to
suggest some new classes of iterative algorithms for solving multivalued
equilibrium problems with trifunction. The convergence of the proposed methods
either requires partially relaxed strongly monotonicity or pseudomonotonicity.
As special cases, we obtain a number of known and new results for solving
various classes of equilibrium and variational inequality problems. Since
multivalued equilibrium problems with trifunction include equilibrium,
variational inequality and complementarity problems as specials cases, our
results continue to hold for these problems.
Paper's Title:
Generalized Fuglede-Putnam Theorem and Orthogonality
Author(s):
A. Bachir and A. Sagres
Department of
Mathematics, Faculty of Science, King Khaled
University, Abha, P.O. Box 9004 Kingdom Saudi Arabia
bachir_ahmed@hotmail.com
sagres@hotmail.com
Abstract:
An asymmetric Fuglede-Putnam’s theorem for dominant operators
and
Paper's Title:
Monotonicity Properties for Generalized Logarithmic Means
Author(s):
Chao-Ping Chen and Feng Qi
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
chenchaoping@hpu.edu.cn
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
qifeng@hpu.edu.cn,
fengqi618@member.ams.org
Url:
http://rgmia.vu.edu.au/qi.html,
http://dami.hpu.edu.cn/qifeng.html
Abstract:
In this paper, we consider the monotonicity properties for ratio of two generalized logarithmic means, and then use it to extend and complement a recently published result of F. Qi and B.-N. Guo.
Paper's Title:
A Majorization Problem for the Subclass of p-Valently Analytic Functions of Complex Order
Author(s):
Sezgin Akbulut
Department of Mathematics, Science and Art Faculty,
Atatürk University, 25240 Erzurum, Turkey
sbulut@atauni.edu.tr
Abstract:
The main purpose of this paper is to investigate a majorization problem for the
class
![]() . Relevant connections of the main result obtained in this paper with those given
by earlier workers on the subject are also pointed out.
. Relevant connections of the main result obtained in this paper with those given
by earlier workers on the subject are also pointed out.
Paper's Title:
Reverses of the Triangle Inequality in Inner Product Spaces
Author(s):
Sever S. Dragomir
School of Computer Science and Mathematics,
Victoria University Of Technology,
PO Box 14428, Mcmc 8001,
Victoria, Australia.
sever@csm.vu.edu.au
Url:
http://rgmia.vu.edu.au/SSDragomirWeb.html
Abstract:
Some new reverses for the generalised triangle inequality in inner product spaces are given. Applications in connection to the Schwarz inequality and for vector-valued integrals are provided as well.
Paper's Title:
Positive Solution For Discrete Three-Point Boundary Value
Problems
Author(s):
Wing-Sum Cheung And Jingli Ren
Department of Mathematics,
The University of Hong Kong,
Pokfulam, Hong Kong
wscheung@hku.hk
Institute of Systems Science,
Chinese Academy of Sciences,
Beijing 100080, P.R. China
renjl@mx.amss.ac.cn
Abstract:
This paper is concerned with the existence of positive solution to the discrete three-point boundary value problem
![]()
![]() ,
,
![]()
![]()
where
![]()
![]() , and f is allowed to change sign. By constructing
available operators, we shall apply the method of lower solution and the method
of topology degree to obtain positive solution of the above problem for
, and f is allowed to change sign. By constructing
available operators, we shall apply the method of lower solution and the method
of topology degree to obtain positive solution of the above problem for
![]() on a suitable interval.
The associated Green’s function is first given.
on a suitable interval.
The associated Green’s function is first given.
Paper's Title:
An alternative proof of monotonicity for the extended mean values
Author(s):
Chao-Ping Chen and Feng Qi
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
chenchaoping@hpu.edu.cn
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
qifeng@hpu.edu.cn,
fengqi618@member.ams.org
Url:
http://rgmia.vu.edu.au/qi.html,
http://dami.hpu.edu.cn/qifeng.html
Abstract:
An alternative proof of monotonicity for the extended mean values is given.
Paper's Title:
Generalizations of two theorems on absolute summability methods
Author(s):
H.S. Özarslan and
H.N. Öğdük
Department of Mathematics,
Erciyes University, 38039 Kayseri,
Turkey
seyhan@erciyes.edu.tr
nogduk@erciyes.edu.tr
URL:
http://fef.erciyes.edu.tr/math/hikmet.htm
Abstract:
In this paper two theorems on ![]() summability methods, which generalize two theorems of Bor on
summability methods, which generalize two theorems of Bor on ![]() summability methods, have been proved.
summability methods, have been proved.
Paper's Title:
Reverse of Martin's Inequality
Author(s):
Chao-Ping Chen, Feng Qi, and Sever S. Dragomir
Department of Applied Mathematics and Informatics,
Research Institute of Applied
Mathematics,
Henan Polytechnic University,
Jiaozuo City, Henan 454010, China
chenchaoping@sohu.com;
chenchaoping@hpu.edu.cn
Department of Applied Mathematics and Informatics,
Research Institute of Applied
Mathematics,
Henan Polytechnic University,
Jiaozuo City, Henan 454010, China
qifeng@hpu.edu.cn
Url: http://rgmia.vu.edu.au/qi.html
School of Computer Science and Mathematics,
Victoria University of Technology,
P. O. Box 14428, Melbourne City Mc,
Victoria 8001, Australia
Sever.Dragomir@vu.edu.au
Url: http://rgmia.vu.edu.au/SSDragomirWeb.html
Abstract:
In this paper, it is proved that
for all natural numbers n, and all real r < 0.

Paper's Title:
On Certain Classes of Harmonic Univalent Functions Based on Salagean Operator
Author(s):
G. Murugusundaramoorthy, Thomas Rosy, and B. A. Stephen
Department of Applied Mathematics and Informatics,
Department of Mathematics, Vellore Institute of Technology,
Deemed University, Vellore - 632014, India.
gmsmoorthy@yahoo.com
Department of Applied Mathematics and Informatics,
Department of Mathematics, Madras Christian College,
Chennai - 600059, India.
drthomasrosy@rediffmail.com
Abstract:
We define and investigate a class of complex-valued harmonic univalent functions of the form f = h + g using Salagean operator where h and g are analytic in the unit disc U = { z : |z| < 1 }. A necessary and sufficient coefficient conditions are given for functions in these classes. Furthermore, distortion theorems, inclusion relations, extreme points, convolution conditions and convex combinations for this family of harmonic functions are obtained.
Paper's Title:
Compactly Supported Interpolatory Orthogonal Multiwavelet Packets
Author(s):
Yang Shouzhi
Department of Mathematics,
Shantou University,
Shantou, Po Box 515063,
P.R.China.
szyang@stu.edu.cn
Abstract:
Compactly supported interpolatory orthogonal multiwavelet packets
are introduced. Precisely, if both the multiscaling function and
the corresponding multiwavelet have the same interpolatory
property, then the multiwavelet packets are also interpolatory
orthogonal. Thus, the coefficients of decomposition or synthesis
of multiwavelet packets can be realized by sampling instead of inner
products. This multiwavelet packets provide a finer decomposition
of multiwavelet packets space and give a better localization.
Paper's Title:
General Oscillations for Some Third Order Differential Systems with Nonlinear Acceleration Term
Author(s):
Awar Simon Ukpera
Department of Mathematics,
Obafemi Awolowo University,
Ile-Ife,
Nigeria.
aukpera@oauife.edu.ng
Abstract:
We generate some general nonuniform hypotheses for third order differential systems
of the form X''' +F(t,X'' )+BX'+CX = P(t), in which B and C are not
necessarily
constant matrices. Some results requiring sharp conditions on this system have recently been
published by the author in
[5]. This work however examines more closely crucial properties
associated with the generalised nature of the nonlinear acceleration term F, which were largely
overlooked in the earlier paper.
Paper's Title:
On the Hohov Convolution Of The Class Sp(α,β)
Author(s):
T. N. Shanmugam and S. Sivasubramanian
Department of Mathematics,
Anna University,
Chennai 600025,
Tamilnadu, India.
shan@annauniv.edu
Department of Mathematics,
Easwari Engineering College,
Chennai-600089,
Tamilnadu, India,
sivasaisastha@rediffmail.com
Abstract:
Let F(a,b;c;z) be the Gaussian hypergeometric function and Ia,b;c(f)=zF(a,b;c;z)*f(z) be the Hohlov operator defined on the class A of all normalized analytic functions. We determine conditions on the parameters a,b,c such that Ia,b;c(f) will be in the class of parabolic starlike functions Sp(α,β). Our results extend several earlier results.
Paper's Title:
Logarithmically complete monotonicity properties for the gamma functions
Author(s):
Chao-Ping Chen and Feng Qi
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University,
Jiaozuo City, Henan 454010,
China.
chenchaoping@hpu.edu.cn
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University,
Jiaozuo City, Henan 454010,
China.
qifeng@hpu.edu.cn
fengqi618@member.ams.org
Abstract:
Some logarithmically completely monotonic functions involving the gamma functions are presented. As a consequence, some known results are proved and refined.
Paper's Title:
Boundedness for Vector-Valued Multilinear Singular Integral Operators on Triebel-Lizorkin Spaces
Author(s):
Liu Lanzhe
College of Mathematics
Changsha University of Science and Technology,
Changsha 410077,
P.R. of China.
lanzheliu@263.net
Abstract:
In this paper, the boundedness for some vector-valued multilinear operators associated to certain
fractional singular integral operators on Triebel-Lizorkin space are obtained. The operators include Calderón-Zygmund
singular integral operator and fractional integral operator.
Paper's Title:
Stability of a Pexiderized Equation
Author(s):
Maryam Amyar
Department of Mathematics,
Islamic Azad University, Rahnamaei Ave,
Mashhad 91735, Iran,
and Banach Mathematical Research Group (BMRG)
amyari@mshdiau.ac.ir
URL: http://amyari.mshdiau.ac.ir
Abstract:
The aim of the paper is to prove the
stability of the Pexiderized equation f(x)=g(y+x)-h(y-x), for any
amenable abelian group.
Paper's Title:
Boundary Value Problems for Fractional Diffusion-Wave equation
Author(s):
Varsha Daftardar-Gejji and Hossein Jafari
Department of Mathematics, University of Pune,
Ganeshkhind, Pune - 411007,
INDIA.
vsgejji@math.unipune.ernet.in
jafari_h@math.com
Abstract:
Non homogeneous fractional diffusion-wave equation has been solved under linear/nonlinear boundary conditions. As the order of time derivative changes from
0 to 2, the process changes from slow diffusion to classical diffusion to mixed diffusion-wave behaviour.
Numerical examples presented here confirm this inference. Orthogonality of eigenfunctions in case of fractional Stürm-Liouville problem has been established
Paper's Title:
Merit Functions and Error Bounds for Mixed Quasivariational Inequalities
Author(s):
Muhammad Aslam Noor
Mathematics Department, COMSATS Institute of Information Technology,
Islamabad, Pakistan
noormaslam@hotmail.com
Abstract:
It is well known that the mixed
quasivariational inequalities are equivalent to the fixed point
problems. We use this equivalent alternative formulation to
construct some merit functions for mixed quasivariational inequalities
and obtain error bounds under some conditions. Since mixed
quasivariational inequalities
include the classical variational inequalities and the complementarity
problems as special cases, our results continue to hold for these
problems.
Paper's Title:
A New Family of Periodic Functions as Explicit Roots of a Class of Polynomial Equations
Author(s):
M. Artzrouni
Department of Mathematics, University of Pau
64013 Pau Cedex
Pau, France
marc.artzrouni@univ-pau.fr
URL: http://www.univ-pau.fr/~artzroun
Abstract:
For any positive integer n a new family of periodic functions in power series form and
of period n is used to solve in closed form a class of polynomial equations of order
n. The n roots are the values of the appropriate function from that family taken at
0, 1, ... , n-1.
Paper's Title:
Some Stability Results For Fixed Point Iteration Processes
Author(s):
M. O. Olatinwo, O. O. Owojori, and C. O. Imoru
Department of Mathematics, Obafemi Awolowo University,
Ile-Ife,
Nigeria.
polatinwo@oauife.edu.ng
walejori@oauife.edu.ng
cimoru@oauife.edu.ng
Abstract:
In this paper, we present some stability results for both the general Krasnoselskij and the Kirk's iteration processes. The method of Berinde \cite{VBE1} is employed but a more general contractive condition than those of Berinde \cite{VBE1}, Harder and Hicks \cite{HAM}, Rhoades \cite{RHO1} and Osilike \cite{OSI1} is considered.
Paper's Title:
Comparison Results for Solutions of Time Scale Matrix Riccati
Equations and Inequalities
Author(s):
R. Hilscher
Department of Mathematical Analysis, Faculty of Science,
Masaryk University, Janáčkovo nám. 2a,
CZ-60200, Brno, Czech Republic.
hilscher@math.muni.cz
URL: http://www.math.muni.cz/~hilscher/
Abstract:
In this paper we derive comparison results for Hermitian solutions of time scale matrix Riccati
equations and Riccati inequalities. Such solutions arise from special conjoined bases
(X,U) of the corresponding time scale symplectic system via the Riccati quotient
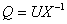 . We also discuss properties of a unitary matrix solution
. We also discuss properties of a unitary matrix solution 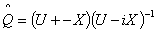 of a certain
associated Riccati equation.
of a certain
associated Riccati equation.
Paper's Title:
A Strengthened Hardy-Hilbert's Type Inequality
Author(s):
Weihong Wang and Bicheng Yang
Department of Mathematics, Guangdong Education Institute,
Guangzhou, Guangdong 520303,
People's Republic Of China
wwh@gdei.edu.cn
bcyang@pub.guangzhou.gd.cn
URL: http://www1.gdei.edu.cn/yangbicheng/index.html
Abstract:
By using the improved Euler-Maclaurin's summation formula and
estimating the weight coefficient, we give a new strengthened
version of the more accurate Hardy-Hilbert's type inequality. As
applications, a strengthened version of the equivalent form is
considered.
Paper's Title:
On Positive Entire Solutions of Second Order Quasilinear Elliptic Equations
Author(s):
Zuodong Yang and Honghui Yin
Institute of Mathematics, School of Mathematics and Computer Science,
Nanjing Normal University, Jiangsu Nanjing 210097,
China;
zdyang_jin@263.net
Department of Mathematics, Huaiyin Teachers College,
Jiangsu Huaian 223001,
China;
School of Mathematics and Computer Sciences,
Nanjing Normal University, Jiangsu Nanjing 210097,
China.
yin_hh@sina.com
Abstract:
In this paper, our main purpose is to establish the existence
theorem of positive entire solutions of second order quasilinear
elliptic equations under new conditions. The main results of the
present paper are new and extend the previously known results.
Paper's Title:
Numerical Studies on Dynamical Systems Method for Solving Ill-posed Problems with Noise
Author(s):
N. H. Sweilam and A. M. Nagy
Mathematics Department, Faculty of Science,
Mathematics Department, Faculty of Science,
Cairo University,
Giza, Egypt.
n_sweilam@yahoo.com
Benha University,
Benha, Egypt.
abdelhameed_nagy@yahoo.com
Abstract:
In this paper, we apply the dynamical systems method proposed by
A. G. RAMM, and the the variational regularization method to
obtain numerical solution to some ill-posed problems with noise.
The results obtained are compared to exact solutions. It is found
that the dynamical systems method is preferable because it is
easier to apply, highly stable, robust, and it always converges to
the solution even for large size models.
Paper's Title:
A New Step Size Rule in Noor's Method for Solving General Variational Inequalities
Author(s):
Abdellah Bnouhachem
School of Management Science and Engineering, Nanjing University,
Nanjing, 210093
P.R. China.
babedallah@yahoo.com
Abstract:
In this paper, we propose a new step size rule in Noor's method
for solving general
variational inequalities. Under suitable conditions, we prove that the
new method is globally convergent. Preliminary numerical
experiments are included to illustrate the advantage and
efficiency of the proposed method.
Paper's Title:
Generalized Quasilinearization Method for the Forced Düffing Equation
Author(s):
Ramzi S. N. Alsaedi
Department of Mathematics, King Abdul Aziz University,
Jeddah P.O. Box 80203,
Saudi Arabia.
ramzialsaedi@yahoo.co.uk
Abstract:
A generalized quasilinearization method for the periodic
problem related to the forced D\"{u}ffing equation is developed and a
sequence of approximate solutions converging monotonically and quadratically
to the solution of the given problem is presented.
Paper's Title:
Iterated Order of Fast Growth Solutions of Linear Differential Equations
Author(s):
Benharrat Belaďdi
Department of Mathematics
Laboratory of Pure and Applied Mathematics
University of Mostaganem
B. P. 227 Mostaganem,
ALGERIA.
belaidi@univ-mosta.dz
Abstract:
In this paper, we investigate the growth of solutions of the differential
equation
f(k) + Ak-1 (z) f(k-1) +...+ A1 (z) f' + A0 (z) f= F (z),
where
Ao (z), ..., Ak-1 (z)
and
F (z)  0
are entire functions. Some estimates are given for the iterated order of solutions of the above quation when one of the coefficients As is being dominant in the sense that it has larger growth than Aj (j≠s) and F.
0
are entire functions. Some estimates are given for the iterated order of solutions of the above quation when one of the coefficients As is being dominant in the sense that it has larger growth than Aj (j≠s) and F.
Paper's Title:
Existence of Solutions for Third Order Nonlinear Boundary Value Problems
Author(s):
Yue Hu and Zuodong Yang
School of Mathematics and Computer Science, Nanjing Normal University, Jiangsu Nanjing 210097,
China.
huu3y2@163.com
College of Zhongbei, Nanjing Normal University, Jiangsu Nanjing 210046,
China.
zdyang_jin@263.net
yangzuodong@njnu.edu.cn
Abstract:
In this paper, the existence of solution for a class of third order quasilinear ordinary differential equations with nonlinear boundary value problems
(Φp(u"))'=f(t,u,u',u"), u(0)=A, u'(0)=B, R(u'(1),u"(1))=0
is established. The results are obtained by using upper and lower solution methods.
Paper's Title:
On Sandwich Theorems for Certain Subclass of Analytic Functions Involving Dziok-Srivastava Operator
Author(s):
T. N. Shanmugam, M. P. Jeyarama and A. Singaravelu
Department of Mathematics
College of Engineering, Anna University
Chennai - 600 025,
India
drtns2001@yahoo.com
Department of Mathematics
Easwari Engineering College
Ramapuram, Chennai - 600089
Tamilnadu, India
jeyaraman-mp@yahoo.co.i
Department of Mathematics
Valliammai Engineering College
Chennai - 603203
Tamilnadu, India.
asing-59@yahoo.com
Abstract:
The purpose of this present paper is to derive some subordination and superordination results for certain normalized analytic functions in the open unit disk, acted upon by Dziok-Srivastava operator. Relevant connections of the results, which are presented in this paper, with various known results are also considered.
Paper's Title:
An Approximation of Jordan Decomposable Functions for a Lipschitz Function
Author(s):
Ibraheem Alolyan
Mathematics Department,
College of Science, King Saud University
P.O.Box: 2455, Riyadh 11451,
Saudi Arabia
ialolyan05@yahoo.com
Abstract:
The well known Jordan decomposition theorem gives the useful characterization that any function of bounded variation can be written as the difference of two increasing functions. Functions which can be expressed in this way can be used to formulate an exclusion test for the recent Cellular Exclusion Algorithms for numerically computing all zero points or the global minima of functions in a given cellular domain [2,8,9]. In this paper we give an algorithm to approximate such increasing functions when only the values of the function of bounded variation can be computed. For this purpose, we are led to introduce the idea of ε-increasing functions. It is shown that for any Lipschitz continuous function, we can find two ε-increasing functions such that the Lipschitz function can be written as the difference of these functions.
Paper's Title:
On a Subclass of Uniformly Convex Functions Defined by the Dziok-Srivastava Operator
Author(s):
M. K. Aouf and G. Murugusundaramoorthy
Mathematics Department, Faculty of Science,
Mansoura University 35516,
Egypt.
mkaouf127@yahoo.com
School of Science and Humanities, VIT University
Vellore - 632014,
India.
gmsmoorthy@yahoo.com
Abstract:
Making use of the Dziok-Srivastava operator, we define a new subclass Tlm([α1];α,β) of uniformly convex function with
negative coefficients. In this paper, we obtain coefficient estimates,
distortion theorems, locate extreme points and obtain radii of
close-to-convexity, starlikeness and convexity for functions belonging to the
class Tlm([α1];α,β) . We
consider integral operators associated with functions belonging to the class
Hlm([α1];α,β) defined via the Dziok-Srivastava
operator. We also obtain several results for the modified Hadamard products of
functions belonging to the class Tlm([α1];α,β)
and we obtain properties associated with generalized fractional calculus
operators.
Paper's Title:
Positive Solutions for Systems of Three-point Nonlinear Boundary Value Problems
Author(s):
J. Henderson and S. K. Ntouyas
Department of Mathematics, Baylor University
Waco, Texas
76798-7328 USA.
Johnny_Henderson@baylor.edu
URL: http://www3.baylor.edu/~Johnny_Henderson
Department of Mathematics, University of Ioannina
451 10 Ioannina,
Greece.
sntouyas@cc.uoi.gr
URL: http://www.math.uoi.gr/~sntouyas
Abstract:
Values of λ are determined for which there exist
positive solutions of the system of three-point boundary value problems,
u''(t)+ λa(t)f(v(t))=0, v''(t)+λb(t)g(u(t))=0,
for 0 < t <1, and
satisfying, u(0) = 0, u(1)=α u(η),
v(0) = 0, v(1)=α v(η). A Guo-Krasnosel'skii fixed
point theorem is applied. Paper's Title:
On Some Remarkable Product of Theta-function
Author(s):
M. S. Mahadeva Naika, M. C. Maheshkumar and K. Sushan Bairy
Department of Mathematics, Abstract:
On pages 338 and 339 in his first notebook, Ramanujan records
eighteen values for a certain product of theta-function. All these
have been proved by B. C. Berndt, H. H. Chan and L-C. Zhang
[4]. Recently M. S. Mahadeva Naika and B. N. Dharmendra
[7,
8] and Mahadeva Naika and M. C. Maheshkumar
[9] have obtained general theorems to establish explicit
evaluations of Ramanujan's remarkable product of theta-function.
Following Ramanujan we define a new function bM,N as
defined in (1.5). The main purpose of this paper is to
establish some new general theorems for explicit evaluations of
product of theta-function.
Paper's Title:
Some Inequalities for a Certain Class of Multivalent Functions
Using Multiplier Transformation Author(s):
K. Suchithra, B. Adolf Stephen, A. Gangadharan and S. Sivasubramanian
Department Of Applied Mathematics
Department Of Mathematics,
Department Of Applied Mathematics
Department Of Mathematics, Abstract:
The object of the present paper is to derive several inequalities
associated with differential subordinations between analytic functions
and a linear operator defined for a certain family of p-valent
functions, which is introduced here by means of a family of extended
multiplier transformations. Some special cases and consequences of
the main results are also considered.
Paper's Title:
The Bernoulli Inequality in Uniformly
Complete f-algebras with Identity Author(s):
Adel Toumi and Mohamed Ali Toumi
Laboratoire de Physique des Liquides Critiques, Département de Physique, Faculté des Sciences de Bizerte,
7021, Zarzouna, Bizerte, TUNISIA
Département de Mathématiques, Faculté des Sciences de Bizerte, 7021, Zarzouna,
Bizerte, TUNISIA Abstract:
The main purpose of this paper is to establish with a constructive proof the
Bernoulli inequality: let A be a uniformly complete f-algebra
with e as unit element, let 1<p<∞, then (e+a)p≥e+pa for all a∈A+. As an
application we prove the Hölder
inequality for positive linear functionals on a uniformly complete f-algebra with identity by using the Minkowski inequality. Paper's Title:
Error Inequalities for Weighted Integration Formulae and Applications
Author(s):
Nenad Ujević and Ivan Lekić
Department of Mathematics Abstract:
Weighted integration formulae are derived. Error inequalities for the
weighted integration formulae are obtained. Applications to some special
functions are also given. Paper's Title:
Some Generalized Difference Sequence Spaces Defined by Orlicz Functions
Author(s):
Ramzi S. N. Alsaedi and Ahmad H. A. Bataineh
Department of Mathematics, King Abdul Aziz University,
Department of Mathematics, Al al-Bayt University, Abstract:
In this paper, we define the sequence spaces: [V,M,p,u,Δ ],[V,M,p,u,Δ]0 and
[V,M,p,u,Δ]∞, where for any sequence x=(xn),
the difference sequence Δx is given by Δx=(Δxn)
Paper's Title:
Regular Variation on Time Scales and Dynamic Equations
Author(s):
Pavel Řehák
Institute of Mathematics, Academy of Sciences of the Czech Republic Abstract:
The purpose of this paper is twofold. First, we want to initiate a study
of regular variation on time scales by introducing this concept in such a
way that it
unifies and extends well studied continuous and discrete cases.
Some basic properties of regularly varying functions on time scales will be
established as well.
Second, we give conditions under which certain solutions of linear second
order
dynamic equations are regularly varying.
Open problems and possible directions for a future research are discussed,
too. Paper's Title:
Contact With Adhesion between a Deformable Body and a Foundation
Author(s):
B. Teniou and M. Sofonea
Laboratoire de Mathematiques Appliquées et Modélisation,
Laboratoire de Mathématiques et Physiques pour les Systémes, Abstract:
The aim of this work is study a dynamic contact problem between a
deformable body and a foundation where the deformations are supposed
to be small. The contact is with adhesion and normal compliance. The
behavior of this body is modeled by a nonlinear
elastic-visco-plastic law. The evolution of bonding field is
described by a nonlinear differential equation. We derive a
variational formulation of the contact problem and we prove the
existence and uniqueness of its solution. The proof is based on the
construction of three intermediate problems and then we construct a
contraction mapping whose unique fixed point will be the weak
solution of the mechanical problem. Paper's Title:
Some Properties of the Solution of a Second Order Elliptic Abstract Differential Equation Author(s):
A. Aibeche and K. Laidoune
Mathematics Department, Faculty of Sciences,
University Ferhat Abbas, Setif,
Abstract:
In this paper we study a class of non regular boundary value
problems for elliptic differential-operator equation of second order with an
operator in boundary conditions. We give conditions which guarantee the
coerciveness of the solution of the considered problem, the completeness of
system of root vectors in Banach-valued functions spaces and we establish
the Abel basis property of this system in Hilbert spaces. Finally, we apply
this abstract results to a partial differential equation in cylindrical
domain.
Paper's Title:
A Method for Solving Systems of Nonlinear Equations
Author(s):
J. Shokri
Department of Mathematics, Urmia University,
Abstract:
In this paper, we suggest and analyze a new two-step iterative
method for solving nonlinear equation systems using the combination
of midpoint quadrature rule and Trapezoidal quadrature rule. We
prove that this method has quadratic convergence. Several examples
are given to illustrate the efficiency of the proposed method.
Paper's Title:
On ε-simultaneous Approximation in Quotient Spaces
Author(s):
H. Alizadeh, Sh. Rezapour, S. M. Vaezpour Department of
Mathematics, Aazad Abstract:
The purpose of this paper is
to develop a theory of best simultaneous approximation to
ε-simultaneous approximation. We shall introduce the
concept of ε-simultaneous pseudo Chebyshev,
ε-simultaneous quasi Chebyshev and
ε-simultaneous weakly Chebyshev subspaces of a Banach
space. Then, it will be determined under what conditions these
subspaces are transmitted to and from quotient spaces.
Paper's Title:
A Double Inequality for Divided Differences and Some Identities of the Psi and Polygamma Functions Author(s):
B. N. Guo and F. Qi School of
Mathematics and Informatics, Henan Polytechnic University, Jiaozuo City, Henan
Province, 454010, China School of
Research Institute of Mathematical Inequality Theory, Henan Polytechnic University, Jiaozuo City, Henan Province, 454010, China Abstract:
In this short note, from the logarithmically completely monotonic property
of the function
Paper's Title:
On a Method of Proving the Hyers-Ulam Stability
of Functional Equations on Restricted Domains Author(s):
Janusz Brzdęk
Department of Mathematics
1: Paper Source
PDF document
Bangalore University, Central College Campus,
Bangalore-560 001,
INDIA
msmnaika@rediffmail.com
softmahe@rediffmail.com
ksbairy@gmail.com
1: Paper Source
PDF document
Sri Venkateswara College Of Engineering
Sriperumbudur, Chennai - 602105,
India.
suchithravenkat@yahoo.co.in
Madras Christian College
Chennai - 600059,
India.
adolfmcc2003@yahoo.co.in
Sri Venkateswara College Of Engineering
Sriperumbudur, Chennai - 602105,
India.
ganga@svce.ac.in
Easwari Engineering College
Ramapuram, Chennai - 600089,
India.
ganga@svce.ac.in
1: Paper Source
PDF document
Adel.Toumi@fst.rnu.tn
MohamedAli.Toumi@fsb.rnu.tn
1: Paper Source
PDF document
University of Split
Teslina 12/III, 21000 Split
CROATIA.
ujevic@pmfst.hr
ivalek@pmfst.hr
1: Paper Source
PDF document
Jeddah P.O.Box 80203,
Saudia Arabia
ramzialsaedi@yahoo.co.uk
Mafraq 25113,
Jordan
ahabf2003@yahoo.ca
= (xn-xn-1)
. We also study some properties and theorems of
these spaces. These are generalizations of those defined and studied by
Savas and Savas and some others before.
1: Paper Source
PDF document
Žižkova 22, CZ61662 Brno,
Czech Republic
rehak@math.muni.cz
URL:http://www.math.muni.cz/~rehak
1: Paper Source
PDF document
Université Mentouri, Constantine 25000,
Algeria
tenioubou2@yahoo.fr
Univesité de Perpignan,
France.
sofonea@univ-perp.fr
1: Paper Source
PDF document
Route de Scipion, 19000,
Setif,
Algeria
aibeche@univ-setif.dz
1: Paper Source
PDF document
P. O. Box 165, Urmia,
Iran
j.shokri@urmia.ac.ir
1: Paper Source
PDF document
Islamic University, Science and Research Branch, Tehran,
Iran
Department of Mathematics, Azarbaidjan
University of Tarbiat Moallem, Tabriz,
Iran
Department of Mathematics, Amirkabir
University of Technology, Tehran,
Iran
alizadehhossain@yahoo.com
sh.rezapour@azaruniv.edu
vaez@aut.ac.ir
URL:http://www.azaruniv.edu/~rezapour
URL:http://math-cs.aut.ac.ir/vaezpour
1: Paper Source
PDF document
bai.ni.guo@gmail.com,
bai.ni.guo@hotmail.com
qifeng618@gmail.com,
qifeng618@hotmail.com,
qifeng618@qq.com
URL:http://qifeng618.spaces.live.com

1: Paper Source
PDF document
Pedagogical University Podchor
30-084 Kraków,
Poland
jbrzdek@ap.krakow.pl
Abstract:
We show that generalizations of some (classical) results on the Hyers-Ulam stability of functional equations, in several variables, can be very easily derived from a simple result on stability of a functional equation in single variable
Paper's Title:
Differentiability of
Distance Functions in p-Normed Spaces
Author(s):
M. S. Moslehian, A. Niknam, S. Shadkam Torbati
Department of Pure Mathematics,
Centre of Excellence in Analysis on Algebraic Structures (CEAAS),,
Ferdowsi University of Mashhad,
P. O. Box
1159, Mashhad,
Iran
moslehian@ferdowsi.um.ac.ir
niknam@math.um.ac.ir
shadkam.s@wali.um.ac.ir
Abstract:
The farthest point mapping in a p-normed space X is studied in virtue of the Gateaux derivative and the Frechet derivative. Let M be a closed bounded subset of X having the uniformly p-Gateaux differentiable norm. Under certain conditions, it is shown that every maximizing sequence is convergent, moreover, if M is a uniquely remotal set then the farthest point mapping is continuous and so M is singleton. In addition, a Hahn--Banach type theorem in $p$-normed spaces is proved.
Paper's Title:
Fixed Points and Stability
of the Cauchy Functional Equation
Author(s):
Choonkil Park and Themistocles M. Rassias
Department of Mathematics, Hanyang University,
Seoul 133-791,
Republic of Korea
Department of Mathematics,
National Technical University of Athens,
Zografou Campus, 15780 Athens,
Greece
baak@hanyang.ac.kr
trassias@math.ntua.gr
Abstract:
Using fixed point methods, we prove the generalized Hyers-Ulam stability of homomorphisms in Banach algebras and of derivations on Banach algebras for the Cauchy functional equation.
Paper's Title:
Hyperbolic Barycentric Coordinates
Author(s):
Abraham A. Ungar
Department of Mathematics, North Dakota State University,
Fargo, ND 58105,
USA
Abraham.Ungar@ndsu.edu
URL: http://math.ndsu.nodak.edu/faculty/ungar/
Abstract:
A powerful and novel way to study Einstein's special theory of relativity and its underlying geometry, the hyperbolic geometry of Bolyai and Lobachevsky, by analogies with classical mechanics and its underlying Euclidean geometry is demonstrated. The demonstration sets the stage for the extension of the notion of barycentric coordinates in Euclidean geometry, first conceived by Möbius in 1827, into hyperbolic geometry. As an example for the application of hyperbolic barycentric coordinates, the hyperbolic midpoint of any hyperbolic segment, and the centroid and orthocenter of any hyperbolic triangle are determined.
Paper's Title:
A Study of the Effect of Density Dependence in a Matrix Population Model
Author(s):
N. Carter and M. Predescu
Department of Mathematical Sciences,
Bentley University,
Waltham, MA 02452,
U.S.A.
ncarter@bentley.edu
mpredescu@bentley.edu
Abstract:
We study the behavior of solutions of a three dimensional discrete time nonlinear matrix population model. We prove results concerning the existence of equilibrium points, boundedness, permanence of solutions, and global stability in special cases of interest. Moreover, numerical simulations are used to compare the dynamics of two main forms of the density dependence function (rational and exponential).
Paper's Title:
Inclusion and Neighborhood
Properties for Certain Subclasses of Analytic Functions Associated with
Convolution Structure
Author(s):
M. K. Aouf
Mathematics Department,
Faculty of Science,
Mansoura University 35516,
Egypt.
mkaouf127@yahoo.com
Abstract:
In this paper we introduce and investigate two new subclasses of multivalently analytic functions of complex order defined by using the familiar convolution structure of analytic functions. In this paper we obtain the coefficient estimates and the consequent inclusion relationships involving the neighborhoods of the p-valently analytic functions.
Paper's Title:
On the Fock Representation of the Central Extensions of the Heisenberg Algebra
Author(s):
L. Accardi and A. Boukas
Centro Vito Volterra, Universitŕ di Roma
Tor Vergata,
via Columbia 2, 00133 Roma,
Italy
accardi@volterra.mat.uniroma2.it
URL: http://volterra.mat.uniroma2.it
Department of Mathematics,
American College of Greece,
Aghia Paraskevi, Athens 15342,
Greece
andreasboukas@acg.edu
Abstract:
We examine the possibility of a direct Fock representation of
the recently obtained non-trivial central extensions
![]() of the Heisenberg algebra, generated by elements
of the Heisenberg algebra, generated by elements
![]() and
E satisfying the commutation relations
and
E satisfying the commutation relations
![]() ,
and
,
and
![]() ,
where a and
,
where a and
![]() are dual, h is self-adjoint, E is the non-zero self-adjoint
central element and
are dual, h is self-adjoint, E is the non-zero self-adjoint
central element and
![]() We define the exponential vectors associated with the
We define the exponential vectors associated with the
![]() Fock space, we compute their Leibniz function (inner product), we describe the
action of a,
Fock space, we compute their Leibniz function (inner product), we describe the
action of a,
![]() and h on the exponential vectors and we compute the moment generating and
characteristic functions of the classical random variable corresponding to the
self-adjoint operator
and h on the exponential vectors and we compute the moment generating and
characteristic functions of the classical random variable corresponding to the
self-adjoint operator
![]()
Paper's Title:
On the product of M-measures in l-groups
Author(s):
A. Boccuto, B. Riěcan, and A. R. Sambucini
Dipartimento di Matematica e Informatica,
via Vanvitelli, 1 I-06123 Perugia,
Italy.
boccuto@dipmat.unipg.it
URL:
http://www.dipmat.unipg.it/~boccuto
Katedra Matematiky, Fakulta Prírodných Vied,
Univerzita Mateja Bela,
Tajovského, 40, Sk-97401 Banská Bystrica,
Slovakia.
riecan@fpv.umb.sk
Dipartimento di Matematica e Informatica,
via Vanvitelli, 1 I-06123 Perugia,
Italy.
matears1@unipg.it
URL:
http://www.unipg.it/~matears1
Abstract:
Some extension-type theorems and compactness
properties for the
product of l-group-valued M-measures are proved.
Paper's Title:
Asymptotic Distribution of Products of Weighted Sums of Dependent
Random Variables
Author(s):
Y. Miao and J. F. Li
College
of Mathematics
and Information
Science,
Henan Normal
University
Henan,
China
yumiao728@yahoo.com.cn
College
of Mathematics
and Information
Science,
Henan Normal
University, 453007
Henan,
China.
junfen_li@yahoo.com.cn
Abstract:
In this paper we establish the asymptotic distribution of products of weighted sums of dependent positive random variable, which extends the results of Rempała and Wesołowski (2002).
Paper's Title:
On a Class of Uniformly Convex Functions Defined by Convolution with Fixed Coefficient
Author(s):
T. N. Shanmugam, S. Sivasubramanian, and G. Murugusundaramoorthy
Department of Mathematics,
College of Engineering,
Anna University,
Chennai - 600 025,
India.
drtns2001@yahoo.com
Department of Mathematics,
University College of Engineering,
Tindivanam
Anna University-Chennai,
Saram-604 703,
India.
sivasaisastha@rediffmail.com
School of Sciences and Humanities,
VIT University, Vellore-632 014,
India.
gmsmoorthy@yahoo.com
Abstract:
We define a new subclass of uniformly convex functions with negative and fixed second coefficients defined by convolution. The main object of this paper is to obtain coefficient estimates distortion bounds, closure theorems and extreme points for functions belong to this new class . The results are generalized to families with fixed finitely many coefficients.
Paper's Title:
Real Interpolation Methods and Quasilogarithmic Operators
Author(s):
Ming Fan
School of Industrial Technology and Management,
Dalarna University, 781 88 Borlänge, Sweden
fmi@du.se
URL: http://users.du.se/~fmi
Abstract:
The purpose of this paper is to deal with nonlinear quasilogarithmic operators, which possesses the uniformly bounded commutator property on various interpolation spaces in the sense of Brudnyi-Krugljak associated with the quasi-power parameter spaces. The duality, and the domain and range spaces of these operators are under consideration. Some known inequalities for the Lebesgue integration spaces and the trace classes are carried over to the non-commutative symmetric spaces of measurable operators affiliated with a semi-finite von Neumann algebra.
Paper's Title:
Solution of One Conjecture on Inequalities with Power-Exponential Functions.
Author(s):
Seiichi Manyama
Graduate School of Science
Osaka University
Japan
manchanr4@gmail.com
Abstract:
In this paper, we prove the open inequality aea+beb≥ aeb+bea for all positive real numbers a and b.
Paper's Title:
Topological Aspects of Scalarization in Vector Optimization Problems.
Author(s):
Peter I. Kogut, Rosanna Manzo and Igor V. Nechay
Department of Differential Equations,
Dnipropetrovsk National University, Naukova
STR.,
13,
49010 Dnipropetrovsk,
Ukraine
p.kogut@i.ua
Universitŕ di Salerno,
Department of Technical Cybernetics,
Dipartimento di Ingegneria dell'Informazione e Matematica Applicata,
Via Ponte don Melillo, 84084 Fisciano (SA),
Italy
manzo@diima.unisa.it
Dnipropetrovsk Technical University,
Acad. Lazarjan
STR., 2,
49010 Dnipropetrovsk,
Ukraine
i.nechay@i.ua
Abstract:
In this paper, we study vector optimization problems in partially ordered Banach spaces. We suppose that the objective mapping possesses a weakened property of lower semicontinuity and make no assumptions on the interior of the ordering cone. We derive sufficient conditions for existence of efficient solutions of the above problems and discuss the role of topological properties of the objective space. We discuss the scalarization of vector optimization problems when the objective functions are vector-valued mappings with a weakened property of lower semicontinuity. We also prove the existence of the so-called generalized efficient solutions via the scalarization process. All principal notions and assertions are illustrated by numerous examples.
Paper's Title:
Shape Diagrams for 2D Compact Sets - Part I: Analytic
Convex Sets.
Author(s):
S. Rivollier, J. Debayle and J.-C. Pinoli
Ecole Nationale Supérieure des Mines de Saint-Etienne,
CIS - LPMG, UMR CNRS 5148, 158 cours Fauriel,
42023 Saint-Etienne Cedex 2, France.
rivollier@emse.fr;
debayle@emse.fr; pinoli@emse.fr
Abstract:
Shape diagrams are representations in the Euclidean plane introduced to study 3-dimensional and 2-dimensional compact convex sets. Such a set is represented by a point within a shape diagram whose coordinates are morphometrical functionals defined as normalized ratios of geometrical functionals. Classically, the geometrical functionals are the area, the perimeter, the radii of the inscribed and circumscribed circles, and the minimum and maximum Feret diameters. They allow thirty-one shape diagrams to be built. Most of these shape diagrams can also been applied to more general compact sets than compact convex sets. Starting from these six classical geometrical functionals, a detailed comparative study has been performed in order to analyze the representation relevance and discrimination power of these thirty-one shape diagrams. The purpose of this paper is to present the first part of this study, by focusing on analytic compact convex sets. A set will be called analytic if its boundary is piecewise defined by explicit functions in such a way that the six geometrical functionals can be straightforwardly calculated. The second and third part of the comparative study are published in two following papers [19.20]. They are focused on analytic simply connected sets and convexity discrimination for analytic and discretized simply connected sets, respectively.
Paper's Title:
Shape Diagrams for 2D Compact Sets - Part II: Analytic
Simply Connected Sets.
Author(s):
S. Rivollier, J. Debayle and J.-C. Pinoli
Ecole Nationale Supérieure des Mines de Saint-Etienne,
CIS - LPMG, UMR CNRS 5148, 158 cours Fauriel,
42023 Saint-Etienne Cedex 2, France.
rivollier@emse.fr;
debayle@emse.fr; pinoli@emse.fr
Abstract:
Shape diagrams are representations in the Euclidean plane introduced to study 3-dimensional and 2-dimensional compact convex sets. However, they can also been applied to more general compact sets than compact convex sets. A compact set is represented by a point within a shape diagram whose coordinates are morphometrical functionals defined as normalized ratios of geometrical functionals. Classically, the geometrical functionals are the area, the perimeter, the radii of the inscribed and circumscribed circles, and the minimum and maximum Feret diameters. They allow twenty-two shape diagrams to be built. Starting from these six classical geometrical functionals, a detailed comparative study has been performed in order to analyze the representation relevance and discrimination power of these twenty-two shape diagrams. The first part of this study is published in a previous paper 16. It focused on analytic compact convex sets. A set will be called analytic if its boundary is piecewise defined by explicit functions in such a way that the six geometrical functionals can be straightforwardly calculated. The purpose of this paper is to present the second part, by focusing on analytic simply connected compact sets. The third part of the comparative study is published in a following paper 17. It is focused on convexity discrimination for analytic and discretized simply connected compact sets.
Paper's Title:
Shape Diagrams for 2D Compact Sets - Part III: Convexity
Discrimination for Analytic and Discretized Simply Connected Sets.
Author(s):
S. Rivollier, J. Debayle and J.-C. Pinoli
Ecole Nationale Supérieure des Mines de Saint-Etienne,
CIS - LPMG, UMR CNRS
5148,
158 cours Fauriel,
42023 Saint-Etienne Cedex 2, France.
rivollier@emse.fr;
debayle@emse.fr; pinoli@emse.fr
Abstract:
Shape diagrams are representations in the Euclidean plane introduced to study 3-dimensional and 2-dimensional compact convex sets. However, they can also been applied to more general compact sets than compact convex sets. A compact set is represented by a point within a shape diagram whose coordinates are morphometrical functionals defined as normalized ratios of geometrical functionals. Classically, the geometrical functionals are the area, the perimeter, the radii of the inscribed and circumscribed circles, and the minimum and maximum Feret diameters. They allow twenty-two shape diagrams to be built. Starting from these six classical geometrical functionals, a detailed comparative study has been performed in order to analyze the representation relevance and discrimination power of these twenty-two shape diagrams. The two first parts of this study are published in previous papers 8,9. They focus on analytic compact convex sets and analytic simply connected compact sets, respectively. The purpose of this paper is to present the third part, by focusing on the convexity discrimination for analytic and discretized simply connected compact sets..
Paper's Title:
The Superstability of the Pexider Type Trigonometric Functional Equation
Author(s):
Gwang Hui Kim and Young Whan Lee
Department of Mathematics, Kangnam
University Yongin, Gyeonggi, 446-702, Korea.
ghkim@kangnam.ac.kr
Department of Computer and Information Security
Daejeon University, Daejeon 300-716, Korea.
ywlee@dju.ac.kr
Abstract:
The aim of this paper is to investigate the stability
problem for
the Pexider type (hyperbolic) trigonometric functional equation
f(x+y)+f(x+σy)=λg(x)h(y) under the conditions :
|f(x+y)+f(x+σy)- λg(x)h(y)|≤φ(x),
φ(y), and min {φ(x), φ (y)}.
As a consequence, we have generalized the results of stability for
the cosine(d'Alembert), sine, and the Wilson functional equations by J.
Baker, P. Găvruta, R. Badora and R. Ger, Pl.~Kannappan, and G.
H. Kim
Paper's Title:
Two Remarks on Commutators of Hardy Operator
Author(s):
Yasuo Komori-Furuya
School of High Technology for Human Welfare
Tokai University
317 Nishino Numazu, Shizuoka 410-0395 Japan
komori@wing.ncc.u-tokai.ac.jp
Abstract:
Fu and Lu showed that
the commutator of multiplication operator by b and
the n-dimensional Hardy operator
is bounded on Lp if b is in some CMO space.
We shall prove the converse of this theorem
and also prove that their result is optimal by giving a counterexample
Paper's Title:
Maximal Inequalities for Multidimensionally Indexed Demimartingales and the Hájek-Rényi Inequality for Associated Random Variables
Author(s):
Tasos C. Christofides and Milto Hadjikyriakou
Department of Mathematics and Statistics
University of Cyprus
P.O.Box 20537, Nicosia 1678, Cyprus
tasos@ucy.ac.cy
miltwh@gmail.com
Abstract:
Demimartingales and demisubmartingales introduced by
Newman and
Wright (1982) generalize the notion of martingales and
submartingales respectively. In this paper we define
multidimensionally indexed demimartingales and demisubmartingales
and prove a maximal inequality for this general class of random
variables. As a corollary we obtain a Hájek-Rényi inequality
for multidimensionally indexed associated random variables, the bound of which,
when reduced to the case of single index, is sharper than the bounds already
known in the literature.
Paper's Title:
Approximation of Common Fixed Points of a Finite Family of Asymptotically Demicontractive Mappings in Banach Spaces
Author(s):
Yuchao Tang, Yong Cai, Liqun Hu and Liwei Liu
Department of Mathematics, NanChang University,
Nanchang 330031, P.R. China
Department of Mathematics, Xi'an Jiaotong University,
Xi'an 710049, P.R.
China
Abstract:
By virtue of new analytic techniques, we analyze and
study
several strong convergence theorems for the approximation of
common fixed points of asymptotically demicontractive mappings
via the multistep iterative sequence with errors in Banach
spaces. Our results improve and extend the corresponding ones
announced by Osilike , Osilike and Aniagbosor, Igbokwe, Cho et
al., Moore and Nnoli, Hu and all the others.
Paper's Title:
Hardy Type Inequalities via Convexity - The Journey so Far
Author(s):
James A.
Oguntuase and Lars-Erik Persson
Department of Mathematics,
University of Agriculture,
P. M. B. 2240, Abeokuta, Nigeria.
Department of
Mathematics, Luleĺ University of Technology,
SE-971 87, Luleĺ , Sweden.
oguntuase@yahoo.com,
larserik@sm.luth.se .
Abstract:
It is nowadays well-known that Hardy's inequality (like many other inequalities) follows directly from Jensen's inequality. Most of the development of Hardy type inequalities has not used this simple fact, which obviously was unknown by Hardy himself and many others. Here we report on some results obtained in this way mostly after 2002 by mainly using this fundamental idea.
Paper's Title:
Some Remarks on a Result of Bougoffa
Author(s):
James A. Oguntuase, Lars-Erik Persson and Josip E. Pečarič
Department of
Mathematics,University of Agriculture,
P M B 2240, Abeokuta, Nigeria
Department of Mathematics,
Luleĺ University of Technology,
SE-971 87, Luleĺ , Sweden
Faculty of Textile Technology, University of Zagreb,
Pierottijeva 6, 10000 Zagreb, Croatia
oguntuase@yahoo.com,
larserik@sm.luth.se,
pecaric@hazu.hr.
Abstract:
Some new generalizations of the result of
L. Bougoffa [J. Inequal. Pure Appl. Math. 7 (2) (2006), Art. 60]
are derived and discussed.
Paper's Title:
Asymptotic Inequalities for the Maximum Modulus of the Derivative of a Polynomial
Author(s):
Clément Frappier
Département de Mathématiques et de Génie industriel École Polytechnique de
Montréal,
C.P.~6079, succ. Centre-ville Montréal (Québec),
H3C 3A7, CANADA
Abstract:
Let
 be an algebraic polynomial of degree
≤n, and let ∥p∥= max {|p(z)|:|z| = 1}.
We study the asymptotic behavior of the best possible constant φn,k (R), for
k = 0 and k=1, in the inequality ∥p'(Rz)∥ + φn,k (R) |ak|
≤ nRn-1 ∥p∥, R → ∞.
be an algebraic polynomial of degree
≤n, and let ∥p∥= max {|p(z)|:|z| = 1}.
We study the asymptotic behavior of the best possible constant φn,k (R), for
k = 0 and k=1, in the inequality ∥p'(Rz)∥ + φn,k (R) |ak|
≤ nRn-1 ∥p∥, R → ∞.
Paper's Title:
The Best Upper Bound for Jensen's Inequality
Author(s):
Vasile Cirtoaje
Department of Automatic Control and Computers
University of Ploiesti
Romania.
Abstract:
In this paper we give the best upper bound for the weighted Jensen's discrete inequality applied to a convex function f defined on a closed interval I in the case when the bound depends on f, I and weights. In addition, we give a simpler expression of the upper bound, which is better than existing similar one.
Paper's Title:
Refinements of the Trace Inequality of Belmega, Lasaulce and Debbah
Author(s):
Shigeru Furuichi and Minghua Lin
Department of Computer Science and System Analysis,
College of Humanities and Sciences, Nihon University,
3-25-40, Sakurajyousui, Setagaya-ku, Tokyo, 156-8550, Japan.
Department of Mathematics and
Statistics,
University of Regina, Regina, Saskatchewan, Canada S4S 0A2.
furuichi@chs.nihon-u.ac.jp, lin243@uregina.ca.
Abstract:
In this short paper, we show a certain matrix trace inequality and then give a refinement of the trace inequality proven by Belmega, Lasaulce and Debbah. In addition, we give an another improvement of their trace inequality.
Paper's Title:
Generalizing Polyhedra to Infinite Dimension
Author(s):
Paolo d'Alessandro
Department of Mathematics, Third University of Rome,
Lgo S.L. Murialdo 1, 00146 Rome, Italy.
URL:
http://www.mat.uniroma3.it/users/dalex/dalex.html.
Abstract:
This paper generalizes polyhedra to infinite dimensional Hilbert spaces as countable intersections of closed semispaces. Highlights are the structure theory that shows that a polyhedron is the sum of compact set (in a suitable topology) plus a closed pointed cone plus a closed subspace, giving the internal representation of polyhedra. In the final part the dual range space technique is extended to the solution of infinite dimensional LP problems.
Paper's Title:
On an Elliptic Over-Determined Problem in Dimension Two
Author(s):
Lakhdar Ragoub
Department of Mathematics and Information of Tiyadhechnology
AL Yamamah University
P.O. Box 45 180, Riyadh 11 512
Saudi Arabia.
Abstract:
We extend the method of Weinberger for a
non-linear over-determined elliptic problem
in R2.
We prove that the domain in consideration is a ball. The
tool of this investigation are maximum principles and P-functions.
Paper's Title:
Some Inequalities Concerning Derivative and Maximum Modulus of Polynomials
Author(s):
N. K. Govil, A. Liman and W. M. Shah
Department of Mathematics & Statistics,
Auburn University, Auburn,
Alabama 36849-5310,
U.S.A
Department of Mathematics,
National Institute of Technology,
Srinagar, Kashmir,
India - 190006
Department of Mathematics,
Kashmir University,
Srinagar, Kashmir,
India - 190006
govilnk@auburn.edu
abliman22@yahoo.com
wmshah@rediffmail.com
Abstract:
In this paper, we prove some compact generalizations of some well-known Bernstein type inequalities concerning the maximum modulus of a polynomial and its derivative in terms of maximum modulus of a polynomial on the unit circle. Besides, an inequality for self-inversive polynomials has also been obtained, which in particular gives some known inequalities for this class of polynomials. All the inequalities obtained are sharp.
Paper's Title:
On the Inequality with Power-Exponential Function
Author(s):
Seiichi Manyama
Graduate School of Science
Osaka University
Japan
manchanr4@gmail.com
Abstract:
In this paper, we prove the inequality
 <
<
 for 0<a<b. Other
related conjectures are also presented.
for 0<a<b. Other
related conjectures are also presented.
Paper's Title:
A-Normal Operators In Semi Hilbertian Spaces
Author(s):
A. Saddi
Department of Mathematics,
College of Education for Girls in Sarat Ebeidah 61914, Abha,
King Khalid University
Saudi Arabia
adel.saddi@fsg.rnu.tn
Abstract:
In this paper we study some properties and inequalities of A-normal operators in semi-Hilbertian spaces by employing some known results for vectors in inner product spaces. We generalize also most of the inequalities of (α,β)-normal operators discussed in Hilbert spaces [7].
Paper's Title:
On Opial's Inequality for Functions of n-Independent Variables
Author(s):
S. A. A. El-Marouf and S. A. AL-Oufi
Department of Mathematics,
Faculty of Science,
Minoufiya University,
Shebin El-Koom,
Egypt
Department of Mathematics,
Faculty of Science, Taibah University,
Madenahmonwarah,
Kingdom of Saudia Arabia
Abstract:
In this paper, we introduce Opial inequalities for functions of n-independent variables. Also, we discuss some different forms of Opial inequality containing functions of n independent variables and their partial derivatives with respect to independent variables.
Paper's Title:
Finite and Infinite Order
Solutions of a Class of Higher Order Linear Differential Equations
Author(s):
Saada Hamouda
Department of Mathematics,
Laboratory of Pure and Applied Mathematics,
University of Mostaganem, B. P 227 Mostaganem,
ALGERIA
hamouda_saada@yahoo.fr
Abstract:
In this paper, we investigate the growth of solutions of higher order linear differential equations where most of the coefficients have the same order and type with each other.
Paper's Title:
Equivalence of the Nonsmooth Nonlinear Complementarity Problems to Unconstrained Minimization
Author(s):
M. A. Tawhid and J. L. Goffin
Department of Mathematics and Statistics,
School of Advanced Technologies and Mathematics,
Thompson Rivers University,
900 McGill Road, PO Box 3010, Kamloops, BC V2C 5N3
Canada
Alexandria University and Egypt Japan University of Science and Technology,
Alexandria-Egypt
mtawhid@tru.ca
Faculty of Management, McGill University,
1001 Sherbrooke Street West, Montreal, Quebec, H3A 1G5
Canada.
Jean-Louis.Goffin@McGill.ca
Abstract:
This paper deals with nonsmooth nonlinear complementarity problem, where the underlying functions are nonsmooth which admit the H-differentiability but not necessarily locally Lipschitzian or directionally differentiable. We consider a reformulation of the nonlinear complementarity problem as an unconstrained minimization problem. We describe H-differentials of the associated penalized Fischer-Burmeister and Kanzow and Kleinmichel merit functions. We show how, under appropriate P0, semimonotone (E0), P, positive definite, and strictly semimonotone (E) -conditions on an H-differential of f, finding local/global minimum of a merit function (or a `stationary point' of a merit function) leads to a solution of the given nonlinear complementarity problem. Our results not only give new results but also unify/extend various similar results proved for C1.
Paper's Title:
Fejér-type Inequalities
Author(s):
Nicuşor Minculete and Flavia-Corina Mitroi
"Dimitrie Cantemir" University,
107 Bisericii Române Street, Braşov, 500068,
România
minculeten@yahoo.com
University of Craiova, Department of Mathematics,
Street A. I. Cuza
13, Craiova, RO-200585,
Romania
fcmitroi@yahoo.com
Abstract:
The aim of this paper is to present some new Fejér-type results for convex functions. Improvements of Young's inequality (the arithmetic-geometric mean inequality) and other applications to special means are pointed as well.
Paper's Title:
Para-chaotic Tuples of Operators
Author(s):
Bahmann Yousefi and Javad Izadi
Department of Mathematics,
Payame Noor University,
P.O. Box 19395-3697, Tehran,
Iran
b_yousefi@pnu.ac.ir
javadie2003@yahoo.com
Abstract:
In this paper, we introduce para-chaotic tuples of operators and we give some relations between para-chaoticity and Hypercyclicity Criterion for a tuple of operators.
Paper's Title:
On the Boundedness of Hardy's Averaging Operators
Author(s):
Dah-Chin Luor
Department of Applied Mathematics,
I-Shou University, Dashu District,
Kaohsiung City 84001,
Taiwan, R.O.C.
dclour@isu.edu.tw
Abstract:
In this paper we establish scales of sufficient conditions for the boundedness of Hardy's averaging operators on weighted Lebesgue spaces. The estimations of the operator norms are also obtained. Included in particular are the Erdélyi-Kober operators.
Paper's Title:
On Generalized Triangle Inequality in p-Freéchet Spaces, 0<p<1
Author(s):
M. A. Latif
Department of Mathematics,
University of Hail, Hail,
Saudi Arabia
m_amer_latif@hotmail.com
Abstract:
In this paper generalized triangle inequality and its reverse in a p-Fréchet space where, 0<p<1 are obtained.
Paper's Title:
A Note on the Ulam stability of Reciprocal Difference and Adjoint Functional Equations
Author(s):
K. Ravi, J. M. Rassias, M. E. Gordji, and B. V. Senthil Kumar
Department of Mathematics,
Sacred Heart College, Tirupattur - 635601,
India
shckavi@yahoo.co.in
Pedagogical Department E. E.,
Section of Mathematics and Informatics,
National and Capodistrian University of Athens,
4, Agamemnonos Str., Aghia Paraskevi,
Athens, Attikis 15342,
GREECE
jrassias@primedu.uoa.gr
Department of Mathematics, Semnan
University,
P.O. Box 35195-363, Semnan,
Iran
madjid.eshaghi@gmail.com
Department of Mathematics,
C.Abdul Hakeem College of Engineering and
Technology, Melvisharam - 632 509,
India
bvssree@yahoo.co.in
Abstract:
This note is an erratum to previous work published as Volume 8, Issue 1, Paper 13, 2011 of The Australian Journal of Mathematical Analysis and Applications.
Paper's Title:
Some Distortion and Other Properties Associated with a Family of the n-Fold Symmetric Koebe Type Functions
Author(s):
H. M. Srivastava, N. Tuneski and E. Georgieva-Celakoska
Department of Mathematics and Statistics,
University of Victoria,
Victoria, British Columbia V8W 3R4,
Canada
Faculty of Mechanical Engineering, St.
Cyril and Methodius University,
Karpo'v s II b.b., MK-1000 Skopje,
Republic of Macedonia
Abstract:
In a recent work by Kamali and Srivastava [5], a certain family of the n-fold symmetric Koebe type functions was introduced and studied systematically. In an earlier investigation, Eguchi and Owa [4] had considered its special case when n=1 (see also [10]). Here, in our present sequel to these earlier works, this general family of the n-fold symmetric Koebe type functions is studied further and several distortion theorems and such other properties as the radii of spirallikeness, the radii of starlikeness and the radii of convexity, which are associated with this family of the n-fold symmetric Koebe type functions, are obtained. We also provide certain criteria that embed this family of the n-fold symmetric Koebe type functions in a function class Gλ which was introduced and studied earlier by Silverman [7].
Paper's Title:
Further Bounds for Two Mappings Related
to the Hermite-Hadamard Inequality
Author(s):
S. S. Dragomir1,2 and I. Gomm1
1Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428,
Melbourne City, MC 8001,
Australia.
2School of Computational & Applied Mathematics,
University of
the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
sever.dragomir@vu.edu.au
ian.gomm@vu.edu.au
URL: http://rgmia.org/dragomir
Abstract:
Some new results concerning two mappings associated to the celebrated Hermite-Hadamard integral inequality for twice differentiable functions with applications for special means are given.
Paper's Title:
Expected Utility with Subjective Events
Author(s):
Jacob Gyntelberg and Frank Hansen
Bank for International Settlements,
Basel,
Switzerland
Tohoku University, Institute for International Education,
Sendai,
Japan
Abstract:
We provide a new theory of expected utility with subjective events modeled by a lattice of projections. This approach allows us to capture the notion of a ``small world'' as a context dependent or local state space embedded into a subjective set of events, the ``grand world''. For each situation the decision makers' subjective ``small world'' reflects the events perceived to be relevant for the act under consideration. The subjective set of events need not be representable by a classical state space. Maintaining preference axioms similar in spirit to the classical axioms, we obtain an expected utility representation which is consistent across local state spaces and separates subjective probability and utility. An added benefit is that this alternative expected utility representation allows for an intuitive distinction between risk and uncertainty.
Paper's Title:
Some Functional Inequalities for the Geometric Operator Mean
Author(s):
Mustapha Raissouli
Taibah University, Faculty of Sciences,
Department of Mathematics,
Al Madinah Al Munawwarah, P.O.Box 30097,
Kingdom of Saudi Arabia.
Abstract:
In this paper, we give some new inequalities of functional type for the power geometric operator mean involving several arguments.
Paper's Title:
New Inequalities of Mill's Ratio and Application to The Inverse Q-function Approximation
Author(s):
Pingyi Fan
Department of Electronic Engineering,
Tsinghua University, Beijing,
China
Abstract:
In this paper, we investigate the Mill's ratio estimation problem and get two new inequalities. Compared to the well known results obtained by Gordon, they becomes tighter. Furthermore, we also discuss the inverse Q-function approximation problem and present some useful results on the inverse solution. Numerical results confirm the validness of our theoretical analysis. In addition, we also present a conjecture on the bounds of inverse solution on Q-function.
Paper's Title:
Numerical Solution of A System of Singularly Perturbed Convection-Diffusion Boundary-Value Problems Using Mesh Equidistribution Technique
Author(s):
Pratibhamoy Das and Srinivasan Natesan
Department of Mathematics,
Indian Institute of Technology Guwahati,
Guwahati - 781 039,
India.
pratibhamoy@gmail.com
natesan@iitg.ernet.in
URL:
http://www.iitg.ernet.in/natesan/
Abstract:
In this article, we consider a system of singularly perturbed weakly coupled convection-diffusion equations having diffusion parameters of different magnitudes. These small parameters give rise to boundary layers. An upwind finite difference scheme on adaptively generated mesh is used to obtain a suitable monitor function that gives first-order convergence which is robust with respect to the diffusion parameters. We present the results of numerical experiments for linear and semilinear system of differential equations to support the effectiveness of our preferred monitor function obtained from theoretical analysis.
Paper's Title:
An Improvement of the Hermite-Hadamard Inequality for Functions Convex on the Coordinates
Author(s):
Milica Klaričić Bakula
Faculty of Science,
University of Split,
Teslina 12, 21000 Split.
Croatia
E-mail: milica@pmfst.hr
Abstract:
An improvement of the Hermite-Hadamard inequality for functions convex on the coordinates is given.
Paper's Title:
On the Sendov Conjecture for a Root Close to the Unit Circle
Author(s):
Indraneel G. Kasmalkar
Department of Mathematics,
University of California,
Berkeley, CA 94720
United States of America
E-mail: indraneelk@berkeley.edu
Abstract:
On Sendov's conjecture, T. Chijiwa quantifies the idea stated by V. Vâjâitu and A. Zaharescu (and M. J. Miller independently), namely that if a polynomial with all roots inside the closed unit disk has a root sufficiently close to the unit circle then there is a critical point at a distance of at most one from that root. Chijiwa provides an estimate of exponential order for the required 'closeness' of the root to the unit circle so that such a critical point may exist. In this paper, we will improve this estimate to polynomial order by making major modifications and strengthening inequalities in Chijiwa's proof.
Paper's Title:
On A Conjecture of A Logarithmically Completely Monotonic Function
Author(s):
Valmir Krasniqi, Armend Sh. Shabani
Department of Mathematics,
University of Prishtina,
Republic of Kosova
E-mail:
vali.99@hotmail.com
armend_shabani@hotmail.com
Abstract:
In this short note we prove a conjecture, related to a logarithmically completely monotonic function, presented in [5]. Then, we extend by proving a more generalized theorem. At the end we pose an open problem on a logarithmically completely monotonic function involving q-Digamma function.
Paper's Title:
A Short Proof of an Open Inequality with Power-Exponential Functions
Author(s):
Mitsuhiro Miyagi and Yusuke Nishizawa
General Education, Ube National College of
Technology,
Tokiwadai 2-14-1, Ube,
Yamaguchi 755-8555,
Japan
E-mail:
miyagi@ube-k.ac.jp
yusuke@ube-k.ac.jp
Abstract:
V. Cîrtoaje conjectured that a3b + b3a + ( (a -b)/2 )4 ≤ 2 holds for all nonnegative numbers a and b with a +b =2. In this short note, we give a proof of the Cîrtoaje's conjecture with power-exponential functions.
Paper's Title:
To a Banach *-algebra in a Semipartial Dynamical System
Author(s):
Bahman Tabatabaie Shourijeh and Seyed Mostafa Zebarjad
Department of Mathematics,
College of Sciences,
Shiraz University, Shiraz 71454,
Iran.
E-mail:
tabataba@math.susc.ac.ir
zebarjad@mail.yu.ac.ir
URL:
http://research.shirazu.ac.ir/faculty/More.asp?ID=207
Abstract:
By a partial dynamical system, we mean a triple containing a C*-algebra A, a discrete group G and a partial action of G on A. There are two C*--algebras associated to a given partial dynamical system. These are nothing but the certain C*-completions of a Banach *-algebra. In constructing such a Banach *-algebra, usually, a tedious limit process is used to apply. In this paper, we prove some theorems in this context without any limit process.
Paper's Title:
Some New Nonlinear Integro-Differential Inequalities of Gronwall-Bellman-Pachpatte Type
Author(s):
A. ABDELDAIM
Department of Mathematics and Computer
Sciences,
Faculty of Science,
Port Said University, Port Said,
EGYPT.
Department of Mathematics,
Faculty of Science and Humanities,
Shaqra University, Dawadmi,
SAUDI ARABIA.
E-mail:
ahassen@su.edu.sa
URL:
http://faculty.ksu.edu.sa/DRABDELDAIM/Pages/Home.aspx
Abstract:
In this paper we establish some new nonlinear integro-differential inequalities of Gronwall-Bellman-Pachpatte type for function of one independent variable. The purpose of this paper is to extend certain results which proved by Pachpatte in [On some fundamental integrodifferential and integral inequalities, An. Sti. Univ. Al. I. Cuza, Iasi, Vol.23 (1977), 77-86]. The inequalities obtained here can be used in the theory of some new classes of nonlinear integro-differential equations. Some applications are also given to illustrate the usefulness of our results.
Paper's Title:
A Dynamic Contact Problem for an Electro Viscoelastic Body
Author(s):
Denche M. and Ait Kaki L.
Laboratoire Equations Differentielles,
Departement de Mathematiques,
Universite Constantine 1,
Algeria.
Ecole Normale Superieure,
Departement des Sciences Exactes et Informatique,
Plateau Mansourah, Constantine.
Algeria.
E-mail:
m.denche@umc.edu.dz
leilaitkaki@yahoo.fr
Abstract:
We consider a dynamic problem which describes a contact between a piezoelectric body and a conductive foundation. The frictionless contact is modelled with the normal compliance, the electric conditions are supposed almost perfect. We prove the existence of a unique weak solution for almost perfect electric contact.
Paper's Title:
Ap Functions and Maximal Operator
Author(s):
Chunping Xie
Department of Mathematics,
Milwaukee School of Engineering,
1025 N. Broadway,
Milwaukee, Wisconsin 53202,
U. S. A.
E-mail: xie@msoe.edu
URL: http://www.msoe.edu/people/chunping.xie
Abstract:
The relationship between Ap functions and Hardy-Littlewood maximal operator on Lp,λ(w), the weighted Morrey space, has been studied. Also the extropolation theorem of Lp,λ(w) has been considered.
Paper's Title:
Weak solutions of non coercive stochastic Navier-Stokes equations in R2
Author(s):
Wilhelm Stannat and Satoshi Yokoyama
Technische Universität Berlin,
Strasse des 17. Juni 136, 10623 Berlin,
Germany.
Graduate School of Mathematical Sciences,
The University of Tokyo,
Komaba, Tokyo 153-8914,
Japan.
E-mail: stannat@math.tu-berlin.de
E-mail: satoshi2@ms.u-tokyo.ac.jp
Abstract:
We prove existence of weak solutions of stochastic Navier-Stokes equations in R2 which do not satisfy the coercivity condition. The equations are formally derived from the critical point of some variational problem defined on the space of volume preserving diffeomorphisms in R2. Since the domain of our equation is unbounded, it is more difficult to get tightness of approximating sequences of solutions in comparison with the case of a bounded domain. Our approach is based on uniform a priori estimates on the enstrophy of weak solutions of the stochastic 2D-Navier-Stokes equations with periodic boundary conditions, where the periodicity is growing to infinity combined with a suitable spatial cutoff-technique.
Paper's Title:
C*-valued metric projection and Moore-Penrose inverse on Hilbert C*-modules
Author(s):
M. Eshaghi Gordji, H. Fathi and S.A.R. Hosseinioun
Department of Mathematics,
Semnan University, P.O. Box 35195-363, Semnan,
Iran.
Center of Excellence in Nonlinear Analysis and Applications (CENAA),
Semnan University,
Iran.
E-mail: Madjid.Eshaghi@gmail.com
Department of Mathematics,
Shahid Beheshti University, Tehran,
Iran.
E-mail: Hedayat.fathi@yahoo.com
Department of Mathematical Sciences,
University of Arkansas, Fayetteville, Arkansas 72701,
USA.
E-mail: shossein@uark.net
Abstract:
Let t be a regular operator between Hilbert C*-modules and t† be its Moore-Penrose inverse. We give some characterizations for t† based on C*-valued metric projection. Moore-Penrose inverse of bounded operators and elements of a C*-algebra is studied as a special case.
Paper's Title:
Some New Generalizations of Jensen's Inequality with Related Results and Applications
Author(s):
Steven G. From
Department of Mathematics
University of Nebraska at Omaha
Omaha, Nebraska 68182-0243.
E-mail: sfrom@unomaha.edu
Abstract:
In this paper, some new generalizations of Jensen's inequality are presented. In particular, upper and lower bounds for the Jensen gap are given and compared analytically and numerically to previously published bounds for both the discrete and continuous Jensen's inequality cases. The new bounds compare favorably to previously proposed bounds. A new method based on a series of locally linear interpolations is given and is the basis for most of the bounds given in this paper. The wide applicability of this method will be demonstrated. As by-products of this method, we shall obtain some new Hermite-Hadamard inequalities for functions which are 3-convex or 3-concave. The new method works to obtain bounds for the Jensen gap for non-convex functions as well, provided one or two derivatives of the nonlinear function are continuous. The mean residual life function of applied probability and reliability theory plays a prominent role in construction of bounds for the Jensen gap. We also present an exact integral representation for the Jensen gap in the continuous case. We briefly discuss some inequalities for other types of convexity, such as convexity in the geometric mean, and briefly discuss applications to reliability theory.
Paper's Title:
Properties of q-gamma and q-beta functions derived from the q-Gauss-Pólya inequalities
Author(s):
Sanja Varošanec
Department of Mathematics,
University of Zagreb,
Zagreb, Croatia
E-mail:
varosans@math.hr
Abstract:
We consider log-convexity and other properties of several functions related to q-gamma and q-beta functions. These properties are consequences of the general inequality, so-called q-analogue of the Gauss-Pólya inequality. Various inequalities involving these special functions are also given.
Paper's Title:
Inequalities for the Area Balance of Functions of Bounded Variation
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
We introduce the area balance function associated to a Lebesgue
integrable function f:[a,b] →C by
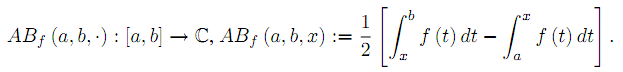
Several sharp bounds for functions of bounded variation are provided. Applications for Lipschitzian and convex functions are also given.
Paper's Title:
On operators for which T2≥-T*2
Author(s):
Messaoud Guesba1 and Mostefa Nadir2
1Department
of Mathematics,
University of El Oued 39000,
Algeria
E-mail: guesbamessaoud2@gmail.com
2Department of Mathematics,
University of Msila 28000,
Algeria
E-mail: mostefanadir@yahoo.fr
Abstract:
In this paper we introduce the new class of operators for which T2≥ -T*2 acting on a complex Hilbert space H. We give some basic properties of these operators. we study the relation between the class and some other well known classes of operators acting on H.
Paper's Title:
Some interesting properties of finite continuous Cesŕro operators
Author(s):
Abdelouahab Mansour and Abderrazak Hechifa
Operator theory laboratory (LABTHOP),
Eloued University,
Algeria.
E-mail:
amansour@math.univ-lyon1.fr
Mathematics Department,
Faculty of Science,
Badji Mokhtar University, -Annaba,
Algeria.
E-mail:
abderrazak02@gmail.com
Abstract:
A complex scalar λ is called an extended eigenvalue of a bounded linear operator T on a complex Banach space if there is a nonzero operator X such that TX = λ XT, the operator X is called extended eigenoperator of T corresponding to the extended eigenvalue λ.
In this paper we prove some properties of extended eigenvalue and extended eigenoperator for
C1 on Lp([0,1]), where C1 is the Cesŕro operator defined on the complex Banach spaces Lp([0 , 1]) for
1<p<∞ by the expression
Paper's Title:
Some New Inequalities of Hermite-Hadamard and Fejér Type for Certain Functions with Higher Convexity Author(s):
Steven G. From Department of Mathematics, Abstract:
In this paper, we present some new inequalities of Hermite-Hadamard or Fejér
type for certain functions satisfying some higher convexity conditions on one or
more derivatives. Paper's Title:
Wavelet Frames in Higher Dimensional Sobolev Spaces Author(s):
Raj Kumar, Manish Chauhan, and Reena Department of Mathematics, Department of Mathematics, Department of Mathematics, Abstract:
In this paper, we present sufficient condition for the sequence
of vectors
Paper's Title:
Euler Series Solutions for Linear Integral Equations Author(s):
Mostefa Nadir and Mustapha Dilmi Department of Mathematics, Abstract:
In this work, we seek the approximate solution of linear integral equations
by truncation Euler series approximation. After substituting the Euler
expansions for the given functions of the equation and the unknown one, the
equation reduces to a linear system, the solution of this latter gives the
Euler coefficients and thereafter the solution of the equation. The
convergence and the error analysis of this method are discussed. Finally, we
compare our numerical results by others. Paper's Title:
MSplit Equality for Monotone Inclusion Problem and Fixed Point Problem in
Real Banach Spaces Author(s):
1,2Christian Chibueze Okeke,
3Abdumalik Usman Bello, 1Chinedu Izuchukwu, and
1Oluwatosin Temitope Mewomo 1School
of Mathematics, 2DST-NRF
Center of Excellence in Mathematical and Statistical Sciences (CoE-Mass) 3Federal
University, Abstract:
In this paper a new iterative algorithm for approximating a common solution of split equality monotone inclusion problem and split equality fixed point problem is introduced. Using our algorithm, we state and prove a strong convergence theorem for approximating an element in the intersection of the set of solutions of a split equality monotone inclusion problem and the set of solutions of a split equality fixed point problem for right Bregman strongly nonexpansive
mappings in the setting of p-uniformly convex Banach spaces which are also uniformly smooth. We also give some applications. Paper's Title:
Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results Author(s):
Sever S. Dragomir1,2 1Mathematics, School of Engineering
& Science Abstract:
In this paper we survey some recent results obtained by the
author in providing various bounds for the celebrated f-divergence
measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation
distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text. Paper's Title:
Relation Between The Set Of Non-decreasing Functions And The Set Of Convex Functions Author(s):
Qefsere Doko Gjonbalaj and Luigj Gjoka Department of Mathematics, Faculty of
Electrical and Computer Engineering, E-mail:
qefsere.gjonbalaj@uni-pr.edu
Department of Engineering Mathematics, E-mail:
luigjgjoka@ymail.com Abstract:
In this article we address the problem of integral presentation
of a convex function. Let I be an interval in R. Here, using the Riemann or Lebesgue’s integration theory, we find the necessary and sufficient condition for a function
f: I→ R to be convex in
I. Paper's Title:
A Comparison Between Two Different Stochastic Epidemic Models with Respect to the Entropy Author(s):
Farzad Fatehi and Tayebe Waezizadeh Department of Mathematics, Department of Pure Mathematics, Faculty
of Mathematics and Computer, Abstract:
In this paper at first a brief history of mathematical models is presented with the aim to clarify the reliability of stochastic models over deterministic models. Next, the necessary background about random variables and stochastic processes, especially Markov chains and the entropy are introduced. After that, entropy of SIR stochastic models is computed and it is proven that an epidemic will disappear after a long time. Entropy of a stochastic mathematical model determines the average uncertainty about the outcome of that random experiment. At the end, we introduce a chain binomial epidemic model and compute its entropy, which is then compared with the DTMC SIR epidemic model to show which one is nearer to reality. Paper's Title:
Existence of Optimal Parameters for Damped Sine-Gordon Equation with Variable Diffusion Coefficient and Neumann Boundary Conditions Author(s):
N. Thapa Department of Mathematical Sciences, Abstract:
The parameter identification problem for sine-Gordon equation is of a major interests among mathematicians and scientists.\ In this work we the consider sine-Gordon equation with variable diffusion coefficient and Neumann boundary data. We show the existence and uniqueness of weak solution for sine-Gordon equation. Then we show that the weak solution continuously depends on parameters. Finally we show the existence of optimal set of parameters. Paper's Title:
A kind of Function Series and Its Applications Author(s):
Yang Tianze
Mechanical Engineering, E-mail:
qdyangtianze@163.com Abstract:
A kind of new function series is obtained in this paper. Their theorems and proofs are shown, and some applications are given. We give the expansion form of general integral and the series expansion form of function and the general expansion form of derivative. Using them in the mathematics,we get some unexpected result. Paper's Title:
Some Inequalities of the Hermite-Hadamard Type for k-Fractional Conformable Integrals Author(s):
C.-J. Huang, G. Rahman, K. S. Nisar, A. Ghaffar and F. Qi Department of Mathematics, Ganzhou Teachers College,
Department of Mathematics, Shaheed Benazir
Bhutto University, Department of Mathematics, College of Arts
and Science at Wadi Aldawaser, 11991, Department of Mathematical Science,
Balochistan University of Information Technology, School of Mathematical Sciences, Tianjin
Polytechnic University, Abstract:
In the paper, the authors deal with generalized k-fractional conformable integrals, establish some inequalities of the Hermite-Hadamard
type for generalized k-fractional conformable integrals for convex functions, and generalize known inequalities of the Hermite-Hadamard type for conformable fractional integrals. Paper's Title:
A Generalization of Ostrowski's Inequality for Functions of Bounded
Variation via a Parameter Author(s):
Seth Kermausuor Department of Mathematics and Computer
Science, Abstract:
In this paper, we provide a generalization of the Ostrowski's inequality for functions of bounded variation for
k points via a parameter λ∈[0,1]. As a by product, we consider some particular cases to obtained some interesting inequalities in these directions. Our results generalizes some of the results by Dragomir in [S. S. DRAGOMIR,
The Ostrowski inequality for mappings of bounded variation,
Bull. Austral. Math. Soc., 60 (1999), pp. 495--508.] Paper's Title:
Dynamical Analysis of HIV/AIDS Epidemic Model with Two Latent Stages, Vertical Transmission and Treatment Author(s):
Nur Shofianah, Isnani Darti, Syaiful Anam Mathematics Department,Faculty of
Mathematics and Natural Sciences. Abstract:
We discuss about dynamical analysis of HIV/AIDS epidemic model with two
latent stages, vertical transmission and treatment. In this model, the spreading
of HIV occurs through both horizontal and vertical transmission. There is also
treatment for individual who has been HIV infected. The latent stage is divided
into slow and fast latent stage based on the immune condition which varies for
each individual. Dynamical analysis result shows that the model has two
equilibrium points: the disease-free equilibrium point and the endemic
equilibrium point. The existence and global stability of equilibrium points
depend on the basic reproduction number R0. When R0
<1, only the disease-free equilibrium point exists. If R0 >1,
there are two equilibrium points, which are the disease-free equilibrium point
and the endemic equilibrium point. Based on the result of stability analysis,
the disease-free equilibrium point is globally asymptotically stable if R0
<1, while if R0 > 1 and p=q, the endemic
equilibrium point will be globally asymptotically stable. In the end, we show
some numerical simulations to support the analytical result. Paper's Title:
A Low Order Least-Squares Nonconforming Finite Element Method for Steady Magnetohydrodynamic Equations Author(s):
Z. Yu, D. Shi and H. Zhu College of Science, School of Mathematics and Statistics, Mathematics Department, Abstract:
A low order least-squares nonconforming finite element (NFE) method is
proposed for magnetohydrodynamic equations with EQ1rot
element and zero-order Raviart-Thomas element. Based on the above element's
typical interpolations properties, the existence and uniqueness of the
approximate solutions are proved and the optimal order error estimates for the
corresponding variables are derived. Paper's Title:
Action of Differential Operators On Chirpsconstruct On L∞ Author(s):
Taoufik El Bouayachi and Naji Yebari Laboratoire de Mathematiques et
applications, Abstract:
We will study in this work the action of differential operators on L∞
chirps and we will give a new definition of logarithmic chirp. Finally we will
study the action of singular integral operators on chirps by wavelet
characterization and Kernel method. Paper's Title:
Some New Mappings Related to Weighted Mean Inequalities Author(s):
Xiu-Fen Ma College of Mathematical and Computer, Abstract:
In this paper, we define four mappings related to weighted mean inequalities, investigate their properties, and obtain some new refinements of weighted mean inequalities. Paper's Title:
Some fixed point results in partial S-metric spaces Author(s):
M. M. Rezaee, S. Sedghi, A. Mukheimer, K. Abodayeh, and Z. D. Mitrovic Department of Mathematics, Qaemshahr
Branch, Department of Mathematics, Qaemshahr
Branch, Department of Mathematics and General
Sciences, Department of Mathematics and General
Sciences, Nonlinear Analysis Research Group, Abstract:
We introduce in this article a new class of generalized metric spaces, called
partial S-metric spaces. In addition, we also give some interesting results on
fixed points in the partial S-metric spaces and some applications. Paper's Title:
Inequalities for Functions of Selfadjoint Operators on Hilbert Spaces:
Author(s):
Sever S. Dragomir1,2 1Mathematics,
College of Engineering
& Science Abstract:
The main aim of this survey is to present recent results concerning
inequalities for continuous functions of selfadjoint operators on complex
Hilbert spaces. It is intended for use by both researchers in various fields
of Linear Operator Theory and Mathematical Inequalities, domains which have
grown exponentially in the last decade, as well as by postgraduate students
and scientists applying inequalities in their specific areas. Paper's Title:
Oblique Projectors from the Simpson Discrete Fourier Transformation Matrix Author(s):
P. Singh and V. Singh School of Mathematics, Computer Science
and Statistics, Abstract:
In this paper we examine the projectors of the Simpson Discrete Fourier Transform matrix of dimension two modulus four and show how they decompose the complex vector space into a direct sum of oblique eigenspaces. These projection operators are used to define a Simpson Discrete Fractional Fourier Transform (SDFRFT). Paper's Title:
Double Difference of Composition Operator on Bloch Spaces Author(s):
Rinchen Tundup Department of Mathematics E-mail:
joneytun123@gmail.com Abstract:
In this paper we characterize the compactness of double difference of three non-compact composition operators on Bloch space induced by three holomorphic self maps on the unit disc. Paper's Title:
Accuracy of Implicit DIMSIMs with Extrapolation Author(s):
A. J. Kadhim, A. Gorgey, N. Arbin and N. Razali Mathematics Department, Faculty of
Science and Mathematics, Unit of Fundamental Engineering Studies, Abstract:
The main aim of this article is to present recent results concerning diagonal implicit multistage integration methods (DIMSIMs) with extrapolation in solving stiff problems. Implicit methods with extrapolation have been proven to be very useful in solving problems with stiff components. There are many articles written on extrapolation of Runge-Kutta methods however fewer articles on extrapolation were written for general linear methods. Passive extrapolation is more stable than active extrapolation as proven in many literature when solving stiff problems by the Runge-Kutta methods. This article takes the first step by investigating the performance of passive extrapolation for DIMSIMs type-2 methods. In the variable stepsize and order codes, order-2 and order-3 DIMSIMs with extrapolation are investigated for Van der Pol and HIRES problems. Comparisons are made with ode23 solver and the numerical experiments showed that implicit DIMSIMs with extrapolation has greater accuracy than the method itself without extrapolation and ode23. Paper's Title:
The Higher Coefficients for Bazilevic Functions B1(α) Author(s):
Marjono, Sa'adatul Fitri, and Krisna Adilia Daniswara Department of Mathematics, Abstract:
Let f be analytic in D{z: |z|< 1} with
Paper's Title:
An Efficient Modification of Differential Transform Method for Solving Integral and Integro-differential Equations Author(s):
S. Al-Ahmad, Ibrahim Mohammed Sulaiman*, and M. Mamat Faculty of Informatics and Computing, Abstract:
In this paper, classes of integral and integro-differential equations are solved using a modified differential transform method. This proposed technique is based on differential transform method (DTM), Laplace transform (LT) procedure and Pad\'{e} approximants (PA). The proposed method which gives a good approximation for the true solution in a large region is referred to modified differential transform method (MDTM). An algorithm was developed to illustrate the flow of the proposed method. Some numerical problems are presented to check the applicability of the proposed scheme and the obtained results from the computations are compared with other existing methods to illustrates its efficiency. Numerical results have shown that the proposed MDTM method is promising compared to other existing methods for solving integral and integro-differential equations. Paper's Title:
Optimization Techniques on Affine Differential Manifolds Author(s):
Ali S Rasheed, Faik Mayah and Ahmed A H AL-Jumaili Ministry of Higher Education and
Scientific Research, Department of Physics, College of
Sciences, Abstract:
In addition to solid ground of Riemannian manifolds fundamentals, this article interviews some popular optimization methods on Riemannian manifolds. Several optimization problems can be better stated on manifolds rather than Euclidean space, such as interior point methods, which in turns based on self-concordant functions (logarithmic barrier functions). Optimization schemes like the steepest descent scheme, the Newton scheme, and others can be extended to Riemannian manifolds. This paper introduces some Riemannian and non-Riemannian schemes on manifolds. Paper's Title:
A Self-adaptive Subgradient Extragradient Algorithm for Variational Inequality Problems and Fixed Point Problems in Banach Spaces Author(s):
F. U. Ogbuisi School of Mathematics, Statistics and
Computer Science, Department of Mathematics, Abstract:
In this paper, we propose and analyze a type of subgradient extragradient algorithm for the approximation of a solution of variational inequality problem which is also a common fixed point of an infinite family of relatively nonexpansive mappings in 2-uniformly convex Banach spaces which are uniformly smooth. By using the generalized projection operator, we prove a strong convergence theorem which does not require the prior knowledge of the Lipschitz constant of cost operator. We further applied our result to constrained convex minimization problem, convex feasibility problem and infinite family of equilibrium problems. Our results improve and complement related results in 2-uniformly convex and uniformly smooth Banach spaces and Hilbert spaces. Paper's Title:
Reduced Generalized Combination Synchronization Between Two n-Dimensional Integer-Order Hyperchaotic Systems and One m-Dimensional Fractional-Order Chaotic System Author(s):
Smail Kaouache, Mohammed Salah Abdelouahab and Rabah Bououden Laboratory of Mathematics and their
interactions, Abstract:
This paper is devoted to investigate the problem of
reduced generalized combination synchronization (RGCS) between two n-dimensional integer-order hyperchaotic drive systems and one m-dimensional
fractional-order chaotic response system. According to the stability theorem of
fractional-order linear system, an active mode controller is proposed to
accomplish this end. Moreover, the proposed synchronization scheme is
applied to synchronize three different chaotic systems, which are the Danca hyperchaotic system, the modified hyperchaotic Rossler system, and the fractional-order Rabinovich-Fabrikant chaotic system. Finally, numerical results are presented to fit our theoretical analysis. Paper's Title:
ψ(m,q)-Isometric Mappings on Metric Spaces Author(s):
Sid Ahmed Ould Beinane, Sidi Hamidou Jah and Sid Ahmed Ould Ahmed Mahmoud Mathematical Analysis and Applications,
Mathematics Department, College of Science, Department of Mathematics, College of
Science Qassim University, Mathematical Analysis and Applications,
Abstract:
The concept of (m,p)-isometric operators on Banach space was extended to
(m,q)-isometric mappings on general metric spaces in [6].
This paper is devoted to define the concept of
ψ(m, q)-isometric, which is the
extension of A(m, p)-isometric operators on Banach spaces introduced in [10].
Let T,ψ: (E,d) -> (E, d) be two mappings.
Paper's Title:
Hermite-Hadamard Type Inequalities for MN-Convex Functions Author(s):
Sever S. Dragomir1,2 1Mathematics,
College of Engineering
& Science Abstract:
The present work endeavours to briefly present some of the fundamental
results connected to the Hermite-Hadamard inequality for special classes of
convex functions such as AG, AH, GA, GG, GH, HA, HG and HH -convex
functions in which the author have been involved during the last five years. For
simplicity, we call these classes of functions such as MN-convex
functions, where M and N stand for any of the Arithmetic (A),
Geometric (G) or Harmonic (H) weighted means of positive real numbers. The survey is
intended for use by both researchers in various fields of Approximation
Theory and Mathematical Inequalities, domains which have grown exponentially
in the last decade, as well as by postgraduate students and scientists
applying inequalities in their specific areas. Paper's Title:
Sweeping Surfaces with Darboux Frame in Euclidean 3-space E3 Author(s):
F. Mofarreh, R. Abdel-Baky and N. Alluhaibi Mathematical Science Department, Faculty
of Science, Department of Mathematics Science and
Arts, College Rabigh Campus, Abstract:
The curve on a regular surface has a moving frame and it is called Darboux frame. We introduce sweeping surfaces along the
curve relating to the this frame and investigate their geometrical properties. Moreover, we obtain the necessary and sufficient conditions for these
surfaces to be developable ruled surfaces. Finally, an example to illustrate the
application of the results is introduced. Paper's Title:
Construction of a Frame Multiresolution Analysis on Locally Compact Abelian Groups Author(s):
R. Kumar and Satyapriya Department of Mathematics, Abstract:
The frame multiresolution analysis (FMRA) on locally compact Abelian groups has been studied and the results concerning classical MRA have been worked upon to obtain new results. All the necessary conditions, which need to be imposed on the scaling function
φ to construct a wavelet frame via FMRA, have been summed up. This process of construction of FMRA has aptly been illustrated by sufficient examples. Paper's Title:
Some criteria for Subspace-hypercyclicity of C0-semigroups Author(s):
Mansooreh Moosapoor Department of Mathematics, Abstract:
We research subspace-hypercyclic C0-semigroups in this paper. We present various types of subspace-hypercyclicity criteria for C0-semigroups. Some of them are stronger than the criteria introduced before. Also, we state that if a C0-semigroup
(Tt}t≥ 0 satisfies in
any of them, then (Tt⊕Tt}t≥ 0 is subspace-hypercyclic. Paper's Title:
Evaluation of a New Class of Double Integrals Involving Generalized Hypergeometric Function
4F3
Author(s):
Joohyung Kim, Insuk Kim and Harsh V. Harsh Department of Mathematics Education, Department of Mathematics, Amity School
of Eng. and Tech., Abstract:
Very recently, Kim evaluated some double integrals involving a generalized hypergeometric function
3F2 with the help of generalization of Edwards's well-known double integral due to Kim,
et al. and generalized classical Watson's summation theorem obtained earlier by Lavoie,
et al.
In this research paper we evaluate one hundred double integrals involving generalized hypergeometric function
4F3 in the form of four master formulas (25 each) viz. in the most general form for any integer.
Some interesting results have also be obtained as special cases of our main findings. Paper's Title:
Some Remarks On Quasinearly Subharmonic Functions Author(s):
Mansour Kalantar Universite Toulouse III-Paul Sabatier,
Abstract:
We prove some basic properties of quasi-nearly subharmonic functions and quasi-nearly subharmonic functions in the narrow sense. Paper's Title:
Nonlinear System of Mixed Ordered Variational Inclusions Involving XOR Operation Author(s):
Iqbal Ahmad, Abdullah and Syed Shakaib Irfan Department of Mechanical Engineering, Zakir Husain Delhi College, Department of Mathematics, Abstract:
In this work, we introduce and solve an NSMOVI frameworks system involving XOR operation with the help of a proposed iterative algorithm in real ordered positive Hilbert spaces. We discuss the existence of a solution of a considered system of inclusions involving XOR operation by applying the resolvent operator technique with XOR operation and also study the strong convergence of the sequences generated by the considered algorithm. Further, we give a numerical example in support of our considered problem which gives the grantee that all the proposed conditions of our main result are fulfilled. Paper's Title:
Semivectorial Bilevel Optimization on Affine-Finsler-Metric Manifolds Author(s):
Faik Mayah1, Ali S Rasheed2 and Naseif J. Al- Jawari3 1Department of Physics, 3Dept.
of Mathematics, Abstract:
A Finsler manifold is a differential manifold together with a Finsler metric, in this paper we construct a new class of Finsler metric affine
manifolds on bilevel semivectorial with optimization problems. The first steps for this purpose involve the study of bilevel optimization on affine manifolds. The bilevel programming problem can
be viewed as a static version of the noncooperative, two-person game which was introduced in the context of unbalanced economic markets.
Bilevel optimization is a special kind of optimization where one problem is embedded within another. Paper's Title:
Coefficient Estimates Of Sakaguchi Kind Functions Using
Lucas Polynomials Author(s):
H. Priya and B. Srutha Keerthi Department of Mathematics, Abstract:
By means of (p,q) Lucas polynomials, we estimate coefficient bounds
and Fekete-Szego inequalities for functions belonging to this
class. Several corollaries and consequences of the main results are
also obtained. Paper's Title:
Hankel Functional Connected to Lemniscate of Bernoulli Author(s):
K. Ramanuja Rao, Rajnesh Lal and Kaushal Singh Fiji National University, Abstract:
The aim of present paper is to derive a higher bound (HB) of 3rd
order Hankel determinant for a collection of holomorphic mappings
connected with exactly to the right side of the lemniscate of Bernoulli,
whose polar coordinates form is r2 = 2cos2(2θ). The method carried
in this paper is more refined than the method adopted by the authors
(see
[1]), who worked on this problem earlier. Paper's Title:
A New Method with Regularization for Solving Split Variational Inequality Problems in Real Hilbert Spaces Author(s):
Francis Akutsah1 and Ojen Kumar Narain2 1School
of Mathematics, 2School
of Mathematics, Abstract:
In this paper, we introduce a new inertial extrapolation method with regularization for approximating solutions of split variational inequality problems in the frame work of real Hilbert spaces. We prove that the proposed method converges strongly to a minimum-norm solution of the problem without using the conventional two cases approach. In addition, we present some numerical experiments to show the efficiency and applicability of the proposed method. The results obtained in this paper extend, generalize and improve several results in this direction. Paper's Title:
Multistage Analytical Approximate Solution of Quasi-Linear Differential- Algebraic System of Index Two Author(s):
Ibrahim M. Albak, F. A.
Abdullah* and Zarita Zainuddin School of Mathematical Sciences, Abstract:
In this paper, a new Multistage Transform Method (MSDTM) has been proposed by utilizing a well-known transformation technique, the Differential Transform Method (DTM), to solve Differential Algebraic Equations (DAEs) with index 2. The advantage of the proposed scheme is that it does not require an index reduction and extends the convergence domain of the solution. Some examples for various types of problems are carried out to show the ability of MSDTM in solving DAEs. The results obtained are in good agreement with the existing literature which demonstrates the effectiveness and efficiency of the proposed method.
Paper's Title:
A Review on Minimally Supported Frequency Wavelets Author(s):
K Pallavi1, M C Lineesh1, A Noufal2 1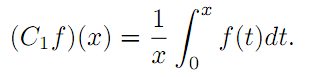
1: Paper Source
PDF document
University of Nebraska at Omaha,
Omaha, Nebraska 68182-0243,
U.S.A.
E-mail: sfrom@unomaha.edu
An open problem is given also.
Some applications to the logarithmic mean are given.
1: Paper Source
PDF document
Kirori Mal College, University of Delhi,
New Delhi-110007,
India.
E-mail: rajkmc@gmail.com
University of Delhi,
New Delhi-110007,
India
E-mail: manish17102021@gmail.com
Hans Raj College, University of Delhi,
New Delhi-110007,
India
E-mail: reena.bhagwat29@gmail.com
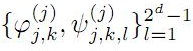 to be a frame for Hs(Rd) are derived. Necessary and
sufficient conditions for the sequence of vectors
to be a frame for Hs(Rd) are derived. Necessary and
sufficient conditions for the sequence of vectors
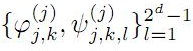 to be tight wavelet frames in Hs(Rd) are obtained.
Further, as an application an example of tight wavelet frames for Hs(R2) as bivariate box spline over 3-direction are given.
to be tight wavelet frames in Hs(Rd) are obtained.
Further, as an application an example of tight wavelet frames for Hs(R2) as bivariate box spline over 3-direction are given.
1: Paper Source
PDF document
University of Msila 28000,
ALGERIA.
E-mail: mostefanadir@yahoo.fr
E-mail: dilmiistapha@yahoo.fr
1: Paper Source
PDF document
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: okekec@ukzn.ac.za
E-mail: izuchukwuc@ukzn.ac.za
E-mail: mewomoo@ukzn.ac.za
Johannesburg,
South Africa.
Dutsin-Ma, Katsina State,
Nigeria.
E-mail:
uabdulmalik@fudutsinma.edu.ng
1: Paper Source
PDF document
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
1: Paper Source
PDF document
University of Prishtina "Hasan Prishtina",
Prishtine 10000,
Kosova
Polytechnic University of Tirana, Tirana,
Albania.
1: Paper Source
PDF document
University of Sussex,
Brighton BN1 9QH,
UK.
E-mail: f.fatehi@sussex.ac.uk
URL:
http://www.sussex.ac.uk/profiles/361251
Shahid Bahonar University of Kerman,
Kerman 76169-14111,
Iran.
E-mail: waezizadeh@uk.ac.ir
URL:
http://academicstaff.uk.ac.ir/en/tavaezizadeh
1: Paper Source
PDF document
Cameron University,
2800 West Gore Blvd,
73505 Lawton, Oklahoma,
USA.
E-mail: nthapa@cameron.edu
URL: http://www.cameron.edu/~nthapa/
1: Paper Source
PDF document
Shandong University, Xinglongshan Campus,
Jinan, Shandong,
China.
1: Paper Source
PDF document
Ganzhou 341000, Jiangxi,
China.
E-mail:
hcj73jx@126.com ,
huangcj1973@qq.com
Sheringal, Upper Dir, Khyber Pakhtoonkhwa,
Pakistan.
E-mail: gauhar55uom@gmail.com
Prince Sattam Bin Abdulaziz University, Riyadh Region,
Kingdom of Saudi Arabia.
E-mail: n.sooppy@psau.edu.sa,
ksnisar1@gmail.com
Engineering and Management Sciences, Quetta,
Pakistan.
E-mail: abdulghaffar.jaffar@gmail.com
Tianjin 300387,
China; Institute of Mathematics,
Henan Polytechnic University, Jiaozuo 454010, Henan,
China.
E-mail: qifeng618@gmail.com,
qifeng618@qq.com
1: Paper Source
PDF document
Alabama State University,
Montgomery, AL 36101,
USA.
E-mail:
skermausour@alasu.edu
1: Paper Source
PDF document
University of Brawijaya,
Jl. Veteran, Malang 65145,
Indonesia.
E-mail:
nur_shofianah@ub.ac.id,
isnanidarti@ub.ac.id,
syaiful@ub.ac.id
1: Paper Source
PDF document
Zhongyuan
University of Technology,
Zhengzhou 450007,
China.
E-mail:
5772@zut.edu.cn
Zhengzhou University,
Zhengzhou 450001,
China.
E-mail:
shi_dy@126.com
University of Southern Mississippi,
Hattiesburg MS, 39406,
U.S.A
E-mail:
huiqing.zhu@usm.edu
1: Paper Source
PDF document
Faculty of sciences and techniques, Tangier,
Morocco.
E-mail:
figo407@gmail.com,
yebarinaji@gmail.com
1: Paper Source
PDF document
Chongqing Normal University Foreign Trade and Business College,
No.9 of Xuefu Road, Hechuan District 401520,
Chongqing City,
The People's Republic of China.
E-mail: maxiufen86@163.com
1: Paper Source
PDF document
Islamic Azad University, Qaemshahr,
Iran.
E-mail: Rezaee.mohammad.m@gmail.com
Islamic Azad University, Qaemshahr,
Iran.
E-mail: sedghi.gh@qaemiau.ac.ir
Prince Sultan University, Riyadh,
KSA.
E-mail: mukheimer@psu.edu.sa
Prince Sultan University, Riyadh,
KSA.
E-mail: kamal@psu.edu.sa
Faculty of Mathematics and Statistics,
Ton Duc Thang University, Ho Chi Minh City,
Vietnam.
E-mail: zoran.mitrovic@tdtu.edu.vn
1: Paper Source
PDF document
a Survey of Recent Results
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
1: Paper Source
PDF document
University of Kwazulu-Natal,
Private Bag X54001, Durban 4001,
South Africa.
E-mail: singhp@ukzn.ac.za,
singhv@ukzn.ac.za
1: Paper Source
PDF document
University of Jammu
Jammu and Kashmir
India.
1: Paper Source
PDF document
Sultan Idris Education University,
35900 Tanjong Malim, Perak,
Malaysia
E-mail: annie_gorgey@fsmt.upsi.edu.my
Faculty of Engineering, Built Environment,
The National University of Malaysia,
43600 Bangi,
Malaysia.
1: Paper Source
PDF document
Faculty of Mathematics and Natural Sciences,,
Brawijaya University, Malang Jawa Timur 65145
Indonesia.
E-mail: marjono@ub.ac.id
saadatulfitri@ub.ac.id
krisnaadiliadaniswara@gmail.com
![]() , and normalized by the conditions f(0)=f'(0)-1=0. We give sharp estimates for the seventh and eighth coefficients for the class of Bazilevic functions with logarithmic growth,
B1α, defined by
, and normalized by the conditions f(0)=f'(0)-1=0. We give sharp estimates for the seventh and eighth coefficients for the class of Bazilevic functions with logarithmic growth,
B1α, defined by
 for
α≥0.
for
α≥0.
1: Paper Source
PDF document
Universiti Sultan Zainal Abidin,
Terengganu, Besut Campus, 22200,
Malaysia.
E-mail: Alahmad.shadi@yahoo.com,
*sulaimanib@unisza.edu.my,
must@unisza.edu.my
1: Paper Source
PDF document
Iraq.
E-mail: ahmedhashem@gmail.com
University of Wasit,
Iraq.
E-mail: faik.mayah@gmail.com
1: Paper Source
PDF document
University of KwaZulu-Natal, Durban,
South Africa.
University of Nigeria, Nsukka,
Nigeria.
E-mail: ferdinard.ogbuisi@unn.edu.ng
fudochukwu@yahoo.com
1: Paper Source
PDF document
Abdelhafid Boussouf University Center, Mila.
Algeria
E-mail: smailkaouache@gmail.com,
medsalah3@yahoo.fr,
rabouden@yahoo.fr
1: Paper Source
PDF document
Jouf University,
Sakaka P.O.Box 2014,
Saudi Arabia.
E-mail: beinane06@gmail.com
P.O. Box 6640, Buraydah 51452,
Saudi Arabia.
E-mail: jahsiidi@yahoo.fr
Mathematics Department, College of Science, Jouf University,
Sakaka P.O.Box 2014,
Saudi Arabia.
E-mail: sidahmed@ju.edu.sa,
sidahmed.sidha@gmail.com
For some positive integer m and q ∈ (0,∞).
T is said to be an ψ(m,q)-isometry,
if for all y,z ∈ E,
1: Paper Source
PDF document
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
1: Paper Source
PDF document
Princess Nourah bint Abdulrahman University
Riyadh 11546,
Saudi Arabia.
E-mail: fyalmofarrah@pnu.edu.sa
Department of Mathematics, Faculty of Science,
University of Assiut,
Assiut 71516,
Egypt.
E-mail: rbaky@live.com
King Abdulaziz University
Jeddah,
Saudi Arabia.
E-mail: nallehaibi@kau.edu.sa
1: Paper Source
PDF document
Kirori Mal College,
University of Delhi,
Delhi,
India.
E-mail: rajkmc@gmail.com
Department of Mathematics,
University of Delhi,
Delhi,
India.
E-mail: kmc.satyapriya@gmail.com
1: Paper Source
PDF document
Farhangian University, Tehran,
Iran.
E-mail: m.mosapour@cfu.ac.ir
mosapor110@gmail.com
1: Paper Source
PDF document
Wonkwang University, Iksan, 570-749,
Korea.
E-mail: joohyung@wku.ac.kr
Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Korea.
E-mail: iki@wku.ac.kr
Amity University Rajasthan
NH-11C, Jaipur-303002, Rajasthan,
India.
E-mail: harshvardhanharsh@gmail.com
1: Paper Source
PDF document
118 Route de Narbonne, 31062 Toulouse,
France.
E-mail:
mansour.kalantar@math.univ-toulouse.fr,
mankalantar12@yahoo.com
1: Paper Source
PDF document
College of Engineering, Qassim University
Buraidah 51452, Al-Qassim,
Saudi Arabia.
E-mail: iqbal@qec.edu.sa,
i.ahmad@qu.edu.sa
University of Delhi,
JLN Marg, New Delhi- 110 002,
India.
E-mail: abdullahdu@qec.edu.sa
Aligarh Muslim University, Aligarh,
India.
E-mail: shakaibirfan@gmail.com
1: Paper Source
PDF document
College of Sciences,
University of Wasit,
Iraq.
E-mail: faik.mayah@gmail.com
2Ministry of Higher Education and Scientific Research,
Iraq.
E-mail: ali.math2018@yahoo.com
ahmedhashem@gmail.com
College of Science,
Mustansiriyah University, Baghdad,
Iraq.
E-mail: nsaif642014@yahoo.com
1: Paper Source
PDF document
School of Advanced Sciences,
VIT Chennai Campus,
Chennai - 600 048,
India.
E-mail:
priyaharikrishnan18@gmail.com
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus,
Chennai - 600 048,
India.
E-mail: isruthilaya06@yahoo.co.in
1: Paper Source
PDF document
Department of Mathematics & Statistics,
P.O. Box 5529, Lautoka,
Fiji.
E-mail: ramanuja.kotti@fnu.ac.fj
rajnesh.lal@fnu.ac.fj
kaushal.singh@fnu.ac.fj
1: Paper Source
PDF document
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 216040405@stu.ukzn.ac.za,
akutsah@gmail.com
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
1: Paper Source
PDF document
Universiti Sains Malaysia,
11800 USM, Penang,
Malaysia.
E-mail: ibra13975@gmail.com,
farahaini@usm.my,
zarita@usm.my
1: Paper Source
PDF document
National Institute of Technology Calicut,
Kerala 673601,
India.
E-mail:
pavikrishnakumar@gmail.com
lineesh@nitc.ac.in
2Department of Mathematics,
Cochin University of Science and Technology,
Kerala 682022,
India.
E-mail: noufal@cusat.ac.in
Abstract:
This paper provides a review on Minimally Supported Frequency (MSF) wavelets that includes the construction and characterization of MSF wavelets. The characterization of MSF wavelets induced from an MRA is discussed and the nature of the low-pass filter associated with it is explained. The concept of wavelet set and dimension function is introduced to study this class of wavelets. Along with MSF wavelets, s-elementary wavelets and unimodular wavelets are also considered due to the similarity in definitions. Examples and illustrations are provided for more clarity.
Paper's Title:
On General Class of Nonlinear Contractive Maps and their Performance Estimates
Author(s):
Olalekan Taofeek Wahab and Salaudeen Alaro Musa
Department of Mathematics and
Statistics
Kwara State University, Malete
P. M. B. 1530 Ilorin,
Nigeria.
E-mail: taofeek.wahab@kwasu.edu.ng
Abstract:
This paper considers two independent general class of nonlinear contractive maps to study the existence properties of nonlinear operators with prior degenerate. The existence properties are proved in the framework of approximate fixed points with the imposition of the general class of contractive conditions in metrical convex spaces without emphasis on completeness or compactness. For computational purposes, the performance estimates and the sensitivity dependence of these conditions are obtained for the Picard operator. Practical examples are also considered to justify the validity of the conditions. The results ensure no term is lost in the operators with prior degenerate and the conditions are strictly larger class when compare with others in the literature.
Paper's Title:
Error Bounds for Numerical Integration of Functions of Lower Smoothness and Gauss-Legendre Quadrature Rule
Author(s):
Samuel A. Surulere and Abiola O. Oladeji
Tshwane University of Technology
Department of Mathematics and Statistics
175, Nelson Mandela drive, Arcadia, Pretoria,
South Africa.
E-mail: samuel.abayomi.sas@gmail.com
Abstract:
The error bounds of the rectangular, trapezoidal and Simpson's rules which are commonly used in approximating the integral of a function (f(x)) over an interval ([a,b]) were estimated. The error bounds of the second, and third generating functions of the Gauss-Legendre quadrature rules were also estimated in this paper. It was shown that for an (f(t)) whose smoothness is increasing, the accuracy of the fourth, sixth and eighth error bound of the second, and third generating functions of the Gauss-Legendre quadrature rule does not increase. It was also shown that the accuracy of the fourth error bound of the Simpson's (1/3) and (3/8) rules does not increase.
Paper's Title:
Trace Inequalities for Operators in Hilbert Spaces: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
School of Engineering
& Science
Victoria University,
PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
In this paper we survey some recent trace inequalities for operators in Hilbert spaces that are connected to Schwarz's, Buzano's and Kato's inequalities and the reverses of Schwarz inequality known in the literature as Cassels' inequality and Shisha-Mond's inequality. Applications for some functionals that are naturally associated to some of these inequalities and for functions of operators defined by power series are given. Further, various trace inequalities for convex functions are presented including refinements of Jensen inequality and several reverses of Jensen's inequality. Hermite-Hadamard type inequalities and the trace version of Slater's inequality are given. Some Lipschitz type inequalities are also surveyed. Examples for fundamental functions such as the power, logarithmic, resolvent and exponential functions are provided as well.
Paper's Title:
Reverse Hölder and Minkowski type integral inequalities for n functions
Author(s):
Panagiotis T. Krasopoulos and Lazhar Bougoffa
Department of Informatics, KEAO,
Electronic National Social Security Fund,
12 Patision St., 10677, Athens,
Greece.
E-mail: pan_kras@yahoo.gr
pankras@teemail.gr
Department of Mathematics,
Faculty of Science, Imam Mohammad Ibn Saud Islamic University,
P.O. Box 90950, Riyadh 11623,
Saudi Arabia.
E-mail: lbbougoffa@imamu.edu.sa
bougoffa@hotmail.com
Abstract:
We present and prove new reverse Hölder and Minkowski type integral inequalities for n functions. We compare our results with other known results from the relative literature in order to test their performance. In this respect, our theorems can be viewed as generalizations of some already known integral inequalities.
Paper's Title:
Conservativeness Criteria of Girsanov Transformation for Non-Symmetric Jump-diffusion
Author(s):
Mila Kurniawaty
DDepartment of Mathematics,
Universitas Brawijaya, Malang,
Indonesia.
E-mail: mila_n12@ub.ac.id
Abstract:
We develop the condition in our previous paper [The Conservativeness of Girsanov transformed for symmetric jump-diffusion process (2018)] in the framework of nonsymmetric Markov process with jumps associated with regular Dirichlet form. We prove the conservativeness of it by relation in duality of Girsanov transformed process and recurrent criteria of Dirichlet form.
Paper's Title:
A Caratheodory's Approximate Solutions of Stochastic Differential Equations Under the Hölder Condition
Author(s):
Bo-Kyeong Kim and Young-Ho Kim
Department of Mathematics,
Changwon National University,
Changwon, Gyeongsangnam-do 51140,
Korea.
E-mail: claire9576@naver.com
yhkim@changwon.ac.kr
Abstract:
In this paper, based on the theorem of the uniqueness of the solution of the stochastic differential equation, the convergence possibility of the Caratheodory's approximate solution was studied by approximating the unique solution. To obtain this convergence theorem, we used a Hölder condition and a weakened linear growth condition. Furthermore, The auxiliary theorems for the existence and continuity of the Caratheodory's approximate solution were investigated as a prerequisite.
Paper's Title:
Corrigendum for Multistage Analytical Approximate Solution of Quasi-Linear Differential- Algebraic System of Index Two
Author(s):
Ibrahim M. Albak, F. A. Abdullah* and Zarita Zainuddin
School of Mathematical Sciences,
Universiti Sains Malaysia,
11800 USM, Penang,
Malaysia.
E-mail: ibra13975@gmail.com,
farahaini@usm.my,
zarita@usm.my
Abstract:
This article is a corrigendum to AJMAA Volume 18, Issue 2, Article 13, {PDF Link}.
Paper's Title:
A Fuzzy Soft Quotient Topology and Its Properties
Author(s):
Haripamyu, Riri Alfakhriati, Monika Rianti Helmi, Jenizon
Department of Mathematics and Data Science, Andalas University, Padang, Indonesia.
E-mail: haripamyu@sci.unand.ac.id
ririalfakhriati123@gmail.com
monikariantihelmi@sci.unand.ac.id
jenizon@gmail.com
Abstract:
This research is to construct a new topology on fuzzy soft set by using the concept of quotient topology. Then we study the concept of quotient map to define the fuzzy soft quotient map and provide some relevant properties of fuzzy soft quotient map. Furthermore, we give some examples related to fuzzy soft quotient topology and fuzzy soft quotient map to apply some properties of fuzzy soft quotient map.
Paper's Title:
Two Geometric Constants Related to Isosceles Orthogonality on Banach Space
Author(s):
Huayou Xie, Qi Liu and Yongjin Li
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P. R. China.
E-mail: xiehy33@mail2.sysu.edu.cn
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P. R. China.
E-mail: liuq325@mail2.sysu.edu.cn
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P. R. China.
E-mail: stslyj@mail.sysu.edu.cn
Abstract:
In this paper, we introduce new geometric constant C(X,ai,bi,ci,2) to measure the difference between isosceles orthogonality and special Carlsson orthogonalities. At the same time, we also present the geometric constant C(X,ai,bi,ci), which is a generalization of the rectangular constant proposed by Joly. According to the inequality on isosceles orthogonality, we give the boundary characterization of these geometric constants. Then the relationship between these geometric constants and uniformly non-square property can also be discussed. Furthermore, we show that there is a close relationship between these geometric constants and some important geometric constants.
Paper's Title:
Fekete Szegö problem on the Class of Bazilevič functions B1(α) related to the Lemniscate Bernoulli
Author(s):
N. M. Asih, Marjono, Sa'adatul Fitri, Ratno Bagus Edy Wibowo
Department of Mathematics,
University of Brawijaya,
Malang 65145,
Indonesia.
Department of Mathematics,
University of Udayana,
Bali,
Indonesia.
E-mail: madeasih@unud.ac.id
Department of Mathematics,
University of Brawijaya,
Malang 65145,
Indonesia.
E-mail: marjono@ub.ac.id
Department of Mathematics,
University of Brawijaya,
Malang 65145,
Indonesia.
E-mail: saadatulfitri@ub.ac.id
Department of Mathematics,
University of Brawijaya,
Malang 65145,
Indonesia.
E-mail: rbagus@ub.ac.id
Abstract:
We provide a sharp boundaries inequalities for Fekete Szegö problem |a3-μ a22|, the coefficients of logarithmic function log~ f(z)/z, and the coefficients of the inverse function f(f'(w)) on the Bazilevič functions B1(α) related to the Lemniscate Bernoulli on the unit disk D={z: |z| < 1}. We obtained the result by using some properties of function with positive real part relates to coefficients problems.
Paper's Title:
Bicomplex Univalent Functions
Author(s):
Mohd Arif, Amjad Ali, Rajat Singh* and Romesh Kumar
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: azizymaths@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: amjadladakhi687@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: *rajat.singh.rs634@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: romeshmath@gmail.com
Abstract:
In this paper we introduce bicomplex univalent functions and also discuss the properties of a specific class of univalent functions.
Paper's Title:
A Unifying View of Some Banach Algebras
Author(s):
R. Kantrowitz
Mathematics & Statistics Department,
Hamilton College,
198 College Hill Road,
Clinton, NY 13323, USA.
E-mail: rkantrow@hamilton.edu
Abstract:
The purpose of this article is to shed light on a unifying framework for some normed algebras and, in particular, for some Banach algebras. The focus is on linear operators T between normed algebras X and Y and specified subalgebras A of Y. When the action of T on products in X satisfies a certain operative equation, the subspace T-1(A) is stable under the multiplication of X and is readily equipped with a family of canonical submultiplicative norms. It turns out that many familiar and important spaces are encompassed under this versatile perspective, and we offer a sampling of several such. In this sense, the article presents an alternative lens through which to view a host of normed algebras. Moreover, recognition that a normed linear space conforms to this general structure provides another avenue to confirming that it is at once stable under multiplication and also outfitted with an abundance of equivalent submultiplicative norms.
Paper's Title:
Semigroup of Linear Operator In Bicomplex Scalars
Author(s):
Stanzin Kunga, Amjad Ali and Aditi Sharma
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: stanzinkunga19@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail:
amjadladakhi687@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: aditi.sharmaro@gmail.com
Abstract:
In this paper, we have studied the generators of C0-semigroups of bicomplex linear operators on BC-Banach modules. This work is based on [5].
Paper's Title:
Some Notes on the Semi-open Subspaces of Topological Spaces
Author(s):
Nicky. K. Tumalun, Philotheus E. A. Tuerah, and Rolles N. S. Palilingan
Department of Mathematics
Universitas Negeri Manado
Tondano 95618
Indonesia.
E-mail: nickytumalun@unima.ac.id
URL: https://fmipa.unima.ac.id/
Department of Mathematics
Universitas Negeri Manado
Tondano 95618
Indonesia.
E-mail: pheatuerah@unima.ac.id
URL: https://fmipa.unima.ac.id/
Department of Physics
Universitas Negeri Manado
Tondano 95618
Indonesia.
E-mail:
rollespalilingan@unima.ac.id
URL: https://fmipa.unima.ac.id/
Abstract:
In this paper, we obtain some new results regarding to the nowhere dense and first category set in the semi-open subspace of a topological space. More precisely, we prove that a nowhere dense set in the semi-open subspace of a topological space is equivalent as a nowhere dense set in that topological space. This implies that a first category set in the semi-open subspace of a topological space is equivalent as a first category set in that topological space. We also give some applications of these results to give some new proofs relating to the properties of semi-open set and Baire space.
Paper's Title:
Higher Order Accurate Compact Schemes for Time Dependent Linear and Nonlinear Convection-Diffusion Equations
Author(s):
S. Thomas, Gopika P.B. and S. K. Nadupuri
Department of Mathematics
National Institute of Technology Calicut
Kerala
673601
India.
E-mail:
sobinputhiyaveettil@gmail.com
pbgopika@gmail.com nsk@nitc.ac.in
Abstract:
The primary objective of this work is to study higher order compact finite difference schemes for finding the numerical solution of convection-diffusion equations which are widely used in engineering applications. The first part of this work is concerned with a higher order exponential scheme for solving unsteady one dimensional linear convection-diffusion equation. The scheme is set up with a fourth order compact exponential discretization for space and cubic $C^1$-spline collocation method for time. The scheme achieves fourth order accuracy in both temporal and spatial variables and is proved to be unconditionally stable. The second part explores the utility of a sixth order compact finite difference scheme in space and Huta's improved sixth order Runge-Kutta scheme in time combined to find the numerical solution of one dimensional nonlinear convection-diffusion equations. Numerical experiments are carried out with Burgers' equation to demonstrate the accuracy of the new scheme which is sixth order in both space and time. Also a sixth order in space predictor-corrector method is proposed. A comparative study is performed of the proposed schemes with existing predictor-corrector method. The investigation of computational order of convergence is presented.
Paper's Title:
Approximately Dual p-Approximate Schauder Frames
Author(s):
K. Mahesh Krishna and P. Sam Johnson
Stat-Math Unit, Indian Statistical
Institute, Bangalore Centre,
Karnataka 560 059
India.
Department of Mathematical and
Computational Sciences,
National Institute of Technology Karnataka (NITK),
Surathkal, Mangaluru 575 025,
India.
E-mail: kmaheshak@gmail.com
sam@nitk.edu.in
Abstract:
Approximately dual frame in Hilbert spaces was introduced by Christensen and Laugesen to overcome difficulties in constructing dual frames for a given Hilbert space frame. It becomes even more difficult in Banach spaces to construct duals. For this purpose, we introduce approximately dual frames for a class of approximate Schauder frames for Banach spaces and develop basic theory. Approximate dual for this subclass is completely characterized and its perturbation is also studied.
Paper's Title:
Results on Bounds of the Spectrum of Positive Definite Matrices by Projections
Author(s):
P. Singh, S. Singh, V. Singh
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
E-mail: singhp@ukzn.ac.za
University of South Africa, Department of
Decision Sciences,
PO Box 392, Pretoria, 0003,
South Africa.
E-mail: singhs2@unisa.ac.za
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
E-mail: singhv@ukzn.ac.za
Abstract:
In this paper, we develop further the theory of trace bounds and show that in some sense that the earlier bounds obtained by various authors on the spectrum of symmetric positive definite matrices are optimal. Our approach is by considering projection operators, from which several mathematical relationships may be derived. Also criteria for positive lower bounds are derived.
Paper's Title:
Li-Yorke and Expansivity for Composition Operators on Lorentz Space
Author(s):
Rajat Singh and Romesh Kumar
Department of Mathematics,
University of Jammu,
Jammu 180006,
INDIA.
E-mail: rajat.singh.rs634@gmail.com
Department of Mathematics,
University of Jammu,
Jammu 180006,
INDIA.
E-mail: romeshmath@gmail.com
Abstract:
In this paper, we investigate Li-Yorke composition operators and some of its variations on Lorentz spaces. Further, we also study expansive composition operators on these spaces. The work of the paper is essentially based on the work in [3], [6], [8] and [15].
Paper's Title:
On the Equiform Geometry of the Involute-evolute Curve Couple in Hyperbolic and de Sitter Spaces
Author(s):
M. Khalifa Saad, H. S. Abdel-Aziz and A. A. Abdel-Salam
Department of Mathematics,
Faculty of Science,
Islamic University of Madinah,
KSA.
E-mail: mohammed.khalifa@iu.edu.sa
Department of Mathematics,
Faculty of Science,
Sohag University, Sohag,
EGYPT.
E-mail: habdelaziz2005@yahoo.com
Department of Mathematics,
Faculty of Science,
Sohag University, Sohag,
EGYPT.
E-mail: asem2e@yahoo.com
Abstract:
In this paper, we aim to investigate the equiform differential geometric properties of the involute-evolute curve couple with constant equiform curvatures in three-dimensional hyperbolic and de Sitter spaces. Also, we obtain some relations between the curvature functions of these curves and investigate some special curves with respect to their equiform curvatures. Finally, we defray two computational examples to support our main findings.
Paper's Title:
The Automatic Continuity of N-Homomorphisms in Certain *-Banach Algebras
Author(s):
M. Aboulekhlef, Y. Tidli
Laboratory of Applied Mathematics and
Information and Communication Technology
Polydisciplinary Faculty of Khouribga
University of Sultan Moulay Slimane
Morocco.
E-mail: aboulekhlef@gmail.com
y.tidli@gmail.com
Abstract:
In this study, we prove the automatic continuity of surjective n-homomorphism between complete p-normed algebras. We show also that if Α and Β are complete *-p-normed algebras, Β is *simple and ψ: Α → Β is a surjective n-homomorphism under certain conditions, then ψ is continuous.
Paper's Title:
A General Fractional Control Scheme for Compound Combination Synchronization Between Different Fractional-Order Identical Chaotic Systems
Author(s):
Soumia Bensimessaoud and Smail Kaouache
Laboratory of Mathematics and their interactions, Abdelhafid Boussouf University Center, Mila, Algeria.
E-mail:
soumiabensimessaoud@gmail.com,
smailkaouache@gmail.com
Abstract:
In this paper, we aim to investigate the problem of compound combination synchronization (CCS) between four different fractional-order identical chaotic systems. Based on Laplace transformation and stability theory of linear dynamical systems, a new control law is proposed to assure the achievement of this kind of synchronization. Secondly, this control scheme is applied to realised CCS between four identical unified chaotic systems. Recall, that the proposed control scheme can be applied to wide classes of chaotic and hyperchaotic systems. Numerical simulations are given to show the effectiveness of the proposed method.
Paper's Title:
On Automorphisms and Bi-derivations of Semiprime Rings
Author(s):
Abu Zaid Ansari, Faiza Shujat, Ahlam Fallatah
Department of Mathematics,
Faculty of Science,
Islamic University of Madinah, Madinah
K.S.A.
E-mail: ansari.abuzaid@gmail.com,
ansari.abuzaid@iu.edu.sa
Department of Mathematics
Faculty of Science
Taibah University, Madinah,
K.S.A.
E-mail: faiza.shujat@gmail.com,
fullahkhan@taibahu.edu.sa
Department of Mathematics
Faculty of Science
Taibah University, Madinah,
K.S.A.
E-mail: Afallatah@taibahu.edu.sa
Abstract:
In this article, our goal is to figure out a functional equation involving automorphisms and bi-derivations on certain semiprime ring. Also, we characterize the structure of automorphism, in case of prime rings.
Paper's Title:
Mass Transportation Approach For Parabolic P-Biharmonic Equations
Author(s):
A. Soglo, K. W. Houedanou, J. Adetola
Institut de Mathematiques et de Sciences
Physiques (IMSP)
Universite d'Abomey-Calavi,
Rep. of Benin
E-mail: ambroiso.soglo@gmail.com
Departement de Mathematiques
Faculte des Sciences et Techniques (FAST)
Universite d'Abomey-Calavi,
Rep. of Benin
E-mail: khouedanou@yahoo.fr
Universite Nationale des Sciences, Technologie, Ingenierie et
Mathematiques (UNSTIM,
Abomey,
Rep. of Benin
E-mail: adetolajamal58@yahoo.com
Abstract:
In this paper, we propose a mass transportation method to solving a parabolic p-biharmonic equations, which generalized the Cahn-Hilliard (CH) equations in RN, N∈N*. By using a time-step optimal approximation in the appropriate Wasserstein space, we define an approximate weak solution which converges to the exact solution of the problem. We also show that the solution under certain conditions may be unique. Therefore, we study the asymptotic behavior of the solution of the parabolic p-biharmonic problem.
Paper's Title:
Commutator For Singular Operators On Variable Exponent Sequence Spaces And Their Corresponding Ergodic Version
Author(s):
A.M. Alphonse and S.S.S. Anupindi
Department of Mathematics,
Birla Institute of Technology And Science- Pilani,
Hyderabad Campus, Jawahar Nagar, Kapra Mandal,
District.-Medchal-500 078, Telangana,
India.
E-mail:
alphonse@hyderabad.bits-pilani.ac.in
p20180442@hyderabad.bits-pilani.ac.in
URL:
https://www.bits-pilani.ac.in/hyderabad/a-michael-alphonse
https://www.bits-pilani.ac.in/research_scholars/sri-sakti-swarup-anupindi
Abstract:
In this paper, we prove strong type inequality for maximal commutator of singular operator on weighted lp spaces. Using these results we prove strong type inequality for the maximal commutator of singular operator on variable exponent sequence spaces. Using Calderon-Coifman-Weiss transference principle we prove strong type inequality for maximal ergodic commutator of singular operator on a probability space equipped with measure preserving transformation U.
Paper's Title:
Using an Euler Type Transform for Accelerating Convergence of Series
Author(s):
Nimete Sh. Berisha, Faton M. Berisha*, Murat Sadiku
Faculty of Economics, University of
Prishtina,
Agim Ramadani st., 10000 Pristina,
Kosovo.
E-mail: nimete.berisha@uni-pr.edu
URL:
https://staff.uni-pr.edu/profile/nimeteberisha
Faculty of Mathematics and Sciences,
University of Prishtina,
Mother Teresa st., 10000 Pristina,
Kosovo.
E-mail: faton.berisha@uni-pr.edu
URL:
https://staff.uni-pr.edu/profile/fatonberisha
Faculty of Business Administration,
South East European University,
Tetovo,
North Macedonia.
E-mail: m.sadiku@seeu.edu.mk
Abstract:
In the paper we give a property of an operator of generalised difference, defined earlier, linear on a set of sequences, and use it to establish Euler type transforms for alternating series. These transforms accelerate the convergence of series under the same conditions as the transforms of non-alternating series. We also give analysis of an algorithm for computing a partial sum of the transformed series by using a higher order operator of generalised difference, and prove a theorem stating its order of complexity.
Paper's Title:
Solving Strongly Nonlinear Fractional Fredholm Integral-Differential Equations in Caputo's Sense Using the SBA Method
Author(s):
Germain Kabore1, Bakari Abbo2, Ousseni So3 and Blaise Some1
1Laboratoire
d'Analyse Numerique, Informatique et de Biomathmathiques (L.N.I.BIO),
Universite Joseph Ki-Zerbo,
Burkina Faso.
E-mail: germainkabore982@gmail.com,
blaisesomeouaga1@gmail.com
2University
of N'Damena, Tchad.
E-mail: bakariabbo@yahoo.fr
3Laboratoire
d'Analyse Numerique, Informatique et de Biomathemathiques (L.N.I.BIO),
Ecole Normale Superieure,
Burkina Faso.
E-mail: sousseni@yahoo.fr
Abstract:
The work addressed in this article consists in constructing the exact solutions, where they exist, of fractional Fredholm-type integro-differential equations in the sense of Caputo. Our results are obtained using the SBA method. The simplification of the approach, the analysis of its convergence, and the generalization of this method to these types of highly nonlinear equations constitute our scientific contribution.
Paper's Title:
Lebesgue Absolutely Continuous Functions Taking Values on C[a,b]
Author(s):
Andrew Felix IV Suarez Cunanan
North Eastern Mindanao State University
E-mail: afccunanan@nemsu.edu.ph
Abstract:
In this paper a version of absolutely continuous function using Lebesgue partition instead of Riemann partition over the field of C[a,b] will be introduced and we call this function as Lebesgue absolutely continuous function on [f,g]. Moreover, some properties of Lebesgue absolutely continuous function on [f,g] will be presented together with its relationship with the other continuous functions.
Paper's Title:
On the Integral Equations via Hartley Superconvolutions
Author(s):
Nguyen Minh Khoa
Department of Mathematics, Electric Power
University,
Ha Noi,
Viet Nam.
E-mail:
khoanm@epu.edu.vn
Abstract:
The new superconvolutions for the Hartley integral transforms are formulated and their properties are studied. Furthermore, we also formulate the Young type theorem for these superconvolutions in the function space Lsαβγ(R) and get its norm estimations. We apply them to solve integral equations and system of integral equations of Toeplitz plus Hankel type.
Paper's Title:
Semicommutative and Semiprime Properties in Bi-amalgamated Rings
Author(s):
1A. Aruldoss, 2C. Selvaraj, 3G. E. Chatzarakis, 4S. L. Panetsos, 5U. Leerawat
1
Department of Mathematics,
Mepco Schlenk Engineering College,
Sivakasi-626 005, Tamilnadu,
India.
aruldossa529@gmail.com
2
Department of Mathematics,
Periyar University,
Salem - 636 011, Tamilnadu,
India.
selvavlr@yahoo.com
3,4
Department of Electrical and Electronic Engineering Educators,
School of Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
geaxatz@otenet.gr
spanetsos@aspete.gr
5
Department of Mathematics,
Faculty of Science, Kasetsart University,
Bangkok 10900,
Thailand.
fsciutl@ku.ac.th
Abstract:
Let α: A→ B and β: A→ C be two ring homomorphisms and I and I' be two ideals of B and C, respectively, such that α{-1}(I)=β{-1}(I'). In this paper, we give a characterization for the bi-amalgamation of A with (B, C) along (I, I') with respect to (α, β) (denoted by A⋈(α, β)(I, I')) to be a SIT, semiprime, semicommutative and semiregular. We also give some characterization for these rings.
Paper's Title:
Dyadic Riesz Wavelets on Local Fields of Positive Characteristics
Author(s):
Kartik Garg, Raj Kumar, Satyapriya
Department of Mathematics,
University of Delhi,
Delhi,
India.
kartikgarg1421@gmail.com,
rajkmc@gmail.com
kmc.satyapriya@gmail.com
Abstract:
In this research paper, we introduce a novel theory for the construction of a Riesz wavelet basis in the space L2(K), where K is a local field with positive characteristics. Our approach is two fold: firstly, we derive some essential characterizations of the scaling function associated with the structure of a Riesz MRA on a local field, and secondly, we review existing methods for constructing wavelet frames in L2(K). We also present a well elaborated example for a better comprehension of our theory. Due to mathematical convenience, we limit ourselves to the case of dyadic dilations only.
Paper's Title:
Indonesia's GDP Forecast: Evidence From Fuzzy Time Series Model Using Particle Swarm Optimization Algorithm
Author(s):
Ismail Djakaria1, Djihad Wungguli2, Regina Sugi Pakadang3, Sri Endang Saleh4, Maman Abdurachman Djauhari5
1,2,3Universitas
Negeri Gorontalo,
Department of Statistics, Gorontalo,
Indonesia.
4Universitas Negeri Gorontalo,
Department of Development Economics, Gorontalo,
Indonesia.
5Indonesian Institute of Education,
Jl. Terusan Pahlawan 32, Garut 44151,
Indonesia.
E-mail: iskar@ung.ac.id
URL:
https://orcid.org/0000-0003-1358-2356
Abstract:
Gross Domestic Product (GDP) is a principal indicator used to measure the economic condition of a country. Indonesia's GDP growth from 2017 to 2019 was approximately 6 percent; however, it experienced a decline in 2020 and 2021, with rates of only -0.02 percent and 2.41 percent, respectively. In the process of economic development planning, a forecasting system is required to determine GDP in the future. The forecasting method employed in this research is fuzzy time series optimized using Particle Swarm Optimization (PSO), to enhance the accuracy and convergence of forecasted values. The dataset used comprises secondary data, specifically 54 sets of Indonesian GDP data spanning from the first quarter of 2010 to the second quarter of 2023. The analysis results indicate that the proposed method is better than the conventional fuzzy time series approach. The former method provides a predictive value for one period in the future with a Mean Absolute Percentage Error (MAPE) value of 4.40%. In contrast, the latter yields higher predictive values with a MAPE value of 7.93%.
Paper's Title:
On Saturation of Norm Convergence of Walsh-Fourier Matrix Transform Means
Author(s):
István Blahota
Institute of Mathematics and Computer Sciences,
University of Nyíregyháza,
H-4400 Nyíregyháza,
Sóstói street 31/b,
Hungary
E-mail: blahota.istvan@nye.hu
Abstract:
In this paper we investigate the saturation of norm convergence issues for regular matrix transform means in case of Walsh-Paley system. The main result is the observation of equality ||σTn (f) - f ||p=0(a)n where an sequence of positive numbers tends to zero and there exists constant $c$, for which t1,n≤ can for every n∈P.
Paper's Title:
On a Novel Class of Advanced Integrals of MacRobert Type Incorporating Generalized Hypergeometric Functions
Author(s):
Shwetha S Shetty and Shantha Kumari Kurumujji
Department of Mathematics, A J Institute
of Engineering and Technology,
(Affiliated to Visvesvaraya Technological University (VTU), Belagavi),
Mangaluru, Karnataka,
India.
E-mail: shwethashetty576@gmail.com,
shanthakk99@gmail.com
Abstract:
The main objective of this study is to evaluate two master formulas expressed as integrals over the interval from zero to π/2. These integrals involve exponential functions and trigonometric functions sine and cosine, along with 3F2 hypergeometric functions parameterized by general variables i and j, where i = j = 0, ± 1, ± 2, .... From these master formulas, we derive twenty-six MacRobert-type integrals by evaluating them at specific values of i and j. The results are expressed using Gamma functions. The findings given here are derived from summation formulas for the series 4 F3 obtained recently by Choi and Rathie along with a general result attributed to MacRobert.
Paper's Title:
Nonlinear Elliptic Problems
Author(s):
Alexander G. Ramm
Department of Mathematics,
Kansas State University,
Manhattan, KS 66506-2602,
USA.
E-mail: ramm@ksu.edu
Abstract:
Let h(u)>0 be a smooth monotonically growing function, limu->∞h(u)|u|^-1=+∞, f(x)≥ 0 is bounded. Consider a nonlinear elliptic problem -Δ u=h(u)+f in D⊂ R3, D is a bounded domain with a smooth boundary S, u=0 on S. We prove the existence of a solution to this problem.
Paper's Title:
Viscosity Approximation Methods for Split Monotone Variational Inclusions and Fixed Point Problems of a Finite Family of ξ-Demimetric Mappings
Author(s):
Prashant Patel and Rahul Shukla
Department of Mathematics,
School of Advanced Sciences,
VIT-AP University, Inavolu,
Beside AP Secretariat,
Amaravati, 522237,
Andhra Pradesh,
India.
E-mail: prashant.patel9999@gmail.com,
prashant.p@vitap.ac.in
Department of Mathematical Sciences & Computing,
Walter Sisulu University,
Mthatha 5117,
South Africa.
E-mail: rshukla@wsu.ac.za
Abstract:
In this paper, we study viscosity approximation methods and present a new algorithm to find a common element of the fixed point of a finite family of ξ-demimetric mappings and the set of solutions of split monotone variational inclusion problem in Hilbert spaces. Under some conditions, we prove a strong convergence theorem which converges to this common solution.
Paper's Title:
Fixed Point Results for Integral Type Contractions in R-Metric Space
Author(s):
Samriddhi Ghosh, Ramakant Bhardwaj, Ritu Shrivastava, Vandana Rathore, Satyendra Narayan
Department of Mathematics,
Amity University, Kolkata, West Bengal,
India.
E-mail: ritha98@gmail.com
Department of Mathematics,
Amity University, Kolkata, West Bengal,
India.
E-mail: drrkbhardwaj100@gmail.com
Department of Mathematics,
Bahrain Polytechnic, Isa Town,
Kingdom of Bahrain
E-mail: ritu.shrivastava@polytechnic.bh
Faculty of Science and Technology,
Jagran Lakecity University, Bhopal, Madhya Pradesh,
India.
E-mail: drvandana@jlu.edu.in
School of Computer Science and
Technology,
Algoma University, Brampton, Ontario,
Canada.
E-mail: narayan.satyendra@gmail.com
Abstract:
The main aim of the research is to establish some invariant point (fixed point) results under the purview of R-Metric Spaces, for integral type R-contractive mappings. To serve this purpose, concepts of R-continuity, R-convergence and R-preservation has been used. Finally, the obtained results has been used to deduce some invariant point results for Banach, Kannan and Chatterjea type mappings in R-Metric Space. Also some examples and applications have been illustrated to support the findings discussed.
Search and serve lasted 0 second(s).