|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Global Analysis on Riemannian Manifolds
Author(s):
Louis Omenyi and Michael Uchenna
Department of Mathematics, Computer
Science, Statistics and Informatics,
Alex Ekwueme Federal University, Ndufu-Alike,
Nigeria.
E-mail: omenyi.louis@funai.edu.ng,
michael.uchenna@funai.edu.ng
URL: http://www.funai.edu.ng
Abstract:
In this paper, an exposition of the central concept of global analysis on a Riemannan manifold is given. We extend the theory of smooth vector fields from open subsets of Euclidean space to Riemannan manifolds. Specifically, we prove that a Riemannian manifold admits a unique solution for a system of ordinary differential equations generated by the flow of smooth tangent vectors. The idea of partial differential equations on Riemannian manifold is highlighted on the unit sphere.
Paper's Title:
Optimization Techniques on Affine Differential Manifolds
Author(s):
Ali S Rasheed, Faik Mayah and Ahmed A H AL-Jumaili
Ministry of Higher Education and
Scientific Research,
Iraq.
E-mail: ahmedhashem@gmail.com
Department of Physics, College of
Sciences,
University of Wasit,
Iraq.
E-mail: faik.mayah@gmail.com
Abstract:
In addition to solid ground of Riemannian manifolds fundamentals, this article interviews some popular optimization methods on Riemannian manifolds. Several optimization problems can be better stated on manifolds rather than Euclidean space, such as interior point methods, which in turns based on self-concordant functions (logarithmic barrier functions). Optimization schemes like the steepest descent scheme, the Newton scheme, and others can be extended to Riemannian manifolds. This paper introduces some Riemannian and non-Riemannian schemes on manifolds.
Paper's Title:
Constraint Qualifications for Multiobjective Programming Problems on Hadamard Manifolds
Author(s):
Arnav Ghosh, Balendu Bhooshan Upadhyay and I.M. Stancu-Minasian
Department of Mathematics,
Indian Institute of Technology Patna,
Patna,
India.
E-mail: arnav_2021ma09@iitp.ac.in
Department of Mathematics,
Indian Institute of Technology Patna,
Patna,
India.
E-mail: bhooshan@iitp.ac.in
"Gheorghe Mihoc-Caius Iacob" Institute of
Mathematical Statistics and Applied Mathematics of the Romanian Academy,
Bucharest,
Romania.
E-mail: stancu_minasian@yahoo.com
Abstract:
The study of optimization methods on manifolds has emerged as an immensely significant topic in mathematics due its ubiquitous applicability as well as various computational advantages associated with it. Motivated by this fact, the present article is devoted to the study of a class of constrained multiobjective programming problems (MOPP) in the framework of Hadamard manifolds. We present the generalized Guignard constraint qualification (GGCQ) in the framework of Hadamard manifolds for (MOPP). Employing (GGCQ), we derive Karush-Kuhn-Tucker type necessary optimality criteria for (MOPP). Moreover, we present several other constraint qualifications (CQs) on Hadamard manifolds, namely, Abadie's CQ, generalized Abadie's CQ, Cottle-type CQ, Slater-type CQ, linear CQ, linear objective CQ and Mangasarian-Fromovitz CQ. Further, we establish various relations between these constraint qualifications. In particular, we show that these constraint qualifications, in turn, become sufficient conditions ensuring that (GGCQ) is satisfied.
Paper's Title:
Semivectorial Bilevel Optimization on Affine-Finsler-Metric Manifolds
Author(s):
Faik Mayah1, Ali S Rasheed2 and Naseif J. Al- Jawari3
1Department of Physics,
College of Sciences,
University of Wasit,
Iraq.
E-mail: faik.mayah@gmail.com
2Ministry of Higher Education and Scientific Research,
Iraq.
E-mail: ali.math2018@yahoo.com
ahmedhashem@gmail.com
3Dept.
of Mathematics,
College of Science,
Mustansiriyah University, Baghdad,
Iraq.
E-mail: nsaif642014@yahoo.com
Abstract:
A Finsler manifold is a differential manifold together with a Finsler metric, in this paper we construct a new class of Finsler metric affine manifolds on bilevel semivectorial with optimization problems. The first steps for this purpose involve the study of bilevel optimization on affine manifolds. The bilevel programming problem can be viewed as a static version of the noncooperative, two-person game which was introduced in the context of unbalanced economic markets. Bilevel optimization is a special kind of optimization where one problem is embedded within another.
Paper's Title:
Applications of Von Neumann Algebras to Rigidity Problems of (2-Step) Riemannian (Nil-)Manifolds
Author(s):
Atefeh Hasan-Zadeh and Hamid-Reza Fanai
DFouman Faculty of Engineering,
College of Engineering, University of Tehran,
Iran.
E-mail: hasanzadeh.a@ut.ac.ir
Department of Mathematical Sciences,
Sharif University of Technology,
Iran
E-mail: fanai@sharif.edu
Abstract:
In this paper, basic notions of von Neumann algebra and its direct analogues in the realm of groupoids and measure spaces have been considered. By recovering the action of a locally compact Lie group from a crossed product of a von Neumann algebra, other proof of one of a geometric propositions of O'Neil and an extension of it has been proposed. Also, using the advanced exploration of nilmanifolds in measure spaces and their corresponding automorphisms (Lie algebraic derivations) a different proof of an analytic theorem of Gordon and Mao has been attained. These two propositions are of the most important ones for rigidity problems of Riemannian manifolds especially 2-step nilmanifolds.
Paper's Title:
Introducing the Dorfmanian: A Powerful Tool for the Calculus Of Variations
Author(s):
Olivier de La Grandville
Department of Management Science and Engineering,
Stanford University,
475 Via Ortega, Stanford, CA 94305,
U. S. A.
E-mail: odelagrandville@gmail.com
Abstract:
We show how a modified Hamiltonian proposed by Robert Dorfman [1] to give intuitive sense
to the Pontryagin maximum principle can be extended to easily obtain all
high-order equations of the calculus of variations. This new concept is
particularly efficient to determine the differential equations leading to
the extremals of functionals defined by n-uple integrals, while a
traditional approach would require -- in some cases repeatedly -- an
extension of Green's theorem to n-space.
Our paper is dedicated to the memory of Robert Dorfman (1916 - 2002).
Paper's Title:
Existence, Global Regularity and Uniqueness of Solutions of the Navier-Stokes Equations in Space Dimension 3 when the Initial Data are Regular
Author(s):
Moulay D. Tidriri
Email: mtctyasa@gmail.com
Abstract:
The existence, regularity, and uniqueness of global solutions of the Navier-Stokes
equations in
are given for when the initial velocity
for all integers q ≥ 0 and div u0
= 0.
Paper's Title:
Ergodic Solenoidal Homology II:
Density of Ergodic Solenoids
Author(s):
Vicente Muñoz and Ricardo Pérez Marco
Instituto de Ciencias Matem
áticas CSIC-UAM-UC3M-UCM,Abstract:
A measured solenoid is a laminated space endowed with a tranversal measure invariant by holonomy. A measured solenoid immersed in a smooth manifold produces a closed current (known as a generalized Ruelle-Sullivan current). Uniquely ergodic solenoids are those for which there is a unique (up to scalars) transversal measure. It is known that for any smooth manifold, any real homology class is represented by a uniquely ergodic solenoid. In this paper, we prove that the currents associated to uniquely ergodic solenoids are dense in the space of closed currents, therefore proving the abundance of such objects.
Paper's Title:
Application of Equivalence Method to Classify Monge-Ampère Equations of Elliptic Type
Author(s):
Moheddine Imsatfia
E-mail: imsatfia@math.jussieu.fr
Abstract:
In this paper, we apply Cartan's equivalence method to give a local classification of Monge-Ampère equations of elliptic type. Then we find a necessary and sufficient conditions such that a Monge-Ampère equation is either contactomorphic to the Laplace equation or to an Euler-Lagrange equation.
Paper's Title:
Certain Coefficient Estimates for Bi-univalent Sakaguchi Type Functions
Author(s):
B. Srutha Keerthi, S. Chinthamani
Department of Applied Mathematics,
Sri Venkateswara College of Engineering,
Sriperumbudur, Chennai - 602105,
India
Abstract:
Estimates on the initial coefficients are obtained for normalized analytic functions f in the open unit disk with f and its inverse g = f-1 satisfying the conditions that zf'(z) / f(z) and zg'(z) / g(z) are both subordinate to a starlike univalent function whose range is symmetric with respect to the real axis. Several related classes of functions are also considered, and connections to earlier known results are made.
Paper's Title:
Countable Ordinal Spaces and Compact Countable Subsets of a Metric Space
Author(s):
B. Alvarez-Samaniego, A. Merino
Nucleo de Investigadores Cientificos
Facultad de Ciencias,
Universidad Central del Ecuador (UCE)
Quito,
Ecuador.
E-mail: borys_yamil@yahoo.com,
balvarez@uce.edu.ec
Escuela de Ciencias Fisicas y Matematica
Facultad de Ciencias Exactas y Naturales
Pontificia Universidad Catolica del Ecuador
Apartado: 17-01-2184, Quito,
Ecuador.
E-mail: aemerinot@puce.edu.ec
Abstract:
We show in detail that every compact countable subset of a metric space is homeomorphic to a countable ordinal number, which extends a result given by Mazurkiewicz and Sierpinski for finite-dimensional Euclidean spaces. In order to achieve this goal, we use Transfinite Induction to construct a specific homeomorphism. In addition, we prove that for all metric space, the cardinality of the set of all the equivalence classes, up to homeomorphisms, of compact countable subsets of this metric space is less than or equal to aleph-one. We also show that for all cardinal number smaller than or equal to aleph-one, there exists a metric space with cardinality equals the aforementioned cardinal number.
Paper's Title:
Quantitative Estimates for Positive Linear Operators Obtained by Means of Piecewise Linear Functions
Author(s):
Vasile Mihesan
Technical University of Cluj-Napoca,
Department of Mathematics,
Str. C. Daicoviciu 15,
Cluj-Napoca,
Romania
Vasile.Mihesan@math.utcluj.ro
Abstract:
In this paper we obtain estimates for the remainder in approximating continuous
functions by positive linear operators, using piecewise linear functions.
Paper's Title:
The Voronovskaja Type Theorem for the Stancu Bivariate
Operators
Author(s):
Ovidiu T. Pop
National College "Mihai Eminescu",
5 Mihai Eminescu Street,
Satu Mare 440014, Romania
Vest University "Vasile Goldis" of
Arad, Branch of Satu Mare,
26 Mihai Viteazul Street
Satu Mare 440030, Romania
ovidiutiberiu@yahoo.com
Abstract:
In this paper, the Voronovskaja type theorem for the Stancu
bivariate operators is established. As particular cases, we shall
obtain the Voronovskaja type theorem for the Bernstein and Schurer
operators.
Paper's Title:
Subordination Results Associated with Hadamard Product
Author(s):
S. Sivasubramanian, C. Ramachandran and B. A. Frasin
Department of Mathematics,
University College of Engineering,
Anna University,
Saram-604 307,
India
Department of Mathematics,
University College of Engineering,
Anna University,
Villupuram,
India
Department of Mathematics,
Al al-Bayt University,
P.O. Box: 130095 Mafraq,
Jordan
Abstract:
In the present investigation, we consider an unified class of functions of complex order using Hadamard's convolution. We obtain a necessary and sufficient condition for functions to be in these classes.
Paper's Title:
Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Some Inequalities of the Hermite-Hadamard Type for k-Fractional Conformable Integrals
Author(s):
C.-J. Huang, G. Rahman, K. S. Nisar, A. Ghaffar and F. Qi
Department of Mathematics, Ganzhou Teachers College,
Ganzhou 341000, Jiangxi,
China.
E-mail:
hcj73jx@126.com ,
huangcj1973@qq.com
Department of Mathematics, Shaheed Benazir
Bhutto University,
Sheringal, Upper Dir, Khyber Pakhtoonkhwa,
Pakistan.
E-mail: gauhar55uom@gmail.com
Department of Mathematics, College of Arts
and Science at Wadi Aldawaser, 11991,
Prince Sattam Bin Abdulaziz University, Riyadh Region,
Kingdom of Saudi Arabia.
E-mail: n.sooppy@psau.edu.sa,
ksnisar1@gmail.com
Department of Mathematical Science,
Balochistan University of Information Technology,
Engineering and Management Sciences, Quetta,
Pakistan.
E-mail: abdulghaffar.jaffar@gmail.com
School of Mathematical Sciences, Tianjin
Polytechnic University,
Tianjin 300387,
China; Institute of Mathematics,
Henan Polytechnic University, Jiaozuo 454010, Henan,
China.
E-mail: qifeng618@gmail.com,
qifeng618@qq.com
Abstract:
In the paper, the authors deal with generalized k-fractional conformable integrals, establish some inequalities of the Hermite-Hadamard type for generalized k-fractional conformable integrals for convex functions, and generalize known inequalities of the Hermite-Hadamard type for conformable fractional integrals.
Paper's Title:
Inequalities for Functions of Selfadjoint Operators on Hilbert Spaces:
a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
College of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning inequalities for continuous functions of selfadjoint operators on complex Hilbert spaces. It is intended for use by both researchers in various fields of Linear Operator Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Differential Sandwich Theorems for Some Subclasses of Analytic Functions
Author(s):
T. N. Shanmugam, V. Ravichandran and S. Sivasubramanian
Department of Mathematics, College of Engineering,
Anna university, Chennai 600 025,
India
shan@annauniv.edu
URL: http://www.annauniv.edu/shan
School of Mathematical Sciences,
Universiti Sains Malaysia,
11800 USM Penang,
Malaysia
vravi@cs.usm.my
URL: http://cs.usm.my/~vravi
Department of Mathematics, Easwari Engineering college,
Ramapuram, Chennai 600 089,
India
sivasaisastha@rediffmail.com
Abstract:
Let 
and 
be univalent in 
with 
We give some applications of first order differential subordination and superordination to obtain sufficient conditions for normalized analytic function 
with 
to satisfy 
Paper's Title:
On Pseudo Almost
Periodic Solutions to Some Neutral Functional-Differential
Equations
Author(s):
Toka Diagana and Eduardo Hernández
Department of Mathematics, Howard University
2441 6th Street NW,
Washington DC 20059,
USA.
tdiagana@howard.edu
Departamento de Matemática, I.C.M.C. Universidade de São Paulo,
Caixa Postal
668, 13560-970, São Carlos SP,
Brazil.
lalohm@icmc.sc.usp.br
Abstract:
This paper discusses the existence and uniqueness of pseudo almost periodic solutions to a class of partial neutral functional-differential equations. Under some suitable assumptions, existence and uniqueness results are obtained. An example is given to illustrate abstract results.
Paper's Title:
Inequalities for
the
Author(s):
S. S. Dragomir
School of Engineering and Science
Victoria University, PO 14428
Melbourne City MC,
Victoria 8001,
Australia
sever.dragomir@vu.edu.au
URL: http://www.staff.vu.edu.au/RGMIA/dragomir/
Abstract:
Some recent inequalities for the Čebyšev functional of two functions of selfadjoint linear operators in Hilbert spaces, under suitable assumptions for the involved functions and operators, are surveyed.
Paper's Title:
Good and Special Weakly Picard Operators for the Stancu Operators with Modified Coefficients
Author(s):
Loredana-Florentina Galea and Alexandru-Mihai Bica
The Agora University of Oradea,
Piata Tineretului no. 8,
410526, Oradea,
Romania
University of Oradea,
Str. Universitatii No. 1,
410087, Oradea,
Romania
loredana.galea@univagora.ro
smbica@yahoo.com
abica@uoradea.ro
Abstract:
In this paper some properties of good and special weakly Picard operators for the Stancu operators with modified coefficients are obtained. In the study of the sequence of iterates of these operators, we obtain the property of dual monotone iteration.
Paper's Title:
An Efficient Modification of Differential Transform Method for Solving Integral and Integro-differential Equations
Author(s):
S. Al-Ahmad, Ibrahim Mohammed Sulaiman*, and M. Mamat
Faculty of Informatics and Computing,
Universiti Sultan Zainal Abidin,
Terengganu, Besut Campus, 22200,
Malaysia.
E-mail: Alahmad.shadi@yahoo.com,
*sulaimanib@unisza.edu.my,
must@unisza.edu.my
Abstract:
In this paper, classes of integral and integro-differential equations are solved using a modified differential transform method. This proposed technique is based on differential transform method (DTM), Laplace transform (LT) procedure and Pad\'{e} approximants (PA). The proposed method which gives a good approximation for the true solution in a large region is referred to modified differential transform method (MDTM). An algorithm was developed to illustrate the flow of the proposed method. Some numerical problems are presented to check the applicability of the proposed scheme and the obtained results from the computations are compared with other existing methods to illustrates its efficiency. Numerical results have shown that the proposed MDTM method is promising compared to other existing methods for solving integral and integro-differential equations.
Paper's Title:
Coexisting Attractors and Bubbling Route to Chaos in Modified Coupled Duffing Oscillators
Author(s):
B. Deruni1, A. S. Hacinliyan1,2, E. Kandiran3, A. C. Keles2, S. Kaouache4, M.-S. Abdelouahab4, N.-E. Hamri4
1Department
of Physics,
University of Yeditepe,
Turkey.
2Department
of Information Systems and Technologies,
University of Yeditepe,
Turkey
3Department
of Software Development,
University of Yeditepe,
Turkey.
4Laboratory
of Mathematics and their interactions,
University Center of Abdelhafid Boussouf,
Mila 43000,
Algeria.
E-mail:
berc890@gmail.com
ahacinliyan@yeditepe.edu.tr
engin.kandiran@yeditepe.edu.tr
cihan.keles@yeditepe.edu.tr
s.kaouache@centr-univ-mila.dz
medsalah3@yahoo.fr
n.hamri@centre-univ-mila.dz
Abstract:
In this article dynamical behavior of coupled Duffing oscillators is analyzed under a small modification. The oscillators have cubic damping instead of linear one. Although single duffing oscillator has complex dynamics, coupled duffing systems possess a much more complex structure. The dynamical behavior of the system is investigated both numerically and analytically. Numerical results indicate that the system has double scroll attractor with suitable parameter values. On the other hand, bifurcation diagrams illustrate rich behavior of the system, and it is seen that, system enters into chaos with different routes. Beside classical bifurcations, bubbling route to chaos is observed for suitable parameter settings. On the other hand, Multistability of the system is indicated with the coexisting attractors, such that under same parameter setting the system shows different periodic and chaotic attractors. Moreover, chaotic synchronization of coupled oscillators is illustrated in final section.
Paper's Title:
A Determinantal Representation of Core EP Inverse
Author(s):
Divya Shenoy Purushothama
Department of Mathematics,
Manipal Institute of Technology,
Manipal Academy of Higher Education,
Manipal -576104, Karnataka,
India.
E-mail: divya.shenoy@manipal.edu
URL:
https://manipal.edu/mit/department-faculty/faculty-list/divya-shenoy-p.html
Abstract:
The notion of Core EP inverse is introduced by Prasad in the article "Core - EP inverse" and proved its existence and uniqueness. Also, a formula for computing the Core EP inverse is obtained from particular linear combination of minors of a given matrix. Here a determinantal representation for Core EP inverse of a matrix A with the help of rank factorization of A is obtained.
Paper's Title:
Parameter dependence of the solution of second order nonlinear ODE's via Perov's fixed point theorem
Author(s):
A. M. Bica, S. Muresan and G. Grebenisan
University of Oradea,
Str. Armatei Romane no.5, 410087,
Oradea, Romania.
smbica@yahoo.com
smuresan@uoradea.ro
grebe@uoradea.ro
Abstract:
Using the Perov's fixed point theorem, the smooth dependence by parameter of
the solution of a two point boundary value problem corresponding to nonlinear
second order ODE's is obtained.
Paper's Title:
On the Fekete-Szeg
Author(s):
T.N. Shanmugam and A. Singaravelu
Department of Mathematics,
Department of Mathematics,
College of Engineering,
Anna University, Chennai-600 025,
Tamilnadu, India
shan@annauniv.edu
Valliammai Engineering College,
Chennai-603 203,
Tamilnadu, India
sivasaisastha@rediffmail.com
Abstract:
In this present investigation, the authors obtainFekete-Szegő's inequality for certain normalized analytic functions 
defined on the open
unit disk for which 
lie in a region starlike with
respect to 1 and symmetric with respect
to the real axis. Also certain applications of the main result for a class of functions
defined by convolution are given. As a special case of this result, Fekete-Szegő's inequality for a class of functions
defined through fractional derivatives is also obtained.
Paper's Title:
Existence of solutions for Neutral Stochastic Functional Differential Systems with Infinite Delay in Abstract Space
Author(s):
P. Balasubramaniam, A. V. A. Kumar and S. K. Ntouyas
Department of Mathematics, Gandhigram Rural Institute,
Deemed University, Gandhigram - 624 302,
Tamil Nadu, India.
pbalgri@rediffmail.com
Department of Mathematics, Gandhigram Rural Institute,
Deemed University, Gandhigram - 624 302,
Tamil Nadu, India.
nnddww@tom.com
Department of Mathematics, University of Ioannina,
451 10 Ioannina,
Greece.
sntouyas@cc.uoi.gr
URL: http://www.math.uoi.gr/~sntouyas
Abstract:
In this paper we prove existence results for semilinear stochastic neutral functional differential systems with unbounded delay in abstract space. Our theory makes use of analytic semigroups and fractional power of closed operators and Sadovskii fixed point theorem.
Paper's Title:
Some Inequalities for a Certain Class of Multivalent Functions
Using Multiplier Transformation
Author(s):
K. Suchithra, B. Adolf Stephen, A. Gangadharan and S. Sivasubramanian
Department Of Applied Mathematics
Sri Venkateswara College Of Engineering
Sriperumbudur, Chennai - 602105,
India.
suchithravenkat@yahoo.co.in
Department Of Mathematics,
Madras Christian College
Chennai - 600059,
India.
adolfmcc2003@yahoo.co.in
Department Of Applied Mathematics
Sri Venkateswara College Of Engineering
Sriperumbudur, Chennai - 602105,
India.
ganga@svce.ac.in
Department Of Mathematics,
Easwari Engineering College
Ramapuram, Chennai - 600089,
India.
ganga@svce.ac.in
Abstract:
The object of the present paper is to derive several inequalities
associated with differential subordinations between analytic functions
and a linear operator defined for a certain family of p-valent
functions, which is introduced here by means of a family of extended
multiplier transformations. Some special cases and consequences of
the main results are also considered.
Paper's Title:
A Study of the Effect of Density Dependence in a Matrix Population Model
Author(s):
N. Carter and M. Predescu
Department of Mathematical Sciences,
Bentley University,
Waltham, MA 02452,
U.S.A.
ncarter@bentley.edu
mpredescu@bentley.edu
Abstract:
We study the behavior of solutions of a three dimensional discrete time nonlinear matrix population model. We prove results concerning the existence of equilibrium points, boundedness, permanence of solutions, and global stability in special cases of interest. Moreover, numerical simulations are used to compare the dynamics of two main forms of the density dependence function (rational and exponential).
Paper's Title:
Neighborhoods of Certain Subclasses of Analytic Functions of Complex Order with Negative Coefficients
Author(s):
B. Srutha Keerthi, B. Adolf Stephen, A. Gangadharan, and S. Sivasubramanian
Department of Applied Mathematics,
Sri Venkateswara College of Engineering,
Sriperumbudur, Chennai - 602105,
India.
sruthilaya06@yahoo.co.in
Department of Mathematics,
Madras Christian College,
Chennai - 600059,
India
adolfmcc2003@yahoo.co.in
Department of Applied Mathematics,
Sri Venkateswara College of Engineering,
Sriperumbudur, Chennai - 602105,
India.
ganga@svce.ac.in
Department of Mathematics,
Easwari Engineering College,
Ramapuram, Chennai - 600089,
India
sivasaisastha@rediffmail.com
Abstract:
The main object of this paper is to prove several inclusion relations associated with the (n, δ) neighborhoods of various subclasses of convex functions of complex order by making use of the known concept of neighborhoods of analytic functions.
Paper's Title:
Sharp Lp Improving Results for Singular Measures on Cn+1
Author(s):
E. Ferreyra, M. Urciuolo
FaMAF-CIEM,
Universidad Nacional de Córdoba-Conicet,
Ciudad Universitaria, 5000 Córdoba,
Argentina
eferrey@famaf.unc.edu.ar
urciuolo@famaf.unc.edu.ar
Abstract:
For j=1,...,n, let Ωj be open sets of the complex plane and let φj be holomorphic functions on Ωj such that φj'' does not vanish identically on Ωj. We consider φ(z1,...,zn) =φ1(z1) +...+φn(zn). We characterize the pairs (p,q) such that the convolution operator with the surface measure supported on a compact subset of the graph of φ is p-q bounded.
Paper's Title:
Fejér-type Inequalities
Author(s):
Nicuşor Minculete and Flavia-Corina Mitroi
"Dimitrie Cantemir" University,
107 Bisericii Române Street, Braşov, 500068,
România
minculeten@yahoo.com
University of Craiova, Department of Mathematics,
Street A. I. Cuza
13, Craiova, RO-200585,
Romania
fcmitroi@yahoo.com
Abstract:
The aim of this paper is to present some new Fejér-type results for convex functions. Improvements of Young's inequality (the arithmetic-geometric mean inequality) and other applications to special means are pointed as well.
Paper's Title:
Lower and Upper Bounds for the Point-Wise Directional Derivative of the Fenchel Duality Map
Author(s):
M. Raissouli1,2, M. Ramezani3
1Department
of Mathematics,
Science Faculty, Taibah University,
P.O. Box 30097, Zip Code 41477, Al Madinah Al Munawwarah,
Saudi Arabia.
2Department
of Mathematics,
Science Faculty, Moulay Ismail University, Meknes,
Morocco.
E-mail:
raissouli.mustapha@gmail.com
3Department
of Mathematics,
University of Bojnord, Bojnord,
Iran.
E-mail: m.ramezani@ub.ac.ir
Abstract:
In this paper, we introduce the point-wise directional derivative of the Fenchel duality map and we study its properties. The best lower and upper bounds of this point-wise directional derivative are also given. We explain how our functional results contain those related to the positive bounded linear operators.
Paper's Title:
Wavelet Frames in Higher Dimensional Sobolev Spaces
Author(s):
Raj Kumar, Manish Chauhan, and Reena
Department of Mathematics,
Kirori Mal College, University of Delhi,
New Delhi-110007,
India.
E-mail: rajkmc@gmail.com
Department of Mathematics,
University of Delhi,
New Delhi-110007,
India
E-mail: manish17102021@gmail.com
Department of Mathematics,
Hans Raj College, University of Delhi,
New Delhi-110007,
India
E-mail: reena.bhagwat29@gmail.com
Abstract:
In this paper, we present sufficient condition for the sequence
of vectors
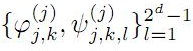to be a frame for Hs(Rd) are derived. Necessary and
sufficient conditions for the sequence of vectors
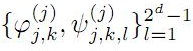to be tight wavelet frames in Hs(Rd) are obtained.
Further, as an application an example of tight wavelet frames for Hs(R2) as bivariate box spline over 3-direction are given.
Paper's Title:
Cubic Alternating Harmonic Number Sums
Author(s):
Anthony Sofo
Victoria University,
College of Engineering and Science,
Melbourne City,
Australia.
E-mail:
Anthony.Sofo@vu.edu.au
Abstract:
We develop new closed form representations of sums of cubic alternating harmonic numbers and reciprocal binomial coefficients. We also identify a new integral representation for the ζ (4) constant.
Paper's Title:
Jordan Canonical Form of Interval Matrices and Applications
Author(s):
S. Hema Surya, T. Nirmala and K. Ganesan
Department of Mathematics, College of
Engineering and Technology,
SRM Institute of Science and Technology,
Kattankulathur,
Chennai-603203,
India.
E-mail: nirmalat@srmist.edu.in
URL:
https://www.srmist.edu.in/faculty/dr-t-nirmala/
Abstract:
A square interval matrix over R can be converted to diagonal form if certain prerequisites are satisfied. However not all square matrices can be diagonalized. As a consequence, we strive the next simplest form to which it can be reduced while retaining important properties such as eigenvalues, rank, nullity, and so on. It turns out that any real interval matrix has a Jordan Canonical Form (JCF) over E if it has n interval eigenvalues in IR. We discuss in this paper a method for computing the Jordan canonical form of an interval matrix using a new pairing technique and a new type of interval arithmetic that will make classifying and analyzing interval matrices easier and more efficient. We conclude with a numerical example that supports the theory and application of predator-prey model.
Paper's Title:
On Sufficient Conditions for Strong Starlikeness
Author(s):
V. Ravichandran, M. H. Khan, M. Darus, And
K. G. Subramanian School of Mathematical Sciences, Universiti Sains Malaysia,
11800 Usm Penang, Malaysia
vravi@cs.usm.my
Url: http://cs.usm.my/~vravi/index.html
Department of Mathematics, Islamiah College, Vaniambadi 635 751, India
khanhussaff@yahoo.co.in
School of Mathematical Sciences, Faculty of Science and Technology, UKM, Bangi
43600,
Malaysia
maslina@pkrisc.cc.ukm.my
Url:
http://www.webspawner.com/users/maslinadarus
Department of Mathematics, Madras Christian College, Tambaram, Chennai 600 059,
India
kgsmani@vsnl.net
Abstract:
In the present investigation, we obtain some sufficient
conditions for a normalized analytic function f(z) defined on the unit disk to
satisfy the condition
Paper's Title:
Fekete-Szegö Inequality for Certain Class of Analytic Functions
Author(s):
V. Ravichandran, Maslina Darus, M. Hussain Khan, and K. G. Subramanian
School of
Mathematical Sciences, Universiti Sains Malaysia,
11800 Usm, Penang, Malaysia
vravi@cs.usm.my
School of
Mathematical Sciences, Faculty of Sciences and Technology,
Ukm, Banki 43600, Malaysia
maslina@pkrisc.cc.ukm.my
Department of
Mathematics, Islamiah College,
Vaniambadi 635 751, India
Department of
Mathematics, Madras Christian College, Tambaram,
Chennai- 600 059, India
kgsmani@vsnl.net
Abstract:
In this present investigation, the authors obtain Fekete-Szegö inequality for a certain
class of analytic functions f(z) for which
lies in a
region starlike with respect to 1 and symmetric with respect to the real axis. Also certain application
of our main result for a class of functions defined by Hadamard product (convolution) is
given. As a special case of our result we obtain Fekete-Szegö inequality for a class of functions
defined through fractional derivatives. Also we obtain Fekete-Szegö inequality for the inverse
functions.
Paper's Title:
Classes of Meromorphic p-valent Parabolic Starlike Functions with Positive Coefficients
Author(s):
S. Sivaprasad Kumar, V. Ravichandran, and G. Murugusundaramoorthy
Department of Applied Mathematics
Delhi College of Engineering,
Delhi 110042, India
sivpk71@yahoo.com
School of Mathematical Sciences
Universiti Sains Malaysia
11800 USM Penang
Malaysia
vravi@cs.usm.my
URL: http://cs.usm.my/~vravi
Department of Mathematics
Vellore Institute of Technology (Deemed University)
Vellore 632 014, India
gmsmoorthy@yahoo.com
Abstract:
In the present paper, we consider two general subclasses of meromorphic p-valent starlike functions with positive coefficients and obtain a necessary and sufficient condition for functions to be in these classes. Also we obtain certain other related results as a consequences of our main results.
Paper's Title:
The successive approximations method and error estimation in terms of at most the first derivative for delay ordinary differential equations
Author(s):
Alexandru Mihai Bica
Department of Mathematics,
University of Oradea,
Str. Armatei Romane no.5,
410087, Oradea,
Romania
smbica@yahoo.com
abica@uoradea.ro
Abstract:
We present here a numerical method for first order delay ordinary differential
equations, which use the Banach's fixed point theorem, the sequence of
successive approximations and the trapezoidal quadrature rule. The error
estimation of the method uses a recent result of P. Cerone and S.S. Dragomir
about the remainder of the trapezoidal quadrature rule for Lipchitzian
functions and for functions with continuous first derivative.
Paper's Title:
Two Mappings Related to Steffensen's Inequalities
Author(s):
Liang-Cheng Wang
School of Mathematical Science,
Chongqing Institute of Technology,
Xingsheng Lu 4,
Yangjiaping 400050, Chongqing City,
China.
wangliangcheng@163.com
Abstract:
In this paper, we define two mappings closely connected with
Steffensen's inequalities, investigate their main properties,
give some refinements for Steffensen's inequalities and obtain new
inequalities.
Paper's Title:
An Easy and Efficient Way for Solving A class of Singular Two Point Boundary Value Problems
Author(s):
Muhammed I. Syam, Muhammed N. Anwar and Basem S. Attili
Mathematical Sciences Department
United Arab Emirates University, P. O. Box 17551
Al-Ain, United Arab Emirates
b.attili@uaeu.ac.ae
Abstract:
We will consider an efficient and easy way for solving a certain
class of singular two point boundary value problems. We will
employ the least squares method which proved to be efficient for
this type of problems. Enough examples that were considered by
others will be solved with comparison with the results presented
there.
Paper's Title:
Komatu Integral Transforms of Analytic Functions Subordinate to Convex Functions
Author(s):
T. N. Shanmugam and C. Ramachandran
Department of Mathematics, College of Engineering,
Anna University, Chennai-600 025, Tamilnadu,
India
shan@annauniv.edu
Department of Mathematics, College of Engineering,
Anna University, Chennai-600 025, Tamilnadu,
India
crjsp2004@yahoo.com
Abstract:
In this paper, we consider the class A of the functions f(z) of the form
which are analytic in an open disk
has some property. Certain inclusion and the closure properties like convolution with convex univalent function etc. are studied.
and study certain subclass of the class A, for which
Paper's Title:
On Sandwich Theorems for Certain Subclass of Analytic Functions Involving Dziok-Srivastava Operator
Author(s):
T. N. Shanmugam, M. P. Jeyarama and A. Singaravelu
Department of Mathematics
College of Engineering, Anna University
Chennai - 600 025,
India
drtns2001@yahoo.com
Department of Mathematics
Easwari Engineering College
Ramapuram, Chennai - 600089
Tamilnadu, India
jeyaraman-mp@yahoo.co.i
Department of Mathematics
Valliammai Engineering College
Chennai - 603203
Tamilnadu, India.
asing-59@yahoo.com
Abstract:
The purpose of this present paper is to derive some subordination and superordination results for certain normalized analytic functions in the open unit disk, acted upon by Dziok-Srivastava operator. Relevant connections of the results, which are presented in this paper, with various known results are also considered.
Paper's Title:
Long Correlations Applied to the Study of Agricultural Indices in Comparison with the S&P500 index
Author(s):
M. C. Mariani, J. Libbin, M.P. Beccar Varela,
V. Kumar Mani, C. Erickson, D.J. Valles Rosales
Department of Mathematical Sciences,
Science Hall 236, New Mexico State University,
Las Cruces, NM 88003-8001,
USA.
mmariani@nmsu.edu
Abstract:
Long-time correlations in agricultural indices are studied and their behavior is compared to the well-established S&P500 index. Hurst exponent and Detrended Fluctuation Analysis (DFA) techniques are used in this analysis. We detected long-correlations in the agricultural indices and briefly discussed some features specific in comparison to the S&P500 index.
Paper's Title:
Hyperbolic Barycentric Coordinates
Author(s):
Abraham A. Ungar
Department of Mathematics, North Dakota State University,
Fargo, ND 58105,
USA
Abraham.Ungar@ndsu.edu
URL: http://math.ndsu.nodak.edu/faculty/ungar/
Abstract:
A powerful and novel way to study Einstein's special theory of relativity and its underlying geometry, the hyperbolic geometry of Bolyai and Lobachevsky, by analogies with classical mechanics and its underlying Euclidean geometry is demonstrated. The demonstration sets the stage for the extension of the notion of barycentric coordinates in Euclidean geometry, first conceived by Möbius in 1827, into hyperbolic geometry. As an example for the application of hyperbolic barycentric coordinates, the hyperbolic midpoint of any hyperbolic segment, and the centroid and orthocenter of any hyperbolic triangle are determined.
Paper's Title:
Superquadracity, Bohr's Inequality and Deviation from a Mean Value
Author(s):
S. Abramovich, J. Barić, and J. Pečarić
Department of Mathematics, University of Haifa,
Haifa, 31905,
Israel
FESB, University of Split,
Rudera Bošcovića,
B.B., 21000, Split,
Croatia
jbaric@fesb.hr
Faculty of Textile Technology,
University of Zagreb,
Prilaz Baruna Filipovića,
30, 10000 Zagreb,
Croatia.
pecaric@hazu.hr
Abstract:
Extensions of Bohr's inequality via superquadracity are obtained, where instead of the power p=2 which appears in Bohr's inequality we get similar results when we deal with p≥ 2 and with p≤ 2. Also, via superquadracity we extend a bound for deviation from a Mean Value.
Paper's Title:
On a Class of Uniformly Convex Functions Defined by Convolution with Fixed Coefficient
Author(s):
T. N. Shanmugam, S. Sivasubramanian, and G. Murugusundaramoorthy
Department of Mathematics,
College of Engineering,
Anna University,
Chennai - 600 025,
India.
drtns2001@yahoo.com
Department of Mathematics,
University College of Engineering,
Tindivanam
Anna University-Chennai,
Saram-604 703,
India.
sivasaisastha@rediffmail.com
School of Sciences and Humanities,
VIT University, Vellore-632 014,
India.
gmsmoorthy@yahoo.com
Abstract:
We define a new subclass of uniformly convex functions with negative and fixed second coefficients defined by convolution. The main object of this paper is to obtain coefficient estimates distortion bounds, closure theorems and extreme points for functions belong to this new class . The results are generalized to families with fixed finitely many coefficients.
Paper's Title:
Some Homogeneous Cyclic Inequalities of Three Variables of Degree Three and Four
Author(s):
TETSUYA ANDO
Department of Mathematics and Informatics,
Chiba University, Chiba 263-8522, JAPAN
ando@math.s.chiba-u.ac.jp
Abstract:
We shall show that the three variable cubic inequality
t2 (a3+b3+c3) + (t4-2t)(ab2+bc2+ca2)
≥ (2t3-1)(a2b+b2c+c2a)
+ (3t4-6t3+3t2-6t+3)abc
holds for non-negative a, b, c, and for any real number t.
We also show some similar three variable cyclic quartic inequalities.
Paper's Title:
A New Property of General Means of Order p with an Application to the Theory of Economic Growth
Author(s):
Olivier de La Grandville
Department of Management Science and Engineering,
Huang Engineering Center, Stanford University,
475 Via Ortega, Stanford, California 94305
U.S.A.
Abstract:
The purpose of this note is to demonstrate a new property of the
general mean of order p of m ordered positive numbers
.
If p < 0 and if
,
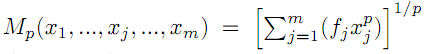
the elasticity of
with
respect to xm, defined by
,
tends towards zero, and therefore
.
This property is then applied to optimal growth theory.
Paper's Title:
A Differential Sandwich Theorem for Analytic Functions Defined by the
Generalized Sălăgean Operator
Author(s):
D. Răducanu and V. O. Nechita
Faculty of Mathematics and Computer
Science,
"Transilvania" University Braşov
Str. Iuliu Maniu 50, 500091 Braşov,
Romania
dorinaraducanu@yahoo.com
Faculty of Mathematics and Computer
Science,
"Babeş-Bolyai" University Cluj-Napoca,
Str. M. Kogalniceanu 1, 400084 Cluj-Napoca,
Romania
URL:
http://math.ubbcluj.ro/~vnechita/
vnechita@math.ubbcluj.ro
Abstract:
We obtain some subordination and superordination results involving the generalized Sălăgean differential operator for certain normalized analytic functions in the open unit disk. Our results extend corresponding previously known results.
Paper's Title:
Szegö Limits and Haar Wavelet Basis
Author(s):
M. N. N. Namboodiri and S. Remadevi
Dept. of Mathematics, Cochin University
of Science and Technology,
Cochin-21, Kerala,
India.
Dept. of Mathematics, College of
Engineering,
Cherthala, Kerala,
India.
Abstract:
This paper deals with Szegö type limits for multiplication operators on L2 (R) with respect to Haar orthonormal basis. Similar studies have been carried out by Morrison for multiplication operators Tf using Walsh System and Legendre polynomials [14]. Unlike the Walsh and Fourier basis functions, the Haar basis functions are local in nature. It is observed that Szegö type limit exist for a class of multiplication operators Tf , f∈ L∞ (R) with respect to Haar (wavelet) system with appropriate ordering. More general classes of orderings of Haar system are identified for which the Szegö type limit exist for certain classes of multiplication operators. Some illustrative examples are also provided.
Paper's Title:
Some Functional Inequalities for the Geometric Operator Mean
Author(s):
Mustapha Raissouli
Taibah University, Faculty of Sciences,
Department of Mathematics,
Al Madinah Al Munawwarah, P.O.Box 30097,
Kingdom of Saudi Arabia.
Abstract:
In this paper, we give some new inequalities of functional type for the power geometric operator mean involving several arguments.
Paper's Title:
Sufficient Conditions for Certain Types of Functions to be Parabolic Starlike
Author(s):
A. Gangadharan and S. Chinthamani
Department of Mathematics,
Easwari Engineering College,
Ramapuram, Chennai - 89,
India.
Research Scholar,
Anna University,
Chennai
E-mail: ganga.megalai@gmail.com
E-mail: chinvicky@rediffmail.com
Abstract:
In this paper sufficient conditions are determined for functions of
the form
and certain other types of functions to be parabolic starlike.
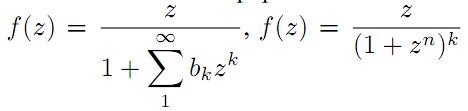
Paper's Title:
Polyanalytic Functions on Subsets of Z[i]
Author(s):
Abtin Daghighi
Linköping University,
SE-581 83,
Sweden.
E-mail: abtindaghighi@gmail.com
Abstract:
For positive integers q we consider the kernel of the powers Lq where L is one of three kinds of discrete analogues of the Cauchy-Riemann operator. The first two kinds are well-studied, but the third kind less so. We give motivations for further study of the third kind especially since its symmetry makes it more appealing for the cases q≥ 2.
From an algebraic perspective it makes sense that the chosen multiplication on the kernels is compatible with the choice of pseudo-powers. We propose such multiplications together with associated pseudo-powers. We develop a proof-tool in terms of certain sets of uniqueness.
Paper's Title:
Hankel Operators on Copson's Spaces
Author(s):
Nicolae Popa
Institute of Mathematics of Romanian Academy,
P.O. BOX 1-764
RO-014700 Bucharest,
Romania.
E-mail: Nicolae.Popa@imar.ro, npopafoc@gmail.com
Abstract:
We give a characterization of boundedness of a Hankel matrix, generated by a pozitive decreasing sequence, acting on Copson's space cop(2).
Paper's Title:
Sweeping Surfaces with Darboux Frame in Euclidean 3-space E3
Author(s):
F. Mofarreh, R. Abdel-Baky and N. Alluhaibi
Mathematical Science Department, Faculty
of Science,
Princess Nourah bint Abdulrahman University
Riyadh 11546,
Saudi Arabia.
E-mail: fyalmofarrah@pnu.edu.sa
Department of Mathematics, Faculty of Science,
University of Assiut,
Assiut 71516,
Egypt.
E-mail: rbaky@live.com
Department of Mathematics Science and
Arts, College Rabigh Campus,
King Abdulaziz University
Jeddah,
Saudi Arabia.
E-mail: nallehaibi@kau.edu.sa
Abstract:
The curve on a regular surface has a moving frame and it is called Darboux frame. We introduce sweeping surfaces along the curve relating to the this frame and investigate their geometrical properties. Moreover, we obtain the necessary and sufficient conditions for these surfaces to be developable ruled surfaces. Finally, an example to illustrate the application of the results is introduced.
Paper's Title:
Linear System of Singularly Perturbed Initial Value Problems with Robin Initial Conditions
Author(s):
S. Dinesh, G. E. Chatzarakis, S. L. Panetsos and S. Sivamani
Department of Mathematics,
Saranathan College of Engineering,
Tiruchirappalli-620012,
Tamil Nadu,
India.
Department of Electrical and Electronic
Engineering Educators,
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail:
geaxatz@otenet.gr,
dineshselvaraj24@gmail.com,
spanetsos@aspete.gr,
winmayi2012@gmail.com
Abstract:
On the interval (0,1], this paper considers an initial value problem for a system of n singularly perturbed differential equations with Robin initial conditions. On a piecewise uniform Shishkin mesh, a computational approach based on a classical finite difference scheme is proposed. This approach is shown to be first-order convergent in the maximum norm uniformly in the perturbation parameters. The theory is illustrated by a numerical example.
Paper's Title:
On the Equiform Geometry of the Involute-evolute Curve Couple in Hyperbolic and de Sitter Spaces
Author(s):
M. Khalifa Saad, H. S. Abdel-Aziz and A. A. Abdel-Salam
Department of Mathematics,
Faculty of Science,
Islamic University of Madinah,
KSA.
E-mail: mohammed.khalifa@iu.edu.sa
Department of Mathematics,
Faculty of Science,
Sohag University, Sohag,
EGYPT.
E-mail: habdelaziz2005@yahoo.com
Department of Mathematics,
Faculty of Science,
Sohag University, Sohag,
EGYPT.
E-mail: asem2e@yahoo.com
Abstract:
In this paper, we aim to investigate the equiform differential geometric properties of the involute-evolute curve couple with constant equiform curvatures in three-dimensional hyperbolic and de Sitter spaces. Also, we obtain some relations between the curvature functions of these curves and investigate some special curves with respect to their equiform curvatures. Finally, we defray two computational examples to support our main findings.
Paper's Title:
Optimal Conditions using Multi-valued G-Presic type Mapping
Author(s):
Deb Sarkar, Ramakant Bhardwaj, Vandana Rathore, and Pulak Konar
Department of Mathematics, Amity
University, Kadampukur, 24PGS(N), Kolkata, West Bengal, 700135,
India.
E-mail: debsarkar1996@gmail.com
Department of Mathematics, Amity
University, Kadampukur, 24PGS(N), Kolkata, West Bengal, 700135,
India.
E-mail: drrkbhardwaj100@gmail.com
School of Engineering and Technology,
Jagran Lakecity University, Bhopal, MP-462044,
India.
E-mail: drvandana@jlu.edu.in
Department of Mathematics,
VIT University, Chennai, Tamil Nadu-600127,
India.
E-mail: pulakkonar@gmail.com
Abstract:
In the present paper, some best proximity results have been presented using the concept of G-Presic type multi-valued mapping. These results are the extensions of Presic's theorem in the non-self mapping. A suitable example has also been given. Here, some applications are presented in θ-chainable space and ordered metric space.
Paper's Title:
Asymptotic Behavior of Mixed Type Functional Equations
Author(s):
J. M. Rassias
Pedagogical Department, E.E., National and
Capodistrian University of Athens, Section of Mathematics And Informatics, 4, Agamemnonos
Str., Aghia Paraskevi, Athens 15342,Greece
jrassias@primedu.uoa.gr
URL:
http://www.primedu.uoa.gr/~jrassias/
Abstract:
In 1983 Skof [24] was the first author to solve the Ulam problem for additive mappings on a restricted domain. In 1998 Jung [14] investigated the Hyers-Ulam stability of additive and quadratic mappings on restricted domains. In this paper we improve the bounds and thus the results obtained by Jung [14], in 1998 and by the author [21], in 2002. Besides we establish new theorems about the Ulam stability of mixed type functional equations on restricted domains. Finally, we apply our recent results to the asymptotic behavior of functional equations of different types.
Paper's Title:
Positive Solutions of Evolution Operator Equations
Author(s):
Radu Precup
Department of Applied Mathematics,
Babes-Bolyai University,
Cluj, Romania
Abstract:
Existence and localization results are derived from Krasnoselskii’s compressionexpansion
fixed point theorem in cones, for operator equations in spaces of continuous functions
from a compact real interval to an abstract space. The main idea, first used in [12], is to handle
two equivalent operator forms of the equation, one of fixed point type giving the operator to
which Krasnoselskii’s theorem applies and an other one of coincidence type which is used to
localize a positive solution in a shell. An application is presented for a boundary value problem
associated to a fourth order partial differential equation on a rectangular domain.
Paper's Title:
On the Ulam Stability for Euler-Lagrange Type Quadratic Functional Equations
Author(s):
Matina John Rassias and John Michael Rassias
Statistics and Modelling Science,
University of Strathclyde,
Livingstone Tower,
26 Richmond Str,
Glasgow, Uk, G1 1xh
Pedagogical Department, E. E., National and Capodistrian University of Athens,
Section of Mathematics and Informatics,
4, Agamemnonos Str, Aghia Paraskevi,
Athens 15342, Greece
Abstract:
In 1940 (and 1968) S. M. Ulam proposed the well-known Ulam stability problem.
In 1941 D.H. Hyers solved the Hyers-Ulam problem for linear mappings. In 1951 D. G. Bourgin
has been the second author treating the Ulam problem for additive mappings. In 1978 according
to P.M. Gruber this kind of stability problems is of particular interest in probability theory and in
the case of functional equations of different types. In 1982-2004 we established the Hyers-Ulam
stability for the Ulam problem for different mappings. In 1992-2000 J.M. Rassias investigated
the Ulam stability for Euler-Lagrange mappings. In this article we solve the Ulam problem
for Euler-Lagrange type quadratic functional equations. These stability results can be applied
in mathematical statistics, stochastic analysis, algebra, geometry, as well as in psychology and
sociology.
Paper's Title:
Multivalued Hemiequilibrium Problems
Author(s):
Muhammad Aslam Noor
Mathematics Department,
COMSATS Institute of Information Technology,
Sector H-8/1, Islamabad,
Pakistan.
noormaslam@hotmail.com
Abstract:
In this paper, we introduce and study a new class of equilibrium problems, known
as multivalued hemiequilibrium problems. The auxiliary principle technique is used to suggest
and analyze some new classes of iterative algorithms for solving multivalued hemiequilibrium
problems. The convergence of the proposed methods either requires partially relaxed strongly
monotonicity or pseudomonotonicity. As special cases, we obtain a number of known and new
results for solving various classes of equilibrium and variational inequality problems. Since
multivalued hemiequilibrium problems include hemiequilibrium, hemivariational inequalities,
variational inequalities and complementarity problems as specials cases, our results still hold for
these problems.
Paper's Title:
On the Hohov Convolution Of The Class Sp(α,β)
Author(s):
T. N. Shanmugam and S. Sivasubramanian
Department of Mathematics,
Anna University,
Chennai 600025,
Tamilnadu, India.
shan@annauniv.edu
Department of Mathematics,
Easwari Engineering College,
Chennai-600089,
Tamilnadu, India,
sivasaisastha@rediffmail.com
Abstract:
Let F(a,b;c;z) be the Gaussian hypergeometric function and Ia,b;c(f)=zF(a,b;c;z)*f(z) be the Hohlov operator defined on the class A of all normalized analytic functions. We determine conditions on the parameters a,b,c such that Ia,b;c(f) will be in the class of parabolic starlike functions Sp(α,β). Our results extend several earlier results.
Paper's Title:
Solution of the Hyers-Ulam Stability Problem for Quadratic Type Functional Equations in Several Variables
Author(s):
John Michael Rassias
Pedagogical Department, E.E., National and Capodistrian University of Athens,
Section of Mathematics and Informatics,
4, Agamemnonos Str., Aghia Paraskevi,
Athens 15342,
Greece
jrassias@primedu.uoa.gr
URL: http://www.primedu.uoa.gr/~jrassias/
Abstract:
In 1940 (and 1968) S. M. Ulam proposed the well-known Ulam stability problem. In 1941 D. H. Hyers solved the Hyers-Ulam problem for linear mappings. In 1951 D. G. Bourgin has been the second author treating the Ulam problem for additive mappings. In 1978 according to P. M. Gruber this kind of stability problems is of particular interest in probability theory and in the case of functional equations of different types. In 1982-2004 we established the Hyers-Ulam stability for the Ulam problem for different mappings. In this article we solve the Hyers-Ulam problem for quadratic type functional equations in several variables. These stability results can be applied in stochastic analysis, financial and actuarial mathematics, as well as in psychology and sociology.
Paper's Title:
A relation between nuclear cones and full nuclear cones
Author(s):
G. Isac and A. B. Nemeth
Department of Mathematics,
Royal Military College of Canada,
P. O. Box 17000 STN Forces Kingston, Ontario,
Canada K7K 7B4.
isac-g@rmc.ca
Faculty of Mathematics and Computer Science,
Babes-Bolyai University,
3400 Cluj-Napoca,
Romania.
nemab@math.ubbcluj.ro
Abstract:
The notion of nuclear cone in locally convex spaces corresponds to the notion of well based cone in normed spaces. Using the bipolar theorem from locally convex spaces it is proved that every closed nuclear cone is a full nuclear cone. Thus every closed nuclear cone can be associated to a mapping from a family of continuous seminorms in the space to the topological dual of the space. The relation with Pareto efficiency is discussed.
Paper's Title:
Boundary Value Problems for Fractional Diffusion-Wave equation
Author(s):
Varsha Daftardar-Gejji and Hossein Jafari
Department of Mathematics, University of Pune,
Ganeshkhind, Pune - 411007,
INDIA.
vsgejji@math.unipune.ernet.in
jafari_h@math.com
Abstract:
Non homogeneous fractional diffusion-wave equation has been solved under linear/nonlinear boundary conditions. As the order of time derivative changes from
0 to 2, the process changes from slow diffusion to classical diffusion to mixed diffusion-wave behaviour.
Numerical examples presented here confirm this inference. Orthogonality of eigenfunctions in case of fractional Stürm-Liouville problem has been established
Paper's Title:
p-valent Meromorphic Functions Involving
Hypergeometric and Koebe Functions by Using Differential Operator
Author(s):
S. Najafzadeh, S. R. Kulkarni and G. Murugusundaramoorthy
Department of Mathematics,
Fergusson College, Pune University,
Pune - 411004,
India.
Najafzadeh1234@yahoo.ie
kulkarni_ferg@yahoo.com
School of Science and Humanities,
Vellore Institute of Technology, Deemed University,
Vellore - 632014,
India.
gmsmoorthy@yahoo.com
Abstract:
New classes of multivalent meromorphic functions involving
hypergeometric and Koebe functions are introduced,we find some
properties of these classes e.g. distortion bounds, radii of
starlikeness and convexity, extreme points, Hadamard product and
verify effect of some integral operator on members of these
classes.
Paper's Title:
Reconstruction of Discontinuities of Functions Given Noisy Data
Author(s):
Eric D. Mbakop
67A Beaver Park Rd,
Framingham, MA, 01702,
U. S. A.
ericsteve86@yahoo.fr
Abstract:
Suppose one is given noisy data of a discontinuous piecewise-smooth
function along with a bound on its second derivative. The locations
of the points of discontinuity of f and their jump sizes are not
assumed known, but are instead retrieved stably from the noisy data.
The novelty of this paper is a numerical method that allows one to
locate some of these points of discontinuity with an accuracy that
can be made arbitrarily small.
Paper's Title:
1-type Pseudo-Chebyshev Subspaces in Generalized 2-normed Spaces
Author(s):
Sh. Rezapour
Department of Mathematics, Azarbaijan University of Tarbiat Moallem,
Azarshahr, Tabriz,
Iran
sh.rezapour@azaruniv.edu
Abstract:
We construct a generalized 2-normed space from every normed space.
We introduce 1-type pseudo-Chebyshev subspaces in generalized
2-normed spaces and give some results in this field.
Paper's Title:
A Coefficient Inequality For Certain Subclasses of Analytic
Functions Related to Complex Order
Author(s):
B. Srutha Keerthi, B. Adolf Stephen and S. Sivasubramanian
Department Of Applied Mathematics, Sri Venkateswara College Of Engineering, Anna University,
Sriperumbudur, Chennai - 602 105,
India.
laya@svce.ac.in
Department of Mathematics, Madras Christian College,
Chennai - 600059,
India
adolfmcc2003@yahoo.co.in
Department of Mathematics, College of Engineering, Anna University,
Tamilnadu, Chennai - 600 025,
India.
sivasaisastha@rediffmail.com
Abstract:
In this present investigation, the authors obtain coefficient
inequality for certain normalized analytic functions of complex order f(z) defined
on the open unit disk for which
(
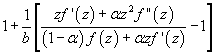and 
be a complex number) lies in a region starlike with respect to 1 and is symmetric with respect to the real axis. Also
certain applications of the main result for a class of functions of complex order
defined by convolution are given. As a special case of this result, coefficient
inequality for a class of functions defined through fractional derivatives is
obtained. The motivation of this paper is to give a generalization of the
coefficient inequalities of the subclasses of starlike and convex functions of
complex order.
Paper's Title:
Iterated Order of Fast Growth Solutions of Linear Differential Equations
Author(s):
Benharrat Belaïdi
Department of Mathematics
Laboratory of Pure and Applied Mathematics
University of Mostaganem
B. P. 227 Mostaganem,
ALGERIA.
belaidi@univ-mosta.dz
Abstract:
In this paper, we investigate the growth of solutions of the differential
equation
f(k) + Ak-1 (z) f(k-1) +...+ A1 (z) f' + A0 (z) f= F (z),
where
Ao (z), ..., Ak-1 (z)
and
F (z) 
0
are entire functions. Some estimates are given for the iterated order of solutions of the above quation when one of the coefficients As is being dominant in the sense that it has larger growth than Aj (j≠s) and F.
Paper's Title:
Local and Global Existence and Uniqueness Results for Second and Higher Order Impulsive Functional Differential Equations with Infinite Delay
Author(s):
Johnny Henderson and Abdelghani Ouahab
Department of Mathematics, Baylor University,
Waco, Texas 76798-7328
USA.
Johnny_Henderson@baylor.edu
Laboratoire de Mathématiques, Université de Sidi Bel Abbés
BP 89, 22000 Sidi Bel Abbées,
Algérie.
ouahab@univ-sba.dz
Abstract:
In this paper, we discuss the local and global existence and
uniqueness results for second and higher order impulsive functional
differential equations with infinite delay. We shall rely on a
nonlinear alternative of Leray-Schauder. For the global existence
and uniqueness we apply a recent Frigon and Granas nonlinear
alternative of Leray-Schauder type in Fréchet spaces.
Paper's Title:
A note on Inequalities due to Martins, Bennett and Alzer
Author(s):
József Sándor
Babeş-Bolyai University of Cluj, Department of Mathematics and Computer Sciences
Kogălniceanu Nr.1, Cluj-Napoca,
Romania.
jjsandor@hotmail.com
jsandor@member.ams.org
Abstract:
A short history of certain inequalities by Martins, Bennett as well as Alzer, is provided. It is shown that, the inequality of Alzer for negative powers [6], or Martin's reverse inequality [7] are due in fact to Alzer [2]. Some related results, as well as a conjecture, are stated.
Paper's Title:
The Convergence of Modified Mann-Ishikawa Iterations when Applied to an Asymptotically Pseudocontractive Map
Author(s):
S. Soltuz
Departamento de Matematicas, Universidad de Los Andes, Carrera 1
No. 18A-10, Bogota,
Colombia
and
``T. Popoviciu" Institute of Numerical Analysis
Cluj-Napoca,
Romania
smsoltuz@gmail.com
URL:http://www.uniandes.edu.co/
Abstract:
We prove that under minimal conditions the modified Mann and Ishikawa iterations converge when dealing with an asymptotically pseudocontractive map. We give an affirmative answer to the open question from C.E. Chidume and H. Zegeye, Approximate fixed point sequences and convergence theorems for asymptotically pseudocontractive mappings, J. Math. Anal. Appl., 278 (2003), 354--366.
Paper's Title:
On a Subclass of Uniformly Convex Functions Defined by the Dziok-Srivastava Operator
Author(s):
M. K. Aouf and G. Murugusundaramoorthy
Mathematics Department, Faculty of Science,
Mansoura University 35516,
Egypt.
mkaouf127@yahoo.com
School of Science and Humanities, VIT University
Vellore - 632014,
India.
gmsmoorthy@yahoo.com
Abstract:
Making use of the Dziok-Srivastava operator, we define a new subclass Tlm([α1];α,β) of uniformly convex function with
negative coefficients. In this paper, we obtain coefficient estimates,
distortion theorems, locate extreme points and obtain radii of
close-to-convexity, starlikeness and convexity for functions belonging to the
class Tlm([α1];α,β) . We
consider integral operators associated with functions belonging to the class
Hlm([α1];α,β) defined via the Dziok-Srivastava
operator. We also obtain several results for the modified Hadamard products of
functions belonging to the class Tlm([α1];α,β)
and we obtain properties associated with generalized fractional calculus
operators.
Paper's Title:
Isoperimetric Inequalities for Dual Harmonic Quermassintegrals
Author(s):
Yuan Jun, Zao Lingzhi and Duan Xibo
School of Mathematics and Computer Science,
Nanjing Normal University, Nanjing, 210097,
China.
yuanjun_math@126.com
Department of Mathematics, Nanjing Xiaozhuang University,
Nanjing, 211171,
China.
lzhzhao@163.com
Department of Mathematics, Shandong Water Polytechnic,
Shandong, 276826,
China
dxb1111@sohu.com
Abstract:
In this paper, some isoperimetric inequalities for the dual harmonic
quermassintegrals are established.
Paper's Title:
Positive Solutions for Systems of Three-point Nonlinear Boundary Value Problems
Author(s):
J. Henderson and S. K. Ntouyas
Department of Mathematics, Baylor University
Waco, Texas
76798-7328 USA.
Johnny_Henderson@baylor.edu
URL: http://www3.baylor.edu/~Johnny_Henderson
Department of Mathematics, University of Ioannina
451 10 Ioannina,
Greece.
sntouyas@cc.uoi.gr
URL: http://www.math.uoi.gr/~sntouyas
Abstract:
Values of λ are determined for which there exist
positive solutions of the system of three-point boundary value problems,
u''(t)+ λa(t)f(v(t))=0, v''(t)+λb(t)g(u(t))=0,
for 0 < t <1, and
satisfying, u(0) = 0, u(1)=α u(η),
v(0) = 0, v(1)=α v(η). A Guo-Krasnosel'skii fixed
point theorem is applied. Paper's Title:
Multivalent Harmonic Mappings Convoluted With a Multivalent Analytic Function
Author(s):
Om P. Ahuja and Özlem Güney
Kent State University, Department of Mathematical Sciences,
University of Dicle, Department of Mathematics, Abstract:
The object of this paper is to study certain geometric properties of
a family of multivalent harmonic mappings in the plane convoluted
with a multivalent analytic function in the open unit disc. Paper's Title:
Reverses of the CBS Integral Inequality in Hilbert Spaces and Related
Results
Author(s):
I. Brnetić, S. S. Dragomir, R. Hoxha and J. Pečarić
Department of Applied Mathematics, Faculty of Electrical
Engineering and Computing,
School of Computer Science & Mathematics, Victoria University
Faculty of Applied Technical Sciences, University of Prishtina,
Faculty of Textile Technology, University of Zagreb, Abstract:
There are many known reverses of the Cauchy-Bunyakovsky-Schwarz (CBS)
inequality in the literature. We obtain here a general integral inequality
comprising some of those results and also provide other related
inequalities. The discrete case, which is of interest in its own turn, is
also analysed. Paper's Title:
On ε-simultaneous Approximation in Quotient Spaces
Author(s):
H. Alizadeh, Sh. Rezapour, S. M. Vaezpour Department of
Mathematics, Aazad Abstract:
The purpose of this paper is
to develop a theory of best simultaneous approximation to
ε-simultaneous approximation. We shall introduce the
concept of ε-simultaneous pseudo Chebyshev,
ε-simultaneous quasi Chebyshev and
ε-simultaneous weakly Chebyshev subspaces of a Banach
space. Then, it will be determined under what conditions these
subspaces are transmitted to and from quotient spaces.
Paper's Title:
Applications of Relations and Relators in the
Extensions of Stability Theorems for Homogeneous and Additive Functions Author(s):
Árpád Száz
Institute of Mathematics, University of Debrecen, Abstract:
By working out an appropriate technique of relations and relators and
extending the ideas of the direct methods of Z. Gajda and R. Ger, we prove
some generalizations of the stability theorems of D. H. Hyers, T. Aoki,
Th. M. Rassias and P. Găvruţă
in terms of the existence and unicity of
2-homogeneous and additive approximate selections of generalized
subadditive relations of semigroups to vector relator spaces. Thus, we
obtain generalizations not only of the selection theorems of Z. Gajda and R.
Ger, but also those of the present author.
Paper's Title:
Inclusion and Neighborhood
Properties for Certain Subclasses of Analytic Functions Associated with
Convolution Structure
Author(s):
M. K. Aouf Mathematics Department, Abstract:
In this paper we introduce and investigate two new subclasses of
multivalently analytic functions of complex order defined by using the
familiar convolution structure of analytic functions. In this paper we
obtain the coefficient estimates and the consequent inclusion relationships
involving the neighborhoods of the p-valently analytic functions.
Paper's Title:
A Coincidence Theorem for Two Kakutani Maps
Author(s):
Mircea Balaj
Department of Mathematics, Abstract:
In this paper we prove the following theorem: Let X be a
nonempty compact convex set in a locally convex Hausdorff
topological vector space, D be the set of its extremal points and F,T:
X―◦X two Kakutani maps; if for each nonempty
finite subset A of D and for any x
∈
coA, F (x)
∩
coA ≠
Ø, then F
and T have a
coincidence point. The proof of this theorem is given first in the
case when X is a simplex, then when X is a polytope and
finally in the general case. Several reformulations of this result
are given in the last part of the paper.
Paper's Title:
Improvement of Jensen's
Inequality for Superquadratic Functions
Author(s):
S. Abramovich, B. Ivanković, and J. Pečarić
Department of Mathematics, Faculty of Transport and
Trafic Engineering, Faculty of Textile,
Abstract:
Since 1907, the famous Jensen's inequality has been refined in different
manners. In our paper, we refine it applying superquadratic functions and
separations of domains for convex functions.
There are convex functions which are not superquadratic and superquadratic
functions which are not convex.
For superquadratic functions which are not convex we get inequalities
analogue to inequalities satisfied by convex functions.
For superquadratic functions which are convex (including many useful
functions) we get refinements of Jensen's inequality and its extensions.
Paper's Title:
Some Inequalities for Gramian Normal
Operators and for Gramian Self-Adjoint Operators in Pseudo-Hilbert Spaces Author(s):
Loredana Ciurdariu Abstract:
Several inequalities for gramian normal operators and for gramian
self-adjoint operators in pseudo-Hilbert spaces are presented.
Paper's Title:
Hardy Type Inequalities via
Convexity - The Journey so Far Author(s):
James A.
Oguntuase and Lars-Erik Persson Department of
Mathematics, Luleå University of Technology, Abstract:
It is nowadays well-known that Hardy's
inequality (like
many other inequalities) follows directly from Jensen's inequality. Most of
the development of Hardy type inequalities has not used this simple fact,
which obviously was unknown by Hardy himself and many others. Here we report
on some results obtained in this way mostly after 2002 by mainly using this
fundamental idea.
Paper's Title:
The Best Upper Bound for Jensen's
Inequality Author(s):
Vasile Cirtoaje Abstract:
In this paper we give the best upper bound
for the weighted Jensen's discrete inequality applied to a convex function f
defined on a closed interval I in the case when the bound depends on f,
I and weights. In addition, we give a simpler expression of the upper
bound, which is better than existing similar one. Paper's Title:
Refinements of the Trace Inequality of
Belmega, Lasaulce and Debbah Author(s):
Shigeru Furuichi and Minghua
Lin Department of Mathematics and
Statistics,
furuichi@chs.nihon-u.ac.jp,
lin243@uregina.ca. Abstract:
In this short paper, we show a
certain matrix trace inequality and then
give a refinement of the trace inequality proven by Belmega, Lasaulce and Debbah.
In addition, we give an another improvement of their trace inequality. Paper's Title:
A Note On The Global Behavior Of A Nonlinear System of Difference Equations Author(s):
Norman H. Josephy, Mihaela Predescu and Samuel W. Woolford
Department of Mathematical Sciences,
mpredescu@bentley.edu Abstract:
This paper deals with the global asymptotic stability character of solutions of a discrete time deterministic model proposed by Wikan and Eide in Bulletin of Mathematical Biology, 66, 2004, 1685-1704. A stochastic extension of this model is proposed and discussed. Computer simulations suggest that the dynamics of the stochastic model includes a mixture of the dynamics observed in the deterministic model.
Paper's Title:
Necessary and Sufficient Conditions for Cyclic Homogeneous Polynomial Inequalities of Degree Four in Real Variables Author(s):
Vasile Cirtoaje and Yuanzhe
Zhou High School Affiliated to Wuhan
University, China Abstract:
In this paper, we give two sets of necessary and sufficient conditions that the inequality f4(x,y,z)
≥ 0 holds for any real numbers x,y,z, where f4(x,y,z) is a cyclic homogeneous polynomial of degree four. In addition, all equality cases of this inequality are analysed. For the particular case in which f4(1,1,1)=0, we get the main result in
[3]. Several applications are given to show the effectiveness of the proposed methods. Paper's Title:
Para-chaotic Tuples of Operators
Author(s):
Bahmann Yousefi and Javad Izadi
Department of Mathematics, Abstract:
In this paper, we introduce para-chaotic tuples
of operators and we give some relations between para-chaoticity
and Hypercyclicity Criterion for a tuple of operators. Paper's Title:
Properties of Certain Multivalent Functions Involving Ruscheweyh Derivatives Author(s):
N-Eng Xu and Ding-Gong Yang
Department of Mathematics, Abstract:
Let Ap(p∈ N) be the class of functions
Paper's Title:
A Geometric Generalization of Busemann-Petty Problem
Author(s):
Liu Rong and Yuan Jun
Shanghai Zhangjiang Group Junior Middle School, Abstract:
The norm defined by Busemann's inequality establishes a class of
star body - intersection body.
This class of star body plays a key role in the solution of Busemann-Petty problem. In 2003,
Giannapoulos [1]
defined a norm for a new class of half-section. Based on this norm, we give a geometric generalization of Busemann-Petty problem, and get its answer as a result
Paper's Title:
On Reformations of 2--Hilbert Spaces Author(s):
M. Eshaghi Gordji, A. Divandari, M. R. Safi and Y. J. Cho Department of Mathematics, Semnan
University,
meshaghi@semnan.ac.ir,
madjid.eshaghi@gmail.com Department of Mathematics, Semnan
University, Department of Mathematics, Semnan
University,
safi@semnan.ac.ir,
SafiMohammadReza@yahoo.com Department of Mathematics Education and
the RINS, Abstract:
In this paper, first, we introduce the new concept of (complex)
2--Hilbert spaces, that is, we define the concept of 2--inner
product spaces with a complex valued 2--inner product by using
the 2--norm. Next, we prove some theorems on Schwartz's
inequality, the polarization identity, the parallelogram laws and
related important properties. Finally, we give some open problems
related to 2--Hilbert spaces.
Paper's Title:
On the Sendov Conjecture for a Root Close to the Unit Circle Author(s):
Indraneel G. Kasmalkar Department of Mathematics, E-mail:
indraneelk@berkeley.edu
Abstract:
On Sendov's conjecture, T. Chijiwa
quantifies the idea stated by V. Vâjâitu and A. Zaharescu (and M. J. Miller independently), namely that if a polynomial with all roots inside the closed unit disk has a root
sufficiently close to the unit circle then there is a critical point at a distance of at most one from that root. Chijiwa provides an estimate of exponential order for the required 'closeness' of the root to the unit circle so that such a critical point may exist. In this paper, we will improve this estimate to polynomial order by making major modifications and strengthening inequalities in Chijiwa's proof. Paper's Title:
Some New Nonlinear Integro-Differential Inequalities of Gronwall-Bellman-Pachpatte Type Author(s):
A. ABDELDAIM Department of Mathematics and Computer
Sciences, Department of Mathematics, E-mail:
ahassen@su.edu.sa
Abstract:
In this paper we establish some new nonlinear integro-differential inequalities of Gronwall-Bellman-Pachpatte type for function of one independent variable. The purpose of this paper is to extend certain results which proved by Pachpatte in [On some fundamental integrodifferential and integral inequalities, An. Sti. Univ. Al. I. Cuza, Iasi, Vol.23 (1977), 77-86]. The inequalities obtained here can be used in the theory of some new classes of nonlinear integro-differential equations. Some applications are also given to illustrate the usefulness of our results. Paper's Title:
On the Regularization of Hammerstein's type Operator Equations
Author(s):
E. Prempeh, I. Owusu-Mensah and K. Piesie-Frimpong Department of Mathematics, Department of Science Education, Department of Mathematics, E-mail:
isaacowusumensah@gmail.com E-mail:
eprempeh.cos@knust.edu.gh E-mail:
piesie74@yahoo.com Abstract:
We have studied Regularization of Hammerstein's Type Operator Equations in general Banach Spaces.
In this paper, the results have been employed to establish regularized solutions to Hammerstein's type operator equations in Hilbert spaces by looking at three cases of regularization. Paper's Title:
Hermite-Hadamard-Fejer Type Inequalities for Harmonically s-convex Functions via Fractional Integrals Author(s):
İmdat İşcan, Mehmet Kunt Department of Mathematics, Abstract:
In this paper, some Hermite-Hadamard-Fejer type integral inequalities for
harmonically s-convex functions in fractional integral forms have been
obtained. Paper's Title:
Some Grüss Type Inequalities in Inner Product Spaces Author(s):
Sever S. Dragomir1,2 1Mathematics, School of Engineering
& Science URL:
http://rgmia.org/dragomir Abstract:
Some inequalities in inner product spaces
where e,f ∈ H with
Paper's Title:
Hyponormal and K-Quasi-Hyponormal Operators On Semi-Hilbertian Spaces Author(s):
Ould Ahmed Mahmoud Sid Ahmed
and Abdelkader Benali Mathematics Department, Mathematics Department, Faculty of
Science, Abstract:
Let H be a Hilbert space and let A be a positive
bounded operator on H. The semi-inner product < u|v>A:=<Au|v>, u,v
∈ H induces a semi-norm || .||A on
H. This makes H into a semi-Hilbertian space. In this paper we
introduce the notions of hyponormalities and k-quasi-hyponormalities for operators on semi Hilbertian space
(H,||.||A), based on the works that studied normal, isometry, unitary and partial isometries operators in these spaces. Also, we generalize
some results which are already known for hyponormal and quasi-hyponormal operators. An
operator T ∈ BA (H) is said to be
(A, k)-quasi-hyponormal if
Paper's Title:
Hermite-Hadamard Type Inequalities for k-Riemann Liouville Fractional Integrals Via Two Kinds of Convexity Author(s):
R. Hussain1, A. Ali2, G. Gulshan3, A. Latif4 and K. Rauf5
1,2,3,4Department
of Mathematics, 5Department
of Mathematics, Abstract:
In this article, a fundamental integral identity including the first order
derivative of a given function via k-Riemann-Liouville fractional integral is established. This is used to obtain further Hermite-Hadamard type inequalities involving left-sided and right-sided
k-Riemann-Liouville fractional integrals for m-convex and (s,m)-convex functions respectively.
Paper's Title:
The Dynamics of an Ebola Epidemic Model with Quarantine of Infectives Author(s):
Eliab Horub Kweyunga Department of Mathematics, E-mail:
hkweyunga@kab.ac.ug Abstract:
The recurrent outbreaks of ebola in Africa present global health challenges. Ebola is a severe, very fatal disease with case fatality rates of up to 90%. In this paper, a theoretical deterministic model for ebola epidemic with quarantine of infectives is proposed and analyzed. The model exhibits two equilibria; the disease free and endemic equilibrium points. The basic reproduction number, R0, which is the main threshold, is obtained and the stability of the equilibrium points established.
Using parameter values drawn from the 2014 West Africa ebola outbreak, a numerical simulation of the model is carried out. It is found that the dynamics of the model are completely determined by R0 and that a quarantine success rate of at least 70% is sufficient to contain the disease outbreak. Paper's Title:
Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results Author(s):
Sever S. Dragomir1,2 1Mathematics, School of Engineering
& Science Abstract:
In this paper we survey some recent results obtained by the
author in providing various bounds for the celebrated f-divergence
measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation
distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text. Paper's Title:
Relation Between The Set Of Non-decreasing Functions And The Set Of Convex Functions Author(s):
Qefsere Doko Gjonbalaj and Luigj Gjoka Department of Mathematics, Faculty of
Electrical and Computer Engineering, E-mail:
qefsere.gjonbalaj@uni-pr.edu
Department of Engineering Mathematics, E-mail:
luigjgjoka@ymail.com Abstract:
In this article we address the problem of integral presentation
of a convex function. Let I be an interval in R. Here, using the Riemann or Lebesgue’s integration theory, we find the necessary and sufficient condition for a function
f: I→ R to be convex in
I. Paper's Title:
Fractional class of analytic functions Defined Using q-Differential Operator
Author(s):
K . R. Karthikeyan, Musthafa Ibrahim and S. Srinivasan Department of Mathematics and
Statistics, College of Engineering, Department of Mathematics, Presidency
College (Autonomous), Abstract:
We define a q-differential fractional operator, which
generalizes Salagean and Ruscheweyh differential operators. We introduce and study a new class of analytic functions involving q-differential fractional operator. We also determine the necessary and sufficient conditions for functions to be in the class. Further, we obtain the coefficient estimates, extreme points, growth and distortion bounds. Paper's Title:
A Multivalued Version of the
Radon-Nikodym Theorem, via the Single-valued Gould Integral Author(s):
Domenico Candeloro1, Anca Croitoru2, Alina Gavriluţ2, Anna Rita Sambucini1 1Dept. of Mathematics and Computer
Sciences, 2Faculty of Mathematics, Abstract:
In this paper we consider a Gould type integral of
real functions with respect to a compact and convex valued not necessarily additive measure.
In particular we will introduce
the concept of integrable multimeasure and, thanks to this notion, we will establish
an exact Radon-Nikodym theorem relative to a fuzzy multisubmeasure which is new also in the finite dimensional case.
Some results concerning the Gould integral are also obtained. Paper's Title:
The Conservativeness of Girsanov Transformed for Symmetric Jump-diffusion Process Author(s):
Mila Kurniawaty and Marjono Department of Mathematics, Abstract:
We study about the Girsanov transformed for symmetric Markov processes with jumps associated with regular Dirichlet form. We prove the conservativeness of it by dividing the regular Dirichlet
form into the "small jump" part and the "big jump" part.
Paper's Title:
Some Convergence Results for Jungck-Am Iterative Process In Hyperbolic Spaces Author(s):
Akindele Adebayo Mebawondu and Oluwatosin Temitope Mewomo School of Mathematics, Statistics and Computer Science,
Abstract:
In this paper, we introduce a new three steps iterative process called Jungck-AM iterative process and show that the proposed iterative process can be used to approximate fixed points of Jungck-contractive type mappings and Jungck-Suzuki type mappings. In addition, we establish some strong and
Δ-convergence results for the approximation of fixed points of Jungck-Suzuki type mappings in the frame work of uniformly convex hyperbolic space. Furthermore, we show that the newly proposed iterative process has a better rate of convergence compare to the Jungck-Noor, Jungck-SP, Jungck-CR and some existing iterative processes in the literature. Finally, stability, data dependency results for Jungck-AM iterative process is established and we present an analytical proof and numerical examples to validate our claim. Paper's Title:
The Concept of Convergence for 2-Dimensional Subspaces Sequence in Normed Spaces Author(s):
M. Manuharawati, D. N. Yunianti, M. Jakfar Mathematics Department, Universitas
Negeri Surabaya, Abstract:
In this paper, we present a concept of convergence of sequence, especially, of
2-dimensional subspaces of normed spaces. The properties of the concept are established. As consequences of our definition in an inner product space, we also obtain the continuity property of the angle between two 2-dimensional subspaces of inner product spaces. Paper's Title:
Bounds on the Jensen Gap, and Implications for Mean-Concentrated Distributions Author(s):
Xiang Gao, Meera Sitharam, Adrian E. Roitberg Department of Chemistry, and Department
of Computer & Information Science & Engineering, Abstract:
This paper gives upper and lower bounds on the gap in Jensen's inequality, i.e., the difference between the expected value of a function of a random variable and the value of the function at the expected value of the random variable.
The bounds depend only on growth properties of the function and specific moments of the random variable. The bounds are particularly useful for distributions that are concentrated around the mean, a commonly occurring scenario such as the average of i.i.d. samples and in statistical mechanics. Paper's Title:
Weyl's theorem for class Q and k - quasi class Q Operators Author(s):
S. Parvatham and D. Senthilkumar Department of Mathematics and Humanities,
Post Graduate and Research Department of
Mathematics, Abstract:
In this paper, we give some properties of class Q
operators. It is proved that every class Q operators satisfies
Weyl's theorem under the condition that T2 is isometry.
Also we proved that every k quasi class Q operators is
Polaroid and the spectral mapping theorem holds for this class of operator. It
will be proved that single valued extension property, Weyl and generalized
Weyl's theorem holds for every k quasi class Q
operators. Paper's Title:
Analysis of a Frictional Contact Problem for Viscoelastic Piezoelectric Materials Author(s):
Meziane Said Ameur, Tedjani Hadj Ammar and Laid Maiza Departement of Mathematics, Departement of Mathematics, Department of Mathematics, Abstract:
In this paper, we consider a mathematical model that describes
the quasi-static process of contact between two thermo-electro-viscoelastic bodies with damage and adhesion. The damage of the materials caused by elastic deformations. The contact is frictional and modeled with a normal compliance condition involving adhesion effect of contact surfaces. Evolution of the
bonding field is described by a first order differential equation. We derive variational formulation for the model and prove an existence and uniqueness result of the weak solution. The proof is based on arguments of evolutionary variational inequalities, parabolic inequalities, differential equations, and fixed point theorem. Paper's Title:
Several Applications of a Local Non-convex Young-type Inequality Author(s):
Loredana Ciurdariu, Sorin Lugojan Department of Mathematics, E-mail:
ltirtirau87@yahoo.com Abstract:
A local version of the Young inequality for positive numbers is used in order to deduce some inequalities about determinants and norms for real quadratic matrices and norms of positive operators on complex Hilbert spaces. Paper's Title:
On Ruled Surfaces According to Quasi-Frame in Euclidean 3-Space Author(s):
M. Khalifa Saad and R. A. Abdel-Baky Department of Mathematics, Faculty of
Science, Department of Mathematics, Faculty of
Science, Abstract:
This paper aims to study the skew ruled surfaces by using the quasi-frame of
Smarandache curves in the Euclidean 3-space. Also, we reveal the
relationship between Serret-Frenet and quasi-frames and give a parametric
representation of a directional ruled surface using the quasi-frame.
Besides, some comparative examples are given and plotted which support our
method and main results. Paper's Title:
Analysis of a Dynamic Elasto-viscoplastic Frictionless Antiplan Contact Problem with Normal Compliance Author(s):
A. Ourahmoun1, B. Bouderah2, T. Serrar3 1,2Applied Mathematics
Laboratory, 3Applied Mathematics
Laboratory, Abstract:
We consider a mathematical model which describes the dynamic evolution of a
thermo elasto viscoplastic contact problem between a body and a rigid
foundation. The mechanical and thermal properties of the obstacle coating
material near its surface. A variational formulation of this dynamic contact
phenomenon is derived in the context of general models of thermo elasto
viscoplastic materials. The displacements and temperatures of the bodies in
contact are governed by the coupled system consisting of a variational
inequality and a parabolic differential equation. The proof is based on a
classical existence and uniqueness result on parabolic
inequalities,differential equations and fixed point arguments. Paper's Title:
Construction of a Frame Multiresolution Analysis on Locally Compact Abelian Groups Author(s):
R. Kumar and Satyapriya Department of Mathematics, Abstract:
The frame multiresolution analysis (FMRA) on locally compact Abelian groups has been studied and the results concerning classical MRA have been worked upon to obtain new results. All the necessary conditions, which need to be imposed on the scaling function
φ to construct a wavelet frame via FMRA, have been summed up. This process of construction of FMRA has aptly been illustrated by sufficient examples. Paper's Title:
Numerical Solution of Certain Types of Fredholm-Volterra Integro-Fractional Differential Equations via Bernstein Polynomials Author(s):
Alias B. Khalaf1, Azhaar H. Sallo2 and Shazad S. Ahmed3 1Department
of Mathematics, College of Science, 2Department
of Mathematics, College of Science, 3Department
of Mathematics, College of Science, Abstract:
In this article we obtain a numerical solution for a certain fractional order integro-differential equations of Fredholm-Volterra type, where the fractional derivative is defined in Caputo sense. The properties of Bernstein polynomials are applied in order to convert the fractional order integro-differential equations to the solution of algebraic equations. Some numerical examples are investigated to illustrate the method. Moreover, the results obtained by this method are compared with the exact solution and with the results of some existing methods as well. Paper's Title:
Multistage Analytical Approximate Solution of Quasi-Linear Differential- Algebraic System of Index Two Author(s):
Ibrahim M. Albak, F. A.
Abdullah* and Zarita Zainuddin School of Mathematical Sciences, Abstract:
In this paper, a new Multistage Transform Method (MSDTM) has been proposed by utilizing a well-known transformation technique, the Differential Transform Method (DTM), to solve Differential Algebraic Equations (DAEs) with index 2. The advantage of the proposed scheme is that it does not require an index reduction and extends the convergence domain of the solution. Some examples for various types of problems are carried out to show the ability of MSDTM in solving DAEs. The results obtained are in good agreement with the existing literature which demonstrates the effectiveness and efficiency of the proposed method.
Paper's Title:
An Integration Technique for Evaluating Quadratic Harmonic Sums Author(s):
J. M. Campbell and K.-W. Chen Department of Mathematics and Statistics, Department of Mathematics, University of Taipei, Abstract:
The modified Abel lemma on summation by parts has been applied in many ways recently to determine closed-form evaluations for
infinite series involving generalized harmonic numbers with an upper parameter of two.
We build upon such results using an integration technique that we apply to ``convert'' a given
evaluation for such a series
into an evaluation for a corresponding series involving squared harmonic numbers. Paper's Title:
On General Class of Nonlinear Contractive Maps and their Performance Estimates Author(s):
Olalekan Taofeek Wahab and Salaudeen Alaro Musa Department of Mathematics and
Statistics Abstract:
This paper considers two independent general class of nonlinear contractive maps to study the existence properties of nonlinear operators with prior degenerate. The existence properties are proved in the framework of approximate fixed points with the imposition of the general class of contractive conditions in metrical convex spaces without emphasis on completeness or compactness. For computational purposes, the performance estimates and the sensitivity dependence of these conditions are obtained for the Picard operator. Practical examples are also considered to justify the validity of the conditions. The results ensure no term is lost in the operators with prior degenerate and the conditions are strictly larger class when compare with others in the literature. Paper's Title:
Several New Closed-form Evaluations of the Generalized Hypergeometric Function with Argument 1/16 Author(s):
B. R. Srivatsa Kumar, Insuk Kim and Arjun K. Rathie Department of Mathematics, Department of Mathematics Education, Department of Mathematics, Abstract:
The main objective of this paper is to establish as many as thirty new closed-form evaluations of the generalized hypergeometric function
q+1Fq(z) for q= 2, 3, 4. This is achieved by means of separating the generalized hypergeometric function
q+1Fq(z) for q=1, 2, 3, 4, 5 into even and odd components together with the use of several known infinite series involving central binomial coefficients obtained earlier by Ji and Hei \& Ji and Zhang. Paper's Title:
Conservativeness Criteria of Girsanov Transformation for Non-Symmetric Jump-diffusion Author(s):
Mila Kurniawaty DDepartment of Mathematics, Abstract:
We develop the condition in our previous paper [The Conservativeness of Girsanov transformed for
symmetric jump-diffusion process (2018)] in the framework of nonsymmetric Markov process with jumps associated with regular Dirichlet form. We prove the conservativeness of it by relation in duality of Girsanov transformed process and
recurrent criteria of Dirichlet form. Paper's Title:
Corrigendum for Multistage Analytical Approximate Solution of Quasi-Linear Differential- Algebraic System of Index Two Author(s):
Ibrahim M. Albak, F. A.
Abdullah* and Zarita Zainuddin School of Mathematical Sciences, Abstract:
This article is a corrigendum to AJMAA Volume 18, Issue 2, Article 13, {PDF Link}. Paper's Title:
Additive Mappings on Semiprime Rings Functioning as Centralizers Author(s):
Abu Zaid Ansari and Faiza Shujat Department of Mathematics, Department of Mathematics, Abstract:
The objective of this research is to prove that an additive
mapping T:R → R is a centralizer on R if it satisfies any one of the following identities:
for all x ∈ R, where n
≥ 1 is a fixed integer and R is any suitably torsion free semiprime ring. Some results on involution
"*" are also presented as consequences of the main theorems. In addition, we will take criticism in account with examples. Paper's Title:
SQIRV Model for Omicron Variant with Time Delay Author(s):
S. Dickson, S. Padmasekaran, G. E. Chatzarakis and S. L. Panetsos Mathematics, Periyar University, Periyar
Palkalai Nagar, Salem, Electrical and Electronic Engineering
Educators, School of Abstract:
In order to examine the dynamics of the Omicron variant, this paper uses mathematical modelling and analysis of a SQIRV model, taking into account the delay in the conversion of susceptible individuals into infected individuals and infected individuals into recovered individuals. The pandemic was eventually controlled as a result of the massive delays. To assure the safety of the host population, this concept incorporates quarantine and the COVID-19 vaccine. Both local and global stability of the model are examined. It is found that the fundamental reproduction number affects both local and global stability conditions. Our findings show that asymptomatic cases caused by an affected population play an important role in increasing Omicron infection in the general population. The most recent data on the pandemic Omicron variant from Tamil Nadu, India, is verified. Paper's Title:
Walrasian Equilibrium for Set-valued Mapping Author(s):
M. Muslikh, R.B.E Wibowo, S. Fitri Department of Mathematics, Abstract:
In this article, we obtain the existence of Walras equilibrium for set-valued demand mappings in a pure exchange economy. In this case, the set-valued mappings are defined by the loss function. Therefore, we shall summarize the features describing the exchange economy system which contain the loss function. Paper's Title:
High Order Collocation Method for the Generalized Kuramoto-Sivashinsky Equation Author(s):
Zanele Mkhize, Nabendra
Parumasur and Pravin Singh School of Mathematics, Statistics and
Computer Sciences, Abstract:
In this paper, we derive the heptic Hermite basis functions and use them as basis functions in the orthogonal collocation on finite elements (OCFE) method. We apply the method to solve the generalized Kuramoto-Sivashinsky equation. Various numerical simulations are presented to justify the computational efficiency of the proposed method. Paper's Title:
Lozi Maps With Max Function and its Application Author(s):
Abdellah Menasri Higher National School of Forests, Abstract:
In this paper, we study the Lozi map by replacing the piecewise linear term
in the first equation by the function max (f(x,y);g(x,y)) such that f and
g are two arbitrary functions in R2. This is a family model that allows us to study several new
piecewise-smooth maps. We demonstrate that these models converge to a robust
chaotic attractor and give some applications of these models in the real
world. Paper's Title:
Li-Yorke and Expansivity for Composition Operators on Lorentz Space Author(s):
Rajat Singh and Romesh Kumar Department of Mathematics, Department of Mathematics, Abstract:
In this paper, we investigate Li-Yorke composition operators and
some of its variations on Lorentz spaces. Further, we also study expansive
composition operators on these spaces. The work of the paper is essentially
based on the work in [3],
[6], [8] and [15]. Paper's Title:
Differential Equations for Indicatrices, Spacelike and Timelike Curves Author(s):
Sameer, Pradeep Kumar Pandey Department of Mathematics, Abstract:
Motivated by the recent work of Deshmukh et al. [20], in this paper we show that Tangent, Binormal, and Principal Normal indicatrices do not form non-trivial differential equations. Finally, we obtain the 4th-order differential equations for spacelike and timelike curves. Paper's Title:
Corrigendum for Differential Equations for Indicatrices, Spacelike and Timelike Curves
Author(s):
Sameer, Pradeep Kumar Pandey Department of Mathematics, ABSTRACT NOT FOUND. WEBSITE ERROR
Abstract:
Paper's Title:
On Automorphisms and Bi-derivations of Semiprime Rings Author(s):
Abu Zaid Ansari, Faiza Shujat, Ahlam Fallatah Department of Mathematics, Department of Mathematics Department of Mathematics Abstract:
In this article, our goal is to figure out a functional equation involving automorphisms and bi-derivations on certain semiprime ring. Also, we characterize the structure of automorphism, in case of prime rings. Search and serve lasted 1 second(s).
1: Paper Source
PDF document
14111, Claridon-Troy Road, Burton, Ohio 44021,
U.S.A.
oahuja@kent.edu
Faculty of Science and Art, 21280 Diyarbakir,
Turkey
ozlemg@dicle.edu.tr
1: Paper Source
PDF document
University of Zagreb, Unska 3, 10 000 Zagreb,
Croatia
andrea@zpm.fer.hr
Po Box 14428, Melbourne Vic 8001
Australia
sever.dragomir@vu.edu.au
URL:http://rgmia.vu.edu.au/dragomir
Mother
Theresa 5, 38 000 Prishtina
Kosova
razimhoxha@yahoo.com
Pierottijeva 6, 10000
Zagreb,
Croatia
pecaric@hazu.hr
1: Paper Source
PDF document
Islamic University, Science and Research Branch, Tehran,
Iran
Department of Mathematics, Azarbaidjan
University of Tarbiat Moallem, Tabriz,
Iran
Department of Mathematics, Amirkabir
University of Technology, Tehran,
Iran
alizadehhossain@yahoo.com
sh.rezapour@azaruniv.edu
vaez@aut.ac.ir
URL:http://www.azaruniv.edu/~rezapour
URL:http://math-cs.aut.ac.ir/vaezpour
1: Paper Source
PDF document
H-4010 Debrecen,
Pf. 12,
Hungary
szaz@math.klte.hu
1: Paper Source
PDF document
Faculty of Science,
Mansoura University 35516,
Egypt.
mkaouf127@yahoo.com
1: Paper Source
PDF document
University of Oradea,
410087, Oradea,
Romania.
mbalaj@uoradea.ro
1: Paper Source
PDF document
University of Haifa,
Haifa 31905,
Israel.
abramos@math.haifa.ac.il
University of Zagreb,
Vukelićeva 4, 10000,
Croatia
bozidar.ivankovic@zg.t-com.hr
University of Zagreb,
Prilaz Baruna Filipovića 30, 10000 Zagreb,
Croatia
pecaric@element.hr
1: Paper Source
PDF document
Department of Mathematics,"Politehnica" University of Timisoara,
P-ta. Victoriei, No.2, 300006-Timisoara,
ROMANIA
cloredana43@yahoo.com.
1: Paper Source
PDF document
Department of Mathematics,
University of Agriculture,
P. M. B. 2240, Abeokuta, Nigeria.
SE-971 87, Luleå , Sweden.
oguntuase@yahoo.com,
larserik@sm.luth.se .
1: Paper Source
PDF document
Department of Automatic Control and Computers
University of Ploiesti
Romania.
1: Paper Source
PDF document
Department of Computer Science and System Analysis,
College of Humanities and Sciences, Nihon University,
3-25-40, Sakurajyousui, Setagaya-ku, Tokyo, 156-8550, Japan.
University of Regina, Regina, Saskatchewan, Canada S4S 0A2.
1: Paper Source
PDF document
Bentley University,
Waltham, MA 02452,
U.S.A.
njosephy@bentley.edu
swoolford@bentley.edu
1: Paper Source
PDF document
Department of Automatic Control and Computers
University of Ploiesti
Romania.
vcirtoaje@upg-ploiesti.ro.
1: Paper Source
PDF document
Payame Noor University,
P.O. Box 19395-3697, Tehran,
Iran
b_yousefi@pnu.ac.ir
javadie2003@yahoo.com
1: Paper Source
PDF document
Changshu Institute of Technology,
Changshu, Jiangsu 215500,
China
which are analytic
in the unit disk. By virtue of the Ruscheweyh derivatives we introduce the new
subclasses Cp(n,α,β,λ,μ) of Ap. Subordination relations, inclusion relations,
convolution properties and a sharp coefficient estimate are
obtained. We also give a sufficient condition for a function to be
in Cp(n,α,β,λ,μ)
1: Paper Source
PDF document
Huo Xiang Road, Shanghai, 201203,
China
1: Paper Source
PDF document
P.O. Box 35195--363, Semnan,
Iran
Iran
Iran
Gyeongsang National University
Chinju 660-701,
Korea
1: Paper Source
PDF document
University of California,
Berkeley, CA 94720
United States of America
1: Paper Source
PDF document
Faculty of Science,
Port Said University, Port Said,
EGYPT.
Faculty of Science and Humanities,
Shaqra University, Dawadmi,
SAUDI ARABIA.
URL:
http://faculty.ksu.edu.sa/DRABDELDAIM/Pages/Home.aspx
1: Paper Source
PDF document
KNUST, Kumasi-
Ghana.
University of Education,
Winneba
Presbyterian University College, Abetifi,
Ghana
1: Paper Source
PDF document
Faculty of Sciences and Arts,
Giresun University, Giresun,
Turkey.
E-mail: imdat.iscan@giresun.edu.tr
Department of Mathematics,
Faculty of Sciences,
Karadeniz Technical University,
61080, Trabzon,
Turkey.
E-mail:
mkunt@ktu.edu.tr
1: Paper Source
PDF document
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
that provide upper bounds for the quantities
and
,
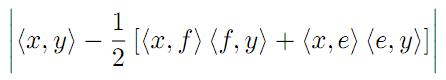
and x,y are vectors in H satisfying some appropriate assumptions are
given. Applications for discrete and integral inequalities are provided as
well.
1: Paper Source
PDF document
College of Science,
Aljouf University,
Aljouf 2014,
Saudi Arabia.
E-mail:
sididahmed@ju.edu.sa
Hassiba Benbouali, University of Chlef,
B.P. 151 Hay Essalem, Chlef 02000,
Algeria.
E-mail:
benali4848@gmail.com 
1: Paper Source
PDF document
Mirpur University of Science and Technology, Mirpur.
Pakistan.
E-mail1:
rashida12@gmail.com
E-mail2:
unigraz2009@yahoo.com
E-mail3:
ghazalagulshan@yahoo.com
E-mail4:
asialatif87@gmail.com
University of Ilorin, Ilorin,
Nigeria.
E-mail5:
krauf@unilorin.edu.ng
1: Paper Source
PDF document
Kabale University,
P.O.Box 317, Kabale,
Uganda.
1: Paper Source
PDF document
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
1: Paper Source
PDF document
University of Prishtina "Hasan Prishtina",
Prishtine 10000,
Kosova
Polytechnic University of Tirana, Tirana,
Albania.
1: Paper Source
PDF document
Caledonian College of Engineering, Muscat,
Sultanate of Oman.
E-mail: kr_karthikeyan1979@yahoo.com
University of Buraimi, Al Buraimi,
Sultanate of Oman.
E-mail: musthafa.ibrahim@gmail.com
Chennai-600005, Tamilnadu,
India.
1: Paper Source
PDF document
University of Perugia,
1, Via Vanvitelli -- 06123, Perugia,
Italy.
E-mail: domenico.candeloro@unipg.it,
anna.sambucini@unipg.it
Al. I. Cuza University,
700506 Iaşi,
Romania.
E-mail: croitoru@uaic.ro,
gavrilut@uaic.ro
1: Paper Source
PDF document
Universitas Brawijaya,
Malang,
Indonesia.
E-mail: mila_n12@ub.ac.id,
marjono@ub.ac.id
1: Paper Source
PDF document
University of KwaZulu-Natal, Durban,
South Africa.
E-mail:
216028272@stu.ukzn.ac.za,
mewomoo@ukzn.ac.za
1: Paper Source
PDF document
Jalan Ketintang Gedung C8,
Surabaya 60321,
Indonesia.
E-mail: manuharawati@unesa.ac.id,
dwiyunianti@unesa.ac.id,
muhammadjakfar@unesa.ac.id
1: Paper Source
PDF document
University of Florida,
Gainesville, FL 32611,
USA.
E-mail: qasdfgtyuiop@gmail.com
URL:
https://scholar.google.com/citations?user=t2nOdxQAAAAJ
1: Paper Source
PDF document
Sri Ramakrishna Institute of Technology, Coimbatore-10, Tamilnadu,
India.
E-mail: parvathasathish@gmail.com
Govt. Arts College, Coimbatore-641018, Tamilnadu,
India.
E-mail: senthilsenkumhari@gmail.com
1: Paper Source
PDF document
El Oued University,
P.O. Box 789, 39000 El Oued,
Algeria.
E-mail:
said-ameur-meziane@univ-eloued.dz
El Oued University,
P.O. Box 789, 39000 El Oued,
Algeria.
E-mail:
hadjammar-tedjani@univ-eloued.dz
Kasdi Merbah University,
30000 Ouargla,
Algeria.
E-mail: maiza.laid@univ-ouargla.dz
1: Paper Source
PDF document
"Politehnica" University of Timisoara,
P-ta. Victoriei, No.2, 300006-Timisoara,
Romania.
1: Paper Source
PDF document
Islamic University of Madinah,
KSA.
Department of Mathematics, Faculty of Science,
Sohag University, Sohag,
EGYPT.
E-mail:
mohamed_khalifa77@science.sohag.edu.eg,
mohammed.khalifa@iu.edu.sa
Assiut University, Assiut,
EGYPT.
E-mail: rbaky@live.com
1: Paper Source
PDF document
M'sila University, 28000,
Algeria.
E-mail: ourahmounabbes@yahoo.fr
Setif 1 University, 19000,
Algeria.
1: Paper Source
PDF document
Kirori Mal College,
University of Delhi,
Delhi,
India.
E-mail: rajkmc@gmail.com
Department of Mathematics,
University of Delhi,
Delhi,
India.
E-mail: kmc.satyapriya@gmail.com
1: Paper Source
PDF document
University of Duhok,
Kurdistan Region,
Iraq.
E-mail: aliasbkhalaf@uod.ac
University of Duhok,
Kurdistan Region,
Iraq.
E-mail: azhaarsallo@uod.ac
University of Sulaimani,
Kurdistan Region,
Iraq.
E-mail: shazad.ahmed@univsul.edu
1: Paper Source
PDF document
Universiti Sains Malaysia,
11800 USM, Penang,
Malaysia.
E-mail: ibra13975@gmail.com,
farahaini@usm.my,
zarita@usm.my
1: Paper Source
PDF document
York University, 4700 Keele St, Toronto,
ON M3J 1P3,
Canada.
E-mail: jmaxwellcampbell@gmail.com
No. 1, Ai-Guo West Road,
Taipei 10048, Taiwan.
E-mail: kwchen@uTaipei.edu.tw
URL:
https://math.utaipei.edu.tw/p/412-1082-22.php
1: Paper Source
PDF document
Kwara State University, Malete
P. M. B. 1530 Ilorin,
Nigeria.
E-mail: taofeek.wahab@kwasu.edu.ng
1: Paper Source
PDF document
Manipal Institute of Technology,
Manipal Academy of Higher Education,
Manipal 576 104,
India.
E-mail: sri_vatsabr@yahoo.com
Wonkwang University,
Iksan, 54538,
Republic of Korea.
E-mail: iki@wku.ac.kr
Vedant College of Engineering and Technology,
Rajasthan Technical University,
Bundi, 323021, Rajasthan,
India.
E-mail: arjunkumarrathie@gmail.com
1: Paper Source
PDF document
Universitas Brawijaya, Malang,
Indonesia.
E-mail: mila_n12@ub.ac.id
1: Paper Source
PDF document
Universiti Sains Malaysia,
11800 USM, Penang,
Malaysia.
E-mail: ibra13975@gmail.com,
farahaini@usm.my,
zarita@usm.my
1: Paper Source
PDF document
Faculty of Science,
Islamic University of Madinah, Madinah
K.S.A.
E-mail: ansari.abuzaid@gmail.com,
ansari.abuzaid@iu.edu.sa
Faculty of Science,
Taibah University, Madinah,
K.S.A.
E-mail: faiza.shujat@gmail.com,
fullahkhan@taibahu.edu.sa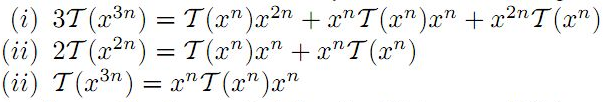 
1: Paper Source
PDF document
636011, Tamilnadu,
India.
E-mail:
dickson@periyaruniversity.ac.in,
padmasekarans@periyaruniversity.ac.in
Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
spanetsos@aspete.gr
1: Paper Source
PDF document
University of Brawijaya,
Malang,
Indonesia.
E-mail: mslk@ub.ac.id
rbagus@ub.ac.id
saadatul@ub.ac.id
1: Paper Source
PDF document
University of KwaZulu-Natal,
Private Bag X 54001,
Durban 4000.
E-mail: mkhizez2@ukzn.ac.za
parumasurn1@ukzn.ac.za
singhp@ukzn.ac.za
URL: https://www.ukzn.ac.za
1: Paper Source
PDF document
Khenchela,
Algeria.
E-mail: abdellah.menasri70@gmail.com
1: Paper Source
PDF document
University of Jammu,
Jammu 180006,
INDIA.
E-mail: rajat.singh.rs634@gmail.com
University of Jammu,
Jammu 180006,
INDIA.
E-mail: romeshmath@gmail.com
1: Paper Source
PDF document
Jaypee University of Information Technology,
Solan, Himachal Pradesh,
India.
E-mail: sksameer08@gmail.com,
pandeypkdelhi@gmail.com
1: Paper Source
PDF document
Jaypee University of Information Technology,
Solan, Himachal Pradesh,
India.
E-mail: sksameer08@gmail.com,
pandeypkdelhi@gmail.com
1: Paper Source
PDF document
Faculty of Science,
Islamic University of Madinah, Madinah
K.S.A.
E-mail: ansari.abuzaid@gmail.com,
ansari.abuzaid@iu.edu.sa
Faculty of Science
Taibah University, Madinah,
K.S.A.
E-mail: faiza.shujat@gmail.com,
fullahkhan@taibahu.edu.sa
Faculty of Science
Taibah University, Madinah,
K.S.A.
E-mail: Afallatah@taibahu.edu.sa
© 2004-2023 Austral Internet Publishing