|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Oscillations of First Order Linear Delay Difference Equations
Author(s):
G. E. Chatzarakis and I. P. Stavroulakis
Department of Mathematics, University of Ioannina,
451 10, Greece
ipstav@cc.uoi.gr
Abstract:
Consider the first order linear delay difference equation of
the form ![]()
![]() where
where
![]() is
a sequence of nonnegative real numbers, k is a positive integer and
is
a sequence of nonnegative real numbers, k is a positive integer and ![]() denotes
the forward difference operator
denotes
the forward difference operator ![]() New
oscillation criteria are established when the well-known oscillation conditions
New
oscillation criteria are established when the well-known oscillation conditions
![]() and
and
![]() are
not satisfied. The results obtained essentially improve known results in the
literature.
are
not satisfied. The results obtained essentially improve known results in the
literature.
Paper's Title:
Integer Sums of Powers of Trigonometric Functions (MOD p), for prime p
Author(s):
G. J. Tee
Department of Mathematics, University of Auckland,
Auckland,
New Zealand
tee@math.auckland.ac.nz
Abstract:
Many multi--parameter families of congruences (mod p) are found for integer
sums of
qth powers of the trigonometric functions over various sets of equidistant
arguments, where
p is any prime factor of q. Those congruences provide sensitive
tests for the accuracy
of software for evaluating trigonometric functions to high precision.
Paper's Title:
A Low Order Least-Squares Nonconforming Finite Element Method for Steady Magnetohydrodynamic Equations
Author(s):
Z. Yu, D. Shi and H. Zhu
College of Science,
Zhongyuan
University of Technology,
Zhengzhou 450007,
China.
E-mail:
5772@zut.edu.cn
School of Mathematics and Statistics,
Zhengzhou University,
Zhengzhou 450001,
China.
E-mail:
shi_dy@126.com
Mathematics Department,
University of Southern Mississippi,
Hattiesburg MS, 39406,
U.S.A
E-mail:
huiqing.zhu@usm.edu
Abstract:
A low order least-squares nonconforming finite element (NFE) method is proposed for magnetohydrodynamic equations with EQ1rot element and zero-order Raviart-Thomas element. Based on the above element's typical interpolations properties, the existence and uniqueness of the approximate solutions are proved and the optimal order error estimates for the corresponding variables are derived.
Paper's Title:
Essential Random Fixed Point Set of Random Operators
Author(s):
Ismat Beg
Centre for Advanced Studies in Mathematics,
Lahore University of Management Sciences (LUMS),
54792-Lahore, PAKISTAN.
ibeg@lums.edu.pk
URL: http://web.lums.edu.pk/~ibeg
Abstract:
We obtain necessary and sufficient conditions for the existence of essential random fixed point of a random operator defined on a compact metric space. The structure of the set of essential random fixed points is also studied.
Paper's Title:
On the Generalized Inverse  over Integral Domains
over Integral Domains
Author(s):
Yaoming Yu and Guorong Wang
College of Education, Shanghai Normal University
Shanghai 200234
People's Republic of China.
yuyaoming@online.sh.cn
grwang@shnu.edu.cn
Abstract:
In this paper, we study further the generalized inverse
 of a matrix A over an integral domain. We give
firstly some necessary and sufficient conditions for the existence
of the generalized inverse
of a matrix A over an integral domain. We give
firstly some necessary and sufficient conditions for the existence
of the generalized inverse  , an explicit expression
for the elements of the generalized inverse
, an explicit expression
for the elements of the generalized inverse  and an
explicit expression for the generalized inverse
and an
explicit expression for the generalized inverse  ,
which reduces to the {1} inverse. Secondly, we verify that the
group inverse, the Drazin inverse, the Moore-Penrose inverse and the
weighted Moore-Penrose inverse are identical with the generalized
inverse
,
which reduces to the {1} inverse. Secondly, we verify that the
group inverse, the Drazin inverse, the Moore-Penrose inverse and the
weighted Moore-Penrose inverse are identical with the generalized
inverse 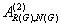 for an appropriate matrix G,
respectively, and then we unify the conditions for the existence and
the expression for the elements of the weighted Moore-Penrose
inverse, the Moore-Penrose inverse, the Drazin inverse and the group
inverse over an integral domain. Thirdly, as a simple application,
we give the relation between some rank equation and the existence of
the generalized inverse
for an appropriate matrix G,
respectively, and then we unify the conditions for the existence and
the expression for the elements of the weighted Moore-Penrose
inverse, the Moore-Penrose inverse, the Drazin inverse and the group
inverse over an integral domain. Thirdly, as a simple application,
we give the relation between some rank equation and the existence of
the generalized inverse  , and a method to compute the
generalized inverse
, and a method to compute the
generalized inverse  . Finally, we give an example of
evaluating the elements of
. Finally, we give an example of
evaluating the elements of  without calculating
without calculating
 .
.
Paper's Title:
Isoperimetric Inequalities for Dual Harmonic Quermassintegrals
Author(s):
Yuan Jun, Zao Lingzhi and Duan Xibo
School of Mathematics and Computer Science,
Nanjing Normal University, Nanjing, 210097,
China.
yuanjun_math@126.com
Department of Mathematics, Nanjing Xiaozhuang University,
Nanjing, 211171,
China.
lzhzhao@163.com
Department of Mathematics, Shandong Water Polytechnic,
Shandong, 276826,
China
dxb1111@sohu.com
Abstract:
In this paper, some isoperimetric inequalities for the dual harmonic
quermassintegrals are established.
Paper's Title:
A Geometric Generalization of Busemann-Petty Problem
Author(s):
Liu Rong and Yuan Jun
Shanghai Zhangjiang Group Junior Middle School,
Huo Xiang Road, Shanghai, 201203,
China
Abstract:
The norm defined by Busemann's inequality establishes a class of star body - intersection body. This class of star body plays a key role in the solution of Busemann-Petty problem. In 2003, Giannapoulos [1] defined a norm for a new class of half-section. Based on this norm, we give a geometric generalization of Busemann-Petty problem, and get its answer as a result
Paper's Title:
Two Further Methods for Deriving Four Results Contiguous to Kummer's Second Theorem
Author(s):
I. Kim and J. Kim
Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Korea.
E-mail: iki@wku.ac.kr
Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Korea.
E-mail: joohyung@wku.ac.kr
Abstract:
In the theory of generalized hypergeometric function, transformation and summation formulas play a key role. In particular, in one of the Kummer's transformation formulas, Kim, et al. in 2012, have obtained ten contiguous results in the form of a single result with the help of generalization of Gauss's second summation theorem obtained earlier by Lavoie, et al.. In this paper, we aim at presenting four of such results by the technique of contiguous function relations and integral method developed by MacRobert.
Paper's Title:
Viability
Theory And Differential Lanchester Type Models For Combat.
Differential Systems.
Author(s):
G. Isac and A. Gosselin
Department Of
Mathematics, Royal Military College Of Canada,
P.O. Box 17000, Stn Forces, Kingston,
Ontario, Canada K7k 7b4
isac-g@rmc.ca
gosselin-a@rmc.ca
URL:
http://www.rmc.ca/academic/math_cs/isac/index_e.html
URL:
http://www.rmc.ca/academic/math_cs/gosselin/index_e.html
Abstract:
In 1914, F.W. Lanchester proposed several mathematical models based on differential equations to describe combat situations [34]. Since then, his work has been extensively modified to represent a variety of competitions including entire wars. Differential Lanchester type models have been studied from many angles by many authors in hundreds of papers and reports. Lanchester type models are used in the planning of optimal strategies, supply and tactics. In this paper, we will show how these models can be studied from a viability theory stand point. We will introduce the notion of winning cone and show that it is a viable cone for these models. In the last part of our paper we will use the viability theory of differential equations to study Lanchester type models from the optimal theory point of view.
Paper's Title:
On the Optimal Buckling Loads of Clamped Columns
Author(s):
Samir Karaa
Department of Mathematics and Statistics
Sultan Qaboos University, P.O. Box 36, Alkhod 123
Muscat, Sultanate of Oman
skaraa@squ.edu.om
URL: http://ajmaa.org/EditorsU/SKaraa.php
Abstract:
We consider the problem of determining the optimal shape of a clamped column of given length and volume, without minimum cross section constraints.
We prove that the necessary condition of optimality derived by
Olhoff
and Rasmussen is sufficient when 0<
Paper's Title:
On Stan Ulam and his Mathematics
Author(s):
Krzysztof Ciesielski and Themistocles M. Rassias
Mathematics Institute, Jagiellonian University,
Abstract:
In this note we give a glimpse of the curriculum vitae of Stan Ulam, his personality and some of the mathematics he was involved in.
Paper's Title:
Topological Aspects of Scalarization in Vector Optimization Problems.
Author(s):
Peter I. Kogut, Rosanna Manzo and Igor V. Nechay
Department of Differential Equations,
Dnipropetrovsk National University, Naukova
STR.,
13,
49010 Dnipropetrovsk,
Ukraine
p.kogut@i.ua
Universitŕ di Salerno,
Department of Technical Cybernetics,
Dipartimento di Ingegneria dell'Informazione e Matematica Applicata,
Via Ponte don Melillo, 84084 Fisciano (SA),
Italy
manzo@diima.unisa.it
Dnipropetrovsk Technical University,
Acad. Lazarjan
STR., 2,
49010 Dnipropetrovsk,
Ukraine
i.nechay@i.ua
Abstract:
In this paper, we study vector optimization problems in partially ordered Banach spaces. We suppose that the objective mapping possesses a weakened property of lower semicontinuity and make no assumptions on the interior of the ordering cone. We derive sufficient conditions for existence of efficient solutions of the above problems and discuss the role of topological properties of the objective space. We discuss the scalarization of vector optimization problems when the objective functions are vector-valued mappings with a weakened property of lower semicontinuity. We also prove the existence of the so-called generalized efficient solutions via the scalarization process. All principal notions and assertions are illustrated by numerous examples.
Paper's Title:
On Some Relations Among the Solutions of the Linear Volterra Integral Equations
Author(s):
Ismet Ozdemir and Faruk Temizer
Inönü Üniversitesi Eğitim Fakültesi,
44280-Malatya,
Turkey
Abstract:
The sufficient conditions for y1(x)≤ y2(x) were given in [1] such that ym(x)=fm(x)+∫ax Km(x, t)ym(t)dt,(m=1,2) and x∈ [a, b]. Some properties such as positivity, boundedness and monotonicity of the solution of the linear Volterra integral equation of the form f(t)=1-∫0tK(t-τ)f(τ)dτ=1-K*f, (0≤ t<∞) were obtained, without solving this equation, in [3,4,5,6]. Also, the boundaries for functions f', f'',..., f(n),(n ∈ N) defined on the infinite interval [0, ∞) were found in [7,8].
In this work, for the given equation f(t)=1-K* f and n≥ 2, it is derived that there exist the functions L2, L3,..., Ln which can be obtained by means of K and some inequalities among the functions f, h2, h3,..., hi for i=2, 3,...., n are satisfied on the infinite interval [0, ∞), where hi is the solution of the equation hi(t)=1-Li* hi and n is a natural number.
Paper's Title:
On a Class of Meromorphic Functions of Janowski Type Related with a Convolution Operator
Author(s):
Abdul Rahman S. Juma, Husamaldin I. Dhayea
Department of
Mathematics,
Alanbar University, Ramadi,
Iraq.
E-mail: dr_juma@hotmail.com
Department of Mathematics,
Tikrit University, Tikrit,
Iraq.
URL: husamaddin@gmail.com
Abstract:
In this paper, we have introduced and studied new operator $Qkλ,m,γ by the Hadamard product (or convolution) of two linear operators Dkλ and Im,γ, then using this operator to study and investigate a new subclass of meromorphic functions of Janowski type, giving the coefficient bounds, a sufficient condition for a function to belong to the considered class and also a convolution property. The results presented provide generalizations of results given in earlier works.
Paper's Title:
The Dynamics of an Ebola Epidemic Model with Quarantine of Infectives
Author(s):
Eliab Horub Kweyunga
Department of Mathematics,
Kabale University,
P.O.Box 317, Kabale,
Uganda.
E-mail: hkweyunga@kab.ac.ug
Abstract:
The recurrent outbreaks of ebola in Africa present global health challenges. Ebola is a severe, very fatal disease with case fatality rates of up to 90%. In this paper, a theoretical deterministic model for ebola epidemic with quarantine of infectives is proposed and analyzed. The model exhibits two equilibria; the disease free and endemic equilibrium points. The basic reproduction number, R0, which is the main threshold, is obtained and the stability of the equilibrium points established. Using parameter values drawn from the 2014 West Africa ebola outbreak, a numerical simulation of the model is carried out. It is found that the dynamics of the model are completely determined by R0 and that a quarantine success rate of at least 70% is sufficient to contain the disease outbreak.
Paper's Title:
The Concept of Convergence for 2-Dimensional Subspaces Sequence in Normed Spaces
Author(s):
M. Manuharawati, D. N. Yunianti, M. Jakfar
Mathematics Department, Universitas
Negeri Surabaya,
Jalan Ketintang Gedung C8,
Surabaya 60321,
Indonesia.
E-mail: manuharawati@unesa.ac.id,
dwiyunianti@unesa.ac.id,
muhammadjakfar@unesa.ac.id
Abstract:
In this paper, we present a concept of convergence of sequence, especially, of 2-dimensional subspaces of normed spaces. The properties of the concept are established. As consequences of our definition in an inner product space, we also obtain the continuity property of the angle between two 2-dimensional subspaces of inner product spaces.
Paper's Title:
A Fuzzy Soft Quotient Topology and Its Properties
Author(s):
Haripamyu, Riri Alfakhriati, Monika Rianti Helmi, Jenizon
Department of Mathematics and Data Science, Andalas University, Padang, Indonesia.
E-mail: haripamyu@sci.unand.ac.id
ririalfakhriati123@gmail.com
monikariantihelmi@sci.unand.ac.id
jenizon@gmail.com
Abstract:
This research is to construct a new topology on fuzzy soft set by using the concept of quotient topology. Then we study the concept of quotient map to define the fuzzy soft quotient map and provide some relevant properties of fuzzy soft quotient map. Furthermore, we give some examples related to fuzzy soft quotient topology and fuzzy soft quotient map to apply some properties of fuzzy soft quotient map.
Paper's Title:
Boundness of the Power Exponential Function a2b +b2a
Author(s):
Yusuke Nishizawa, Yukuhito Yasuda
Faculty of Education, Saitama University,
Shimo-okubo 255, Sakura-ku, Saitama-city, Saitama,
Japan.
E-mail:
ynishizawa@mail.saitama-u.ac.jp
Faculty of Education, Saitama University,
Shimo-okubo 255, Sakura-ku, Saitama-city, Saitama,
Japan.
E-mail: y.yasuda.694@ms.saitama-u.ac.jp
Abstract:
In this paper, we consider the boundness of the power exponential function a2b +b2a for nonnegative real numbers a and b. The author proved that the function has the maximum value 1 for a + b = ˝, but it is no known that the minimum value for a + b = ˝. In this paper, we give the new proof of the function has the maximum value 1 and show that a2b +b2a > 0.989905 for a + b = ˝.
Paper's Title:
The Drazin-star and Star-Drazin Solutions to Quaternion Matrix Equations
Author(s):
Ivan I. Kyrchei, Dijana Mosić, Predrag Stanimirović
Pidstryhach Institute for Applied Problems
of Mechanics and Mathematics
of NAS of Ukraine, L'viv, 79060,
Ukraine.
E-mail:
ivankyrchei26@gmail.com
Faculty of Sciences and Mathematics,
University of Niš, P.O.
Box 224, 18000, Niš, Serbia.
E-mail: dijana@pmf.ni.ac.rs
Faculty of Sciences and Mathematics,
University of Niš, P.O.
Box 224, 18000, Niš, Serbia.
E-mail: pecko@pmf.ni.ac.rs
Abstract:
The notions of the Drazin-star and star-Drazin matrices are expanded to quaternion matrices in this paper. Their determinantal representations are developed in both cases in terms of noncommutative row-column determinants of quaternion matrices and for minors of appropriate complex matrices. We study all possible two-sided quaternion matrix equations with their one-sided partial cases whose uniquely determined solutions are based on the Drazin-star and star-Drazin matrices. Solutions of these equations are represented by Cramer's rules in both cases for quaternion and complex matrix equations. A numerical example is presented to illustrate our results.
Paper's Title:
Analytical and Numerical Solutions of the Inhomogenous Wave Equation
Author(s):
T. Matsuura and S. Saitoh
Department of Mechanical Engineering, Faculty of Engineering,
Gunma University, Kiryu 376-8515, Japan
matsuura@me.gunma-u.ac.jp
Department of Mathematics, Faculty of Engineering,
Gunma University, Kiryu 376-8515, Japan
ssaitoh@math.sci.gunma-u.ac.jp
Abstract:
In this paper, by a new concept and method we give approximate
solutions of the inhomogenous wave equation on multidimensional spaces.
Numerical experiments are conducted as well.
Paper's Title:
Norm Estimates for the Difference between Bochner’s Integral and the Convex Combination of Function’s Values
Author(s):
P. Cerone, Y.J. Cho, S.S. Dragomir, J.K. Kim, and S.S. Kim
School of
Computer Science and Mathematics,
Victoria University of Technology,
Po Box 14428, Mcmc 8001, Victoria, Australia.
pietro.cerone@vu.edu.au
URL:
http://rgmia.vu.edu.au/cerone/index.html
Department of
Mathematics Education, College of Education,
Gyeongsang National University, Chinju 660-701, Korea
yjcho@nongae.gsnu.ac.kr
School of
Computer Science and Mathematics,
Victoria University of Technology,
Po Box 14428, Mcmc 8001, Victoria, Australia.
sever.dragomir@vu.edu.au
URL:
http://rgmia.vu.edu.au/SSDragomirWeb.html
Department of
Mathematics, Kyungnam University,
Masan,, Kyungnam 631-701, Korea
jongkyuk@kyungnam.ac.kr
Department of
Mathematics, Dongeui University,
Pusan 614-714, Korea
sskim@dongeui.ac.kr
Abstract:
Norm estimates are developed between the Bochner integral of a vector-valued function in Banach spaces having the Radon-Nikodym property and the convex combination of function values taken on a division of the interval [a, b].
Paper's Title:
On Pseudo Almost
Periodic Solutions to Some Neutral Functional-Differential
Equations
Author(s):
Toka Diagana and Eduardo Hernández
Department of Mathematics, Howard University
2441 6th Street NW,
Washington DC 20059,
USA.
tdiagana@howard.edu
Departamento de Matemática, I.C.M.C. Universidade de Săo Paulo,
Caixa Postal
668, 13560-970, Săo Carlos SP,
Brazil.
lalohm@icmc.sc.usp.br
Abstract:
This paper discusses the existence and uniqueness of pseudo almost periodic solutions to a class of partial neutral functional-differential equations. Under some suitable assumptions, existence and uniqueness results are obtained. An example is given to illustrate abstract results.
Paper's Title:
Existence Results for Perturbed Fractional Differential
Inclusions
Author(s):
Y.-K. Chang
Department of Mathematics,
Lanzhou Jiaotong University, Lanzhou, Gansu 730070, People's
Republic of China
lzchangyk@163.com
Abstract:
This paper is mainly concerned with the following fractional differential
inclusions with boundary condition
A sufficient condition is established for the existence of solutions of the
above problem by using a fixed point theorem for multivalued maps due to
Dhage. Our result is proved under the mixed generalized Lipschitz and
Carathéodory conditions.
Paper's Title:
A Short Proof of an Open Inequality with Power-Exponential Functions
Author(s):
Mitsuhiro Miyagi and Yusuke Nishizawa
General Education, Ube National College of
Technology,
Tokiwadai 2-14-1, Ube,
Yamaguchi 755-8555,
Japan
E-mail:
miyagi@ube-k.ac.jp
yusuke@ube-k.ac.jp
Abstract:
V. Cîrtoaje conjectured that a3b + b3a + ( (a -b)/2 )4 ≤ 2 holds for all nonnegative numbers a and b with a +b =2. In this short note, we give a proof of the Cîrtoaje's conjecture with power-exponential functions.
Paper's Title:
The Effect of Harvesting Activities on Prey-Predator Fishery Model with Holling type II in Toxicant Aquatic Ecosystem
Author(s):
Moh Nurul Huda, Fidia Deny Tisna Amijaya, Ika Purnamasari
Department of Mathematics, Faculty of
Mathematics and Natural Science,
Mulawarman University,
Samarinda, East Kalimantan,75123
Indonesia.
E-mail: muh.nurulhuda@fmipa.unmul.ac.id
fidiadta@fmipa.unmul.ac.id
ika.purnamasari@fmipa.unmul.ac.id
Abstract:
This paper discussed prey-predator fishery models, in particular by analysing the effects of toxic substances on aquatic ecosystems. It is assumed in this model, that the prey population is plankton and the predator population is fish.\ Interaction between the two populations uses the Holling type II function. The existence of local and global critical points of the system are shown and their stability properties are analysed. Furthermore, Bionomic equilibrium and optimal control of harvesting are discussed. Finally, numerical simulations have been carried out to show in the interpretation of results.
Paper's Title:
Riemann-Stieltjes Integrals and Some Ostrowski Type Inequalities
Author(s):
W. G. Alshanti
Department of General Studies,
Jubail University College,
KSA.
E-mail: shantiw@ucj.edu.sa
Abstract:
In this article, we investigate new integral inequalities of Ostrowski's type of various functional aspects. For mapping's second derivative, we assume two cases, namely, L1 and L∞ spaces. Moreover, for first derivative, we investigate two different characteristics, namely, bounded variation and locally Lipchitz continuity. Applications to special means and composite quadrature rules are also carried out.
Paper's Title:
An Integration Technique for Evaluating Quadratic Harmonic Sums
Author(s):
J. M. Campbell and K.-W. Chen
Department of Mathematics and Statistics,
York University, 4700 Keele St, Toronto,
ON M3J 1P3,
Canada.
E-mail: jmaxwellcampbell@gmail.com
Department of Mathematics, University of Taipei,
No. 1, Ai-Guo West Road,
Taipei 10048, Taiwan.
E-mail: kwchen@uTaipei.edu.tw
URL:
https://math.utaipei.edu.tw/p/412-1082-22.php
Abstract:
The modified Abel lemma on summation by parts has been applied in many ways recently to determine closed-form evaluations for infinite series involving generalized harmonic numbers with an upper parameter of two. We build upon such results using an integration technique that we apply to ``convert'' a given evaluation for such a series into an evaluation for a corresponding series involving squared harmonic numbers.
Paper's Title:
Finite Volume Approximation of a Class of 2D Elliptic Equations with Discontinuous and Highly Oscillating Coefficients
Author(s):
J. D. Bambi Pemba and B. Ondami
Université Marien Ngouabi
Factuté des Sciences et Techniques
BP 69 Brazzaville,
Congo.
E-mail: bondami@gmail.com
URL:
https://www.researchgate.net/profile/Bienvenu-Ondami
https://www.linkedin.com/in/bienvenu-ondami
Abstract:
In this paper, we are interested in the Finite Volume approximation of a second-order two-dimensional elliptic equation in heterogeneous porous medium with a periodic structure. The equation's coefficients are therefore discontinuous and highly oscillating. This class of problems has been extensively studied in the literature, where various methods proposed for determining the so-called homogenized problem. What we are particularly interested in is the direct numerical approximation of the problem, which has received little attention in the literature. We use the cell-centered finite volume approach for this purpose. Error estimates are established, and numerical simulations are conducted for both the isotropic and anisotropic media cases. The obtained solution is compared to the homogenized solution, and the results show that this approach provides an adequate approximation of the exact solution.
Paper's Title:
A Note on Evaluation of a New Class of Integrals Involving Generalized Hypergeometric Function
Author(s):
Madhav Prasad Poudel, Dongkyu Lim*, Narayan Prasad Pahari, Arjun K. Rathie
School of Engineering,
Pokhara University, Pokhara-30, Kaski,
Nepal.
E-mail: pdmadav@gmail.com
Department of Mathematics Education,
Andong National University, Andong 36729,
Republic of Korea.
E-mail: dklim@anu.ac.kr
Central Department of Mathematics,
Tribhuvan University, Kirtipur, Kathmandu,
Nepal.
E-mail: nppahari@gmail.com
Department of Mathematics,
Vedant College of Engineering & Technology (Rajasthan Technical University),
Village: Tulsi,
Jakhamund, Dist. Bundi, Rajasthan State,
India.
E-mail:
arjunkumarrathie@gmail.com
Abstract:
In the theory of hypergeometric and generalized hypergeometric series, classical summation theorems such as those of Gauss, Gauss second, Bailey and Kummer for the series
2F1; Watson, Dixon, Whipple and Saalshutz play a key role. Applications of the above mentioned summation theorems are well known for the series
3F2. In our present investigation, we aim to evaluate twenty five new class of integrals involving generalized hypergeometric function in the form of a single integral of the form:
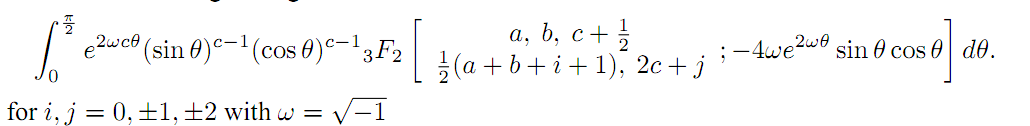
The results are established with the help of the generalizations of the classical Watson's summation theorem obtained earlier by Lavoie et al.. Fifty interesting integrals in the form of two integrals (twenty five each) have also been given as special cases of our main findings.
Paper's Title:
Portfolio Optimization of Sharia and Non-Sharia Stocks Using Single Index Model (Case study: Jakarta Sharia Index and Kompas 100 Index)
Author(s):
Kwardiniya Andawaningtyas, Muhammad Luthfi, Marjono, Endang Wahyu Handamari, Umu S'adah, Evi Ardiyani
Department of Mathematics,
Brawijaya University, Malang,
Indonesia.
Department of Mathematics,
IPB University, Bogor,
Indonesia.
E-mail:
dina_math@ub.ac.id
muhammadluthfi@student.ub.ac.id
marjono@ub.ac.id
ewahyu-math@ub.ac.id
u.saadah@ub.ac.id
ardiyanievi@apps.ipb.ac.id
Abstract:
Stocks are instruments with high returns but also have increased risks. One way to overcome this risk is to form a stock portfolio. This study observed 30 sharia stocks listed on the Jakarta Islamic Index (JII) and 28 non-shariah stocks listed on the Kompas 100 Index from March 2020 to September 2022. The data used is the daily closing price of stocks, the number of stock dividends, and the daily closing price of the Jakarta Composite Index (JCI) from 3rd March 2020, to 31st August 2022. In addition, interest rate of Bank Indonesia Certificate (SBI) is used as risk-free rate. This study aims to optimize the sharia and non-sharia stocks portfolio using the Single Index Model (SIM), which will then be evaluated using the Sharpe, Treynor, and Jensen ratio. The result is that the optimal portfolio of sharia stocks have better performance than the optimal portfolio of non-sharia stocks based on the Treynor ratio. Meanwhile, the optimal portfolio of non-sharia stocks have better performance than the optimal portfolio of sharia stocks based on the Sharpe and Jensen ratio.
Paper's Title:
On Vector Variational Inequality Problem in Terms of Bifunctions
Author(s):
C. S. Lalitha and Monika Mehta
Department of Mathematics, Rajdhani College,
Department of Mathematics, Satyawati College,
University of Delhi, Raja Garden,
Delhi 110015, India
cslalitha@rediffmail.com
University Of Delhi, Ashok Vihar,
Phase-III, Delhi 110052, India
mridul_in@yahoo.com
Abstract:
In this paper, we consider a generalized vector variational
inequality problem expressed in terms of a bifunction and establish
existence theorems for this problem by using the concepts of cone
convexity and cone strong quasiconvexity and employing the
celebrated Fan's Lemma. We also give two types of gap functions for this problem.
Paper's Title:
Local and Global Existence and Uniqueness Results for Second and Higher Order Impulsive Functional Differential Equations with Infinite Delay
Author(s):
Johnny Henderson and Abdelghani Ouahab
Department of Mathematics, Baylor University,
Waco, Texas 76798-7328
USA.
Johnny_Henderson@baylor.edu
Laboratoire de Mathématiques, Université de Sidi Bel Abbés
BP 89, 22000 Sidi Bel Abbées,
Algérie.
ouahab@univ-sba.dz
Abstract:
In this paper, we discuss the local and global existence and
uniqueness results for second and higher order impulsive functional
differential equations with infinite delay. We shall rely on a
nonlinear alternative of Leray-Schauder. For the global existence
and uniqueness we apply a recent Frigon and Granas nonlinear
alternative of Leray-Schauder type in Fréchet spaces.
Paper's Title:
Existence of Solutions for Third Order Nonlinear Boundary Value Problems
Author(s):
Yue Hu and Zuodong Yang
School of Mathematics and Computer Science, Nanjing Normal University, Jiangsu Nanjing 210097,
China.
huu3y2@163.com
College of Zhongbei, Nanjing Normal University, Jiangsu Nanjing 210046,
China.
zdyang_jin@263.net
yangzuodong@njnu.edu.cn
Abstract:
In this paper, the existence of solution for a class of third order quasilinear ordinary differential equations with nonlinear boundary value problems
(Φp(u"))'=f(t,u,u',u"), u(0)=A, u'(0)=B, R(u'(1),u"(1))=0
is established. The results are obtained by using upper and lower solution methods.
Paper's Title:
The Convergence of Modified Mann-Ishikawa Iterations when Applied to an Asymptotically Pseudocontractive Map
Author(s):
S. Soltuz
Departamento de Matematicas, Universidad de Los Andes, Carrera 1
No. 18A-10, Bogota,
Colombia
and
``T. Popoviciu" Institute of Numerical Analysis
Cluj-Napoca,
Romania
smsoltuz@gmail.com
URL:http://www.uniandes.edu.co/
Abstract:
We prove that under minimal conditions the modified Mann and Ishikawa iterations converge when dealing with an asymptotically pseudocontractive map. We give an affirmative answer to the open question from C.E. Chidume and H. Zegeye, Approximate fixed point sequences and convergence theorems for asymptotically pseudocontractive mappings, J. Math. Anal. Appl., 278 (2003), 354--366.
Paper's Title:
On a Subclass of Uniformly Convex Functions Defined by the Dziok-Srivastava Operator
Author(s):
M. K. Aouf and G. Murugusundaramoorthy
Mathematics Department, Faculty of Science,
Mansoura University 35516,
Egypt.
mkaouf127@yahoo.com
School of Science and Humanities, VIT University
Vellore - 632014,
India.
gmsmoorthy@yahoo.com
Abstract:
Making use of the Dziok-Srivastava operator, we define a new subclass Tlm([α1];α,β) of uniformly convex function with
negative coefficients. In this paper, we obtain coefficient estimates,
distortion theorems, locate extreme points and obtain radii of
close-to-convexity, starlikeness and convexity for functions belonging to the
class Tlm([α1];α,β) . We
consider integral operators associated with functions belonging to the class
Hlm([α1];α,β) defined via the Dziok-Srivastava
operator. We also obtain several results for the modified Hadamard products of
functions belonging to the class Tlm([α1];α,β)
and we obtain properties associated with generalized fractional calculus
operators.
Paper's Title:
Applications of Relations and Relators in the
Extensions of Stability Theorems for Homogeneous and Additive Functions
Author(s):
Árpád Száz
Institute of Mathematics, University of Debrecen,
H-4010 Debrecen,
Pf. 12,
Hungary
szaz@math.klte.hu
Abstract:
By working out an appropriate technique of relations and relators and extending the ideas of the direct methods of Z. Gajda and R. Ger, we prove some generalizations of the stability theorems of D. H. Hyers, T. Aoki, Th. M. Rassias and P. Găvruţă in terms of the existence and unicity of 2-homogeneous and additive approximate selections of generalized subadditive relations of semigroups to vector relator spaces. Thus, we obtain generalizations not only of the selection theorems of Z. Gajda and R. Ger, but also those of the present author.
Paper's Title:
Ellipses of Minimal Area and of Minimal Eccentricity Circumscribed About a Convex Quadrilateral
Author(s):
Alan Horwitz
Penn State University,
25 Yearsley Mill Rd.,
Media, PA 19063,
U.S.A
alh4@psu.edu
Abstract:
First, we fill in key gaps in Steiner's nice characterization of
the most nearly circular ellipse which passes through the vertices of a convex
quadrilateral,
![]() . Steiner proved that there is only one pair of conjugate
directions, M1 and M2, that belong to all ellipses of circumscription.
Then he proves that if there is an ellipse, E, whose equal
conjugate diameters possess the directional constants M1 and M2,
then E must be an ellipse of circumscription which has minimal eccentricity.
However, Steiner does not show the existence or uniqueness of such an ellipse.
We prove that there is a unique ellipse of minimal eccentricity which passes
through the vertices of
. Steiner proved that there is only one pair of conjugate
directions, M1 and M2, that belong to all ellipses of circumscription.
Then he proves that if there is an ellipse, E, whose equal
conjugate diameters possess the directional constants M1 and M2,
then E must be an ellipse of circumscription which has minimal eccentricity.
However, Steiner does not show the existence or uniqueness of such an ellipse.
We prove that there is a unique ellipse of minimal eccentricity which passes
through the vertices of
![]() . We also show that there exists an ellipse which passes through the vertices of
. We also show that there exists an ellipse which passes through the vertices of
![]() and whose
equal conjugate diameters
possess the directional constants M1 and M2. We also show
that there exists a unique ellipse of minimal area which passes through the
vertices of
and whose
equal conjugate diameters
possess the directional constants M1 and M2. We also show
that there exists a unique ellipse of minimal area which passes through the
vertices of
![]() . Finally, we call a convex quadrilateral,
. Finally, we call a convex quadrilateral,
![]() , bielliptic if the unique
inscribed and circumscribed ellipses of minimal eccentricity have the same
eccentricity. This generalizes the notion of bicentric quadrilaterals. In
particular, we show the existence of a bielliptic convex quadrilateral which is
not bicentric.
, bielliptic if the unique
inscribed and circumscribed ellipses of minimal eccentricity have the same
eccentricity. This generalizes the notion of bicentric quadrilaterals. In
particular, we show the existence of a bielliptic convex quadrilateral which is
not bicentric.
Paper's Title:
Generalized Efficient Solutions to One Class of Vector Optimization Problems in Banach Space
Author(s):
Peter I. Kogut, Rosanna Manzo, and Igor V. Nechay
Department of Differential Equations,
Dnipropetrovsk National University,
Naukova str., 13,
49050 Dnipropetrovsk,
Ukraine
p.kogut@i.ua
Dipartimento di Ingegneria
Dell’informazione e Matematica Applicata,
Universitŕ di Salerno,
Via
Ponte
Don Melillo,
84084 Fisciano
(Sa),
Italy
manzo@diima.unisa.it
Department of Technical Cybernetics,
Dnipropetrovsk Technical University,
Acad. Lazarjan str., 2,
49010
Dnipropetrovsk,
Ukraine
i.nechay@i.ua
Abstract:
In this paper, we study vector optimization problems in Banach spaces for essentially nonlinear operator equations with additional control and state constraints. We assume that an objective mapping possesses a weakened property of lower semicontinuity and make no assumptions on the interior of the ordering cone. Using the penalization approach we derive both sufficient and necessary conditions for the existence of efficient solutions of the above problems. We also prove the existence of the so-called generalized efficient solutions via the scalarization of some penalized vector optimization problem.
Paper's Title:
Approximation of Common Fixed Points of a Finite Family of Asymptotically Demicontractive Mappings in Banach Spaces
Author(s):
Yuchao Tang, Yong Cai, Liqun Hu and Liwei Liu
Department of Mathematics, NanChang University,
Nanchang 330031, P.R. China
Department of Mathematics, Xi'an Jiaotong University,
Xi'an 710049, P.R.
China
Abstract:
By virtue of new analytic techniques, we analyze and
study
several strong convergence theorems for the approximation of
common fixed points of asymptotically demicontractive mappings
via the multistep iterative sequence with errors in Banach
spaces. Our results improve and extend the corresponding ones
announced by Osilike , Osilike and Aniagbosor, Igbokwe, Cho et
al., Moore and Nnoli, Hu and all the others.
Paper's Title:
Necessary and Sufficient Conditions for Cyclic Homogeneous Polynomial Inequalities of Degree Four in Real Variables
Author(s):
Vasile Cirtoaje and Yuanzhe Zhou
Department of Automatic Control and Computers
University of Ploiesti
Romania.
vcirtoaje@upg-ploiesti.ro.
High School Affiliated to Wuhan University, China
Abstract:
In this paper, we give two sets of necessary and sufficient conditions that the inequality f4(x,y,z) ≥ 0 holds for any real numbers x,y,z, where f4(x,y,z) is a cyclic homogeneous polynomial of degree four. In addition, all equality cases of this inequality are analysed. For the particular case in which f4(1,1,1)=0, we get the main result in [3]. Several applications are given to show the effectiveness of the proposed methods.
Paper's Title:
Asymptotic Analysis of Positive Decreasing Solutions of a Class of Systems of Second Order Nonlinear Differential Equations in the Framework of Regular Variation
Author(s):
Jaroslav Jaroš, Kusano Takaŝi, Tomoyuki Tanigawa
Department of Mathematical Analysis and
Numerical Mathematics,
Faculty of Mathematics, Physics and Informatics,
Comenius Universiy, 842 48 Bratislava,
Slovakia.
E-mail: ksntksjm4@gmail.com
Professor Emeritus at: Hiroshima
University,
Department of Mathematics, Faculty of Science,
Higashi-Hiroshima 739-8526,
Japan.
E-mail: jaros@fmph.uniba.sk
Department of Mathematics, Faculty of
Education,
Kumamoto University, Kumamoto 860-8555,
Japan.
E-mail:
tanigawa@educ.kumamoto-u.ac.jp
Abstract:
The system of nonlinear differential equations
is under consideration, where αi
and βi are positive constants and
pi(t) and qi(t) are continuous regularly varying functions
on [a,∞). Two kinds of criteria are established for
the existence of strongly decreasing regularly varying solutions with negative
indices of (A) with precise asymptotic behavior at infinity. Fixed point
techniques and basic theory of regular variation are utilized for this purpose.
Paper's Title:
Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.
Paper's Title:
Integrating Factors and First Integrals of a Class of Third Order Differential Equations
Author(s):
Mohammadkheer Al-Jararha
Department of Mathematics,
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: mohammad.ja@yu.edu.jo
Abstract:
The principle of finding an integrating factor for a none exact differential equations is extended to a class of third order differential equations. If the third order equation is not exact, under certain conditions, an integrating factor exists which transforms it to an exact one. Hence, it can be reduced into a second order differential equation. In this paper, we give explicit forms for certain integrating factors of a class of the third order differential equations.
Paper's Title:
A Method of the Study of the Cauchy Problem for~a~Singularly Perturbed Linear Inhomogeneous Differential Equation
Author(s):
E. E. Bukzhalev and A. V. Ovchinnikov
Faculty of Physics,
Moscow State University,
1 Leninskie Gory,
Moscow, 119991,
Russia
E-mail: bukzhalev@mail.ru
Russian Institute for Scientific and
Technical Information of the Russian Academy of Sciences,
20 Usievicha St., Moscow, 125190,
Russia
E-mail: ovchinnikov@viniti.ru
Abstract:
We construct a sequence that converges to a solution of the Cauchy problem for a singularly perturbed linear inhomogeneous differential equation of an arbitrary order. This sequence is also an asymptotic sequence in the following sense: the deviation (in the norm of the space of continuous functions) of its nth element from the solution of the problem is proportional to the (n+1)th power of the parameter of perturbation. This sequence can be used for justification of asymptotics obtained by the method of boundary functions.
Paper's Title:
On Finding Integrating Factors and First Integrals for a Class of Higher Order Differential Equations
Author(s):
Mohammadkheer M. Al-Jararha
Department of Mathematics,
Yarmouk University,
Irbid, 21163,
Jordan.
E-mail: mohammad.ja@yu.edu.jo
Abstract:
If the $n-th$ order differential equation is not exact, under certain
conditions, an integrating factor exists which transforms the differential
equation into an exact one. Thus, the order of differential equation can be
reduced to the lower order. In this paper, we present a technique for finding
integrating factors of the following class of differential equations:
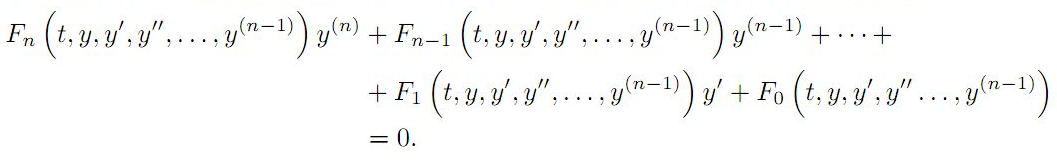
Here, the functions F0,F1,F2,
…,Fn are assumed to be continuous
functions with their first partial derivatives on some simply connected domain
Ω ⊂ Rn+1.
We also presented some demonstrative examples
Paper's Title:
On a New Class of Eulerian's Type Integrals Involving Generalized Hypergeometric Functions
Author(s):
Sungtae Jun, Insuk Kim and Arjun K. Rathie
General Education Institute,
Konkuk University, Chungju 380-701,
Republic of Korea.
Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Republic of Korea.
Department of Mathematics,
Vedant College of Engineering and Technology (Rajasthan Technical University),
Bundi-323021, Rajasthan,
India.
E-mail: sjun@kku.ac.kr, iki@wku.ac.kr, arjunkumarrathie@gmail.com
Abstract:
Very recently Masjed-Jamei and Koepf established interesting and useful generalizations of various classical summation theorems for the 2F1, 3F2, 4F3, 5F4 and 6F5 generalized hypergeometric series. The main aim of this paper is to establish eleven Eulerian's type integrals involving generalized hypergeometric functions by employing these theorems. Several special cases have also been given.
Paper's Title:
On an extension of Edwards's double integral with applications
Author(s):
I. Kim, S. Jun, Y. Vyas and A. K. Rathie
Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Republic of Korea.
General Education Institute,
Konkuk University,
Chungju 380-701,
Republic of Korea.
Department of Mathematics, School of
Engineering,
Sir Padampat Singhania University,
Bhatewar, Udaipur, 313601, Rajasthan State,
India.
Department of Mathematics,
Vedant College of Engineering and Technology,
(Rajasthan Technical University),
Bundi-323021, Rajasthan,
India.
E-mail: iki@wku.ac.kr
sjun@kku.ac.kr
yashoverdhan.vyas@spsu.ac.in
arjunkumarrathie@gmail.com
Abstract:
The aim of this note is to provide an extension of the well known and useful Edwards's double integral. As an application, new class of twelve double integrals involving hypergeometric function have been evaluated in terms of gamma function. The results are established with the help of classical summation theorems for the series 3F2 due to Watson, Dixon and Whipple. Several new and interesting integrals have also been obtained from our main findings.
Paper's Title:
On the Polyconvolution of Hartley Integral Transforms H1, H2, H1 and Integral Equations
Author(s):
Nguyen Minh Khoa and Dau Xuan Luong
Department of Mathematics,
Electric Power University,
Ha Noi, and Faculty of Fundamental Science,
Ha Long University, Quang Ninh,
Viet Nam.
E-mail: khoanm@epu.edu.vn,
dauxuanluong@gmail.com
Abstract:
In this paper, we construct and study a new polyconvolution * (f,g,h)(x) of functions f, g, h. We will show that the polyconvolution satisfy the following factorization equality
H1[*(f,g,h)](y)=(H2f)(y)(H1g)(y)(H1h)(y), ∀y∈ R.
We prove the existence of this polyconvolution in the space L(R). As examples, applications to solve an integral equation of polyconvolution type and two systems of integral equations of polyconvolution type are presented.
Paper's Title:
Bounds on the Jensen Gap, and Implications for Mean-Concentrated Distributions
Author(s):
Xiang Gao, Meera Sitharam, Adrian E. Roitberg
Department of Chemistry, and Department
of Computer & Information Science & Engineering,
University of Florida,
Gainesville, FL 32611,
USA.
E-mail: qasdfgtyuiop@gmail.com
URL:
https://scholar.google.com/citations?user=t2nOdxQAAAAJ
Abstract:
This paper gives upper and lower bounds on the gap in Jensen's inequality, i.e., the difference between the expected value of a function of a random variable and the value of the function at the expected value of the random variable. The bounds depend only on growth properties of the function and specific moments of the random variable. The bounds are particularly useful for distributions that are concentrated around the mean, a commonly occurring scenario such as the average of i.i.d. samples and in statistical mechanics.
Paper's Title:
Some fixed point results in partial S-metric spaces
Author(s):
M. M. Rezaee, S. Sedghi, A. Mukheimer, K. Abodayeh, and Z. D. Mitrovic
Department of Mathematics, Qaemshahr
Branch,
Islamic Azad University, Qaemshahr,
Iran.
E-mail: Rezaee.mohammad.m@gmail.com
Department of Mathematics, Qaemshahr
Branch,
Islamic Azad University, Qaemshahr,
Iran.
E-mail: sedghi.gh@qaemiau.ac.ir
Department of Mathematics and General
Sciences,
Prince Sultan University, Riyadh,
KSA.
E-mail: mukheimer@psu.edu.sa
Department of Mathematics and General
Sciences,
Prince Sultan University, Riyadh,
KSA.
E-mail: kamal@psu.edu.sa
Nonlinear Analysis Research Group,
Faculty of Mathematics and Statistics,
Ton Duc Thang University, Ho Chi Minh City,
Vietnam.
E-mail: zoran.mitrovic@tdtu.edu.vn
Abstract:
We introduce in this article a new class of generalized metric spaces, called partial S-metric spaces. In addition, we also give some interesting results on fixed points in the partial S-metric spaces and some applications.
Paper's Title:
Numerical Approximation by the Method of Lines with Finite-volume Approach of a Solute Transport Equation in Periodic Heterogeneous Porous Medium
Author(s):
D. J. Bambi Pemba and B. Ondami
Université Marien Ngouabi,
Factuté des Sciences et Techniques,
BP 69, Brazzaville,
Congo.
E-mail: bondami@gmail.com
Abstract:
In this paper we are interested in the numerical approximation of a two-dimensional solute transport equation in heterogeneous porous media having periodic structures. It is a class of problems which has been the subject of various works in the literature, where different methods are proposed for the determination of the so-called homogenized problem. We are interested in this paper, in the direct resolution of the problem, and we use the method of lines with a finite volume approach to discretize this equation. This discretization leads to an ordinary differential equation (ODE) that we discretize by the Euler implicit scheme. Numerical experiments comparing the obtained solution and the homogenized problem solution are presented. They show that the precision and robustness of this method depend on the ratio between, the mesh size and the parameter involved in the periodic homogenization.
Paper's Title:
Solving Non-Autonomous Nonlinear Systems of Ordinary Differential Equations Using Multi-Stage Differential Transform Method
Author(s):
K. A. Ahmad, Z. Zainuddin, F. A. Abdullah
School of Mathematical Sciences
Universiti Sains Malaysia
11800 USM Penang
Malaysia.
E-mail: abumohmmadkh@hotmail.com
zarita@usm.my
farahaini@usm.my
Abstract:
Differential equations are basic tools to describe a wide variety of phenomena in nature such as, electrostatics, physics, chemistry, economics, etc. In this paper, a technique is developed to solve nonlinear and linear systems of ordinary differential equations based on the standard Differential Transform Method (DTM) and Multi-stage Differential Transform Method (MsDTM). Comparative numerical results that we are obtained by MsDTM and Runge-Kutta method are proposed. The numerical results showed that the MsDTM gives more accurate approximation as compared to the Runge-Kutta numerical method for the solutions of nonlinear and linear systems of ordinary differential equations
Paper's Title:
Inequalities of Gamma Function Appearing in Generalizing Probability Sampling Design
Author(s):
Mohammadkheer M. Al-Jararha And Jehad M. Al-Jararha
Department of Mathematics,
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: mohammad.ja@yu.edu.jo
Department of Statistics,
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: jehad@yu.edu.jo
Abstract:
In this paper, we investigate the complete monotonicity of some functions involving gamma function. Using the monotonic properties of these functions, we derived some inequalities involving gamma and beta functions. Such inequalities can be used to generalize different probability distribution functions. Also, they can be used to generalize some statistical designs, e.g., the probability proportional to the size without replacement design.
Paper's Title:
Rational Expressions of Arithmetic and Geometric Means for the Sequence
npn ∈ N and the Geometric Progression
Author(s):
M. Kinegawa, S. Miyamoto and Y. Nishizawa
Faculty of Education, Saitama University,
Shimo-okubo 255, Sakura-ku, Saitama-city, Saitama,
Japan.
E-mail: m.kinegawa.645@ms.saitama-u.ac.jp
Faculty of Education, Saitama University,
Shimo-okubo 255, Sakura-ku, Saitama-city, Saitama,
Japan.
E-mail: s.miyamoto.245@ms.saitama-u.ac.jp
Faculty of Education, Saitama University,
Shimo-okubo 255, Sakura-ku, Saitama-city, Saitama,
Japan.
E-mail:
ynishizawa@mail.saitama-u.ac.jp
Abstract:
In this paper, we consider the arithmetic and geometric means for the sequence npn ∈ N and the geometric progression. We obtain the results associated with the rational expressions of the means.
Paper's Title:
Evaluation of a New Class of Double Integrals Involving Generalized Hypergeometric Function
4F3
Author(s):
Joohyung Kim, Insuk Kim and Harsh V. Harsh
Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Korea.
E-mail: joohyung@wku.ac.kr
Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Korea.
E-mail: iki@wku.ac.kr
Department of Mathematics, Amity School
of Eng. and Tech.,
Amity University Rajasthan
NH-11C, Jaipur-303002, Rajasthan,
India.
E-mail: harshvardhanharsh@gmail.com
Abstract:
Very recently, Kim evaluated some double integrals involving a generalized hypergeometric function 3F2 with the help of generalization of Edwards's well-known double integral due to Kim, et al. and generalized classical Watson's summation theorem obtained earlier by Lavoie, et al. In this research paper we evaluate one hundred double integrals involving generalized hypergeometric function 4F3 in the form of four master formulas (25 each) viz. in the most general form for any integer. Some interesting results have also be obtained as special cases of our main findings.
Paper's Title:
Oscillatory Behavior of Second-Order Non-Canonical
Retarded Difference Equations
Author(s):
G.E. Chatzarakis1, N. Indrajith2, E. Thandapani3 and K.S. Vidhyaa4
1Department
of Electrical and Electronic Engineering Educators,
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail: gea.xatz@aspete.gr,
geaxatz@otenet.gr
2Department
of Mathematics,
Presidency College, Chennai - 600 005,
India.
E-mail: indrajithna@gmail.com
3Ramanujan
Institute for Advanced Study in Mathematics,
University of Madras,
Chennai - 600 005,
India.
E-mail: ethandapani@yahoo.co.in
4
Department of Mathematics,Abstract:
Using monotonic properties of nonoscillatory solutions, we obtain new oscillatory criteria for the second-order non-canonical difference equation with retarded argument
![]()
Our oscillation results improve and extend the earlier ones. Examples illustrating the results are provided.
Paper's Title:
Preserver of Local Spectrum of Skew-product Operators
Author(s):
Rohollah Parvinianzadeh1,*, Meysam Asadipour2 and Jumakhan Pazhman3
1Department
of Mathematics,
College of Sciences,
University of Yasouj,
Yasouj, 75918-74934,
Iran.
E-mail: r.parvinian@yu.ac.ir
2Department
of Mathematics,
College of Sciences,
University of Yasouj,
Yasouj, 75918-74934,
Iran.
E-mail: Asadipour@yu.ac.ir
3Department
of Mathematics,
Ghor Institute of higher education,
Afghanistan.
E-mail: jumapazhman@gmail.com
Abstract:
Let H and K be infinite-dimensional complex Hilbert spaces, and B(H) (resp. B(K)) be the algebra of all bounded linear operators on H (resp. on K). For an operator T∈ B(H) and a vector h∈ H, let σT(h) denote the local spectrum of T at h. For two nonzero vectors h0∈ H and k0∈ K, we show that if two maps φ1 and φ2 from B(H) into B(K) satisfy
σφ1(T)φ2(S)*(k0)= σTS*(h0})
for all T, S ∈ B(H), and their range containing all operators of rank at most two, then there exist bijective linear maps P : H→ K and Q : K→ H such that φ1(T) = PTQ and φ2(T)* =Q-1T*P-1 for all T ∈ B(H). Also, we obtain some interesting results in this direction.
Paper's Title:
SQIRV Model for Omicron Variant with Time Delay
Author(s):
S. Dickson, S. Padmasekaran, G. E. Chatzarakis and S. L. Panetsos
Mathematics, Periyar University, Periyar
Palkalai Nagar, Salem,
636011, Tamilnadu,
India.
E-mail:
dickson@periyaruniversity.ac.in,
padmasekarans@periyaruniversity.ac.in
Electrical and Electronic Engineering
Educators, School of
Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
spanetsos@aspete.gr
Abstract:
In order to examine the dynamics of the Omicron variant, this paper uses mathematical modelling and analysis of a SQIRV model, taking into account the delay in the conversion of susceptible individuals into infected individuals and infected individuals into recovered individuals. The pandemic was eventually controlled as a result of the massive delays. To assure the safety of the host population, this concept incorporates quarantine and the COVID-19 vaccine. Both local and global stability of the model are examined. It is found that the fundamental reproduction number affects both local and global stability conditions. Our findings show that asymptomatic cases caused by an affected population play an important role in increasing Omicron infection in the general population. The most recent data on the pandemic Omicron variant from Tamil Nadu, India, is verified.
Paper's Title:
Higher Order Accurate Compact Schemes for Time Dependent Linear and Nonlinear Convection-Diffusion Equations
Author(s):
S. Thomas, Gopika P.B. and S. K. Nadupuri
Department of Mathematics
National Institute of Technology Calicut
Kerala
673601
India.
E-mail:
sobinputhiyaveettil@gmail.com
pbgopika@gmail.com nsk@nitc.ac.in
Abstract:
The primary objective of this work is to study higher order compact finite difference schemes for finding the numerical solution of convection-diffusion equations which are widely used in engineering applications. The first part of this work is concerned with a higher order exponential scheme for solving unsteady one dimensional linear convection-diffusion equation. The scheme is set up with a fourth order compact exponential discretization for space and cubic $C^1$-spline collocation method for time. The scheme achieves fourth order accuracy in both temporal and spatial variables and is proved to be unconditionally stable. The second part explores the utility of a sixth order compact finite difference scheme in space and Huta's improved sixth order Runge-Kutta scheme in time combined to find the numerical solution of one dimensional nonlinear convection-diffusion equations. Numerical experiments are carried out with Burgers' equation to demonstrate the accuracy of the new scheme which is sixth order in both space and time. Also a sixth order in space predictor-corrector method is proposed. A comparative study is performed of the proposed schemes with existing predictor-corrector method. The investigation of computational order of convergence is presented.
Paper's Title:
The arithmetic-geometric mean inequality from the integral of 1/t
Author(s):
Kuniya Ibaragi, Yusuke Nishizawa and Noriyuki Ohira
Faculty of Education,
Saitama University,
Shimo-okubo 255, Sakura-ku, Saitama-city, Saitama,
Japan.
k.ibaragi.896@ms.saitama-u.ac.jp
Faculty of Education,
Saitama University,
Shimo-okubo 255, Sakura-ku, Saitama-city, Saitama,
Japan.
ynishizawa@mail.saitama-u.ac.jp
Faculty of Education,
Saitama University,
Shimo-okubo 255, Sakura-ku, Saitama-city, Saitama,
Japan.
n.ohira.677@ms.saitama-u.ac.jp
Abstract:
In this short note, we improve the arithmetic-geometric mean inequality using by the integral of 1/t.
Paper's Title:
Indonesia's GDP Forecast: Evidence From Fuzzy Time Series Model Using Particle Swarm Optimization Algorithm
Author(s):
Ismail Djakaria1, Djihad Wungguli2, Regina Sugi Pakadang3, Sri Endang Saleh4, Maman Abdurachman Djauhari5
1,2,3Universitas
Negeri Gorontalo,
Department of Statistics, Gorontalo,
Indonesia.
4Universitas Negeri Gorontalo,
Department of Development Economics, Gorontalo,
Indonesia.
5Indonesian Institute of Education,
Jl. Terusan Pahlawan 32, Garut 44151,
Indonesia.
E-mail: iskar@ung.ac.id
URL:
https://orcid.org/0000-0003-1358-2356
Abstract:
Gross Domestic Product (GDP) is a principal indicator used to measure the economic condition of a country. Indonesia's GDP growth from 2017 to 2019 was approximately 6 percent; however, it experienced a decline in 2020 and 2021, with rates of only -0.02 percent and 2.41 percent, respectively. In the process of economic development planning, a forecasting system is required to determine GDP in the future. The forecasting method employed in this research is fuzzy time series optimized using Particle Swarm Optimization (PSO), to enhance the accuracy and convergence of forecasted values. The dataset used comprises secondary data, specifically 54 sets of Indonesian GDP data spanning from the first quarter of 2010 to the second quarter of 2023. The analysis results indicate that the proposed method is better than the conventional fuzzy time series approach. The former method provides a predictive value for one period in the future with a Mean Absolute Percentage Error (MAPE) value of 4.40%. In contrast, the latter yields higher predictive values with a MAPE value of 7.93%.
Paper's Title:
On Saturation of Norm Convergence of Walsh-Fourier Matrix Transform Means
Author(s):
István Blahota
Institute of Mathematics and Computer Sciences,
University of Nyíregyháza,
H-4400 Nyíregyháza,
Sóstói street 31/b,
Hungary
E-mail: blahota.istvan@nye.hu
Abstract:
In this paper we investigate the saturation of norm convergence issues for regular matrix transform means in case of Walsh-Paley system. The main result is the observation of equality ||σTn (f) - f ||p=0(a)n where an sequence of positive numbers tends to zero and there exists constant $c$, for which t1,n≤ can for every n∈P.
Paper's Title:
New Reverses of Schwarz, Triangle and Bessel Inequalities in Inner Product Spaces
Author(s):
S. S. Dragomir
School of Computer Science and Mathematics, Victoria
University of Technology, PO BOX
14428, MCMC 8001, VICTORIA, AUSTRALIA.
sever.dragomir@vu.edu.au
URL:
http://rgmia.vu.edu.au/SSDragomirWeb.html
Abstract:
New reverses of the Schwarz, triangle and Bessel inequalities in inner product spaces are pointed out. These results complement the recent ones obtained by the author in the earlier paper [13]. Further, they are employed to establish new Grüss type inequalities. Finally, some natural integral inequalities are stated as well.
Paper's Title:
On an Extension of Hilbert’s Integral Inequality with Some Parameters
Author(s):
Bicheng Yang
Department of
Mathematics, Guangdong Education College, Guangzhou, Guangdong 510303, People’s
Republic of China.
bcyang@pub.guangzhou.gd.cn
URL:
http://www1.gdei.edu.cn/yangbicheng/index.html
Abstract:
In this paper, by introducing some parameters and estimating the
weight function, we give an extension of Hilbert’s integral inequality with a
best constant factor. As applications, we consider the equivalent form and some
particular results.
Paper's Title:
Fekete-Szegö Inequality for Certain Class of Analytic Functions
Author(s):
V. Ravichandran, Maslina Darus, M. Hussain Khan, and K. G. Subramanian
School of
Mathematical Sciences, Universiti Sains Malaysia,
11800 Usm, Penang, Malaysia
vravi@cs.usm.my
School of
Mathematical Sciences, Faculty of Sciences and Technology,
Ukm, Banki 43600, Malaysia
maslina@pkrisc.cc.ukm.my
Department of
Mathematics, Islamiah College,
Vaniambadi 635 751, India
Department of
Mathematics, Madras Christian College, Tambaram,
Chennai- 600 059, India
kgsmani@vsnl.net
Abstract:
In this present investigation, the authors obtain Fekete-Szegö inequality for a certain
class of analytic functions f(z) for which
 lies in a
region starlike with respect to 1 and symmetric with respect to the real axis. Also certain application
of our main result for a class of functions defined by Hadamard product (convolution) is
given. As a special case of our result we obtain Fekete-Szegö inequality for a class of functions
defined through fractional derivatives. Also we obtain Fekete-Szegö inequality for the inverse
functions.
lies in a
region starlike with respect to 1 and symmetric with respect to the real axis. Also certain application
of our main result for a class of functions defined by Hadamard product (convolution) is
given. As a special case of our result we obtain Fekete-Szegö inequality for a class of functions
defined through fractional derivatives. Also we obtain Fekete-Szegö inequality for the inverse
functions.
Paper's Title:
Reverses of the Triangle Inequality in Inner Product Spaces
Author(s):
Sever S. Dragomir
School of Computer Science and Mathematics,
Victoria University Of Technology,
PO Box 14428, Mcmc 8001,
Victoria, Australia.
sever@csm.vu.edu.au
Url:
http://rgmia.vu.edu.au/SSDragomirWeb.html
Abstract:
Some new reverses for the generalised triangle inequality in inner product spaces are given. Applications in connection to the Schwarz inequality and for vector-valued integrals are provided as well.
Paper's Title:
Positive Solution For Discrete Three-Point Boundary Value
Problems
Author(s):
Wing-Sum Cheung And Jingli Ren
Department of Mathematics,
The University of Hong Kong,
Pokfulam, Hong Kong
wscheung@hku.hk
Institute of Systems Science,
Chinese Academy of Sciences,
Beijing 100080, P.R. China
renjl@mx.amss.ac.cn
Abstract:
This paper is concerned with the existence of positive solution to the discrete three-point boundary value problem
![]()
![]() ,
,
![]()
![]()
where
![]()
![]() , and f is allowed to change sign. By constructing
available operators, we shall apply the method of lower solution and the method
of topology degree to obtain positive solution of the above problem for
, and f is allowed to change sign. By constructing
available operators, we shall apply the method of lower solution and the method
of topology degree to obtain positive solution of the above problem for
![]() on a suitable interval.
The associated Green’s function is first given.
on a suitable interval.
The associated Green’s function is first given.
Paper's Title:
A Simple New Proof of Fan-Taussky-Todd Inequalities
Author(s):
Zhi-Hua Zhang and Zhen-Gang Xiao
Zixing Educational Research Section,
Chenzhou City, Hunan 423400, P. R. China.
Zhi-hua Zhang
Url: http://www.hnzxslzx.com/zzhweb/
Department Of Mathematics, Hunan Institute Of Science And Technology,
Yueyang City, Hunan 423400, P. R. China.
Zhen-gang Xiao
Abstract:
In this paper we present simple new proofs of the inequalities:
which holds for all real numbers a0 = 0, a1, · · · , an, an+1 = 0 and the coefficients
2(1 - cos(π/(n + 1))) and 2(1 + cos(π/(n + 1))) are the best possible; and
which holds for all real numbers a0 = 0, a1, · · · , an and the coefficients
2(1-cos(π/(2n + 1))) and 2(1 + cos(π/(2n + 1))) are the best possible.

Paper's Title:
Weak Solution for Hyperbolic Equations with a Non-Local Condition
Author(s):
Lazhar Bougoffa
King Khalid
University, Faculty of Science, Department of Mathematics,
P.O.Box 9004, Abha, Saudi Arabia
abogafah@kku.edu.sa
Abstract:
In this paper, we study hyperbolic equations with a non-local condition. We prove
the existence and uniqueness of weak solutions, using energy inequality and the density of the
range of the operator generated by the problem.
Paper's Title:
Meromorphic P-Valent Functions With Positive And Fixed Second Coefficients
Author(s):
B.A. Frasin and G. Murugusundaramoorthy
Department of Mathematics,
Al Al-Bayt University,
P.O. Box: 130095,
Mafraq, Jordan.
bafrasin@yahoo.com
URL: http://www.geocities.com/bafrasin/techie.html
Department of Mathematics,
Vellore Institute of Technology,
Deemed University,
Vellore - 632014,
India.
gmsmoorthy@yahoo.com
Abstract:
We introduce the classes ![]() and
and ![]() of meromorphic univalent functions ith positive and fixed second coefficients. The aim of the present paper is to obtain coefficient inequalities and closure theorems for these classes. Furthermore, the radii of convexity and starlikeness for functions the classes
of meromorphic univalent functions ith positive and fixed second coefficients. The aim of the present paper is to obtain coefficient inequalities and closure theorems for these classes. Furthermore, the radii of convexity and starlikeness for functions the classes ![]() and
and ![]() are determined.
are determined.
Paper's Title:
The successive approximations method and error estimation in terms of at most the first derivative for delay ordinary differential equations
Author(s):
Alexandru Mihai Bica
Department of Mathematics,
University of Oradea,
Str. Armatei Romane no.5,
410087, Oradea,
Romania
smbica@yahoo.com
abica@uoradea.ro
Abstract:
We present here a numerical method for first order delay ordinary differential
equations, which use the Banach's fixed point theorem, the sequence of
successive approximations and the trapezoidal quadrature rule. The error
estimation of the method uses a recent result of P. Cerone and S.S. Dragomir
about the remainder of the trapezoidal quadrature rule for Lipchitzian
functions and for functions with continuous first derivative.
Paper's Title:
On Zeros of Diagonally Quasiconvex Multifunctions
Author(s):
Zoran D. Mitrović
Faculty of Electrical Engineering,
University of Banja Luka,
78000 Banja Luka, Patre 5
Bosnia and Herzegovina
zmitrovic@etfbl.net
Abstract:
In this paper, we extended the notion of diagonally quasiconvexity
for multifunctions and established several existence results for
zeros of diagonally quasiconvex multifunctions. As applications we
obtain the results of fixed points, coincidence points and best
approximations for multifunctions. Using our result we also prove
the existence of solutions to the variational-like inequality
problem and generalized vector equilibrium problem. The results
of this paper generalize some known results in the literature.
Paper's Title:
Positive Periodic Time-Scale Solutions for Functional Dynamic Equations
Author(s):
Douglas R. Anderson and Joan Hoffacker
Department of Mathematics and Computer Science
Concordia College
Moorhead, MN 56562 USA
andersod@cord.edu
URL: http://www.cord.edu/faculty/andersod/
Department of Mathematical Sciences
Clemson University
Clemson, SC 29634 USA
johoff@clemson.edu
URL: http://www.math.clemson.edu/facstaff/johoff.htm
Abstract:
Using Krasnoselskii's fixed point theorem, we establish the existence of positive periodic solutions
to two pairs of related nonautonomous functional delta dynamic equations on periodic time scales, and then extend the discussion to higher-dimensional equations. Two pairs of corresponding nabla equations
are also provided in an analogous manner.
Paper's Title:
Notes on Sakaguchi Functions
Author(s):
Shigeyoshi Owa, Tadayuki Sekine and Rikuo Yamakawa
Department of Mathematics, Kinki University,
Higashi-Osaka, Osaka 577-8502,
Japan.
owa@math.kindai.ac.jp
Office of Mathematics, College of Pharmacy, Nihon University,
7-1 Narashinodai, Funabashi-city,
Chiba, 274-8555, Japan.
tsekine@pha.nihon-u.ac.jp
Department of Mathematics, Shibaura Institute of Technology,
Minuma, Saitama-city,
Saitama 337-8570, Japan.
yamakawa@sic.shibaura-it.ac.jp
Abstract:
By using the definition for certain
univalent functions f(z) in the open unit disk U given by K. Sakaguchi
[2], two classes S(α) and T(α) of analytic functions in U
are introduced. The object of the present paper is to discuss some properties of
functions f(z) belonging to the classes S(α) and T(α).
Paper's Title:
Boundary Value Problems for Fractional Diffusion-Wave equation
Author(s):
Varsha Daftardar-Gejji and Hossein Jafari
Department of Mathematics, University of Pune,
Ganeshkhind, Pune - 411007,
INDIA.
vsgejji@math.unipune.ernet.in
jafari_h@math.com
Abstract:
Non homogeneous fractional diffusion-wave equation has been solved under linear/nonlinear boundary conditions. As the order of time derivative changes from
0 to 2, the process changes from slow diffusion to classical diffusion to mixed diffusion-wave behaviour.
Numerical examples presented here confirm this inference. Orthogonality of eigenfunctions in case of fractional Stürm-Liouville problem has been established
Paper's Title:
Uniqueness of Meromorphic Functions that Share Three Values
Author(s):
Abhijit Banerjee
Department of Mathematics
Kalyani Government Engineering College
West Bengal 741235
India.
abanerjee_kal@yahoo.co.in
abanerjee@mail15.com
abanerjee_kal@rediffmail.com
Abstract:
In the paper dealing with the uniqueness problem of meromorphic functions we prove five theorems one of which will improve a result given by Lahiri \cite{5} and the remaining will supplement some previous results.
Paper's Title:
A Reverse
of the Triangle Inequality in Inner Product Spaces and Applications for
Polynomials
Author(s):
I. Brnetić, S. S. Dragomir, R. Hoxha and J. Pečarić
Department of Applied Mathematics, Faculty of Electrical
Engineering and Computing,
University of Zagreb, Unska 3, 10 000 Zagreb,
Croatia
andrea@zpm.fer.hr
School of Computer Science & Mathematics, Victoria University
Po Box 14428, Melbourne Vic 8001
Australia
sever.dragomir@vu.edu.au
URL:http://rgmia.vu.edu.au/dragomir
Faculty of Applied Technical Sciences, University of Prishtina,
Mother
Theresa 5, 38 000 Prishtina
Kosova
razimhoxha@yahoo.com
Faculty of Textile Technology, University of Zagreb,
Pierottijeva 6, 10000
Zagreb,
Croatia
pecaric@hazu.hr
Abstract:
A reverse of the triangle inequality in inner product spaces related to the
celebrated Diaz-Metcalf inequality with applications for complex polynomials
is given.
Paper's Title:
On the Fekete-Szeg
Author(s):
T.N. Shanmugam and A. Singaravelu
Department of Mathematics,
Department of Mathematics,
College of Engineering,
Anna University, Chennai-600 025,
Tamilnadu, India
shan@annauniv.edu
Valliammai Engineering College,
Chennai-603 203,
Tamilnadu, India
sivasaisastha@rediffmail.com
Abstract:
In this present investigation, the authors obtainFekete-Szegő's inequality for certain normalized analytic functions ![]() defined on the open
unit disk for which
defined on the open
unit disk for which ![]() lie in a region starlike with
respect to 1 and symmetric with respect
to the real axis. Also certain applications of the main result for a class of functions
defined by convolution are given. As a special case of this result, Fekete-Szegő's inequality for a class of functions
defined through fractional derivatives is also obtained.
lie in a region starlike with
respect to 1 and symmetric with respect
to the real axis. Also certain applications of the main result for a class of functions
defined by convolution are given. As a special case of this result, Fekete-Szegő's inequality for a class of functions
defined through fractional derivatives is also obtained.
Paper's Title:
Komatu Integral Transforms of Analytic Functions Subordinate to Convex Functions
Author(s):
T. N. Shanmugam and C. Ramachandran
Department of Mathematics, College of Engineering,
Anna University, Chennai-600 025, Tamilnadu,
India
shan@annauniv.edu
Department of Mathematics, College of Engineering,
Anna University, Chennai-600 025, Tamilnadu,
India
crjsp2004@yahoo.com
Abstract:
In this paper, we consider the class A of the functions f(z) of the form
which are analytic in an open disk
has some property. Certain inclusion and the closure properties like convolution with convex univalent function etc. are studied.

 and study certain subclass of the class A, for which
and study certain subclass of the class A, for which
Paper's Title:
A Coefficient Inequality For Certain Subclasses of Analytic
Functions Related to Complex Order
Author(s):
B. Srutha Keerthi, B. Adolf Stephen and S. Sivasubramanian
Department Of Applied Mathematics, Sri Venkateswara College Of Engineering, Anna University,
Sriperumbudur, Chennai - 602 105,
India.
laya@svce.ac.in
Department of Mathematics, Madras Christian College,
Chennai - 600059,
India
adolfmcc2003@yahoo.co.in
Department of Mathematics, College of Engineering, Anna University,
Tamilnadu, Chennai - 600 025,
India.
sivasaisastha@rediffmail.com
Abstract:
In this present investigation, the authors obtain coefficient
inequality for certain normalized analytic functions of complex order f(z) defined
on the open unit disk for which
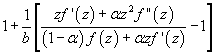 (
(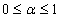 and
and  be a complex number) lies in a region starlike with respect to 1 and is symmetric with respect to the real axis. Also
certain applications of the main result for a class of functions of complex order
defined by convolution are given. As a special case of this result, coefficient
inequality for a class of functions defined through fractional derivatives is
obtained. The motivation of this paper is to give a generalization of the
coefficient inequalities of the subclasses of starlike and convex functions of
complex order.
be a complex number) lies in a region starlike with respect to 1 and is symmetric with respect to the real axis. Also
certain applications of the main result for a class of functions of complex order
defined by convolution are given. As a special case of this result, coefficient
inequality for a class of functions defined through fractional derivatives is
obtained. The motivation of this paper is to give a generalization of the
coefficient inequalities of the subclasses of starlike and convex functions of
complex order.
Paper's Title:
Construction of Lyapunov Functionals In Functional Differential Equations With Applications To Exponential Stability In Volterra Integro-differential Equations
Author(s):
Youssef N. Raffoul
Department of Mathematics, University of Dayton,
Dayton OH 45469-2316,
USA
youssef.raffoul@notes.udayton.edu
URL:http://academic.udayton.edu/YoussefRaffoul
Abstract:
Non-negative definite Lyapunov functionals are employed to obtain
sufficient conditions that guarantee the exponential asymptotic
stability and uniform exponential asymptotic stability of the zero
solution of nonlinear functional differential systems. The theory
is applied to Volterra integro-differential equations in the form
of proposition examples.
Paper's Title:
On Oscillation of
Second-Order Delay Dynamic Equations on Time Scales
Author(s):
S. H. Saker
Department of Mathematics, Faculty of Science,
Mansoura University, Mansoura, 35516,
Egypt.
shsaker@mans.edu.eg
Abstract:
Some new oscillation criteria for second-order linear delay dynamic equation
on a time scale T are established. Our results improve the
recent results for delay dynamic equations and in the special case when
T=R, the results include the oscillation results established by Hille [1948,
Trans. Amer. Math. Soc. 64 (1948), 234-252] and Erbe [Canad. Math. Bull. 16
(1973), 49-56.] for differential equations. When T=Z the
results include and improve some oscillation criteria for difference
equations. When T=hZ, h>0, T=qN and T=N2, i.e., for generalized second order delay difference equations our
results are essentially new and can be applied on different types of time
scales. An example is considered to illustrate the main results.
Paper's Title:
Some Inequalities for a Certain Class of Multivalent Functions
Using Multiplier Transformation
Author(s):
K. Suchithra, B. Adolf Stephen, A. Gangadharan and S. Sivasubramanian
Department Of Applied Mathematics
Sri Venkateswara College Of Engineering
Sriperumbudur, Chennai - 602105,
India.
suchithravenkat@yahoo.co.in
Department Of Mathematics,
Madras Christian College
Chennai - 600059,
India.
adolfmcc2003@yahoo.co.in
Department Of Applied Mathematics
Sri Venkateswara College Of Engineering
Sriperumbudur, Chennai - 602105,
India.
ganga@svce.ac.in
Department Of Mathematics,
Easwari Engineering College
Ramapuram, Chennai - 600089,
India.
ganga@svce.ac.in
Abstract:
The object of the present paper is to derive several inequalities
associated with differential subordinations between analytic functions
and a linear operator defined for a certain family of p-valent
functions, which is introduced here by means of a family of extended
multiplier transformations. Some special cases and consequences of
the main results are also considered.
Paper's Title:
Multivalent Harmonic Mappings Convoluted With a Multivalent Analytic Function
Author(s):
Om P. Ahuja and Özlem Güney
Kent State University, Department of Mathematical Sciences,
14111, Claridon-Troy Road, Burton, Ohio 44021,
U.S.A.
oahuja@kent.edu
University of Dicle, Department of Mathematics, Abstract:
The object of this paper is to study certain geometric properties of
a family of multivalent harmonic mappings in the plane convoluted
with a multivalent analytic function in the open unit disc. Paper's Title:
A Subclass of Meromorphically Multivalent Functions with Applications to Generalized Hypergeometric Functions Author(s):
M. K. Aouf
Mathematics Department,
Faculty of Science,
Abstract:
In this paper a new subclass of meromorphically multivalent functions, which
is defined by means of a Hadamard product (or convolution) involving some
suitably normalized meromorphically p-valent functions. The main object of
the present paper is to investigate the various important properties and
characteristics of this subclass of meromorphically multivalent functions.
We also derive many interesting results for the Hadamard products of
functions belonging to this subclass. Also we consider several applications
of our main results to generalized hypergeomtric functions.
Paper's Title:
Ulam Stability of Functional Equations Author(s):
Stefan Czerwik and Krzysztof Król
Institute of Mathematics Abstract:
In this survey paper we present some of the main results on Ulam-Hyers-Rassias stability
for important functional equations.
Paper's Title:
On the product of M-measures in l-groups Author(s):
A. Boccuto, B. Riěcan, and A. R. Sambucini
Dipartimento di Matematica e Informatica,
Abstract:
Some extension-type theorems and compactness
properties for the Paper's Title:
Asymptotic Distribution of Products of Weighted Sums of Dependent
Random Variables
Author(s):
Y. Miao and J. F. Li
College
of Mathematics
and Information
Science,
College
of Mathematics
and Information
Science,
Abstract:
In this paper we establish the asymptotic distribution of products
of weighted sums of dependent positive random variable, which
extends the results of Rempała and Wesołowski (2002).
Paper's Title:
Fractional Integral Operators and Olsen Inequalities on
Non-Homogeneous Spaces
Author(s):
Idha Sihwaningrum, Herry P. Suryawan, Hendra Gunawan
Analysis and Geometry Group, Abstract:
We prove the boundedness of the fractional
integral operator Iα
on generalized Morrey spaces of non-homogeneous type. In addition, we also
present Olsen-type inequalities for a multiplication operator involving Iα.
Our proof uses a result of García-Cuerva and Martell
[3]. Paper's Title:
Real Interpolation Methods and Quasilogarithmic Operators
Author(s):
Ming Fan
School of Industrial Technology and Management, Abstract:
The purpose of this paper is to deal with nonlinear quasilogarithmic operators, which possesses
the uniformly bounded commutator
property on various interpolation spaces in the sense of Brudnyi-Krugljak associated
with the quasi-power parameter spaces. The duality, and the domain and range spaces
of these operators are under consideration. Some known inequalities
for the Lebesgue integration spaces and the trace
classes are carried over to the non-commutative symmetric spaces of measurable operators
affiliated with a semi-finite von Neumann algebra.
Paper's Title:
Hardy Type Inequalities via
Convexity - The Journey so Far Author(s):
James A.
Oguntuase and Lars-Erik Persson Department of
Mathematics, Luleĺ University of Technology, Abstract:
It is nowadays well-known that Hardy's
inequality (like
many other inequalities) follows directly from Jensen's inequality. Most of
the development of Hardy type inequalities has not used this simple fact,
which obviously was unknown by Hardy himself and many others. Here we report
on some results obtained in this way mostly after 2002 by mainly using this
fundamental idea.
Paper's Title:
On an Elliptic Over-Determined Problem in
Dimension Two Author(s):
Lakhdar Ragoub Abstract:
We extend the method of Weinberger for a
non-linear over-determined elliptic problem Paper's Title:
On Opial's Inequality for Functions of n-Independent Variables
Author(s):
S. A. A. El-Marouf and S. A.
AL-Oufi Department of Mathematics, Department of Mathematics, Abstract:
In this paper, we introduce Opial inequalities for functions of
n-independent variables. Also, we discuss some different forms of Opial
inequality containing functions of n independent variables and their partial
derivatives with respect to independent variables. Paper's Title:
Existence Results for Second Order Impulsive Functional Differential Equations with Infinite Delay Author(s):
M. Lakrib, A. Oumansour and K. Yadi
Laboratoire de Mathématiques, Université Djillali Laboratoire de Mathématiques, Université Abou Bekr Abstract:
In this paper we study the existence of solutions for second order
impulsive functional differential equations with infinite delay.
To obtain our results, we apply fixed point methods. Paper's Title:
Stability Problems for Generalized Additive Mappings and Euler-Lagrange Type Mappings Author(s):
M. Todoroki, K. Kumahara, T. Miura and S.-E. Takahasi
The Open University of Japan, Toho University, Yamagata University, Abstract:
We introduce a generalized additivity of a mapping between Banach
spaces and establish the Ulam type stability problem for a
generalized additive mapping. The obtained results are somewhat
different from the Ulam type stability result of Euler-Lagrange
type mappings obtained by H. -M. Kim, K. -W. Jun and J. M. Rassias. Paper's Title:
Szegö Limits and Haar Wavelet Basis Author(s):
M. N. N. Namboodiri and S. Remadevi Dept. of Mathematics, Cochin University
of Science and Technology, Dept. of Mathematics, College of
Engineering, Abstract:
This paper deals with Szegö type limits for multiplication operators on
L2 (R) with respect to Haar orthonormal basis. Similar studies have
been carried out by Morrison for multiplication operators Tf using Walsh System and Legendre polynomials
[14]. Unlike the
Walsh and Fourier basis functions, the Haar basis functions are local in
nature. It is observed that Szegö type limit exist for a class of
multiplication operators Tf , f∈ L∞ (R) with respect to Haar
(wavelet) system with appropriate ordering. More general classes of orderings of Haar system are
identified for which the Szegö type limit exist for certain classes of
multiplication operators. Some illustrative examples are also provided.
Paper's Title:
Some Identities for Ramanujan - Göllnitz - Gordon Continued fraction
Author(s):
M. S. Mahadeva Naika, B. N. Dharmendra and S. Chandan Kumar Department of Mathematics, Department of Mathematics, Abstract:
In this paper, we obtain certain P--Q eta--function identities, using which we establish identities providing modular relations between Ramanujan-Göllnitz-Gordon
continued fraction H(q) and H(q^n)
for n= 2, 3, 4, 5, 7, 8, 9, 11, 13, 15, 17, 19, 23, 25, 29 and 55.
Paper's Title:
To a Banach *-algebra in a Semipartial Dynamical System Author(s):
Bahman Tabatabaie Shourijeh and Seyed Mostafa Zebarjad Department of Mathematics,
E-mail:
tabataba@math.susc.ac.ir
Abstract:
By a partial dynamical system, we mean a triple containing a C*-algebra A, a discrete group G and a partial action of G on A. There are two C*--algebras associated to a given partial dynamical system. These are nothing but the certain C*-completions of a Banach *-algebra. In constructing such a Banach *-algebra, usually, a tedious limit process is used to apply. In this paper, we prove some theorems in this context without any limit process. Paper's Title:
On Eigenvalues and Boundary Curvature of the C*-algebra Numerical Rang Author(s):
M. T. Heydari Department of Mathematics, E-mail:
heydari@yu.ac.ir Abstract:
Let A be a C*-algebra with unit 1 and
a∈A be a nilpotent. By Donoghue's Theorem, all corner points of
its numerical range V(a) belong to the spectrum σ(a). It is therefore natural to expect that, more
generally, the distance from a point p on the boundary ∂ V(a) of
V(a) to σ(a) should be in some sense bounded by the radius of
curvature of ∂ V(a) at p. Paper's Title:
The boundedness of Bessel-Riesz operators on generalized Morrey spaces Author(s):
Mochammad Idris, Hendra Gunawan and Eridani Department of Mathematics, Department of Mathematics, Department of Mathematics, Abstract:
In this paper, we prove the boundedness of Bessel-Riesz operators
on generalized Morrey spaces. The proof uses the usual dyadic
decomposition, a Hedberg-type inequality for the operators, and the boundedness
of Hardy-Littlewood maximal operator. Our results reveal that the norm of
the operators is dominated by the norm of the kernels. Paper's Title:
Stability of the D-Bar Reconstruction Method for Complex Conductivities Author(s):
1S.
El Kontar, 1T.
El Arwadi, 1H.
Chrayteh, 2J.-M.
Sac-Épée 1Department of Mathematics and
Computer Science, 2Institut Élie Cartan de
Lorraine, Abstract:
In 2000, Francini solved the inverse conductivity problem for twice-differentiable conductivities and
permittivities. This solution was considered to be the first approach using D-bar methods with complex
conductivities. In 2012, based on Francini's work, Hamilton introduced a reconstruction method of the
conductivity distribution with complex values. The method consists of six steps. A voltage potential
is applied on the boundary. Solving a D-Bar equation gives the complex conductivity. In this paper,
the stability of the D-Bar equation is studied via two approximations, texp and tB, for
the scattering transform. The study is based on rewriting the reconstruction method in terms of
continuous operators. The conductivity is considered to be non smooth. Paper's Title:
A Note on Divergent Fourier Series and λ-Permutations Author(s):
A. Castillo, J. Chavez and H. Kim Tufts University, Texas Tech University, University of Michigan-Dearborn, Abstract:
We present a continuous function on [-π,π] whose Fourier series diverges and it cannot be rearranged to converge by a
λ-permutation. Paper's Title:
Existence of Positive Solutions for
Nonlinear Fractional Differential Equations
with Multi-point Boundary Conditions Author(s):
N. Adjeroud Khenchela University, Department of
Mathematics, Abstract:
This paper is devoted to the existence results of positive solutions for a nonlinear fractional differential equations with multi-point boundary
conditions. By means of the Schauder fixed point theorem, some results on the existence are obtained. Paper's Title:
Polyanalytic Functions on Subsets of Z[i]
Author(s):
Abtin Daghighi Linköping University,
E-mail:
abtindaghighi@gmail.com Abstract:
For positive integers q we consider the kernel of the
powers Lq where L is one of three kinds of discrete analogues of the Cauchy-Riemann operator. The first two kinds are well-studied, but the third kind less so.
We give motivations for further study of the third kind especially since its symmetry makes it more appealing for the cases
q≥ 2. From an algebraic perspective it makes sense that the chosen
multiplication on the kernels is compatible with the choice of pseudo-powers. We
propose such multiplications together with associated pseudo-powers. We develop
a proof-tool in terms of certain sets of uniqueness. Paper's Title:
Fractional class of analytic functions Defined Using q-Differential Operator
Author(s):
K . R. Karthikeyan, Musthafa Ibrahim and S. Srinivasan Department of Mathematics and
Statistics, College of Engineering, Department of Mathematics, Presidency
College (Autonomous), Abstract:
We define a q-differential fractional operator, which
generalizes Salagean and Ruscheweyh differential operators. We introduce and study a new class of analytic functions involving q-differential fractional operator. We also determine the necessary and sufficient conditions for functions to be in the class. Further, we obtain the coefficient estimates, extreme points, growth and distortion bounds. Paper's Title:
On Commutator of Aluthge Transforms and Fuglede-Putnam Property Author(s):
(Manzar Maleki, Ali Reza Janfada and Seyed Mohammad Sadegh Nabavi Sales International Campus, Faculty of
Mathematical Sciences, Faculty of Mathematics and Statistics,
Department of Mathematics, Department of Pure Mathematics, Hakim
Sabzevari University, Abstract:
We deal with the well-known Fuglede-Putnam theorem and related FP-property. We show that if
(A,B) has the FP-property, then so has
Paper's Title:
An Analytical Solution of Perturbed Fisher's Equation Using Homotopy Perturbation Method (HPM), Regular Perturbation Method (RPM) and Adomian Decomposition Method (ADM) Author(s):
Moussa Bagayogo, Youssouf Minoungou, Youssouf Pare Departement de Mathematique, Abstract:
In this paper, Homotopy Perturbation Method (HPM), Regular Pertubation Method (RPM) and Adomian decomposition Method (ADM) are applied to Fisher equation. Then, the solution yielding the given initial conditions is gained. Finally, the solutions obtained by each method are compared Paper's Title:
Dynamical Analysis of HIV/AIDS Epidemic Model with Two Latent Stages, Vertical Transmission and Treatment Author(s):
Nur Shofianah, Isnani Darti, Syaiful Anam Mathematics Department,Faculty of
Mathematics and Natural Sciences. Abstract:
We discuss about dynamical analysis of HIV/AIDS epidemic model with two
latent stages, vertical transmission and treatment. In this model, the spreading
of HIV occurs through both horizontal and vertical transmission. There is also
treatment for individual who has been HIV infected. The latent stage is divided
into slow and fast latent stage based on the immune condition which varies for
each individual. Dynamical analysis result shows that the model has two
equilibrium points: the disease-free equilibrium point and the endemic
equilibrium point. The existence and global stability of equilibrium points
depend on the basic reproduction number R0. When R0
<1, only the disease-free equilibrium point exists. If R0 >1,
there are two equilibrium points, which are the disease-free equilibrium point
and the endemic equilibrium point. Based on the result of stability analysis,
the disease-free equilibrium point is globally asymptotically stable if R0
<1, while if R0 > 1 and p=q, the endemic
equilibrium point will be globally asymptotically stable. In the end, we show
some numerical simulations to support the analytical result. Paper's Title:
An Existence of the Solution to Neutral Stochastic Functional Differential Equations Under the Holder Condition Author(s):
Young-Ho Kim Department of Mathematics, E-mail: iyhkim@changwon.ac.kr
Abstract:
In this paper, we show the existence and uniqueness of solution of
the neutral stochastic functional differential equations under
weakened H\"{o}lder condition, a weakened linear growth condition,
and a contractive condition. Furthermore, in order to obtain the
existence of a solution to the equation we used the Picard sequence. Paper's Title:
Weyl's theorem for class Q and k - quasi class Q Operators Author(s):
S. Parvatham and D. Senthilkumar Department of Mathematics and Humanities,
Post Graduate and Research Department of
Mathematics, Abstract:
In this paper, we give some properties of class Q
operators. It is proved that every class Q operators satisfies
Weyl's theorem under the condition that T2 is isometry.
Also we proved that every k quasi class Q operators is
Polaroid and the spectral mapping theorem holds for this class of operator. It
will be proved that single valued extension property, Weyl and generalized
Weyl's theorem holds for every k quasi class Q
operators. Paper's Title:
On Ruled Surfaces According to Quasi-Frame in Euclidean 3-Space Author(s):
M. Khalifa Saad and R. A. Abdel-Baky Department of Mathematics, Faculty of
Science, Department of Mathematics, Faculty of
Science, Abstract:
This paper aims to study the skew ruled surfaces by using the quasi-frame of
Smarandache curves in the Euclidean 3-space. Also, we reveal the
relationship between Serret-Frenet and quasi-frames and give a parametric
representation of a directional ruled surface using the quasi-frame.
Besides, some comparative examples are given and plotted which support our
method and main results. Paper's Title:
Antiderivatives and Integrals Involving Incomplete Beta Functions with Applications Author(s):
R. AlAhmad1,2 and H. Almefleh1 Mathematics Department, Faculty of Engineering, Abstract:
In this paper, we prove that incomplete beta functions are antiderivatives of several products and powers of trigonometric functions, we give formulas for antiderivatives for products and powers of trigonometric functions in term of incomplete beta functions, and we evaluate integrals involving trigonometric functions using incomplete beta functions. Also, we extend some properties of the beta functions to the incomplete beta functions. As an application for the above results, we find the moments for certain probability distributions. Paper's Title:
Reduced Generalized Combination Synchronization Between Two n-Dimensional Integer-Order Hyperchaotic Systems and One m-Dimensional Fractional-Order Chaotic System Author(s):
Smail Kaouache, Mohammed Salah Abdelouahab and Rabah Bououden Laboratory of Mathematics and their
interactions, Abstract:
This paper is devoted to investigate the problem of
reduced generalized combination synchronization (RGCS) between two n-dimensional integer-order hyperchaotic drive systems and one m-dimensional
fractional-order chaotic response system. According to the stability theorem of
fractional-order linear system, an active mode controller is proposed to
accomplish this end. Moreover, the proposed synchronization scheme is
applied to synchronize three different chaotic systems, which are the Danca hyperchaotic system, the modified hyperchaotic Rossler system, and the fractional-order Rabinovich-Fabrikant chaotic system. Finally, numerical results are presented to fit our theoretical analysis. Paper's Title:
Existence and Approximation of Traveling Wavefronts for the Diffusive Mackey-Glass Equation Author(s):
C. Ramirez-Carrasco and J. Molina-Garay Facultad de Ciencias Basicas, Abstract:
In this paper, we consider the diffusive Mackey-Glass model with discrete delay. This equation describes the dynamics of the blood cell production. We investigate the existence of traveling wavefronts solutions connecting the two steady states of the model. We develop an alternative proof of the existence of such solutions and we also demonstrate the existence of traveling wavefronts moving at minimum speed. The proposed approach is based on the use technique of upper-lower solutions. Finally, through an iterative procedure, we show numerical simulations that approximate the traveling wavefronts, thus confirming our theoretical results. Paper's Title:
Coexisting Attractors and Bubbling Route to Chaos in Modified Coupled Duffing Oscillators Author(s):
B. Deruni1, A. S. Hacinliyan1,2, E. Kandiran3, A. C. Keles2, S. Kaouache4, M.-S. Abdelouahab4, N.-E. Hamri4 1Department
of Physics, 2Department
of Information Systems and Technologies, 3Department
of Software Development, 4Laboratory
of Mathematics and their interactions, E-mail:
berc890@gmail.com Abstract:
In this article dynamical behavior of coupled Duffing oscillators is analyzed under a small modification. The oscillators have cubic damping instead of linear one. Although single duffing oscillator has complex dynamics, coupled duffing systems possess a much more complex structure. The dynamical behavior of the system is investigated both numerically and analytically. Numerical results indicate that the system has double scroll attractor with suitable parameter values. On the other hand, bifurcation diagrams illustrate rich behavior of the system, and it is seen that, system enters into chaos with different routes. Beside classical bifurcations, bubbling route to chaos is observed for suitable parameter settings. On the other hand, Multistability of the system is indicated with the coexisting attractors, such that under same parameter setting the system shows different periodic and chaotic attractors. Moreover, chaotic synchronization of coupled oscillators is illustrated in final section. Paper's Title:
Pointwise Convergence of Fourier-type Series with Exponential Weights
Author(s):
Hee Sun Jung and Ryozi Sakai Department of Mathematics Education,
Sungkyunkwan University, Department of Mathematics, Abstract:
Let R = ( - ∞,∞), and let Q∈C1(R):R→[0,∞)
be an even function. We consider the exponential weights w(x)=e-Q(x),
x∈R. In this paper we obtain a pointwise convergence theorem for the Fourier-type series with respect to the orthonormal
polynomials {pn(w2;x)}. Paper's Title:
On Euler's First Transformation Formula for k-hypergeometric Function Author(s):
Sungtae Jun and Insuk Kim General Education Institute, Abstract:
Mubeen et al. obtained Kummer's first transformation for the
k-hypergeometric function. The aim of this note is to provide the Euler-type first transformation for the
k-hypergeometric function. As a limiting case, we recover the results of Mubeen
et al. In addition to this, an alternate and easy derivation of Kummer's first transformation for the
k-hypergeometric function is also given. Paper's Title:
Hankel Functional Connected to Lemniscate of Bernoulli Author(s):
K. Ramanuja Rao, Rajnesh Lal and Kaushal Singh Fiji National University, Abstract:
The aim of present paper is to derive a higher bound (HB) of 3rd
order Hankel determinant for a collection of holomorphic mappings
connected with exactly to the right side of the lemniscate of Bernoulli,
whose polar coordinates form is r2 = 2cos2(2θ). The method carried
in this paper is more refined than the method adopted by the authors
(see
[1]), who worked on this problem earlier. Paper's Title:
Locally Bicomplex Convex Module and Their Applications Author(s):
Stanzin Kunga and Aditi Sharma Department of Mathematics, Department of Mathematics, Abstract:
Let X be a locally BC convex module and L(X) be the family of all continuous bicomplex linear operators on
X. In this paper, we study some concepts of D-valued seminorms on
locally BC convex module. Further, we study the bicomplex version of Co and
(Co,1) semigroup. The work of this paper is inspired by the work in
[2] and
[6]. Paper's Title:
Algorithms for Nonlinear Problems Involving Strictly Pseudocontractive Mappings Author(s):
Mathew Olajiire Aibinu1, Surendra Colin Thakur2, Sibusiso Moyo3 1Institute for Systems Science
& KZN E-Skill CoLab, 1DSI-NRF
Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS), 2 KZN E-Skill CoLab,
3Institute for Systems Science & Office of the DVC Research,
Innovation & Engagement Milena Court, Abstract:
The puzzles in approximating a fixed point of nonlinear problems involving the class of strictly pseudocontractive mappings are conquered in this paper through viscosity implicit rules. Using generalized contraction mappings, a new viscosity iterative algorithm which is implicit in nature is proposed and analysed in Banach spaces for the class of strictly pseudocontractive mappings. The computations and analysis which are used in the proposed scheme are easy to follow and this gives rooms for a broad application of the scheme. It is obtained that the proposed iterative algorithm converges strongly to a fixed point of a
μ-strictly pseudocontractive mapping which also solves a variational inequality problem. The result is also shown to hold for finite family of strictly pseudocontractive mappings. A numerical example is given to show the skillfulness of the proposed scheme and its implementation.
Paper's Title:
A Review on Minimally Supported Frequency Wavelets Author(s):
K Pallavi1, M C Lineesh1, A Noufal2 1
Faculty of Science and Art, 21280 Diyarbakir,
Turkey
ozlemg@dicle.edu.tr
1: Paper Source
PDF document
Mansoura University 35516,
Egypt
mkaouf127@yahoo.com
1: Paper Source
PDF document
Silesian University of Technology
Kaszubska 23,
44-100 Gliwice,
Poland
Stefan.Czerwik@polsl.pl
Krzysztof.Krol@polsl.pl
1: Paper Source
PDF document
via Vanvitelli, 1 I-06123 Perugia,
Italy.
boccuto@dipmat.unipg.it
URL:
http://www.dipmat.unipg.it/~boccuto
Katedra Matematiky, Fakulta Prírodných Vied,
Univerzita Mateja Bela,
Tajovského, 40, Sk-97401 Banská Bystrica,
Slovakia.
riecan@fpv.umb.sk
Dipartimento di Matematica e Informatica,
via Vanvitelli, 1 I-06123 Perugia,
Italy.
matears1@unipg.it
URL:
http://www.unipg.it/~matears1
product of l-group-valued M-measures are proved.
1: Paper Source
PDF document
Henan Normal
University
Henan,
China
yumiao728@yahoo.com.cn
Henan Normal
University, 453007
Henan,
China.
junfen_li@yahoo.com.cn
1: Paper Source
PDF document
Faculty of Mathematics and Natural Sciences,
Bandung Institute of Technology, Bandung 40132,
Indonesia
hgunawan@math.itb.ac.id
URL:
http://personal.fmipa.itb.ac.id/hgunawan/
1: Paper Source
PDF document
Dalarna University, 781 88 Borlänge, Sweden
fmi@du.se
URL: http://users.du.se/~fmi
1: Paper Source
PDF document
Department of Mathematics,
University of Agriculture,
P. M. B. 2240, Abeokuta, Nigeria.
SE-971 87, Luleĺ , Sweden.
oguntuase@yahoo.com,
larserik@sm.luth.se .
1: Paper Source
PDF document
Department of Mathematics and Information of Tiyadhechnology
AL Yamamah University
P.O. Box 45 180, Riyadh 11 512
Saudi Arabia.
in R2.
We prove that the domain in consideration is a ball. The
tool of this investigation are maximum principles and P-functions.
1: Paper Source
PDF document
Faculty of Science,
Minoufiya University,
Shebin El-Koom,
Egypt
Faculty of Science, Taibah University,
Madenahmonwarah,
Kingdom of Saudia Arabia
1: Paper Source
PDF document
Liabées, B.P. 89 Sidi Bel Abbčs 22000, Algérie
mlakrib@univ-sba.dz
oumansour@univ-sba.dz
Belkaid, B.P. 119 Tlemcen 13000, Algérie
k_yadi@mail.univ-tlemcen.dz
1: Paper Source
PDF document
Chiba, 261-8586,
Japan
tomamiyu3232@sky.sannet.ne.jp
kumahara@ouj.ac.jp
Yamagata University,
Yonezawa 992-8510,
Japan
miura@yz.yamagata-u.ac.jp
Chiba, 273-0866,
Japan
sin_ei1@yahoo.co.jp
1: Paper Source
PDF document
Cochin-21, Kerala,
India.
Cherthala, Kerala,
India.
1: Paper Source
PDF document
Bangalore University,
Central College Campus,
Bangalore-560 001,
INDIA
Maharani's Science College for Women,
J. L. B. Road, Mysore-570 001,
INDIA
1: Paper Source
PDF document
College of Sciences,
Shiraz University, Shiraz 71454,
Iran.
zebarjad@mail.yu.ac.ir
URL:
http://research.shirazu.ac.ir/faculty/More.asp?ID=207
1: Paper Source
PDF document
College of Sciences,
Yasouj University,
Yasouj, 75914-74831,
Iran.
1: Paper Source
PDF document
Bandung Institute of Technology,
Bandung 40132,
Indonesia.
E-mail:
mochidris@students.itb.ac.id
Bandung Institute of Technology,
Bandung 40132,
Indonesia.
E-mail: hgunawan@math.itb.ac.id
URL:
http://personal.fmipa.itb.ac.id/hgunawan/
Airlangga University,
Surabaya 60115,
Indonesia.
E-mail: eridani.dinadewi@gmail.com
1: Paper Source
PDF document
Faculty of Science, Beirut Arab University,
P.O. Box: 11-5020, Beirut,
Lebanon.
E-mail: srs915@student.bau.edu.lb
Université de Lorraine - Metz,
France.
1: Paper Source
PDF document
Department of Mathematics,
Medford, MA 02155,
USA
E-mail: angel.castillo@tufts.edu
Department of Mathematics and Statistics,
Lubbock, TX 79409,
USA
E-mail: josechavez5@my.unt.edu
Department of Mathematics and Statistics,
Dearborn, MI 48128,
USA.
E-mail: khyejin@umich.edu
1: Paper Source
PDF document
Khenchela, 40000,
Algeria.
E-mail: adjnac@gmail.com
1: Paper Source
PDF document
SE-581 83,
Sweden.
1: Paper Source
PDF document
Caledonian College of Engineering, Muscat,
Sultanate of Oman.
E-mail: kr_karthikeyan1979@yahoo.com
University of Buraimi, Al Buraimi,
Sultanate of Oman.
E-mail: musthafa.ibrahim@gmail.com
Chennai-600005, Tamilnadu,
India.
1: Paper Source
PDF document
Ferdowsi University of Mashhad, Mashhad,
Iran.
E-mail: manzar.maleki@gmail.com
University of Birjand,
P. O. Box 414, Birjand 9717851367,
Iran.
E-mail: ajanfada@birjand.ac.ir
P.O. Box 397, Sabzevar,
Iran.
E-mail: sadegh.nabavi@hsu.ac.ir
![]() where 0≤
t1,t2≤1 are arbitrary.
We first prove that
where 0≤
t1,t2≤1 are arbitrary.
We first prove that
 if and only if
AX=XB for all X, whenever (A,B) has the FP-property. We
prove some similar results for
if and only if
AX=XB for all X, whenever (A,B) has the FP-property. We
prove some similar results for
 instead of $
instead of $![]() as well. Also we introduce the sequence of generalized iterations of Aluthge transform of operators and express some results for this notion associated to the FP-property.
as well. Also we introduce the sequence of generalized iterations of Aluthge transform of operators and express some results for this notion associated to the FP-property.
1: Paper Source
PDF document
Universite Ouaga I Pr Joseph Ki-Zerbo,
Burkina Faso.
E-mail:
moussabagayogo94@gmail.com,
m.youl@yahoo.fr,
pareyoussouf@yahoo.fr.
1: Paper Source
PDF document
University of Brawijaya,
Jl. Veteran, Malang 65145,
Indonesia.
E-mail:
nur_shofianah@ub.ac.id,
isnanidarti@ub.ac.id,
syaiful@ub.ac.id
1: Paper Source
PDF document
Changwon National University,
Changwon, Gyeongsangnam-do 51140,
Korea.
1: Paper Source
PDF document
Sri Ramakrishna Institute of Technology, Coimbatore-10, Tamilnadu,
India.
E-mail: parvathasathish@gmail.com
Govt. Arts College, Coimbatore-641018, Tamilnadu,
India.
E-mail: senthilsenkumhari@gmail.com
1: Paper Source
PDF document
Islamic University of Madinah,
KSA.
Department of Mathematics, Faculty of Science,
Sohag University, Sohag,
EGYPT.
E-mail:
mohamed_khalifa77@science.sohag.edu.eg,
mohammed.khalifa@iu.edu.sa
Assiut University, Assiut,
EGYPT.
E-mail: rbaky@live.com
1: Paper Source
PDF document
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: rami_thenat@yu.edu.jo
Higher Colleges of Technology,
Ras Alkhaimah,
UAE.
1: Paper Source
PDF document
Abdelhafid Boussouf University Center, Mila.
Algeria
E-mail: smailkaouache@gmail.com,
medsalah3@yahoo.fr,
rabouden@yahoo.fr
1: Paper Source
PDF document
Universidad Catolica del Maule, Talca,
Chile
E-mail: carloshrc1989@gmail.com
molina@imca.edu.pe
1: Paper Source
PDF document
University of Yeditepe,
Turkey.
University of Yeditepe,
Turkey
University of Yeditepe,
Turkey.
University Center of Abdelhafid Boussouf,
Mila 43000,
Algeria.
ahacinliyan@yeditepe.edu.tr
engin.kandiran@yeditepe.edu.tr
cihan.keles@yeditepe.edu.tr
s.kaouache@centr-univ-mila.dz
medsalah3@yahoo.fr
n.hamri@centre-univ-mila.dz
1: Paper Source
PDF document
Seoul 110-745,
Republic of Korea.
E-mail: hsun90@skku.edu
Meijo University, Nagoya 468-8502,
Japan.
E-mail: ryozi@hm.aitai.ne.jp
1: Paper Source
PDF document
Konkuk University, Chungju 380-701,
Republic of Korea.
E-mail: sjun@kku.ac.kr
Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Republic of Korea.
E-mail: iki@wku.ac.kr
1: Paper Source
PDF document
Department of Mathematics & Statistics,
P.O. Box 5529, Lautoka,
Fiji.
E-mail: ramanuja.kotti@fnu.ac.fj
rajnesh.lal@fnu.ac.fj
kaushal.singh@fnu.ac.fj
1: Paper Source
PDF document
University of Jammu,
Jammu And Kashmir,
India.
E-mail: stanzinkunga19@gmail.com
University of Jammu,
Jammu And Kashmir,
India.
E-mail: aditi.sharmaro@gmail.com
1: Paper Source
PDF document
Durban University of Technology,
Durban 4000,
South Africa.
Johannesburg,
South Africa.
E-mail: moaibinu@yahoo.com
mathewa@dut.ac.za
Durban University of Technology,
Durban 4000,
South Africa.
E-mail: thakur@dut.ac.za
Durban University of Technology,
Durban 4000,
South Africa.
E-mail: dvcrie@dut.ac.za
1: Paper Source
PDF document
National Institute of Technology Calicut,
Kerala 673601,
India.
E-mail:
pavikrishnakumar@gmail.com
lineesh@nitc.ac.in
2Department of Mathematics,
Cochin University of Science and Technology,
Kerala 682022,
India.
E-mail: noufal@cusat.ac.in
Abstract:
This paper provides a review on Minimally Supported Frequency (MSF) wavelets that includes the construction and characterization of MSF wavelets. The characterization of MSF wavelets induced from an MRA is discussed and the nature of the low-pass filter associated with it is explained. The concept of wavelet set and dimension function is introduced to study this class of wavelets. Along with MSF wavelets, s-elementary wavelets and unimodular wavelets are also considered due to the similarity in definitions. Examples and illustrations are provided for more clarity.
Paper's Title:
On General Class of Nonlinear Contractive Maps and their Performance Estimates
Author(s):
Olalekan Taofeek Wahab and Salaudeen Alaro Musa
Department of Mathematics and
Statistics
Kwara State University, Malete
P. M. B. 1530 Ilorin,
Nigeria.
E-mail: taofeek.wahab@kwasu.edu.ng
Abstract:
This paper considers two independent general class of nonlinear contractive maps to study the existence properties of nonlinear operators with prior degenerate. The existence properties are proved in the framework of approximate fixed points with the imposition of the general class of contractive conditions in metrical convex spaces without emphasis on completeness or compactness. For computational purposes, the performance estimates and the sensitivity dependence of these conditions are obtained for the Picard operator. Practical examples are also considered to justify the validity of the conditions. The results ensure no term is lost in the operators with prior degenerate and the conditions are strictly larger class when compare with others in the literature.
Paper's Title:
On Trigonometric Approximation of Continuous Functions by Deferred Matrix Means
Author(s):
Xhevat Zahir Krasniqi
Faculty of Education,
University of Prishtina "Hasan Prishtina",
Avenue "Mother Theresa " no. 5, Prishtinë
10000,
Republic of Kosovo.
E-mail: xhevat.krasniqi@uni-pr.edu
URL:
https://staff.uni-pr.edu/profile/xhevatkrasniqi
Abstract:
In this paper, for the first time, we introduce the deferred matrix means which contain the well-known generalized deferred Nörlund, deferred Nörlund, deferred Riesz, deferred Cesŕro means introduced earlier by others, and a new class of sequences (predominantly a wider class than the class of Head Bounded Variation Sequences). In addition, using the deferred matrix means of Fourier series of a continuous function, we determine the degree of approximation of such function via its modulus of continuity and a positive mediate function.
Paper's Title:
Three Inequalities Associated with Rado Inequality
Author(s):
Rin Miyao, Yusuke Nishizawa, Keigo Takamura
Faculty of Education,
Saitama University,
Shimo-okubo 255, Sakura-ku, Saitama-city, Saitama,
Japan.
E-mail: r.miyao.242@ms.saitama-u.ac.jp
Faculty of Education,
Saitama University,
Shimo-okubo 255, Sakura-ku, Saitama-city, Saitama,
Japan.
E-mail:
ynishizawa@mail.saitama-u.ac.jp
Faculty of Education,
Saitama University,
Shimo-okubo 255, Sakura-ku, Saitama-city, Saitama,
Japan.
E-mail: k.takamura.442@ms.saitama-u.ac.jp
Abstract:
In this short note we estimate three inequalities associated with Rado inequality and show the refinement and reverse of Arithmetic mean- Geometric mean inequality.
Paper's Title:
Several New Closed-form Evaluations of the Generalized Hypergeometric Function with Argument 1/16
Author(s):
B. R. Srivatsa Kumar, Insuk Kim and Arjun K. Rathie
Department of Mathematics,
Manipal Institute of Technology,
Manipal Academy of Higher Education,
Manipal 576 104,
India.
E-mail: sri_vatsabr@yahoo.com
Department of Mathematics Education,
Wonkwang University,
Iksan, 54538,
Republic of Korea.
E-mail: iki@wku.ac.kr
Department of Mathematics,
Vedant College of Engineering and Technology,
Rajasthan Technical University,
Bundi, 323021, Rajasthan,
India.
E-mail: arjunkumarrathie@gmail.com
Abstract:
The main objective of this paper is to establish as many as thirty new closed-form evaluations of the generalized hypergeometric function q+1Fq(z) for q= 2, 3, 4. This is achieved by means of separating the generalized hypergeometric function q+1Fq(z) for q=1, 2, 3, 4, 5 into even and odd components together with the use of several known infinite series involving central binomial coefficients obtained earlier by Ji and Hei \& Ji and Zhang.
Paper's Title:
Application of Chebyshev Polynomials to Volterra-Fredholm Integral Equations
Author(s):
Aissa Lakhal, Mostefa Nadir and Mohamed Nasseh Nadir
Department of Mathematics,
Faculty of Mathematics and
Informatics,
University of Msila,
Algeria.
E-mail:
aissa.lakhal@univ-msila.dz
mostefa.nadir@univ-msila.dz
nadir.mohamednasseh@yahoo.com
URL: https://www.mostefanadir.com
Abstract:
The goal of this work is to examine the numerical solution of linear Volterra-Fredholm integral equations of the second kind using the first, second, third and fourth Chebyshev polynomials. Noting that, the approximate solution is given in the form of series which converges to the exact one. Numerical examples are compared with other methods, in order to prove the applicability and the efficiency of this technical.
Paper's Title:
Fractional Integral Inequalities of Hermite-Hadamard Type for P-convex and Quasi-Convex Stochastic Process
Author(s):
Oualid Rholam, Mohammed Barmaki and Driss Gretet
National School of Applied Sciences (ENSA),
University Ibn Tofail,
B.P 242 Kenitra 14000,
phone number : +212606257757,
Morocco.
E-mail: oualid.rholam@uit.ac.ma
Science Faculty Ben M'sik,
University Hassan II,
B.P 7955 Av Driss El Harti Sidi Othmane 20700,
phone number : +212 5 22 70 46 71 ,
Morocco.
E-mail: mohammed.barmaki@uit.ac.ma
National School of Applied Sciences (ENSA),
University Ibn Tofail,
B.P 242 Kenitra 14000,
phone number : +212661403557,
Morocco.
E-mail: driss.gretete@uit.ac.ma
Abstract:
In this paper we consider the class of P-convex and Quasi-convex stochastic processes on witch we apply a general class of generalized fractional integral operator in order to establish new integral inequalities of Hermite-Hadammard type. then we obtain some results for well known types of fractional integrals. Results obtained in this paper may be starting point as well as a useful source of inspiration for further research in convex analysis.
Paper's Title:
Complete Analysis of Global Behavior of Certain System of Piecewise Linear Difference Equations
Author(s):
Atiratch Laoharenoo, Ratinan Boonklurb and Watcharapol Rewlirdsirikul
Department of Mathematics and Computer
Science,
Kamnoetvidya Science Academy, Rayong 21210
Thailand.
E-mail: atiratch.l@kvis.ac.th
Department of Mathematics and Computer Science,
Faculty of Science, Chulalongkorn University, Bangkok 10330
Thailand.
E-mail: ratinan.b@chula.ac.th
Department of Mathematics and Computer
Science,
Faculty of Science, Chulalongkorn University, Bangkok 10330
Thailand.
E-mail:
6570104323@student.chula.ac.th
Abstract:
Our goal is to study the system of piecewise linear difference equations x{n+1} = |xn|-yn-b and y{n+1} = xn - |yn| + 1 where n ≥ 0 and b ≥ 6. We can prove that the behavior of the solution can be divided into 2 types depending on the region of initial condition (x0,y0). That is, the solution eventually becomes the equilibrium point. Otherwise, the solution eventually becomes the periodic solution of prime period 5. All regions of initial condition for each type of solution are determined.
Paper's Title:
Differential Equations for Indicatrices, Spacelike and Timelike Curves
Author(s):
Sameer, Pradeep Kumar Pandey
Department of Mathematics,
Jaypee University of Information Technology,
Solan, Himachal Pradesh,
India.
E-mail: sksameer08@gmail.com,
pandeypkdelhi@gmail.com
Abstract:
Motivated by the recent work of Deshmukh et al. [20], in this paper we show that Tangent, Binormal, and Principal Normal indicatrices do not form non-trivial differential equations. Finally, we obtain the 4th-order differential equations for spacelike and timelike curves.
Paper's Title:
A General Fractional Control Scheme for Compound Combination Synchronization Between Different Fractional-Order Identical Chaotic Systems
Author(s):
Soumia Bensimessaoud and Smail Kaouache
Laboratory of Mathematics and their interactions, Abdelhafid Boussouf University Center, Mila, Algeria.
E-mail:
soumiabensimessaoud@gmail.com,
smailkaouache@gmail.com
Abstract:
In this paper, we aim to investigate the problem of compound combination synchronization (CCS) between four different fractional-order identical chaotic systems. Based on Laplace transformation and stability theory of linear dynamical systems, a new control law is proposed to assure the achievement of this kind of synchronization. Secondly, this control scheme is applied to realised CCS between four identical unified chaotic systems. Recall, that the proposed control scheme can be applied to wide classes of chaotic and hyperchaotic systems. Numerical simulations are given to show the effectiveness of the proposed method.
Paper's Title:
Corrigendum for Differential Equations for Indicatrices, Spacelike and Timelike Curves
Author(s):
Sameer, Pradeep Kumar Pandey
Department of Mathematics,
Jaypee University of Information Technology,
Solan, Himachal Pradesh,
India.
E-mail: sksameer08@gmail.com,
pandeypkdelhi@gmail.com
ABSTRACT NOT FOUND. WEBSITE ERROR
Abstract:
Paper's Title:
ℵ0 Algebra and its Novel Application in Edge Detection
Author(s):
G. E. Chatzarakis1, S. Dickson2, S. Padmasekaran2, S. L. Panetsos1, and J. Ravi3
1Electrical
and Electronic Engineering Educators,
School of Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
spanetsos@aspete.gr
2Mathematics,
Periyar University,
Periyar Palkalai Nagar, Salem, 636011, Tamilnadu,
India.
E-mail: dix.bern@gmail.com,
padmasekarans@periyaruniversity.ac.in
3Department
of Mathematics, Amity University,
Bengaluru, Karnataka,
India.
E-mail:
jravistat@gmail.com
Abstract:
In this paper a new type of ℵ0-algebra has been defined. With its help, the fuzzy cross subalgebra and the fuzzy η-relation on the ℵ0-algebra are introduced and their respective properties are derived. Moreover, the fuzzy cross ℵ0-ideal of the ℵ0-algebra is defined with some theorems and intuitionistic fuzzy ℵ0-ideals of the ℵ0-algebra are introduced. This fuzzy algebra concept is applied in image processing to detect edges. This ℵ0-algebra is a novelty in the field of research.
Paper's Title:
New Fast Extragradient-like Methods for Non-Lipschitzian Pseudo-monotone Variational Inequalities
Author(s):
Morad Ali Peyvand
Department of Mathematics
Yasouj University
Yasouj,
Iran.
E-mail: peyvand@yu.ac.ir
Abstract:
An efficient double-projection method, with a new search strategy, is designed for solving variational inequalities in real Hilbert spaces with pseudo-monotone cost operator. Our proposed method uses a computationally inexpensive simple line search procedure based on local information of the operator and very weak conditions of parameters to obtain larger step sizes. A description of the algorithm along with its weak convergence is provided without assuming Lipschitz continuity. Also, a modification to the proposed method is presented, wherein the second projection onto the closed and convex subset is replaced with the one onto a subgradient half space. Numerical experiments and comparisons with related methods demonstrate the reliability and benefits of the proposed schemes.
Paper's Title:
Refinement of Jensen's Inequality for Analytical Convex (Concave) Functions
Author(s):
P. Kórus, Z. Retkes
Institute of Applied Pedagogy,
Juhász Gyula Faculty of Education,
University of Szeged,
Hattyas utca 10, H-6725 Szeged,
Hungary.
E-mail: korus.peter@szte.hu
65 Manor Road, Desford, LE9 9JQ,
United Kingdom.
E-mail:
tigris35711@gmail.com
Abstract:
The well-known Jensen inequality and Hermite--Hadamard inequality were extended using iterated integrals by Z. Retkes in 2008 and then by P. Kórus in 2019. In this paper, we consider analytical convex (concave) functions in order to obtain new refinements of Jensen's inequality. We apply the main result to the classical HM--GM--AM, AM--RMS, triangle inequalities and present an application to the geometric series. We also give Mercer type variants of Jensen's inequality.
Paper's Title:
A Multi-Stage Differential Transform Approach for Solving Differential Algebraic Systems Without Index Reduction
Author(s):
Khalil Al Ahmad, Farah Abdulla Aini, Amirah Azmi, Muhammad Abbas
School of Mathematical Sciences
Universiti Sains Malaysia
11800 USM Penang
Malaysia.
Department of Mathematics,
University of Sargodha,
40100 Sargodha,
Pakistan
E-mail:
abumohmmadkh@hotmail.com
farahaini@usm.my
amirahazmi@usm.my
muhammad.abbas@uos.edu.pk
Abstract:
This paper aims to solve differential algebraic systems without the need to reduce the index, which causes a defect in the behavior of the approximate solution. The differential transform method was developed to solve differential algebraic systems. The differential algebraic system is transferred to the algebraic system by applying the differential transform method. Then the Multi-stage differential transform method is applied to extend the interval of the convergence. The numerical results show the new technique is an efficient and flexible tool to obtain accurate results that meet the initial conditions and keep the behavior of the approximate solution consistent.
Paper's Title:
On the Construction of Dyadic Wavelet Frames in Local Fields of Positive Characteristic
Author(s):
Vishal Dhawan, Khalil Ahmad, Satyapriya, Raj Kumar
Department of Mathematics,
Kirori Mal College,
University of Delhi, Delhi,
India.
E-mail: dhawanmathskmc@gmail.com
Department of Mathematics,
Al-Falah University,
Faridabad, Haryana,
India.
E-mail: kahmad49@gmail.com
Department of Mathematics,
University of Delhi, Delhi,
India.
E-mail: kmc.satyapriya@gmail.com
Department of Mathematics,
Kirori Mal College,
University of Delhi, Delhi,
India.
E-mail: rajkmc@gmail.com
Abstract:
This paper explores the construction of dyadic wavelet frames in (L2(K)), where (K) is a local field with positive characteristic. Using frame multiresolution analysis (FMRA), we establish a systematic method for generating wavelet frames within this setting. While conventional results indicate that two functions are necessary for constructing wavelet frames, we demonstrate that under specific conditions, a single function is sufficient. By leveraging properties of local fields, we provide a detailed characterization of the refinement equation and necessary frame conditions. These results enhance the theoretical understanding of wavelet frames and open new directions for applications in harmonic analysis and signal representation over non-Archimedean fields.
Paper's Title:
A Posteriori Error Analysis for a Pollution Model in a Bounded Domain of the Atmosphere
Author(s):
Abdou Wahidi Bello, Jamal Adetola, Djibo Moustapha, Saley Bisso
Université d'Abomey-Calavi,
Département de Mathématiques, Abomey-Calavi,
Republic of Benin.
E-mail: wahidi.bello@fast.uac.bj
Université Nationale des Sciences
Technologie,
Ingénierie et Mathématiques (UNSTIM),
Ecole Nationale Supérieure de Génie Mathématique et Modélisation (ENSGMM),
Republic of Benin.
E-mail: adetolajamal@unstim.bj
Département de Sciences Fondamentales,
École Supérieure Des Sciences Du Numérique,
Université de Dosso, Dosso,
Niger.
E-mail: moustaphad530@gmail.com
Département de Mathématiques et
Informatique,
Faculté des Sciences et Techniques,
Université Abdou Moumouni, Niamey,
Niger.
E-mail: bisso.saley@uam.edu.ne
Abstract:
This study conducts an a posteriori error analysis for a mathematical model of atmospheric pollution in a bounded domain. The finite element method is employed to approximate solutions to convection-diffusion-reaction equations, commonly used to model pollutant transport and transformation. The analysis focuses on deriving reliable and efficient error indicators for both temporal and spatial discretizations. Theoretical results establish upper and lower bounds for the discretization errors, ensuring optimal mesh refinement. Numerical simulations, supported by graphical representations, validate the theoretical findings by demonstrating the convergence of error indicators. These results confirm the effectiveness of the finite element method for solving atmospheric pollution models and highlight the importance of adaptive techniques for improving numerical accuracy.
Paper's Title:
Rational Functions of Chebyshev Polynomials for Volterra-Fredholm Integral Equations
Author(s):
Fakhreddine Seghiri and Mostefa Nadir
Department of Mathematics University of
Msila,
University Pole, Rode Bordj Bou Arreridj Msila 28000
Algeria.
E-mail: Fakhreddine.seghiri@univ-msila.dz
mostefa.nadir@univ-msila.dz
Abstract:
In this work, we treat a new numerical method for solving Volterra-Fredholm integral equations of the second kind. This method is based on orthogonal basis of rational functions derived from Chebyshev polynomials of the first kind. The approximate solution by this series converges to the exact solution. Numerical examples are presented and compared with other methods, in the goal to show the applicability and the efficiency of this method.
Paper's Title:
The Difference Between Two Approximate and Accurate Solutions of the Stochastic Differential Delay Equation Under Weak Conditions
Author(s):
Jin-Hyeong Kim and Young-Ho Kim
Department of Mathematics, Changwon
National University,
Changwon, Gyeongsangnam 51140,
Korea.
E-mail: ginhyung5647@changwon.ac.kr
yhkim@changwon.ac.k
Abstract:
In this paper we investigates the existence of approximate solutions derived from the Caratheodory's and the Euler-Maruyama's scheme under a uniform Lipschitz condition and a weakened linear growth condition. And by analyzing the continuity and convergence of these approximate solutions, we would like to provide reliable results to approximate the unique solutions of stochastic functional differential delay equations. In particular, we investigate how quickly the approximate solution by the Carateodori and Euler-Maruyama approximation methods approaches the accurate solution of the equation.
Search and serve lasted 0 second(s).