|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Attempts to Define a Baum--Connes Map Via Localization of Categories for Inverse Semigroups
Author(s):
Bernhard Burgstaller
Departamento de Matematica,
Universidade Federal de Santa Catarina,
CEP 88.040-900 Florianopolis-SC,
Brasil.
E-mail:
bernhardburgstaller@yahoo.de
URL:
http://mathematik.work/bernhardburgstaller/index.html
Abstract:
An induction functor in inverse semigroup equivariant KK-theory is considered, and together with %a restriction functors certain results similar to those known from the Mackey machinery are shown. It is also verified that for any so-called E-continuous inverse semigroup its equivariant KK-theory satisfies the universal property and is a triangulated category.
Paper's Title:
Viability
Theory And Differential Lanchester Type Models For Combat.
Differential Systems.
Author(s):
G. Isac and A. Gosselin
Department Of
Mathematics, Royal Military College Of Canada,
P.O. Box 17000, Stn Forces, Kingston,
Ontario, Canada K7k 7b4
isac-g@rmc.ca
gosselin-a@rmc.ca
URL:
http://www.rmc.ca/academic/math_cs/isac/index_e.html
URL:
http://www.rmc.ca/academic/math_cs/gosselin/index_e.html
Abstract:
In 1914, F.W. Lanchester proposed several mathematical models based on differential equations to describe combat situations [34]. Since then, his work has been extensively modified to represent a variety of competitions including entire wars. Differential Lanchester type models have been studied from many angles by many authors in hundreds of papers and reports. Lanchester type models are used in the planning of optimal strategies, supply and tactics. In this paper, we will show how these models can be studied from a viability theory stand point. We will introduce the notion of winning cone and show that it is a viable cone for these models. In the last part of our paper we will use the viability theory of differential equations to study Lanchester type models from the optimal theory point of view.
Paper's Title:
Asymptotic Behavior of Mixed Type Functional Equations
Author(s):
J. M. Rassias
Pedagogical Department, E.E., National and
Capodistrian University of Athens, Section of Mathematics And Informatics, 4, Agamemnonos
Str., Aghia Paraskevi, Athens 15342,Greece
jrassias@primedu.uoa.gr
URL:
http://www.primedu.uoa.gr/~jrassias/
Abstract:
In 1983 Skof [24] was the first author to solve the Ulam problem for additive mappings on a restricted domain. In 1998 Jung [14] investigated the Hyers-Ulam stability of additive and quadratic mappings on restricted domains. In this paper we improve the bounds and thus the results obtained by Jung [14], in 1998 and by the author [21], in 2002. Besides we establish new theorems about the Ulam stability of mixed type functional equations on restricted domains. Finally, we apply our recent results to the asymptotic behavior of functional equations of different types.
Paper's Title:
On Singular Numbers of Hankel Matrices of Markov Functions
Author(s):
Vasily A. Prokhorov
Department of Mathematics and Statistics,
University of South Alabama,
Mobile, Alabama 36688-0002,
USA.
E-mail: prokhoro@southalabama.edu
URL:
http://www.southalabama.edu/mathstat/people/prokhorov.shtml
Abstract:
Let E ⊂ (01,1) be a compact set and let μ be a positive Borel measure with support supp μ=E. Let
In the case when E=[a,b]⊂ (-1,1) and μ satisfies the condition dμ/dx>0 a.e. on E, we investigate asymptotic behavior of singular numbers σkn,n of the Hankel matrix Dn, where kn/n→θ∈[0,1] as n→∞. Moreover, we obtain asymptotics of the Kolmogorov, Gelfand and linear k-widths, k=kn, of the unit ball An,2 of Pn∩L2(Γ) in the space L2(μ,E), where Γ={z:|z|=1} and Pn is the class of all polynomials of the degree at most n.
Paper's Title:
Optimization and Approximation for Polyhedra in Separable Hilbert Spaces
Author(s):
Paolo d'Alessandro
Department of Mathematics,
Third University of Rome,
Italy.
E-mail: pdalex45@gmail.com
Abstract:
This paper studies infinite dimensional polyhedra, covering the case in which range spaces of operators defining inequality systems are not closed. A rangespace method of linear programming is generalized to infinite dimensions and finite dimensional methods of approximation are introduced.
Paper's Title:
Inequalities for Functions of Selfadjoint Operators on Hilbert Spaces:
a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
College of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning inequalities for continuous functions of selfadjoint operators on complex Hilbert spaces. It is intended for use by both researchers in various fields of Linear Operator Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Generalizing Polyhedra to Infinite Dimension
Author(s):
Paolo d'Alessandro
Department of Mathematics, Third University of Rome,
Lgo S.L. Murialdo 1, 00146 Rome, Italy.
URL:
http://www.mat.uniroma3.it/users/dalex/dalex.html.
Abstract:
This paper generalizes polyhedra to infinite dimensional Hilbert spaces as countable intersections of closed semispaces. Highlights are the structure theory that shows that a polyhedron is the sum of compact set (in a suitable topology) plus a closed pointed cone plus a closed subspace, giving the internal representation of polyhedra. In the final part the dual range space technique is extended to the solution of infinite dimensional LP problems.
Paper's Title:
Expected Utility with Subjective Events
Author(s):
Jacob Gyntelberg and Frank Hansen
Bank for International Settlements,
Basel,
Switzerland
Tohoku University, Institute for International Education,
Sendai,
Japan
Abstract:
We provide a new theory of expected utility with subjective events modeled by a lattice of projections. This approach allows us to capture the notion of a ``small world'' as a context dependent or local state space embedded into a subjective set of events, the ``grand world''. For each situation the decision makers' subjective ``small world'' reflects the events perceived to be relevant for the act under consideration. The subjective set of events need not be representable by a classical state space. Maintaining preference axioms similar in spirit to the classical axioms, we obtain an expected utility representation which is consistent across local state spaces and separates subjective probability and utility. An added benefit is that this alternative expected utility representation allows for an intuitive distinction between risk and uncertainty.
Paper's Title:
The Drazin-star and Star-Drazin Solutions to Quaternion Matrix Equations
Author(s):
Ivan I. Kyrchei, Dijana Mosić, Predrag Stanimirović
Pidstryhach Institute for Applied Problems
of Mechanics and Mathematics
of NAS of Ukraine, L'viv, 79060,
Ukraine.
E-mail:
ivankyrchei26@gmail.com
Faculty of Sciences and Mathematics,
University of Niš, P.O.
Box 224, 18000, Niš, Serbia.
E-mail: dijana@pmf.ni.ac.rs
Faculty of Sciences and Mathematics,
University of Niš, P.O.
Box 224, 18000, Niš, Serbia.
E-mail: pecko@pmf.ni.ac.rs
Abstract:
The notions of the Drazin-star and star-Drazin matrices are expanded to quaternion matrices in this paper. Their determinantal representations are developed in both cases in terms of noncommutative row-column determinants of quaternion matrices and for minors of appropriate complex matrices. We study all possible two-sided quaternion matrix equations with their one-sided partial cases whose uniquely determined solutions are based on the Drazin-star and star-Drazin matrices. Solutions of these equations are represented by Cramer's rules in both cases for quaternion and complex matrix equations. A numerical example is presented to illustrate our results.
Paper's Title:
On the Generalized Stability and
Asymptotic Behavior of Quadratic Mappings
Author(s):
Hark-Mahn Kim, Sang-Baek Lee and Eunyoung Son
Department of Mathematics
Chungnam National University
Daejeon,
305-764,
Republic of Korea
hmkim@cnu.ac.kr
Abstract:
We extend the stability of quadratic mappings to the stability of general quadratic mappings with several variables, and then obtain an improved asymptotic property of quadratic mappings on restricted domains.
Paper's Title:
Shape Diagrams for 2D Compact Sets - Part II: Analytic
Simply Connected Sets.
Author(s):
S. Rivollier, J. Debayle and J.-C. Pinoli
Ecole Nationale Supérieure des Mines de Saint-Etienne,
CIS - LPMG, UMR CNRS 5148, 158 cours Fauriel,
42023 Saint-Etienne Cedex 2, France.
rivollier@emse.fr;
debayle@emse.fr; pinoli@emse.fr
Abstract:
Shape diagrams are representations in the Euclidean plane introduced to study 3-dimensional and 2-dimensional compact convex sets. However, they can also been applied to more general compact sets than compact convex sets. A compact set is represented by a point within a shape diagram whose coordinates are morphometrical functionals defined as normalized ratios of geometrical functionals. Classically, the geometrical functionals are the area, the perimeter, the radii of the inscribed and circumscribed circles, and the minimum and maximum Feret diameters. They allow twenty-two shape diagrams to be built. Starting from these six classical geometrical functionals, a detailed comparative study has been performed in order to analyze the representation relevance and discrimination power of these twenty-two shape diagrams. The first part of this study is published in a previous paper 16. It focused on analytic compact convex sets. A set will be called analytic if its boundary is piecewise defined by explicit functions in such a way that the six geometrical functionals can be straightforwardly calculated. The purpose of this paper is to present the second part, by focusing on analytic simply connected compact sets. The third part of the comparative study is published in a following paper 17. It is focused on convexity discrimination for analytic and discretized simply connected compact sets.
Paper's Title:
Equilibria and Periodic Solutions of Projected Dynamical Systems on Sets with Corners
Author(s):
Matthew D. Johnston and Monica-Gabriela Cojocaru
Department of Applied Mathematics, University of Waterloo,
Ontario, Canada
mdjohnst@math.uwaterloo.ca
Department of Mathematics & Statistics, University of
Guelph,
Ontario, Canada
mcojocar@uoguelph.ca
Abstract:
Projected dynamical systems theory represents a bridge between the
static worlds of variational inequalities and equilibrium
problems, and the dynamic world of ordinary differential
equations. A projected dynamical system (PDS) is given by the flow
of a projected differential equation, an ordinary differential
equation whose trajectories are restricted to a constraint set
K. Projected differential equations are defined by discontinuous
vector fields and so standard differential equations theory cannot
apply. The formal study of PDS began in the 90's, although some
results existed in the literature since the 70's. In this paper we
present a novel result regarding existence of equilibria and
periodic cycles of a finite dimensional PDS on constraint sets
K, whose points satisfy a corner condition. The novelty is due
to proving existence of boundary equilibria without using a
variational inequality approach or monotonicity type conditions.
Paper's Title:
Applications of Relations and Relators in the
Extensions of Stability Theorems for Homogeneous and Additive Functions
Author(s):
Árpád Száz
Institute of Mathematics, University of Debrecen,
H-4010 Debrecen,
Pf. 12,
Hungary
szaz@math.klte.hu
Abstract:
By working out an appropriate technique of relations and relators and extending the ideas of the direct methods of Z. Gajda and R. Ger, we prove some generalizations of the stability theorems of D. H. Hyers, T. Aoki, Th. M. Rassias and P. Găvruţă in terms of the existence and unicity of 2-homogeneous and additive approximate selections of generalized subadditive relations of semigroups to vector relator spaces. Thus, we obtain generalizations not only of the selection theorems of Z. Gajda and R. Ger, but also those of the present author.
Paper's Title:
Existence, Global Regularity and Uniqueness of Solutions of the Navier-Stokes Equations in Space Dimension 3 when the Initial Data are Regular
Author(s):
Moulay D. Tidriri
Email: mtctyasa@gmail.com
Abstract:
The existence, regularity, and uniqueness of global solutions of the Navier-Stokes
equations in
![]() are given for when the initial velocity
are given for when the initial velocity
![]() for all integers q ≥ 0 and div u0
= 0.
for all integers q ≥ 0 and div u0
= 0.
Paper's Title:
Additive Mappings on Semiprime Rings Functioning as Centralizers
Author(s):
Abu Zaid Ansari and Faiza Shujat
Department of Mathematics,
Faculty of Science,
Islamic University of Madinah, Madinah
K.S.A.
E-mail: ansari.abuzaid@gmail.com,
ansari.abuzaid@iu.edu.sa
Department of Mathematics,
Faculty of Science,
Taibah University, Madinah,
K.S.A.
E-mail: faiza.shujat@gmail.com,
fullahkhan@taibahu.edu.sa
Abstract:
The objective of this research is to prove that an additive mapping T:R → R is a centralizer on R if it satisfies any one of the following identities:
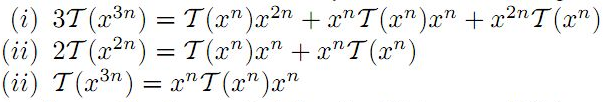
for all x ∈ R, where n ≥ 1 is a fixed integer and R is any suitably torsion free semiprime ring. Some results on involution "*" are also presented as consequences of the main theorems. In addition, we will take criticism in account with examples.
Paper's Title:
Global Implicit Function Theorems and Critical Point Theory in Frechet Spaces
Author(s):
Kaveh Eftekharinasab
Algebra and Topology Department,
Institute of Mathematics of National Academy of Sciences of Ukraine
Tereshchenkivska st., 01024, Kyiv,
Ukraine.
E-mail: kaveh@imath.kiev.ua
URL:
https://www.imath.kiev.ua/people/profile.php?pid=485\&lang=en
Abstract:
We prove two versions of a global implicit function theorem, which involve no loss of derivative, for Keller's Cc1 -mappings between arbitrary Fréchet spaces. Subsequently, within this framework, we apply these theorems to establish the global existence and uniqueness of solutions to initial value problems that involve the loss of one derivative. Moreover, we prove a Lagrange multiplier theorem by employing indirect applications of the global implicit function theorems through submersions and transversality.
Paper's Title:
On a Method of Proving the Hyers-Ulam Stability
of Functional Equations on Restricted Domains
Author(s):
Janusz Brzdęk
Department of Mathematics
Pedagogical University Podchor
Abstract:
We show that generalizations of some (classical) results on the Hyers-Ulam stability of functional equations, in several variables, can be very easily derived from a simple result on stability of a functional equation in single variable
Paper's Title:
Generalized Efficient Solutions to One Class of Vector Optimization Problems in Banach Space
Author(s):
Peter I. Kogut, Rosanna Manzo, and Igor V. Nechay
Department of Differential Equations,
Dnipropetrovsk National University,
Naukova str., 13,
49050 Dnipropetrovsk,
Ukraine
p.kogut@i.ua
Dipartimento di Ingegneria
Dell’informazione e Matematica Applicata,
Università di Salerno,
Via
Ponte
Don Melillo,
84084 Fisciano
(Sa),
Italy
manzo@diima.unisa.it
Department of Technical Cybernetics,
Dnipropetrovsk Technical University,
Acad. Lazarjan str., 2,
49010
Dnipropetrovsk,
Ukraine
i.nechay@i.ua
Abstract:
In this paper, we study vector optimization problems in Banach spaces for essentially nonlinear operator equations with additional control and state constraints. We assume that an objective mapping possesses a weakened property of lower semicontinuity and make no assumptions on the interior of the ordering cone. Using the penalization approach we derive both sufficient and necessary conditions for the existence of efficient solutions of the above problems. We also prove the existence of the so-called generalized efficient solutions via the scalarization of some penalized vector optimization problem.
Paper's Title:
Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.
Paper's Title:
Generalised Models for Torsional Spine Reconnection
Author(s):
Ali Khalaf Hussain Al-Hachami
Department of Mathematics,
College of Education For Pure Sciences,
Wasit University,
Iraq.
E-mail: alhachamia@uowasit.edu.iq
Abstract:
Three-dimensional (3D) null points are available in wealth in the solar corona, and the equivalent is probably going to be valid in other astrophysical situations. On-going outcomes from sun oriented perceptions and from reproductions propose that reconnection at such 3D nulls may assume a significant job in the coronal dynamics. The properties of the torsional spine method of magnetic reconnection at 3D nulls are researched. Kinematic model are created, which incorporate the term ηJ that is spatially localised around the null, stretching out along the spine of the null. The null point is to research the impact of shifting the level of asymmetry of the null point magnetic field on the subsequent reconnection process where past examinations constantly considered a non-nonexclusive radially symmetric null. Specifically we analyse the rate of reconnection of magnetic flux at the spine of null point. Logical arrangements are determined for the enduring kinematic equation, and contrasted and the after effects of torsional spine reconnection models when the current is restricted in which the Maxwell conditions are illuminated. The geometry of the current layers inside which torsional spine reconnection happen is autonomous on the symmetry of the magnetic field. Torsional spine reconnection happens in a thin cylinder around the spine, with circular cross-segment when the fan eigenvalues are extraordinary. The short axis of the circle being along the solid field bearing. Just as it was discovered that the fundamental structure of the method of attractive reconnection considered is unaffected by changing the magnetic field symmetry, that is, the plasma flow is discovered rotational around the spine of null point. The spatiotemporal pinnacle current, and the pinnacle reconnection rate achieved, are found not to rely upon the level of asymmetry.
Paper's Title:
On some Strongly Nonlinear Elliptic Problems
in L¹-data with a Nonlinearity Having a Constant Sign in Orlicz
Spaces via Penalization Methods
Author(s):
E. Azroul, A. Benkirane and M. Rhoudaf
Dep. Math., Faculté des Sciences
Dhar-Mahraz,
B.P 1796 Atlas Fès,
Maroc
Departement of Mathematics,
Faculty of Sciences and Techniques of Tangier,
B.P. 416, Tangier,
Morocco.
rhoudaf_mohamed@yahoo.fr
Abstract:
This paper is concerned with the existence result of the
unilateral problem associated to the equations of the type
![]()
in Orlicz spaces, without
assuming the sign condition in the nonlinearity g. The source term f belongs to L¹(Ώ).
Paper's Title:
Shape Diagrams for 2D Compact Sets - Part III: Convexity
Discrimination for Analytic and Discretized Simply Connected Sets.
Author(s):
S. Rivollier, J. Debayle and J.-C. Pinoli
Ecole Nationale Supérieure des Mines de Saint-Etienne,
CIS - LPMG, UMR CNRS
5148,
158 cours Fauriel,
42023 Saint-Etienne Cedex 2, France.
rivollier@emse.fr;
debayle@emse.fr; pinoli@emse.fr
Abstract:
Shape diagrams are representations in the Euclidean plane introduced to study 3-dimensional and 2-dimensional compact convex sets. However, they can also been applied to more general compact sets than compact convex sets. A compact set is represented by a point within a shape diagram whose coordinates are morphometrical functionals defined as normalized ratios of geometrical functionals. Classically, the geometrical functionals are the area, the perimeter, the radii of the inscribed and circumscribed circles, and the minimum and maximum Feret diameters. They allow twenty-two shape diagrams to be built. Starting from these six classical geometrical functionals, a detailed comparative study has been performed in order to analyze the representation relevance and discrimination power of these twenty-two shape diagrams. The two first parts of this study are published in previous papers 8,9. They focus on analytic compact convex sets and analytic simply connected compact sets, respectively. The purpose of this paper is to present the third part, by focusing on the convexity discrimination for analytic and discretized simply connected compact sets..
Paper's Title:
On a Problem on Periodic Functions
Author(s):
Adel A. Abdelkarim
Mathematics Department, Faculty of
Science,
Jerash Private University, Jerash,
Jordan.
E-mail:
adelafifo_afifo@yahoo.com
Abstract:
Given a continuous periodic real function f with n translates f1 ,..., fn , where fi(x)=f(x+ai), i=1,...,n. We solve a problem by Erdos and Chang and show that there are rational numbers r,s such that f(r)≥ fi(r), f(s)≤ fi(s), i=1,...,n. No restrictions on the constants or any further restriction on the function f are necessary as was imposed earlier.
Paper's Title:
A Multivalued Version of the
Radon-Nikodym Theorem, via the Single-valued Gould Integral
Author(s):
Domenico Candeloro1, Anca Croitoru2, Alina Gavriluţ2, Anna Rita Sambucini1
1Dept. of Mathematics and Computer
Sciences,
University of Perugia,
1, Via Vanvitelli -- 06123, Perugia,
Italy.
E-mail: domenico.candeloro@unipg.it,
anna.sambucini@unipg.it
2Faculty of Mathematics,
Al. I. Cuza University,
700506 Iaşi,
Romania.
E-mail: croitoru@uaic.ro,
gavrilut@uaic.ro
Abstract:
In this paper we consider a Gould type integral of real functions with respect to a compact and convex valued not necessarily additive measure. In particular we will introduce the concept of integrable multimeasure and, thanks to this notion, we will establish an exact Radon-Nikodym theorem relative to a fuzzy multisubmeasure which is new also in the finite dimensional case. Some results concerning the Gould integral are also obtained.
Paper's Title:
Generalized Fuglede-Putnam Theorem and Orthogonality
Author(s):
A. Bachir and A. Sagres
Department of
Mathematics, Faculty of Science, King Khaled
University, Abha, P.O. Box 9004 Kingdom Saudi Arabia
bachir_ahmed@hotmail.com
sagres@hotmail.com
Abstract:
An asymmetric Fuglede-Putnam’s theorem for dominant operators
and
Paper's Title:
An Algorithm to Compute Gaussian-Type Quadrature Formulae
that Integrate Polynomials and Some Spline Functions Exactly
Author(s):
Allal Guessab
Laboratoire de Mathématiques Appliquées,
Université de Pau, 64000, Pau,
France.
allal.guessab@univ-pau.fr
URL: http://www.univ-pau.fr/~aguessab/
Abstract:
It is well-known that for sufficiently smooth integrands on an interval, numerical integration can be performed stably and efficiently via the classical (polynomial) Gauss quadrature formulae. However, for many other sets of integrands these quadrature formulae do not perform well. A very natural way of avoiding this problem is to include a wide class among arbitrary functions (not necessary polynomials) to be integrated exactly. The spline functions are natural candidates for such problems. In this paper, after studying Gaussian type quadrature formulae which are exact for spline functions and which contain boundary terms involving derivatives at both end points, we present a fast algorithm for computing their nodes and weights. It is also shown, taking advantage of the close connection with ordinary Gauss quadrature formula, that the latter are computed, via eigenvalues and eigenvectors of real symmetric tridiagonal matrices. Hence a new class of quadrature formulae can then be computed directly by standard software for ordinary Gauss quadrature formula. Comparative results with classical Gauss quadrature formulae are given to illustrate the numerical performance of the approach.
Paper's Title:
On the Ulam Stability for Euler-Lagrange Type Quadratic Functional Equations
Author(s):
Matina John Rassias and John Michael Rassias
Statistics and Modelling Science,
University of Strathclyde,
Livingstone Tower,
26 Richmond Str,
Glasgow, Uk, G1 1xh
Pedagogical Department, E. E., National and Capodistrian University of Athens,
Section of Mathematics and Informatics,
4, Agamemnonos Str, Aghia Paraskevi,
Athens 15342, Greece
Abstract:
In 1940 (and 1968) S. M. Ulam proposed the well-known Ulam stability problem.
In 1941 D.H. Hyers solved the Hyers-Ulam problem for linear mappings. In 1951 D. G. Bourgin
has been the second author treating the Ulam problem for additive mappings. In 1978 according
to P.M. Gruber this kind of stability problems is of particular interest in probability theory and in
the case of functional equations of different types. In 1982-2004 we established the Hyers-Ulam
stability for the Ulam problem for different mappings. In 1992-2000 J.M. Rassias investigated
the Ulam stability for Euler-Lagrange mappings. In this article we solve the Ulam problem
for Euler-Lagrange type quadratic functional equations. These stability results can be applied
in mathematical statistics, stochastic analysis, algebra, geometry, as well as in psychology and
sociology.
Paper's Title:
Solution of the Hyers-Ulam Stability Problem for Quadratic Type Functional Equations in Several Variables
Author(s):
John Michael Rassias
Pedagogical Department, E.E., National and Capodistrian University of Athens,
Section of Mathematics and Informatics,
4, Agamemnonos Str., Aghia Paraskevi,
Athens 15342,
Greece
jrassias@primedu.uoa.gr
URL: http://www.primedu.uoa.gr/~jrassias/
Abstract:
In 1940 (and 1968) S. M. Ulam proposed the well-known Ulam stability problem. In 1941 D. H. Hyers solved the Hyers-Ulam problem for linear mappings. In 1951 D. G. Bourgin has been the second author treating the Ulam problem for additive mappings. In 1978 according to P. M. Gruber this kind of stability problems is of particular interest in probability theory and in the case of functional equations of different types. In 1982-2004 we established the Hyers-Ulam stability for the Ulam problem for different mappings. In this article we solve the Hyers-Ulam problem for quadratic type functional equations in several variables. These stability results can be applied in stochastic analysis, financial and actuarial mathematics, as well as in psychology and sociology.
Paper's Title:
A relation between nuclear cones and full nuclear cones
Author(s):
G. Isac and A. B. Nemeth
Department of Mathematics,
Royal Military College of Canada,
P. O. Box 17000 STN Forces Kingston, Ontario,
Canada K7K 7B4.
isac-g@rmc.ca
Faculty of Mathematics and Computer Science,
Babes-Bolyai University,
3400 Cluj-Napoca,
Romania.
nemab@math.ubbcluj.ro
Abstract:
The notion of nuclear cone in locally convex spaces corresponds to the notion of well based cone in normed spaces. Using the bipolar theorem from locally convex spaces it is proved that every closed nuclear cone is a full nuclear cone. Thus every closed nuclear cone can be associated to a mapping from a family of continuous seminorms in the space to the topological dual of the space. The relation with Pareto efficiency is discussed.
Paper's Title:
Ergodic Solenoidal Homology II:
Density of Ergodic Solenoids
Author(s):
Vicente Muñoz and Ricardo Pérez Marco
Instituto de Ciencias Matem
áticas CSIC-UAM-UC3M-UCM,Abstract:
A measured solenoid is a laminated space endowed with a tranversal measure invariant by holonomy. A measured solenoid immersed in a smooth manifold produces a closed current (known as a generalized Ruelle-Sullivan current). Uniquely ergodic solenoids are those for which there is a unique (up to scalars) transversal measure. It is known that for any smooth manifold, any real homology class is represented by a uniquely ergodic solenoid. In this paper, we prove that the currents associated to uniquely ergodic solenoids are dense in the space of closed currents, therefore proving the abundance of such objects.
Paper's Title:
Hardy Type Inequalities via Convexity - The Journey so Far
Author(s):
James A.
Oguntuase and Lars-Erik Persson
Department of Mathematics,
University of Agriculture,
P. M. B. 2240, Abeokuta, Nigeria.
Department of
Mathematics, Luleå University of Technology,
SE-971 87, Luleå , Sweden.
oguntuase@yahoo.com,
larserik@sm.luth.se .
Abstract:
It is nowadays well-known that Hardy's inequality (like many other inequalities) follows directly from Jensen's inequality. Most of the development of Hardy type inequalities has not used this simple fact, which obviously was unknown by Hardy himself and many others. Here we report on some results obtained in this way mostly after 2002 by mainly using this fundamental idea.
Paper's Title:
The Best Upper Bound for Jensen's Inequality
Author(s):
Vasile Cirtoaje
Department of Automatic Control and Computers
University of Ploiesti
Romania.
Abstract:
In this paper we give the best upper bound for the weighted Jensen's discrete inequality applied to a convex function f defined on a closed interval I in the case when the bound depends on f, I and weights. In addition, we give a simpler expression of the upper bound, which is better than existing similar one.
Paper's Title:
An Lp Inequality for `Self-Reciprocal' Polynomials. II
Author(s):
M. A. Qazi
Department of Mathematics,
Tuskegee University,
Tuskegee, Alabama 36088
U.S.A.
Abstract:
The main result of this paper is a sharp integral mean inequality for the derivative of a `self-reciprocal' polynomial.
Paper's Title:
L∞- Error Estimate of Schwarz Algorithm for Elliptic Quasi-Variational Inequalities Related to Impulse Control Problem
Author(s):
Saadi Samira and Mehri Allaoua
Lab. LANOS, Department of Mathematics,
University Badji Mokhtar Annaba,
P.O.Box 12, Annaba 23000,
Algeria.
Lab. LAIG, Department of Mathematics,
University May 8th 1945,
P.O.Box 401, Guelma 24000,
Algeria.
E-mail:
saadisamira69@yahoo.fr
allmehri@yahoo.fr
Abstract:
In this work, we study Schwarz method for a class of elliptic quasi-variational inequalities. The principal result of this investigation is to prove the error estimate in ∞-norm for two domains with overlapping nonmatching grids, using the geometrical convergence, and the uniform convergence of Cortey Dumont.
Paper's Title:
Action of Differential Operators On Chirpsconstruct On L∞
Author(s):
Taoufik El Bouayachi and Naji Yebari
Laboratoire de Mathematiques et
applications,
Faculty of sciences and techniques, Tangier,
Morocco.
E-mail:
figo407@gmail.com,
yebarinaji@gmail.com
Abstract:
We will study in this work the action of differential operators on L∞ chirps and we will give a new definition of logarithmic chirp. Finally we will study the action of singular integral operators on chirps by wavelet characterization and Kernel method.
Paper's Title:
Analysis of a Frictional Contact Problem for Viscoelastic Piezoelectric Materials
Author(s):
Meziane Said Ameur, Tedjani Hadj Ammar and Laid Maiza
Departement of Mathematics,
El Oued University,
P.O. Box 789, 39000 El Oued,
Algeria.
E-mail:
said-ameur-meziane@univ-eloued.dz
Departement of Mathematics,
El Oued University,
P.O. Box 789, 39000 El Oued,
Algeria.
E-mail:
hadjammar-tedjani@univ-eloued.dz
Department of Mathematics,
Kasdi Merbah University,
30000 Ouargla,
Algeria.
E-mail: maiza.laid@univ-ouargla.dz
Abstract:
In this paper, we consider a mathematical model that describes the quasi-static process of contact between two thermo-electro-viscoelastic bodies with damage and adhesion. The damage of the materials caused by elastic deformations. The contact is frictional and modeled with a normal compliance condition involving adhesion effect of contact surfaces. Evolution of the bonding field is described by a first order differential equation. We derive variational formulation for the model and prove an existence and uniqueness result of the weak solution. The proof is based on arguments of evolutionary variational inequalities, parabolic inequalities, differential equations, and fixed point theorem.
Paper's Title:
Optimization Techniques on Affine Differential Manifolds
Author(s):
Ali S Rasheed, Faik Mayah and Ahmed A H AL-Jumaili
Ministry of Higher Education and
Scientific Research,
Iraq.
E-mail: ahmedhashem@gmail.com
Department of Physics, College of
Sciences,
University of Wasit,
Iraq.
E-mail: faik.mayah@gmail.com
Abstract:
In addition to solid ground of Riemannian manifolds fundamentals, this article interviews some popular optimization methods on Riemannian manifolds. Several optimization problems can be better stated on manifolds rather than Euclidean space, such as interior point methods, which in turns based on self-concordant functions (logarithmic barrier functions). Optimization schemes like the steepest descent scheme, the Newton scheme, and others can be extended to Riemannian manifolds. This paper introduces some Riemannian and non-Riemannian schemes on manifolds.
Paper's Title:
A Review on Minimally Supported Frequency Wavelets
Author(s):
K Pallavi1, M C Lineesh1, A Noufal2
1
Department of Mathematics,2Department of Mathematics,
Cochin University of Science and Technology,
Kerala 682022,
India.
E-mail: noufal@cusat.ac.in
Abstract:
This paper provides a review on Minimally Supported Frequency (MSF) wavelets that includes the construction and characterization of MSF wavelets. The characterization of MSF wavelets induced from an MRA is discussed and the nature of the low-pass filter associated with it is explained. The concept of wavelet set and dimension function is introduced to study this class of wavelets. Along with MSF wavelets, s-elementary wavelets and unimodular wavelets are also considered due to the similarity in definitions. Examples and illustrations are provided for more clarity.
Paper's Title:
On the Class of Totally Polynomially Posinormal Operators
Author(s):
E. Shine Lal, T. Prasad, P. Ramya
Department of Mathematics,University
College,
Thiruvananthapuram, Kerala, 695034.
India.
E-mail: shinelal.e@gmail.com
Department of Mathematics,
University of Calicut,
Malapuram, Kerala 673635,
India.
E-mail: prasadvalapil@gmail.com
Department of Mathematics,
N.S.S College,
Nemmara, Kerala, 678508
India.
E-mail: ramyagcc@gmail.com
Abstract:
In this paper, we proved that if T ∈
B(H) is totally P-posinormal operator with
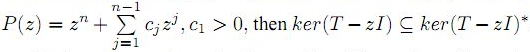 . Moreover, we study spectral continuity and range kernel orthogonality of these class of operators.
. Moreover, we study spectral continuity and range kernel orthogonality of these class of operators.
Paper's Title:
On the Optimal Buckling Loads of Clamped Columns
Author(s):
Samir Karaa
Department of Mathematics and Statistics
Sultan Qaboos University, P.O. Box 36, Alkhod 123
Muscat, Sultanate of Oman
skaraa@squ.edu.om
URL: http://ajmaa.org/EditorsU/SKaraa.php
Abstract:
We consider the problem of determining the optimal shape of a clamped column of given length and volume, without minimum cross section constraints.
We prove that the necessary condition of optimality derived by
Olhoff
and Rasmussen is sufficient when 0<
Paper's Title:
On a Generalized Biharmonic Equation in Plane Polars with Applications to Functionally Graded Materials
Author(s):
Ciro D'Apice
Department of Information Engineering and Applied Mathematics (DIIMA),
University of Salerno, 84084 Fisciano (SA),
Salerno, Italy.
dapice@diima.unisa.it
Abstract:
In this paper we consider a generalized biharmonic
equation modelling a two-dimensional inhomogeneous
elastic state in the curvilinear rectangle ![]()
![]() where
where ![]() denote plane polar
coordinates. Such an arch--like region is maintained in equilibrium under
self--equilibrated traction applied on the edge
denote plane polar
coordinates. Such an arch--like region is maintained in equilibrium under
self--equilibrated traction applied on the edge ![]() while the other three
edges
while the other three
edges ![]()
![]() and
and ![]() are traction free. Our
aim is to derive some explicit spatial exponential decay bounds for the
specific Airy stress function and its derivatives. Two types of smoothly
varying inhomogeneity are considered: (i) the elastic moduli vary
smoothly with the polar angle, (ii) they vary smoothly
with the polar distance. Such types of smoothly varying inhomogeneous elastic
materials provide a model for technological important functionally graded
materials. The results of the present paper prove how the spatial decay rate
varies with the constitutive profile.
are traction free. Our
aim is to derive some explicit spatial exponential decay bounds for the
specific Airy stress function and its derivatives. Two types of smoothly
varying inhomogeneity are considered: (i) the elastic moduli vary
smoothly with the polar angle, (ii) they vary smoothly
with the polar distance. Such types of smoothly varying inhomogeneous elastic
materials provide a model for technological important functionally graded
materials. The results of the present paper prove how the spatial decay rate
varies with the constitutive profile.
Paper's Title:
Existence of solutions for Neutral Stochastic Functional Differential Systems with Infinite Delay in Abstract Space
Author(s):
P. Balasubramaniam, A. V. A. Kumar and S. K. Ntouyas
Department of Mathematics, Gandhigram Rural Institute,
Deemed University, Gandhigram - 624 302,
Tamil Nadu, India.
pbalgri@rediffmail.com
Department of Mathematics, Gandhigram Rural Institute,
Deemed University, Gandhigram - 624 302,
Tamil Nadu, India.
nnddww@tom.com
Department of Mathematics, University of Ioannina,
451 10 Ioannina,
Greece.
sntouyas@cc.uoi.gr
URL: http://www.math.uoi.gr/~sntouyas
Abstract:
In this paper we prove existence results for semilinear stochastic neutral functional differential systems with unbounded delay in abstract space. Our theory makes use of analytic semigroups and fractional power of closed operators and Sadovskii fixed point theorem.
Paper's Title:
On the Generalized Inverse  over Integral Domains
over Integral Domains
Author(s):
Yaoming Yu and Guorong Wang
College of Education, Shanghai Normal University
Shanghai 200234
People's Republic of China.
yuyaoming@online.sh.cn
grwang@shnu.edu.cn
Abstract:
In this paper, we study further the generalized inverse
 of a matrix A over an integral domain. We give
firstly some necessary and sufficient conditions for the existence
of the generalized inverse
of a matrix A over an integral domain. We give
firstly some necessary and sufficient conditions for the existence
of the generalized inverse  , an explicit expression
for the elements of the generalized inverse
, an explicit expression
for the elements of the generalized inverse  and an
explicit expression for the generalized inverse
and an
explicit expression for the generalized inverse  ,
which reduces to the {1} inverse. Secondly, we verify that the
group inverse, the Drazin inverse, the Moore-Penrose inverse and the
weighted Moore-Penrose inverse are identical with the generalized
inverse
,
which reduces to the {1} inverse. Secondly, we verify that the
group inverse, the Drazin inverse, the Moore-Penrose inverse and the
weighted Moore-Penrose inverse are identical with the generalized
inverse 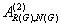 for an appropriate matrix G,
respectively, and then we unify the conditions for the existence and
the expression for the elements of the weighted Moore-Penrose
inverse, the Moore-Penrose inverse, the Drazin inverse and the group
inverse over an integral domain. Thirdly, as a simple application,
we give the relation between some rank equation and the existence of
the generalized inverse
for an appropriate matrix G,
respectively, and then we unify the conditions for the existence and
the expression for the elements of the weighted Moore-Penrose
inverse, the Moore-Penrose inverse, the Drazin inverse and the group
inverse over an integral domain. Thirdly, as a simple application,
we give the relation between some rank equation and the existence of
the generalized inverse  , and a method to compute the
generalized inverse
, and a method to compute the
generalized inverse  . Finally, we give an example of
evaluating the elements of
. Finally, we give an example of
evaluating the elements of  without calculating
without calculating
 .
.
Paper's Title:
Local and Global Existence and Uniqueness Results for Second and Higher Order Impulsive Functional Differential Equations with Infinite Delay
Author(s):
Johnny Henderson and Abdelghani Ouahab
Department of Mathematics, Baylor University,
Waco, Texas 76798-7328
USA.
Johnny_Henderson@baylor.edu
Laboratoire de Mathématiques, Université de Sidi Bel Abbés
BP 89, 22000 Sidi Bel Abbées,
Algérie.
ouahab@univ-sba.dz
Abstract:
In this paper, we discuss the local and global existence and
uniqueness results for second and higher order impulsive functional
differential equations with infinite delay. We shall rely on a
nonlinear alternative of Leray-Schauder. For the global existence
and uniqueness we apply a recent Frigon and Granas nonlinear
alternative of Leray-Schauder type in Fréchet spaces.
Paper's Title:
The Convergence of Modified Mann-Ishikawa Iterations when Applied to an Asymptotically Pseudocontractive Map
Author(s):
S. Soltuz
Departamento de Matematicas, Universidad de Los Andes, Carrera 1
No. 18A-10, Bogota,
Colombia
and
``T. Popoviciu" Institute of Numerical Analysis
Cluj-Napoca,
Romania
smsoltuz@gmail.com
URL:http://www.uniandes.edu.co/
Abstract:
We prove that under minimal conditions the modified Mann and Ishikawa iterations converge when dealing with an asymptotically pseudocontractive map. We give an affirmative answer to the open question from C.E. Chidume and H. Zegeye, Approximate fixed point sequences and convergence theorems for asymptotically pseudocontractive mappings, J. Math. Anal. Appl., 278 (2003), 354--366.
Paper's Title:
Existence of Bounded Solutions for a Class of
Strongly Nonlinear Elliptic Equations in Orlicz-Sobolev Spaces
Author(s):
Abdelmoujib Benkirane and Ahmed Youssfi
Department of Mathematics and Informatics, Faculty of Sciences
Dhar El Mahraz
University Sidi Mohammed Ben Abdallah
PB 1796 Fez-Atlas, Fez
Morocco
a.benkirane@menara.ma
ahmed.youssfi@caramail.com
Abstract:
We prove, in the setting of Orlicz-Sobolev spaces, the existence of
bounded solutions for some strongly nonlinear elliptic equations
with operator of the principal part having degenerate coercivity and
lower order terms not satisfying the sign condition. The data have a
suitable summability and no Δ2-condition is needed for the
considered N-functions.
Paper's Title:
Linearly Transformable Minimal Surfaces
Author(s):
Harold R. Parks and Walter B. Woods
Department of Mathematics,
Oregon State University,
Corvallis, Oregon 97331--4605,
USA
parks@math.oregonstate.edu
URL: http://www.math.oregonstate.edu/people/view/parks/
Abstract:
We give a complete description of a nonplanar minimal surface in R3 with the surprising property that the surface remains minimal after mapping by a linear transformation that dilates by three distinct factors in three orthogonal directions. The surface is defined in closed form using Jacobi elliptic functions.
Paper's Title:
Differentiability of
Distance Functions in p-Normed Spaces
Author(s):
M. S. Moslehian, A. Niknam, S. Shadkam Torbati
Department of Pure Mathematics,
Centre of Excellence in Analysis on Algebraic Structures (CEAAS),,
Ferdowsi University of Mashhad,
P. O. Box
1159, Mashhad,
Iran
moslehian@ferdowsi.um.ac.ir
niknam@math.um.ac.ir
shadkam.s@wali.um.ac.ir
Abstract:
The farthest point mapping in a p-normed space X is studied in virtue of the Gateaux derivative and the Frechet derivative. Let M be a closed bounded subset of X having the uniformly p-Gateaux differentiable norm. Under certain conditions, it is shown that every maximizing sequence is convergent, moreover, if M is a uniquely remotal set then the farthest point mapping is continuous and so M is singleton. In addition, a Hahn--Banach type theorem in $p$-normed spaces is proved.
Paper's Title:
Some Open Problems in Analysis
Author(s):
A.G. Ramm
Mathematics Department, Kansas State University,
Manhattan, KS 66506-2602,
USA
ramm@math.ksu.edu
URL: http://www.math.ksu.edu/~ramm
Abstract:
In this paper some open problems in analysis are formulated. These problems were formulated and discussed by the author at ICMAA6.
Paper's Title:
Shape Diagrams for 2D Compact Sets - Part I: Analytic
Convex Sets.
Author(s):
S. Rivollier, J. Debayle and J.-C. Pinoli
Ecole Nationale Supérieure des Mines de Saint-Etienne,
CIS - LPMG, UMR CNRS 5148, 158 cours Fauriel,
42023 Saint-Etienne Cedex 2, France.
rivollier@emse.fr;
debayle@emse.fr; pinoli@emse.fr
Abstract:
Shape diagrams are representations in the Euclidean plane introduced to study 3-dimensional and 2-dimensional compact convex sets. Such a set is represented by a point within a shape diagram whose coordinates are morphometrical functionals defined as normalized ratios of geometrical functionals. Classically, the geometrical functionals are the area, the perimeter, the radii of the inscribed and circumscribed circles, and the minimum and maximum Feret diameters. They allow thirty-one shape diagrams to be built. Most of these shape diagrams can also been applied to more general compact sets than compact convex sets. Starting from these six classical geometrical functionals, a detailed comparative study has been performed in order to analyze the representation relevance and discrimination power of these thirty-one shape diagrams. The purpose of this paper is to present the first part of this study, by focusing on analytic compact convex sets. A set will be called analytic if its boundary is piecewise defined by explicit functions in such a way that the six geometrical functionals can be straightforwardly calculated. The second and third part of the comparative study are published in two following papers [19.20]. They are focused on analytic simply connected sets and convexity discrimination for analytic and discretized simply connected sets, respectively.
Paper's Title:
The Superstability of the Pexider Type Trigonometric Functional Equation
Author(s):
Gwang Hui Kim and Young Whan Lee
Department of Mathematics, Kangnam
University Yongin, Gyeonggi, 446-702, Korea.
ghkim@kangnam.ac.kr
Department of Computer and Information Security
Daejeon University, Daejeon 300-716, Korea.
ywlee@dju.ac.kr
Abstract:
The aim of this paper is to investigate the stability
problem for
the Pexider type (hyperbolic) trigonometric functional equation
f(x+y)+f(x+σy)=λg(x)h(y) under the conditions :
|f(x+y)+f(x+σy)- λg(x)h(y)|≤φ(x),
φ(y), and min {φ(x), φ (y)}.
As a consequence, we have generalized the results of stability for
the cosine(d'Alembert), sine, and the Wilson functional equations by J.
Baker, P. Găvruta, R. Badora and R. Ger, Pl.~Kannappan, and G.
H. Kim
Paper's Title:
Approximation of Common Fixed Points of a Finite Family of Asymptotically Demicontractive Mappings in Banach Spaces
Author(s):
Yuchao Tang, Yong Cai, Liqun Hu and Liwei Liu
Department of Mathematics, NanChang University,
Nanchang 330031, P.R. China
Department of Mathematics, Xi'an Jiaotong University,
Xi'an 710049, P.R.
China
Abstract:
By virtue of new analytic techniques, we analyze and
study
several strong convergence theorems for the approximation of
common fixed points of asymptotically demicontractive mappings
via the multistep iterative sequence with errors in Banach
spaces. Our results improve and extend the corresponding ones
announced by Osilike , Osilike and Aniagbosor, Igbokwe, Cho et
al., Moore and Nnoli, Hu and all the others.
Paper's Title:
Hyperbolic Models Arising in the Theory of Longitudinal Vibration of Elastic Bars
Author(s):
1I. Fedotov, 1J. Marais, 1,2M. Shatalov and 1H.M. Tenkam
1Department of Mathematics and Statistics,
Tshwane University
of
Technology
Private Bag X6680, Pretoria 0001
South Africa.
fedotovi@tut.ac.za,
julian.marais@gmail.com,
djouosseutenkamhm@tut.ac.za.
2Manufacturing and
Materials
Council of Scientific and Industrial
Research (CSIR)
P.O. Box 395, Pretoria, 0001
South Africa.
mshatlov@csir.co.za
Abstract:
In this paper a unified approach to the
derivation of families of one
dimensional hyperbolic differential equations and boundary conditions describing
the longitudinal vibration of elastic bars is outlined. The longitudinal and
lateral displacements are expressed in the form of a power series expansion in
the lateral coordinate. Equations of motion and boundary conditions are derived
using Hamilton's variational principle. Most of the well known models in this
field fall within the frames of the proposed theory, including the classical
model, and the more elaborated models proposed by by Rayleigh, Love, Bishop,
Mindlin, Herrmann and McNiven. The exact solution is presented for the
Mindlin-Herrmann case in terms of Green functions. Finally, deductions regarding
the accuracy of the models are made by comparison with the exact
Pochhammer-Chree solution for an isotropic cylinder.
Paper's Title:
A Note On The Global Behavior Of A Nonlinear System of Difference Equations
Author(s):
Norman H. Josephy, Mihaela Predescu and Samuel W. Woolford
Department of Mathematical Sciences,
Bentley University,
Waltham, MA 02452,
U.S.A.
mpredescu@bentley.edu
njosephy@bentley.edu
swoolford@bentley.edu
Abstract:
This paper deals with the global asymptotic stability character of solutions of a discrete time deterministic model proposed by Wikan and Eide in Bulletin of Mathematical Biology, 66, 2004, 1685-1704. A stochastic extension of this model is proposed and discussed. Computer simulations suggest that the dynamics of the stochastic model includes a mixture of the dynamics observed in the deterministic model.
Paper's Title:
Growth and Products of Subharmonic Functions in the Unit Ball
Author(s):
R. Supper
Université de Strasbourg,
UFR de Mathématique et Informatique, URA CNRS 001,
7 rue René Descartes,
F--67 084 Strasbourg Cedex,
France
raphaele.supper@math.unistra.fr
Abstract:
The purpose of this paper is to link information on the application u→gu with some growth conditions on the functions u and g subharmonic in the unit ball of RN. Two kinds of growth are considered: the Bloch--type growth and growth conditions expressed through integrals involving involutions of the unit ball.
Paper's Title:
Existence Results for Second Order Impulsive Functional Differential Equations with Infinite Delay
Author(s):
M. Lakrib, A. Oumansour and K. Yadi
Laboratoire de Mathématiques, Université Djillali
Liabées, B.P. 89 Sidi Bel Abbès 22000, Algérie
mlakrib@univ-sba.dz
oumansour@univ-sba.dz
Laboratoire de Mathématiques, Université Abou Bekr
Belkaid, B.P. 119 Tlemcen 13000, Algérie
k_yadi@mail.univ-tlemcen.dz
Abstract:
In this paper we study the existence of solutions for second order impulsive functional differential equations with infinite delay. To obtain our results, we apply fixed point methods.
Paper's Title:
Szegö Limits and Haar Wavelet Basis
Author(s):
M. N. N. Namboodiri and S. Remadevi
Dept. of Mathematics, Cochin University
of Science and Technology,
Cochin-21, Kerala,
India.
Dept. of Mathematics, College of
Engineering,
Cherthala, Kerala,
India.
Abstract:
This paper deals with Szegö type limits for multiplication operators on L2 (R) with respect to Haar orthonormal basis. Similar studies have been carried out by Morrison for multiplication operators Tf using Walsh System and Legendre polynomials [14]. Unlike the Walsh and Fourier basis functions, the Haar basis functions are local in nature. It is observed that Szegö type limit exist for a class of multiplication operators Tf , f∈ L∞ (R) with respect to Haar (wavelet) system with appropriate ordering. More general classes of orderings of Haar system are identified for which the Szegö type limit exist for certain classes of multiplication operators. Some illustrative examples are also provided.
Paper's Title:
Traub-Potra-Type Method for Set-Valued Maps
Author(s):
Ioannis K. Argyros and Saïd Hilout
Cameron University,
Department of Mathematics Sciences,
Lawton, OK 73505,
USA
URL: http://www.cameron.edu/~ioannisa/
Poitiers University,
Laboratoire de Mathematiques et Applications,
Bd. Pierre et Marie Curie, Teleport 2, B.P. 30179,
86962 Futuroscope Chasseneuil Cedex,
France
said.hilout@math.univ-poitiers.fr
http://www-math.univ-poitiers.fr/~hilout/
Abstract:
We introduce a new iterative method for approximating a locally unique solution of variational inclusions in Banach spaces by using generalized divided differences of the first order. This method extends a method considered by Traub (in the scalar case) and by Potra (in the Banach spaces case) for solving nonlinear equations to variational inclusions. An existence-convergence theorem and a radius of convergence are given under some conditions on divided differences operator and Lipschitz-like continuity property of set-valued mappings. The R-order of the method is equal to the unique positive root of a certain cubic equation, which is $1.839..., and as such it compares favorably to related methods such as the Secant method which is only of order $1.618....
Paper's Title:
Properties of Certain Multivalent Functions Involving Ruscheweyh Derivatives
Author(s):
N-Eng Xu and Ding-Gong Yang
Department of Mathematics,
Changshu Institute of Technology,
Changshu, Jiangsu 215500,
China
Abstract:
Let Ap(p∈ N) be the class of functions
which are analytic
in the unit disk. By virtue of the Ruscheweyh derivatives we introduce the new
subclasses Cp(n,α,β,λ,μ) of Ap. Subordination relations, inclusion relations,
convolution properties and a sharp coefficient estimate are
obtained. We also give a sufficient condition for a function to be
in Cp(n,α,β,λ,μ)
Paper's Title:
Polyanalytic Functions on Subsets of Z[i]
Author(s):
Abtin Daghighi
Linköping University,
SE-581 83,
Sweden.
E-mail: abtindaghighi@gmail.com
Abstract:
For positive integers q we consider the kernel of the powers Lq where L is one of three kinds of discrete analogues of the Cauchy-Riemann operator. The first two kinds are well-studied, but the third kind less so. We give motivations for further study of the third kind especially since its symmetry makes it more appealing for the cases q≥ 2.
From an algebraic perspective it makes sense that the chosen multiplication on the kernels is compatible with the choice of pseudo-powers. We propose such multiplications together with associated pseudo-powers. We develop a proof-tool in terms of certain sets of uniqueness.
Paper's Title:
Kinematic Model for Magnetic Null-points in 2 Dimensions
Author(s):
Ali Khalaf Hussain Al-Hachami
Department of Mathematics,
College of Education For Pure Sciences,
Wasit University,
Iraq.
E-mail: alhachamia@uowasit.edu.iq
Abstract:
The adjacent configurations of two-dimensional magnetic null point centers are analyzed by an immediate examination about the null. The configurations are classified as either potential or non-potential. By then the non-potential cases are subdivided into three cases depending upon whether the component of current is less than, equal to or greater than a threshold current. In addition the essential structure of reconnection in 2D is examined. It unfolds that the manner by which the magnetic flux is rebuilt. In this paper, we center on the ramifications of kinematic arrangements; that is, we fathom just Maxwell's conditions and a resistive Ohm's law.
Paper's Title:
Existence of Compositional Square Roots of Circle Maps
Author(s):
K. Ali Akbar and T. Mubeena
Department of Mathematics,
School of Physical Sciences,
Central University of Kerala,
Periya - 671320,
Kasaragod,
Kerala,
India.
E-mail: aliakbar.pkd@gmail.com,
aliakbar@cukerala.ac.in
Department of Mathematics,
School of Mathematics and Computational Sciences,
University of Calicut,
Thenhipalam-673635,
Malappuram,
Kerala,
India.
E-mail: mubeenatc@gmail.com,
mubeenatc@uoc.ac.in
Abstract:
In this paper, we discuss the existence of compositional square roots of circle maps. If f and g are two maps such that g ○ g = f, we say that g is a compositional square root of f.
Paper's Title:
Conservativeness Criteria of Girsanov Transformation for Non-Symmetric Jump-diffusion
Author(s):
Mila Kurniawaty
DDepartment of Mathematics,
Universitas Brawijaya, Malang,
Indonesia.
E-mail: mila_n12@ub.ac.id
Abstract:
We develop the condition in our previous paper [The Conservativeness of Girsanov transformed for symmetric jump-diffusion process (2018)] in the framework of nonsymmetric Markov process with jumps associated with regular Dirichlet form. We prove the conservativeness of it by relation in duality of Girsanov transformed process and recurrent criteria of Dirichlet form.
Paper's Title:
Generalized Composition Operators On Besov Spaces
Author(s):
Vishal Sharma, Sanjay Kumar and Stanzin Dolkar
Department of Mathematics,
Central University of Jammu,
Jammu and Kashmir,
India.
E-mail: sharmavishal911@gmail.com
Department of Mathematics,
Central University of Jammu,
Jammu and Kashmir,
India.
E-mail: sanjaykmath@gmail.com
Department of Mathematics,
Central University of Jammu,
Jammu and Kashmir,
India.
E-mail: stanzin.math@cujammu.ac.in
Abstract:
In this paper, we characterize boundedness, compactness and find the essential norm estimates for generalized composition operators between Besov spaces and Sp spaces.
Paper's Title:
Higher Order Accurate Compact Schemes for Time Dependent Linear and Nonlinear Convection-Diffusion Equations
Author(s):
S. Thomas, Gopika P.B. and S. K. Nadupuri
Department of Mathematics
National Institute of Technology Calicut
Kerala
673601
India.
E-mail:
sobinputhiyaveettil@gmail.com
pbgopika@gmail.com nsk@nitc.ac.in
Abstract:
The primary objective of this work is to study higher order compact finite difference schemes for finding the numerical solution of convection-diffusion equations which are widely used in engineering applications. The first part of this work is concerned with a higher order exponential scheme for solving unsteady one dimensional linear convection-diffusion equation. The scheme is set up with a fourth order compact exponential discretization for space and cubic $C^1$-spline collocation method for time. The scheme achieves fourth order accuracy in both temporal and spatial variables and is proved to be unconditionally stable. The second part explores the utility of a sixth order compact finite difference scheme in space and Huta's improved sixth order Runge-Kutta scheme in time combined to find the numerical solution of one dimensional nonlinear convection-diffusion equations. Numerical experiments are carried out with Burgers' equation to demonstrate the accuracy of the new scheme which is sixth order in both space and time. Also a sixth order in space predictor-corrector method is proposed. A comparative study is performed of the proposed schemes with existing predictor-corrector method. The investigation of computational order of convergence is presented.
Paper's Title:
Generalized Triangular and Symmetric Splitting Method for Steady State Probability Vector of Stochastic Matrices
Author(s):
B. Harika, D. Rajaiah, L. P. RajKumar, Malla Reddy Perati
Department of Mathematics,
Kakatiya University
E-mail: hbolledla@gmail.com
Department of Mathematics,
Kakatiya Institute of Technology and Science
E-mail: dr.mh@kitsw.ac.in
Department of Mathematics,
Kakatiya University
E-mail: ladalla@gmail.com
Department of Mathematics,
Kakatiya University
E-mail: mperati@yahoo.com
Abstract:
To find the steady state probability vector of homogenous linear system π Q=0 of stochastic rate matrix Q, generalized triangular and symmetric (GTS) splitting method is presented. Convergence analysis and choice of parameters are given when the regularized matrix A=QT+ε I of the regularized linear system Ax=b is positive definite. Analysis shows that the iterative solution of GTS method converges unconditionally to the unique solution of the regularized linear system. From the numerical results, it is clear that the solution of proposed method converges rapidly when compared to the existing methods.
Paper's Title:
Commutator For Singular Operators On Variable Exponent Sequence Spaces And Their Corresponding Ergodic Version
Author(s):
A.M. Alphonse and S.S.S. Anupindi
Department of Mathematics,
Birla Institute of Technology And Science- Pilani,
Hyderabad Campus, Jawahar Nagar, Kapra Mandal,
District.-Medchal-500 078, Telangana,
India.
E-mail:
alphonse@hyderabad.bits-pilani.ac.in
p20180442@hyderabad.bits-pilani.ac.in
URL:
https://www.bits-pilani.ac.in/hyderabad/a-michael-alphonse
https://www.bits-pilani.ac.in/research_scholars/sri-sakti-swarup-anupindi
Abstract:
In this paper, we prove strong type inequality for maximal commutator of singular operator on weighted lp spaces. Using these results we prove strong type inequality for the maximal commutator of singular operator on variable exponent sequence spaces. Using Calderon-Coifman-Weiss transference principle we prove strong type inequality for maximal ergodic commutator of singular operator on a probability space equipped with measure preserving transformation U.
Paper's Title:
Dyadic Riesz Wavelets on Local Fields of Positive Characteristics
Author(s):
Kartik Garg, Raj Kumar, Satyapriya
Department of Mathematics,
University of Delhi,
Delhi,
India.
kartikgarg1421@gmail.com,
rajkmc@gmail.com
kmc.satyapriya@gmail.com
Abstract:
In this research paper, we introduce a novel theory for the construction of a Riesz wavelet basis in the space L2(K), where K is a local field with positive characteristics. Our approach is two fold: firstly, we derive some essential characterizations of the scaling function associated with the structure of a Riesz MRA on a local field, and secondly, we review existing methods for constructing wavelet frames in L2(K). We also present a well elaborated example for a better comprehension of our theory. Due to mathematical convenience, we limit ourselves to the case of dyadic dilations only.
Paper's Title:
Robust Layer Resolving Scheme for a System of Two Singularly Perturbed Time-Dependent Delay Initial Value Problems with Robin Initial Conditions
Author(s):
1K. Ramiya Bharathi, 2G. E. Chatzarakis, 2S. L. Panetsos, and 1M. Joseph Paramasivam
1PG & Research Department of
Mathematics,
Bishop Heber College (Affiliated to Bharathidasan University),
Tiruchirappalli - 620 017, Tamil Nadu,
India.
E-mail: ramiyabharathik28@gmail.com,
paramasivam.ma@bhc.edu.i
2Department of Electrical and Electronic Engineering Educators,
School of Pedagogical \& Technological Education (ASPETE),
Marousi, 15122, Athens,
Greece.
E-mail: gea.xatz@aspete.gr,
spanetsos@aspete.gr
Abstract:
This paper aimed at proving first order convergence for system of two singularly perturbed time-dependent initial value problems with delay in spatial variable and robin initial conditions. A Classical layer resolving finite difference scheme is developed by implementing uniform mesh for time discretization; Shishkin-mesh, a piecewise uniform mesh for spatial discretization. Shishkin-mesh is constructed is such way it captures the intricacies behavior of the layers. The interior layer is induced by the presence of a delay term in the space term. Error estimate is carried out to prove first order convergence with the help of maximum principle, stability analysis, solution bounds and sharper estimates of the singular components of the solutions. Finally, the numerical illustration is computed for the problem to bolster the scheme.
Paper's Title:
Necessary and Sufficient Conditions for the Boundedness of Fractional Integral Operators on Hypergroups
Author(s):
Ari Wardayani, Mutia Nur Estri, Wihantoro, Idha Sihwaningrum
Faculty of Mathematics and Natural
Sciences,
Jenderal Soedirman University,
Indonesia.
E-mail: ari.wardayani@unsoed.ac.id
mutia.estri@unsoed.ac.id
wihantoro@unsoed.ac.id
idha.sihwaningrum@unsoed.ac.id
Abstract:
We prove in this paper the necessary and sufficient conditions for the boundedness of the fractional integral operators on Lebesgue spaces over commutative hypergroups. The necessity proofs take into account the Haar measure, meanwhile the sufficiency proofs employ the maximal operators.
Paper's Title:
Pseudomonotonicity and Quasimonotonicity
by Translations versus Monotonicity in Hilbert Spaces
Author(s):
George Isac and Dumitru Motreanu
Department of
Mathematics, Royal Military College of Canada, P.O. Box 17000 Stn Forces
Kingston, Ontario, Canada, K7k 7b4.
gisac@juno.com
Département de Mathématiques, Université de Perpignan, 66860
Perpignan, France.
motreanu@univ-perp.fr
Abstract:
Let ![]() be a Gâteaux differentiable mapping on
an open convex subset
be a Gâteaux differentiable mapping on
an open convex subset ![]() of a
Hilbert space
of a
Hilbert space![]() . If there exists a straight line
. If there exists a straight line ![]() such that
such that ![]() is pseudomonotone for any
is pseudomonotone for any ![]() then
then ![]() is monotone. Related results using a
regularity condition are given.
is monotone. Related results using a
regularity condition are given.
Paper's Title:
Positive Solution For Discrete Three-Point Boundary Value
Problems
Author(s):
Wing-Sum Cheung And Jingli Ren
Department of Mathematics,
The University of Hong Kong,
Pokfulam, Hong Kong
wscheung@hku.hk
Institute of Systems Science,
Chinese Academy of Sciences,
Beijing 100080, P.R. China
renjl@mx.amss.ac.cn
Abstract:
This paper is concerned with the existence of positive solution to the discrete three-point boundary value problem
![]()
![]() ,
,
![]()
![]()
where
![]()
![]() , and f is allowed to change sign. By constructing
available operators, we shall apply the method of lower solution and the method
of topology degree to obtain positive solution of the above problem for
, and f is allowed to change sign. By constructing
available operators, we shall apply the method of lower solution and the method
of topology degree to obtain positive solution of the above problem for
![]() on a suitable interval.
The associated Green’s function is first given.
on a suitable interval.
The associated Green’s function is first given.
Paper's Title:
Quantitative Estimates for Positive Linear Operators Obtained by Means of Piecewise Linear Functions
Author(s):
Vasile Mihesan
Technical University of Cluj-Napoca,
Department of Mathematics,
Str. C. Daicoviciu 15,
Cluj-Napoca,
Romania
Vasile.Mihesan@math.utcluj.ro
Abstract:
In this paper we obtain estimates for the remainder in approximating continuous
functions by positive linear operators, using piecewise linear functions.
Paper's Title:
On Perturbed Reflection Coefficients
Author(s):
J. L. Díaz-Barrero and J. J. Egozcue
Applied Mathematics III,
Universidad Politécnica de Cataluña,
Barcelona, Spain
jose.luis.diaz@upc.edu
juan.jose.egozcue@upc.edu
Abstract:
Many control and signal processing applications require testing
stability of polynomials. Classical tests for locating zeros of
polynomials are recursive, but they must be stopped whenever the so
called "singular polynomials" appear. These ``singular cases'' are
often avoided by perturbing the "singular polynomial".
Perturbation techniques although always successful are not proven to
be well-founded. Our aim is to give a mathematical foundation to a
perturbation method in order to overcome "singular cases" when
using Levinson recursion as a testing method. The non-singular
polynomials are proven to be dense in the set of all polynomials
respect the L²-norm on the unit circle . The proof is
constructive and can be used algorithmically.
Paper's Title:
Stability of a Pexiderized Equation
Author(s):
Maryam Amyar
Department of Mathematics,
Islamic Azad University, Rahnamaei Ave,
Mashhad 91735, Iran,
and Banach Mathematical Research Group (BMRG)
amyari@mshdiau.ac.ir
URL: http://amyari.mshdiau.ac.ir
Abstract:
The aim of the paper is to prove the
stability of the Pexiderized equation f(x)=g(y+x)-h(y-x), for any
amenable abelian group.
Paper's Title:
Positive Periodic Time-Scale Solutions for Functional Dynamic Equations
Author(s):
Douglas R. Anderson and Joan Hoffacker
Department of Mathematics and Computer Science
Concordia College
Moorhead, MN 56562 USA
andersod@cord.edu
URL: http://www.cord.edu/faculty/andersod/
Department of Mathematical Sciences
Clemson University
Clemson, SC 29634 USA
johoff@clemson.edu
URL: http://www.math.clemson.edu/facstaff/johoff.htm
Abstract:
Using Krasnoselskii's fixed point theorem, we establish the existence of positive periodic solutions
to two pairs of related nonautonomous functional delta dynamic equations on periodic time scales, and then extend the discussion to higher-dimensional equations. Two pairs of corresponding nabla equations
are also provided in an analogous manner.
Paper's Title:
Existence of Non-spurious Solutions to Discrete Boundary Value Problems
Author(s):
Irena Rachunkova and Christopher C. Tisdell
Department of Mathematics
School of Mathematics
Palacky University
771 46 Olomouc, Czech Republic.
rachunko@risc.upol.cz
URL: http://phoenix.inf.upol.cz/~rachunekl/mathair/matha-en.htm
The University of New South Wales
Sydney 2052, Australia.
cct@unsw.edu.au
URL: http://www.maths.unsw.edu.au/~cct
Abstract:
This paper investigates discrete boundary value problems (BVPs) involving second-order difference equations and two-point boundary conditions.
General theorems guaranteeing the existence and uniqueness of solutions to the discrete BVP are established. The methods involve a sufficient growth condition to yield an a priori bound on solutions to a certain family of discrete BVPs. The em a priori bounds on solutions to the discrete BVP do not depend on the step-size and thus there are no ``spurious'' solutions. It is shown that solutions of the discrete BVP will converge to solutions of ordinary differential equations.
Paper's Title:
Generalized Hypergeometric Functions Defined on the Class of Univalent Functions
Author(s):
N. Marikkannan, A. Gangadharan and C. Ganesamoorthy
Department of Applied Mathematics,
Sri Venkateswara College of Engineering,
Sriperumbudur 602105,
India.
mari@svce.ac.in
Department of Applied mathematics,
Sri Venkateswara College of Engineering,
Sriperumbudur 602105,
India.
ganga@svce.ac.in
Department of Mathematics,
Alagappa university,
Karaikudi,
India.
ganesamoorthyc@yahoo.com
Abstract:
Let A denotes the class of all analytic functions
f(z), normalized by the condition f'(0)-1=f(0)=0 defined on
the open unit disk
Paper's Title:
A Different Proof for the non-Existence of Hilbert-Schmidt Hankel Operators with
Anti-Holomorphic Symbols on the Bergman Space
Author(s):
Georg Schneider
Universität Wien, Brünnerstr. 72 A-1210 Wien,
Austria.
georg.schneider@univie.ac.at
URL: http://www.univie.ac.at/bwl/cont/mitarbeiter/schneider.htm
Abstract:
We show that there are no (non-trivial) Hilbert-Schmidt Hankel
operators with anti-holomorphic symbols on the Bergman space of
the unit-ball B2(Bl) for l≥2. The result dates back to
[6]. However, we give a different proof. The methodology can
be easily applied to other more general settings. Especially, as
indicated in the section containing generalizations, the new
methodology allows to prove some robustness results for existing
ones.
Paper's Title:
The Iterated Variational Method for the Eigenelements of a Class of Two-Point Boundary Value Problems
Author(s):
Muhammed I. Syam and Qasem M. Al-Mdallal
Department of Mathematical Sciences, College of Science, UAE University,
P. O. Box 17551, Al-Ain,
United Arab Emirates
Q.Almdallal@uaeu.ac.ae
M.Syam@uaeu.ac.ae
Abstract:
The iterated variational method is considered in the approximation
of eigenvalues and eigenfunctions for a class of two point boundary
value problems. The implementation of this method is easy and
competes well with other methods. Numerical examples are presented
to show the efficiency of the method proposed. Comparison with the
work of others is also illustrated.
Paper's Title:
Existence of Large Solutions to Non-Monotone Semilinear Elliptic Equations
Author(s):
Alan V. Lair, Zachary J. Proano, and Aihua W. Wood
Air Force Institute of Technology
2950 Hobson Way, AFIT/ENC
Wright-Patterson Air Force Base, OH, 45433-7765,
USA.
Aihua.Wood@afit.edu
URL: www.afit.edu
Abstract:
We study the existence of large solutions of the semilinear elliptic equation Δu=p(x)f(u) where f is not monotonic. We prove existence, on bounded and unbounded domains, under the assumption that f is Lipschitz continuous, f(0) = 0, f(s) > 0 for s > 0 and there exists a nonnegative, nondecreasing Hölder continuous function g and a constant M such that g(s) ≤ f(s) ≤ Mg(s) for large s. The nonnegative function p is allowed to be zero on much of the domain.
Paper's Title:
On Oscillation of
Second-Order Delay Dynamic Equations on Time Scales
Author(s):
S. H. Saker
Department of Mathematics, Faculty of Science,
Mansoura University, Mansoura, 35516,
Egypt.
shsaker@mans.edu.eg
Abstract:
Some new oscillation criteria for second-order linear delay dynamic equation
on a time scale T are established. Our results improve the
recent results for delay dynamic equations and in the special case when
T=R, the results include the oscillation results established by Hille [1948,
Trans. Amer. Math. Soc. 64 (1948), 234-252] and Erbe [Canad. Math. Bull. 16
(1973), 49-56.] for differential equations. When T=Z the
results include and improve some oscillation criteria for difference
equations. When T=hZ, h>0, T=qN and T=N2, i.e., for generalized second order delay difference equations our
results are essentially new and can be applied on different types of time
scales. An example is considered to illustrate the main results.
Paper's Title:
The Invariant Subspace Problem for Linear Relations on Hilbert Spaces
Author(s):
Daniel Grixti-Cheng
Department of Mathematics and Statistics,
The University of Melbourne,
Melbourne, VIC, 3010
Australia.
D.Grixti@ms.unimelb.edu.au
Abstract:
We consider the invariant subspace problem for linear relations on Hilbert spaces with the aim of promoting interest in the problem as viewed from the theory of linear relations. We present an equivalence between the single valued and multivalued invariant subspace problems and give some new theorems pertaining to the invariant subspace problem for linear relations on a Hilbert space.
Paper's Title:
A Sum Form Functional Equation and Its Relevance in Information Theory
Author(s):
Prem Nath and Dhiraj Kumar Singh
Department of Mathematics
University of Delhi
Delhi - 110007
India
pnathmaths@gmail.com
dksingh@maths.du.ac.in
Abstract:
The general solutions of a sum form functional equation containing four unknown mappings have been investigated. The importance of these solutions in relation to various entropies in information theory has been emphasised.
Paper's Title:
The Bernoulli Inequality in Uniformly
Complete f-algebras with Identity
Author(s):
Adel Toumi and Mohamed Ali Toumi
Laboratoire de Physique des Liquides Critiques, Département de Physique, Faculté des Sciences de Bizerte,
7021, Zarzouna, Bizerte, TUNISIA
Adel.Toumi@fst.rnu.tn
Département de Mathématiques, Faculté des Sciences de Bizerte, 7021, Zarzouna,
Bizerte, TUNISIA
MohamedAli.Toumi@fsb.rnu.tn
Abstract:
The main purpose of this paper is to establish with a constructive proof the
Bernoulli inequality: let A be a uniformly complete f-algebra
with e as unit element, let 1<p<∞, then (e+a)p≥e+pa for all a∈A+. As an
application we prove the Hölder
inequality for positive linear functionals on a uniformly complete f-algebra with identity by using the Minkowski inequality. Paper's Title:
Multivalent Harmonic Mappings Convoluted With a Multivalent Analytic Function
Author(s):
Om P. Ahuja and Özlem Güney
Kent State University, Department of Mathematical Sciences,
University of Dicle, Department of Mathematics, Abstract:
The object of this paper is to study certain geometric properties of
a family of multivalent harmonic mappings in the plane convoluted
with a multivalent analytic function in the open unit disc. Paper's Title:
The ε-Small Ball Drop Property
Author(s):
C. Donnini and A. Martellotti Dipartimento
di Statistica e Matematica per la Ricerca Economica,
{Dipartimento di Matematica e Informatica, Abstract:
We continue the investigation on classes of small sets in a
Banach space that give alternative formulations of the Drop
Property. The small sets here considered are the set having the
small ball property, and we show that for sets having non-empty
intrinsic core and whose affine hull contains a closed affine space
of infinite dimension the Drop Property can be equivalently
formulated in terms of the small ball property. Paper's Title:
Stability of a Mixed Additive, Quadratic and Cubic Functional Equation In Quasi-Banach Spaces
Author(s):
A. Najati and F. Moradlou
Department of Mathematics, Faculty of Sciences,
Faculty of Mathematical Sciences, Abstract:
In this paper we establish the general solution of a mixed additive,
quadratic and cubic functional equation and investigate the
Hyers--Ulam--Rassias stability of this equation in quasi-Banach
spaces. The concept of Hyers-Ulam-Rassias stability originated from
Th. M. Rassias' stability theorem that appeared in his paper: On the
stability of the linear mapping in Banach spaces, Proc. Amer. Math.
Soc. 72 (1978), 297--300. Paper's Title:
Integer Sums of Powers of Trigonometric Functions (MOD p), for prime p
Author(s):
G. J. Tee
Department of Mathematics, University of Auckland,
Auckland, Abstract:
Many multi--parameter families of congruences (mod p) are found for integer
sums of
qth powers of the trigonometric functions over various sets of equidistant
arguments, where
p is any prime factor of q. Those congruences provide sensitive
tests for the accuracy
of software for evaluating trigonometric functions to high precision. Paper's Title:
Some Properties of the Solution of a Second Order Elliptic Abstract Differential Equation Author(s):
A. Aibeche and K. Laidoune
Mathematics Department, Faculty of Sciences,
University Ferhat Abbas, Setif,
Abstract:
In this paper we study a class of non regular boundary value
problems for elliptic differential-operator equation of second order with an
operator in boundary conditions. We give conditions which guarantee the
coerciveness of the solution of the considered problem, the completeness of
system of root vectors in Banach-valued functions spaces and we establish
the Abel basis property of this system in Hilbert spaces. Finally, we apply
this abstract results to a partial differential equation in cylindrical
domain.
Paper's Title:
Ulam Stability of Functional Equations Author(s):
Stefan Czerwik and Krzysztof Król
Institute of Mathematics Abstract:
In this survey paper we present some of the main results on Ulam-Hyers-Rassias stability
for important functional equations.
Paper's Title:
Stability of Almost Multiplicative Functionals Author(s):
Norio Niwa, Hirokazu Oka, Takeshi Miura and Sin-Ei Takahasi
Faculty of Engineering, Osaka Electro-Communication University, Abstract:
Let
δ
and p be non-negative real numbers. Let
then we show that
φ
is multiplicative or
for some p≠1, then by using Hyers-Ulam-Rassias
stability of additive Cauchy equation, we show that
φ
is a ring homomorphism or
Paper's Title:
Hyperbolic Barycentric Coordinates Author(s):
Abraham A. Ungar
1: Paper Source
PDF document
14111, Claridon-Troy Road, Burton, Ohio 44021,
U.S.A.
oahuja@kent.edu
Faculty of Science and Art, 21280 Diyarbakir,
Turkey
ozlemg@dicle.edu.tr
1: Paper Source
PDF document
Università degli Studi di Napoli "Parthenope",
Via Medina, 80133 Napoli,
Italy
chiara.donnini@uniarthenope.it
Università degli Studi di Perugia,
Via Pascoli - 06123 Perugia,
Italy.
amart@dipmat.unipg.it
URL:
www.dipmat.unipg.it/~amart/
1: Paper Source
PDF document
University of Mohaghegh Ardabili, Ardabil,
Iran
a.nejati@yahoo.com
University of Tabriz, Tabriz,
Iran
moradlou@tabrizu.ac.ir
1: Paper Source
PDF document
New Zealand
tee@math.auckland.ac.nz
1: Paper Source
PDF document
Route de Scipion, 19000,
Setif,
Algeria
aibeche@univ-setif.dz
1: Paper Source
PDF document
Silesian University of Technology
Kaszubska 23,
44-100 Gliwice,
Poland
Stefan.Czerwik@polsl.pl
Krzysztof.Krol@polsl.pl
1: Paper Source
PDF document
Neyagawa 572-8530,
Japan
Faculty of Engineering, Ibaraki University,
Hitachi 316-8511,
Japan
Department of Applied Mathematics and Physics, Graduate School of
Science and Engineering,
Yamagata University,
Yonezawa 992-8510
Japan
oka@mx.ibaraki.ac.jp
miura@yz.yamagata-u.ac.jp
sin-ei@emperor.yz.yamagata-u.ac.jp
![]() be the
real or complex number field and
be the
real or complex number field and
![]() a normed algebra
over
a normed algebra
over ![]() . If a mapping
. If a mapping
![]() satisfies
satisfies![]()
![]() for all
for all ![]() If, in
addition,
φ
satisfies
If, in
addition,
φ
satisfies![]()
![]() for all
for all
![]() In other words,
φ
is a ring homomorphism, or an approximately zero
mapping. The results of this paper are inspired by Th.M. Rassias' stability
theorem.
In other words,
φ
is a ring homomorphism, or an approximately zero
mapping. The results of this paper are inspired by Th.M. Rassias' stability
theorem.
1: Paper Source
PDF document
Department of Mathematics, North Dakota State University,
Fargo, ND 58105,
USA
Abraham.Ungar@ndsu.edu
URL: http://math.ndsu.nodak.edu/faculty/ungar/
Abstract:
A powerful and novel way to study Einstein's special theory of relativity and its underlying geometry, the hyperbolic geometry of Bolyai and Lobachevsky, by analogies with classical mechanics and its underlying Euclidean geometry is demonstrated. The demonstration sets the stage for the extension of the notion of barycentric coordinates in Euclidean geometry, first conceived by Möbius in 1827, into hyperbolic geometry. As an example for the application of hyperbolic barycentric coordinates, the hyperbolic midpoint of any hyperbolic segment, and the centroid and orthocenter of any hyperbolic triangle are determined.
Paper's Title:
The Riemann-Stieltjes Integral on Time Scales
Author(s):
D. Mozyrska, E. Pawłuszewicz, D. Torres
Faculty Of Computer Science,
Białystok University Of Technology,
15-351 Białystok,
Poland
d.mozyrska@pb.edu.pl
Department Of Mathematics,
University Of Aveiro,
3810-193 Aveiro,
Portugal
ewa@ua.pt
Department Of Mathematics,
University Of Aveiro,
3810-193 Aveiro,
Portugal
delfim@ua.pt
Abstract:
We study the process of integration on time scales in the sense of Riemann-Stieltjes. Analogues of the classical properties are proved for a generic time scale, and examples are given
Paper's Title:
Topological Aspects of Scalarization in Vector Optimization Problems.
Author(s):
Peter I. Kogut, Rosanna Manzo and Igor V. Nechay
Department of Differential Equations,
Dnipropetrovsk National University, Naukova
STR.,
13,
49010 Dnipropetrovsk,
Ukraine
p.kogut@i.ua
Università di Salerno,
Department of Technical Cybernetics,
Dipartimento di Ingegneria dell'Informazione e Matematica Applicata,
Via Ponte don Melillo, 84084 Fisciano (SA),
Italy
manzo@diima.unisa.it
Dnipropetrovsk Technical University,
Acad. Lazarjan
STR., 2,
49010 Dnipropetrovsk,
Ukraine
i.nechay@i.ua
Abstract:
In this paper, we study vector optimization problems in partially ordered Banach spaces. We suppose that the objective mapping possesses a weakened property of lower semicontinuity and make no assumptions on the interior of the ordering cone. We derive sufficient conditions for existence of efficient solutions of the above problems and discuss the role of topological properties of the objective space. We discuss the scalarization of vector optimization problems when the objective functions are vector-valued mappings with a weakened property of lower semicontinuity. We also prove the existence of the so-called generalized efficient solutions via the scalarization process. All principal notions and assertions are illustrated by numerous examples.
Paper's Title:
Inclusion Properties of a Certain Subclass of Strongly Close-To-Convex Functions
Author(s):
S. M. Khairnar and M. More
Department of Mathematics,
Maharashtra Academy of Engineerring,
Alandi -412 105, Pune, Maharashtra,
INDIA.
smkhairnar2007@gmail.com,
meenamores@gmail.com.
Abstract:
The purpose of this paper is to derive some inclusion and argument properties of a new subclass of strongly close-to-convex functions in the open unit disc. We have considered an integral operator defined by convolution involving hypergeometric function in the subclass definition. The subclass also extends to the class of α-spirallike functions of complex order.
Paper's Title:
Sharp Lp Improving Results for Singular Measures on Cn+1
Author(s):
E. Ferreyra, M. Urciuolo
FaMAF-CIEM,
Universidad Nacional de Córdoba-Conicet,
Ciudad Universitaria, 5000 Córdoba,
Argentina
eferrey@famaf.unc.edu.ar
urciuolo@famaf.unc.edu.ar
Abstract:
For j=1,...,n, let Ωj be open sets of the complex plane and let φj be holomorphic functions on Ωj such that φj'' does not vanish identically on Ωj. We consider φ(z1,...,zn) =φ1(z1) +...+φn(zn). We characterize the pairs (p,q) such that the convolution operator with the surface measure supported on a compact subset of the graph of φ is p-q bounded.
Paper's Title:
Equivalence of the Nonsmooth Nonlinear Complementarity Problems to Unconstrained Minimization
Author(s):
M. A. Tawhid and J. L. Goffin
Department of Mathematics and Statistics,
School of Advanced Technologies and Mathematics,
Thompson Rivers University,
900 McGill Road, PO Box 3010, Kamloops, BC V2C 5N3
Canada
Alexandria University and Egypt Japan University of Science and Technology,
Alexandria-Egypt
mtawhid@tru.ca
Faculty of Management, McGill University,
1001 Sherbrooke Street West, Montreal, Quebec, H3A 1G5
Canada.
Jean-Louis.Goffin@McGill.ca
Abstract:
This paper deals with nonsmooth nonlinear complementarity problem, where the underlying functions are nonsmooth which admit the H-differentiability but not necessarily locally Lipschitzian or directionally differentiable. We consider a reformulation of the nonlinear complementarity problem as an unconstrained minimization problem. We describe H-differentials of the associated penalized Fischer-Burmeister and Kanzow and Kleinmichel merit functions. We show how, under appropriate P0, semimonotone (E0), P, positive definite, and strictly semimonotone (E) -conditions on an H-differential of f, finding local/global minimum of a merit function (or a `stationary point' of a merit function) leads to a solution of the given nonlinear complementarity problem. Our results not only give new results but also unify/extend various similar results proved for C1.
Paper's Title:
Unital Compact Homomorphisms Between Extended Analytic Uniform Algebras
Author(s):
D. Alimohammadi and M. Mayghani
Department of Mathematics,
Faculty of Science, Arak University,
PO Box 38156-8-8349, Arak,
Iran.
Abstract:
Let X and K be compact plane sets with K⊆X. We denote by A(X,K) and A(X) the algebras of all continuous complex-valued functions on X which are analytic on int(K) and int(X), respectively. It is known that A(X,K) and A(X) are natural uniform algebras on X. A(X) and A(X,K) are called analytic uniform algebra and extended analytic uniform algebra on X, respectively. In this paper we study unital homomorphisms between extended analytic uniform algebras and investigate necessary and sufficient conditions for which these homomorphisms to be compact. We also determine the spectrum of unital compact endomorphisms of extended analytic uniform algebras.
Paper's Title:
A Geometric Generalization of Busemann-Petty Problem
Author(s):
Liu Rong and Yuan Jun
Shanghai Zhangjiang Group Junior Middle School,
Huo Xiang Road, Shanghai, 201203,
China
Abstract:
The norm defined by Busemann's inequality establishes a class of star body - intersection body. This class of star body plays a key role in the solution of Busemann-Petty problem. In 2003, Giannapoulos [1] defined a norm for a new class of half-section. Based on this norm, we give a geometric generalization of Busemann-Petty problem, and get its answer as a result
Paper's Title:
Certain Compact Generalizations of Well-Known Polynomial Inequalities
Author(s):
N. A. Rather and Suhail Gulzar
Department of Mathematics,
University of Kashmir, Hazratbal Srinagar-190006,
India.
Abstract:
In this paper, certain sharp compact generalizations of well-known Bernstien-type inequalities for polynomials, from which a variety of interesting results follow as special cases, are obtained.
Paper's Title:
C*-algebras Associated Noncommutative Circle and Their K-theory
Author(s):
Saleh Omran
Taif University,
Faculty of Science,
Taif,
KSA
South Valley University,
Faculty of Science,
Math. Dep.
Qena,
Egypt
Abstract:
In this article we investigate the universal C*-algebras associated to certain 1 - dimensional simplicial flag complexes which describe the noncommutative circle. We denote it by S1nc. We examine the K-theory of this algebra and the subalgebras S1nc/Ik, Ik . Where Ik, for each k, is the ideal in S1nc generated by all products of generators hs containing at least k+1 pairwise different generators. Moreover we prove that such algebra divided by the ideal I2 is commutative.
Paper's Title:
Application of Equivalence Method to Classify Monge-Ampère Equations of Elliptic Type
Author(s):
Moheddine Imsatfia
E-mail: imsatfia@math.jussieu.fr
Abstract:
In this paper, we apply Cartan's equivalence method to give a local classification of Monge-Ampère equations of elliptic type. Then we find a necessary and sufficient conditions such that a Monge-Ampère equation is either contactomorphic to the Laplace equation or to an Euler-Lagrange equation.
Paper's Title:
On Some Constructive Method of Rational Approximation
Author(s):
Vasiliy A. Prokhorov
Department of Mathematics and Statistics
University of South Alabama
Mobile, Alabama 36688-0002,
USA.
E-mail:
prokhoro@southalabama.edu
URL:
http://www.southalabama.edu/mathstat/people/prokhorov.shtml
Abstract:
We study a constructive method of rational approximation of analytic functions based on ideas of the theory of Hankel operators. Some properties of the corresponding Hankel operator are investigated. We also consider questions related to the convergence of rational approximants. Analogues of Montessus de Ballore's and Gonchars's theorems on the convergence of rows of Padé approximants are proved.
Paper's Title:
C*-valued metric projection and Moore-Penrose inverse on Hilbert C*-modules
Author(s):
M. Eshaghi Gordji, H. Fathi and S.A.R. Hosseinioun
Department of Mathematics,
Semnan University, P.O. Box 35195-363, Semnan,
Iran.
Center of Excellence in Nonlinear Analysis and Applications (CENAA),
Semnan University,
Iran.
E-mail: Madjid.Eshaghi@gmail.com
Department of Mathematics,
Shahid Beheshti University, Tehran,
Iran.
E-mail: Hedayat.fathi@yahoo.com
Department of Mathematical Sciences,
University of Arkansas, Fayetteville, Arkansas 72701,
USA.
E-mail: shossein@uark.net
Abstract:
Let t be a regular operator between Hilbert C*-modules and t† be its Moore-Penrose inverse. We give some characterizations for t† based on C*-valued metric projection. Moore-Penrose inverse of bounded operators and elements of a C*-algebra is studied as a special case.
Paper's Title:
Some New Generalizations of Jensen's Inequality with Related Results and Applications
Author(s):
Steven G. From
Department of Mathematics
University of Nebraska at Omaha
Omaha, Nebraska 68182-0243.
E-mail: sfrom@unomaha.edu
Abstract:
In this paper, some new generalizations of Jensen's inequality are presented. In particular, upper and lower bounds for the Jensen gap are given and compared analytically and numerically to previously published bounds for both the discrete and continuous Jensen's inequality cases. The new bounds compare favorably to previously proposed bounds. A new method based on a series of locally linear interpolations is given and is the basis for most of the bounds given in this paper. The wide applicability of this method will be demonstrated. As by-products of this method, we shall obtain some new Hermite-Hadamard inequalities for functions which are 3-convex or 3-concave. The new method works to obtain bounds for the Jensen gap for non-convex functions as well, provided one or two derivatives of the nonlinear function are continuous. The mean residual life function of applied probability and reliability theory plays a prominent role in construction of bounds for the Jensen gap. We also present an exact integral representation for the Jensen gap in the continuous case. We briefly discuss some inequalities for other types of convexity, such as convexity in the geometric mean, and briefly discuss applications to reliability theory.
Paper's Title:
On the Constant in a Transference Inequality for the Vector-valued Fourier Transform
Author(s):
Dion Gijswijt and Jan van Neerven
Delft University of Technology,
Faculty EEMCS/DIAM,
P.O. Box 5031,
2600 GA Delft,
The Netherlands.
URL:
http://aw.twi.tudelft.nl/~neerven/
URL:
http://homepage.tudelft.nl/64a8q/
E-mail:
J.M.A.M.vanNeerven@TUDelft.nl
E-mail: D.C.Gijswijt@TUDelft.nl
Abstract:
The standard proof of the equivalence of Fourier type on Rd and on the torus Td is usually stated in terms of an implicit constant, defined as the minimum of a sum of powers of sinc functions. In this note we compute this minimum explicitly.
Paper's Title:
Lower and Upper Bounds for the Point-Wise Directional Derivative of the Fenchel Duality Map
Author(s):
M. Raissouli1,2, M. Ramezani3
1Department
of Mathematics,
Science Faculty, Taibah University,
P.O. Box 30097, Zip Code 41477, Al Madinah Al Munawwarah,
Saudi Arabia.
2Department
of Mathematics,
Science Faculty, Moulay Ismail University, Meknes,
Morocco.
E-mail:
raissouli.mustapha@gmail.com
3Department
of Mathematics,
University of Bojnord, Bojnord,
Iran.
E-mail: m.ramezani@ub.ac.ir
Abstract:
In this paper, we introduce the point-wise directional derivative of the Fenchel duality map and we study its properties. The best lower and upper bounds of this point-wise directional derivative are also given. We explain how our functional results contain those related to the positive bounded linear operators.
Paper's Title:
Some New Inequalities of Hermite-Hadamard and Fejér Type for Certain Functions with Higher Convexity
Author(s):
Steven G. From
Department of Mathematics,
University of Nebraska at Omaha,
Omaha, Nebraska 68182-0243,
U.S.A.
E-mail: sfrom@unomaha.edu
Abstract:
In this paper, we present some new inequalities of Hermite-Hadamard or Fejér
type for certain functions satisfying some higher convexity conditions on one or
more derivatives.
An open problem is given also.
Some applications to the logarithmic mean are given.
Paper's Title:
On Closed Range C*-modular Operators
Author(s):
Javad Farokhi-Ostad and Ali Reza Janfada
Department of Mathematics,
Faculty of Mathematics and Statistics Sciences,
University of Birjand, Birjand,
Iran.
E-mail: j.farokhi@birjand.ac.ir
ajanfada@birjand.ac.ir
Abstract:
In this paper, for the class of the modular operators on Hilbert C*-modules, we give the conditions to closedness of their ranges. Also, the equivalence conditions for the closedness of the range of the modular projections on Hilbert C*-modules are discussed. Moreover, the mixed reverse order law for the Moore-Penrose invertible modular operators are given.
Paper's Title:
Invariant Subspaces Close to Almost Invariant Subspaces for Bounded Linear Operators
Author(s):
M. A. Farzaneh, A. Assadi and H. M. Mohammadinejad
Department of Mathematical and
Statistical Sciences,
University of Birjand,
PO Box 97175/615, Birjand,
Iran.
E-mail: farzaneh@birjand.ac.ir
Department of Mathematical and
Statistical Sciences,
University of Birjand,
PO Box 97175/615, Birjand,
Iran.
E-mail: assadi-aman@birjand.ac.ir
Department of Mathematical and
Statistical Sciences,
University of Birjand,
PO Box 97175/615, Birjand,
Iran.
E-mail: hmohammadin@birjand.ac.ir
Abstract:
In this paper, we consider some features of almost invariant subspace notion. At first, we restate the notion of almost invariant subspace and obtain some results. Then we try to achieve an invariant subspace completely close to an almost invariant subspace. Also, we introduce the notion of "almost equivalent subspaces" to simply the subject related to almost invariant subspaces and apply it.
Paper's Title:
Existence of Optimal Parameters for Damped Sine-Gordon Equation with Variable Diffusion Coefficient and Neumann Boundary Conditions
Author(s):
N. Thapa
Department of Mathematical Sciences,
Cameron University,
2800 West Gore Blvd,
73505 Lawton, Oklahoma,
USA.
E-mail: nthapa@cameron.edu
URL: http://www.cameron.edu/~nthapa/
Abstract:
The parameter identification problem for sine-Gordon equation is of a major interests among mathematicians and scientists.\ In this work we the consider sine-Gordon equation with variable diffusion coefficient and Neumann boundary data. We show the existence and uniqueness of weak solution for sine-Gordon equation. Then we show that the weak solution continuously depends on parameters. Finally we show the existence of optimal set of parameters.
Paper's Title:
A Method of the Study of the Cauchy Problem for~a~Singularly Perturbed Linear Inhomogeneous Differential Equation
Author(s):
E. E. Bukzhalev and A. V. Ovchinnikov
Faculty of Physics,
Moscow State University,
1 Leninskie Gory,
Moscow, 119991,
Russia
E-mail: bukzhalev@mail.ru
Russian Institute for Scientific and
Technical Information of the Russian Academy of Sciences,
20 Usievicha St., Moscow, 125190,
Russia
E-mail: ovchinnikov@viniti.ru
Abstract:
We construct a sequence that converges to a solution of the Cauchy problem for a singularly perturbed linear inhomogeneous differential equation of an arbitrary order. This sequence is also an asymptotic sequence in the following sense: the deviation (in the norm of the space of continuous functions) of its nth element from the solution of the problem is proportional to the (n+1)th power of the parameter of perturbation. This sequence can be used for justification of asymptotics obtained by the method of boundary functions.
Paper's Title:
Euler-Maclaurin Formulas for Functions of Bounded Variation
Author(s):
G. De Marco, M. De Zotti, C. Mariconda
Dipartimento di Matematica Tullio Levi-Civita,
Universita degli Studi di Padova
Via Trieste 63, Padova 35121,
Italy.
E-mail: carlo.mariconda@unipd.it
URL: http://www.math.unipd.it
Abstract:
The first-order Euler-Maclaurin formula relates the sum of the values of a smooth function on an interval of integers with its integral on the same interval on R. We formulate here the analogue for functions that are just of bounded variation.
Paper's Title:
Numerical Radius Isometries between Hermitian Banach Algebras
Author(s):
Mohamed Mabrouk and Ashwaq Albideewi
Department of Mathematics,
Faculty of Sciences Cite Erriadh,
University of Gabes,
6072 Zrig, Gabes,
Tunisia.
E-mail: mohamed.mabrouk@fsg.rnu.tn
Department of Mathematics,
College of Applied Sciences,
Umm Al-Qura University,
P. O. Box 715,
Makkah 21955,
Saudi Arabia.
Email: Ashwaq.F.B@hotmail.com
Abstract:
In the case of C*-algebras, the author in [2] showed that any linear unital and surjective numerical radius isometry is a Jordan *-isomorphism. In this paper, we generalize this result to the case of Hermitian Banach algebras.
Paper's Title:
A Note on Taylor Expansions Without the Differentiability Assumption
Author(s):
Moawia Alghalith
Economics Dept.,
University of the West Indies,
St Augustine,
Trinidad and Tobago.
E-mail: malghalith@gmail.com
Abstract:
We introduce new Taylor expansions when the function is not differentiable.
Retraction
This article has been retracted under the authority of the Editor on Chief on 1 April, 2021. The PDF file is no longer available, but can be obtained from the editorial office upon request.
Paper's Title:
Formulation of Approximate Mathematical Model for Incoming Water to Some Dams on Tigris and Euphrates Rivers Using Spline Function
Author(s):
Nadia M. J. Ibrahem, Heba A. Abd Al-Razak, and Muna M. Mustafa
Mathematics Department,
College of Sciences for Women,
University of Baghdad, Baghdad,
Iraq.
E-mail:
Nadiamj_math@csw.uobaghdad.edu.iq
Abstract:
In this paper, we formulate three mathematical models using spline functions, such as linear, quadratic and cubic functions to approximate the mathematical model for incoming water to some dams. We will implement this model on dams of both rivers; dams on the Tigris are Mosul and Amara while dams on the Euphrates are Hadetha and Al-Hindya.
Paper's Title:
Solving Two Point Boundary Value Problems by Modified Sumudu Transform Homotopy Perturbation Method
Author(s):
Asem AL Nemrat and Zarita Zainuddin
School of Mathematical Sciences,
Universiti Sains Malaysia,
11800 Penang,
Malaysia.
E-mail: alnemrata@yahoo.com
zarita@usm.my
Abstract:
This paper considers a combined form of the Sumudu transform with the modified homotopy perturbation method (MHPM) to find approximate and analytical solutions for nonlinear two point boundary value problems. This method is called the modified Sumudu transform homotopy perturbation method (MSTHPM). The suggested technique avoids the round-off errors and finds the solution without any restrictive assumptions or discretization. We will introduce an appropriate initial approximation and furthermore, the residual error will be canceled in some points of the interval (RECP). Only a first order approximation of MSTHPM will be required, as compared to STHPM, which needs more iterations for the same cases of study. After comparing figures between approximate, MSTHPM, STHPM and numerical solutions, it is found through the solutions we have obtained that they are highly accurate, indicating that the MSTHPM is very effective, simple and can be used to solve other types of nonlinear boundary value problems (BVPs).
Paper's Title:
Global Analysis on Riemannian Manifolds
Author(s):
Louis Omenyi and Michael Uchenna
Department of Mathematics, Computer
Science, Statistics and Informatics,
Alex Ekwueme Federal University, Ndufu-Alike,
Nigeria.
E-mail: omenyi.louis@funai.edu.ng,
michael.uchenna@funai.edu.ng
URL: http://www.funai.edu.ng
Abstract:
In this paper, an exposition of the central concept of global analysis on a Riemannan manifold is given. We extend the theory of smooth vector fields from open subsets of Euclidean space to Riemannan manifolds. Specifically, we prove that a Riemannian manifold admits a unique solution for a system of ordinary differential equations generated by the flow of smooth tangent vectors. The idea of partial differential equations on Riemannian manifold is highlighted on the unit sphere.
Paper's Title:
Weyl's theorem for class Q and k - quasi class Q Operators
Author(s):
S. Parvatham and D. Senthilkumar
Department of Mathematics and Humanities,
Sri Ramakrishna Institute of Technology, Coimbatore-10, Tamilnadu,
India.
E-mail: parvathasathish@gmail.com
Post Graduate and Research Department of
Mathematics,
Govt. Arts College, Coimbatore-641018, Tamilnadu,
India.
E-mail: senthilsenkumhari@gmail.com
Abstract:
In this paper, we give some properties of class Q operators. It is proved that every class Q operators satisfies Weyl's theorem under the condition that T2 is isometry. Also we proved that every k quasi class Q operators is Polaroid and the spectral mapping theorem holds for this class of operator. It will be proved that single valued extension property, Weyl and generalized Weyl's theorem holds for every k quasi class Q operators.
Paper's Title:
Accuracy of Implicit DIMSIMs with Extrapolation
Author(s):
A. J. Kadhim, A. Gorgey, N. Arbin and N. Razali
Mathematics Department, Faculty of
Science and Mathematics,
Sultan Idris Education University,
35900 Tanjong Malim, Perak,
Malaysia
E-mail: annie_gorgey@fsmt.upsi.edu.my
Unit of Fundamental Engineering Studies,
Faculty of Engineering, Built Environment,
The National University of Malaysia,
43600 Bangi,
Malaysia.
Abstract:
The main aim of this article is to present recent results concerning diagonal implicit multistage integration methods (DIMSIMs) with extrapolation in solving stiff problems. Implicit methods with extrapolation have been proven to be very useful in solving problems with stiff components. There are many articles written on extrapolation of Runge-Kutta methods however fewer articles on extrapolation were written for general linear methods. Passive extrapolation is more stable than active extrapolation as proven in many literature when solving stiff problems by the Runge-Kutta methods. This article takes the first step by investigating the performance of passive extrapolation for DIMSIMs type-2 methods. In the variable stepsize and order codes, order-2 and order-3 DIMSIMs with extrapolation are investigated for Van der Pol and HIRES problems. Comparisons are made with ode23 solver and the numerical experiments showed that implicit DIMSIMs with extrapolation has greater accuracy than the method itself without extrapolation and ode23.
Paper's Title:
Inequalities of Gamma Function Appearing in Generalizing Probability Sampling Design
Author(s):
Mohammadkheer M. Al-Jararha And Jehad M. Al-Jararha
Department of Mathematics,
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: mohammad.ja@yu.edu.jo
Department of Statistics,
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: jehad@yu.edu.jo
Abstract:
In this paper, we investigate the complete monotonicity of some functions involving gamma function. Using the monotonic properties of these functions, we derived some inequalities involving gamma and beta functions. Such inequalities can be used to generalize different probability distribution functions. Also, they can be used to generalize some statistical designs, e.g., the probability proportional to the size without replacement design.
Paper's Title:
Sweeping Surfaces with Darboux Frame in Euclidean 3-space E3
Author(s):
F. Mofarreh, R. Abdel-Baky and N. Alluhaibi
Mathematical Science Department, Faculty
of Science,
Princess Nourah bint Abdulrahman University
Riyadh 11546,
Saudi Arabia.
E-mail: fyalmofarrah@pnu.edu.sa
Department of Mathematics, Faculty of Science,
University of Assiut,
Assiut 71516,
Egypt.
E-mail: rbaky@live.com
Department of Mathematics Science and
Arts, College Rabigh Campus,
King Abdulaziz University
Jeddah,
Saudi Arabia.
E-mail: nallehaibi@kau.edu.sa
Abstract:
The curve on a regular surface has a moving frame and it is called Darboux frame. We introduce sweeping surfaces along the curve relating to the this frame and investigate their geometrical properties. Moreover, we obtain the necessary and sufficient conditions for these surfaces to be developable ruled surfaces. Finally, an example to illustrate the application of the results is introduced.
Paper's Title:
Rational Expressions of Arithmetic and Geometric Means for the Sequence
npn ∈ N and the Geometric Progression
Author(s):
M. Kinegawa, S. Miyamoto and Y. Nishizawa
Faculty of Education, Saitama University,
Shimo-okubo 255, Sakura-ku, Saitama-city, Saitama,
Japan.
E-mail: m.kinegawa.645@ms.saitama-u.ac.jp
Faculty of Education, Saitama University,
Shimo-okubo 255, Sakura-ku, Saitama-city, Saitama,
Japan.
E-mail: s.miyamoto.245@ms.saitama-u.ac.jp
Faculty of Education, Saitama University,
Shimo-okubo 255, Sakura-ku, Saitama-city, Saitama,
Japan.
E-mail:
ynishizawa@mail.saitama-u.ac.jp
Abstract:
In this paper, we consider the arithmetic and geometric means for the sequence npn ∈ N and the geometric progression. We obtain the results associated with the rational expressions of the means.
Paper's Title:
Coexisting Attractors and Bubbling Route to Chaos in Modified Coupled Duffing Oscillators
Author(s):
B. Deruni1, A. S. Hacinliyan1,2, E. Kandiran3, A. C. Keles2, S. Kaouache4, M.-S. Abdelouahab4, N.-E. Hamri4
1Department
of Physics,
University of Yeditepe,
Turkey.
2Department
of Information Systems and Technologies,
University of Yeditepe,
Turkey
3Department
of Software Development,
University of Yeditepe,
Turkey.
4Laboratory
of Mathematics and their interactions,
University Center of Abdelhafid Boussouf,
Mila 43000,
Algeria.
E-mail:
berc890@gmail.com
ahacinliyan@yeditepe.edu.tr
engin.kandiran@yeditepe.edu.tr
cihan.keles@yeditepe.edu.tr
s.kaouache@centr-univ-mila.dz
medsalah3@yahoo.fr
n.hamri@centre-univ-mila.dz
Abstract:
In this article dynamical behavior of coupled Duffing oscillators is analyzed under a small modification. The oscillators have cubic damping instead of linear one. Although single duffing oscillator has complex dynamics, coupled duffing systems possess a much more complex structure. The dynamical behavior of the system is investigated both numerically and analytically. Numerical results indicate that the system has double scroll attractor with suitable parameter values. On the other hand, bifurcation diagrams illustrate rich behavior of the system, and it is seen that, system enters into chaos with different routes. Beside classical bifurcations, bubbling route to chaos is observed for suitable parameter settings. On the other hand, Multistability of the system is indicated with the coexisting attractors, such that under same parameter setting the system shows different periodic and chaotic attractors. Moreover, chaotic synchronization of coupled oscillators is illustrated in final section.
Paper's Title:
Nonlinear System of Mixed Ordered Variational Inclusions Involving XOR Operation
Author(s):
Iqbal Ahmad, Abdullah and Syed Shakaib Irfan
Department of Mechanical Engineering,
College of Engineering, Qassim University
Buraidah 51452, Al-Qassim,
Saudi Arabia.
E-mail: iqbal@qec.edu.sa,
i.ahmad@qu.edu.sa
Zakir Husain Delhi College,
University of Delhi,
JLN Marg, New Delhi- 110 002,
India.
E-mail: abdullahdu@qec.edu.sa
Department of Mathematics,
Aligarh Muslim University, Aligarh,
India.
E-mail: shakaibirfan@gmail.com
Abstract:
In this work, we introduce and solve an NSMOVI frameworks system involving XOR operation with the help of a proposed iterative algorithm in real ordered positive Hilbert spaces. We discuss the existence of a solution of a considered system of inclusions involving XOR operation by applying the resolvent operator technique with XOR operation and also study the strong convergence of the sequences generated by the considered algorithm. Further, we give a numerical example in support of our considered problem which gives the grantee that all the proposed conditions of our main result are fulfilled.
Paper's Title:
Locally Bicomplex Convex Module and Their Applications
Author(s):
Stanzin Kunga and Aditi Sharma
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: stanzinkunga19@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: aditi.sharmaro@gmail.com
Abstract:
Let X be a locally BC convex module and L(X) be the family of all continuous bicomplex linear operators on X. In this paper, we study some concepts of D-valued seminorms on locally BC convex module. Further, we study the bicomplex version of Co and (Co,1) semigroup. The work of this paper is inspired by the work in [2] and [6].
Paper's Title:
An Integration Technique for Evaluating Quadratic Harmonic Sums
Author(s):
J. M. Campbell and K.-W. Chen
Department of Mathematics and Statistics,
York University, 4700 Keele St, Toronto,
ON M3J 1P3,
Canada.
E-mail: jmaxwellcampbell@gmail.com
Department of Mathematics, University of Taipei,
No. 1, Ai-Guo West Road,
Taipei 10048, Taiwan.
E-mail: kwchen@uTaipei.edu.tw
URL:
https://math.utaipei.edu.tw/p/412-1082-22.php
Abstract:
The modified Abel lemma on summation by parts has been applied in many ways recently to determine closed-form evaluations for infinite series involving generalized harmonic numbers with an upper parameter of two. We build upon such results using an integration technique that we apply to ``convert'' a given evaluation for such a series into an evaluation for a corresponding series involving squared harmonic numbers.
Paper's Title:
Introducing the Picard-S3 Iteration for Fixed Points
Author(s):
Pravin Singh, Virath Singh and Shivani Singh
University of KwaZulu-Natal,
School of Mathematics Statistics and Computer Sciences,
Private Bag X54001,
Durban, 4000
South Africa.
Unisa,
Department of Decision Sciences,
PO Box 392,
Pretoria, 0003
South Africa.
E-mail: singhprook@gmail.com
singhv@ukzn.ac.za
shivstarsingh@gmail.com
Abstract:
In this paper we introduce a three step iteration method and show that it can be used to approximate the fixed point of a weak contraction mapping. Furthermore, we prove that this scheme is equivalent to the Mann iterative scheme. A comparison is made with other three step iterative methods by examining the speed of convergence. Results are presented in tables to support our conclusion.
Paper's Title:
Eigenvalue Bounds based on Projections
Author(s):
Pravin Singh, Shivani Singh, Virath Singh
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
University of South Africa,
Department of Decision Sciences, PO Box 392,
Pretoria,0003,
South Africa.
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
E-mail:
singhp@ukzn.ac.za,
singhs2@unisa.ac.za,
singhv@ukzn.ac.za
Abstract:
In this paper, we derive expressions for the bounds of the extremal eigenvalues of positive definite matrices. Our approach is to use a symmetric projection operator onto an n-2 dimensional subspace of the real space of n tuples. These bounds are based on traces of the matrix and its powers. They are relatively easy and inexpensive to compute.
Paper's Title:
On Automorphisms and Bi-derivations of Semiprime Rings
Author(s):
Abu Zaid Ansari, Faiza Shujat, Ahlam Fallatah
Department of Mathematics,
Faculty of Science,
Islamic University of Madinah, Madinah
K.S.A.
E-mail: ansari.abuzaid@gmail.com,
ansari.abuzaid@iu.edu.sa
Department of Mathematics
Faculty of Science
Taibah University, Madinah,
K.S.A.
E-mail: faiza.shujat@gmail.com,
fullahkhan@taibahu.edu.sa
Department of Mathematics
Faculty of Science
Taibah University, Madinah,
K.S.A.
E-mail: Afallatah@taibahu.edu.sa
Abstract:
In this article, our goal is to figure out a functional equation involving automorphisms and bi-derivations on certain semiprime ring. Also, we characterize the structure of automorphism, in case of prime rings.
Paper's Title:
Growth and Approximation of Entire Solutions of Linear Partial Differential Equation in Terms of Bessel Polynomial Approximation Errors in Lp-norm, 1 ≤ p ≤ ∞
Author(s):
Devendra Kumar
Department of Mathematics, Faculty of
Sciences
Al-Baha University,
P.O.Box-7738 Alaqiq, Al-Baha-65799,
Saudi Arabia.
E-mail:
d_kumar001@rediffmail.com,
dsingh@bu.edu.sa
Abstract:
We deal with entire solutions of some special type linear homogeneous partial differential equations that are represented in convergent series of Bessel polynomials. We determine the growth orders and types of the solutions, in terms of Bessel polynomial approximation errors in both sup norm and Lp-norm, 1 ≤ p ≤ ∞.
Paper's Title:
A New Look at the Equations of the Calculus of Variations
Author(s):
Olivier de La Grandville
Faculty of Economics, Goethe University
Frankfurt,
Theodore Adorno Platz 4, 60323 Frankfurt,
Germany.
E-mail: odelagrandville@gmail.com
Abstract:
We first offer an entirely new way to derive the celebrated Euler equation of the calculus of variations. The advantage of this approach is two-fold. On the one hand, it entirely eschews the two hurdles encountered by Lagrange, which become challenging in the case of elaborate functionals: getting rid of the arbitrary character of the perturbation given to the optimal function, and demonstrating the fundamental lemma of the calculus of variations. On the other hand, it leads in a direct way to the remarkable discovery made by Robert Dorfman ( 1969) when he introduced a modified Hamiltonian, which we called a Dorfmanian (2018) to honor his memory. In turn, extending the Dorfmanian enables to obtain readily the fundamental equations of the calculus of variations for the optimization of high-order functionals, or multiple integrals.
Paper's Title:
Maximal Singular Operators On Variable Exponent Sequence Spaces and Their Corresponding Ergodic Version
Author(s):
Sri Sakti Swarup Anupindi and Michael A. Alphonse
Department of Mathematics, Birla Institute
of Technology And Science- Pilani,
Hyderabad Campus, Jawahar Nagar, Kapra Mandal,
District.-Medchal-500 078 Telangana,
India.
E-mail:
p20180442@hyderabad.bits-pilani.ac.in
alphonse@hyderabad.bits-pilani.ac.in
URL:
https://www.bits-pilani.ac.in/hyderabad/a-michael-alphonse
https://www.bits-pilani.ac.in/research_scholars/sri-sakti-swarup-anupindi
Abstract:
In this paper, we prove strong and weak type inequalities of singular operators on weighted lwp(Z)$. Using these results, we prove strong type and weak type inequalities of the maximal singular operator of Calderon-Zygmund type on variable exponent sequence spaces lp(·)(Z). Using the Calderon-Coifman-Weiss transference principle, we prove strong type, weak type inequalities of the maximal ergodic singular operator on Lwp(X,B,μ) spaces, where (X,B,μ) is a probability space equipped with measure preserving transformation U.
Paper's Title:
New Fast Extragradient-like Methods for Non-Lipschitzian Pseudo-monotone Variational Inequalities
Author(s):
Morad Ali Peyvand
Department of Mathematics
Yasouj University
Yasouj,
Iran.
E-mail: peyvand@yu.ac.ir
Abstract:
An efficient double-projection method, with a new search strategy, is designed for solving variational inequalities in real Hilbert spaces with pseudo-monotone cost operator. Our proposed method uses a computationally inexpensive simple line search procedure based on local information of the operator and very weak conditions of parameters to obtain larger step sizes. A description of the algorithm along with its weak convergence is provided without assuming Lipschitz continuity. Also, a modification to the proposed method is presented, wherein the second projection onto the closed and convex subset is replaced with the one onto a subgradient half space. Numerical experiments and comparisons with related methods demonstrate the reliability and benefits of the proposed schemes.
Paper's Title:
Discrete-time Evolution and Stable Equilibria of Multi-compartment Dengue Tracker: Nonlinear Dynamics Modulated by Controlled Stochasticity
Author(s):
M. Bhaduri and M. Predescu
Department of Mathematical Sciences,
Bentley University,
Waltham, MA 02452,
U.S.A.
E-mail: mbhaduri@bentley.edu,
mpredescu@bentley.edu
Abstract:
We discuss the dynamics of solutions of a nonlinear discrete time model that will be useful in Dengue control. The proposed model may be utilized to analyze the dynamics of three variables (mosquito population, habitats and consciousness) across different parameters. Stochasticity has been introduced in realistic ways to highlight combinations of random parameters (on education and recollection) which limits the oscillatory recurrence of habitats and awareness. We propose optimal methods for implementing potential intervention strategies and offer interactive dashboards for vizualizing varied scenarios.
Search and serve lasted 1 second(s).