|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Differential Equations for Indicatrices, Spacelike and Timelike Curves
Author(s):
Sameer, Pradeep Kumar Pandey
Department of Mathematics,
Jaypee University of Information Technology,
Solan, Himachal Pradesh,
India.
E-mail: sksameer08@gmail.com,
pandeypkdelhi@gmail.com
Abstract:
Motivated by the recent work of Deshmukh et al. [20], in this paper we show that Tangent, Binormal, and Principal Normal indicatrices do not form non-trivial differential equations. Finally, we obtain the 4th-order differential equations for spacelike and timelike curves.
Paper's Title:
Global Implicit Function Theorems and Critical Point Theory in Frechet Spaces
Author(s):
Kaveh Eftekharinasab
Algebra and Topology Department,
Institute of Mathematics of National Academy of Sciences of Ukraine
Tereshchenkivska st., 01024, Kyiv,
Ukraine.
E-mail: kaveh@imath.kiev.ua
URL:
https://www.imath.kiev.ua/people/profile.php?pid=485\&lang=en
Abstract:
We prove two versions of a global implicit function theorem, which involve no loss of derivative, for Keller's Cc1 -mappings between arbitrary Fréchet spaces. Subsequently, within this framework, we apply these theorems to establish the global existence and uniqueness of solutions to initial value problems that involve the loss of one derivative. Moreover, we prove a Lagrange multiplier theorem by employing indirect applications of the global implicit function theorems through submersions and transversality.
Paper's Title:
Applications of Relations and Relators in the
Extensions of Stability Theorems for Homogeneous and Additive Functions
Author(s):
Árpád Száz
Institute of Mathematics, University of Debrecen,
H-4010 Debrecen,
Pf. 12,
Hungary
szaz@math.klte.hu
Abstract:
By working out an appropriate technique of relations and relators and extending the ideas of the direct methods of Z. Gajda and R. Ger, we prove some generalizations of the stability theorems of D. H. Hyers, T. Aoki, Th. M. Rassias and P. Găvruţă in terms of the existence and unicity of 2-homogeneous and additive approximate selections of generalized subadditive relations of semigroups to vector relator spaces. Thus, we obtain generalizations not only of the selection theorems of Z. Gajda and R. Ger, but also those of the present author.
Paper's Title:
On Saturation of Norm Convergence of Walsh-Fourier Matrix Transform Means
Author(s):
István Blahota
Institute of Mathematics and Computer Sciences,
University of Nyíregyháza,
H-4400 Nyíregyháza,
Sóstói street 31/b,
Hungary
E-mail: blahota.istvan@nye.hu
Abstract:
In this paper we investigate the saturation of norm convergence issues for regular matrix transform means in case of Walsh-Paley system. The main result is the observation of equality ||σTn (f) - f ||p=0(a)n where an sequence of positive numbers tends to zero and there exists constant $c$, for which t1,n≤ can for every n∈P.
Paper's Title:
Sweeping Surfaces with Darboux Frame in Euclidean 3-space E3
Author(s):
F. Mofarreh, R. Abdel-Baky and N. Alluhaibi
Mathematical Science Department, Faculty
of Science,
Princess Nourah bint Abdulrahman University
Riyadh 11546,
Saudi Arabia.
E-mail: fyalmofarrah@pnu.edu.sa
Department of Mathematics, Faculty of Science,
University of Assiut,
Assiut 71516,
Egypt.
E-mail: rbaky@live.com
Department of Mathematics Science and
Arts, College Rabigh Campus,
King Abdulaziz University
Jeddah,
Saudi Arabia.
E-mail: nallehaibi@kau.edu.sa
Abstract:
The curve on a regular surface has a moving frame and it is called Darboux frame. We introduce sweeping surfaces along the curve relating to the this frame and investigate their geometrical properties. Moreover, we obtain the necessary and sufficient conditions for these surfaces to be developable ruled surfaces. Finally, an example to illustrate the application of the results is introduced.
Paper's Title:
Oscillation and Boundedness of Solutions to First and Second Order Forced Dynamic Equations with Mixed Nonlinearities
Author(s):
Ravi P. Agarwal and Martin Bohner
Department of Mathematical Sciences, Florida Institute of Technology
Melbourne, FL 32901,
U.S.A.
bohner@mst.edu
URL:http://web.mst.edu/~bohner
Department of Economics and Finance, Missouri University of Science and Technology
Rolla, MO 65401,
U.S.A.
agarwal@fit.edu
Abstract:
Some oscillation and boundedness criteria for solutions to certain
first and second order forced dynamic equations
with mixed nonlinearities are established. The main tool in the proofs
is an inequality due to Hardy, Littlewood and Pólya.
The obtained results can be applied to differential equations,
difference equations and q-difference equations. The results
are illustrated with numerous examples.
Paper's Title:
Ulam Stability of Functional Equations
Author(s):
Stefan Czerwik and Krzysztof Król
Institute of Mathematics
Silesian University of Technology
Kaszubska 23,
44-100 Gliwice,
Poland
Stefan.Czerwik@polsl.pl
Krzysztof.Krol@polsl.pl
Abstract:
In this survey paper we present some of the main results on Ulam-Hyers-Rassias stability for important functional equations.
Paper's Title:
Finite Volume Approximation of a Class of 2D Elliptic Equations with Discontinuous and Highly Oscillating Coefficients
Author(s):
J. D. Bambi Pemba and B. Ondami
Université Marien Ngouabi
Factuté des Sciences et Techniques
BP 69 Brazzaville,
Congo.
E-mail: bondami@gmail.com
URL:
https://www.researchgate.net/profile/Bienvenu-Ondami
https://www.linkedin.com/in/bienvenu-ondami
Abstract:
In this paper, we are interested in the Finite Volume approximation of a second-order two-dimensional elliptic equation in heterogeneous porous medium with a periodic structure. The equation's coefficients are therefore discontinuous and highly oscillating. This class of problems has been extensively studied in the literature, where various methods proposed for determining the so-called homogenized problem. What we are particularly interested in is the direct numerical approximation of the problem, which has received little attention in the literature. We use the cell-centered finite volume approach for this purpose. Error estimates are established, and numerical simulations are conducted for both the isotropic and anisotropic media cases. The obtained solution is compared to the homogenized solution, and the results show that this approach provides an adequate approximation of the exact solution.
Paper's Title:
Some Properties of the Solution of a Second Order Elliptic Abstract Differential Equation
Author(s):
A. Aibeche and K. Laidoune
Mathematics Department, Faculty of Sciences,
University Ferhat Abbas, Setif,
Route de Scipion, 19000,
Setif,
Algeria
aibeche@univ-setif.dz
Abstract:
In this paper we study a class of non regular boundary value
problems for elliptic differential-operator equation of second order with an
operator in boundary conditions. We give conditions which guarantee the
coerciveness of the solution of the considered problem, the completeness of
system of root vectors in Banach-valued functions spaces and we establish
the Abel basis property of this system in Hilbert spaces. Finally, we apply
this abstract results to a partial differential equation in cylindrical
domain.
Paper's Title:
Asymptotic Inequalities for the Maximum Modulus of the Derivative of a Polynomial
Author(s):
Clément Frappier
Département de Mathématiques et de Génie industriel École Polytechnique de
Montréal,
C.P.~6079, succ. Centre-ville Montréal (Québec),
H3C 3A7, CANADA
Abstract:
Let
 be an algebraic polynomial of degree
≤n, and let ∥p∥= max {|p(z)|:|z| = 1}.
We study the asymptotic behavior of the best possible constant φn,k (R), for
k = 0 and k=1, in the inequality ∥p'(Rz)∥ + φn,k (R) |ak|
≤ nRn-1 ∥p∥, R → ∞.
be an algebraic polynomial of degree
≤n, and let ∥p∥= max {|p(z)|:|z| = 1}.
We study the asymptotic behavior of the best possible constant φn,k (R), for
k = 0 and k=1, in the inequality ∥p'(Rz)∥ + φn,k (R) |ak|
≤ nRn-1 ∥p∥, R → ∞.
Paper's Title:
Sharp Lp Improving Results for Singular Measures on Cn+1
Author(s):
E. Ferreyra, M. Urciuolo
FaMAF-CIEM,
Universidad Nacional de Córdoba-Conicet,
Ciudad Universitaria, 5000 Córdoba,
Argentina
eferrey@famaf.unc.edu.ar
urciuolo@famaf.unc.edu.ar
Abstract:
For j=1,...,n, let Ωj be open sets of the complex plane and let φj be holomorphic functions on Ωj such that φj'' does not vanish identically on Ωj. We consider φ(z1,...,zn) =φ1(z1) +...+φn(zn). We characterize the pairs (p,q) such that the convolution operator with the surface measure supported on a compact subset of the graph of φ is p-q bounded.
Paper's Title:
A Determinantal Representation of Core EP Inverse
Author(s):
Divya Shenoy Purushothama
Department of Mathematics,
Manipal Institute of Technology,
Manipal Academy of Higher Education,
Manipal -576104, Karnataka,
India.
E-mail: divya.shenoy@manipal.edu
URL:
https://manipal.edu/mit/department-faculty/faculty-list/divya-shenoy-p.html
Abstract:
The notion of Core EP inverse is introduced by Prasad in the article "Core - EP inverse" and proved its existence and uniqueness. Also, a formula for computing the Core EP inverse is obtained from particular linear combination of minors of a given matrix. Here a determinantal representation for Core EP inverse of a matrix A with the help of rank factorization of A is obtained.
Paper's Title:
The Drazin-star and Star-Drazin Solutions to Quaternion Matrix Equations
Author(s):
Ivan I. Kyrchei, Dijana Mosić, Predrag Stanimirović
Pidstryhach Institute for Applied Problems
of Mechanics and Mathematics
of NAS of Ukraine, L'viv, 79060,
Ukraine.
E-mail:
ivankyrchei26@gmail.com
Faculty of Sciences and Mathematics,
University of Ni, P.O.
Box 224, 18000, Ni, Serbia.
E-mail: dijana@pmf.ni.ac.rs
Faculty of Sciences and Mathematics,
University of Ni, P.O.
Box 224, 18000, Ni, Serbia.
E-mail: pecko@pmf.ni.ac.rs
Abstract:
The notions of the Drazin-star and star-Drazin matrices are expanded to quaternion matrices in this paper. Their determinantal representations are developed in both cases in terms of noncommutative row-column determinants of quaternion matrices and for minors of appropriate complex matrices. We study all possible two-sided quaternion matrix equations with their one-sided partial cases whose uniquely determined solutions are based on the Drazin-star and star-Drazin matrices. Solutions of these equations are represented by Cramer's rules in both cases for quaternion and complex matrix equations. A numerical example is presented to illustrate our results.
Paper's Title:
Oscillation Criteria for Second Order Delay Difference Equations via Canonical Transformations and Some New Monotonic Properties
Author(s):
R. Deepalakhmi, S. Saravanan, J. R. Graef, and E. Thandapani
Department of Interdisciplinary Studies
Tamil Nadu Dr. Ambedkar Law University
Chennai-600113,
India.
profdeepalakshmi@gmail.com
Madras School of Economics,
Chennai-600025,
India.
profsaran11@gmail.com
Department of Mathematics,
University of Tennessee at Chattanooga,
Chattanooga,TN 37403,
USA.
john-graef@utc.edu
Ramanujan Institute for Advanced Study in
Mathematics,
University of Madras,
Chennai - 600 005,
India.
ethandapani@yahoo.co.in
Abstract:
This paper is concerned with second-order linear noncanonical delay difference equations of the form
Δ(μ(t)Δ y(t))+ p(t)y(φ(t))=0.
The authors prove new oscillation criteria by first transforming the equation into canonical form and then obtaining some new monotonic properties of the positive solutions of the transformed equation. By using a comparison with first-order delay difference equations and a generalization of a technique developed by Koplatadze, they obtain their main results. Examples illustrating the improvement over known results in the literature are presented.
Paper's Title:
Uniqueness of Meromorphic Functions and
Weighted Sharing
Author(s):
Indrajit Lahiri and Rupa Pal
Department of Mathematics, University of
Kalyani, West Bengal 741235, India
indr9431@dataone.in
Jhargram Raj College,
Jhargram, Midnapur(W),
West Bengal 721507,
India
rupa.a.pal@gmail.com
Abstract:
With the help of the notion of weighted sharing of values, we prove a result on uniqueness of meromorphic functions and as a consequence we improve a result of P. Li
Paper's Title:
A New Method for Comparing Closed Intervals
Author(s):
Ibraheem Alolyan
Department of Mathematics, College of Sciences,
King Saud University, P. O. Box 2455, Riyadh 11451,
Saudi Arabia
ialolyan@ksu.edu.sa
URL:http://faculty.ksu.edu.sa/ALolyan
Abstract:
The usual ordering ``≤" on R is a total ordering, that is, for any two real numbers in R, we can determine their order without difficulty. However, for any two closed intervals in R, there is not a natural ordering among the set of all closed intervals in R. Several methods have been developed to compare two intervals. In this paper, we define the μ-ordering which is a new method for ordering closed intervals.
Paper's Title:
Solving Fractional Transport Equation via Walsh Function
Author(s):
A. Kadem
L. M. F. N., Mathematics Department,
University of Setif,
Algeria
abdelouahak@yahoo.fr
Abstract:
In this paper we give a complete proof of A method for the solution of fractional transport equation in three-dimensional case by using Walsh function is presented. The main characteristic of this technique is that it reduces these problems to those of solving a system of algebraic equations, thus greatly simplifying the problem.
Paper's Title:
Existence and Approximation of Traveling Wavefronts for the Diffusive Mackey-Glass Equation
Author(s):
C. Ramirez-Carrasco and J. Molina-Garay
Facultad de Ciencias Basicas,
Universidad Catolica del Maule, Talca,
Chile
E-mail: carloshrc1989@gmail.com
molina@imca.edu.pe
Abstract:
In this paper, we consider the diffusive Mackey-Glass model with discrete delay. This equation describes the dynamics of the blood cell production. We investigate the existence of traveling wavefronts solutions connecting the two steady states of the model. We develop an alternative proof of the existence of such solutions and we also demonstrate the existence of traveling wavefronts moving at minimum speed. The proposed approach is based on the use technique of upper-lower solutions. Finally, through an iterative procedure, we show numerical simulations that approximate the traveling wavefronts, thus confirming our theoretical results.
Paper's Title:
Timelike Surfaces with a Common Line of Curvature in Minkowski 3-Space
Author(s):
M.K. Saad, A.Z. Ansari, M. Akram and F. Alharbi
Department of Mathematics ,
Faculty of Science,
Islamic University of Madinah,
KSA
Abstract:
In this paper, we analyze the problem of constructing a timelike surface family from a given non-null curve line of curvature. Using the Frenet frame of the non-null curve in Minkowski space E13 we express the family of surfaces as a linear combination of the components of this frame, and derive the necessary and sufficient conditions for the coefficients to satisfy both the line of curvature and the isoparametric requirements. In addition, a necessary and sufficient condition for the given non-null curve to satisfy the line of curvature and the geodesic requirements is investigated. The extension to timelike surfaces of revolution is also outlined. Meanwhile, some representative non-null curves are chosen to construct the corresponding timelike surfaces which possessing these curves as lines of curvature. Results presented in this paper have applications in geometric modeling and the manufacturing of products. In addition, some computational examples are given and plotted.
Paper's Title:
Topological Aspects of Discrete Switch Dynamical Systems
Author(s):
Faiz Imam and Sharan Gopal
Department of Mathematics,
BITS - Pilani, Hyderabad Campus,
India.
E-mail: mefaizy@gmail.com
Department of Mathematics,
BITS - Pilani, Hyderabad Campus,
India.
E-mail: sharanraghu@gmail.com
ABSTRACT NOT FOUND. WEBSITE ERROR
Abstract:
Paper's Title:
Fixed Point Results for Integral Type Contractions in R-Metric Space
Author(s):
Samriddhi Ghosh, Ramakant Bhardwaj, Ritu Shrivastava, Vandana Rathore, Satyendra Narayan
Department of Mathematics,
Amity University, Kolkata, West Bengal,
India.
E-mail: ritha98@gmail.com
Department of Mathematics,
Amity University, Kolkata, West Bengal,
India.
E-mail: drrkbhardwaj100@gmail.com
Department of Mathematics,
Bahrain Polytechnic, Isa Town,
Kingdom of Bahrain
E-mail: ritu.shrivastava@polytechnic.bh
Faculty of Science and Technology,
Jagran Lakecity University, Bhopal, Madhya Pradesh,
India.
E-mail: drvandana@jlu.edu.in
School of Computer Science and
Technology,
Algoma University, Brampton, Ontario,
Canada.
E-mail: narayan.satyendra@gmail.com
Abstract:
The main aim of the research is to establish some invariant point (fixed point) results under the purview of R-Metric Spaces, for integral type R-contractive mappings. To serve this purpose, concepts of R-continuity, R-convergence and R-preservation has been used. Finally, the obtained results has been used to deduce some invariant point results for Banach, Kannan and Chatterjea type mappings in R-Metric Space. Also some examples and applications have been illustrated to support the findings discussed.
Paper's Title:
Essential Random Fixed Point Set of Random Operators
Author(s):
Ismat Beg
Centre for Advanced Studies in Mathematics,
Lahore University of Management Sciences (LUMS),
54792-Lahore, PAKISTAN.
ibeg@lums.edu.pk
URL: http://web.lums.edu.pk/~ibeg
Abstract:
We obtain necessary and sufficient conditions for the existence of essential random fixed point of a random operator defined on a compact metric space. The structure of the set of essential random fixed points is also studied.
Paper's Title:
On the Hohov Convolution Of The Class Sp(α,β)
Author(s):
T. N. Shanmugam and S. Sivasubramanian
Department of Mathematics,
Anna University,
Chennai 600025,
Tamilnadu, India.
shan@annauniv.edu
Department of Mathematics,
Easwari Engineering College,
Chennai-600089,
Tamilnadu, India,
sivasaisastha@rediffmail.com
Abstract:
Let F(a,b;c;z) be the Gaussian hypergeometric function and Ia,b;c(f)=zF(a,b;c;z)*f(z) be the Hohlov operator defined on the class A of all normalized analytic functions. We determine conditions on the parameters a,b,c such that Ia,b;c(f) will be in the class of parabolic starlike functions Sp(α,β). Our results extend several earlier results.
Paper's Title:
Generalized Hypergeometric Functions Defined on the Class of Univalent Functions
Author(s):
N. Marikkannan, A. Gangadharan and C. Ganesamoorthy
Department of Applied Mathematics,
Sri Venkateswara College of Engineering,
Sriperumbudur 602105,
India.
mari@svce.ac.in
Department of Applied mathematics,
Sri Venkateswara College of Engineering,
Sriperumbudur 602105,
India.
ganga@svce.ac.in
Department of Mathematics,
Alagappa university,
Karaikudi,
India.
ganesamoorthyc@yahoo.com
Abstract:
Let A denotes the class of all analytic functions
f(z), normalized by the condition f'(0)-1=f(0)=0 defined on
the open unit disk
Paper's Title:
Strongly Nonlinear Variational Parabolic Problems in Weighted Sobolev Spaces
Author(s):
L. Aharouch, E. Azroul and M. Rhoudaf
Dép. Math. Faculté des Sciences Dhar-Mahraz
B.P 1796 Atlas Fés,
Maroc.
rhoudaf_mohamed@yahoo.fr
Abstract:
In this paper , we study the existence of a weak solutions for the
initial-boundary value problems of the strongly nonlinear degenerated parabolic
equation,
where
A is a Leray-lions operator acted from
Lp(0,T,W01,p(Ώ,w)) into its dual. g(x,t,u,∇ u)
is a nonlinear term with critical growth condition with respect to ∇ u
and no growth with respect to u.
The source term f is assumed to belong to Lp'(0,T,W-1,p'(Ώ,w*)).
∂u
+A(u)+g(x,t,u,∇ u)=f
∂t
Paper's Title:
On Stan Ulam and his Mathematics
Author(s):
Krzysztof Ciesielski and Themistocles M. Rassias
Mathematics Institute, Jagiellonian University,
Abstract:
In this note we give a glimpse of the curriculum vitae of Stan Ulam, his personality and some of the mathematics he was involved in.
Paper's Title:
On a Method of Proving the Hyers-Ulam Stability
of Functional Equations on Restricted Domains
Author(s):
Janusz Brzdęk
Department of Mathematics
Pedagogical University Podchor
Abstract:
We show that generalizations of some (classical) results on the Hyers-Ulam stability of functional equations, in several variables, can be very easily derived from a simple result on stability of a functional equation in single variable
Paper's Title:
Fixed Points and Stability
of the Cauchy Functional Equation
Author(s):
Choonkil Park and Themistocles M. Rassias
Department of Mathematics, Hanyang University,
Seoul 133-791,
Republic of Korea
Department of Mathematics,
National Technical University of Athens,
Zografou Campus, 15780 Athens,
Greece
baak@hanyang.ac.kr
trassias@math.ntua.gr
Abstract:
Using fixed point methods, we prove the generalized Hyers-Ulam stability of homomorphisms in Banach algebras and of derivations on Banach algebras for the Cauchy functional equation.
Paper's Title:
Hyperbolic Barycentric Coordinates
Author(s):
Abraham A. Ungar
Department of Mathematics, North Dakota State University,
Fargo, ND 58105,
USA
Abraham.Ungar@ndsu.edu
URL: http://math.ndsu.nodak.edu/faculty/ungar/
Abstract:
A powerful and novel way to study Einstein's special theory of relativity and its underlying geometry, the hyperbolic geometry of Bolyai and Lobachevsky, by analogies with classical mechanics and its underlying Euclidean geometry is demonstrated. The demonstration sets the stage for the extension of the notion of barycentric coordinates in Euclidean geometry, first conceived by Möbius in 1827, into hyperbolic geometry. As an example for the application of hyperbolic barycentric coordinates, the hyperbolic midpoint of any hyperbolic segment, and the centroid and orthocenter of any hyperbolic triangle are determined.
Paper's Title:
Hyers-Ulam-Rassias Stability
of a Generalized Jensen Functional Equation
Author(s):
A. Charifi, B. Bouikhalene, E. Elqorachi and A. Redouani
Department of
Mathematics, Faculty of Sciences,
Ibn Tofail University,
Kenitra, Morocco
charifi2000@yahoo.fr
bbouikhalene@yahoo.fr
Department of
Mathematics, Faculty of Sciences,
Ibn Zohr University,
Agadir, Morocco
elqorachi@hotmail.com
Redouani-ahmed@yahoo.fr
Abstract:
In this paper we obtain the Hyers-Ulam-Rassias stability for the generalized Jensen's functional equation in abelian group (G,+). Furthermore we discuss the case where G is amenable and we give a note on the Hyers-Ulam-stability of the K-spherical (n × n)-matrix functional equation.
Paper's Title:
Topological Aspects of Scalarization in Vector Optimization Problems.
Author(s):
Peter I. Kogut, Rosanna Manzo and Igor V. Nechay
Department of Differential Equations,
Dnipropetrovsk National University, Naukova
STR.,
13,
49010 Dnipropetrovsk,
Ukraine
p.kogut@i.ua
Università di Salerno,
Department of Technical Cybernetics,
Dipartimento di Ingegneria dell'Informazione e Matematica Applicata,
Via Ponte don Melillo, 84084 Fisciano (SA),
Italy
manzo@diima.unisa.it
Dnipropetrovsk Technical University,
Acad. Lazarjan
STR., 2,
49010 Dnipropetrovsk,
Ukraine
i.nechay@i.ua
Abstract:
In this paper, we study vector optimization problems in partially ordered Banach spaces. We suppose that the objective mapping possesses a weakened property of lower semicontinuity and make no assumptions on the interior of the ordering cone. We derive sufficient conditions for existence of efficient solutions of the above problems and discuss the role of topological properties of the objective space. We discuss the scalarization of vector optimization problems when the objective functions are vector-valued mappings with a weakened property of lower semicontinuity. We also prove the existence of the so-called generalized efficient solutions via the scalarization process. All principal notions and assertions are illustrated by numerous examples.
Paper's Title:
Para-chaotic Tuples of Operators
Author(s):
Bahmann Yousefi and Javad Izadi
Department of Mathematics,
Payame Noor University,
P.O. Box 19395-3697, Tehran,
Iran
b_yousefi@pnu.ac.ir
javadie2003@yahoo.com
Abstract:
In this paper, we introduce para-chaotic tuples of operators and we give some relations between para-chaoticity and Hypercyclicity Criterion for a tuple of operators.
Paper's Title:
Existence and Regularity of Minima of an Integral Functional in Unbounded Domain
Author(s):
L. Aharouch, J. Bennouna and A. Bouajaja
King Khalid University
Faculty of Arts and Science Mha'l Asir
Saudi Arabia.
E-mail: laharouch@gmail.com
Université Sidi Mohammed Ben Abdellah
Faculté des Sciences Dhar-Mahraz
B.P 1796 Atlas Fès,
Maroc.
Email: jbennouna@hotmail.com
E-mail: kadabouajaja@hotmail.com
Abstract:
We prove the existence and the regularity of minima for a functional defined on a suitable Sobolev space.
Paper's Title:
Local Boundedness of Weak Solutions for Singular Parabolic Systems of p-Laplacian Type
Author(s):
Corina Karim, Marjono
Department of Mathematics,
Universitas Brawijaya,
Indonesia.
E-mail: co_mathub@ub.ac.id,
marjono@ub.ac.id
Abstract:
We study the local boundedness of weak solutions for evolutional p-Laplacian systems in the singular case. The initial data is belonging to Lebesgue space L∞ (0,T;W(1,p) (Ω,Rn )). We use intrinsic scaling method to treat the boundedness of weak solutions. The main result is to make the local boundedness of weak solution for the systems well-worked in the intrinsic scaling.
Paper's Title:
On the Polyconvolution of Hartley Integral Transforms H1, H2, H1 and Integral Equations
Author(s):
Nguyen Minh Khoa and Dau Xuan Luong
Department of Mathematics,
Electric Power University,
Ha Noi, and Faculty of Fundamental Science,
Ha Long University, Quang Ninh,
Viet Nam.
E-mail: khoanm@epu.edu.vn,
dauxuanluong@gmail.com
Abstract:
In this paper, we construct and study a new polyconvolution * (f,g,h)(x) of functions f, g, h. We will show that the polyconvolution satisfy the following factorization equality
H1[*(f,g,h)](y)=(H2f)(y)(H1g)(y)(H1h)(y), ∀y∈ R.
We prove the existence of this polyconvolution in the space L(R). As examples, applications to solve an integral equation of polyconvolution type and two systems of integral equations of polyconvolution type are presented.
Paper's Title:
A New Relaxed b-metric Type and Fixed Point Results
Author(s):
P. Singh, V. Singh and Thokozani Cyprian Martin Jele
Department of Mathematics,
University of KwaZulu-Natal,
Private Bag X54001, Durban,
South Africa.
E-mail: singhp@ukzn.ac.za,
singhv@ukzn.ac.za,
thokozani.jele@nwu.ac.za
Abstract:
The purpose of this paper is to introduce a new relaxed α, β b-metric type by relaxing the triangle inequality. We investigate the effect that this generalization has on fixed point theorems.
Paper's Title:
A Review on Minimally Supported Frequency Wavelets
Author(s):
K Pallavi1, M C Lineesh1, A Noufal2
1
Department of Mathematics,2Department of Mathematics,
Cochin University of Science and Technology,
Kerala 682022,
India.
E-mail: noufal@cusat.ac.in
Abstract:
This paper provides a review on Minimally Supported Frequency (MSF) wavelets that includes the construction and characterization of MSF wavelets. The characterization of MSF wavelets induced from an MRA is discussed and the nature of the low-pass filter associated with it is explained. The concept of wavelet set and dimension function is introduced to study this class of wavelets. Along with MSF wavelets, s-elementary wavelets and unimodular wavelets are also considered due to the similarity in definitions. Examples and illustrations are provided for more clarity.
Paper's Title:
Corrigendum for A Review on Minimally Supported Frequency Wavelets
Author(s):
K Pallavi1, M C Lineesh1, A Noufal2
1
Department of Mathematics,2Department of Mathematics,
Cochin University of Science and Technology,
Kerala 682022,
India.
E-mail: noufal@cusat.ac.in
Abstract:
This article is a corrigendum to AJMAA Volume 18, Issue 2, Article 17, {PDF Link}.
Paper's Title:
Linear System of Singularly Perturbed Initial Value Problems with Robin Initial Conditions
Author(s):
S. Dinesh, G. E. Chatzarakis, S. L. Panetsos and S. Sivamani
Department of Mathematics,
Saranathan College of Engineering,
Tiruchirappalli-620012,
Tamil Nadu,
India.
Department of Electrical and Electronic
Engineering Educators,
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail:
geaxatz@otenet.gr,
dineshselvaraj24@gmail.com,
spanetsos@aspete.gr,
winmayi2012@gmail.com
Abstract:
On the interval (0,1], this paper considers an initial value problem for a system of n singularly perturbed differential equations with Robin initial conditions. On a piecewise uniform Shishkin mesh, a computational approach based on a classical finite difference scheme is proposed. This approach is shown to be first-order convergent in the maximum norm uniformly in the perturbation parameters. The theory is illustrated by a numerical example.
Paper's Title:
Some Notes on the Semi-open Subspaces of Topological Spaces
Author(s):
Nicky. K. Tumalun, Philotheus E. A. Tuerah, and Rolles N. S. Palilingan
Department of Mathematics
Universitas Negeri Manado
Tondano 95618
Indonesia.
E-mail: nickytumalun@unima.ac.id
URL: https://fmipa.unima.ac.id/
Department of Mathematics
Universitas Negeri Manado
Tondano 95618
Indonesia.
E-mail: pheatuerah@unima.ac.id
URL: https://fmipa.unima.ac.id/
Department of Physics
Universitas Negeri Manado
Tondano 95618
Indonesia.
E-mail:
rollespalilingan@unima.ac.id
URL: https://fmipa.unima.ac.id/
Abstract:
In this paper, we obtain some new results regarding to the nowhere dense and first category set in the semi-open subspace of a topological space. More precisely, we prove that a nowhere dense set in the semi-open subspace of a topological space is equivalent as a nowhere dense set in that topological space. This implies that a first category set in the semi-open subspace of a topological space is equivalent as a first category set in that topological space. We also give some applications of these results to give some new proofs relating to the properties of semi-open set and Baire space.
Paper's Title:
On Infinite Unions and Intersections of Sets in a Metric Space
Author(s):
Spiros Konstantogiannis
Ronin Institute,
Montclair, New Jersey,
United States.
E-mail:
spiros.konstantogiannis@ronininstitute.org
URL:
https://www.researchgate.net/profile/Spiros-Konstantogiannis
Abstract:
The aim of this paper is to examine infinite unions and intersections of sets in a general metric space, with a view to explaining when an infinite intersection of open sets is an open set and when an infinite union of closed sets is a closed set.
Paper's Title:
Corrigendum for Differential Equations for Indicatrices, Spacelike and Timelike Curves
Author(s):
Sameer, Pradeep Kumar Pandey
Department of Mathematics,
Jaypee University of Information Technology,
Solan, Himachal Pradesh,
India.
E-mail: sksameer08@gmail.com,
pandeypkdelhi@gmail.com
ABSTRACT NOT FOUND. WEBSITE ERROR
Abstract:
Paper's Title:
Optimal Conditions using Multi-valued G-Presic type Mapping
Author(s):
Deb Sarkar, Ramakant Bhardwaj, Vandana Rathore, and Pulak Konar
Department of Mathematics, Amity
University, Kadampukur, 24PGS(N), Kolkata, West Bengal, 700135,
India.
E-mail: debsarkar1996@gmail.com
Department of Mathematics, Amity
University, Kadampukur, 24PGS(N), Kolkata, West Bengal, 700135,
India.
E-mail: drrkbhardwaj100@gmail.com
School of Engineering and Technology,
Jagran Lakecity University, Bhopal, MP-462044,
India.
E-mail: drvandana@jlu.edu.in
Department of Mathematics,
VIT University, Chennai, Tamil Nadu-600127,
India.
E-mail: pulakkonar@gmail.com
Abstract:
In the present paper, some best proximity results have been presented using the concept of G-Presic type multi-valued mapping. These results are the extensions of Presic's theorem in the non-self mapping. A suitable example has also been given. Here, some applications are presented in θ-chainable space and ordered metric space.
Paper's Title:
Maximal Singular Operators On Variable Exponent Sequence Spaces and Their Corresponding Ergodic Version
Author(s):
Sri Sakti Swarup Anupindi and Michael A. Alphonse
Department of Mathematics, Birla Institute
of Technology And Science- Pilani,
Hyderabad Campus, Jawahar Nagar, Kapra Mandal,
District.-Medchal-500 078 Telangana,
India.
E-mail:
p20180442@hyderabad.bits-pilani.ac.in
alphonse@hyderabad.bits-pilani.ac.in
URL:
https://www.bits-pilani.ac.in/hyderabad/a-michael-alphonse
https://www.bits-pilani.ac.in/research_scholars/sri-sakti-swarup-anupindi
Abstract:
In this paper, we prove strong and weak type inequalities of singular operators on weighted lwp(Z)$. Using these results, we prove strong type and weak type inequalities of the maximal singular operator of Calderon-Zygmund type on variable exponent sequence spaces lp(·)(Z). Using the Calderon-Coifman-Weiss transference principle, we prove strong type, weak type inequalities of the maximal ergodic singular operator on Lwp(X,B,μ) spaces, where (X,B,μ) is a probability space equipped with measure preserving transformation U.
Paper's Title:
A Note on Evaluation of a New Class of Integrals Involving Generalized Hypergeometric Function
Author(s):
Madhav Prasad Poudel, Dongkyu Lim*, Narayan Prasad Pahari, Arjun K. Rathie
School of Engineering,
Pokhara University, Pokhara-30, Kaski,
Nepal.
E-mail: pdmadav@gmail.com
Department of Mathematics Education,
Andong National University, Andong 36729,
Republic of Korea.
E-mail: dklim@anu.ac.kr
Central Department of Mathematics,
Tribhuvan University, Kirtipur, Kathmandu,
Nepal.
E-mail: nppahari@gmail.com
Department of Mathematics,
Vedant College of Engineering & Technology (Rajasthan Technical University),
Village: Tulsi,
Jakhamund, Dist. Bundi, Rajasthan State,
India.
E-mail:
arjunkumarrathie@gmail.com
Abstract:
In the theory of hypergeometric and generalized hypergeometric series, classical summation theorems such as those of Gauss, Gauss second, Bailey and Kummer for the series
2F1; Watson, Dixon, Whipple and Saalshutz play a key role. Applications of the above mentioned summation theorems are well known for the series
3F2. In our present investigation, we aim to evaluate twenty five new class of integrals involving generalized hypergeometric function in the form of a single integral of the form:
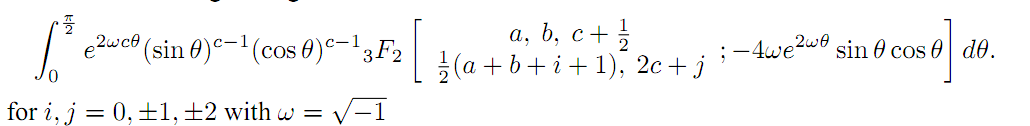
The results are established with the help of the generalizations of the classical Watson's summation theorem obtained earlier by Lavoie et al.. Fifty interesting integrals in the form of two integrals (twenty five each) have also been given as special cases of our main findings.
Paper's Title:
Results Concerning Fixed Point for Soft Weakly Contraction In Soft Metric Spaces
Author(s):
Abid Khan, Santosh Kumar Sharma, Anurag Choubey, Girraj Kumar Verma, Umashankar Sharma, Ramakant Bhardwaj
Department of Mathematics,
AUMP, Gwalior,
India.
abid69304@gmail.com
Department of Mathematics,
AUMP, Gwalior,
India.
sksharma1@gwa.amity.edu
Department of Computer Science,
Technocrats Institute of Technology,
Bhopal, MP,
India.
directoracademicstit@gmail.com
Department of Mathematics,
AUMP, Gwalior,
India.
gkverma@gwa.amity.edu
Department of Physics,
RJIT BSF Tekanpur, MP,
India.
ussharma001@gmail.com
School of Applied Science
AUK, WB,
India.
rkbhardwaj100@gmail.com
Abstract:
The basic objective of the proposed research work is to make people acquainted with the concept of soft metric space by generalizing the notions of soft (ψ,φ)-weakly contractive mappings in soft metric space, as well as to look at specific fundamental and topological parts of the underlying spaces. A compatible example is given to explain the idea of said space structure. The theory is very useful in decision making problems and secure transmission as fixed point provides exact output. The fixed-point theorems on subsets of Rm that are useful in game theoretic settings.
Paper's Title:
On the Construction of Dyadic Wavelet Frames in Local Fields of Positive Characteristic
Author(s):
Vishal Dhawan, Khalil Ahmad, Satyapriya, Raj Kumar
Department of Mathematics,
Kirori Mal College,
University of Delhi, Delhi,
India.
E-mail: dhawanmathskmc@gmail.com
Department of Mathematics,
Al-Falah University,
Faridabad, Haryana,
India.
E-mail: kahmad49@gmail.com
Department of Mathematics,
University of Delhi, Delhi,
India.
E-mail: kmc.satyapriya@gmail.com
Department of Mathematics,
Kirori Mal College,
University of Delhi, Delhi,
India.
E-mail: rajkmc@gmail.com
Abstract:
This paper explores the construction of dyadic wavelet frames in (L2(K)), where (K) is a local field with positive characteristic. Using frame multiresolution analysis (FMRA), we establish a systematic method for generating wavelet frames within this setting. While conventional results indicate that two functions are necessary for constructing wavelet frames, we demonstrate that under specific conditions, a single function is sufficient. By leveraging properties of local fields, we provide a detailed characterization of the refinement equation and necessary frame conditions. These results enhance the theoretical understanding of wavelet frames and open new directions for applications in harmonic analysis and signal representation over non-Archimedean fields.
Paper's Title:
Divergence Conditions for Continued Reciprocal Powers
Author(s):
Dixon J. Jones
Coralville IA
USA 52241.
E-mail: d.j.jones.1798@gmail.com
URL: https://dixonjjones.com/math/
Abstract:
We derive conditions on a continued reciprocal power's (strictly positive) terms sufficient for its divergence. The work involves reviewing and extending convergence criteria for continued supraunitary powers. We close with a brief comment on the history of a convergence condition for continued roots.
Paper's Title:
New Coincidence and Fixed Point Theorems for Strictly Contractive Hybrid Maps
Author(s):
S. L. Singh and Amal M. Hashim
21, Govind Nagar, Rishikesh 249201,
Ua, India
vedicmri@sancharnet.in
Dept. of Math., College of Science,
Univ. of Basarah,
Iraq.
Abstract:
The purpose of this paper is to study the (EA)-property and noncompatible maps
of a hybrid pair of single-valued and multivalued maps in fixed point considerations. Such maps
have the remarkable property that they need not be continuous at their common fixed points. We
use this property to obtain some coincidence and fixed point theorems for strictly contractive
hybrid maps without using their continuity and completeness or compactness of the space.
Paper's Title:
General Oscillations for Some Third Order Differential Systems with Nonlinear Acceleration Term
Author(s):
Awar Simon Ukpera
Department of Mathematics,
Obafemi Awolowo University,
Ile-Ife,
Nigeria.
aukpera@oauife.edu.ng
Abstract:
We generate some general nonuniform hypotheses for third order differential systems
of the form X''' +F(t,X'' )+BX'+CX = P(t), in which B and C are not
necessarily
constant matrices. Some results requiring sharp conditions on this system have recently been
published by the author in
[5]. This work however examines more closely crucial properties
associated with the generalised nature of the nonlinear acceleration term F, which were largely
overlooked in the earlier paper.
Paper's Title:
The successive approximations method and error estimation in terms of at most the first derivative for delay ordinary differential equations
Author(s):
Alexandru Mihai Bica
Department of Mathematics,
University of Oradea,
Str. Armatei Romane no.5,
410087, Oradea,
Romania
smbica@yahoo.com
abica@uoradea.ro
Abstract:
We present here a numerical method for first order delay ordinary differential
equations, which use the Banach's fixed point theorem, the sequence of
successive approximations and the trapezoidal quadrature rule. The error
estimation of the method uses a recent result of P. Cerone and S.S. Dragomir
about the remainder of the trapezoidal quadrature rule for Lipchitzian
functions and for functions with continuous first derivative.
Paper's Title:
Boundedness for Vector-Valued Multilinear Singular Integral Operators on Triebel-Lizorkin Spaces
Author(s):
Liu Lanzhe
College of Mathematics
Changsha University of Science and Technology,
Changsha 410077,
P.R. of China.
lanzheliu@263.net
Abstract:
In this paper, the boundedness for some vector-valued multilinear operators associated to certain
fractional singular integral operators on Triebel-Lizorkin space are obtained. The operators include Calderón-Zygmund
singular integral operator and fractional integral operator.
Paper's Title:
A relation between nuclear cones and full nuclear cones
Author(s):
G. Isac and A. B. Nemeth
Department of Mathematics,
Royal Military College of Canada,
P. O. Box 17000 STN Forces Kingston, Ontario,
Canada K7K 7B4.
isac-g@rmc.ca
Faculty of Mathematics and Computer Science,
Babes-Bolyai University,
3400 Cluj-Napoca,
Romania.
nemab@math.ubbcluj.ro
Abstract:
The notion of nuclear cone in locally convex spaces corresponds to the notion of well based cone in normed spaces. Using the bipolar theorem from locally convex spaces it is proved that every closed nuclear cone is a full nuclear cone. Thus every closed nuclear cone can be associated to a mapping from a family of continuous seminorms in the space to the topological dual of the space. The relation with Pareto efficiency is discussed.
Paper's Title:
Existence of Non-spurious Solutions to Discrete Boundary Value Problems
Author(s):
Irena Rachunkova and Christopher C. Tisdell
Department of Mathematics
School of Mathematics
Palacky University
771 46 Olomouc, Czech Republic.
rachunko@risc.upol.cz
URL: http://phoenix.inf.upol.cz/~rachunekl/mathair/matha-en.htm
The University of New South Wales
Sydney 2052, Australia.
cct@unsw.edu.au
URL: http://www.maths.unsw.edu.au/~cct
Abstract:
This paper investigates discrete boundary value problems (BVPs) involving second-order difference equations and two-point boundary conditions.
General theorems guaranteeing the existence and uniqueness of solutions to the discrete BVP are established. The methods involve a sufficient growth condition to yield an a priori bound on solutions to a certain family of discrete BVPs. The em a priori bounds on solutions to the discrete BVP do not depend on the step-size and thus there are no ``spurious'' solutions. It is shown that solutions of the discrete BVP will converge to solutions of ordinary differential equations.
Paper's Title:
Some Stability Results For Fixed Point Iteration Processes
Author(s):
M. O. Olatinwo, O. O. Owojori, and C. O. Imoru
Department of Mathematics, Obafemi Awolowo University,
Ile-Ife,
Nigeria.
polatinwo@oauife.edu.ng
walejori@oauife.edu.ng
cimoru@oauife.edu.ng
Abstract:
In this paper, we present some stability results for both the general Krasnoselskij and the Kirk's iteration processes. The method of Berinde \cite{VBE1} is employed but a more general contractive condition than those of Berinde \cite{VBE1}, Harder and Hicks \cite{HAM}, Rhoades \cite{RHO1} and Osilike \cite{OSI1} is considered.
Paper's Title:
Coincidences and Fixed Points of Hybrid Maps in Symmetric Spaces
Author(s):
S. L. Singh and Bhagwati Prasad
Vedic MRI, 21 Govind Nagar,
Department of Mathematics, Gurukula Kangri University,
Rishikesh 249201
India
vedicmri@gmail.com
Hardwar 249404,
India
Abstract:
The purpose of this paper is to obtain a new coincidence theorem for a
single-valued and two multivalued operators in symmetric spaces. We derive
fixed point theorems and discuss some special cases and applications.
Paper's Title:
On the Generalized Inverse  over Integral Domains
over Integral Domains
Author(s):
Yaoming Yu and Guorong Wang
College of Education, Shanghai Normal University
Shanghai 200234
People's Republic of China.
yuyaoming@online.sh.cn
grwang@shnu.edu.cn
Abstract:
In this paper, we study further the generalized inverse
 of a matrix A over an integral domain. We give
firstly some necessary and sufficient conditions for the existence
of the generalized inverse
of a matrix A over an integral domain. We give
firstly some necessary and sufficient conditions for the existence
of the generalized inverse  , an explicit expression
for the elements of the generalized inverse
, an explicit expression
for the elements of the generalized inverse  and an
explicit expression for the generalized inverse
and an
explicit expression for the generalized inverse  ,
which reduces to the {1} inverse. Secondly, we verify that the
group inverse, the Drazin inverse, the Moore-Penrose inverse and the
weighted Moore-Penrose inverse are identical with the generalized
inverse
,
which reduces to the {1} inverse. Secondly, we verify that the
group inverse, the Drazin inverse, the Moore-Penrose inverse and the
weighted Moore-Penrose inverse are identical with the generalized
inverse  for an appropriate matrix G,
respectively, and then we unify the conditions for the existence and
the expression for the elements of the weighted Moore-Penrose
inverse, the Moore-Penrose inverse, the Drazin inverse and the group
inverse over an integral domain. Thirdly, as a simple application,
we give the relation between some rank equation and the existence of
the generalized inverse
for an appropriate matrix G,
respectively, and then we unify the conditions for the existence and
the expression for the elements of the weighted Moore-Penrose
inverse, the Moore-Penrose inverse, the Drazin inverse and the group
inverse over an integral domain. Thirdly, as a simple application,
we give the relation between some rank equation and the existence of
the generalized inverse  , and a method to compute the
generalized inverse
, and a method to compute the
generalized inverse  . Finally, we give an example of
evaluating the elements of
. Finally, we give an example of
evaluating the elements of  without calculating
without calculating
 .
.
Paper's Title:
Local and Global Existence and Uniqueness Results for Second and Higher Order Impulsive Functional Differential Equations with Infinite Delay
Author(s):
Johnny Henderson and Abdelghani Ouahab
Department of Mathematics, Baylor University,
Waco, Texas 76798-7328
USA.
Johnny_Henderson@baylor.edu
Laboratoire de Mathématiques, Université de Sidi Bel Abbés
BP 89, 22000 Sidi Bel Abbées,
Algérie.
ouahab@univ-sba.dz
Abstract:
In this paper, we discuss the local and global existence and
uniqueness results for second and higher order impulsive functional
differential equations with infinite delay. We shall rely on a
nonlinear alternative of Leray-Schauder. For the global existence
and uniqueness we apply a recent Frigon and Granas nonlinear
alternative of Leray-Schauder type in Fréchet spaces.
Paper's Title:
Normalized Truncated Levy models applied to the study of Financial Markets
Author(s):
M. C. Mariani, K. Martin, D. W. Dombrowski and D. Martinez
Department of Mathematical Sciences and Department of Finance,
New Mexico State University, P.O. Box 30001
Department 3MB Las Cruces, New Mexico 88003-8001
USA.
mmariani@nmsu.edu
kjmartin@nmsu.edu
Abstract:
This work is devoted to the study of the statistical properties of financial instruments from developed markets. We performed a new analysis of the behavior of companies corresponding to the DJIA index, and of the index itself, by using a normalized Truncated Levy walk model. We conclude that the Truncated Levy distribution describes perfectly the evolution of the companies and of the index near a crash.
Paper's Title:
Existence of Bounded Solutions for a Class of
Strongly Nonlinear Elliptic Equations in Orlicz-Sobolev Spaces
Author(s):
Abdelmoujib Benkirane and Ahmed Youssfi
Department of Mathematics and Informatics, Faculty of Sciences
Dhar El Mahraz
University Sidi Mohammed Ben Abdallah
PB 1796 Fez-Atlas, Fez
Morocco
a.benkirane@menara.ma
ahmed.youssfi@caramail.com
Abstract:
We prove, in the setting of Orlicz-Sobolev spaces, the existence of
bounded solutions for some strongly nonlinear elliptic equations
with operator of the principal part having degenerate coercivity and
lower order terms not satisfying the sign condition. The data have a
suitable summability and no Δ2-condition is needed for the
considered N-functions.
Paper's Title:
Integer Sums of Powers of Trigonometric Functions (MOD p), for prime p
Author(s):
G. J. Tee
Department of Mathematics, University of Auckland,
Auckland,
New Zealand
tee@math.auckland.ac.nz
Abstract:
Many multi--parameter families of congruences (mod p) are found for integer
sums of
qth powers of the trigonometric functions over various sets of equidistant
arguments, where
p is any prime factor of q. Those congruences provide sensitive
tests for the accuracy
of software for evaluating trigonometric functions to high precision.
Paper's Title:
A Subclass of Meromorphically Multivalent Functions with Applications to Generalized Hypergeometric Functions
Author(s):
M. K. Aouf
Mathematics Department,
Faculty of Science,
Mansoura University 35516,
Egypt
mkaouf127@yahoo.com
Abstract:
In this paper a new subclass of meromorphically multivalent functions, which
is defined by means of a Hadamard product (or convolution) involving some
suitably normalized meromorphically p-valent functions. The main object of
the present paper is to investigate the various important properties and
characteristics of this subclass of meromorphically multivalent functions.
We also derive many interesting results for the Hadamard products of
functions belonging to this subclass. Also we consider several applications
of our main results to generalized hypergeomtric functions.
Paper's Title:
A Fixed Point Approach to
the Stability of the Equation
![]()
Author(s):
Soon-Mo Jung
Mathematics Section, College of Science and Technology
Hong-Ik
University, 339-701 Chochiwon
Republic of Korea.
smjung@hongik.ac.kr
Abstract:
We will apply a fixed point method for proving the Hyers--Ulam stability of
the functional equation
![]() .
.
Paper's Title:
On some Strongly Nonlinear Elliptic Problems
in L¹-data with a Nonlinearity Having a Constant Sign in Orlicz
Spaces via Penalization Methods
Author(s):
E. Azroul, A. Benkirane and M. Rhoudaf
Dep. Math., Faculté des Sciences
Dhar-Mahraz,
B.P 1796 Atlas Fès,
Maroc
Departement of Mathematics,
Faculty of Sciences and Techniques of Tangier,
B.P. 416, Tangier,
Morocco.
rhoudaf_mohamed@yahoo.fr
Abstract:
This paper is concerned with the existence result of the
unilateral problem associated to the equations of the type
![]()
in Orlicz spaces, without
assuming the sign condition in the nonlinearity g. The source term f belongs to L¹(Ώ).
Paper's Title:
Approximation of Derivatives in a Singularly Perturbed Second Order Ordinary Differential Equation with Discontinuous Terms Arising in Chemical Reactor Theory
Author(s):
R. Mythili Priyadharshini and N. Ramanujam
Department of Mathematics, Bharathidasan University,
Tiruchirappalli - 620 024, Tamilnadu, India.
matram2k3@yahoo.com
URL:
http://www.bdu.ac.in/depa/science/ramanujam.htm
Abstract:
In this paper, a singularly perturbed second order ordinary differential equation with a discontinuous convection coefficient arising in chemical reactor theory is considered. A robust-layer-resolving numerical method is suggested. An ε-uniform global error estimate for the numerical solution and also to the numerical derivative are established. Numerical results are provided to illustrate the theoretical results.
Paper's Title:
On an Elliptic Over-Determined Problem in Dimension Two
Author(s):
Lakhdar Ragoub
Department of Mathematics and Information of Tiyadhechnology
AL Yamamah University
P.O. Box 45 180, Riyadh 11 512
Saudi Arabia.
Abstract:
We extend the method of Weinberger for a
non-linear over-determined elliptic problem
in R2.
We prove that the domain in consideration is a ball. The
tool of this investigation are maximum principles and P-functions.
Paper's Title:
Approximation of an AQCQ-Functional Equation and its Applications
Author(s):
Choonkil Park and Jung Rye Lee
Department of Mathematics,
Research Institute for Natural Sciences,
Hanyang University, Seoul 133-791,
Korea;
Department of Mathematics,
Daejin University,
Kyeonggi 487-711,
Korea
baak@hanyang.ac.kr
jrlee@daejin.ac.kr
Abstract:
This paper is a survey on the generalized Hyers-Ulam stability of an AQCQ-functional equation in several spaces. Its content is divided into the following sections:
1. Introduction and preliminaries.
2. Generalized Hyers-Ulam stability of an AQCQ-functional equation in Banach spaces: direct method.
3. Generalized Hyers-Ulam stability of an AQCQ-functional equation in Banach spaces: fixed point method.
4. Generalized Hyers-Ulam stability of an AQCQ-functional equation in random Banach spaces: direct method.
5. Generalized Hyers-Ulam stability of an AQCQ-functional equation in random Banach spaces: fixed point method.
6. Generalized Hyers-Ulam stability of an AQCQ-functional equation in non-Archi-medean Banach spaces: direct method.
7. Generalized Hyers-Ulam stability of an AQCQ-functional equation in non-Archi-medean Banach spaces: fixed point method.
Paper's Title:
On the Three Variable Reciprocity Theorem and Its Applications
Author(s):
D. D. Somashekara and D. Mamta
Department of Studies in Mathematics,
University of Mysore,
Manasagangotri, Mysore-570 006
India
dsomashekara@yahoo.com
Department of Mathematics,
The National Institute of Engineering,
Mysore-570 008,
India
mathsmamta@yahoo.com
Abstract:
In this paper we show how the three variable reciprocity theorem can be easily derived from the well known two variable reciprocity theorem of Ramanujan by parameter augmentation. Further we derive some q-gamma, q-beta and eta-function identities from the three variable reciprocity theorem.
Paper's Title:
Traub-Potra-Type Method for Set-Valued Maps
Author(s):
Ioannis K. Argyros and Saïd Hilout
Cameron University,
Department of Mathematics Sciences,
Lawton, OK 73505,
USA
URL: http://www.cameron.edu/~ioannisa/
Poitiers University,
Laboratoire de Mathematiques et Applications,
Bd. Pierre et Marie Curie, Teleport 2, B.P. 30179,
86962 Futuroscope Chasseneuil Cedex,
France
said.hilout@math.univ-poitiers.fr
http://www-math.univ-poitiers.fr/~hilout/
Abstract:
We introduce a new iterative method for approximating a locally unique solution of variational inclusions in Banach spaces by using generalized divided differences of the first order. This method extends a method considered by Traub (in the scalar case) and by Potra (in the Banach spaces case) for solving nonlinear equations to variational inclusions. An existence-convergence theorem and a radius of convergence are given under some conditions on divided differences operator and Lipschitz-like continuity property of set-valued mappings. The R-order of the method is equal to the unique positive root of a certain cubic equation, which is $1.839..., and as such it compares favorably to related methods such as the Secant method which is only of order $1.618....
Paper's Title:
Uniform Continuity and k-Convexity
Author(s):
Adel Afif Abdelkarim
Mathematics Department, Faculty of Science,
J
erash University, Jerash
Jordan.
Abstract:
A closed arcwise-connected subset A of Rn is called k-convex if for each positive number a and for all elements x and y in A there is a positive number b such that if the norm of x-y is less than or equal to b then the length of the shortest curve l(x,y) in A is less than k times the norm of x-y plus a. We show that a union of two non disjoint closed finite convex subsets need not be k-convex. Let f(x) be a uniformly continuous functions on a finite number of closed subsets A_{1},...,A_{n} of R^{n} such that the union of A_{j},...,A_{n},j=1,...,n-1 is k-convex. We show that f is uniformly continuous on the union of the sets A_{i},i=1,...,n. We give counter examples if this condition is not satisfied. As a corollary we show that if f(x) is uniformly continuous on each of two closed convex sets A,B then f(x) is uniformly continuous on the union of A and B.
Paper's Title:
L∞- Error Estimate of Schwarz Algorithm for Elliptic Quasi-Variational Inequalities Related to Impulse Control Problem
Author(s):
Saadi Samira and Mehri Allaoua
Lab. LANOS, Department of Mathematics,
University Badji Mokhtar Annaba,
P.O.Box 12, Annaba 23000,
Algeria.
Lab. LAIG, Department of Mathematics,
University May 8th 1945,
P.O.Box 401, Guelma 24000,
Algeria.
E-mail:
saadisamira69@yahoo.fr
allmehri@yahoo.fr
Abstract:
In this work, we study Schwarz method for a class of elliptic quasi-variational inequalities. The principal result of this investigation is to prove the error estimate in ∞-norm for two domains with overlapping nonmatching grids, using the geometrical convergence, and the uniform convergence of Cortey Dumont.
Paper's Title:
Application of Equivalence Method to Classify Monge-Ampère Equations of Elliptic Type
Author(s):
Moheddine Imsatfia
E-mail: imsatfia@math.jussieu.fr
Abstract:
In this paper, we apply Cartan's equivalence method to give a local classification of Monge-Ampère equations of elliptic type. Then we find a necessary and sufficient conditions such that a Monge-Ampère equation is either contactomorphic to the Laplace equation or to an Euler-Lagrange equation.
Paper's Title:
Examples of Fractals Satisfying the Quasihyperbolic Boundary Condition
Author(s):
Petteri Harjulehto and Riku Klén
Department of Mathematics and Statistics,
FI-20014 University of Turku,
Finland
E-mail: petteri.harjulehto@utu.fi
E-mail: riku.klen@utu.fi
Abstract:
In this paper we give explicit examples of bounded domains that satisfy the quasihyperbolic boundary condition and calculate the values for the constants. These domains are also John domains and we calculate John constants as well. The authors do not know any other paper where exact values of parameters has been estimated.
Paper's Title:
On the Hyers-Ulam Stability of Homomorphisms and Lie Derivations
Author(s):
Javad Izadi and Bahmann Yousefi
Department of Mathematics, Payame Noor
University,
P.O. Box: 19395-3697, Tehran,
Iran.
E-mail: javadie2003@yahoo.com,
b_yousefi@pnu.ac.ir
Abstract:
Let A be a Lie Banach*-algebra. For each elements (a, b) and (c, d) in A2:= A * A, by definitions
(a, b) (c, d)= (ac, bd),
|(a, b)|= |a|+ |b|,
(a, b)*= (a*, b*),
A2 can be considered as a Banach*-algebra. This Banach*-algebra is called a Lie Banach*-algebra whenever it is equipped with the following definitions of Lie product:
for all a, b, c, d in A. Also, if A is a Lie Banach*-algebra, then D: A2→A2 satisfying
D ([ (a, b), (c, d)])= [ D (a, b), (c, d)]+ [(a, b), D (c, d)]
for all $a, b, c, d∈A, is a Lie derivation on A2. Furthermore, if A is a Lie Banach*-algebra, then D is called a Lie* derivation on A2 whenever D is a Lie derivation with D (a, b)*= D (a*, b*) for all a, b∈A. In this paper, we investigate the Hyers-Ulam stability of Lie Banach*-algebra homomorphisms and Lie* derivations on the Banach*-algebra A2.
Paper's Title:
Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Convergence and Stability Results for New Three Step Iteration Process
in Modular Spaces
Author(s):
Naresh Kumar and Renu Chugh
Department of Mathematics,
M.D. University,
Rohtak-124001, Haryana,
India.
E-mail: nks280@gmail.com
E-mail: chugh.r1@gmail.com
Abstract:
The aim of this paper is to introduce a new iteration process (5) for ρ-contraction mappings in Modular spaces. We obtain some analytical proof for convergence and stability of our iteration process (5). We show that our iteration process (5) gives faster convergence results than the leading AK iteration process (4) for contraction mappings. Moreover, a numerical example (using the Matlab Software) is presented to compare the rate of convergence for existing iteration processes with our new iteration process (5).
Paper's Title:
Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.
Paper's Title:
Euler-Maclaurin Formulas for Functions of Bounded Variation
Author(s):
G. De Marco, M. De Zotti, C. Mariconda
Dipartimento di Matematica Tullio Levi-Civita,
Universita degli Studi di Padova
Via Trieste 63, Padova 35121,
Italy.
E-mail: carlo.mariconda@unipd.it
URL: http://www.math.unipd.it
Abstract:
The first-order Euler-Maclaurin formula relates the sum of the values of a smooth function on an interval of integers with its integral on the same interval on R. We formulate here the analogue for functions that are just of bounded variation.
Paper's Title:
Action of Differential Operators On Chirpsconstruct On L∞
Author(s):
Taoufik El Bouayachi and Naji Yebari
Laboratoire de Mathematiques et
applications,
Faculty of sciences and techniques, Tangier,
Morocco.
E-mail:
figo407@gmail.com,
yebarinaji@gmail.com
Abstract:
We will study in this work the action of differential operators on L∞ chirps and we will give a new definition of logarithmic chirp. Finally we will study the action of singular integral operators on chirps by wavelet characterization and Kernel method.
Paper's Title:
Extension of Factorization Theorems of Maurey to s-positively Homogeneous Operators
Author(s):
Abdelmoumen Tiaiba
Department of Physics,
University of M'sila,
Algeria.
E-mail: tiaiba05@yahoo.fr
Abstract:
In the present work, we prove that the class of s-positively homogeneous operators is a Banach space. As application, we give the generalization of some Maurey factorization theorems to T which is a s-positively homogeneous operator from X a Banach space into Lp. Where we establish necessary and sufficient conditions to proof that T factors through Lq. After this we give extend result of dual factorization theorem to same class of operators above.
Paper's Title:
Global Analysis on Riemannian Manifolds
Author(s):
Louis Omenyi and Michael Uchenna
Department of Mathematics, Computer
Science, Statistics and Informatics,
Alex Ekwueme Federal University, Ndufu-Alike,
Nigeria.
E-mail: omenyi.louis@funai.edu.ng,
michael.uchenna@funai.edu.ng
URL: http://www.funai.edu.ng
Abstract:
In this paper, an exposition of the central concept of global analysis on a Riemannan manifold is given. We extend the theory of smooth vector fields from open subsets of Euclidean space to Riemannan manifolds. Specifically, we prove that a Riemannian manifold admits a unique solution for a system of ordinary differential equations generated by the flow of smooth tangent vectors. The idea of partial differential equations on Riemannian manifold is highlighted on the unit sphere.
Paper's Title:
The Concept of Convergence for 2-Dimensional Subspaces Sequence in Normed Spaces
Author(s):
M. Manuharawati, D. N. Yunianti, M. Jakfar
Mathematics Department, Universitas
Negeri Surabaya,
Jalan Ketintang Gedung C8,
Surabaya 60321,
Indonesia.
E-mail: manuharawati@unesa.ac.id,
dwiyunianti@unesa.ac.id,
muhammadjakfar@unesa.ac.id
Abstract:
In this paper, we present a concept of convergence of sequence, especially, of 2-dimensional subspaces of normed spaces. The properties of the concept are established. As consequences of our definition in an inner product space, we also obtain the continuity property of the angle between two 2-dimensional subspaces of inner product spaces.
Paper's Title:
A new approach to the study of fixed point for simulation functions with application in G-metric spaces
Author(s):
Komi Afassinou and Ojen Kumar Narain
Department of Mathematical Sciences,
University of Zululand,
KwaDlangezwa,
South Africa.
E-mail: komia@aims.ac.za
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
The purpose of this work is to generalize the fixed point results of Kumar et al. [11] by introducing the concept of (α,β)-Z-contraction mapping, Suzuki generalized (α,β)-Z-contraction mapping, (α,β)-admissible mapping and triangular (α,β)-admissible mapping in the frame work of G-metric spaces. Fixed point theorems for these class of mappings are established in the frame work of a complete G-metric spaces and we establish a generalization of the fixed point result of Kumar et al. [11] and a host of others in the literature. Finally, we apply our fixed point result to solve an integral equation.
Paper's Title:
Generalised Models for Torsional Spine Reconnection
Author(s):
Ali Khalaf Hussain Al-Hachami
Department of Mathematics,
College of Education For Pure Sciences,
Wasit University,
Iraq.
E-mail: alhachamia@uowasit.edu.iq
Abstract:
Three-dimensional (3D) null points are available in wealth in the solar corona, and the equivalent is probably going to be valid in other astrophysical situations. On-going outcomes from sun oriented perceptions and from reproductions propose that reconnection at such 3D nulls may assume a significant job in the coronal dynamics. The properties of the torsional spine method of magnetic reconnection at 3D nulls are researched. Kinematic model are created, which incorporate the term ηJ that is spatially localised around the null, stretching out along the spine of the null. The null point is to research the impact of shifting the level of asymmetry of the null point magnetic field on the subsequent reconnection process where past examinations constantly considered a non-nonexclusive radially symmetric null. Specifically we analyse the rate of reconnection of magnetic flux at the spine of null point. Logical arrangements are determined for the enduring kinematic equation, and contrasted and the after effects of torsional spine reconnection models when the current is restricted in which the Maxwell conditions are illuminated. The geometry of the current layers inside which torsional spine reconnection happen is autonomous on the symmetry of the magnetic field. Torsional spine reconnection happens in a thin cylinder around the spine, with circular cross-segment when the fan eigenvalues are extraordinary. The short axis of the circle being along the solid field bearing. Just as it was discovered that the fundamental structure of the method of attractive reconnection considered is unaffected by changing the magnetic field symmetry, that is, the plasma flow is discovered rotational around the spine of null point. The spatiotemporal pinnacle current, and the pinnacle reconnection rate achieved, are found not to rely upon the level of asymmetry.
Paper's Title:
On Ruled Surfaces According to Quasi-Frame in Euclidean 3-Space
Author(s):
M. Khalifa Saad and R. A. Abdel-Baky
Department of Mathematics, Faculty of
Science,
Islamic University of Madinah,
KSA.
Department of Mathematics, Faculty of Science,
Sohag University, Sohag,
EGYPT.
E-mail:
mohamed_khalifa77@science.sohag.edu.eg,
mohammed.khalifa@iu.edu.sa
Department of Mathematics, Faculty of
Science,
Assiut University, Assiut,
EGYPT.
E-mail: rbaky@live.com
Abstract:
This paper aims to study the skew ruled surfaces by using the quasi-frame of Smarandache curves in the Euclidean 3-space. Also, we reveal the relationship between Serret-Frenet and quasi-frames and give a parametric representation of a directional ruled surface using the quasi-frame. Besides, some comparative examples are given and plotted which support our method and main results.
Paper's Title:
Attempts to Define a Baum--Connes Map Via Localization of Categories for Inverse Semigroups
Author(s):
Bernhard Burgstaller
Departamento de Matematica,
Universidade Federal de Santa Catarina,
CEP 88.040-900 Florianopolis-SC,
Brasil.
E-mail:
bernhardburgstaller@yahoo.de
URL:
http://mathematik.work/bernhardburgstaller/index.html
Abstract:
An induction functor in inverse semigroup equivariant KK-theory is considered, and together with %a restriction functors certain results similar to those known from the Mackey machinery are shown. It is also verified that for any so-called E-continuous inverse semigroup its equivariant KK-theory satisfies the universal property and is a triangulated category.
Paper's Title:
Construction of a Frame Multiresolution Analysis on Locally Compact Abelian Groups
Author(s):
R. Kumar and Satyapriya
Department of Mathematics,
Kirori Mal College,
University of Delhi,
Delhi,
India.
E-mail: rajkmc@gmail.com
Department of Mathematics,
University of Delhi,
Delhi,
India.
E-mail: kmc.satyapriya@gmail.com
Abstract:
The frame multiresolution analysis (FMRA) on locally compact Abelian groups has been studied and the results concerning classical MRA have been worked upon to obtain new results. All the necessary conditions, which need to be imposed on the scaling function φ to construct a wavelet frame via FMRA, have been summed up. This process of construction of FMRA has aptly been illustrated by sufficient examples.
Paper's Title:
Coexisting Attractors and Bubbling Route to Chaos in Modified Coupled Duffing Oscillators
Author(s):
B. Deruni1, A. S. Hacinliyan1,2, E. Kandiran3, A. C. Keles2, S. Kaouache4, M.-S. Abdelouahab4, N.-E. Hamri4
1Department
of Physics,
University of Yeditepe,
Turkey.
2Department
of Information Systems and Technologies,
University of Yeditepe,
Turkey
3Department
of Software Development,
University of Yeditepe,
Turkey.
4Laboratory
of Mathematics and their interactions,
University Center of Abdelhafid Boussouf,
Mila 43000,
Algeria.
E-mail:
berc890@gmail.com
ahacinliyan@yeditepe.edu.tr
engin.kandiran@yeditepe.edu.tr
cihan.keles@yeditepe.edu.tr
s.kaouache@centr-univ-mila.dz
medsalah3@yahoo.fr
n.hamri@centre-univ-mila.dz
Abstract:
In this article dynamical behavior of coupled Duffing oscillators is analyzed under a small modification. The oscillators have cubic damping instead of linear one. Although single duffing oscillator has complex dynamics, coupled duffing systems possess a much more complex structure. The dynamical behavior of the system is investigated both numerically and analytically. Numerical results indicate that the system has double scroll attractor with suitable parameter values. On the other hand, bifurcation diagrams illustrate rich behavior of the system, and it is seen that, system enters into chaos with different routes. Beside classical bifurcations, bubbling route to chaos is observed for suitable parameter settings. On the other hand, Multistability of the system is indicated with the coexisting attractors, such that under same parameter setting the system shows different periodic and chaotic attractors. Moreover, chaotic synchronization of coupled oscillators is illustrated in final section.
Paper's Title:
Coefficient Estimates Of Sakaguchi Kind Functions Using
Lucas Polynomials
Author(s):
H. Priya and B. Srutha Keerthi
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus,
Chennai - 600 048,
India.
E-mail:
priyaharikrishnan18@gmail.com
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus,
Chennai - 600 048,
India.
E-mail: isruthilaya06@yahoo.co.in
Abstract:
By means of (p,q) Lucas polynomials, we estimate coefficient bounds and Fekete-Szego inequalities for functions belonging to this class. Several corollaries and consequences of the main results are also obtained.
Paper's Title:
Numerical Solution of Certain Types of Fredholm-Volterra Integro-Fractional Differential Equations via Bernstein Polynomials
Author(s):
Alias B. Khalaf1, Azhaar H. Sallo2 and Shazad S. Ahmed3
1Department
of Mathematics, College of Science,
University of Duhok,
Kurdistan Region,
Iraq.
E-mail: aliasbkhalaf@uod.ac
2Department
of Mathematics, College of Science,
University of Duhok,
Kurdistan Region,
Iraq.
E-mail: azhaarsallo@uod.ac
3Department
of Mathematics, College of Science,
University of Sulaimani,
Kurdistan Region,
Iraq.
E-mail: shazad.ahmed@univsul.edu
Abstract:
In this article we obtain a numerical solution for a certain fractional order integro-differential equations of Fredholm-Volterra type, where the fractional derivative is defined in Caputo sense. The properties of Bernstein polynomials are applied in order to convert the fractional order integro-differential equations to the solution of algebraic equations. Some numerical examples are investigated to illustrate the method. Moreover, the results obtained by this method are compared with the exact solution and with the results of some existing methods as well.
Paper's Title:
An Integration Technique for Evaluating Quadratic Harmonic Sums
Author(s):
J. M. Campbell and K.-W. Chen
Department of Mathematics and Statistics,
York University, 4700 Keele St, Toronto,
ON M3J 1P3,
Canada.
E-mail: jmaxwellcampbell@gmail.com
Department of Mathematics, University of Taipei,
No. 1, Ai-Guo West Road,
Taipei 10048, Taiwan.
E-mail: kwchen@uTaipei.edu.tw
URL:
https://math.utaipei.edu.tw/p/412-1082-22.php
Abstract:
The modified Abel lemma on summation by parts has been applied in many ways recently to determine closed-form evaluations for infinite series involving generalized harmonic numbers with an upper parameter of two. We build upon such results using an integration technique that we apply to ``convert'' a given evaluation for such a series into an evaluation for a corresponding series involving squared harmonic numbers.
Paper's Title:
Existence of Compositional Square Roots of Circle Maps
Author(s):
K. Ali Akbar and T. Mubeena
Department of Mathematics,
School of Physical Sciences,
Central University of Kerala,
Periya - 671320,
Kasaragod,
Kerala,
India.
E-mail: aliakbar.pkd@gmail.com,
aliakbar@cukerala.ac.in
Department of Mathematics,
School of Mathematics and Computational Sciences,
University of Calicut,
Thenhipalam-673635,
Malappuram,
Kerala,
India.
E-mail: mubeenatc@gmail.com,
mubeenatc@uoc.ac.in
Abstract:
In this paper, we discuss the existence of compositional square roots of circle maps. If f and g are two maps such that g ○ g = f, we say that g is a compositional square root of f.
Paper's Title:
Improved Oscillation Criteria of Second-Order Advanced Non-canonical Difference Equation
Author(s):
G. E. Chatzarakis1, N. Indrajith2, S. L. Panetsos1, E. Thandapani3
1Department
of Electrical and Electronic Engineering Educators
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail: gea.xatz@aspete.gr,
geaxatz@otenet.gr
spanetsos@aspete.gr
2Department
of Mathematics,
Presidency College, Chennai - 600 005,
India.
E-mail: indrajithna@gmail.com
3Ramanujan
Institute for Advanced Study in Mathematics,
University of Madras Chennai - 600 005,
India.
E-mail: ethandapani@yahoo.co.in
Abstract:
Employing monotonic properties of nonoscillatory solutions, we derive some new oscillation criteria for the second-order advanced non-canonical difference equation
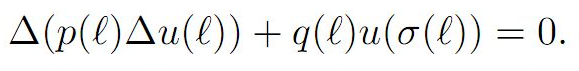
Our results extend and improve the earlier ones. The outcome is illustrated via some particular difference equations.
Paper's Title:
Several New Closed-form Evaluations of the Generalized Hypergeometric Function with Argument 1/16
Author(s):
B. R. Srivatsa Kumar, Insuk Kim and Arjun K. Rathie
Department of Mathematics,
Manipal Institute of Technology,
Manipal Academy of Higher Education,
Manipal 576 104,
India.
E-mail: sri_vatsabr@yahoo.com
Department of Mathematics Education,
Wonkwang University,
Iksan, 54538,
Republic of Korea.
E-mail: iki@wku.ac.kr
Department of Mathematics,
Vedant College of Engineering and Technology,
Rajasthan Technical University,
Bundi, 323021, Rajasthan,
India.
E-mail: arjunkumarrathie@gmail.com
Abstract:
The main objective of this paper is to establish as many as thirty new closed-form evaluations of the generalized hypergeometric function q+1Fq(z) for q= 2, 3, 4. This is achieved by means of separating the generalized hypergeometric function q+1Fq(z) for q=1, 2, 3, 4, 5 into even and odd components together with the use of several known infinite series involving central binomial coefficients obtained earlier by Ji and Hei \& Ji and Zhang.
Paper's Title:
Bounds for the Extremal Eigenvalues of Positive Definite Matrices
Author(s):
Shivani Singh and Pravin Singh
Unisa, Department of Decision Sciences,
PO Box 392,
Pretoria,
0003,
South Africa.
E-mail: singhs2@unisa.ac.za
University of KwaZulu-Natal,
School of Mathematics Statistics and Computer Sciences
Private Bag X54001,
Durban,
4000,
South Africa.
E-mail: singhprook@gmail.com
Abstract:
We use a projection to achieve bounds for a vector function of the eigenvalues of a positive definite matrix. For various choices of the monotonic function we are able to obtain bounds for the extremal eigenvalues in terms of the traces of the matrix and its powers. These bounds are relatively simple to compute.
Paper's Title:
On Statistically Φ-Convergence
Author(s):
Supama
Department of Mathematics,
Gadjah Mada
University,
Yogyakarta 55281,
Indonesia.
E-mail: supama@ugm.ac.id
Abstract:
The idea of statistical convergence was introduced by Antoni Zygmund in 1935. Based on in the idea of Zygmund, Henry Fast and Hugo Steinhaus independently introduced a concept of statistical convergence as a generalization of an ordinary convergence in the same year 1951. In this paper, by using the Orlicz function, we introduce a concept of statistical Φ-convergence, as a generalization of the statistical convergence. Further, we observe some basic properties and some topological properties of the statistical Φ-convergent sequences
Paper's Title:
SQIRV Model for Omicron Variant with Time Delay
Author(s):
S. Dickson, S. Padmasekaran, G. E. Chatzarakis and S. L. Panetsos
Mathematics, Periyar University, Periyar
Palkalai Nagar, Salem,
636011, Tamilnadu,
India.
E-mail:
dickson@periyaruniversity.ac.in,
padmasekarans@periyaruniversity.ac.in
Electrical and Electronic Engineering
Educators, School of
Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
spanetsos@aspete.gr
Abstract:
In order to examine the dynamics of the Omicron variant, this paper uses mathematical modelling and analysis of a SQIRV model, taking into account the delay in the conversion of susceptible individuals into infected individuals and infected individuals into recovered individuals. The pandemic was eventually controlled as a result of the massive delays. To assure the safety of the host population, this concept incorporates quarantine and the COVID-19 vaccine. Both local and global stability of the model are examined. It is found that the fundamental reproduction number affects both local and global stability conditions. Our findings show that asymptomatic cases caused by an affected population play an important role in increasing Omicron infection in the general population. The most recent data on the pandemic Omicron variant from Tamil Nadu, India, is verified.
Paper's Title:
Bicomplex Univalent Functions
Author(s):
Mohd Arif, Amjad Ali, Rajat Singh* and Romesh Kumar
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: azizymaths@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: amjadladakhi687@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: *rajat.singh.rs634@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: romeshmath@gmail.com
Abstract:
In this paper we introduce bicomplex univalent functions and also discuss the properties of a specific class of univalent functions.
Paper's Title:
Coefficient Bounds for Sakaguchi Kind of Functions Associated with Sine Function
Author(s):
Serap Bulut, H. Priya and B. Srutha Keerth
Kocaeli University,
Faculty of Aviation and Space Sciences,
Arslanbey Campus, 41285 Kartepe-Kocaeli,
Turkey.
E-mail: serap.bulut@kocaeli.edu.tr
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus, Chennai - 600 048,
India.
E-mail: priyaharikrishnan18@gmail.com,
priya.h2020@vitstudent.ac.in
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus, Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com,
sruthakeerthi.b@vit.ac.in
Abstract:
In this paper, we introduce a new general subclass of analytic functions with respect to symmetric points in the domain of sine function. We obtain sharp coefficient bounds and upper bounds for the Fekete-Szegö functional. Also we get sharp bounds for the logarithmic coefficients of functions belonging to this new class.
Paper's Title:
Commutator For Singular Operators On Variable Exponent Sequence Spaces And Their Corresponding Ergodic Version
Author(s):
A.M. Alphonse and S.S.S. Anupindi
Department of Mathematics,
Birla Institute of Technology And Science- Pilani,
Hyderabad Campus, Jawahar Nagar, Kapra Mandal,
District.-Medchal-500 078, Telangana,
India.
E-mail:
alphonse@hyderabad.bits-pilani.ac.in
p20180442@hyderabad.bits-pilani.ac.in
URL:
https://www.bits-pilani.ac.in/hyderabad/a-michael-alphonse
https://www.bits-pilani.ac.in/research_scholars/sri-sakti-swarup-anupindi
Abstract:
In this paper, we prove strong type inequality for maximal commutator of singular operator on weighted lp spaces. Using these results we prove strong type inequality for the maximal commutator of singular operator on variable exponent sequence spaces. Using Calderon-Coifman-Weiss transference principle we prove strong type inequality for maximal ergodic commutator of singular operator on a probability space equipped with measure preserving transformation U.
Paper's Title:
Some Nonlinear Gronwall-Bellman Type Retarded Integral Inequalities with Power and Their Applications
Author(s):
Ammar Boudeliou
Department of Mathematics, University of Constantine 1
Brothers Mentouri,
BP, 325, Ain El Bey Street, 25017,
Algeria.
E-mail: ammar_boudeliou@umc.edu.dz
Abstract:
In this paper, we investigate a certain class of nonlinear Gronwall-Bellman type integral inequalities with power in more general cases involving retarded term and more general nonlinearities. Our results generalize some known integral inequalities and other results obtained very recently. The inequalities given here can be used to estimate the bound on the solutions of retarded integral equation of Volterra type and integro-differential equations (IDE) with power. Two examples are given to show the validity of our established theorems.
Paper's Title:
A New Iterative Approximation of a Split Fixed Point Constraint Equilibrium Problem
Author(s):
Musa Adewale Olona1, Adhir Maharaj2 and Ojen Kumar Narain3
1School
of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 219095783@stu.ukzn.ac.za
2Department
of Mathematics,
Durban University of Technology, Durban,
South Africa.
E-mail: adhirm@dut.ac.za
3School
of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
The purpose of this paper is to introduce an iterative algorithm for approximating an element in the solution set of the common split feasibility problem for fixed points of demimetric mappings and equilibrium problem for monotone mapping in real Hilbert spaces. Motivated by self-adaptive step size method, we incorporate the inertial technique to accelerate the convergence of the proposed method and establish a strong convergence of the sequence generated by the proposed algorithm. Finally, we present a numerical example to illustrate the significant performance of our method. Our results extend and improve some existing results in the literature.
Paper's Title:
Recursive Bounds for the Eigenvalues of Symmetric Positive Definite Matrices
Author(s):
Pravin Singh, Shivani Singh, Virath Singh
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
University of South Africa,
Department of Decision Sciences, PO Box 392,
Pretoria,0003,
South Africa.
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
E-mail:
singhp@ukzn.ac.za,
singhs2@unisa.ac.za,
singhv@ukzn.ac.za
Abstract:
In this paper, we bound the extremal eigenvalues of a positive definite real symmetric matrix by considering a part of the characteristic equation in the region of the smallest and largest eigenvalues. An expansion around these values leads to a sequence of monotonic functions, whose zeros coincide with the extremal zeros of associated polynomials. The latter is shown to yield bounds that are fairly accurate.
Paper's Title:
ℵ0 Algebra and its Novel Application in Edge Detection
Author(s):
G. E. Chatzarakis1, S. Dickson2, S. Padmasekaran2, S. L. Panetsos1, and J. Ravi3
1Electrical
and Electronic Engineering Educators,
School of Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
spanetsos@aspete.gr
2Mathematics,
Periyar University,
Periyar Palkalai Nagar, Salem, 636011, Tamilnadu,
India.
E-mail: dix.bern@gmail.com,
padmasekarans@periyaruniversity.ac.in
3Department
of Mathematics, Amity University,
Bengaluru, Karnataka,
India.
E-mail:
jravistat@gmail.com
Abstract:
In this paper a new type of ℵ0-algebra has been defined. With its help, the fuzzy cross subalgebra and the fuzzy η-relation on the ℵ0-algebra are introduced and their respective properties are derived. Moreover, the fuzzy cross ℵ0-ideal of the ℵ0-algebra is defined with some theorems and intuitionistic fuzzy ℵ0-ideals of the ℵ0-algebra are introduced. This fuzzy algebra concept is applied in image processing to detect edges. This ℵ0-algebra is a novelty in the field of research.
Paper's Title:
Solving Fixed Point Problems and Variational Inclusions Using Viscosity Approximations
Author(s):
P. Patel, R. Shukla
Department of Mathematics, School of
Advanced Sciences, VIT-AP University\\
Amaravati, 522237, Andhra Pradesh,
India.
E-mail:
prashant.patel9999@gmail.com,
prashant.p@vitap.ac.in
Department of Mathematical Sciences &
Computing, Walter Sisulu University,
Mthatha 5117,
South Africa.
E-mail: rshukla@wsu.ac.za
Abstract:
This paper proposes a new algorithm to find a common element of the fixed point set of a finite family of demimetric mappings and the set of solutions of a general split variational inclusion problem in Hilbert spaces. The algorithm is based on the viscosity approximation method, which is a powerful tool for solving fixed point problems and variational inclusion problems. Under some conditions, we prove that the sequence generated by the algorithm converges strongly to this common solution.
Paper's Title:
Dyadic Riesz Wavelets on Local Fields of Positive Characteristics
Author(s):
Kartik Garg, Raj Kumar, Satyapriya
Department of Mathematics,
University of Delhi,
Delhi,
India.
kartikgarg1421@gmail.com,
rajkmc@gmail.com
kmc.satyapriya@gmail.com
Abstract:
In this research paper, we introduce a novel theory for the construction of a Riesz wavelet basis in the space L2(K), where K is a local field with positive characteristics. Our approach is two fold: firstly, we derive some essential characterizations of the scaling function associated with the structure of a Riesz MRA on a local field, and secondly, we review existing methods for constructing wavelet frames in L2(K). We also present a well elaborated example for a better comprehension of our theory. Due to mathematical convenience, we limit ourselves to the case of dyadic dilations only.
Paper's Title:
Indonesia's GDP Forecast: Evidence From Fuzzy Time Series Model Using Particle Swarm Optimization Algorithm
Author(s):
Ismail Djakaria1, Djihad Wungguli2, Regina Sugi Pakadang3, Sri Endang Saleh4, Maman Abdurachman Djauhari5
1,2,3Universitas
Negeri Gorontalo,
Department of Statistics, Gorontalo,
Indonesia.
4Universitas Negeri Gorontalo,
Department of Development Economics, Gorontalo,
Indonesia.
5Indonesian Institute of Education,
Jl. Terusan Pahlawan 32, Garut 44151,
Indonesia.
E-mail: iskar@ung.ac.id
URL:
https://orcid.org/0000-0003-1358-2356
Abstract:
Gross Domestic Product (GDP) is a principal indicator used to measure the economic condition of a country. Indonesia's GDP growth from 2017 to 2019 was approximately 6 percent; however, it experienced a decline in 2020 and 2021, with rates of only -0.02 percent and 2.41 percent, respectively. In the process of economic development planning, a forecasting system is required to determine GDP in the future. The forecasting method employed in this research is fuzzy time series optimized using Particle Swarm Optimization (PSO), to enhance the accuracy and convergence of forecasted values. The dataset used comprises secondary data, specifically 54 sets of Indonesian GDP data spanning from the first quarter of 2010 to the second quarter of 2023. The analysis results indicate that the proposed method is better than the conventional fuzzy time series approach. The former method provides a predictive value for one period in the future with a Mean Absolute Percentage Error (MAPE) value of 4.40%. In contrast, the latter yields higher predictive values with a MAPE value of 7.93%.
Paper's Title:
Fuzzy Ideal Congruences of ADL's
Author(s):
G. Prakasam Babu, K. Ramanuja Rao, G. Srikanya and Ch. Santhi Sundar Raj
1,4Department of Engineering
Mathematics,
Andhra University,
Visakhapatnam-A.P,
India.
E-mail: prakash.g368@gmail.com,
santhisundarraj@yahoo.com
2Department of Mathematics,
Solomon Islands National University,
Panatina Campus, Honiara,
Solomon Islands.
E-mail: ramanuja.kotti@sinu.edu.sb
3Department of Mathematics,
Raghu Engineering College (A),
Visakhapatnam-A.P.,
India.
E-mail:
srikanya.gonnabhaktula@raghuenggcollege.in
Abstract:
The concept of fuzzy congruence of an ADL is introduced. Established a correspondence between fuzzy ideals and fuzzy congruences of an ADL and obtained an equivalent condition for an ADL with a maximal element is a Boolean algebra.
Paper's Title:
Robust Layer Resolving Scheme for a System of Two Singularly Perturbed Time-Dependent Delay Initial Value Problems with Robin Initial Conditions
Author(s):
1K. Ramiya Bharathi, 2G. E. Chatzarakis, 2S. L. Panetsos, and 1M. Joseph Paramasivam
1PG & Research Department of
Mathematics,
Bishop Heber College (Affiliated to Bharathidasan University),
Tiruchirappalli - 620 017, Tamil Nadu,
India.
E-mail: ramiyabharathik28@gmail.com,
paramasivam.ma@bhc.edu.i
2Department of Electrical and Electronic Engineering Educators,
School of Pedagogical \& Technological Education (ASPETE),
Marousi, 15122, Athens,
Greece.
E-mail: gea.xatz@aspete.gr,
spanetsos@aspete.gr
Abstract:
This paper aimed at proving first order convergence for system of two singularly perturbed time-dependent initial value problems with delay in spatial variable and robin initial conditions. A Classical layer resolving finite difference scheme is developed by implementing uniform mesh for time discretization; Shishkin-mesh, a piecewise uniform mesh for spatial discretization. Shishkin-mesh is constructed is such way it captures the intricacies behavior of the layers. The interior layer is induced by the presence of a delay term in the space term. Error estimate is carried out to prove first order convergence with the help of maximum principle, stability analysis, solution bounds and sharper estimates of the singular components of the solutions. Finally, the numerical illustration is computed for the problem to bolster the scheme.
Paper's Title:
Viscosity Approximation Methods for Split Monotone Variational Inclusions and Fixed Point Problems of a Finite Family of ξ-Demimetric Mappings
Author(s):
Prashant Patel and Rahul Shukla
Department of Mathematics,
School of Advanced Sciences,
VIT-AP University, Inavolu,
Beside AP Secretariat,
Amaravati, 522237,
Andhra Pradesh,
India.
E-mail: prashant.patel9999@gmail.com,
prashant.p@vitap.ac.in
Department of Mathematical Sciences & Computing,
Walter Sisulu University,
Mthatha 5117,
South Africa.
E-mail: rshukla@wsu.ac.za
Abstract:
In this paper, we study viscosity approximation methods and present a new algorithm to find a common element of the fixed point of a finite family of ξ-demimetric mappings and the set of solutions of split monotone variational inclusion problem in Hilbert spaces. Under some conditions, we prove a strong convergence theorem which converges to this common solution.
Paper's Title:
A New Method for Eigenvalue Computations for Positive Definite Matrices
Author(s):
Pravin Singh, Shivani Singh, Virath Singh
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4000,
South Africa.
E-mail: singhp@ukzn.ac.za
University of South Africa, Department of
Decision Sciences,
PO Box 392, Pretoria, 0003,
South Africa.
E-mail: singhs2@unisa.ac.za
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4000,
South Africa.
E-mail: singhv@ukzn.ac.za
Abstract:
In this paper, we derive and analyse a new method to compute the first few dominant eigenvalues of real positive definite matrices. It involves a variant of the power method, shifted inverse iteration and the innerproduct functional. Our method is shown to reconstruct the minimal polynomial of the matrix.
Paper's Title:
On the Pathwise Uniqueness of Solutions to Stochastic Integral Equations of Ito Type
Author(s):
Romeo Negrea
Department of Mathematics,
Politehnica University of Timisoara,
P-ta Victoriei 2, 300006, Timisoara,
Romania.
E-mail: romeo.negrea@upt.ro
Abstract:
We give sufficient conditions for the pathwise uniqueness of solutions to nonlinear stochastic integral equations of Itô type. The result concerns a relaxation of the classical Lipschitz condition by allowing for a Nagumo-type fast-growing time dependence as the initial time is approached. We also propose a special subclass of functions N ⊂ M which shows that our considerations go beyond the classical contraction case. Moreover, they assure the facilities for to prove the existence and uniqueness of solutions and for the existence of the fixed points for some class of operators associated to stochastic integral equations.
Search and serve lasted 1 second(s).