|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Constraint Qualifications for Multiobjective Programming Problems on Hadamard Manifolds
Author(s):
Arnav Ghosh, Balendu Bhooshan Upadhyay and I.M. Stancu-Minasian
Department of Mathematics,
Indian Institute of Technology Patna,
Patna,
India.
E-mail: arnav_2021ma09@iitp.ac.in
Department of Mathematics,
Indian Institute of Technology Patna,
Patna,
India.
E-mail: bhooshan@iitp.ac.in
"Gheorghe Mihoc-Caius Iacob" Institute of
Mathematical Statistics and Applied Mathematics of the Romanian Academy,
Bucharest,
Romania.
E-mail: stancu_minasian@yahoo.com
Abstract:
The study of optimization methods on manifolds has emerged as an immensely significant topic in mathematics due its ubiquitous applicability as well as various computational advantages associated with it. Motivated by this fact, the present article is devoted to the study of a class of constrained multiobjective programming problems (MOPP) in the framework of Hadamard manifolds. We present the generalized Guignard constraint qualification (GGCQ) in the framework of Hadamard manifolds for (MOPP). Employing (GGCQ), we derive Karush-Kuhn-Tucker type necessary optimality criteria for (MOPP). Moreover, we present several other constraint qualifications (CQs) on Hadamard manifolds, namely, Abadie's CQ, generalized Abadie's CQ, Cottle-type CQ, Slater-type CQ, linear CQ, linear objective CQ and Mangasarian-Fromovitz CQ. Further, we establish various relations between these constraint qualifications. In particular, we show that these constraint qualifications, in turn, become sufficient conditions ensuring that (GGCQ) is satisfied.
Paper's Title:
On Zeros of Diagonally Quasiconvex Multifunctions
Author(s):
Zoran D. Mitrović
Faculty of Electrical Engineering,
University of Banja Luka,
78000 Banja Luka, Patre 5
Bosnia and Herzegovina
zmitrovic@etfbl.net
Abstract:
In this paper, we extended the notion of diagonally quasiconvexity
for multifunctions and established several existence results for
zeros of diagonally quasiconvex multifunctions. As applications we
obtain the results of fixed points, coincidence points and best
approximations for multifunctions. Using our result we also prove
the existence of solutions to the variational-like inequality
problem and generalized vector equilibrium problem. The results
of this paper generalize some known results in the literature.
Paper's Title:
On Vector Variational Inequality Problem in Terms of Bifunctions
Author(s):
C. S. Lalitha and Monika Mehta
Department of Mathematics, Rajdhani College,
Department of Mathematics, Satyawati College,
University of Delhi, Raja Garden,
Delhi 110015, India
cslalitha@rediffmail.com
University Of Delhi, Ashok Vihar,
Phase-III, Delhi 110052, India
mridul_in@yahoo.com
Abstract:
In this paper, we consider a generalized vector variational
inequality problem expressed in terms of a bifunction and establish
existence theorems for this problem by using the concepts of cone
convexity and cone strong quasiconvexity and employing the
celebrated Fan's Lemma. We also give two types of gap functions for this problem.
Paper's Title:
Generalizing Polyhedra to Infinite Dimension
Author(s):
Paolo d'Alessandro
Department of Mathematics, Third University of Rome,
Lgo S.L. Murialdo 1, 00146 Rome, Italy.
URL:
http://www.mat.uniroma3.it/users/dalex/dalex.html.
Abstract:
This paper generalizes polyhedra to infinite dimensional Hilbert spaces as countable intersections of closed semispaces. Highlights are the structure theory that shows that a polyhedron is the sum of compact set (in a suitable topology) plus a closed pointed cone plus a closed subspace, giving the internal representation of polyhedra. In the final part the dual range space technique is extended to the solution of infinite dimensional LP problems.
Paper's Title:
Existence, Global Regularity and Uniqueness of Solutions of the Navier-Stokes Equations in Space Dimension 3 when the Initial Data are Regular
Author(s):
Moulay D. Tidriri
Email: mtctyasa@gmail.com
Abstract:
The existence, regularity, and uniqueness of global solutions of the Navier-Stokes
equations in
![]() are given for when the initial velocity
are given for when the initial velocity
![]() for all integers q ≥ 0 and div u0
= 0.
for all integers q ≥ 0 and div u0
= 0.
Paper's Title:
Additive Mappings on Semiprime Rings Functioning as Centralizers
Author(s):
Abu Zaid Ansari and Faiza Shujat
Department of Mathematics,
Faculty of Science,
Islamic University of Madinah, Madinah
K.S.A.
E-mail: ansari.abuzaid@gmail.com,
ansari.abuzaid@iu.edu.sa
Department of Mathematics,
Faculty of Science,
Taibah University, Madinah,
K.S.A.
E-mail: faiza.shujat@gmail.com,
fullahkhan@taibahu.edu.sa
Abstract:
The objective of this research is to prove that an additive mapping T:R → R is a centralizer on R if it satisfies any one of the following identities:
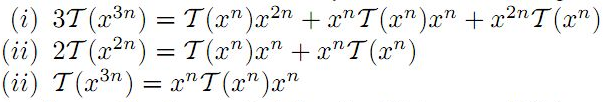
for all x ∈ R, where n ≥ 1 is a fixed integer and R is any suitably torsion free semiprime ring. Some results on involution "*" are also presented as consequences of the main theorems. In addition, we will take criticism in account with examples.
Paper's Title:
Applications of Relations and Relators in the
Extensions of Stability Theorems for Homogeneous and Additive Functions
Author(s):
Árpád Száz
Institute of Mathematics, University of Debrecen,
H-4010 Debrecen,
Pf. 12,
Hungary
szaz@math.klte.hu
Abstract:
By working out an appropriate technique of relations and relators and extending the ideas of the direct methods of Z. Gajda and R. Ger, we prove some generalizations of the stability theorems of D. H. Hyers, T. Aoki, Th. M. Rassias and P. Găvruţă in terms of the existence and unicity of 2-homogeneous and additive approximate selections of generalized subadditive relations of semigroups to vector relator spaces. Thus, we obtain generalizations not only of the selection theorems of Z. Gajda and R. Ger, but also those of the present author.
Paper's Title:
Shape Diagrams for 2D Compact Sets - Part I: Analytic
Convex Sets.
Author(s):
S. Rivollier, J. Debayle and J.-C. Pinoli
Ecole Nationale Supérieure des Mines de Saint-Etienne,
CIS - LPMG, UMR CNRS 5148, 158 cours Fauriel,
42023 Saint-Etienne Cedex 2, France.
rivollier@emse.fr;
debayle@emse.fr; pinoli@emse.fr
Abstract:
Shape diagrams are representations in the Euclidean plane introduced to study 3-dimensional and 2-dimensional compact convex sets. Such a set is represented by a point within a shape diagram whose coordinates are morphometrical functionals defined as normalized ratios of geometrical functionals. Classically, the geometrical functionals are the area, the perimeter, the radii of the inscribed and circumscribed circles, and the minimum and maximum Feret diameters. They allow thirty-one shape diagrams to be built. Most of these shape diagrams can also been applied to more general compact sets than compact convex sets. Starting from these six classical geometrical functionals, a detailed comparative study has been performed in order to analyze the representation relevance and discrimination power of these thirty-one shape diagrams. The purpose of this paper is to present the first part of this study, by focusing on analytic compact convex sets. A set will be called analytic if its boundary is piecewise defined by explicit functions in such a way that the six geometrical functionals can be straightforwardly calculated. The second and third part of the comparative study are published in two following papers [19.20]. They are focused on analytic simply connected sets and convexity discrimination for analytic and discretized simply connected sets, respectively.
Paper's Title:
Expected Utility with Subjective Events
Author(s):
Jacob Gyntelberg and Frank Hansen
Bank for International Settlements,
Basel,
Switzerland
Tohoku University, Institute for International Education,
Sendai,
Japan
Abstract:
We provide a new theory of expected utility with subjective events modeled by a lattice of projections. This approach allows us to capture the notion of a ``small world'' as a context dependent or local state space embedded into a subjective set of events, the ``grand world''. For each situation the decision makers' subjective ``small world'' reflects the events perceived to be relevant for the act under consideration. The subjective set of events need not be representable by a classical state space. Maintaining preference axioms similar in spirit to the classical axioms, we obtain an expected utility representation which is consistent across local state spaces and separates subjective probability and utility. An added benefit is that this alternative expected utility representation allows for an intuitive distinction between risk and uncertainty.
Paper's Title:
Some Inequalities of the Hermite-Hadamard Type for k-Fractional Conformable Integrals
Author(s):
C.-J. Huang, G. Rahman, K. S. Nisar, A. Ghaffar and F. Qi
Department of Mathematics, Ganzhou Teachers College,
Ganzhou 341000, Jiangxi,
China.
E-mail:
hcj73jx@126.com ,
huangcj1973@qq.com
Department of Mathematics, Shaheed Benazir
Bhutto University,
Sheringal, Upper Dir, Khyber Pakhtoonkhwa,
Pakistan.
E-mail: gauhar55uom@gmail.com
Department of Mathematics, College of Arts
and Science at Wadi Aldawaser, 11991,
Prince Sattam Bin Abdulaziz University, Riyadh Region,
Kingdom of Saudi Arabia.
E-mail: n.sooppy@psau.edu.sa,
ksnisar1@gmail.com
Department of Mathematical Science,
Balochistan University of Information Technology,
Engineering and Management Sciences, Quetta,
Pakistan.
E-mail: abdulghaffar.jaffar@gmail.com
School of Mathematical Sciences, Tianjin
Polytechnic University,
Tianjin 300387,
China; Institute of Mathematics,
Henan Polytechnic University, Jiaozuo 454010, Henan,
China.
E-mail: qifeng618@gmail.com,
qifeng618@qq.com
Abstract:
In the paper, the authors deal with generalized k-fractional conformable integrals, establish some inequalities of the Hermite-Hadamard type for generalized k-fractional conformable integrals for convex functions, and generalize known inequalities of the Hermite-Hadamard type for conformable fractional integrals.
Paper's Title:
Existence of Solution of Differential and Riemann-Liouville Equation Via Fixed Point Approach in Complex Valued b-Metric Spaces
Author(s):
K. Afassinou, A. A. Mebawondu, H. A. Abass and O. K. Narain
Department of Science Access,
University of Zululand, KwaDlangezwa,
South Africa.
E-mail: komia@aims.ac.za
DST-NRF Centre of Excellence in
Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: dele@aims.ac.za
DST-NRF Centre of Excellence in
Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: hammedabass548@gmail.com
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
In this paper, we establish some fixed point and common fixed point results for a new type of generalized contractive mapping using the notion of C-class function in the framework of complex valued b-metric spaces. As an application, we establish the existence and uniqueness of a solution for Riemann-Liouville integral and ordinary differential equation in the framework of a complete complex valued b-metric spaces. The obtained results generalize and improve some fixed point results in the literature.
Paper's Title:
Shape Diagrams for 2D Compact Sets - Part II: Analytic
Simply Connected Sets.
Author(s):
S. Rivollier, J. Debayle and J.-C. Pinoli
Ecole Nationale Supérieure des Mines de Saint-Etienne,
CIS - LPMG, UMR CNRS 5148, 158 cours Fauriel,
42023 Saint-Etienne Cedex 2, France.
rivollier@emse.fr;
debayle@emse.fr; pinoli@emse.fr
Abstract:
Shape diagrams are representations in the Euclidean plane introduced to study 3-dimensional and 2-dimensional compact convex sets. However, they can also been applied to more general compact sets than compact convex sets. A compact set is represented by a point within a shape diagram whose coordinates are morphometrical functionals defined as normalized ratios of geometrical functionals. Classically, the geometrical functionals are the area, the perimeter, the radii of the inscribed and circumscribed circles, and the minimum and maximum Feret diameters. They allow twenty-two shape diagrams to be built. Starting from these six classical geometrical functionals, a detailed comparative study has been performed in order to analyze the representation relevance and discrimination power of these twenty-two shape diagrams. The first part of this study is published in a previous paper 16. It focused on analytic compact convex sets. A set will be called analytic if its boundary is piecewise defined by explicit functions in such a way that the six geometrical functionals can be straightforwardly calculated. The purpose of this paper is to present the second part, by focusing on analytic simply connected compact sets. The third part of the comparative study is published in a following paper 17. It is focused on convexity discrimination for analytic and discretized simply connected compact sets.
Paper's Title:
Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.
Paper's Title:
A Multivalued Version of the
Radon-Nikodym Theorem, via the Single-valued Gould Integral
Author(s):
Domenico Candeloro1, Anca Croitoru2, Alina Gavriluţ2, Anna Rita Sambucini1
1Dept. of Mathematics and Computer
Sciences,
University of Perugia,
1, Via Vanvitelli -- 06123, Perugia,
Italy.
E-mail: domenico.candeloro@unipg.it,
anna.sambucini@unipg.it
2Faculty of Mathematics,
Al. I. Cuza University,
700506 Iaşi,
Romania.
E-mail: croitoru@uaic.ro,
gavrilut@uaic.ro
Abstract:
In this paper we consider a Gould type integral of real functions with respect to a compact and convex valued not necessarily additive measure. In particular we will introduce the concept of integrable multimeasure and, thanks to this notion, we will establish an exact Radon-Nikodym theorem relative to a fuzzy multisubmeasure which is new also in the finite dimensional case. Some results concerning the Gould integral are also obtained.
Paper's Title:
Riemann-Stieltjes Integrals and Some Ostrowski Type Inequalities
Author(s):
W. G. Alshanti
Department of General Studies,
Jubail University College,
KSA.
E-mail: shantiw@ucj.edu.sa
Abstract:
In this article, we investigate new integral inequalities of Ostrowski's type of various functional aspects. For mapping's second derivative, we assume two cases, namely, L1 and L∞ spaces. Moreover, for first derivative, we investigate two different characteristics, namely, bounded variation and locally Lipchitz continuity. Applications to special means and composite quadrature rules are also carried out.
Paper's Title:
On Stable Numerical Differentiation
Author(s):
N. S. Hoang and A. G. Ramm
Mathematics Department, Kansas State University Abstract:
Based on a regularized Volterra equation, two different approaches for numerical differentiation are considered.
The first approach consists of solving a regularized Volterra equation while the second approach is based on solving a disretized version of the regularized Volterra equation.
Numerical experiments show that these methods are efficient and compete favorably with the variational regularization method for stable calculating the derivatives of noisy functions.
Paper's Title:
Real Interpolation Methods and Quasilogarithmic Operators
Author(s):
Ming Fan
School of Industrial Technology and Management, Abstract:
The purpose of this paper is to deal with nonlinear quasilogarithmic operators, which possesses
the uniformly bounded commutator
property on various interpolation spaces in the sense of Brudnyi-Krugljak associated
with the quasi-power parameter spaces. The duality, and the domain and range spaces
of these operators are under consideration. Some known inequalities
for the Lebesgue integration spaces and the trace
classes are carried over to the non-commutative symmetric spaces of measurable operators
affiliated with a semi-finite von Neumann algebra.
Paper's Title:
Equivalence of the Nonsmooth Nonlinear Complementarity Problems to Unconstrained Minimization
Author(s):
M. A. Tawhid and J. L. Goffin
Manhattan, KS 66506-2602,
U. S. A.
nguyenhs@math.ksu.edu
ramm@math.ksu.edu
URL:http://math.ksu.edu/~ramm
3: Paper Source
PDF document
Dalarna University, 781 88 Borlänge, Sweden
fmi@du.se
URL: http://users.du.se/~fmi
3: Paper Source
PDF document
Department of Mathematics and Statistics,
School of Advanced Technologies and Mathematics,
Thompson Rivers University,
900 McGill Road, PO Box 3010, Kamloops, BC V2C 5N3
Canada
Alexandria University and Egypt Japan University of Science and Technology,
Alexandria-Egypt
mtawhid@tru.ca
Faculty of Management, McGill University,
1001 Sherbrooke Street West, Montreal, Quebec, H3A 1G5
Canada.
Jean-Louis.Goffin@McGill.ca
Abstract:
This paper deals with nonsmooth nonlinear complementarity problem, where the underlying functions are nonsmooth which admit the H-differentiability but not necessarily locally Lipschitzian or directionally differentiable. We consider a reformulation of the nonlinear complementarity problem as an unconstrained minimization problem. We describe H-differentials of the associated penalized Fischer-Burmeister and Kanzow and Kleinmichel merit functions. We show how, under appropriate P0, semimonotone (E0), P, positive definite, and strictly semimonotone (E) -conditions on an H-differential of f, finding local/global minimum of a merit function (or a `stationary point' of a merit function) leads to a solution of the given nonlinear complementarity problem. Our results not only give new results but also unify/extend various similar results proved for C1.
Paper's Title:
On Generalization of Hardy-type Inequalities
Author(s):
K. Rauf, S. Ponnusamy and J. O. Omolehin
Department of Mathematics,
University of Ilorin, Ilorin,
Nigeria
krauf@unilorin.edu.ng
Department of Mathematics,
Indian Institute of Technology Madras,
Chennai- 600 036,
India
samy@iitm.ac.in
Department of Mathematics,
University of Ilorin, Ilorin,
Nigeria
omolehin_joseph@yahoo.com
Abstract:
This paper is devoted to some new generalization of Hardy-type integral inequalities and the reversed forms. The study is to determine conditions on which the generalized inequalities hold using some known hypothesis. Improvement of some inequalities are also presented.
Paper's Title:
C*-valued metric projection and Moore-Penrose inverse on Hilbert C*-modules
Author(s):
M. Eshaghi Gordji, H. Fathi and S.A.R. Hosseinioun
Department of Mathematics,
Semnan University, P.O. Box 35195-363, Semnan,
Iran.
Center of Excellence in Nonlinear Analysis and Applications (CENAA),
Semnan University,
Iran.
E-mail: Madjid.Eshaghi@gmail.com
Department of Mathematics,
Shahid Beheshti University, Tehran,
Iran.
E-mail: Hedayat.fathi@yahoo.com
Department of Mathematical Sciences,
University of Arkansas, Fayetteville, Arkansas 72701,
USA.
E-mail: shossein@uark.net
Abstract:
Let t be a regular operator between Hilbert C*-modules and t† be its Moore-Penrose inverse. We give some characterizations for t† based on C*-valued metric projection. Moore-Penrose inverse of bounded operators and elements of a C*-algebra is studied as a special case.
Paper's Title:
Some fixed point results in partial S-metric spaces
Author(s):
M. M. Rezaee, S. Sedghi, A. Mukheimer, K. Abodayeh, and Z. D. Mitrovic
Department of Mathematics, Qaemshahr
Branch,
Islamic Azad University, Qaemshahr,
Iran.
E-mail: Rezaee.mohammad.m@gmail.com
Department of Mathematics, Qaemshahr
Branch,
Islamic Azad University, Qaemshahr,
Iran.
E-mail: sedghi.gh@qaemiau.ac.ir
Department of Mathematics and General
Sciences,
Prince Sultan University, Riyadh,
KSA.
E-mail: mukheimer@psu.edu.sa
Department of Mathematics and General
Sciences,
Prince Sultan University, Riyadh,
KSA.
E-mail: kamal@psu.edu.sa
Nonlinear Analysis Research Group,
Faculty of Mathematics and Statistics,
Ton Duc Thang University, Ho Chi Minh City,
Vietnam.
E-mail: zoran.mitrovic@tdtu.edu.vn
Abstract:
We introduce in this article a new class of generalized metric spaces, called partial S-metric spaces. In addition, we also give some interesting results on fixed points in the partial S-metric spaces and some applications.
Paper's Title:
The Effect of Harvesting Activities on Prey-Predator Fishery Model with Holling type II in Toxicant Aquatic Ecosystem
Author(s):
Moh Nurul Huda, Fidia Deny Tisna Amijaya, Ika Purnamasari
Department of Mathematics, Faculty of
Mathematics and Natural Science,
Mulawarman University,
Samarinda, East Kalimantan,75123
Indonesia.
E-mail: muh.nurulhuda@fmipa.unmul.ac.id
fidiadta@fmipa.unmul.ac.id
ika.purnamasari@fmipa.unmul.ac.id
Abstract:
This paper discussed prey-predator fishery models, in particular by analysing the effects of toxic substances on aquatic ecosystems. It is assumed in this model, that the prey population is plankton and the predator population is fish.\ Interaction between the two populations uses the Holling type II function. The existence of local and global critical points of the system are shown and their stability properties are analysed. Furthermore, Bionomic equilibrium and optimal control of harvesting are discussed. Finally, numerical simulations have been carried out to show in the interpretation of results.
Paper's Title:
On Automorphisms and Bi-derivations of Semiprime Rings
Author(s):
Abu Zaid Ansari, Faiza Shujat, Ahlam Fallatah
Department of Mathematics,
Faculty of Science,
Islamic University of Madinah, Madinah
K.S.A.
E-mail: ansari.abuzaid@gmail.com,
ansari.abuzaid@iu.edu.sa
Department of Mathematics
Faculty of Science
Taibah University, Madinah,
K.S.A.
E-mail: faiza.shujat@gmail.com,
fullahkhan@taibahu.edu.sa
Department of Mathematics
Faculty of Science
Taibah University, Madinah,
K.S.A.
E-mail: Afallatah@taibahu.edu.sa
Abstract:
In this article, our goal is to figure out a functional equation involving automorphisms and bi-derivations on certain semiprime ring. Also, we characterize the structure of automorphism, in case of prime rings.
Paper's Title:
Solving Fixed Point Problems and Variational Inclusions Using Viscosity Approximations
Author(s):
P. Patel, R. Shukla
Department of Mathematics, School of
Advanced Sciences, VIT-AP University\\
Amaravati, 522237, Andhra Pradesh,
India.
E-mail:
prashant.patel9999@gmail.com,
prashant.p@vitap.ac.in
Department of Mathematical Sciences &
Computing, Walter Sisulu University,
Mthatha 5117,
South Africa.
E-mail: rshukla@wsu.ac.za
Abstract:
This paper proposes a new algorithm to find a common element of the fixed point set of a finite family of demimetric mappings and the set of solutions of a general split variational inclusion problem in Hilbert spaces. The algorithm is based on the viscosity approximation method, which is a powerful tool for solving fixed point problems and variational inclusion problems. Under some conditions, we prove that the sequence generated by the algorithm converges strongly to this common solution.
Paper's Title:
Long Time Behavior for a Viscoelastic Problem with a Positive Definite Kernel
Author(s):
Nasser-eddine Tatar
King Fahd
University of Petroleum and Mineral, Department of Mathematical Sciences,
Dhahran, 31261 Saudi Arabia
tatarn@kfupm.edu.sa
Abstract:
We study the asymptotic behavior of solutions for an integro-differential problem which arises in the theory of viscoelasticity. It is proved that solutions go to rest in an exponential manner under new assumptions on the relaxation function in the memory term. In particular, we consider a new family of kernels which are not necessarily decreasing.
Paper's Title:
General Oscillations for Some Third Order Differential Systems with Nonlinear Acceleration Term
Author(s):
Awar Simon Ukpera
Department of Mathematics,
Obafemi Awolowo University,
Ile-Ife,
Nigeria.
aukpera@oauife.edu.ng
Abstract:
We generate some general nonuniform hypotheses for third order differential systems
of the form X''' +F(t,X'' )+BX'+CX = P(t), in which B and C are not
necessarily
constant matrices. Some results requiring sharp conditions on this system have recently been
published by the author in
[5]. This work however examines more closely crucial properties
associated with the generalised nature of the nonlinear acceleration term F, which were largely
overlooked in the earlier paper.
Paper's Title:
A general theory of decision making
Author(s):
Frank Hansen
Department of Economics,
University of Copenhagen,
Studiestraede 6, DK-1455 Copenhagen K
Denmark
Frank.Hansen@econ.ku.dk
URL: http://www.econ.ku.dk/okofh
Abstract:
We formulate a general theory of decision making based on a lattice of observable events, and we exhibit
a large class of representations called the general model. Some of the representations are equivalent to
the so called standard model in which observable events are modelled by
an algebra of measurable subsets of a state space, while others are not compatible with such a description.
We show that the general model collapses to the standard model, if and only if an additional axiom
is satisfied. We argue that this axiom is not very
natural and thus assert that the standard model may not be general enough to model all relevant
phenomena in economics. Using the general model we are
(as opposed to Schmeidler [16]) able to rationalize Ellsberg's paradox
without the introduction of non-additive measures.
Paper's Title:
A Reverse
of the Triangle Inequality in Inner Product Spaces and Applications for
Polynomials
Author(s):
I. Brnetić, S. S. Dragomir, R. Hoxha and J. Pečarić
Department of Applied Mathematics, Faculty of Electrical
Engineering and Computing,
University of Zagreb, Unska 3, 10 000 Zagreb,
Croatia
andrea@zpm.fer.hr
School of Computer Science & Mathematics, Victoria University
Po Box 14428, Melbourne Vic 8001
Australia
sever.dragomir@vu.edu.au
URL:http://rgmia.vu.edu.au/dragomir
Faculty of Applied Technical Sciences, University of Prishtina,
Mother
Theresa 5, 38 000 Prishtina
Kosova
razimhoxha@yahoo.com
Faculty of Textile Technology, University of Zagreb,
Pierottijeva 6, 10000
Zagreb,
Croatia
pecaric@hazu.hr
Abstract:
A reverse of the triangle inequality in inner product spaces related to the
celebrated Diaz-Metcalf inequality with applications for complex polynomials
is given.
Paper's Title:
Comparison Results for Solutions of Time Scale Matrix Riccati
Equations and Inequalities
Author(s):
R. Hilscher
Department of Mathematical Analysis, Faculty of Science,
Masaryk University, Janáčkovo nám. 2a,
CZ-60200, Brno, Czech Republic.
hilscher@math.muni.cz
URL: http://www.math.muni.cz/~hilscher/
Abstract:
In this paper we derive comparison results for Hermitian solutions of time scale matrix Riccati
equations and Riccati inequalities. Such solutions arise from special conjoined bases
(X,U) of the corresponding time scale symplectic system via the Riccati quotient
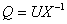 . We also discuss properties of a unitary matrix solution
. We also discuss properties of a unitary matrix solution 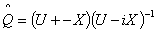 of a certain
associated Riccati equation.
of a certain
associated Riccati equation.
Paper's Title:
Hyers-Ulam-Rassias Stability
of a Generalized Jensen Functional Equation
Author(s):
A. Charifi, B. Bouikhalene, E. Elqorachi and A. Redouani
Department of
Mathematics, Faculty of Sciences,
Ibn Tofail University,
Kenitra, Morocco
charifi2000@yahoo.fr
bbouikhalene@yahoo.fr
Department of
Mathematics, Faculty of Sciences,
Ibn Zohr University,
Agadir, Morocco
elqorachi@hotmail.com
Redouani-ahmed@yahoo.fr
Abstract:
In this paper we obtain the Hyers-Ulam-Rassias stability for the generalized Jensen's functional equation in abelian group (G,+). Furthermore we discuss the case where G is amenable and we give a note on the Hyers-Ulam-stability of the K-spherical (n × n)-matrix functional equation.
Paper's Title:
Improvement of Jensen's
Inequality for Superquadratic Functions
Author(s):
S. Abramovich, B. Ivanković, and J. Pečarić
Department of Mathematics,
University of Haifa,
Haifa 31905,
Israel.
abramos@math.haifa.ac.il
Faculty of Transport and
Trafic Engineering,
University of Zagreb,
Vukelićeva 4, 10000,
Croatia
bozidar.ivankovic@zg.t-com.hr
Faculty of Textile,
University of Zagreb,
Prilaz Baruna Filipovića 30, 10000 Zagreb,
Croatia
pecaric@element.hr
Abstract:
Since 1907, the famous Jensen's inequality has been refined in different manners. In our paper, we refine it applying superquadratic functions and separations of domains for convex functions. There are convex functions which are not superquadratic and superquadratic functions which are not convex. For superquadratic functions which are not convex we get inequalities analogue to inequalities satisfied by convex functions. For superquadratic functions which are convex (including many useful functions) we get refinements of Jensen's inequality and its extensions.
Paper's Title:
Common Fixed Point Results for Banach Operator Pairs and Applications to Best Approximation
Author(s):
Hemant Kumar Nashine
Department of Mathematics,
Disha Institute of Management and Technology,
Satya Vihar, Vidhansabha - Chandrakhuri Marg (Baloda Bazar Road),
Mandir Hasaud,
Raipur - 492101(Chhattisgarh), India.
hemantnashine@rediffmail.com
nashine_09@rediffmail.com
Abstract:
The common fixed point results for Banach operator pair with generalized nonexpansive mappings in q-normed space have been obtained in the present work. As application, some more general best approximation results have also been determined without the assumption of linearity or affinity of mappings. These results unify and generalize various existing known results with the aid of more general class of noncommuting mappings.
Paper's Title:
On Generalized Triangle Inequality in p-Freéchet Spaces, 0<p<1
Author(s):
M. A. Latif
Department of Mathematics,
University of Hail, Hail,
Saudi Arabia
m_amer_latif@hotmail.com
Abstract:
In this paper generalized triangle inequality and its reverse in a p-Fréchet space where, 0<p<1 are obtained.
Paper's Title:
A One-Line Derivation of the Euler and Ostrogradski Equations
Author(s):
Olivier de La Grandville
Stanford University,
Department of Management Science and Engineering,
Stanford, CA 94305,
U. S. A
Abstract:
At the very heart of major results of classical physics, the Euler and Ostrogradski equations have apparently no intuitive interpretation. In this paper we show that this is not so. Relying on Euler's initial geometric approach, we show that they can be obtained through a direct reasoning that does not imply any calculation. The intuitive approach we suggest offers two benefits: it gives immediate significance to these fundamental second-order non-linear differential equations; and second, it allows to obtain a property of the calculus of variations that does not seem to have been uncovered until now: the Euler and Ostrogradski equations can be derived not necessarily by giving a variation to the optimal function -- as is always done; one could equally well start by giving a variation to their derivative(s).
Paper's Title:
Hermite-Hadamard-Fejer Type Inequalities for Harmonically s-convex Functions via Fractional Integrals
Author(s):
İmdat İşcan, Mehmet Kunt
Department of Mathematics,
Faculty of Sciences and Arts,
Giresun University, Giresun,
Turkey.
E-mail: imdat.iscan@giresun.edu.tr
Department of Mathematics,
Faculty of Sciences,
Karadeniz Technical University,
61080, Trabzon,
Turkey.
E-mail:
mkunt@ktu.edu.tr
Abstract:
In this paper, some Hermite-Hadamard-Fejer type integral inequalities for harmonically s-convex functions in fractional integral forms have been obtained.
Paper's Title:
On the Hyers-Ulam Stability of Homomorphisms and Lie Derivations
Author(s):
Javad Izadi and Bahmann Yousefi
Department of Mathematics, Payame Noor
University,
P.O. Box: 19395-3697, Tehran,
Iran.
E-mail: javadie2003@yahoo.com,
b_yousefi@pnu.ac.ir
Abstract:
Let A be a Lie Banach*-algebra. For each elements (a, b) and (c, d) in A2:= A * A, by definitions
(a, b) (c, d)= (ac, bd),
|(a, b)|= |a|+ |b|,
(a, b)*= (a*, b*),
A2 can be considered as a Banach*-algebra. This Banach*-algebra is called a Lie Banach*-algebra whenever it is equipped with the following definitions of Lie product:
for all a, b, c, d in A. Also, if A is a Lie Banach*-algebra, then D: A2→A2 satisfying
D ([ (a, b), (c, d)])= [ D (a, b), (c, d)]+ [(a, b), D (c, d)]
for all $a, b, c, d∈A, is a Lie derivation on A2. Furthermore, if A is a Lie Banach*-algebra, then D is called a Lie* derivation on A2 whenever D is a Lie derivation with D (a, b)*= D (a*, b*) for all a, b∈A. In this paper, we investigate the Hyers-Ulam stability of Lie Banach*-algebra homomorphisms and Lie* derivations on the Banach*-algebra A2.
Paper's Title:
Hermite-Hadamard Type Inequalities for k-Riemann Liouville Fractional Integrals Via Two Kinds of Convexity
Author(s):
R. Hussain1, A. Ali2, G. Gulshan3, A. Latif4 and K. Rauf5
1,2,3,4Department
of Mathematics,
Mirpur University of Science and Technology, Mirpur.
Pakistan.
E-mail1:
rashida12@gmail.com
E-mail2:
unigraz2009@yahoo.com
E-mail3:
ghazalagulshan@yahoo.com
E-mail4:
asialatif87@gmail.com
5Department
of Mathematics,
University of Ilorin, Ilorin,
Nigeria.
E-mail5:
krauf@unilorin.edu.ng
Abstract:
In this article, a fundamental integral identity including the first order derivative of a given function via k-Riemann-Liouville fractional integral is established. This is used to obtain further Hermite-Hadamard type inequalities involving left-sided and right-sided k-Riemann-Liouville fractional integrals for m-convex and (s,m)-convex functions respectively.
Paper's Title:
Weakly Compact Composition Operators on Real Lipschitz Spaces of Complex-valued Functions on Compact Metric Spaces with Lipschitz Involutions
Author(s):
D. Alimohammadi and H. Alihoseini
Department of Mathematics,
Faculty of Science,
Arak University
P. O. Box,38156-8-8349,
Arak,
Iran.
E-mail: d-alimohammadi@araku.ac.ir
E-mail:
hr_alihoseini@yahoo.com
URL: http://www.araku.ac.ir
Abstract:
We first show that a bounded linear operator T on a real Banach space E is weakly compact if and only if the complex linear operator T on the complex Banach space EC is weakly compact, where EC is a suitable complexification of E and iT' is the complex linear operator on EC associated with T. Next we show that every weakly compact composition operator on real Lipschitz spaces of complex-valued functions on compact metric spaces with Lipschitz involutions is compact.
Paper's Title:
On Closed Range C*-modular Operators
Author(s):
Javad Farokhi-Ostad and Ali Reza Janfada
Department of Mathematics,
Faculty of Mathematics and Statistics Sciences,
University of Birjand, Birjand,
Iran.
E-mail: j.farokhi@birjand.ac.ir
ajanfada@birjand.ac.ir
Abstract:
In this paper, for the class of the modular operators on Hilbert C*-modules, we give the conditions to closedness of their ranges. Also, the equivalence conditions for the closedness of the range of the modular projections on Hilbert C*-modules are discussed. Moreover, the mixed reverse order law for the Moore-Penrose invertible modular operators are given.
Paper's Title:
A New Adomian Approach to Solving Integral Equations of Fredholm and Volterra Second Kind
Author(s):
Ouedraogo Seny, Nebie Abdoul Wassiha, Youssouf Pare, Blaise Some
Departement de mathematiques,
Universite Joseph Ki-Zerbo,
Burkina Faso.
E-mail: oseny@yahoo.fr,
nebwass@yahoo.fr
pareyoussouf@yahoo.fr,
some@univ-ouaga.bf
Abstract:
In order to simplify the resolution of Fredholm and Volterra's second type integral equations, we propose a new approach based on the Adomian Decompositional Method (ADM). We test the new approach on several examples with success.
Paper's Title:
Weyl's theorem for class Q and k - quasi class Q Operators
Author(s):
S. Parvatham and D. Senthilkumar
Department of Mathematics and Humanities,
Sri Ramakrishna Institute of Technology, Coimbatore-10, Tamilnadu,
India.
E-mail: parvathasathish@gmail.com
Post Graduate and Research Department of
Mathematics,
Govt. Arts College, Coimbatore-641018, Tamilnadu,
India.
E-mail: senthilsenkumhari@gmail.com
Abstract:
In this paper, we give some properties of class Q operators. It is proved that every class Q operators satisfies Weyl's theorem under the condition that T2 is isometry. Also we proved that every k quasi class Q operators is Polaroid and the spectral mapping theorem holds for this class of operator. It will be proved that single valued extension property, Weyl and generalized Weyl's theorem holds for every k quasi class Q operators.
Paper's Title:
Inequalities for Functions of Selfadjoint Operators on Hilbert Spaces:
a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
College of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning inequalities for continuous functions of selfadjoint operators on complex Hilbert spaces. It is intended for use by both researchers in various fields of Linear Operator Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Attempts to Define a Baum--Connes Map Via Localization of Categories for Inverse Semigroups
Author(s):
Bernhard Burgstaller
Departamento de Matematica,
Universidade Federal de Santa Catarina,
CEP 88.040-900 Florianopolis-SC,
Brasil.
E-mail:
bernhardburgstaller@yahoo.de
URL:
http://mathematik.work/bernhardburgstaller/index.html
Abstract:
An induction functor in inverse semigroup equivariant KK-theory is considered, and together with %a restriction functors certain results similar to those known from the Mackey machinery are shown. It is also verified that for any so-called E-continuous inverse semigroup its equivariant KK-theory satisfies the universal property and is a triangulated category.
Paper's Title:
On Subspace-Supercyclic Operators
Author(s):
Mansooreh Moosapoor
Assistant Professor,
Department of Mathematics,
Farhangian University, Tehran,
Iran.
E-mail: mosapor110@gmail.com
m.mosapour@cfu.ac.ir
Abstract:
In this paper, we prove that supercyclic operators are subspace-supercyclic and by this we give a positive answer to a question posed in ( L. Zhang, Z. H. Zhou, Notes about subspace-supercyclic operators, Ann. Funct. Anal., 6 (2015), pp. 60--68). We give examples of subspace-supercyclic operators that are not subspace-hypercyclic. We state that if T is an invertible supercyclic operator then Tn and T-n is subspace-supercyclic for any positive integer n. We give two subspace-supercyclicity criteria. Surprisingly, we show that subspace-supercyclic operators exist on finite-dimensional spaces.
Paper's Title:
Optimal Control Analysis of HIV/AIDS Epidemic Model with an Antiretroviral Treatment
Author(s):
U. Habibah and R. A. Sari
Mathematics Department and Reseach Group
of Biomathematics,
Faculty of Mathematics and Natural Science,
Brawijaya University, Jl. Veteran Malang 65145,
Indonesia.
E-mail: ummu_habibah@ub.ac.id
Abstract:
A mathematical model of HIV/AIDS is governed by a system of ordinary differential equations in the presence of an antiretroviral treatment (ARV). The theory of optimal control is applied to an epidemic model of HIV/AIDS which an ARV is used as a control strategy in order to prevent the spread of HIV/AIDS. The optimality system is derived by applying the Pontryagin's Minimum Principle. We analyze the boundedness and positivity of solutions, and an existence of the optimal control. Numerical simulations are conducted to obtain numerical solution of the optimally system.
Paper's Title:
Hermite-Hadamard Type Inequalities for MN-Convex Functions
Author(s):
Sever S. Dragomir1,2
1Mathematics,
College of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
The present work endeavours to briefly present some of the fundamental results connected to the Hermite-Hadamard inequality for special classes of convex functions such as AG, AH, GA, GG, GH, HA, HG and HH -convex functions in which the author have been involved during the last five years. For simplicity, we call these classes of functions such as MN-convex functions, where M and N stand for any of the Arithmetic (A), Geometric (G) or Harmonic (H) weighted means of positive real numbers. The survey is intended for use by both researchers in various fields of Approximation Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
A New Method with Regularization for Solving Split Variational Inequality Problems in Real Hilbert Spaces
Author(s):
Francis Akutsah1 and Ojen Kumar Narain2
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 216040405@stu.ukzn.ac.za,
akutsah@gmail.com
2School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
In this paper, we introduce a new inertial extrapolation method with regularization for approximating solutions of split variational inequality problems in the frame work of real Hilbert spaces. We prove that the proposed method converges strongly to a minimum-norm solution of the problem without using the conventional two cases approach. In addition, we present some numerical experiments to show the efficiency and applicability of the proposed method. The results obtained in this paper extend, generalize and improve several results in this direction.
Paper's Title:
Timelike Surfaces with a Common Line of Curvature in Minkowski 3-Space
Author(s):
M.K. Saad, A.Z. Ansari, M. Akram and F. Alharbi
Department of Mathematics ,
Faculty of Science,
Islamic University of Madinah,
KSA
Abstract:
In this paper, we analyze the problem of constructing a timelike surface family from a given non-null curve line of curvature. Using the Frenet frame of the non-null curve in Minkowski space E13 we express the family of surfaces as a linear combination of the components of this frame, and derive the necessary and sufficient conditions for the coefficients to satisfy both the line of curvature and the isoparametric requirements. In addition, a necessary and sufficient condition for the given non-null curve to satisfy the line of curvature and the geodesic requirements is investigated. The extension to timelike surfaces of revolution is also outlined. Meanwhile, some representative non-null curves are chosen to construct the corresponding timelike surfaces which possessing these curves as lines of curvature. Results presented in this paper have applications in geometric modeling and the manufacturing of products. In addition, some computational examples are given and plotted.
Paper's Title:
Two Geometric Constants Related to Isosceles Orthogonality on Banach Space
Author(s):
Huayou Xie, Qi Liu and Yongjin Li
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P. R. China.
E-mail: xiehy33@mail2.sysu.edu.cn
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P. R. China.
E-mail: liuq325@mail2.sysu.edu.cn
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P. R. China.
E-mail: stslyj@mail.sysu.edu.cn
Abstract:
In this paper, we introduce new geometric constant C(X,ai,bi,ci,2) to measure the difference between isosceles orthogonality and special Carlsson orthogonalities. At the same time, we also present the geometric constant C(X,ai,bi,ci), which is a generalization of the rectangular constant proposed by Joly. According to the inequality on isosceles orthogonality, we give the boundary characterization of these geometric constants. Then the relationship between these geometric constants and uniformly non-square property can also be discussed. Furthermore, we show that there is a close relationship between these geometric constants and some important geometric constants.
Paper's Title:
SQIRV Model for Omicron Variant with Time Delay
Author(s):
S. Dickson, S. Padmasekaran, G. E. Chatzarakis and S. L. Panetsos
Mathematics, Periyar University, Periyar
Palkalai Nagar, Salem,
636011, Tamilnadu,
India.
E-mail:
dickson@periyaruniversity.ac.in,
padmasekarans@periyaruniversity.ac.in
Electrical and Electronic Engineering
Educators, School of
Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
spanetsos@aspete.gr
Abstract:
In order to examine the dynamics of the Omicron variant, this paper uses mathematical modelling and analysis of a SQIRV model, taking into account the delay in the conversion of susceptible individuals into infected individuals and infected individuals into recovered individuals. The pandemic was eventually controlled as a result of the massive delays. To assure the safety of the host population, this concept incorporates quarantine and the COVID-19 vaccine. Both local and global stability of the model are examined. It is found that the fundamental reproduction number affects both local and global stability conditions. Our findings show that asymptomatic cases caused by an affected population play an important role in increasing Omicron infection in the general population. The most recent data on the pandemic Omicron variant from Tamil Nadu, India, is verified.
Paper's Title:
Fractional Integral Inequalities of Hermite-Hadamard Type for P-convex and Quasi-Convex Stochastic Process
Author(s):
Oualid Rholam, Mohammed Barmaki and Driss Gretet
National School of Applied Sciences (ENSA),
University Ibn Tofail,
B.P 242 Kenitra 14000,
phone number : +212606257757,
Morocco.
E-mail: oualid.rholam@uit.ac.ma
Science Faculty Ben M'sik,
University Hassan II,
B.P 7955 Av Driss El Harti Sidi Othmane 20700,
phone number : +212 5 22 70 46 71 ,
Morocco.
E-mail: mohammed.barmaki@uit.ac.ma
National School of Applied Sciences (ENSA),
University Ibn Tofail,
B.P 242 Kenitra 14000,
phone number : +212661403557,
Morocco.
E-mail: driss.gretete@uit.ac.ma
Abstract:
In this paper we consider the class of P-convex and Quasi-convex stochastic processes on witch we apply a general class of generalized fractional integral operator in order to establish new integral inequalities of Hermite-Hadammard type. then we obtain some results for well known types of fractional integrals. Results obtained in this paper may be starting point as well as a useful source of inspiration for further research in convex analysis.
Paper's Title:
Fuzzy Ideal Congruences of ADL's
Author(s):
G. Prakasam Babu, K. Ramanuja Rao, G. Srikanya and Ch. Santhi Sundar Raj
1,4Department of Engineering
Mathematics,
Andhra University,
Visakhapatnam-A.P,
India.
E-mail: prakash.g368@gmail.com,
santhisundarraj@yahoo.com
2Department of Mathematics,
Solomon Islands National University,
Panatina Campus, Honiara,
Solomon Islands.
E-mail: ramanuja.kotti@sinu.edu.sb
3Department of Mathematics,
Raghu Engineering College (A),
Visakhapatnam-A.P.,
India.
E-mail:
srikanya.gonnabhaktula@raghuenggcollege.in
Abstract:
The concept of fuzzy congruence of an ADL is introduced. Established a correspondence between fuzzy ideals and fuzzy congruences of an ADL and obtained an equivalent condition for an ADL with a maximal element is a Boolean algebra.
Paper's Title:
Integrability of Sine and Cosine Series Having Coefficients of a New Class
Author(s):
L. Leindler Bolyai Institute,
University of Szeged, Aradi Vértanúk Tere 1, H-6720 Szeged, Hungary
leindler@math.u-szeged.hu
Abstract:
Some integrability theorems or only their sufficient part are
generalized such that the coefficients of the sine and cosine series belong to a
new class of sequences being wider than the class of sequences of rest bounded
variation, which itself is a generalization of the monotone decreasing
sequences, but a subclass of the almost monotone decreasing sequences. It is
also verified that the new class of sequences and the class of almost monotone
decreasing sequences are not comparable.
Paper's Title:
An Algorithm to Compute Gaussian-Type Quadrature Formulae
that Integrate Polynomials and Some Spline Functions Exactly
Author(s):
Allal Guessab
Laboratoire de Mathématiques Appliquées,
Université de Pau, 64000, Pau,
France.
allal.guessab@univ-pau.fr
URL: http://www.univ-pau.fr/~aguessab/
Abstract:
It is well-known that for sufficiently smooth integrands on an interval, numerical integration can be performed stably and efficiently via the classical (polynomial) Gauss quadrature formulae. However, for many other sets of integrands these quadrature formulae do not perform well. A very natural way of avoiding this problem is to include a wide class among arbitrary functions (not necessary polynomials) to be integrated exactly. The spline functions are natural candidates for such problems. In this paper, after studying Gaussian type quadrature formulae which are exact for spline functions and which contain boundary terms involving derivatives at both end points, we present a fast algorithm for computing their nodes and weights. It is also shown, taking advantage of the close connection with ordinary Gauss quadrature formula, that the latter are computed, via eigenvalues and eigenvectors of real symmetric tridiagonal matrices. Hence a new class of quadrature formulae can then be computed directly by standard software for ordinary Gauss quadrature formula. Comparative results with classical Gauss quadrature formulae are given to illustrate the numerical performance of the approach.
Paper's Title:
Positive Solutions of Evolution Operator Equations
Author(s):
Radu Precup
Department of Applied Mathematics,
Babes-Bolyai University,
Cluj, Romania
Abstract:
Existence and localization results are derived from Krasnoselskii’s compressionexpansion
fixed point theorem in cones, for operator equations in spaces of continuous functions
from a compact real interval to an abstract space. The main idea, first used in [12], is to handle
two equivalent operator forms of the equation, one of fixed point type giving the operator to
which Krasnoselskii’s theorem applies and an other one of coincidence type which is used to
localize a positive solution in a shell. An application is presented for a boundary value problem
associated to a fourth order partial differential equation on a rectangular domain.
Paper's Title:
Ellipses of Maximal Area and of Minimal Eccentricity Inscribed in a Convex Quadrilateral
Author(s):
Alan Horwitz
Penn State University,
25 Yearsley Mill Rd., Media, Pa 19063
alh4@psu.edu
Url: www.math.psu.edu/horwitz
Abstract:
Let Ð be a convex quadrilateral in the plane and let M1 and M2 be the midpoints
of the diagonals of Ð. It is well–known that if E is an ellipse inscribed in Ð, then the center of
E must lie on Z, the open line segment connecting M1 and M2 . We use a theorem of Marden
relating the foci of an ellipse tangent to the lines thru the sides of a triangle and the zeros of a
partial fraction expansion to prove the converse: If P lies on Z, then there is a unique ellipse with
center P inscribed in Ð. This completely characterizes the locus of centers of ellipses inscribed
in Ð. We also show that there is a unique ellipse of maximal area inscribed in Ð. Finally, we
prove our most signifigant results: There is a unique ellipse of minimal eccentricity inscribed in
Ð.
Paper's Title:
Some Approximation for the linear combinations of modified Beta operators
Author(s):
Naokant Deo
Department of Applied Mathematics
Delhi College of Engineering
Bawana Road, Delhi - 110042,
India.
dr_naokant_deo@yahoo.com
Abstract:
In this paper, we propose a sequence of new positive linear operators βn to study the ordinary approximation of unbounded functions by using some properties of the Steklov means.
Paper's Title:
On the Optimal Buckling Loads of Clamped Columns
Author(s):
Samir Karaa
Department of Mathematics and Statistics
Sultan Qaboos University, P.O. Box 36, Alkhod 123
Muscat, Sultanate of Oman
skaraa@squ.edu.om
URL: http://ajmaa.org/EditorsU/SKaraa.php
Abstract:
We consider the problem of determining the optimal shape of a clamped column of given length and volume, without minimum cross section constraints.
We prove that the necessary condition of optimality derived by
Olhoff
and Rasmussen is sufficient when 0<
Paper's Title:
Note on the Rank of Birkhoff Interpolation
Author(s):
J. Rubió-Massegú
Applied Mathematics III, Universitat Politècnica de Catalunya,
Colom 1, 08222, Terrassa,
Spain
josep.rubio@upc.edu
Abstract:
The relationship between a variant of the rank of a univariate
Birkhoff interpolation problem, called normal rank, and other
numbers of interest associated to the interpolation problem is
studied.
Paper's Title:
Coincidences and Fixed Points of Hybrid Maps in Symmetric Spaces
Author(s):
S. L. Singh and Bhagwati Prasad
Vedic MRI, 21 Govind Nagar,
Department of Mathematics, Gurukula Kangri University,
Rishikesh 249201
India
vedicmri@gmail.com
Hardwar 249404,
India
Abstract:
The purpose of this paper is to obtain a new coincidence theorem for a
single-valued and two multivalued operators in symmetric spaces. We derive
fixed point theorems and discuss some special cases and applications.
Paper's Title:
Generalizations of Hermite-Hadamard's Inequalities for Log-Convex Functions
Author(s):
Ai-Jun Li
School of Mathematics and Informatics,
Henan Polytechnic University,
Jiaozuo City, Henan Province,
454010, China.
liaijun72@163.com
Abstract:
In this article, Hermite-Hadamard's inequalities are extended in
terms of the weighted power mean and log-convex
function. Several refinements, generalizations and related
inequalities are obtained.
Paper's Title:
Existence of Bounded Solutions for a Class of
Strongly Nonlinear Elliptic Equations in Orlicz-Sobolev Spaces
Author(s):
Abdelmoujib Benkirane and Ahmed Youssfi
Department of Mathematics and Informatics, Faculty of Sciences
Dhar El Mahraz
University Sidi Mohammed Ben Abdallah
PB 1796 Fez-Atlas, Fez
Morocco
a.benkirane@menara.ma
ahmed.youssfi@caramail.com
Abstract:
We prove, in the setting of Orlicz-Sobolev spaces, the existence of
bounded solutions for some strongly nonlinear elliptic equations
with operator of the principal part having degenerate coercivity and
lower order terms not satisfying the sign condition. The data have a
suitable summability and no Δ2-condition is needed for the
considered N-functions.
Paper's Title:
Differentiability of
Distance Functions in p-Normed Spaces
Author(s):
M. S. Moslehian, A. Niknam, S. Shadkam Torbati
Department of Pure Mathematics,
Centre of Excellence in Analysis on Algebraic Structures (CEAAS),,
Ferdowsi University of Mashhad,
P. O. Box
1159, Mashhad,
Iran
moslehian@ferdowsi.um.ac.ir
niknam@math.um.ac.ir
shadkam.s@wali.um.ac.ir
Abstract:
The farthest point mapping in a p-normed space X is studied in virtue of the Gateaux derivative and the Frechet derivative. Let M be a closed bounded subset of X having the uniformly p-Gateaux differentiable norm. Under certain conditions, it is shown that every maximizing sequence is convergent, moreover, if M is a uniquely remotal set then the farthest point mapping is continuous and so M is singleton. In addition, a Hahn--Banach type theorem in $p$-normed spaces is proved.
Paper's Title:
Stability of Almost Multiplicative Functionals
Author(s):
Norio Niwa, Hirokazu Oka, Takeshi Miura and Sin-Ei Takahasi
Faculty of Engineering, Osaka Electro-Communication University,
Neyagawa 572-8530,
Japan
Faculty of Engineering, Ibaraki University,
Hitachi 316-8511,
Japan
Department of Applied Mathematics and Physics, Graduate School of
Science and Engineering,
Yamagata University,
Yonezawa 992-8510
Japan
oka@mx.ibaraki.ac.jp
miura@yz.yamagata-u.ac.jp
sin-ei@emperor.yz.yamagata-u.ac.jp
Abstract:
Let
δ
and p be non-negative real numbers. Let
![]() be the
real or complex number field and
be the
real or complex number field and
![]() a normed algebra
over
a normed algebra
over ![]() . If a mapping
. If a mapping
![]() satisfies
satisfies
![]()
then we show that
φ
is multiplicative or
![]() for all
for all ![]() If, in
addition,
φ
satisfies
If, in
addition,
φ
satisfies
![]()
for some p≠1, then by using Hyers-Ulam-Rassias
stability of additive Cauchy equation, we show that
φ
is a ring homomorphism or
![]() for all
for all
![]() In other words,
φ
is a ring homomorphism, or an approximately zero
mapping. The results of this paper are inspired by Th.M. Rassias' stability
theorem.
In other words,
φ
is a ring homomorphism, or an approximately zero
mapping. The results of this paper are inspired by Th.M. Rassias' stability
theorem.
Paper's Title:
On Some
Mapping Properties of M
Author(s):
Nihal Yilmaz Özgür
Balkesir University,
Faculty of Arts and Sciences, Department of Mathematics,
10145 Balkesir,
TURKEY
nihal@balikesir.edu.tr
URL: http://w3.balikesir.edu.tr/~nihal/
Abstract:
We consider spheres corresponding to any norm function on the complex plane and their images under the Möbius transformations. We see that the sphere preserving property is not an invariant characteristic property of Möbius transformations except in the Euclidean case.
Paper's Title:
Hyperbolic Barycentric Coordinates
Author(s):
Abraham A. Ungar
Department of Mathematics, North Dakota State University,
Fargo, ND 58105,
USA
Abraham.Ungar@ndsu.edu
URL: http://math.ndsu.nodak.edu/faculty/ungar/
Abstract:
A powerful and novel way to study Einstein's special theory of relativity and its underlying geometry, the hyperbolic geometry of Bolyai and Lobachevsky, by analogies with classical mechanics and its underlying Euclidean geometry is demonstrated. The demonstration sets the stage for the extension of the notion of barycentric coordinates in Euclidean geometry, first conceived by Möbius in 1827, into hyperbolic geometry. As an example for the application of hyperbolic barycentric coordinates, the hyperbolic midpoint of any hyperbolic segment, and the centroid and orthocenter of any hyperbolic triangle are determined.
Paper's Title:
On the product of M-measures in l-groups
Author(s):
A. Boccuto, B. Riěcan, and A. R. Sambucini
Dipartimento di Matematica e Informatica,
via Vanvitelli, 1 I-06123 Perugia,
Italy.
boccuto@dipmat.unipg.it
URL:
http://www.dipmat.unipg.it/~boccuto
Katedra Matematiky, Fakulta Prírodných Vied,
Univerzita Mateja Bela,
Tajovského, 40, Sk-97401 Banská Bystrica,
Slovakia.
riecan@fpv.umb.sk
Dipartimento di Matematica e Informatica,
via Vanvitelli, 1 I-06123 Perugia,
Italy.
matears1@unipg.it
URL:
http://www.unipg.it/~matears1
Abstract:
Some extension-type theorems and compactness
properties for the
product of l-group-valued M-measures are proved.
Paper's Title:
The Riemann-Stieltjes Integral on Time Scales
Author(s):
D. Mozyrska, E. Pawłuszewicz, D. Torres
Faculty Of Computer Science,
Białystok University Of Technology,
15-351 Białystok,
Poland
d.mozyrska@pb.edu.pl
Department Of Mathematics,
University Of Aveiro,
3810-193 Aveiro,
Portugal
ewa@ua.pt
Department Of Mathematics,
University Of Aveiro,
3810-193 Aveiro,
Portugal
delfim@ua.pt
Abstract:
We study the process of integration on time scales in the sense of Riemann-Stieltjes. Analogues of the classical properties are proved for a generic time scale, and examples are given
Paper's Title:
Approximation of Derivatives in a Singularly Perturbed Second Order Ordinary Differential Equation with Discontinuous Terms Arising in Chemical Reactor Theory
Author(s):
R. Mythili Priyadharshini and N. Ramanujam
Department of Mathematics, Bharathidasan University,
Tiruchirappalli - 620 024, Tamilnadu, India.
matram2k3@yahoo.com
URL:
http://www.bdu.ac.in/depa/science/ramanujam.htm
Abstract:
In this paper, a singularly perturbed second order ordinary differential equation with a discontinuous convection coefficient arising in chemical reactor theory is considered. A robust-layer-resolving numerical method is suggested. An ε-uniform global error estimate for the numerical solution and also to the numerical derivative are established. Numerical results are provided to illustrate the theoretical results.
Paper's Title:
Uniqueness of Meromorphic Functions and
Weighted Sharing
Author(s):
Indrajit Lahiri and Rupa Pal
Department of Mathematics, University of
Kalyani, West Bengal 741235, India
indr9431@dataone.in
Jhargram Raj College,
Jhargram, Midnapur(W),
West Bengal 721507,
India
rupa.a.pal@gmail.com
Abstract:
With the help of the notion of weighted sharing of values, we prove a result on uniqueness of meromorphic functions and as a consequence we improve a result of P. Li
Paper's Title:
Two Remarks on Commutators of Hardy Operator
Author(s):
Yasuo Komori-Furuya
School of High Technology for Human Welfare
Tokai University
317 Nishino Numazu, Shizuoka 410-0395 Japan
komori@wing.ncc.u-tokai.ac.jp
Abstract:
Fu and Lu showed that
the commutator of multiplication operator by b and
the n-dimensional Hardy operator
is bounded on Lp if b is in some CMO space.
We shall prove the converse of this theorem
and also prove that their result is optimal by giving a counterexample
Paper's Title:
On an Elliptic Over-Determined Problem in Dimension Two
Author(s):
Lakhdar Ragoub
Department of Mathematics and Information of Tiyadhechnology
AL Yamamah University
P.O. Box 45 180, Riyadh 11 512
Saudi Arabia.
Abstract:
We extend the method of Weinberger for a
non-linear over-determined elliptic problem
in R2.
We prove that the domain in consideration is a ball. The
tool of this investigation are maximum principles and P-functions.
Paper's Title:
Uniform Convergence of Schwarz Method for Noncoercive Variational Inequalities Simple Proof
Author(s):
M. Haiour and E. Hadidi.
Department of mathematics, LANOS Laboratory,
Faculty of the Sciences, University Badji Mokhtar,
P.O 23000 Annaba,
Algeria.
haiourm@yahoo.fr,
ehadidi71@yahoo.fr
Abstract:
In this paper we study noncoercive variational inequalities, using the Schwarz method. The main idea of this method consists in decomposing the domain in two subdomains. We give a simple proof for the main result concerning L∞ error estimates, using the Zhou geometrical convergence and the L∞ approximation given for finite element methods by Courty-Dumont.
Paper's Title:
Sharp Lp Improving Results for Singular Measures on Cn+1
Author(s):
E. Ferreyra, M. Urciuolo
FaMAF-CIEM,
Universidad Nacional de Córdoba-Conicet,
Ciudad Universitaria, 5000 Córdoba,
Argentina
eferrey@famaf.unc.edu.ar
urciuolo@famaf.unc.edu.ar
Abstract:
For j=1,...,n, let Ωj be open sets of the complex plane and let φj be holomorphic functions on Ωj such that φj'' does not vanish identically on Ωj. We consider φ(z1,...,zn) =φ1(z1) +...+φn(zn). We characterize the pairs (p,q) such that the convolution operator with the surface measure supported on a compact subset of the graph of φ is p-q bounded.
Paper's Title:
Para-chaotic Tuples of Operators
Author(s):
Bahmann Yousefi and Javad Izadi
Department of Mathematics,
Payame Noor University,
P.O. Box 19395-3697, Tehran,
Iran
b_yousefi@pnu.ac.ir
javadie2003@yahoo.com
Abstract:
In this paper, we introduce para-chaotic tuples of operators and we give some relations between para-chaoticity and Hypercyclicity Criterion for a tuple of operators.
Paper's Title:
Multilinear Fractional Integral Operators on Herz Spaces
Author(s):
Yasuo Komori-Furuya
School of High Technology and Human Welfare,
Tokai University,
317 Nishino Numazu Shizuoka, 410-0395
Japan
Abstract:
We prove the boundedness of the multilinear fractional integral operators of Kenig and Stein type on Herz spaces. We also show that our results are optimal.
Paper's Title:
Schwarz Method
for Variational Inequalities Related to Ergodic Control Problems
Author(s):
S. Saadi, H. Mécheri
Department of Mathematics, Badji Mokhtar
University, Annaba 23000,
P.O.Box. 12, Annaba 23000, Algeria
Abstract:
In this paper, we study variational inequalities related to ergodic control problems studied by M. Boulbrachène and H. Sissaoui [11], where the "discount factor" (i.e., the zero order term) is set to 0, we use an overlapping Schwarz method on nomatching grid which consists in decomposing the domain in two subdomains. For α ∈ ]0.1[ we provide the discretization on each subdomain converges in L∞ -norm.
Paper's Title:
An Improvement of the Hermite-Hadamard Inequality for Functions Convex on the Coordinates
Author(s):
Milica Klaričić Bakula
Faculty of Science,
University of Split,
Teslina 12, 21000 Split.
Croatia
E-mail: milica@pmfst.hr
Abstract:
An improvement of the Hermite-Hadamard inequality for functions convex on the coordinates is given.
Paper's Title:
L∞- Error Estimate of Schwarz Algorithm for Elliptic Quasi-Variational Inequalities Related to Impulse Control Problem
Author(s):
Saadi Samira and Mehri Allaoua
Lab. LANOS, Department of Mathematics,
University Badji Mokhtar Annaba,
P.O.Box 12, Annaba 23000,
Algeria.
Lab. LAIG, Department of Mathematics,
University May 8th 1945,
P.O.Box 401, Guelma 24000,
Algeria.
E-mail:
saadisamira69@yahoo.fr
allmehri@yahoo.fr
Abstract:
In this work, we study Schwarz method for a class of elliptic quasi-variational inequalities. The principal result of this investigation is to prove the error estimate in ∞-norm for two domains with overlapping nonmatching grids, using the geometrical convergence, and the uniform convergence of Cortey Dumont.
Paper's Title:
New Stochastic Calculus
Author(s):
Moawia Alghalith
Department of Economics,
University of the West Indies, St. Augustine,
Trinidad and Tobago.
E-mail:
malghalith@gmail.com
Abstract:
We present new stochastic differential equations, that are more general and simpler than the existing Ito-based stochastic differential equations. As an example, we apply our approach to the investment (portfolio) model.
Paper's Title:
Optimization and Approximation for Polyhedra in Separable Hilbert Spaces
Author(s):
Paolo d'Alessandro
Department of Mathematics,
Third University of Rome,
Italy.
E-mail: pdalex45@gmail.com
Abstract:
This paper studies infinite dimensional polyhedra, covering the case in which range spaces of operators defining inequality systems are not closed. A rangespace method of linear programming is generalized to infinite dimensions and finite dimensional methods of approximation are introduced.
Paper's Title:
Ostrowski Type Fractional Integral Inequalities for Generalized (s,m,
Author(s):
Artion Kashuri and Rozana Liko
University of Vlora "Ismail Qemali",
Faculty of Technical Science,
Department of Mathematics, 9400,
Albania.
E-mail:
artionkashuri@gmail.com
E-mail: rozanaliko86@gmail.com
Abstract:
In the present paper, the notion of generalized (s,m,φ)-preinvex function is introduced and some new integral inequalities for the left hand side of Gauss-Jacobi type quadrature formula involving generalized (s,m,φ)-preinvex functions along with beta function are given. Moreover, some generalizations of Ostrowski type inequalities for generalized (s,m,φ)-preinvex functions via Riemann-Liouville fractional integrals are established.
Paper's Title:
On The Rayleigh-Love Rod Accreting In Both Length And
Cross-Sectional Area: Forced And Damped Vibrations
Author(s):
M.L.G. Lekalakala1, M. Shatalov2, I. Fedotov3, S.V. Joubert4
1Department
of Mathematics, Vaal University of Technology, P.O. Box 1889, Secunda, 2302,
South Africa.
E-mail1:
glen@vut.ac.za
2,3,4Department of Mathematics and Statistics, Tshwane University of Technology, Pretoria, South Africa.
Abstract:
In this paper an elastic cylindrical rod that is subjected to forced and damped vibrations is considered. The rod is assumed to be isotropic. The applied external force of excitation is assumed to be harmonic, and the damping force is that of Kelvin-Voigt. The longitudinally vibrating rod is fixed at the left end and free at the other end. The rod is assumed to be accreting in length and cross-sectional area as it vibrates. The problem arising and the dynamics of the vibrating rod are described and investigated within the Rayleigh-Love theories of the rod. A partial differential equation describing the longitudinal displacement of the rod is formulated. The formulated partial differential equation, together with the corresponding boundary conditions as per the configuration of the rod, is solved numerically using the Galerkin-Kantorovich method. The frequency of vibration of the harmonic exciting force is kept constant in this investigation.
It is shown that in this periodically forced viscoelastic damped vibration, all the modes of vibration are subjected to the resonance behaviour within a proper time interval, depending on the length of the accreting rod.
Paper's Title:
Birkhoff-James orthogonality and Best Approximant in L1(X)
Author(s):
Mecheri Hacene and Rebiai Belgacem
Department of Mathematics and
Informatics,
LAMIS laboratory, University of Tebessa,
Algeria.
E-mail: mecherih2000@yahoo.fr
Department of Mathematics and
Informatics,
LAMIS laboratory, University of Tebessa,
Algeria.
E-mail: brebiai@gmail.com
Abstract:
Let X be a complex Banach space and let (X,ρ) be a positive measure space. The Birkhoff-James orthogonality is a generalization of Hilbert space orthogonality to Banach spaces. We use this notion of orthogonality to establish a new characterization of Birkhoff-James orthogonality of bounded linear operators in L1(X,ρ) also implies best approximation has been proved.
Paper's Title:
Some Convergence Results for Jungck-Am Iterative Process In Hyperbolic Spaces
Author(s):
Akindele Adebayo Mebawondu and Oluwatosin Temitope Mewomo
School of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail:
216028272@stu.ukzn.ac.za,
mewomoo@ukzn.ac.za
Abstract:
In this paper, we introduce a new three steps iterative process called Jungck-AM iterative process and show that the proposed iterative process can be used to approximate fixed points of Jungck-contractive type mappings and Jungck-Suzuki type mappings. In addition, we establish some strong and Δ-convergence results for the approximation of fixed points of Jungck-Suzuki type mappings in the frame work of uniformly convex hyperbolic space. Furthermore, we show that the newly proposed iterative process has a better rate of convergence compare to the Jungck-Noor, Jungck-SP, Jungck-CR and some existing iterative processes in the literature. Finally, stability, data dependency results for Jungck-AM iterative process is established and we present an analytical proof and numerical examples to validate our claim.
Paper's Title:
Action of Differential Operators On Chirpsconstruct On L∞
Author(s):
Taoufik El Bouayachi and Naji Yebari
Laboratoire de Mathematiques et
applications,
Faculty of sciences and techniques, Tangier,
Morocco.
E-mail:
figo407@gmail.com,
yebarinaji@gmail.com
Abstract:
We will study in this work the action of differential operators on L∞ chirps and we will give a new definition of logarithmic chirp. Finally we will study the action of singular integral operators on chirps by wavelet characterization and Kernel method.
Paper's Title:
A new approach to the study of fixed point for simulation functions with application in G-metric spaces
Author(s):
Komi Afassinou and Ojen Kumar Narain
Department of Mathematical Sciences,
University of Zululand,
KwaDlangezwa,
South Africa.
E-mail: komia@aims.ac.za
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
The purpose of this work is to generalize the fixed point results of Kumar et al. [11] by introducing the concept of (α,β)-Z-contraction mapping, Suzuki generalized (α,β)-Z-contraction mapping, (α,β)-admissible mapping and triangular (α,β)-admissible mapping in the frame work of G-metric spaces. Fixed point theorems for these class of mappings are established in the frame work of a complete G-metric spaces and we establish a generalization of the fixed point result of Kumar et al. [11] and a host of others in the literature. Finally, we apply our fixed point result to solve an integral equation.
Paper's Title:
Applications of Von Neumann Algebras to Rigidity Problems of (2-Step) Riemannian (Nil-)Manifolds
Author(s):
Atefeh Hasan-Zadeh and Hamid-Reza Fanai
DFouman Faculty of Engineering,
College of Engineering, University of Tehran,
Iran.
E-mail: hasanzadeh.a@ut.ac.ir
Department of Mathematical Sciences,
Sharif University of Technology,
Iran
E-mail: fanai@sharif.edu
Abstract:
In this paper, basic notions of von Neumann algebra and its direct analogues in the realm of groupoids and measure spaces have been considered. By recovering the action of a locally compact Lie group from a crossed product of a von Neumann algebra, other proof of one of a geometric propositions of O'Neil and an extension of it has been proposed. Also, using the advanced exploration of nilmanifolds in measure spaces and their corresponding automorphisms (Lie algebraic derivations) a different proof of an analytic theorem of Gordon and Mao has been attained. These two propositions are of the most important ones for rigidity problems of Riemannian manifolds especially 2-step nilmanifolds.
Paper's Title:
Composite Variational-Like Inequalities Given By Weakly Relaxed
Author(s):
Syed Shakaib Irfan, Iqbal Ahmad, Zubair Khan and Preeti Shukla
College of Engineering, Qassim University
Buraidah, Al-Qassim,
Saudi Arabia.
E-mail: shakaib@qec.edu.sa
College of Engineering, Qassim University
Buraidah, Al-Qassim,
Saudi Arabia.
E-mail: iqbal@qec.edu.sa
Department of Mathematics,
Integral University Lucknow,
India.
E-mail: zkhan@iul.ac.in
Department of Mathematics,
Integral University Lucknow,
India.
E-mail: shuklapreeti1991@gmail.com
Abstract:
In this article, we introduce a composite variational-like inequalities with weakly relaxed ζ-pseudomonotone multi-valued maping in reflexive Banach spaces. We obtain existence of solutions to the composite variational-like inequalities with weakly relaxed ζ-pseudomon -otone multi-valued maps in reflexive Banach spaces by using KKM theorem. We have also checked the solvability of the composite variational-like inequalities with weakly relaxed ζ-semi-pseudomonotone multi-valued maps in arbitrary Banach spaces using Kakutani-Fan-Glicksberg fixed point theorem.
Paper's Title:
A Self-adaptive Subgradient Extragradient Algorithm for Variational Inequality Problems and Fixed Point Problems in Banach Spaces
Author(s):
F. U. Ogbuisi
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
Department of Mathematics,
University of Nigeria, Nsukka,
Nigeria.
E-mail: ferdinard.ogbuisi@unn.edu.ng
fudochukwu@yahoo.com
Abstract:
In this paper, we propose and analyze a type of subgradient extragradient algorithm for the approximation of a solution of variational inequality problem which is also a common fixed point of an infinite family of relatively nonexpansive mappings in 2-uniformly convex Banach spaces which are uniformly smooth. By using the generalized projection operator, we prove a strong convergence theorem which does not require the prior knowledge of the Lipschitz constant of cost operator. We further applied our result to constrained convex minimization problem, convex feasibility problem and infinite family of equilibrium problems. Our results improve and complement related results in 2-uniformly convex and uniformly smooth Banach spaces and Hilbert spaces.
Paper's Title:
ψ(m,q)-Isometric Mappings on Metric Spaces
Author(s):
Sid Ahmed Ould Beinane, Sidi Hamidou Jah and Sid Ahmed Ould Ahmed Mahmoud
Mathematical Analysis and Applications,
Mathematics Department, College of Science,
Jouf University,
Sakaka P.O.Box 2014,
Saudi Arabia.
E-mail: beinane06@gmail.com
Department of Mathematics, College of
Science Qassim University,
P.O. Box 6640, Buraydah 51452,
Saudi Arabia.
E-mail: jahsiidi@yahoo.fr
Mathematical Analysis and Applications,
Mathematics Department, College of Science, Jouf University,
Sakaka P.O.Box 2014,
Saudi Arabia.
E-mail: sidahmed@ju.edu.sa,
sidahmed.sidha@gmail.com
Abstract:
The concept of (m,p)-isometric operators on Banach space was extended to
(m,q)-isometric mappings on general metric spaces in [6].
This paper is devoted to define the concept of
ψ(m, q)-isometric, which is the
extension of A(m, p)-isometric operators on Banach spaces introduced in [10].
Let T,ψ: (E,d) -> (E, d) be two mappings.
For some positive integer m and q ∈ (0,∞).
T is said to be an ψ(m,q)-isometry,
if for all y,z ∈ E,

Paper's Title:
Existence and Approximation of Traveling Wavefronts for the Diffusive Mackey-Glass Equation
Author(s):
C. Ramirez-Carrasco and J. Molina-Garay
Facultad de Ciencias Basicas,
Universidad Catolica del Maule, Talca,
Chile
E-mail: carloshrc1989@gmail.com
molina@imca.edu.pe
Abstract:
In this paper, we consider the diffusive Mackey-Glass model with discrete delay. This equation describes the dynamics of the blood cell production. We investigate the existence of traveling wavefronts solutions connecting the two steady states of the model. We develop an alternative proof of the existence of such solutions and we also demonstrate the existence of traveling wavefronts moving at minimum speed. The proposed approach is based on the use technique of upper-lower solutions. Finally, through an iterative procedure, we show numerical simulations that approximate the traveling wavefronts, thus confirming our theoretical results.
Paper's Title:
Pointwise Convergence of Fourier-type Series with Exponential Weights
Author(s):
Hee Sun Jung and Ryozi Sakai
Department of Mathematics Education,
Sungkyunkwan University,
Seoul 110-745,
Republic of Korea.
E-mail: hsun90@skku.edu
Department of Mathematics,
Meijo University, Nagoya 468-8502,
Japan.
E-mail: ryozi@hm.aitai.ne.jp
Abstract:
Let R = ( - ∞,∞), and let Q∈C1(R):R→[0,∞) be an even function. We consider the exponential weights w(x)=e-Q(x), x∈R. In this paper we obtain a pointwise convergence theorem for the Fourier-type series with respect to the orthonormal polynomials {pn(w2;x)}.
Paper's Title:
Algorithms for Nonlinear Problems Involving Strictly Pseudocontractive Mappings
Author(s):
Mathew Olajiire Aibinu1, Surendra Colin Thakur2, Sibusiso Moyo3
1Institute for Systems Science
& KZN E-Skill CoLab,
Durban University of Technology,
Durban 4000,
South Africa.
1DSI-NRF
Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: moaibinu@yahoo.com
mathewa@dut.ac.za
2 KZN E-Skill CoLab,
Durban University of Technology,
Durban 4000,
South Africa.
E-mail: thakur@dut.ac.za
3Institute for Systems Science & Office of the DVC Research,
Innovation & Engagement Milena Court,
Durban University of Technology,
Durban 4000,
South Africa.
E-mail: dvcrie@dut.ac.za
Abstract:
The puzzles in approximating a fixed point of nonlinear problems involving the class of strictly pseudocontractive mappings are conquered in this paper through viscosity implicit rules. Using generalized contraction mappings, a new viscosity iterative algorithm which is implicit in nature is proposed and analysed in Banach spaces for the class of strictly pseudocontractive mappings. The computations and analysis which are used in the proposed scheme are easy to follow and this gives rooms for a broad application of the scheme. It is obtained that the proposed iterative algorithm converges strongly to a fixed point of a μ-strictly pseudocontractive mapping which also solves a variational inequality problem. The result is also shown to hold for finite family of strictly pseudocontractive mappings. A numerical example is given to show the skillfulness of the proposed scheme and its implementation.
Paper's Title:
An Integration Technique for Evaluating Quadratic Harmonic Sums
Author(s):
J. M. Campbell and K.-W. Chen
Department of Mathematics and Statistics,
York University, 4700 Keele St, Toronto,
ON M3J 1P3,
Canada.
E-mail: jmaxwellcampbell@gmail.com
Department of Mathematics, University of Taipei,
No. 1, Ai-Guo West Road,
Taipei 10048, Taiwan.
E-mail: kwchen@uTaipei.edu.tw
URL:
https://math.utaipei.edu.tw/p/412-1082-22.php
Abstract:
The modified Abel lemma on summation by parts has been applied in many ways recently to determine closed-form evaluations for infinite series involving generalized harmonic numbers with an upper parameter of two. We build upon such results using an integration technique that we apply to ``convert'' a given evaluation for such a series into an evaluation for a corresponding series involving squared harmonic numbers.
Paper's Title:
Trace Inequalities for Operators in Hilbert Spaces: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
School of Engineering
& Science
Victoria University,
PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
In this paper we survey some recent trace inequalities for operators in Hilbert spaces that are connected to Schwarz's, Buzano's and Kato's inequalities and the reverses of Schwarz inequality known in the literature as Cassels' inequality and Shisha-Mond's inequality. Applications for some functionals that are naturally associated to some of these inequalities and for functions of operators defined by power series are given. Further, various trace inequalities for convex functions are presented including refinements of Jensen inequality and several reverses of Jensen's inequality. Hermite-Hadamard type inequalities and the trace version of Slater's inequality are given. Some Lipschitz type inequalities are also surveyed. Examples for fundamental functions such as the power, logarithmic, resolvent and exponential functions are provided as well.
Paper's Title:
Uniqueness Problems for Difference Polynomials Sharing a Non-Zero Polynomial of Certain Degree With Finite Weight
Author(s):
V. Priyanka, S. Rajeshwari and V. Husna
Department of Mathematics,
School of Engineering,
Presidency University,
Bangalore-560064,
India.
E-mail:
priyapriyankaram1994@gmail.com
rajeshwaripreetham@gmail.com
husnav43@gmail.com
Abstract:
In this paper, we prove a result on the value distribution of difference polynomials sharing higher order derivatives of meromorphic functions which improves some earlier results. At the same time, we also prove possible uniqueness relation of entire functions when the difference polynomial generated by them sharing a non zero polynomial of certain degree. The result obtained in the paper will improve and generalize a number of recent results in a compact and convenient way.
Paper's Title:
On the Oldest Problem in the Calculus of Variations: A New Message from Queen Dido
Author(s):
Olivier de La Grandville
Faculty of Economics,
Goethe University Frankfurt,
Theodore Adorno Platz 4, 60323 Frankfurt,
Germany.
E-mail: odelagrandville@gmail.com
Abstract:
We consider the problem of finding the optimal curve of given length linking two points in a plane such as it encloses a maximal area. We show that if the curve is not described by a single-valued function, its determination does not necessarily imply to work with a parametric representation of the curve. We show that a simpler approach is at hand -- and, who knows? -- this might well be the method Queen Dido used.
Paper's Title:
A Self Adaptive Method for Solving Split Bilevel Variational Inequalities Problem in Hilbert Spaces
Author(s):
Francis Akutsah1, Ojen Kumar Narain2, Funmilayo Abibat Kasali3 Olawale Kazeem Oyewole4 and Akindele Adebayo Mebawondu5
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 216040405@stu.ukzn.ac.za,
akutsah@gmail.com
2School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
3Mountain Top University,
Prayer City, Ogun State,
Nigeria.
E-mail: fkasali@mtu.edu.ng
4Technion-Israel
Institute of Technology.
E-mail: 217079141@stu.ukzn.ac.za,
oyewoleolawalekazeem@gmail.co
5School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
DST-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
Mountain Top University,
Prayer City, Ogun State,
Nigeria.
E-mail: dele@aims.ac.za
Abstract:
In this work, we study the split bilevel variational inequality problem in two real Hilbert spaces. We propose a new modified inertial projection and contraction method for solving the aforementioned problem when one of the operators is pseudomonotone and Lipschitz continuous while the other operator is α-strongly monotone. The use of the weakly sequential continuity condition on the Pseudomonotone operator is removed in this work. A Strong convergence theorem of the proposed method is proved under some mild conditions. In addition, some numerical experiments are presented to show the efficiency and implementation of our method in comparison with other methods in the literature in the framework of infinite dimensional Hilbert spaces. The results obtained in this paper extend, generalize and improve several.
Paper's Title:
Lozi Maps With Max Function and its Application
Author(s):
Abdellah Menasri
Higher National School of Forests,
Khenchela,
Algeria.
E-mail: abdellah.menasri70@gmail.com
Abstract:
In this paper, we study the Lozi map by replacing the piecewise linear term in the first equation by the function max (f(x,y);g(x,y)) such that f and g are two arbitrary functions in R2. This is a family model that allows us to study several new piecewise-smooth maps. We demonstrate that these models converge to a robust chaotic attractor and give some applications of these models in the real world.
Paper's Title:
Metric Functionals for the Hästö Metric
Author(s):
G. Bettencourt and S. Mendes
Departamento de Matemática,
Universidade da Beira Interior -
Covilhã Portugal,
Centro de Matemática e Aplicações
Universidade da Beira Interior -
Covilhã Portugal.
E-mail: gastao@ubi.pt
ISCTE - University Institute of Lisbon - Lisbon Portugal,
Centro de Matemática e Aplicações
Universidade da Beira Interior -
Covilhã Portugal.
E-mail: sergio.mendes@iscte-iul.pt
Abstract:
In 2002, new classes of weighted metrics on Rn were introduced by Peter Hästö. In this article we compute the metric functionals for such classes of metrics.
Paper's Title:
Higher Order Accurate Compact Schemes for Time Dependent Linear and Nonlinear Convection-Diffusion Equations
Author(s):
S. Thomas, Gopika P.B. and S. K. Nadupuri
Department of Mathematics
National Institute of Technology Calicut
Kerala
673601
India.
E-mail:
sobinputhiyaveettil@gmail.com
pbgopika@gmail.com nsk@nitc.ac.in
Abstract:
The primary objective of this work is to study higher order compact finite difference schemes for finding the numerical solution of convection-diffusion equations which are widely used in engineering applications. The first part of this work is concerned with a higher order exponential scheme for solving unsteady one dimensional linear convection-diffusion equation. The scheme is set up with a fourth order compact exponential discretization for space and cubic $C^1$-spline collocation method for time. The scheme achieves fourth order accuracy in both temporal and spatial variables and is proved to be unconditionally stable. The second part explores the utility of a sixth order compact finite difference scheme in space and Huta's improved sixth order Runge-Kutta scheme in time combined to find the numerical solution of one dimensional nonlinear convection-diffusion equations. Numerical experiments are carried out with Burgers' equation to demonstrate the accuracy of the new scheme which is sixth order in both space and time. Also a sixth order in space predictor-corrector method is proposed. A comparative study is performed of the proposed schemes with existing predictor-corrector method. The investigation of computational order of convergence is presented.
Paper's Title:
Approximately Dual p-Approximate Schauder Frames
Author(s):
K. Mahesh Krishna and P. Sam Johnson
Stat-Math Unit, Indian Statistical
Institute, Bangalore Centre,
Karnataka 560 059
India.
Department of Mathematical and
Computational Sciences,
National Institute of Technology Karnataka (NITK),
Surathkal, Mangaluru 575 025,
India.
E-mail: kmaheshak@gmail.com
sam@nitk.edu.in
Abstract:
Approximately dual frame in Hilbert spaces was introduced by Christensen and Laugesen to overcome difficulties in constructing dual frames for a given Hilbert space frame. It becomes even more difficult in Banach spaces to construct duals. For this purpose, we introduce approximately dual frames for a class of approximate Schauder frames for Banach spaces and develop basic theory. Approximate dual for this subclass is completely characterized and its perturbation is also studied.
Paper's Title:
Geometrical Properties of Subclass of Analytic Function with Odd Degree
Author(s):
K. Sivagami Sundari and B. Srutha Keerthi
Divison of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology, Chennai Campus, Chennai - 600 127,
India.
E-mail: sivagamisundari.2298@gmail.com
Divison of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology, Chennai Campus, Chennai - 600 127,
India.
E-mail: keerthivitmaths@gmail.com
Abstract:
The objective of the paper is to study the geometrical
properties of the class B(λ, t).
For which we have proved that the radius
 is optimal ,(i.e)
the number
is optimal ,(i.e)
the number
 cannot be replaced by a larger one. Additionally, the graphs for various values of t and
λ are compared in order to study the sharpness of the coefficient bounds.
cannot be replaced by a larger one. Additionally, the graphs for various values of t and
λ are compared in order to study the sharpness of the coefficient bounds.
Paper's Title:
Differential Equations for Indicatrices, Spacelike and Timelike Curves
Author(s):
Sameer, Pradeep Kumar Pandey
Department of Mathematics,
Jaypee University of Information Technology,
Solan, Himachal Pradesh,
India.
E-mail: sksameer08@gmail.com,
pandeypkdelhi@gmail.com
Abstract:
Motivated by the recent work of Deshmukh et al. [20], in this paper we show that Tangent, Binormal, and Principal Normal indicatrices do not form non-trivial differential equations. Finally, we obtain the 4th-order differential equations for spacelike and timelike curves.
Paper's Title:
The Automatic Continuity of N-Homomorphisms in Certain *-Banach Algebras
Author(s):
M. Aboulekhlef, Y. Tidli
Laboratory of Applied Mathematics and
Information and Communication Technology
Polydisciplinary Faculty of Khouribga
University of Sultan Moulay Slimane
Morocco.
E-mail: aboulekhlef@gmail.com
y.tidli@gmail.com
Abstract:
In this study, we prove the automatic continuity of surjective n-homomorphism between complete p-normed algebras. We show also that if Α and Β are complete *-p-normed algebras, Β is *simple and ψ: Α → Β is a surjective n-homomorphism under certain conditions, then ψ is continuous.
Paper's Title:
On Infinite Unions and Intersections of Sets in a Metric Space
Author(s):
Spiros Konstantogiannis
Ronin Institute,
Montclair, New Jersey,
United States.
E-mail:
spiros.konstantogiannis@ronininstitute.org
URL:
https://www.researchgate.net/profile/Spiros-Konstantogiannis
Abstract:
The aim of this paper is to examine infinite unions and intersections of sets in a general metric space, with a view to explaining when an infinite intersection of open sets is an open set and when an infinite union of closed sets is a closed set.
Paper's Title:
Generalized Triangular and Symmetric Splitting Method for Steady State Probability Vector of Stochastic Matrices
Author(s):
B. Harika, D. Rajaiah, L. P. RajKumar, Malla Reddy Perati
Department of Mathematics,
Kakatiya University
E-mail: hbolledla@gmail.com
Department of Mathematics,
Kakatiya Institute of Technology and Science
E-mail: dr.mh@kitsw.ac.in
Department of Mathematics,
Kakatiya University
E-mail: ladalla@gmail.com
Department of Mathematics,
Kakatiya University
E-mail: mperati@yahoo.com
Abstract:
To find the steady state probability vector of homogenous linear system π Q=0 of stochastic rate matrix Q, generalized triangular and symmetric (GTS) splitting method is presented. Convergence analysis and choice of parameters are given when the regularized matrix A=QT+ε I of the regularized linear system Ax=b is positive definite. Analysis shows that the iterative solution of GTS method converges unconditionally to the unique solution of the regularized linear system. From the numerical results, it is clear that the solution of proposed method converges rapidly when compared to the existing methods.
Paper's Title:
Using an Euler Type Transform for Accelerating Convergence of Series
Author(s):
Nimete Sh. Berisha, Faton M. Berisha*, Murat Sadiku
Faculty of Economics, University of
Prishtina,
Agim Ramadani st., 10000 Pristina,
Kosovo.
E-mail: nimete.berisha@uni-pr.edu
URL:
https://staff.uni-pr.edu/profile/nimeteberisha
Faculty of Mathematics and Sciences,
University of Prishtina,
Mother Teresa st., 10000 Pristina,
Kosovo.
E-mail: faton.berisha@uni-pr.edu
URL:
https://staff.uni-pr.edu/profile/fatonberisha
Faculty of Business Administration,
South East European University,
Tetovo,
North Macedonia.
E-mail: m.sadiku@seeu.edu.mk
Abstract:
In the paper we give a property of an operator of generalised difference, defined earlier, linear on a set of sequences, and use it to establish Euler type transforms for alternating series. These transforms accelerate the convergence of series under the same conditions as the transforms of non-alternating series. We also give analysis of an algorithm for computing a partial sum of the transformed series by using a higher order operator of generalised difference, and prove a theorem stating its order of complexity.
Paper's Title:
Automatic Continuity of Generalized Derivations in Certain *-Banach Algebras
Author(s):
M. Aboulekhlef, Y. Tidli and M. Belam
Laboratory of Applied Mathematics and
Information and Communication Technology Polydisciplinary
Faculty of Khouribga University of Sultan Moulay Slimane
Morocco.
E-mail:
aboulekhlef@gmail.com
y.tidli@gmail.com
m.belam@gmail.com
Abstract:
Consider the map φ of the Banach algebra Β in Β, if there exists a derivation δ of Β in Β so that for every x, y ∈ Β , φ(xy) =φ(x)y+xδ(y) . φ is called a generalized derivation of Β. In [9], Bresar introduced the concept of generalized derivations. We prove several results about the automatic continuity of generalized derivations on certain Banach algebras.
Paper's Title:
Global Implicit Function Theorems and Critical Point Theory in Frechet Spaces
Author(s):
Kaveh Eftekharinasab
Algebra and Topology Department,
Institute of Mathematics of National Academy of Sciences of Ukraine
Tereshchenkivska st., 01024, Kyiv,
Ukraine.
E-mail: kaveh@imath.kiev.ua
URL:
https://www.imath.kiev.ua/people/profile.php?pid=485\&lang=en
Abstract:
We prove two versions of a global implicit function theorem, which involve no loss of derivative, for Keller's Cc1 -mappings between arbitrary Fréchet spaces. Subsequently, within this framework, we apply these theorems to establish the global existence and uniqueness of solutions to initial value problems that involve the loss of one derivative. Moreover, we prove a Lagrange multiplier theorem by employing indirect applications of the global implicit function theorems through submersions and transversality.
Paper's Title:
Fixed Point Results for Integral Type Contractions in R-Metric Space
Author(s):
Samriddhi Ghosh, Ramakant Bhardwaj, Ritu Shrivastava, Vandana Rathore, Satyendra Narayan
Department of Mathematics,
Amity University, Kolkata, West Bengal,
India.
E-mail: ritha98@gmail.com
Department of Mathematics,
Amity University, Kolkata, West Bengal,
India.
E-mail: drrkbhardwaj100@gmail.com
Department of Mathematics,
Bahrain Polytechnic, Isa Town,
Kingdom of Bahrain
E-mail: ritu.shrivastava@polytechnic.bh
Faculty of Science and Technology,
Jagran Lakecity University, Bhopal, Madhya Pradesh,
India.
E-mail: drvandana@jlu.edu.in
School of Computer Science and
Technology,
Algoma University, Brampton, Ontario,
Canada.
E-mail: narayan.satyendra@gmail.com
Abstract:
The main aim of the research is to establish some invariant point (fixed point) results under the purview of R-Metric Spaces, for integral type R-contractive mappings. To serve this purpose, concepts of R-continuity, R-convergence and R-preservation has been used. Finally, the obtained results has been used to deduce some invariant point results for Banach, Kannan and Chatterjea type mappings in R-Metric Space. Also some examples and applications have been illustrated to support the findings discussed.
Search and serve lasted 1 second(s).