|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Inequalities for Functions of Selfadjoint Operators on Hilbert Spaces:
a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
College of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning inequalities for continuous functions of selfadjoint operators on complex Hilbert spaces. It is intended for use by both researchers in various fields of Linear Operator Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.
Paper's Title:
Trace Inequalities for Operators in Hilbert Spaces: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
School of Engineering
& Science
Victoria University,
PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
In this paper we survey some recent trace inequalities for operators in Hilbert spaces that are connected to Schwarz's, Buzano's and Kato's inequalities and the reverses of Schwarz inequality known in the literature as Cassels' inequality and Shisha-Mond's inequality. Applications for some functionals that are naturally associated to some of these inequalities and for functions of operators defined by power series are given. Further, various trace inequalities for convex functions are presented including refinements of Jensen inequality and several reverses of Jensen's inequality. Hermite-Hadamard type inequalities and the trace version of Slater's inequality are given. Some Lipschitz type inequalities are also surveyed. Examples for fundamental functions such as the power, logarithmic, resolvent and exponential functions are provided as well.
Paper's Title:
Hermite-Hadamard Type Inequalities for MN-Convex Functions
Author(s):
Sever S. Dragomir1,2
1Mathematics,
College of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
The present work endeavours to briefly present some of the fundamental results connected to the Hermite-Hadamard inequality for special classes of convex functions such as AG, AH, GA, GG, GH, HA, HG and HH -convex functions in which the author have been involved during the last five years. For simplicity, we call these classes of functions such as MN-convex functions, where M and N stand for any of the Arithmetic (A), Geometric (G) or Harmonic (H) weighted means of positive real numbers. The survey is intended for use by both researchers in various fields of Approximation Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Inequalities for
the
Author(s):
S. S. Dragomir
School of Engineering and Science
Victoria University, PO 14428
Melbourne City MC,
Victoria 8001,
Australia
sever.dragomir@vu.edu.au
URL: http://www.staff.vu.edu.au/RGMIA/dragomir/
Abstract:
Some recent inequalities for the Čebyšev functional of two functions of selfadjoint linear operators in Hilbert spaces, under suitable assumptions for the involved functions and operators, are surveyed.
Paper's Title:
Some Grüss Type Inequalities in Inner Product Spaces
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir
Abstract:
Some inequalities in inner product spaces
that provide upper bounds for the quantities
and
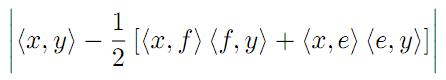
where e,f ∈ H with
and x,y are vectors in H satisfying some appropriate assumptions are
given. Applications for discrete and integral inequalities are provided as
well.
Paper's Title:
New Reverses of Schwarz, Triangle and Bessel Inequalities in Inner Product Spaces
Author(s):
S. S. Dragomir
School of Computer Science and Mathematics, Victoria
University of Technology, PO BOX
14428, MCMC 8001, VICTORIA, AUSTRALIA.
sever.dragomir@vu.edu.au
URL:
http://rgmia.vu.edu.au/SSDragomirWeb.html
Abstract:
New reverses of the Schwarz, triangle and Bessel inequalities in inner product spaces are pointed out. These results complement the recent ones obtained by the author in the earlier paper [13]. Further, they are employed to establish new Grüss type inequalities. Finally, some natural integral inequalities are stated as well.
Paper's Title:
Some Operator Order Inequalities for Continuous Functions of Selfadjoint Operators in Hilbert Spaces
Author(s):
S. S. Dragomir1,2 and Charles E. M. Pearce3
1Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428,
Melbourne City, MC 8001,
Australia.
2School of Computational & Applied Mathematics,
University of
the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
sever.dragomir@vu.edu.au
URL: http://rgmia.org/dragomir
3School
of Mathematical Sciences,
The University of Adelaide,
Adelaide,
Australia
Abstract:
Various bounds in the operator order for the following operator transform
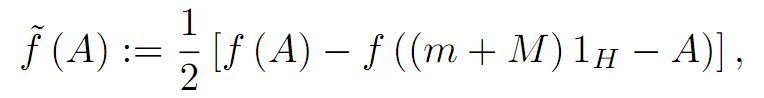
where A is a selfadjoint operator in the Hilbert space H with the
spectrum Sp( A) ⊆ [ m,M]
and f:[m,M] -> C is a continuous function on [m,M]
are given. Applications for the power and logarithmic functions are provided as
well.
Paper's Title:
Further Bounds for Two Mappings Related
to the Hermite-Hadamard Inequality
Author(s):
S. S. Dragomir1,2 and I. Gomm1
1Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428,
Melbourne City, MC 8001,
Australia.
2School of Computational & Applied Mathematics,
University of
the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
sever.dragomir@vu.edu.au
ian.gomm@vu.edu.au
URL: http://rgmia.org/dragomir
Abstract:
Some new results concerning two mappings associated to the celebrated Hermite-Hadamard integral inequality for twice differentiable functions with applications for special means are given.
Paper's Title:
Inequalities for the Area Balance of Functions of Bounded Variation
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
We introduce the area balance function associated to a Lebesgue
integrable function f:[a,b] →C by
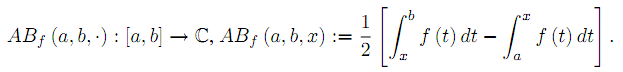
Several sharp bounds for functions of bounded variation are provided. Applications for Lipschitzian and convex functions are also given.
Paper's Title:
Some New Inequalities for Hypo-q-Norms on a Cartesian Product of Normed Linear Spaces
Author(s):
Sever S. Dragomir1,2
1Applied
Mathematics Research Group, ISILC,
Victoria University,
PO Box 14428, Melbourne City, MC 8001,
Australia.
E-mail: sever.dragomir@vu.edu.au
URL:
http://rgmia.org/dragomir
2School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
Abstract:
Let ( E,|| · ||) be a normed
linear space over the real or complex number field K. If by
Sn,p with p∈[ 1,∞]
we denote the spheres generated by the $p$-norms ||
· ||n,p on Kn, then we consider
the following hypo-q-norms on
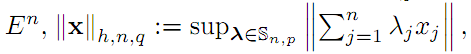 with q>1 and
with q>1 and
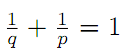 if p>1, q=1 if
p=∞
and q=∞ if p=1. For p=2, we also consider the hypo-Euclidean norm on En, i.e.,
if p>1, q=1 if
p=∞
and q=∞ if p=1. For p=2, we also consider the hypo-Euclidean norm on En, i.e.,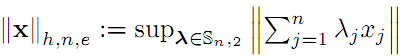
In this paper we have obtained among others the following inequalities
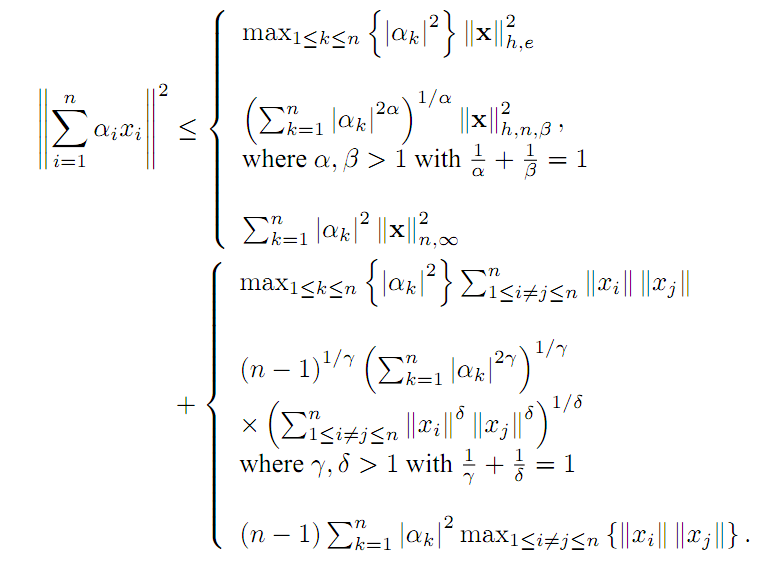
The case for n=2 and the connection with the following new norms
![]() and
and
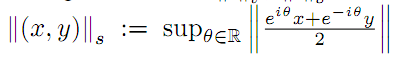
are also investigated. When the norm || · || is generated by an inner product, further bounds are given as well.
Paper's Title:
Reverses of the CBS Integral Inequality in Hilbert Spaces and Related
Results
Author(s):
I. Brnetić, S. S. Dragomir, R. Hoxha and J. Pečarić
Department of Applied Mathematics, Faculty of Electrical
Engineering and Computing,
University of Zagreb, Unska 3, 10 000 Zagreb,
Croatia
andrea@zpm.fer.hr
School of Computer Science & Mathematics, Victoria University
Po Box 14428, Melbourne Vic 8001
Australia
sever.dragomir@vu.edu.au
URL:http://rgmia.vu.edu.au/dragomir
Faculty of Applied Technical Sciences, University of Prishtina,
Mother
Theresa 5, 38 000 Prishtina
Kosova
razimhoxha@yahoo.com
Faculty of Textile Technology, University of Zagreb,
Pierottijeva 6, 10000
Zagreb,
Croatia
pecaric@hazu.hr
Abstract:
There are many known reverses of the Cauchy-Bunyakovsky-Schwarz (CBS)
inequality in the literature. We obtain here a general integral inequality
comprising some of those results and also provide other related
inequalities. The discrete case, which is of interest in its own turn, is
also analysed.
Paper's Title:
Bounds for Two Mappings Associated to
the Hermite-Hadamard Inequality
Author(s):
S. S. Dragomir1,2 and I. Gomm1
1Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428,
Melbourne City, MC 8001,
Australia.
2School of Computational & Applied Mathematics,
University of
the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
sever.dragomir@vu.edu.au
ian.gomm@vu.edu.au
URL: http://rgmia.org/dragomir
Abstract:
Some inequalities concerning two mappings associated to the celebrated Hermite-Hadamard integral inequality for convex function with applications for special means are given.
Paper's Title:
Some Applications of Fejér's Inequality for Convex Functions (I)
Author(s):
S.S. Dragomir1,2 and I. Gomm1
1Mathematics, School of
Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia.
URL: http://rgmia.org/dragomir
2School of Computational &
Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
Abstract:
Some applications of Fejér's inequality for convex functions are explored. Upper and lower bounds for the weighted integral
under various assumptions for f with applications to the trapezoidal quadrature rule are given. Some inequalities for special means are also provided
Paper's Title:
Some New Generalizations of Jensen's Inequality with Related Results and Applications
Author(s):
Steven G. From
Department of Mathematics
University of Nebraska at Omaha
Omaha, Nebraska 68182-0243.
E-mail: sfrom@unomaha.edu
Abstract:
In this paper, some new generalizations of Jensen's inequality are presented. In particular, upper and lower bounds for the Jensen gap are given and compared analytically and numerically to previously published bounds for both the discrete and continuous Jensen's inequality cases. The new bounds compare favorably to previously proposed bounds. A new method based on a series of locally linear interpolations is given and is the basis for most of the bounds given in this paper. The wide applicability of this method will be demonstrated. As by-products of this method, we shall obtain some new Hermite-Hadamard inequalities for functions which are 3-convex or 3-concave. The new method works to obtain bounds for the Jensen gap for non-convex functions as well, provided one or two derivatives of the nonlinear function are continuous. The mean residual life function of applied probability and reliability theory plays a prominent role in construction of bounds for the Jensen gap. We also present an exact integral representation for the Jensen gap in the continuous case. We briefly discuss some inequalities for other types of convexity, such as convexity in the geometric mean, and briefly discuss applications to reliability theory.
Paper's Title:
Norm Estimates for the Difference between Bochner’s Integral and the Convex Combination of Function’s Values
Author(s):
P. Cerone, Y.J. Cho, S.S. Dragomir, J.K. Kim, and S.S. Kim
School of
Computer Science and Mathematics,
Victoria University of Technology,
Po Box 14428, Mcmc 8001, Victoria, Australia.
pietro.cerone@vu.edu.au
URL:
http://rgmia.vu.edu.au/cerone/index.html
Department of
Mathematics Education, College of Education,
Gyeongsang National University, Chinju 660-701, Korea
yjcho@nongae.gsnu.ac.kr
School of
Computer Science and Mathematics,
Victoria University of Technology,
Po Box 14428, Mcmc 8001, Victoria, Australia.
sever.dragomir@vu.edu.au
URL:
http://rgmia.vu.edu.au/SSDragomirWeb.html
Department of
Mathematics, Kyungnam University,
Masan,, Kyungnam 631-701, Korea
jongkyuk@kyungnam.ac.kr
Department of
Mathematics, Dongeui University,
Pusan 614-714, Korea
sskim@dongeui.ac.kr
Abstract:
Norm estimates are developed between the Bochner integral of a vector-valued function in Banach spaces having the Radon-Nikodym property and the convex combination of function values taken on a division of the interval [a, b].
Paper's Title:
Some Ostrowski Type Inequalities for Two Cos-Integral Transforms of Absolutely Continuous Functions
Author(s):
S. S. Dragomir and G. Sorrentino
Mathematics, College Sport, Health and
Engineering,
Victoria University, PO Box 14428,
Melbourne City, MC 8001,
Australia.
DST-NRF Centre of Excellence in the
Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
E-mail: sever.dragomir@vu.edu.au
URL: http://rgmia.org/dragomir
Mathematics, First Year College,
Victoria University, PO Box 14428,
Melbourne City, MC 8001,
Australia.
Abstract:
For a Lebesgue integrable function f:[a,b] ⊂[0,π]→C
we consider the cos-integral transforms

and

We provide in this paper some upper bounds for the quantities

and

for
x ∈ [ a,b], in terms of the p-norms of the derivative
f ' for absolutely continuous functions f:[a,b] ⊂[0,π]→C.
Applications for approximating Steklov cos-average functions and Steklov
split cos-average functions are also provided.
Paper's Title:
A Generalization of Ostrowski's Inequality for Functions of Bounded
Variation via a Parameter
Author(s):
Seth Kermausuor
Department of Mathematics and Computer
Science,
Alabama State University,
Montgomery, AL 36101,
USA.
E-mail:
skermausour@alasu.edu
Abstract:
In this paper, we provide a generalization of the Ostrowski's inequality for functions of bounded variation for k points via a parameter λ∈[0,1]. As a by product, we consider some particular cases to obtained some interesting inequalities in these directions. Our results generalizes some of the results by Dragomir in [S. S. DRAGOMIR, The Ostrowski inequality for mappings of bounded variation, Bull. Austral. Math. Soc., 60 (1999), pp. 495--508.]
Paper's Title:
A Reverse
of the Triangle Inequality in Inner Product Spaces and Applications for
Polynomials
Author(s):
I. Brnetić, S. S. Dragomir, R. Hoxha and J. Pečarić
Department of Applied Mathematics, Faculty of Electrical
Engineering and Computing,
University of Zagreb, Unska 3, 10 000 Zagreb,
Croatia
andrea@zpm.fer.hr
School of Computer Science & Mathematics, Victoria University
Po Box 14428, Melbourne Vic 8001
Australia
sever.dragomir@vu.edu.au
URL:http://rgmia.vu.edu.au/dragomir
Faculty of Applied Technical Sciences, University of Prishtina,
Mother
Theresa 5, 38 000 Prishtina
Kosova
razimhoxha@yahoo.com
Faculty of Textile Technology, University of Zagreb,
Pierottijeva 6, 10000
Zagreb,
Croatia
pecaric@hazu.hr
Abstract:
A reverse of the triangle inequality in inner product spaces related to the
celebrated Diaz-Metcalf inequality with applications for complex polynomials
is given.
Paper's Title:
Some New Inequalities of Hermite-Hadamard and Fejér Type for Certain Functions with Higher Convexity
Author(s):
Steven G. From
Department of Mathematics,
University of Nebraska at Omaha,
Omaha, Nebraska 68182-0243,
U.S.A.
E-mail: sfrom@unomaha.edu
Abstract:
In this paper, we present some new inequalities of Hermite-Hadamard or Fejér
type for certain functions satisfying some higher convexity conditions on one or
more derivatives.
An open problem is given also.
Some applications to the logarithmic mean are given.
Paper's Title:
Bounds on the Jensen Gap, and Implications for Mean-Concentrated Distributions
Author(s):
Xiang Gao, Meera Sitharam, Adrian E. Roitberg
Department of Chemistry, and Department
of Computer & Information Science & Engineering,
University of Florida,
Gainesville, FL 32611,
USA.
E-mail: qasdfgtyuiop@gmail.com
URL:
https://scholar.google.com/citations?user=t2nOdxQAAAAJ
Abstract:
This paper gives upper and lower bounds on the gap in Jensen's inequality, i.e., the difference between the expected value of a function of a random variable and the value of the function at the expected value of the random variable. The bounds depend only on growth properties of the function and specific moments of the random variable. The bounds are particularly useful for distributions that are concentrated around the mean, a commonly occurring scenario such as the average of i.i.d. samples and in statistical mechanics.
Paper's Title:
Error Bounds for Numerical Integration of Functions of Lower Smoothness and Gauss-Legendre Quadrature Rule
Author(s):
Samuel A. Surulere and Abiola O. Oladeji
Tshwane University of Technology
Department of Mathematics and Statistics
175, Nelson Mandela drive, Arcadia, Pretoria,
South Africa.
E-mail: samuel.abayomi.sas@gmail.com
Abstract:
The error bounds of the rectangular, trapezoidal and Simpson's rules which are commonly used in approximating the integral of a function (f(x)) over an interval ([a,b]) were estimated. The error bounds of the second, and third generating functions of the Gauss-Legendre quadrature rules were also estimated in this paper. It was shown that for an (f(t)) whose smoothness is increasing, the accuracy of the fourth, sixth and eighth error bound of the second, and third generating functions of the Gauss-Legendre quadrature rule does not increase. It was also shown that the accuracy of the fourth error bound of the Simpson's (1/3) and (3/8) rules does not increase.
Paper's Title:
Generalizations of Hermite-Hadamard's Inequalities for Log-Convex Functions
Author(s):
Ai-Jun Li
School of Mathematics and Informatics,
Henan Polytechnic University,
Jiaozuo City, Henan Province,
454010, China.
liaijun72@163.com
Abstract:
In this article, Hermite-Hadamard's inequalities are extended in
terms of the weighted power mean and log-convex
function. Several refinements, generalizations and related
inequalities are obtained.
Paper's Title:
Several Applications of a Local Non-convex Young-type Inequality
Author(s):
Loredana Ciurdariu, Sorin Lugojan
Department of Mathematics,
"Politehnica" University of Timisoara,
P-ta. Victoriei, No.2, 300006-Timisoara,
Romania.
E-mail: ltirtirau87@yahoo.com
Abstract:
A local version of the Young inequality for positive numbers is used in order to deduce some inequalities about determinants and norms for real quadratic matrices and norms of positive operators on complex Hilbert spaces.
Paper's Title:
Reverse Hölder and Minkowski type integral inequalities for n functions
Author(s):
Panagiotis T. Krasopoulos and Lazhar Bougoffa
Department of Informatics, KEAO,
Electronic National Social Security Fund,
12 Patision St., 10677, Athens,
Greece.
E-mail: pan_kras@yahoo.gr
pankras@teemail.gr
Department of Mathematics,
Faculty of Science, Imam Mohammad Ibn Saud Islamic University,
P.O. Box 90950, Riyadh 11623,
Saudi Arabia.
E-mail: lbbougoffa@imamu.edu.sa
bougoffa@hotmail.com
Abstract:
We present and prove new reverse Hölder and Minkowski type integral inequalities for n functions. We compare our results with other known results from the relative literature in order to test their performance. In this respect, our theorems can be viewed as generalizations of some already known integral inequalities.
Paper's Title:
Refinement Inequalities Among Symmetric Divergence Measures
Author(s):
Inder Jeet Taneja
Departamento de Matemática,
Universidade Federal de Santa Catarina, 88.040-900
Florianópolis, Sc, Brazil
taneja@mtm.ufsc.br
URL: http://www.mtm.ufsc.br/~taneja
Abstract:
There are three classical divergence measures in the literature
on information theory and statistics, namely, Jeffryes-Kullback-Leiber’s
J-divergence, Sibson-Burbea-Rao’s Jensen- Shannon divegernce and
Taneja’s arithemtic - geometric mean divergence. These bear an
interesting relationship among each other and are based on logarithmic
expressions. The divergence measures like Hellinger discrimination,
symmetric χ2−divergence, and triangular discrimination
are not based on logarithmic expressions. These six divergence measures are
symmetric with respect to probability distributions. In this paper some
interesting inequalities among these symmetric divergence measures are studied.
Refinements of these inequalities are also given. Some inequalities due to
Dragomir et al. [6]
are also improved.
Paper's Title:
Improvement of Jensen's
Inequality for Superquadratic Functions
Author(s):
S. Abramovich, B. Ivanković, and J. Pečarić
Department of Mathematics,
University of Haifa,
Haifa 31905,
Israel.
abramos@math.haifa.ac.il
Faculty of Transport and
Trafic Engineering,
University of Zagreb,
Vukelićeva 4, 10000,
Croatia
bozidar.ivankovic@zg.t-com.hr
Faculty of Textile,
University of Zagreb,
Prilaz Baruna Filipovića 30, 10000 Zagreb,
Croatia
pecaric@element.hr
Abstract:
Since 1907, the famous Jensen's inequality has been refined in different manners. In our paper, we refine it applying superquadratic functions and separations of domains for convex functions. There are convex functions which are not superquadratic and superquadratic functions which are not convex. For superquadratic functions which are not convex we get inequalities analogue to inequalities satisfied by convex functions. For superquadratic functions which are convex (including many useful functions) we get refinements of Jensen's inequality and its extensions.
Paper's Title:
Fejér-type Inequalities
Author(s):
Nicuşor Minculete and Flavia-Corina Mitroi
"Dimitrie Cantemir" University,
107 Bisericii Române Street, Braşov, 500068,
România
minculeten@yahoo.com
University of Craiova, Department of Mathematics,
Street A. I. Cuza
13, Craiova, RO-200585,
Romania
fcmitroi@yahoo.com
Abstract:
The aim of this paper is to present some new Fejér-type results for convex functions. Improvements of Young's inequality (the arithmetic-geometric mean inequality) and other applications to special means are pointed as well.
Paper's Title:
Reverses of the Triangle Inequality in Inner Product Spaces
Author(s):
Sever S. Dragomir
School of Computer Science and Mathematics,
Victoria University Of Technology,
PO Box 14428, Mcmc 8001,
Victoria, Australia.
sever@csm.vu.edu.au
Url:
http://rgmia.vu.edu.au/SSDragomirWeb.html
Abstract:
Some new reverses for the generalised triangle inequality in inner product spaces are given. Applications in connection to the Schwarz inequality and for vector-valued integrals are provided as well.
Paper's Title:
A note on Inequalities due to Martins, Bennett and Alzer
Author(s):
József Sándor
Babeş-Bolyai University of Cluj, Department of Mathematics and Computer Sciences
Kogălniceanu Nr.1, Cluj-Napoca,
Romania.
jjsandor@hotmail.com
jsandor@member.ams.org
Abstract:
A short history of certain inequalities by Martins, Bennett as well as Alzer, is provided. It is shown that, the inequality of Alzer for negative powers [6], or Martin's reverse inequality [7] are due in fact to Alzer [2]. Some related results, as well as a conjecture, are stated.
Paper's Title:
Inequalities of Gamma Function Appearing in Generalizing Probability Sampling Design
Author(s):
Mohammadkheer M. Al-Jararha And Jehad M. Al-Jararha
Department of Mathematics,
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: mohammad.ja@yu.edu.jo
Department of Statistics,
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: jehad@yu.edu.jo
Abstract:
In this paper, we investigate the complete monotonicity of some functions involving gamma function. Using the monotonic properties of these functions, we derived some inequalities involving gamma and beta functions. Such inequalities can be used to generalize different probability distribution functions. Also, they can be used to generalize some statistical designs, e.g., the probability proportional to the size without replacement design.
Paper's Title:
Riemann-Stieltjes Integrals and Some Ostrowski Type Inequalities
Author(s):
W. G. Alshanti
Department of General Studies,
Jubail University College,
KSA.
E-mail: shantiw@ucj.edu.sa
Abstract:
In this article, we investigate new integral inequalities of Ostrowski's type of various functional aspects. For mapping's second derivative, we assume two cases, namely, L1 and L∞ spaces. Moreover, for first derivative, we investigate two different characteristics, namely, bounded variation and locally Lipchitz continuity. Applications to special means and composite quadrature rules are also carried out.
Paper's Title:
Fractional Integral Inequalities of Hermite-Hadamard Type for P-convex and Quasi-Convex Stochastic Process
Author(s):
Oualid Rholam, Mohammed Barmaki and Driss Gretet
National School of Applied Sciences (ENSA),
University Ibn Tofail,
B.P 242 Kenitra 14000,
phone number : +212606257757,
Morocco.
E-mail: oualid.rholam@uit.ac.ma
Science Faculty Ben M'sik,
University Hassan II,
B.P 7955 Av Driss El Harti Sidi Othmane 20700,
phone number : +212 5 22 70 46 71 ,
Morocco.
E-mail: mohammed.barmaki@uit.ac.ma
National School of Applied Sciences (ENSA),
University Ibn Tofail,
B.P 242 Kenitra 14000,
phone number : +212661403557,
Morocco.
E-mail: driss.gretete@uit.ac.ma
Abstract:
In this paper we consider the class of P-convex and Quasi-convex stochastic processes on witch we apply a general class of generalized fractional integral operator in order to establish new integral inequalities of Hermite-Hadammard type. then we obtain some results for well known types of fractional integrals. Results obtained in this paper may be starting point as well as a useful source of inspiration for further research in convex analysis.
Paper's Title:
Reverse of Martin's Inequality
Author(s):
Chao-Ping Chen, Feng Qi, and Sever S. Dragomir
Department of Applied Mathematics and Informatics,
Research Institute of Applied
Mathematics,
Henan Polytechnic University,
Jiaozuo City, Henan 454010, China
chenchaoping@sohu.com;
chenchaoping@hpu.edu.cn
Department of Applied Mathematics and Informatics,
Research Institute of Applied
Mathematics,
Henan Polytechnic University,
Jiaozuo City, Henan 454010, China
qifeng@hpu.edu.cn
Url: http://rgmia.vu.edu.au/qi.html
School of Computer Science and Mathematics,
Victoria University of Technology,
P. O. Box 14428, Melbourne City Mc,
Victoria 8001, Australia
Sever.Dragomir@vu.edu.au
Url: http://rgmia.vu.edu.au/SSDragomirWeb.html
Abstract:
In this paper, it is proved that
for all natural numbers n, and all real r < 0.

Paper's Title:
The successive approximations method and error estimation in terms of at most the first derivative for delay ordinary differential equations
Author(s):
Alexandru Mihai Bica
Department of Mathematics,
University of Oradea,
Str. Armatei Romane no.5,
410087, Oradea,
Romania
smbica@yahoo.com
abica@uoradea.ro
Abstract:
We present here a numerical method for first order delay ordinary differential
equations, which use the Banach's fixed point theorem, the sequence of
successive approximations and the trapezoidal quadrature rule. The error
estimation of the method uses a recent result of P. Cerone and S.S. Dragomir
about the remainder of the trapezoidal quadrature rule for Lipchitzian
functions and for functions with continuous first derivative.
Paper's Title:
Some Inequalities for Gramian Normal Operators and for Gramian Self-Adjoint Operators in Pseudo-Hilbert Spaces
Author(s):
Loredana Ciurdariu
Department of Mathematics,"Politehnica" University of Timisoara,
P-ta. Victoriei, No.2, 300006-Timisoara,
ROMANIA
cloredana43@yahoo.com.
Abstract:
Several inequalities for gramian normal operators and for gramian self-adjoint operators in pseudo-Hilbert spaces are presented.
Paper's Title:
A-Normal Operators In Semi Hilbertian Spaces
Author(s):
A. Saddi
Department of Mathematics,
College of Education for Girls in Sarat Ebeidah 61914, Abha,
King Khalid University
Saudi Arabia
adel.saddi@fsg.rnu.tn
Abstract:
In this paper we study some properties and inequalities of A-normal operators in semi-Hilbertian spaces by employing some known results for vectors in inner product spaces. We generalize also most of the inequalities of (α,β)-normal operators discussed in Hilbert spaces [7].
Paper's Title:
On the Hyers-Ulam Stability of Homomorphisms and Lie Derivations
Author(s):
Javad Izadi and Bahmann Yousefi
Department of Mathematics, Payame Noor
University,
P.O. Box: 19395-3697, Tehran,
Iran.
E-mail: javadie2003@yahoo.com,
b_yousefi@pnu.ac.ir
Abstract:
Let A be a Lie Banach*-algebra. For each elements (a, b) and (c, d) in A2:= A * A, by definitions
(a, b) (c, d)= (ac, bd),
|(a, b)|= |a|+ |b|,
(a, b)*= (a*, b*),
A2 can be considered as a Banach*-algebra. This Banach*-algebra is called a Lie Banach*-algebra whenever it is equipped with the following definitions of Lie product:
for all a, b, c, d in A. Also, if A is a Lie Banach*-algebra, then D: A2→A2 satisfying
D ([ (a, b), (c, d)])= [ D (a, b), (c, d)]+ [(a, b), D (c, d)]
for all $a, b, c, d∈A, is a Lie derivation on A2. Furthermore, if A is a Lie Banach*-algebra, then D is called a Lie* derivation on A2 whenever D is a Lie derivation with D (a, b)*= D (a*, b*) for all a, b∈A. In this paper, we investigate the Hyers-Ulam stability of Lie Banach*-algebra homomorphisms and Lie* derivations on the Banach*-algebra A2.
Paper's Title:
Hermite-Hadamard Type Inequalities for k-Riemann Liouville Fractional Integrals Via Two Kinds of Convexity
Author(s):
R. Hussain1, A. Ali2, G. Gulshan3, A. Latif4 and K. Rauf5
1,2,3,4Department
of Mathematics,
Mirpur University of Science and Technology, Mirpur.
Pakistan.
E-mail1:
rashida12@gmail.com
E-mail2:
unigraz2009@yahoo.com
E-mail3:
ghazalagulshan@yahoo.com
E-mail4:
asialatif87@gmail.com
5Department
of Mathematics,
University of Ilorin, Ilorin,
Nigeria.
E-mail5:
krauf@unilorin.edu.ng
Abstract:
In this article, a fundamental integral identity including the first order derivative of a given function via k-Riemann-Liouville fractional integral is established. This is used to obtain further Hermite-Hadamard type inequalities involving left-sided and right-sided k-Riemann-Liouville fractional integrals for m-convex and (s,m)-convex functions respectively.
Paper's Title:
Some Inequalities of the Hermite-Hadamard Type for k-Fractional Conformable Integrals
Author(s):
C.-J. Huang, G. Rahman, K. S. Nisar, A. Ghaffar and F. Qi
Department of Mathematics, Ganzhou Teachers College,
Ganzhou 341000, Jiangxi,
China.
E-mail:
hcj73jx@126.com ,
huangcj1973@qq.com
Department of Mathematics, Shaheed Benazir
Bhutto University,
Sheringal, Upper Dir, Khyber Pakhtoonkhwa,
Pakistan.
E-mail: gauhar55uom@gmail.com
Department of Mathematics, College of Arts
and Science at Wadi Aldawaser, 11991,
Prince Sattam Bin Abdulaziz University, Riyadh Region,
Kingdom of Saudi Arabia.
E-mail: n.sooppy@psau.edu.sa,
ksnisar1@gmail.com
Department of Mathematical Science,
Balochistan University of Information Technology,
Engineering and Management Sciences, Quetta,
Pakistan.
E-mail: abdulghaffar.jaffar@gmail.com
School of Mathematical Sciences, Tianjin
Polytechnic University,
Tianjin 300387,
China; Institute of Mathematics,
Henan Polytechnic University, Jiaozuo 454010, Henan,
China.
E-mail: qifeng618@gmail.com,
qifeng618@qq.com
Abstract:
In the paper, the authors deal with generalized k-fractional conformable integrals, establish some inequalities of the Hermite-Hadamard type for generalized k-fractional conformable integrals for convex functions, and generalize known inequalities of the Hermite-Hadamard type for conformable fractional integrals.
Paper's Title:
Error estimates for aproximations of the Fourier transform of functions in Lp spaces
Author(s):
A. Aglic
Aljinovic and J. Pecaric Department of Applied Mathematics,
Faculty of Electrical Engineering and Computing,
University Of Zagreb, Unska 3, 10 000 Zagreb,
Croatia
andrea@zpm.fer.hr
Faculty of Textile Technology,
University of Zagreb, Pierottijeva 6, 10000 Zagreb,
Croatia
pecaric@hazu.hr
Abstract:
New inequalities concerning the Fourier transform are given. Estimates of the difference between two Fourier transforms and even bounds to the associated numerical quadrature formulae are provided as well.
Paper's Title:
Weighted Generalization of the Trapezoidal Rule via Fink Identity
Author(s):
S. Kovač, J. Pečarić and A. Vukelić
Faculty of Geotechnical Engineering, University of Zagreb,
Hallerova aleja 7, 42000 Varaždin,
Croatia.
sanja.kovac@gtfvz.hr
Faculty of Textile Technology, University of Zagreb,
Pierottijeva 6, 10000 Zagreb,
Croatia.
pecaric@hazu.hr
Faculty of Food Technology and Biotechnology, Mathematics department, University of Zagreb,
Pierottijeva 6, 10000 Zagreb,
Croatia.
avukelic@pbf.hr
Abstract:
The weighted Fink identity is given and used to obtain generalized
weighted trapezoidal formula for n-time differentiable functions.
Also, an error estimate is obtained for this formula.
Paper's Title:
On the Asymptotic Behavior of Solutions of Third Order Nonlinear Differential Equations
Author(s):
Ivan Mojsej and Alena Tartaľová
Institute of Mathematics,
Faculty of Science, P. J. Šafárik University,
Jesenná 5, 041 54 Košice,
Slovak Republic
ivan.mojsej@upjs.sk
Department of Applied Mathematics and Business Informatics,
Faculty of Economics,
Technical University,
Nemcovej 32, 040 01 Košice,
Slovak Republic
alena.tartalova@tuke.sk
Abstract:
This paper is concerned with the asymptotic behavior of solutions of nonlinear differential equations of the
third order with quasiderivatives. Mainly, we present the necessary and sufficient conditions for the existence
of nonoscillatory solutions with specified asymptotic behavior as Paper's Title:
The Riemann-Stieltjes Integral on Time Scales Author(s):
D. Mozyrska, E. Pawłuszewicz,
D. Torres
Faculty Of Computer Science,
Abstract:
We study the process of integration on time
scales in the sense of Riemann-Stieltjes. Analogues of the classical properties
are proved for a generic time scale, and examples are given Paper's Title:
The Best Upper Bound for Jensen's
Inequality Author(s):
Vasile Cirtoaje Abstract:
In this paper we give the best upper bound
for the weighted Jensen's discrete inequality applied to a convex function f
defined on a closed interval I in the case when the bound depends on f,
I and weights. In addition, we give a simpler expression of the upper
bound, which is better than existing similar one. Paper's Title:
On Generalized Triangle Inequality in p-Freéchet Spaces, 0<p<1
Author(s):
M. A. Latif Department of Mathematics, Abstract:
In this paper generalized triangle inequality and its reverse in a
p-Fréchet space where, 0<p<1 are obtained. Paper's Title:
On Reformations of 2--Hilbert Spaces Author(s):
M. Eshaghi Gordji, A. Divandari, M. R. Safi and Y. J. Cho Department of Mathematics, Semnan
University,
meshaghi@semnan.ac.ir,
madjid.eshaghi@gmail.com Department of Mathematics, Semnan
University, Department of Mathematics, Semnan
University,
safi@semnan.ac.ir,
SafiMohammadReza@yahoo.com Department of Mathematics Education and
the RINS, Abstract:
In this paper, first, we introduce the new concept of (complex)
2--Hilbert spaces, that is, we define the concept of 2--inner
product spaces with a complex valued 2--inner product by using
the 2--norm. Next, we prove some theorems on Schwartz's
inequality, the polarization identity, the parallelogram laws and
related important properties. Finally, we give some open problems
related to 2--Hilbert spaces.
Paper's Title:
An Improvement of the Hermite-Hadamard Inequality for Functions Convex on the Coordinates Author(s):
Milica Klaričić Bakula Faculty of Science, E-mail: milica@pmfst.hr
Abstract:
An improvement of the Hermite-Hadamard inequality for functions convex on the coordinates is given. Paper's Title:
Birkhoff-James orthogonality and Best Approximant in L1(X) Author(s):
Mecheri Hacene and Rebiai Belgacem Department of Mathematics and
Informatics, Department of Mathematics and
Informatics, Abstract:
Let X be a complex Banach space and let (X,ρ) be a positive measure space. The Birkhoff-James orthogonality is a generalization of Hilbert space orthogonality to Banach spaces. We use this notion of orthogonality to establish a new characterization of Birkhoff-James orthogonality of bounded linear operators in L1(X,ρ) also implies best approximation has been proved. Paper's Title:
The RAFU remainder in Taylor's formula Author(s):
A. C. Sanchez ''Santa Eulalia'' High School, Abstract:
This work is about the remainder in Taylor's formula.
Specifically, the RAFU remainder is studied. Its mathematical expression is
given. Some examples are shown. Different ways to obtain this remainder are developed. Paper's Title:
New Proofs of the Grüss Inequality Author(s):
A.Mc.D. Mercer
and Peter R.
Mercer
Dept. Mathematics and Statistics,
Abstract:
We present new proofs of the Grüss inequality in its original form and in its linear
functional form.
Paper's Title:
Quantitative Estimates for Positive Linear Operators Obtained by Means of Piecewise Linear Functions
Author(s):
Vasile Mihesan
Technical University of Cluj-Napoca, Abstract:
In this paper we obtain estimates for the remainder in approximating continuous
functions by positive linear operators, using piecewise linear functions.
Paper's Title:
On the Hohov Convolution Of The Class Sp(α,β)
Author(s):
T. N. Shanmugam and S. Sivasubramanian
Department of Mathematics,
Department of Mathematics, Abstract:
Let F(a,b;c;z) be the Gaussian hypergeometric function and Ia,b;c(f)=zF(a,b;c;z)*f(z) be the Hohlov operator defined on the class A of all normalized analytic functions. We determine conditions on the parameters a,b,c such that Ia,b;c(f) will be in the class of parabolic starlike functions Sp(α,β). Our results extend several earlier results.
Paper's Title:
Solution of the Hyers-Ulam Stability Problem for Quadratic Type Functional Equations in Several Variables
Author(s):
John Michael Rassias
Pedagogical Department, E.E., National and Capodistrian University of Athens, Abstract:
In 1940 (and 1968) S. M. Ulam proposed the well-known Ulam stability problem. In 1941 D. H. Hyers solved the Hyers-Ulam problem for linear mappings. In 1951 D. G. Bourgin has been the second author treating the Ulam problem for additive mappings. In 1978 according to P. M. Gruber this kind of stability problems is of particular interest in probability theory and in the case of functional equations of different types. In 1982-2004 we established the Hyers-Ulam stability for the Ulam problem for different mappings. In this article we solve the Hyers-Ulam problem for quadratic type functional equations in several variables. These stability results can be applied in stochastic analysis, financial and actuarial mathematics, as well as in psychology and sociology. Paper's Title:
Parameter dependence of the solution of second order nonlinear ODE's via Perov's fixed point theorem
Author(s):
A. M. Bica, S. Muresan and G. Grebenisan
University of Oradea,
2: Paper Source
PDF document
Białystok University Of Technology,
15-351 Białystok,
Poland
d.mozyrska@pb.edu.pl
Department Of Mathematics,
University Of Aveiro,
3810-193 Aveiro,
Portugal
ewa@ua.pt
Department Of Mathematics,
University Of Aveiro,
3810-193 Aveiro,
Portugal
delfim@ua.pt
2: Paper Source
PDF document
Department of Automatic Control and Computers
University of Ploiesti
Romania.
2: Paper Source
PDF document
University of Hail, Hail,
Saudi Arabia
m_amer_latif@hotmail.com
2: Paper Source
PDF document
P.O. Box 35195--363, Semnan,
Iran
Iran
Iran
Gyeongsang National University
Chinju 660-701,
Korea
2: Paper Source
PDF document
University of Split,
Teslina 12, 21000 Split.
Croatia
2: Paper Source
PDF document
LAMIS laboratory, University of Tebessa,
Algeria.
E-mail: mecherih2000@yahoo.fr
LAMIS laboratory, University of Tebessa,
Algeria.
E-mail: brebiai@gmail.com
2: Paper Source
PDF document
Spain
E-mail: csanchezalicia@gmail.com
1: Paper Source
PDF document
University of Guelph, Guelph, Ontario,
Canada.
amercer@reach.net
Dept. Mathematics,
S.U.N.Y. College at Buffalo, Buffalo, NY,
U.S.A.
mercerpr@math.buffalostate.edu
1: Paper Source
PDF document
Department of Mathematics,
Str. C. Daicoviciu 15,
Cluj-Napoca,
Romania
Vasile.Mihesan@math.utcluj.ro
1: Paper Source
PDF document
Anna University,
Chennai 600025,
Tamilnadu, India.
shan@annauniv.edu
Easwari Engineering College,
Chennai-600089,
Tamilnadu, India,
sivasaisastha@rediffmail.com
1: Paper Source
PDF document
Section of Mathematics and Informatics,
4, Agamemnonos Str., Aghia Paraskevi,
Athens 15342,
Greece
jrassias@primedu.uoa.gr
URL: http://www.primedu.uoa.gr/~jrassias/
1: Paper Source
PDF document
Str. Armatei Romane no.5, 410087,
Oradea, Romania.
smbica@yahoo.com
smuresan@uoradea.ro
grebe@uoradea.ro
Abstract:
Using the Perov's fixed point theorem, the smooth dependence by parameter of
the solution of a two point boundary value problem corresponding to nonlinear
second order ODE's is obtained.
Paper's Title:
Notes on Sakaguchi Functions
Author(s):
Shigeyoshi Owa, Tadayuki Sekine and Rikuo Yamakawa
Department of Mathematics, Kinki University,
Higashi-Osaka, Osaka 577-8502,
Japan.
owa@math.kindai.ac.jp
Office of Mathematics, College of Pharmacy, Nihon University,
7-1 Narashinodai, Funabashi-city,
Chiba, 274-8555, Japan.
tsekine@pha.nihon-u.ac.jp
Department of Mathematics, Shibaura Institute of Technology,
Minuma, Saitama-city,
Saitama 337-8570, Japan.
yamakawa@sic.shibaura-it.ac.jp
Abstract:
By using the definition for certain
univalent functions f(z) in the open unit disk U given by K. Sakaguchi
[2], two classes S(α) and T(α) of analytic functions in U
are introduced. The object of the present paper is to discuss some properties of
functions f(z) belonging to the classes S(α) and T(α).
Paper's Title:
Coincidences and Fixed Points of Hybrid Maps in Symmetric Spaces
Author(s):
S. L. Singh and Bhagwati Prasad
Vedic MRI, 21 Govind Nagar,
Department of Mathematics, Gurukula Kangri University,
Rishikesh 249201
India
vedicmri@gmail.com
Hardwar 249404,
India
Abstract:
The purpose of this paper is to obtain a new coincidence theorem for a
single-valued and two multivalued operators in symmetric spaces. We derive
fixed point theorems and discuss some special cases and applications.
Paper's Title:
Existence of solutions for Neutral Stochastic Functional Differential Systems with Infinite Delay in Abstract Space
Author(s):
P. Balasubramaniam, A. V. A. Kumar and S. K. Ntouyas
Department of Mathematics, Gandhigram Rural Institute,
Deemed University, Gandhigram - 624 302,
Tamil Nadu, India.
pbalgri@rediffmail.com
Department of Mathematics, Gandhigram Rural Institute,
Deemed University, Gandhigram - 624 302,
Tamil Nadu, India.
nnddww@tom.com
Department of Mathematics, University of Ioannina,
451 10 Ioannina,
Greece.
sntouyas@cc.uoi.gr
URL: http://www.math.uoi.gr/~sntouyas
Abstract:
In this paper we prove existence results for semilinear stochastic neutral functional differential systems with unbounded delay in abstract space. Our theory makes use of analytic semigroups and fractional power of closed operators and Sadovskii fixed point theorem.
Paper's Title:
A Coefficient Inequality For Certain Subclasses of Analytic
Functions Related to Complex Order
Author(s):
B. Srutha Keerthi, B. Adolf Stephen and S. Sivasubramanian
Department Of Applied Mathematics, Sri Venkateswara College Of Engineering, Anna University,
Sriperumbudur, Chennai - 602 105,
India.
laya@svce.ac.in
Department of Mathematics, Madras Christian College,
Chennai - 600059,
India
adolfmcc2003@yahoo.co.in
Department of Mathematics, College of Engineering, Anna University,
Tamilnadu, Chennai - 600 025,
India.
sivasaisastha@rediffmail.com
Abstract:
In this present investigation, the authors obtain coefficient
inequality for certain normalized analytic functions of complex order f(z) defined
on the open unit disk for which
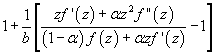 (
( and
and  be a complex number) lies in a region starlike with respect to 1 and is symmetric with respect to the real axis. Also
certain applications of the main result for a class of functions of complex order
defined by convolution are given. As a special case of this result, coefficient
inequality for a class of functions defined through fractional derivatives is
obtained. The motivation of this paper is to give a generalization of the
coefficient inequalities of the subclasses of starlike and convex functions of
complex order.
be a complex number) lies in a region starlike with respect to 1 and is symmetric with respect to the real axis. Also
certain applications of the main result for a class of functions of complex order
defined by convolution are given. As a special case of this result, coefficient
inequality for a class of functions defined through fractional derivatives is
obtained. The motivation of this paper is to give a generalization of the
coefficient inequalities of the subclasses of starlike and convex functions of
complex order.
Paper's Title:
Product Formulas Involving Gauss Hypergeometric Functions
Author(s):
Edward Neuman
Department of Mathematics, Mailcode 4408,
Southern Illinois University,
1245 Lincoln Drive,
Carbondale, IL 62901,
USA.
edneuman@math.siu.edu
URL: http://www.math.siu.edu/neuman/personal.html
Abstract:
New formulas for a product of two Gauss hypergeometric functions are derived.
Applications to special functions, with emphasis on Jacobi polynomials, Jacobi functions, and Bessel functions of the first kind, are included.
Most of the results are obtained with the aid of the double Dirichlet average of a univariate function.
Paper's Title:
On Interaction of Discontinuous Waves in a Gas with Dust Particles
Author(s):
J. Jena
Department of Mathematics, Netaji Subhas institute of technology,
Sector-3, Dwarka, New Delhi - 110 075,
India.
jjena67@rediffmail.com
jjena@nsit.ac.in
Abstract:
In this paper, the interaction of the strong shock with the weak discontinuity has been investigated for the system of partial differential equations describing one dimensional unsteady plane flow of an inviscid gas with large number of dust particles. The amplitudes of the reflected and transmitted waves after interaction of the weak discontinuity through a strong shock are evaluated by exploiting the results of general theory of wave interaction.
Paper's Title:
Existence of Large Solutions to Non-Monotone Semilinear Elliptic Equations
Author(s):
Alan V. Lair, Zachary J. Proano, and Aihua W. Wood
Air Force Institute of Technology
2950 Hobson Way, AFIT/ENC
Wright-Patterson Air Force Base, OH, 45433-7765,
USA.
Aihua.Wood@afit.edu
URL: www.afit.edu
Abstract:
We study the existence of large solutions of the semilinear elliptic equation Δu=p(x)f(u) where f is not monotonic. We prove existence, on bounded and unbounded domains, under the assumption that f is Lipschitz continuous, f(0) = 0, f(s) > 0 for s > 0 and there exists a nonnegative, nondecreasing Hölder continuous function g and a constant M such that g(s) ≤ f(s) ≤ Mg(s) for large s. The nonnegative function p is allowed to be zero on much of the domain.
Paper's Title:
On a Subclass of Uniformly Convex Functions Defined by the Dziok-Srivastava Operator
Author(s):
M. K. Aouf and G. Murugusundaramoorthy
Mathematics Department, Faculty of Science,
Mansoura University 35516,
Egypt.
mkaouf127@yahoo.com
School of Science and Humanities, VIT University
Vellore - 632014,
India.
gmsmoorthy@yahoo.com
Abstract:
Making use of the Dziok-Srivastava operator, we define a new subclass Tlm([α1];α,β) of uniformly convex function with
negative coefficients. In this paper, we obtain coefficient estimates,
distortion theorems, locate extreme points and obtain radii of
close-to-convexity, starlikeness and convexity for functions belonging to the
class Tlm([α1];α,β) . We
consider integral operators associated with functions belonging to the class
Hlm([α1];α,β) defined via the Dziok-Srivastava
operator. We also obtain several results for the modified Hadamard products of
functions belonging to the class Tlm([α1];α,β)
and we obtain properties associated with generalized fractional calculus
operators.
Paper's Title:
On Stable Numerical Differentiation
Author(s):
N. S. Hoang and A. G. Ramm
Mathematics Department, Kansas State University Abstract:
Based on a regularized Volterra equation, two different approaches for numerical differentiation are considered.
The first approach consists of solving a regularized Volterra equation while the second approach is based on solving a disretized version of the regularized Volterra equation.
Numerical experiments show that these methods are efficient and compete favorably with the variational regularization method for stable calculating the derivatives of noisy functions.
Paper's Title:
Existence of Bounded Solutions for a Class of
Strongly Nonlinear Elliptic Equations in Orlicz-Sobolev Spaces
Author(s):
Abdelmoujib Benkirane and Ahmed Youssfi
Department of Mathematics and Informatics, Faculty of Sciences
Dhar El Mahraz Abstract:
We prove, in the setting of Orlicz-Sobolev spaces, the existence of
bounded solutions for some strongly nonlinear elliptic equations
with operator of the principal part having degenerate coercivity and
lower order terms not satisfying the sign condition. The data have a
suitable summability and no Δ2-condition is needed for the
considered N-functions.
Paper's Title:
Positive Solutions for Systems of Three-point Nonlinear Boundary Value Problems Author(s):
J. Henderson and S. K. Ntouyas
Department of Mathematics, Baylor University
Department of Mathematics, University of Ioannina Abstract:
Values of λ are determined for which there exist
positive solutions of the system of three-point boundary value problems,
u''(t)+ λa(t)f(v(t))=0, v''(t)+λb(t)g(u(t))=0,
for 0 < t <1, and
satisfying, u(0) = 0, u(1)=α u(η),
v(0) = 0, v(1)=α v(η). A Guo-Krasnosel'skii fixed
point theorem is applied. Paper's Title:
Error Inequalities for Weighted Integration Formulae and Applications
Author(s):
Nenad Ujević and Ivan Lekić
Department of Mathematics Abstract:
Weighted integration formulae are derived. Error inequalities for the
weighted integration formulae are obtained. Applications to some special
functions are also given. Paper's Title:
Some Properties of the Solution of a Second Order Elliptic Abstract Differential Equation Author(s):
A. Aibeche and K. Laidoune
Mathematics Department, Faculty of Sciences,
University Ferhat Abbas, Setif,
Abstract:
In this paper we study a class of non regular boundary value
problems for elliptic differential-operator equation of second order with an
operator in boundary conditions. We give conditions which guarantee the
coerciveness of the solution of the considered problem, the completeness of
system of root vectors in Banach-valued functions spaces and we establish
the Abel basis property of this system in Hilbert spaces. Finally, we apply
this abstract results to a partial differential equation in cylindrical
domain.
Paper's Title:
Hyers-Ulam-Rassias Stability
of a Generalized Jensen Functional Equation Author(s):
A. Charifi, B. Bouikhalene, E.
Elqorachi and A. Redouani
Department of Abstract:
In this paper we obtain the
Hyers-Ulam-Rassias stability for the generalized Jensen's functional equation in
abelian group (G,+). Furthermore we discuss the case where G is amenable and we
give a note on the Hyers-Ulam-stability of the K-spherical (n
× n)-matrix functional
equation. Paper's Title:
Superquadracity, Bohr's Inequality and Deviation from a Mean Value Author(s):
S. Abramovich, J. Barić,
and J. Pečarić
Department of Mathematics, University of Haifa,
Manhattan, KS 66506-2602,
U. S. A.
nguyenhs@math.ksu.edu
ramm@math.ksu.edu
URL:http://math.ksu.edu/~ramm
1: Paper Source
PDF document
University Sidi Mohammed Ben Abdallah
PB 1796 Fez-Atlas, Fez
Morocco
a.benkirane@menara.ma
ahmed.youssfi@caramail.com
1: Paper Source
PDF document
Waco, Texas
76798-7328 USA.
Johnny_Henderson@baylor.edu
URL: http://www3.baylor.edu/~Johnny_Henderson
451 10 Ioannina,
Greece.
sntouyas@cc.uoi.gr
URL: http://www.math.uoi.gr/~sntouyas
1: Paper Source
PDF document
University of Split
Teslina 12/III, 21000 Split
CROATIA.
ujevic@pmfst.hr
ivalek@pmfst.hr
1: Paper Source
PDF document
Route de Scipion, 19000,
Setif,
Algeria
aibeche@univ-setif.dz
1: Paper Source
PDF document
Mathematics, Faculty of Sciences,
Ibn Tofail University,
Kenitra, Morocco
charifi2000@yahoo.fr
bbouikhalene@yahoo.fr
Department of
Mathematics, Faculty of Sciences,
Ibn Zohr University,
Agadir, Morocco
elqorachi@hotmail.com
Redouani-ahmed@yahoo.fr
1: Paper Source
PDF document
Haifa, 31905,
Israel
abramos@math.haifa.ac.il
FESB, University of Split,
Rudera Bošcovića,
B.B., 21000, Split,
Croatia
jbaric@fesb.hr
Faculty of Textile Technology,
University of Zagreb,
Prilaz Baruna Filipovića,
30, 10000 Zagreb,
Croatia.
pecaric@hazu.hr
Abstract:
Extensions of Bohr's inequality via superquadracity are obtained, where instead of the power p=2 which appears in Bohr's inequality we get similar results when we deal with p≥ 2 and with p≤ 2. Also, via superquadracity we extend a bound for deviation from a Mean Value.
Paper's Title:
The Superstability of the Pexider Type Trigonometric Functional Equation
Author(s):
Gwang Hui Kim and Young Whan Lee
Department of Mathematics, Kangnam
University Yongin, Gyeonggi, 446-702, Korea.
ghkim@kangnam.ac.kr
Department of Computer and Information Security
Daejeon University, Daejeon 300-716, Korea.
ywlee@dju.ac.kr
Abstract:
The aim of this paper is to investigate the stability
problem for
the Pexider type (hyperbolic) trigonometric functional equation
f(x+y)+f(x+σy)=λg(x)h(y) under the conditions :
|f(x+y)+f(x+σy)- λg(x)h(y)|≤φ(x),
φ(y), and min {φ(x), φ (y)}.
As a consequence, we have generalized the results of stability for
the cosine(d'Alembert), sine, and the Wilson functional equations by J.
Baker, P. Găvruta, R. Badora and R. Ger, Pl.~Kannappan, and G.
H. Kim
Paper's Title:
Error Estimates for Approximations of the Laplace transform of Functions in Lp Spaces
Author(s):
Andrea Aglić Aljinović
Department of Applied Mathematics,
Faculty of Electrical Engineering and Computing,
University of Zagreb,
Unska 3, 10 000 Zagreb,
Croatia
Abstract:
In this paper error estimates of approximations in complex domain for the Laplace transform are given for functions which vanish beyond a finite domain and whose derivatives belongs to Lp spaces. New inequalities concerning the Laplace transform, as well as estimates of the difference between the two Laplace transforms are presented and used to obtain two associated numerical rules and error bounds of their remainders.
Paper's Title:
On Generalization of Hardy-type Inequalities
Author(s):
K. Rauf, S. Ponnusamy and J. O. Omolehin
Department of Mathematics,
University of Ilorin, Ilorin,
Nigeria
krauf@unilorin.edu.ng
Department of Mathematics,
Indian Institute of Technology Madras,
Chennai- 600 036,
India
samy@iitm.ac.in
Department of Mathematics,
University of Ilorin, Ilorin,
Nigeria
omolehin_joseph@yahoo.com
Abstract:
This paper is devoted to some new generalization of Hardy-type integral inequalities and the reversed forms. The study is to determine conditions on which the generalized inequalities hold using some known hypothesis. Improvement of some inequalities are also presented.
Paper's Title:
On A Conjecture of A Logarithmically Completely Monotonic Function
Author(s):
Valmir Krasniqi, Armend Sh. Shabani
Department of Mathematics,
University of Prishtina,
Republic of Kosova
E-mail:
vali.99@hotmail.com
armend_shabani@hotmail.com
Abstract:
In this short note we prove a conjecture, related to a logarithmically completely monotonic function, presented in [5]. Then, we extend by proving a more generalized theorem. At the end we pose an open problem on a logarithmically completely monotonic function involving q-Digamma function.
Paper's Title:
Some New Nonlinear Integro-Differential Inequalities of Gronwall-Bellman-Pachpatte Type
Author(s):
A. ABDELDAIM
Department of Mathematics and Computer
Sciences,
Faculty of Science,
Port Said University, Port Said,
EGYPT.
Department of Mathematics,
Faculty of Science and Humanities,
Shaqra University, Dawadmi,
SAUDI ARABIA.
E-mail:
ahassen@su.edu.sa
URL:
http://faculty.ksu.edu.sa/DRABDELDAIM/Pages/Home.aspx
Abstract:
In this paper we establish some new nonlinear integro-differential inequalities of Gronwall-Bellman-Pachpatte type for function of one independent variable. The purpose of this paper is to extend certain results which proved by Pachpatte in [On some fundamental integrodifferential and integral inequalities, An. Sti. Univ. Al. I. Cuza, Iasi, Vol.23 (1977), 77-86]. The inequalities obtained here can be used in the theory of some new classes of nonlinear integro-differential equations. Some applications are also given to illustrate the usefulness of our results.
Paper's Title:
A Nonhomogeneous Subdiffusion Heat Equation
Author(s):
Joel-Arturo Rodriguez-Ceballos, Ana-Magnolia Marin, Ruben-Dario Ortiz
Instituto Tecnológico de Morelia,
Morelia, Michoacan,
Mexico
E-mail: joel@ifm.umich.mx
Universidad de Cartagena,
Campus San Pablo,
Cartagena de Indias, Bolivar,
Colombia
E-mail: amarinr@unicartagena.edu.co
E-mail: joel@ifm.umich.mx
Abstract:
In this paper we consider a nonhomogeneous subdiffusion heat equation of fractional order with Dirichlet boundary conditions.
Paper's Title:
Weak solutions of non coercive stochastic Navier-Stokes equations in R2
Author(s):
Wilhelm Stannat and Satoshi Yokoyama
Technische Universität Berlin,
Strasse des 17. Juni 136, 10623 Berlin,
Germany.
Graduate School of Mathematical Sciences,
The University of Tokyo,
Komaba, Tokyo 153-8914,
Japan.
E-mail: stannat@math.tu-berlin.de
E-mail: satoshi2@ms.u-tokyo.ac.jp
Abstract:
We prove existence of weak solutions of stochastic Navier-Stokes equations in R2 which do not satisfy the coercivity condition. The equations are formally derived from the critical point of some variational problem defined on the space of volume preserving diffeomorphisms in R2. Since the domain of our equation is unbounded, it is more difficult to get tightness of approximating sequences of solutions in comparison with the case of a bounded domain. Our approach is based on uniform a priori estimates on the enstrophy of weak solutions of the stochastic 2D-Navier-Stokes equations with periodic boundary conditions, where the periodicity is growing to infinity combined with a suitable spatial cutoff-technique.
Paper's Title:
Examples of Fractals Satisfying the Quasihyperbolic Boundary Condition
Author(s):
Petteri Harjulehto and Riku Klén
Department of Mathematics and Statistics,
FI-20014 University of Turku,
Finland
E-mail: petteri.harjulehto@utu.fi
E-mail: riku.klen@utu.fi
Abstract:
In this paper we give explicit examples of bounded domains that satisfy the quasihyperbolic boundary condition and calculate the values for the constants. These domains are also John domains and we calculate John constants as well. The authors do not know any other paper where exact values of parameters has been estimated.
Paper's Title:
Hermite-Hadamard-Fejer Type Inequalities for Harmonically s-convex Functions via Fractional Integrals
Author(s):
İmdat İşcan, Mehmet Kunt
Department of Mathematics,
Faculty of Sciences and Arts,
Giresun University, Giresun,
Turkey.
E-mail: imdat.iscan@giresun.edu.tr
Department of Mathematics,
Faculty of Sciences,
Karadeniz Technical University,
61080, Trabzon,
Turkey.
E-mail:
mkunt@ktu.edu.tr
Abstract:
In this paper, some Hermite-Hadamard-Fejer type integral inequalities for harmonically s-convex functions in fractional integral forms have been obtained.
Paper's Title:
On the Biharmonic Equation with Nonlinear Boundary Integral Conditions
Author(s):
R. Hamdouche and H. Saker
L.M.A. Department of Mathematics, Faculty
of Sciences,
University of Badji Mokhtar,
P.O.Box 12. Annaba 23000,
Algeria.
E-mail: h_saker@yahoo.fr,
hmdch.rahma16@gmail.com
Abstract:
In the present work, we deal with the biharmonic problems in a bounded domain in the plane with the nonlinear boundary integral conditions. After applying the Boundary integral method, a system of nonlinear boundary integral equations is obtained. The result show that when the nonlinearity satisfies some conditions lead the existence and uniqueness of the solution.
Paper's Title:
Hyponormal and K-Quasi-Hyponormal Operators On Semi-Hilbertian Spaces
Author(s):
Ould Ahmed Mahmoud Sid Ahmed and Abdelkader Benali
Mathematics Department,
College of Science,
Aljouf University,
Aljouf 2014,
Saudi Arabia.
E-mail:
sididahmed@ju.edu.sa
Mathematics Department, Faculty of
Science,
Hassiba Benbouali, University of Chlef,
B.P. 151 Hay Essalem, Chlef 02000,
Algeria.
E-mail:
benali4848@gmail.com
Abstract:
Let H be a Hilbert space and let A be a positive bounded operator on H. The semi-inner product < u|v>A:=<Au|v>, u,v ∈ H induces a semi-norm || .||A on H. This makes H into a semi-Hilbertian space. In this paper we introduce the notions of hyponormalities and k-quasi-hyponormalities for operators on semi Hilbertian space (H,||.||A), based on the works that studied normal, isometry, unitary and partial isometries operators in these spaces. Also, we generalize some results which are already known for hyponormal and quasi-hyponormal operators. An operator T ∈ BA (H) is said to be (A, k)-quasi-hyponormal if
![]()
Paper's Title:
Partial Semigroup Algebras Associated to Partial Action
Author(s):
Bahman Tabatabaie Shourijeh and Sahar Moayeri Rahni
Department of Mathematics,
College of Sciences, Shiraz University,
Shiraz, 71454,
Iran.
E-mail:
tabataba@math.susc.ac.ir
Department of Mathematics,
College of Sciences, Shiraz University,
Shiraz, 71454,
Iran.
E-mail: smoayeri@shirazu.ac.ir
Abstract:
For a given inverse semigroup S, we introduce the notion of algebraic crossed product by using a given partial action of S, and we will prove that under some condition it is associative. Also we will introduce the concept of partial semigroup algebra KPar(S), and we show that the suitable quotient of KPar(S) is a kind of crossed product.
Paper's Title:
Strong Convergence Theorem for a Common Fixed Point of an
Infinite Family of J-nonexpansive Maps with Applications
Author(s):
Charlse Ejike Chidume, Otubo Emmanuel Ezzaka and Chinedu Godwin Ezea
African University of Science and
Technology,
Abuja,
Nigeria.
E-mail:
cchidume@aust.edu.ng
Ebonyi State University,
Abakaliki,
Nigeria.
E-mail: mrzzaka@yahoo.com
Nnamdi Azikiwe University,
Awka,
Nigeria.
E-mail: chinedu.ezea@gmail.com
Abstract:
Let E be a uniformly convex and uniformly smooth real Banach space with dual space E*. Let {Ti}∞i=1 be a family of J-nonexpansive maps, where, for each i,~Ti maps E to 2E*. A new class of maps, J-nonexpansive maps from E to E*, an analogue of nonexpansive self maps of E, is introduced. Assuming that the set of common J-fixed points of {Ti}∞i=1 is nonempty, an iterative scheme is constructed and proved to converge strongly to a point x* in ∩∞n=1FJTi. This result is then applied, in the case that E is a real Hilbert space to obtain a strong convergence theorem for approximation of a common fixed point for an infinite family of nonexpansive maps, assuming existences. The theorem obtained is compared with some important results in the literature. Finally, the technique of proof is also of independent interest.
Paper's Title:
Ostrowski Type Fractional Integral Inequalities for Generalized (s,m,
Author(s):
Artion Kashuri and Rozana Liko
University of Vlora "Ismail Qemali",
Faculty of Technical Science,
Department of Mathematics, 9400,
Albania.
E-mail:
artionkashuri@gmail.com
E-mail: rozanaliko86@gmail.com
Abstract:
In the present paper, the notion of generalized (s,m,φ)-preinvex function is introduced and some new integral inequalities for the left hand side of Gauss-Jacobi type quadrature formula involving generalized (s,m,φ)-preinvex functions along with beta function are given. Moreover, some generalizations of Ostrowski type inequalities for generalized (s,m,φ)-preinvex functions via Riemann-Liouville fractional integrals are established.
Paper's Title:
Convergence and Stability Results for New Three Step Iteration Process
in Modular Spaces
Author(s):
Naresh Kumar and Renu Chugh
Department of Mathematics,
M.D. University,
Rohtak-124001, Haryana,
India.
E-mail: nks280@gmail.com
E-mail: chugh.r1@gmail.com
Abstract:
The aim of this paper is to introduce a new iteration process (5) for ρ-contraction mappings in Modular spaces. We obtain some analytical proof for convergence and stability of our iteration process (5). We show that our iteration process (5) gives faster convergence results than the leading AK iteration process (4) for contraction mappings. Moreover, a numerical example (using the Matlab Software) is presented to compare the rate of convergence for existing iteration processes with our new iteration process (5).
Paper's Title:
On Commutator of Aluthge Transforms and Fuglede-Putnam Property
Author(s):
(Manzar Maleki, Ali Reza Janfada and Seyed Mohammad Sadegh Nabavi Sales
International Campus, Faculty of
Mathematical Sciences,
Ferdowsi University of Mashhad, Mashhad,
Iran.
E-mail: manzar.maleki@gmail.com
Faculty of Mathematics and Statistics,
Department of Mathematics,
University of Birjand,
P. O. Box 414, Birjand 9717851367,
Iran.
E-mail: ajanfada@birjand.ac.ir
Department of Pure Mathematics, Hakim
Sabzevari University,
P.O. Box 397, Sabzevar,
Iran.
E-mail: sadegh.nabavi@hsu.ac.ir
Abstract:
We deal with the well-known Fuglede-Putnam theorem and related FP-property. We show that if
(A,B) has the FP-property, then so has
![]() where 0≤
t1,t2≤1 are arbitrary.
We first prove that
where 0≤
t1,t2≤1 are arbitrary.
We first prove that
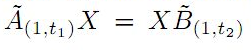 if and only if
AX=XB for all X, whenever (A,B) has the FP-property. We
prove some similar results for
if and only if
AX=XB for all X, whenever (A,B) has the FP-property. We
prove some similar results for
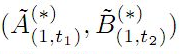 instead of $
instead of $![]() as well. Also we introduce the sequence of generalized iterations of Aluthge transform of operators and express some results for this notion associated to the FP-property.
as well. Also we introduce the sequence of generalized iterations of Aluthge transform of operators and express some results for this notion associated to the FP-property.
Paper's Title:
On Closed Range C*-modular Operators
Author(s):
Javad Farokhi-Ostad and Ali Reza Janfada
Department of Mathematics,
Faculty of Mathematics and Statistics Sciences,
University of Birjand, Birjand,
Iran.
E-mail: j.farokhi@birjand.ac.ir
ajanfada@birjand.ac.ir
Abstract:
In this paper, for the class of the modular operators on Hilbert C*-modules, we give the conditions to closedness of their ranges. Also, the equivalence conditions for the closedness of the range of the modular projections on Hilbert C*-modules are discussed. Moreover, the mixed reverse order law for the Moore-Penrose invertible modular operators are given.
Paper's Title:
Iterative Algorithm for Split Generalized Mixed Equilibrium Problem Involving Relaxed Monotone Mappings in Real Hilbert Spaces
Author(s):
1U.A. Osisiogu, F.L. Adum, and 2C. Izuchukwu
1Department of Mathematics and
Computer Science,
Ebonyi State University, Abakaliki,
Nigeria.
E-mail: uosisiogu@gmail.com,
adumson2@yahoo.com
2School of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: izuchukwuc@ukzn.ac.za,
izuchukwu_c@yahoo.com
Abstract:
The main purpose of this paper is to introduce a certain class of split generalized mixed equilibrium problem involving relaxed monotone mappings. To solve our proposed problem, we introduce an iterative algorithm and obtain its strong convergence to a solution of the split generalized mixed equilibrium problems in Hilbert spaces. As special cases of the proposed problem, we studied the proximal split feasibility problem and variational inclusion problem.
Paper's Title:
An Existence of the Solution to Neutral Stochastic Functional Differential Equations Under the Holder Condition
Author(s):
Young-Ho Kim
Department of Mathematics,
Changwon National University,
Changwon, Gyeongsangnam-do 51140,
Korea.
E-mail: iyhkim@changwon.ac.kr
Abstract:
In this paper, we show the existence and uniqueness of solution of the neutral stochastic functional differential equations under weakened H\"{o}lder condition, a weakened linear growth condition, and a contractive condition. Furthermore, in order to obtain the existence of a solution to the equation we used the Picard sequence.
Paper's Title:
Some fixed point results in partial S-metric spaces
Author(s):
M. M. Rezaee, S. Sedghi, A. Mukheimer, K. Abodayeh, and Z. D. Mitrovic
Department of Mathematics, Qaemshahr
Branch,
Islamic Azad University, Qaemshahr,
Iran.
E-mail: Rezaee.mohammad.m@gmail.com
Department of Mathematics, Qaemshahr
Branch,
Islamic Azad University, Qaemshahr,
Iran.
E-mail: sedghi.gh@qaemiau.ac.ir
Department of Mathematics and General
Sciences,
Prince Sultan University, Riyadh,
KSA.
E-mail: mukheimer@psu.edu.sa
Department of Mathematics and General
Sciences,
Prince Sultan University, Riyadh,
KSA.
E-mail: kamal@psu.edu.sa
Nonlinear Analysis Research Group,
Faculty of Mathematics and Statistics,
Ton Duc Thang University, Ho Chi Minh City,
Vietnam.
E-mail: zoran.mitrovic@tdtu.edu.vn
Abstract:
We introduce in this article a new class of generalized metric spaces, called partial S-metric spaces. In addition, we also give some interesting results on fixed points in the partial S-metric spaces and some applications.
Paper's Title:
Composite Variational-Like Inequalities Given By Weakly Relaxed
Author(s):
Syed Shakaib Irfan, Iqbal Ahmad, Zubair Khan and Preeti Shukla
College of Engineering, Qassim University
Buraidah, Al-Qassim,
Saudi Arabia.
E-mail: shakaib@qec.edu.sa
College of Engineering, Qassim University
Buraidah, Al-Qassim,
Saudi Arabia.
E-mail: iqbal@qec.edu.sa
Department of Mathematics,
Integral University Lucknow,
India.
E-mail: zkhan@iul.ac.in
Department of Mathematics,
Integral University Lucknow,
India.
E-mail: shuklapreeti1991@gmail.com
Abstract:
In this article, we introduce a composite variational-like inequalities with weakly relaxed ζ-pseudomonotone multi-valued maping in reflexive Banach spaces. We obtain existence of solutions to the composite variational-like inequalities with weakly relaxed ζ-pseudomon -otone multi-valued maps in reflexive Banach spaces by using KKM theorem. We have also checked the solvability of the composite variational-like inequalities with weakly relaxed ζ-semi-pseudomonotone multi-valued maps in arbitrary Banach spaces using Kakutani-Fan-Glicksberg fixed point theorem.
Paper's Title:
Double Difference of Composition Operator on Bloch Spaces
Author(s):
Rinchen Tundup
Department of Mathematics
University of Jammu
Jammu and Kashmir
India.
E-mail: joneytun123@gmail.com
Abstract:
In this paper we characterize the compactness of double difference of three non-compact composition operators on Bloch space induced by three holomorphic self maps on the unit disc.
Paper's Title:
Attempts to Define a Baum--Connes Map Via Localization of Categories for Inverse Semigroups
Author(s):
Bernhard Burgstaller
Departamento de Matematica,
Universidade Federal de Santa Catarina,
CEP 88.040-900 Florianopolis-SC,
Brasil.
E-mail:
bernhardburgstaller@yahoo.de
URL:
http://mathematik.work/bernhardburgstaller/index.html
Abstract:
An induction functor in inverse semigroup equivariant KK-theory is considered, and together with %a restriction functors certain results similar to those known from the Mackey machinery are shown. It is also verified that for any so-called E-continuous inverse semigroup its equivariant KK-theory satisfies the universal property and is a triangulated category.
Paper's Title:
Estimates of Norms on Krein Spaces
Author(s):
Satheesh K. Athira, P. Sam Johnson and K. Kamaraj
Department of Mathematical and Computational Sciences,
National Institute of Technology Karnataka,
Surathkal, Mangaluru 575 025,
India.
E-mail: athirachandri@gmail.com
Department of Mathematical and
Computational Sciences,
National Institute of Technology Karnataka,
Surathkal, Mangaluru 575 025,
India.
E-mail:sam@nitk.edu.in
Department of Mathematics,
University College of Engineering Arni,
Anna University, Arni 632 326,
India.
E-mail: krajkj@yahoo.com
Abstract:
Various norms can be defined on a Krein space by choosing different underlying fundamental decompositions. Some estimates of norms on Krein spaces are discussed and a few results in Bognar's paper are generalized.
Paper's Title:
Sharp Inequalities Between Hölder and Stolarsky Means of Two Positive Numbers
Author(s):
M. Bustos Gonzalez and A. I. Stan
The University of Iowa,
Department of Mathematics,
14 MacLean Hall,
Iowa City, Iowa,
USA.
E-mail:
margarita-bustosgonzalez@uiowa.edu
The Ohio State University at Marion,
Department of Mathematics,
1465 Mount Vernon Avenue,
Marion, Ohio,
USA.
E-mail: stan.7@osu.edu
Abstract:
Given any index of the Stolarsky means, we find the greatest and least indexes of the H\"older means, such that for any two positive numbers, the Stolarsky mean with the given index is bounded from below and above by the Hölder means with those indexes, of the two positive numbers. Finally, we present a geometric application of this inequality involving the Fermat-Torricelli point of a triangle.
Paper's Title:
Estimation for Bounded Solutions of Some Nonlinear Integral Inequalities with Delay in Several Variables
Author(s):
Smakdji Mohamed Elhadi, Denche Mouhamed and Khellaf Hassane
Department of Mathematics
University of Frčres Mentouri
PO Box 25000, Ain Elbay,
Constantine,
Algeria.
E-mail: khellafhassane@umc.edu.dz
Abstract:
In this paper, some new nonlinear retarded integral inequalities of Gronwall-Bellman type for functions of two and n-independents variables are investigated. The derived results can be applied in the study of differential-integral equations with time delay. An example is given to illustrate the application of our results.
Paper's Title:
Uniqueness Problems for Difference Polynomials Sharing a Non-Zero Polynomial of Certain Degree With Finite Weight
Author(s):
V. Priyanka, S. Rajeshwari and V. Husna
Department of Mathematics,
School of Engineering,
Presidency University,
Bangalore-560064,
India.
E-mail:
priyapriyankaram1994@gmail.com
rajeshwaripreetham@gmail.com
husnav43@gmail.com
Abstract:
In this paper, we prove a result on the value distribution of difference polynomials sharing higher order derivatives of meromorphic functions which improves some earlier results. At the same time, we also prove possible uniqueness relation of entire functions when the difference polynomial generated by them sharing a non zero polynomial of certain degree. The result obtained in the paper will improve and generalize a number of recent results in a compact and convenient way.
Paper's Title:
Jordan Canonical Form of Interval Matrices and Applications
Author(s):
S. Hema Surya, T. Nirmala and K. Ganesan
Department of Mathematics, College of
Engineering and Technology,
SRM Institute of Science and Technology,
Kattankulathur,
Chennai-603203,
India.
E-mail: nirmalat@srmist.edu.in
URL:
https://www.srmist.edu.in/faculty/dr-t-nirmala/
Abstract:
A square interval matrix over R can be converted to diagonal form if certain prerequisites are satisfied. However not all square matrices can be diagonalized. As a consequence, we strive the next simplest form to which it can be reduced while retaining important properties such as eigenvalues, rank, nullity, and so on. It turns out that any real interval matrix has a Jordan Canonical Form (JCF) over E if it has n interval eigenvalues in IR. We discuss in this paper a method for computing the Jordan canonical form of an interval matrix using a new pairing technique and a new type of interval arithmetic that will make classifying and analyzing interval matrices easier and more efficient. We conclude with a numerical example that supports the theory and application of predator-prey model.
Paper's Title:
Eigenvalue Bounds based on Projections
Author(s):
Pravin Singh, Shivani Singh, Virath Singh
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
University of South Africa,
Department of Decision Sciences, PO Box 392,
Pretoria,0003,
South Africa.
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
E-mail:
singhp@ukzn.ac.za,
singhs2@unisa.ac.za,
singhv@ukzn.ac.za
Abstract:
In this paper, we derive expressions for the bounds of the extremal eigenvalues of positive definite matrices. Our approach is to use a symmetric projection operator onto an n-2 dimensional subspace of the real space of n tuples. These bounds are based on traces of the matrix and its powers. They are relatively easy and inexpensive to compute.
Paper's Title:
Generalized Triangular and Symmetric Splitting Method for Steady State Probability Vector of Stochastic Matrices
Author(s):
B. Harika, D. Rajaiah, L. P. RajKumar, Malla Reddy Perati
Department of Mathematics,
Kakatiya University
E-mail: hbolledla@gmail.com
Department of Mathematics,
Kakatiya Institute of Technology and Science
E-mail: dr.mh@kitsw.ac.in
Department of Mathematics,
Kakatiya University
E-mail: ladalla@gmail.com
Department of Mathematics,
Kakatiya University
E-mail: mperati@yahoo.com
Abstract:
To find the steady state probability vector of homogenous linear system π Q=0 of stochastic rate matrix Q, generalized triangular and symmetric (GTS) splitting method is presented. Convergence analysis and choice of parameters are given when the regularized matrix A=QT+ε I of the regularized linear system Ax=b is positive definite. Analysis shows that the iterative solution of GTS method converges unconditionally to the unique solution of the regularized linear system. From the numerical results, it is clear that the solution of proposed method converges rapidly when compared to the existing methods.
Paper's Title:
Recursive Bounds for the Eigenvalues of Symmetric Positive Definite Matrices
Author(s):
Pravin Singh, Shivani Singh, Virath Singh
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
University of South Africa,
Department of Decision Sciences, PO Box 392,
Pretoria,0003,
South Africa.
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
E-mail:
singhp@ukzn.ac.za,
singhs2@unisa.ac.za,
singhv@ukzn.ac.za
Abstract:
In this paper, we bound the extremal eigenvalues of a positive definite real symmetric matrix by considering a part of the characteristic equation in the region of the smallest and largest eigenvalues. An expansion around these values leads to a sequence of monotonic functions, whose zeros coincide with the extremal zeros of associated polynomials. The latter is shown to yield bounds that are fairly accurate.
Paper's Title:
Refinement of Jensen's Inequality for Analytical Convex (Concave) Functions
Author(s):
P. Kórus, Z. Retkes
Institute of Applied Pedagogy,
Juhász Gyula Faculty of Education,
University of Szeged,
Hattyas utca 10, H-6725 Szeged,
Hungary.
E-mail: korus.peter@szte.hu
65 Manor Road, Desford, LE9 9JQ,
United Kingdom.
E-mail:
tigris35711@gmail.com
Abstract:
The well-known Jensen inequality and Hermite--Hadamard inequality were extended using iterated integrals by Z. Retkes in 2008 and then by P. Kórus in 2019. In this paper, we consider analytical convex (concave) functions in order to obtain new refinements of Jensen's inequality. We apply the main result to the classical HM--GM--AM, AM--RMS, triangle inequalities and present an application to the geometric series. We also give Mercer type variants of Jensen's inequality.
Paper's Title:
On the Pathwise Uniqueness of Solutions to Stochastic Integral Equations of Ito Type
Author(s):
Romeo Negrea
Department of Mathematics,
Politehnica University of Timisoara,
P-ta Victoriei 2, 300006, Timisoara,
Romania.
E-mail: romeo.negrea@upt.ro
Abstract:
We give sufficient conditions for the pathwise uniqueness of solutions to nonlinear stochastic integral equations of Itô type. The result concerns a relaxation of the classical Lipschitz condition by allowing for a Nagumo-type fast-growing time dependence as the initial time is approached. We also propose a special subclass of functions N ⊂ M which shows that our considerations go beyond the classical contraction case. Moreover, they assure the facilities for to prove the existence and uniqueness of solutions and for the existence of the fixed points for some class of operators associated to stochastic integral equations.
Search and serve lasted 1 second(s).