|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
An Integration Technique for Evaluating Quadratic Harmonic Sums
Author(s):
J. M. Campbell and K.-W. Chen
Department of Mathematics and Statistics,
York University, 4700 Keele St, Toronto,
ON M3J 1P3,
Canada.
E-mail: jmaxwellcampbell@gmail.com
Department of Mathematics, University of Taipei,
No. 1, Ai-Guo West Road,
Taipei 10048, Taiwan.
E-mail: kwchen@uTaipei.edu.tw
URL:
https://math.utaipei.edu.tw/p/412-1082-22.php
Abstract:
The modified Abel lemma on summation by parts has been applied in many ways recently to determine closed-form evaluations for infinite series involving generalized harmonic numbers with an upper parameter of two. We build upon such results using an integration technique that we apply to ``convert'' a given evaluation for such a series into an evaluation for a corresponding series involving squared harmonic numbers.
Paper's Title:
Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
On the Generalized Inverse  over Integral Domains
over Integral Domains
Author(s):
Yaoming Yu and Guorong Wang
College of Education, Shanghai Normal University
Shanghai 200234
People's Republic of China.
yuyaoming@online.sh.cn
grwang@shnu.edu.cn
Abstract:
In this paper, we study further the generalized inverse
 of a matrix A over an integral domain. We give
firstly some necessary and sufficient conditions for the existence
of the generalized inverse
of a matrix A over an integral domain. We give
firstly some necessary and sufficient conditions for the existence
of the generalized inverse  , an explicit expression
for the elements of the generalized inverse
, an explicit expression
for the elements of the generalized inverse  and an
explicit expression for the generalized inverse
and an
explicit expression for the generalized inverse  ,
which reduces to the {1} inverse. Secondly, we verify that the
group inverse, the Drazin inverse, the Moore-Penrose inverse and the
weighted Moore-Penrose inverse are identical with the generalized
inverse
,
which reduces to the {1} inverse. Secondly, we verify that the
group inverse, the Drazin inverse, the Moore-Penrose inverse and the
weighted Moore-Penrose inverse are identical with the generalized
inverse 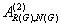 for an appropriate matrix G,
respectively, and then we unify the conditions for the existence and
the expression for the elements of the weighted Moore-Penrose
inverse, the Moore-Penrose inverse, the Drazin inverse and the group
inverse over an integral domain. Thirdly, as a simple application,
we give the relation between some rank equation and the existence of
the generalized inverse
for an appropriate matrix G,
respectively, and then we unify the conditions for the existence and
the expression for the elements of the weighted Moore-Penrose
inverse, the Moore-Penrose inverse, the Drazin inverse and the group
inverse over an integral domain. Thirdly, as a simple application,
we give the relation between some rank equation and the existence of
the generalized inverse  , and a method to compute the
generalized inverse
, and a method to compute the
generalized inverse  . Finally, we give an example of
evaluating the elements of
. Finally, we give an example of
evaluating the elements of  without calculating
without calculating
 .
.
Paper's Title:
Positive Solutions for Systems of Three-point Nonlinear Boundary Value Problems
Author(s):
J. Henderson and S. K. Ntouyas
Department of Mathematics, Baylor University
Waco, Texas
76798-7328 USA.
Johnny_Henderson@baylor.edu
URL: http://www3.baylor.edu/~Johnny_Henderson
Department of Mathematics, University of Ioannina
451 10 Ioannina,
Greece.
sntouyas@cc.uoi.gr
URL: http://www.math.uoi.gr/~sntouyas
Abstract:
Values of λ are determined for which there exist
positive solutions of the system of three-point boundary value problems,
u''(t)+ λa(t)f(v(t))=0, v''(t)+λb(t)g(u(t))=0,
for 0 < t <1, and
satisfying, u(0) = 0, u(1)=α u(η),
v(0) = 0, v(1)=α v(η). A Guo-Krasnosel'skii fixed
point theorem is applied. Paper's Title:
On a Class of Meromorphic Functions of Janowski Type Related with a Convolution Operator Author(s):
Abdul Rahman S. Juma, Husamaldin I. Dhayea Department of
Mathematics, Department of Mathematics, Abstract:
In this paper, we have introduced and studied new operator $Qkλ,m,γ by the Hadamard product (or convolution) of two linear operators Dkλ
and Im,γ, then using this operator to study and investigate a new subclass of meromorphic functions of Janowski type, giving the coefficient bounds, a sufficient condition for a function to belong to the considered class and also a convolution property. The results presented provide generalizations of results given in earlier works. Paper's Title:
Sweeping Surfaces with Darboux Frame in Euclidean 3-space E3 Author(s):
F. Mofarreh, R. Abdel-Baky and N. Alluhaibi Mathematical Science Department, Faculty
of Science, Department of Mathematics Science and
Arts, College Rabigh Campus, Abstract:
The curve on a regular surface has a moving frame and it is called Darboux frame. We introduce sweeping surfaces along the
curve relating to the this frame and investigate their geometrical properties. Moreover, we obtain the necessary and sufficient conditions for these
surfaces to be developable ruled surfaces. Finally, an example to illustrate the
application of the results is introduced. Paper's Title:
Positive Periodic Solutions for
Second-Order Differential Equations with Generalized Neutral Operator Author(s):
Wing-Sum Cheung, Jingli Ren and Weiwei Han
6: Paper Source
PDF document
Alanbar University, Ramadi,
Iraq.
E-mail: dr_juma@hotmail.com
Tikrit University, Tikrit,
Iraq.
URL: husamaddin@gmail.com
6: Paper Source
PDF document
Princess Nourah bint Abdulrahman University
Riyadh 11546,
Saudi Arabia.
E-mail: fyalmofarrah@pnu.edu.sa
Department of Mathematics, Faculty of Science,
University of Assiut,
Assiut 71516,
Egypt.
E-mail: rbaky@live.com
King Abdulaziz University
Jeddah,
Saudi Arabia.
E-mail: nallehaibi@kau.edu.sa
5: Paper Source
PDF document
Department of Mathematics,
The University of Hong Kong
Pokfulam
Road,
Hong Kong
Department of Mathematics, Zhengzhou University
Zhengzhou 450001,
P.R. China
wscheung@hkucc.hku.hk
renjl@zzu.edu.cn
Abstract:
By some analysis of the neutral operator
![]() and an application of the fixed-point
index theorem, we obtain sufficient conditions for the existence,
multiplicity and nonexistence of periodic solutions to a second-order
differential equation with the prescribed neutral operator, which improve
and extend some recent results of Lu-Ge, Wu-Wang, and Zhang. An example is
given to illustrate our results. Moreover, the analysis of the generalized
neutral operator will be helpful for other types of differential equations.
and an application of the fixed-point
index theorem, we obtain sufficient conditions for the existence,
multiplicity and nonexistence of periodic solutions to a second-order
differential equation with the prescribed neutral operator, which improve
and extend some recent results of Lu-Ge, Wu-Wang, and Zhang. An example is
given to illustrate our results. Moreover, the analysis of the generalized
neutral operator will be helpful for other types of differential equations.
Paper's Title:
Maximal Inequalities for Multidimensionally Indexed Demimartingales and the Hájek-Rényi Inequality for Associated Random Variables
Author(s):
Tasos C. Christofides and Milto Hadjikyriakou
Department of Mathematics and Statistics
University of Cyprus
P.O.Box 20537, Nicosia 1678, Cyprus
tasos@ucy.ac.cy
miltwh@gmail.com
Abstract:
Demimartingales and demisubmartingales introduced by
Newman and
Wright (1982) generalize the notion of martingales and
submartingales respectively. In this paper we define
multidimensionally indexed demimartingales and demisubmartingales
and prove a maximal inequality for this general class of random
variables. As a corollary we obtain a Hájek-Rényi inequality
for multidimensionally indexed associated random variables, the bound of which,
when reduced to the case of single index, is sharper than the bounds already
known in the literature.
Paper's Title:
New Refinements of Hölder's Inequality
Author(s):
Xiu-Fen Ma
College of Mathematical and Computer,
Chongqing Normal University Foreign Trade and Business College,
No.9 of Xuefu Road, Hechuan District 401520,
Chongqing City,
The People's Republic of China.
E-mail: maxiufen86@163.com
Abstract:
In this paper, we define two mappings, investigate their properties, obtain some new refinements of Hölder's inequality.
Paper's Title:
Iterative Algorithm for Split Generalized Mixed Equilibrium Problem Involving Relaxed Monotone Mappings in Real Hilbert Spaces
Author(s):
1U.A. Osisiogu, F.L. Adum, and 2C. Izuchukwu
1Department of Mathematics and
Computer Science,
Ebonyi State University, Abakaliki,
Nigeria.
E-mail: uosisiogu@gmail.com,
adumson2@yahoo.com
2School of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: izuchukwuc@ukzn.ac.za,
izuchukwu_c@yahoo.com
Abstract:
The main purpose of this paper is to introduce a certain class of split generalized mixed equilibrium problem involving relaxed monotone mappings. To solve our proposed problem, we introduce an iterative algorithm and obtain its strong convergence to a solution of the split generalized mixed equilibrium problems in Hilbert spaces. As special cases of the proposed problem, we studied the proximal split feasibility problem and variational inclusion problem.
Paper's Title:
Timelike Surfaces with a Common Line of Curvature in Minkowski 3-Space
Author(s):
M.K. Saad, A.Z. Ansari, M. Akram and F. Alharbi
Department of Mathematics ,
Faculty of Science,
Islamic University of Madinah,
KSA
Abstract:
In this paper, we analyze the problem of constructing a timelike surface family from a given non-null curve line of curvature. Using the Frenet frame of the non-null curve in Minkowski space E13 we express the family of surfaces as a linear combination of the components of this frame, and derive the necessary and sufficient conditions for the coefficients to satisfy both the line of curvature and the isoparametric requirements. In addition, a necessary and sufficient condition for the given non-null curve to satisfy the line of curvature and the geodesic requirements is investigated. The extension to timelike surfaces of revolution is also outlined. Meanwhile, some representative non-null curves are chosen to construct the corresponding timelike surfaces which possessing these curves as lines of curvature. Results presented in this paper have applications in geometric modeling and the manufacturing of products. In addition, some computational examples are given and plotted.
Paper's Title:
Several New Closed-form Evaluations of the Generalized Hypergeometric Function with Argument 1/16
Author(s):
B. R. Srivatsa Kumar, Insuk Kim and Arjun K. Rathie
Department of Mathematics,
Manipal Institute of Technology,
Manipal Academy of Higher Education,
Manipal 576 104,
India.
E-mail: sri_vatsabr@yahoo.com
Department of Mathematics Education,
Wonkwang University,
Iksan, 54538,
Republic of Korea.
E-mail: iki@wku.ac.kr
Department of Mathematics,
Vedant College of Engineering and Technology,
Rajasthan Technical University,
Bundi, 323021, Rajasthan,
India.
E-mail: arjunkumarrathie@gmail.com
Abstract:
The main objective of this paper is to establish as many as thirty new closed-form evaluations of the generalized hypergeometric function q+1Fq(z) for q= 2, 3, 4. This is achieved by means of separating the generalized hypergeometric function q+1Fq(z) for q=1, 2, 3, 4, 5 into even and odd components together with the use of several known infinite series involving central binomial coefficients obtained earlier by Ji and Hei \& Ji and Zhang.
Paper's Title:
New Refinements for Integral and Sum Forms of Generalized Hölder Inequality For N Term
Author(s):
M. Jakfar, Manuharawati, D. Savitri
Mathematics Department,
Universitas Negeri Surabaya
Jalan Ketintang Gedung C8, Surabaya, 60321
Indonesia.
E-mail: muhammadjakfar@unesa.ac.id
manuharawati@unesa.ac.id
diansavitri@unesa.ac.id
Abstract:
We know that in the field of functional analysis, Hölder inequality is very well known, important, and very applicable. So many researchers are interested in discussing these inequalities. Many world mathematicians try to improve these inequalities. In general, the Hölder inequality has two forms, namely the integral form and the sum form. In this paper, we will introduce a new refinement of the generalization of Hölder inequalities in both integral and addition forms. Especially in the sum form, improvements will be introduced that are better than the previous improvements that have been published by Jing-feng Tian, Ming-hu Ha, and Chao Wang.
Paper's Title:
A General Fractional Control Scheme for Compound Combination Synchronization Between Different Fractional-Order Identical Chaotic Systems
Author(s):
Soumia Bensimessaoud and Smail Kaouache
Laboratory of Mathematics and their interactions, Abdelhafid Boussouf University Center, Mila, Algeria.
E-mail:
soumiabensimessaoud@gmail.com,
smailkaouache@gmail.com
Abstract:
In this paper, we aim to investigate the problem of compound combination synchronization (CCS) between four different fractional-order identical chaotic systems. Based on Laplace transformation and stability theory of linear dynamical systems, a new control law is proposed to assure the achievement of this kind of synchronization. Secondly, this control scheme is applied to realised CCS between four identical unified chaotic systems. Recall, that the proposed control scheme can be applied to wide classes of chaotic and hyperchaotic systems. Numerical simulations are given to show the effectiveness of the proposed method.
Paper's Title:
Two Mappings Related to Steffensen's Inequalities
Author(s):
Liang-Cheng Wang
School of Mathematical Science,
Chongqing Institute of Technology,
Xingsheng Lu 4,
Yangjiaping 400050, Chongqing City,
China.
wangliangcheng@163.com
Abstract:
In this paper, we define two mappings closely connected with
Steffensen's inequalities, investigate their main properties,
give some refinements for Steffensen's inequalities and obtain new
inequalities.
Paper's Title:
On a Problem on Periodic Functions
Author(s):
Adel A. Abdelkarim
Mathematics Department, Faculty of
Science,
Jerash Private University, Jerash,
Jordan.
E-mail:
adelafifo_afifo@yahoo.com
Abstract:
Given a continuous periodic real function f with n translates f1 ,..., fn , where fi(x)=f(x+ai), i=1,...,n. We solve a problem by Erdos and Chang and show that there are rational numbers r,s such that f(r)≥ fi(r), f(s)≤ fi(s), i=1,...,n. No restrictions on the constants or any further restriction on the function f are necessary as was imposed earlier.
Paper's Title:
MSplit Equality for Monotone Inclusion Problem and Fixed Point Problem in
Real Banach Spaces
Author(s):
1,2Christian Chibueze Okeke, 3Abdumalik Usman Bello, 1Chinedu Izuchukwu, and 1Oluwatosin Temitope Mewomo
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: okekec@ukzn.ac.za
E-mail: izuchukwuc@ukzn.ac.za
E-mail: mewomoo@ukzn.ac.za
2DST-NRF
Center of Excellence in Mathematical and Statistical Sciences (CoE-Mass)
Johannesburg,
South Africa.
3Federal
University,
Dutsin-Ma, Katsina State,
Nigeria.
E-mail:
uabdulmalik@fudutsinma.edu.ng
Abstract:
In this paper a new iterative algorithm for approximating a common solution of split equality monotone inclusion problem and split equality fixed point problem is introduced. Using our algorithm, we state and prove a strong convergence theorem for approximating an element in the intersection of the set of solutions of a split equality monotone inclusion problem and the set of solutions of a split equality fixed point problem for right Bregman strongly nonexpansive mappings in the setting of p-uniformly convex Banach spaces which are also uniformly smooth. We also give some applications.
Paper's Title:
Inequalities for Functions of Selfadjoint Operators on Hilbert Spaces:
a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
College of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning inequalities for continuous functions of selfadjoint operators on complex Hilbert spaces. It is intended for use by both researchers in various fields of Linear Operator Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Coexisting Attractors and Bubbling Route to Chaos in Modified Coupled Duffing Oscillators
Author(s):
B. Deruni1, A. S. Hacinliyan1,2, E. Kandiran3, A. C. Keles2, S. Kaouache4, M.-S. Abdelouahab4, N.-E. Hamri4
1Department
of Physics,
University of Yeditepe,
Turkey.
2Department
of Information Systems and Technologies,
University of Yeditepe,
Turkey
3Department
of Software Development,
University of Yeditepe,
Turkey.
4Laboratory
of Mathematics and their interactions,
University Center of Abdelhafid Boussouf,
Mila 43000,
Algeria.
E-mail:
berc890@gmail.com
ahacinliyan@yeditepe.edu.tr
engin.kandiran@yeditepe.edu.tr
cihan.keles@yeditepe.edu.tr
s.kaouache@centr-univ-mila.dz
medsalah3@yahoo.fr
n.hamri@centre-univ-mila.dz
Abstract:
In this article dynamical behavior of coupled Duffing oscillators is analyzed under a small modification. The oscillators have cubic damping instead of linear one. Although single duffing oscillator has complex dynamics, coupled duffing systems possess a much more complex structure. The dynamical behavior of the system is investigated both numerically and analytically. Numerical results indicate that the system has double scroll attractor with suitable parameter values. On the other hand, bifurcation diagrams illustrate rich behavior of the system, and it is seen that, system enters into chaos with different routes. Beside classical bifurcations, bubbling route to chaos is observed for suitable parameter settings. On the other hand, Multistability of the system is indicated with the coexisting attractors, such that under same parameter setting the system shows different periodic and chaotic attractors. Moreover, chaotic synchronization of coupled oscillators is illustrated in final section.
Paper's Title:
Fractional Integral Inequalities of Hermite-Hadamard Type for P-convex and Quasi-Convex Stochastic Process
Author(s):
Oualid Rholam, Mohammed Barmaki and Driss Gretet
National School of Applied Sciences (ENSA),
University Ibn Tofail,
B.P 242 Kenitra 14000,
phone number : +212606257757,
Morocco.
E-mail: oualid.rholam@uit.ac.ma
Science Faculty Ben M'sik,
University Hassan II,
B.P 7955 Av Driss El Harti Sidi Othmane 20700,
phone number : +212 5 22 70 46 71 ,
Morocco.
E-mail: mohammed.barmaki@uit.ac.ma
National School of Applied Sciences (ENSA),
University Ibn Tofail,
B.P 242 Kenitra 14000,
phone number : +212661403557,
Morocco.
E-mail: driss.gretete@uit.ac.ma
Abstract:
In this paper we consider the class of P-convex and Quasi-convex stochastic processes on witch we apply a general class of generalized fractional integral operator in order to establish new integral inequalities of Hermite-Hadammard type. then we obtain some results for well known types of fractional integrals. Results obtained in this paper may be starting point as well as a useful source of inspiration for further research in convex analysis.
Paper's Title:
A New Iterative Approximation of a Split Fixed Point Constraint Equilibrium Problem
Author(s):
Musa Adewale Olona1, Adhir Maharaj2 and Ojen Kumar Narain3
1School
of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 219095783@stu.ukzn.ac.za
2Department
of Mathematics,
Durban University of Technology, Durban,
South Africa.
E-mail: adhirm@dut.ac.za
3School
of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
The purpose of this paper is to introduce an iterative algorithm for approximating an element in the solution set of the common split feasibility problem for fixed points of demimetric mappings and equilibrium problem for monotone mapping in real Hilbert spaces. Motivated by self-adaptive step size method, we incorporate the inertial technique to accelerate the convergence of the proposed method and establish a strong convergence of the sequence generated by the proposed algorithm. Finally, we present a numerical example to illustrate the significant performance of our method. Our results extend and improve some existing results in the literature.
Paper's Title:
Positive Solutions of Evolution Operator Equations
Author(s):
Radu Precup
Department of Applied Mathematics,
Babes-Bolyai University,
Cluj, Romania
Abstract:
Existence and localization results are derived from Krasnoselskii’s compressionexpansion
fixed point theorem in cones, for operator equations in spaces of continuous functions
from a compact real interval to an abstract space. The main idea, first used in [12], is to handle
two equivalent operator forms of the equation, one of fixed point type giving the operator to
which Krasnoselskii’s theorem applies and an other one of coincidence type which is used to
localize a positive solution in a shell. An application is presented for a boundary value problem
associated to a fourth order partial differential equation on a rectangular domain.
Paper's Title:
A Generalization of Ostrowski's Inequality for Functions of Bounded
Variation via a Parameter
Author(s):
Seth Kermausuor
Department of Mathematics and Computer
Science,
Alabama State University,
Montgomery, AL 36101,
USA.
E-mail:
skermausour@alasu.edu
Abstract:
In this paper, we provide a generalization of the Ostrowski's inequality for functions of bounded variation for k points via a parameter λ∈[0,1]. As a by product, we consider some particular cases to obtained some interesting inequalities in these directions. Our results generalizes some of the results by Dragomir in [S. S. DRAGOMIR, The Ostrowski inequality for mappings of bounded variation, Bull. Austral. Math. Soc., 60 (1999), pp. 495--508.]
Paper's Title:
Fractional exp(-φ(ξ))- Expansion Method and its Application to Space--Time Nonlinear Fractional Equations
Author(s):
A. A. Moussa and L. A. Alhakim
Department of Management Information
System and Production Management,
College of Business and Economics, Qassim University,
P.O. BOX 6666, Buraidah: 51452,
Saudi Arabia.
E-mail: Alaamath81@gmail.com
URL:
https://scholar.google.com/citations?user=ccztZdsAAAAJ&hl=ar
Department of Management Information
System and Production Management,
College of Business and Economics, Qassim University,
P.O. BOX 6666, Buraidah: 51452,
Saudi Arabia.
E-mail: Lama2736@gmail.com
URL:
https://scholar.google.com/citations?user=OSiSh1AAAAAJ&hl=ar
Abstract:
In this paper, we mainly suggest a new method that depends on the fractional derivative proposed by Katugampola for solving nonlinear fractional partial differential equations. Using this method, we obtained numerous useful and surprising solutions for the space--time fractional nonlinear Whitham--Broer--Kaup equations and space--time fractional generalized nonlinear Hirota--Satsuma coupled KdV equations. The solutions obtained varied between hyperbolic, trigonometric, and rational functions, and we hope those interested in the real-life applications of the previous two equations will find this approach useful.
Paper's Title:
Reduced Generalized Combination Synchronization Between Two n-Dimensional Integer-Order Hyperchaotic Systems and One m-Dimensional Fractional-Order Chaotic System
Author(s):
Smail Kaouache, Mohammed Salah Abdelouahab and Rabah Bououden
Laboratory of Mathematics and their
interactions,
Abdelhafid Boussouf University Center, Mila.
Algeria
E-mail: smailkaouache@gmail.com,
medsalah3@yahoo.fr,
rabouden@yahoo.fr
Abstract:
This paper is devoted to investigate the problem of reduced generalized combination synchronization (RGCS) between two n-dimensional integer-order hyperchaotic drive systems and one m-dimensional fractional-order chaotic response system. According to the stability theorem of fractional-order linear system, an active mode controller is proposed to accomplish this end. Moreover, the proposed synchronization scheme is applied to synchronize three different chaotic systems, which are the Danca hyperchaotic system, the modified hyperchaotic Rossler system, and the fractional-order Rabinovich-Fabrikant chaotic system. Finally, numerical results are presented to fit our theoretical analysis.
Paper's Title:
Existence and Approximation of Traveling Wavefronts for the Diffusive Mackey-Glass Equation
Author(s):
C. Ramirez-Carrasco and J. Molina-Garay
Facultad de Ciencias Basicas,
Universidad Catolica del Maule, Talca,
Chile
E-mail: carloshrc1989@gmail.com
molina@imca.edu.pe
Abstract:
In this paper, we consider the diffusive Mackey-Glass model with discrete delay. This equation describes the dynamics of the blood cell production. We investigate the existence of traveling wavefronts solutions connecting the two steady states of the model. We develop an alternative proof of the existence of such solutions and we also demonstrate the existence of traveling wavefronts moving at minimum speed. The proposed approach is based on the use technique of upper-lower solutions. Finally, through an iterative procedure, we show numerical simulations that approximate the traveling wavefronts, thus confirming our theoretical results.
Paper's Title:
Evaluation of a New Class of Double Integrals Involving Generalized Hypergeometric Function
4F3
Author(s):
Joohyung Kim, Insuk Kim and Harsh V. Harsh
Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Korea.
E-mail: joohyung@wku.ac.kr
Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Korea.
E-mail: iki@wku.ac.kr
Department of Mathematics, Amity School
of Eng. and Tech.,
Amity University Rajasthan
NH-11C, Jaipur-303002, Rajasthan,
India.
E-mail: harshvardhanharsh@gmail.com
Abstract:
Very recently, Kim evaluated some double integrals involving a generalized hypergeometric function 3F2 with the help of generalization of Edwards's well-known double integral due to Kim, et al. and generalized classical Watson's summation theorem obtained earlier by Lavoie, et al. In this research paper we evaluate one hundred double integrals involving generalized hypergeometric function 4F3 in the form of four master formulas (25 each) viz. in the most general form for any integer. Some interesting results have also be obtained as special cases of our main findings.
Paper's Title:
A Review on Minimally Supported Frequency Wavelets
Author(s):
K Pallavi1, M C Lineesh1, A Noufal2
1
Department of Mathematics,2Department of Mathematics,
Cochin University of Science and Technology,
Kerala 682022,
India.
E-mail: noufal@cusat.ac.in
Abstract:
This paper provides a review on Minimally Supported Frequency (MSF) wavelets that includes the construction and characterization of MSF wavelets. The characterization of MSF wavelets induced from an MRA is discussed and the nature of the low-pass filter associated with it is explained. The concept of wavelet set and dimension function is introduced to study this class of wavelets. Along with MSF wavelets, s-elementary wavelets and unimodular wavelets are also considered due to the similarity in definitions. Examples and illustrations are provided for more clarity.
Paper's Title:
Estimation for Bounded Solutions of Some Nonlinear Integral Inequalities with Delay in Several Variables
Author(s):
Smakdji Mohamed Elhadi, Denche Mouhamed and Khellaf Hassane
Department of Mathematics
University of Frères Mentouri
PO Box 25000, Ain Elbay,
Constantine,
Algeria.
E-mail: khellafhassane@umc.edu.dz
Abstract:
In this paper, some new nonlinear retarded integral inequalities of Gronwall-Bellman type for functions of two and n-independents variables are investigated. The derived results can be applied in the study of differential-integral equations with time delay. An example is given to illustrate the application of our results.
Paper's Title:
SQIRV Model for Omicron Variant with Time Delay
Author(s):
S. Dickson, S. Padmasekaran, G. E. Chatzarakis and S. L. Panetsos
Mathematics, Periyar University, Periyar
Palkalai Nagar, Salem,
636011, Tamilnadu,
India.
E-mail:
dickson@periyaruniversity.ac.in,
padmasekarans@periyaruniversity.ac.in
Electrical and Electronic Engineering
Educators, School of
Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
spanetsos@aspete.gr
Abstract:
In order to examine the dynamics of the Omicron variant, this paper uses mathematical modelling and analysis of a SQIRV model, taking into account the delay in the conversion of susceptible individuals into infected individuals and infected individuals into recovered individuals. The pandemic was eventually controlled as a result of the massive delays. To assure the safety of the host population, this concept incorporates quarantine and the COVID-19 vaccine. Both local and global stability of the model are examined. It is found that the fundamental reproduction number affects both local and global stability conditions. Our findings show that asymptomatic cases caused by an affected population play an important role in increasing Omicron infection in the general population. The most recent data on the pandemic Omicron variant from Tamil Nadu, India, is verified.
Paper's Title:
Two Further Methods for Deriving Four Results Contiguous to Kummer's Second Theorem
Author(s):
I. Kim and J. Kim
Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Korea.
E-mail: iki@wku.ac.kr
Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Korea.
E-mail: joohyung@wku.ac.kr
Abstract:
In the theory of generalized hypergeometric function, transformation and summation formulas play a key role. In particular, in one of the Kummer's transformation formulas, Kim, et al. in 2012, have obtained ten contiguous results in the form of a single result with the help of generalization of Gauss's second summation theorem obtained earlier by Lavoie, et al.. In this paper, we aim at presenting four of such results by the technique of contiguous function relations and integral method developed by MacRobert.
Paper's Title:
Some Nonlinear Gronwall-Bellman Type Retarded Integral Inequalities with Power and Their Applications
Author(s):
Ammar Boudeliou
Department of Mathematics, University of Constantine 1
Brothers Mentouri,
BP, 325, Ain El Bey Street, 25017,
Algeria.
E-mail: ammar_boudeliou@umc.edu.dz
Abstract:
In this paper, we investigate a certain class of nonlinear Gronwall-Bellman type integral inequalities with power in more general cases involving retarded term and more general nonlinearities. Our results generalize some known integral inequalities and other results obtained very recently. The inequalities given here can be used to estimate the bound on the solutions of retarded integral equation of Volterra type and integro-differential equations (IDE) with power. Two examples are given to show the validity of our established theorems.
Paper's Title:
Finite Volume Approximation of a Class of 2D Elliptic Equations with Discontinuous and Highly Oscillating Coefficients
Author(s):
J. D. Bambi Pemba and B. Ondami
Université Marien Ngouabi
Factuté des Sciences et Techniques
BP 69 Brazzaville,
Congo.
E-mail: bondami@gmail.com
URL:
https://www.researchgate.net/profile/Bienvenu-Ondami
https://www.linkedin.com/in/bienvenu-ondami
Abstract:
In this paper, we are interested in the Finite Volume approximation of a second-order two-dimensional elliptic equation in heterogeneous porous medium with a periodic structure. The equation's coefficients are therefore discontinuous and highly oscillating. This class of problems has been extensively studied in the literature, where various methods proposed for determining the so-called homogenized problem. What we are particularly interested in is the direct numerical approximation of the problem, which has received little attention in the literature. We use the cell-centered finite volume approach for this purpose. Error estimates are established, and numerical simulations are conducted for both the isotropic and anisotropic media cases. The obtained solution is compared to the homogenized solution, and the results show that this approach provides an adequate approximation of the exact solution.
Paper's Title:
The Drazin-star and Star-Drazin Solutions to Quaternion Matrix Equations
Author(s):
Ivan I. Kyrchei, Dijana Mosić, Predrag Stanimirović
Pidstryhach Institute for Applied Problems
of Mechanics and Mathematics
of NAS of Ukraine, L'viv, 79060,
Ukraine.
E-mail:
ivankyrchei26@gmail.com
Faculty of Sciences and Mathematics,
University of Niš, P.O.
Box 224, 18000, Niš, Serbia.
E-mail: dijana@pmf.ni.ac.rs
Faculty of Sciences and Mathematics,
University of Niš, P.O.
Box 224, 18000, Niš, Serbia.
E-mail: pecko@pmf.ni.ac.rs
Abstract:
The notions of the Drazin-star and star-Drazin matrices are expanded to quaternion matrices in this paper. Their determinantal representations are developed in both cases in terms of noncommutative row-column determinants of quaternion matrices and for minors of appropriate complex matrices. We study all possible two-sided quaternion matrix equations with their one-sided partial cases whose uniquely determined solutions are based on the Drazin-star and star-Drazin matrices. Solutions of these equations are represented by Cramer's rules in both cases for quaternion and complex matrix equations. A numerical example is presented to illustrate our results.
Paper's Title:
On an Extension of Hilbert’s Integral Inequality with Some Parameters
Author(s):
Bicheng Yang
Department of
Mathematics, Guangdong Education College, Guangzhou, Guangdong 510303, People’s
Republic of China.
bcyang@pub.guangzhou.gd.cn
URL:
http://www1.gdei.edu.cn/yangbicheng/index.html
Abstract:
In this paper, by introducing some parameters and estimating the
weight function, we give an extension of Hilbert’s integral inequality with a
best constant factor. As applications, we consider the equivalent form and some
particular results.
Paper's Title:
Norm Estimates for the Difference between Bochner’s Integral and the Convex Combination of Function’s Values
Author(s):
P. Cerone, Y.J. Cho, S.S. Dragomir, J.K. Kim, and S.S. Kim
School of
Computer Science and Mathematics,
Victoria University of Technology,
Po Box 14428, Mcmc 8001, Victoria, Australia.
pietro.cerone@vu.edu.au
URL:
http://rgmia.vu.edu.au/cerone/index.html
Department of
Mathematics Education, College of Education,
Gyeongsang National University, Chinju 660-701, Korea
yjcho@nongae.gsnu.ac.kr
School of
Computer Science and Mathematics,
Victoria University of Technology,
Po Box 14428, Mcmc 8001, Victoria, Australia.
sever.dragomir@vu.edu.au
URL:
http://rgmia.vu.edu.au/SSDragomirWeb.html
Department of
Mathematics, Kyungnam University,
Masan,, Kyungnam 631-701, Korea
jongkyuk@kyungnam.ac.kr
Department of
Mathematics, Dongeui University,
Pusan 614-714, Korea
sskim@dongeui.ac.kr
Abstract:
Norm estimates are developed between the Bochner integral of a vector-valued function in Banach spaces having the Radon-Nikodym property and the convex combination of function values taken on a division of the interval [a, b].
Paper's Title:
A New Hardy-Hilbert's Type Inequality for Double Series and its Applications
Author(s):
Mingzhe Gao
Department of Mathematics and Computer Science, Normal College Jishou University,
Jishou Hunan, 416000,
People's Republic of China
mingzhegao1940@yahoo.com.cn
Abstract:
In this paper, it is shown that a new Hardy-Hilbert’s type
inequality for double series can be established by introducing a parameter ![]() and the weight function of the form
and the weight function of the form ![]() where c is Euler
constant and
where c is Euler
constant and ![]() And
the coefficient
And
the coefficient ![]() and
and ![]() appear simultaneously in the coefficient and the weight
function when
appear simultaneously in the coefficient and the weight
function when ![]() In particular, for
case
In particular, for
case ![]() some new Hilbert’s
type inequalities are obtained. As applications, some extensions of Hardy-Littlewood’s inequality are given.
some new Hilbert’s
type inequalities are obtained. As applications, some extensions of Hardy-Littlewood’s inequality are given.
Paper's Title:
Oscillations of First Order Linear Delay Difference Equations
Author(s):
G. E. Chatzarakis and I. P. Stavroulakis
Department of Mathematics, University of Ioannina,
451 10, Greece
ipstav@cc.uoi.gr
Abstract:
Consider the first order linear delay difference equation of
the form ![]()
![]() where
where
![]() is
a sequence of nonnegative real numbers, k is a positive integer and
is
a sequence of nonnegative real numbers, k is a positive integer and ![]() denotes
the forward difference operator
denotes
the forward difference operator ![]() New
oscillation criteria are established when the well-known oscillation conditions
New
oscillation criteria are established when the well-known oscillation conditions
![]() and
and
![]() are
not satisfied. The results obtained essentially improve known results in the
literature.
are
not satisfied. The results obtained essentially improve known results in the
literature.
Paper's Title:
A Stability of the G-type Functional Equation
Author(s):
Gwang Hui Kim
Department of Mathematics, Kangnam University
Suwon 449-702, Korea.
ghkim@kangnam.ac.kr
Abstract:
We will investigate the stability in the sense of G
Paper's Title:
The Iterated Variational Method for the Eigenelements of a Class of Two-Point Boundary Value Problems
Author(s):
Muhammed I. Syam and Qasem M. Al-Mdallal
Department of Mathematical Sciences, College of Science, UAE University,
P. O. Box 17551, Al-Ain,
United Arab Emirates
Q.Almdallal@uaeu.ac.ae
M.Syam@uaeu.ac.ae
Abstract:
The iterated variational method is considered in the approximation
of eigenvalues and eigenfunctions for a class of two point boundary
value problems. The implementation of this method is easy and
competes well with other methods. Numerical examples are presented
to show the efficiency of the method proposed. Comparison with the
work of others is also illustrated.
Paper's Title:
Existence of Solutions for Third Order Nonlinear Boundary Value Problems
Author(s):
Yue Hu and Zuodong Yang
School of Mathematics and Computer Science, Nanjing Normal University, Jiangsu Nanjing 210097,
China.
huu3y2@163.com
College of Zhongbei, Nanjing Normal University, Jiangsu Nanjing 210046,
China.
zdyang_jin@263.net
yangzuodong@njnu.edu.cn
Abstract:
In this paper, the existence of solution for a class of third order quasilinear ordinary differential equations with nonlinear boundary value problems
(Φp(u"))'=f(t,u,u',u"), u(0)=A, u'(0)=B, R(u'(1),u"(1))=0
is established. The results are obtained by using upper and lower solution methods.
Paper's Title:
Nontrivial Solutions of Singular Superlinear Three-point
Boundary Value Problems at Resonance
Author(s):
Feng Wang, Fang Zhang
School of Mathematics and Physics,
Changzou University,
Changzhou, 213164,
China.
fengwang188@163.com
Abstract:
The singular superlinear second order three-point boundary value problems at resonance
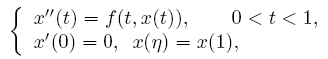
are considered under some conditions concerning the first eigenvalues corresponding to the relevant linear operators, where n ∈ (0,1) is a constant, f is allowed to be singular at both t=0 and t=1. The existence results of nontrivial solutions are given by means of the topological degree theory.
Paper's Title:
Two Remarks on Commutators of Hardy Operator
Author(s):
Yasuo Komori-Furuya
School of High Technology for Human Welfare
Tokai University
317 Nishino Numazu, Shizuoka 410-0395 Japan
komori@wing.ncc.u-tokai.ac.jp
Abstract:
Fu and Lu showed that
the commutator of multiplication operator by b and
the n-dimensional Hardy operator
is bounded on Lp if b is in some CMO space.
We shall prove the converse of this theorem
and also prove that their result is optimal by giving a counterexample
Paper's Title:
On a Hilbert-type Inequality with the Polygamma Function
Author(s):
Bing He and Bicheng Yang
Department of Mathematics, Guangdong Education College,
Guangzhou, 510303,
China.
Department of Mathematics, Guangdong Education College,
Guangzhou, 510303,
China.
Abstract:
By applying the method of weight function and the technique of real analysis, a Hilbert-type inequality with a best constant factor is established, where the best constant factor is made of the polygamma function. Furthermore, the inverse form is given.
Paper's Title:
Hermite-Hadamard-Fejer Type Inequalities for Harmonically s-convex Functions via Fractional Integrals
Author(s):
İmdat İşcan, Mehmet Kunt
Department of Mathematics,
Faculty of Sciences and Arts,
Giresun University, Giresun,
Turkey.
E-mail: imdat.iscan@giresun.edu.tr
Department of Mathematics,
Faculty of Sciences,
Karadeniz Technical University,
61080, Trabzon,
Turkey.
E-mail:
mkunt@ktu.edu.tr
Abstract:
In this paper, some Hermite-Hadamard-Fejer type integral inequalities for harmonically s-convex functions in fractional integral forms have been obtained.
Paper's Title:
Presentation a mathematical model for bone metastases control by using tamoxifen
Author(s):
Maryam Nikbakht, Alireza Fakharzadeh Jahromi and Aghileh Heydari
Department of Mathematics,
Payame Noor University,
P.O.Box 19395-3697, Tehran,
Iran.
.E-mail:
maryam_nikbakht@pnu.ac.ir
Department of Mathematics,
Faculty of Basic Science,
Shiraz University of Technology.
E-mail:
a_fakharzadeh@sutech.ac.ir
Department of Mathematics,
Payame Noor University,
P.O.Box 19395-3697, Tehran,
Iran.
E-mail: a-heidari@pnu.ac.ir
Abstract:
Bone is a common site for metastases (secondary tumor) because of breast and prostate cancer. According to our evaluations the mathematical aspect of the effect of drug in bone metastases has not been studied yet. Hence, this paper suggested a new mathematical model for bone metastases control by using tamoxifen. The proposed model is a system of nonlinear partial differential equations. In this paper our purpose is to present a control model for bone metastases. At end by some numerical simulations, the proposed model is examined by using physician.
Paper's Title:
Existence of Positive Solutions for
Nonlinear Fractional Differential Equations
with Multi-point Boundary Conditions
Author(s):
N. Adjeroud
Khenchela University, Department of
Mathematics,
Khenchela, 40000,
Algeria.
E-mail: adjnac@gmail.com
Abstract:
This paper is devoted to the existence results of positive solutions for a nonlinear fractional differential equations with multi-point boundary conditions. By means of the Schauder fixed point theorem, some results on the existence are obtained.
Paper's Title:
The Functional Equation With an Exponential Polynomial Solution and its Stability
Author(s):
Young Whan Lee1, Gwang Hui Kim2*, and Jeong Il Kim3
1Department of Computer
Hacking and Information Security,
College of Engineering, Daejeon University,
Daejeon, 34520,
Korea(Republic of).
E-mail: ywlee@dju.ac.kr
2Department of Mathematics,
Kangnam University,
Yongin, Gyeonggi, 16979,
Korea(Republic of).
E-mail: ighkim@kangnam.ac.kr
3Department of Statistics,
Daejeon University,
Daejeon 34520,
Korea(Republic of).
E-mail: jlkim@dju.ac.kr
Abstract:
In this paper, we prove that the unique continuous solution of the functional equation

is

where pn(x) is a polynomial with degree n and

We also obtain the superstability and stability of the functional equation with the following forms, respectively:

and

Paper's Title:
Some Inequalities of the Hermite-Hadamard Type for k-Fractional Conformable Integrals
Author(s):
C.-J. Huang, G. Rahman, K. S. Nisar, A. Ghaffar and F. Qi
Department of Mathematics, Ganzhou Teachers College,
Ganzhou 341000, Jiangxi,
China.
E-mail:
hcj73jx@126.com ,
huangcj1973@qq.com
Department of Mathematics, Shaheed Benazir
Bhutto University,
Sheringal, Upper Dir, Khyber Pakhtoonkhwa,
Pakistan.
E-mail: gauhar55uom@gmail.com
Department of Mathematics, College of Arts
and Science at Wadi Aldawaser, 11991,
Prince Sattam Bin Abdulaziz University, Riyadh Region,
Kingdom of Saudi Arabia.
E-mail: n.sooppy@psau.edu.sa,
ksnisar1@gmail.com
Department of Mathematical Science,
Balochistan University of Information Technology,
Engineering and Management Sciences, Quetta,
Pakistan.
E-mail: abdulghaffar.jaffar@gmail.com
School of Mathematical Sciences, Tianjin
Polytechnic University,
Tianjin 300387,
China; Institute of Mathematics,
Henan Polytechnic University, Jiaozuo 454010, Henan,
China.
E-mail: qifeng618@gmail.com,
qifeng618@qq.com
Abstract:
In the paper, the authors deal with generalized k-fractional conformable integrals, establish some inequalities of the Hermite-Hadamard type for generalized k-fractional conformable integrals for convex functions, and generalize known inequalities of the Hermite-Hadamard type for conformable fractional integrals.
Paper's Title:
Cubic Alternating Harmonic Number Sums
Author(s):
Anthony Sofo
Victoria University,
College of Engineering and Science,
Melbourne City,
Australia.
E-mail:
Anthony.Sofo@vu.edu.au
Abstract:
We develop new closed form representations of sums of cubic alternating harmonic numbers and reciprocal binomial coefficients. We also identify a new integral representation for the ζ (4) constant.
Paper's Title:
Dynamical Analysis of HIV/AIDS Epidemic Model with Two Latent Stages, Vertical Transmission and Treatment
Author(s):
Nur Shofianah, Isnani Darti, Syaiful Anam
Mathematics Department,Faculty of
Mathematics and Natural Sciences.
University of Brawijaya,
Jl. Veteran, Malang 65145,
Indonesia.
E-mail:
nur_shofianah@ub.ac.id,
isnanidarti@ub.ac.id,
syaiful@ub.ac.id
Abstract:
We discuss about dynamical analysis of HIV/AIDS epidemic model with two latent stages, vertical transmission and treatment. In this model, the spreading of HIV occurs through both horizontal and vertical transmission. There is also treatment for individual who has been HIV infected. The latent stage is divided into slow and fast latent stage based on the immune condition which varies for each individual. Dynamical analysis result shows that the model has two equilibrium points: the disease-free equilibrium point and the endemic equilibrium point. The existence and global stability of equilibrium points depend on the basic reproduction number R0. When R0 <1, only the disease-free equilibrium point exists. If R0 >1, there are two equilibrium points, which are the disease-free equilibrium point and the endemic equilibrium point. Based on the result of stability analysis, the disease-free equilibrium point is globally asymptotically stable if R0 <1, while if R0 > 1 and p=q, the endemic equilibrium point will be globally asymptotically stable. In the end, we show some numerical simulations to support the analytical result.
Paper's Title:
On an extension of Edwards's double integral with applications
Author(s):
I. Kim, S. Jun, Y. Vyas and A. K. Rathie
Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Republic of Korea.
General Education Institute,
Konkuk University,
Chungju 380-701,
Republic of Korea.
Department of Mathematics, School of
Engineering,
Sir Padampat Singhania University,
Bhatewar, Udaipur, 313601, Rajasthan State,
India.
Department of Mathematics,
Vedant College of Engineering and Technology,
(Rajasthan Technical University),
Bundi-323021, Rajasthan,
India.
E-mail: iki@wku.ac.kr
sjun@kku.ac.kr
yashoverdhan.vyas@spsu.ac.in
arjunkumarrathie@gmail.com
Abstract:
The aim of this note is to provide an extension of the well known and useful Edwards's double integral. As an application, new class of twelve double integrals involving hypergeometric function have been evaluated in terms of gamma function. The results are established with the help of classical summation theorems for the series 3F2 due to Watson, Dixon and Whipple. Several new and interesting integrals have also been obtained from our main findings.
Paper's Title:
On Ruled Surfaces According to Quasi-Frame in Euclidean 3-Space
Author(s):
M. Khalifa Saad and R. A. Abdel-Baky
Department of Mathematics, Faculty of
Science,
Islamic University of Madinah,
KSA.
Department of Mathematics, Faculty of Science,
Sohag University, Sohag,
EGYPT.
E-mail:
mohamed_khalifa77@science.sohag.edu.eg,
mohammed.khalifa@iu.edu.sa
Department of Mathematics, Faculty of
Science,
Assiut University, Assiut,
EGYPT.
E-mail: rbaky@live.com
Abstract:
This paper aims to study the skew ruled surfaces by using the quasi-frame of Smarandache curves in the Euclidean 3-space. Also, we reveal the relationship between Serret-Frenet and quasi-frames and give a parametric representation of a directional ruled surface using the quasi-frame. Besides, some comparative examples are given and plotted which support our method and main results.
Paper's Title:
Optimal Control Analysis of HIV/AIDS Epidemic Model with an Antiretroviral Treatment
Author(s):
U. Habibah and R. A. Sari
Mathematics Department and Reseach Group
of Biomathematics,
Faculty of Mathematics and Natural Science,
Brawijaya University, Jl. Veteran Malang 65145,
Indonesia.
E-mail: ummu_habibah@ub.ac.id
Abstract:
A mathematical model of HIV/AIDS is governed by a system of ordinary differential equations in the presence of an antiretroviral treatment (ARV). The theory of optimal control is applied to an epidemic model of HIV/AIDS which an ARV is used as a control strategy in order to prevent the spread of HIV/AIDS. The optimality system is derived by applying the Pontryagin's Minimum Principle. We analyze the boundedness and positivity of solutions, and an existence of the optimal control. Numerical simulations are conducted to obtain numerical solution of the optimally system.
Paper's Title:
A New Method with Regularization for Solving Split Variational Inequality Problems in Real Hilbert Spaces
Author(s):
Francis Akutsah1 and Ojen Kumar Narain2
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 216040405@stu.ukzn.ac.za,
akutsah@gmail.com
2School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
In this paper, we introduce a new inertial extrapolation method with regularization for approximating solutions of split variational inequality problems in the frame work of real Hilbert spaces. We prove that the proposed method converges strongly to a minimum-norm solution of the problem without using the conventional two cases approach. In addition, we present some numerical experiments to show the efficiency and applicability of the proposed method. The results obtained in this paper extend, generalize and improve several results in this direction.
Paper's Title:
Additive Mappings on Semiprime Rings Functioning as Centralizers
Author(s):
Abu Zaid Ansari and Faiza Shujat
Department of Mathematics,
Faculty of Science,
Islamic University of Madinah, Madinah
K.S.A.
E-mail: ansari.abuzaid@gmail.com,
ansari.abuzaid@iu.edu.sa
Department of Mathematics,
Faculty of Science,
Taibah University, Madinah,
K.S.A.
E-mail: faiza.shujat@gmail.com,
fullahkhan@taibahu.edu.sa
Abstract:
The objective of this research is to prove that an additive mapping T:R → R is a centralizer on R if it satisfies any one of the following identities:
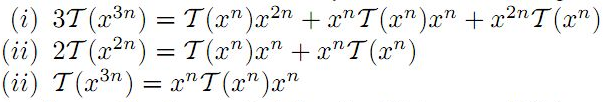
for all x ∈ R, where n ≥ 1 is a fixed integer and R is any suitably torsion free semiprime ring. Some results on involution "*" are also presented as consequences of the main theorems. In addition, we will take criticism in account with examples.
Paper's Title:
Higher Order Accurate Compact Schemes for Time Dependent Linear and Nonlinear Convection-Diffusion Equations
Author(s):
S. Thomas, Gopika P.B. and S. K. Nadupuri
Department of Mathematics
National Institute of Technology Calicut
Kerala
673601
India.
E-mail:
sobinputhiyaveettil@gmail.com
pbgopika@gmail.com nsk@nitc.ac.in
Abstract:
The primary objective of this work is to study higher order compact finite difference schemes for finding the numerical solution of convection-diffusion equations which are widely used in engineering applications. The first part of this work is concerned with a higher order exponential scheme for solving unsteady one dimensional linear convection-diffusion equation. The scheme is set up with a fourth order compact exponential discretization for space and cubic $C^1$-spline collocation method for time. The scheme achieves fourth order accuracy in both temporal and spatial variables and is proved to be unconditionally stable. The second part explores the utility of a sixth order compact finite difference scheme in space and Huta's improved sixth order Runge-Kutta scheme in time combined to find the numerical solution of one dimensional nonlinear convection-diffusion equations. Numerical experiments are carried out with Burgers' equation to demonstrate the accuracy of the new scheme which is sixth order in both space and time. Also a sixth order in space predictor-corrector method is proposed. A comparative study is performed of the proposed schemes with existing predictor-corrector method. The investigation of computational order of convergence is presented.
Paper's Title:
Solving Strongly Nonlinear Fractional Fredholm Integral-Differential Equations in Caputo's Sense Using the SBA Method
Author(s):
Germain Kabore1, Bakari Abbo2, Ousseni So3 and Blaise Some1
1Laboratoire
d'Analyse Numerique, Informatique et de Biomathmathiques (L.N.I.BIO),
Universite Joseph Ki-Zerbo,
Burkina Faso.
E-mail: germainkabore982@gmail.com,
blaisesomeouaga1@gmail.com
2University
of N'Damena, Tchad.
E-mail: bakariabbo@yahoo.fr
3Laboratoire
d'Analyse Numerique, Informatique et de Biomathemathiques (L.N.I.BIO),
Ecole Normale Superieure,
Burkina Faso.
E-mail: sousseni@yahoo.fr
Abstract:
The work addressed in this article consists in constructing the exact solutions, where they exist, of fractional Fredholm-type integro-differential equations in the sense of Caputo. Our results are obtained using the SBA method. The simplification of the approach, the analysis of its convergence, and the generalization of this method to these types of highly nonlinear equations constitute our scientific contribution.
Paper's Title:
Solving Fixed Point Problems and Variational Inclusions Using Viscosity Approximations
Author(s):
P. Patel, R. Shukla
Department of Mathematics, School of
Advanced Sciences, VIT-AP University\\
Amaravati, 522237, Andhra Pradesh,
India.
E-mail:
prashant.patel9999@gmail.com,
prashant.p@vitap.ac.in
Department of Mathematical Sciences &
Computing, Walter Sisulu University,
Mthatha 5117,
South Africa.
E-mail: rshukla@wsu.ac.za
Abstract:
This paper proposes a new algorithm to find a common element of the fixed point set of a finite family of demimetric mappings and the set of solutions of a general split variational inclusion problem in Hilbert spaces. The algorithm is based on the viscosity approximation method, which is a powerful tool for solving fixed point problems and variational inclusion problems. Under some conditions, we prove that the sequence generated by the algorithm converges strongly to this common solution.
Paper's Title:
The Projective Riccati Equations Method for Solving Nonlinear Schrodinger Equation in Bi-Isotropic Fiber
Author(s):
A. Ourahmoun, Z. Mezache
Optics and Precision Mechanics
Institute of Setif,
Algeria.
E-mail:
abbes.ourahmoun@univ-setif.dz
zinemezaache@yahoo.fr
Abstract:
Bi-isotropic materials, characterized by their chiral and non-reciprocal nature, present unique challenges and opportunities in scientific research, driving the development of cutting-edge applications. In this paper, we explore the influence of chirality using a newly developed framework that emphasizes the nonlinear effects arising from the magnetization vector under a strong electric field. Our research introduces a novel formulation of constitutive relations and delves into the analysis of solutions for the nonlinear Schr\"{o}dinger equation, which governs pulse propagation in nonlinear bi-isotropic media. By employing the Projective Riccati Equation Method with variable dispersion and nonlinearity, we systematically derive families of solutions to the nonlinear Schr\"{o}dinger equation in chiral and non-reciprocal optical fibers. This approach provides valuable insights into the propagation of light in two polarization modes right circularly polarized (RCP) and left circularly polarized (LCP) each associated with distinct wave vectors in nonlinear bi-isotropic environments. The study presents several new exact solutions of optical solitons within these media.
Paper's Title:
A New Proof of Classical Watson's Summation Theorem for the Series 3F2(1)
Author(s):
Insuk Kim, Arjun K. Rathie
Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Korea.
E-mail: iki@wku.ac.kr
Department of Mathematics,
Vedant College of Engineering and Technology (Rajasthan Technical University),
Bundi, Rajasthan,
India.
E-mail:
arjunkumarrathie@gmail.com
Abstract:
The aim of this short research note is to provide a new proof of classical Watson's summation theorem for the series 3F2(1). The theorem is obtained by evaluating an infinite integral and making use of classical Gauss's first and second summation theorems for the series 2F1.
Paper's Title:
A general theory of decision making
Author(s):
Frank Hansen
Department of Economics,
University of Copenhagen,
Studiestraede 6, DK-1455 Copenhagen K
Denmark
Frank.Hansen@econ.ku.dk
URL: http://www.econ.ku.dk/okofh
Abstract:
We formulate a general theory of decision making based on a lattice of observable events, and we exhibit
a large class of representations called the general model. Some of the representations are equivalent to
the so called standard model in which observable events are modelled by
an algebra of measurable subsets of a state space, while others are not compatible with such a description.
We show that the general model collapses to the standard model, if and only if an additional axiom
is satisfied. We argue that this axiom is not very
natural and thus assert that the standard model may not be general enough to model all relevant
phenomena in economics. Using the general model we are
(as opposed to Schmeidler [16]) able to rationalize Ellsberg's paradox
without the introduction of non-additive measures.
Paper's Title:
Positive Periodic Time-Scale Solutions for Functional Dynamic Equations
Author(s):
Douglas R. Anderson and Joan Hoffacker
Department of Mathematics and Computer Science
Concordia College
Moorhead, MN 56562 USA
andersod@cord.edu
URL: http://www.cord.edu/faculty/andersod/
Department of Mathematical Sciences
Clemson University
Clemson, SC 29634 USA
johoff@clemson.edu
URL: http://www.math.clemson.edu/facstaff/johoff.htm
Abstract:
Using Krasnoselskii's fixed point theorem, we establish the existence of positive periodic solutions
to two pairs of related nonautonomous functional delta dynamic equations on periodic time scales, and then extend the discussion to higher-dimensional equations. Two pairs of corresponding nabla equations
are also provided in an analogous manner.
Paper's Title:
On Vector Variational Inequality Problem in Terms of Bifunctions
Author(s):
C. S. Lalitha and Monika Mehta
Department of Mathematics, Rajdhani College,
Department of Mathematics, Satyawati College,
University of Delhi, Raja Garden,
Delhi 110015, India
cslalitha@rediffmail.com
University Of Delhi, Ashok Vihar,
Phase-III, Delhi 110052, India
mridul_in@yahoo.com
Abstract:
In this paper, we consider a generalized vector variational
inequality problem expressed in terms of a bifunction and establish
existence theorems for this problem by using the concepts of cone
convexity and cone strong quasiconvexity and employing the
celebrated Fan's Lemma. We also give two types of gap functions for this problem.
Paper's Title:
A Strengthened Hardy-Hilbert's Type Inequality
Author(s):
Weihong Wang and Bicheng Yang
Department of Mathematics, Guangdong Education Institute,
Guangzhou, Guangdong 520303,
People's Republic Of China
wwh@gdei.edu.cn
bcyang@pub.guangzhou.gd.cn
URL: http://www1.gdei.edu.cn/yangbicheng/index.html
Abstract:
By using the improved Euler-Maclaurin's summation formula and
estimating the weight coefficient, we give a new strengthened
version of the more accurate Hardy-Hilbert's type inequality. As
applications, a strengthened version of the equivalent form is
considered.
Paper's Title:
The Superstability of the Pexider Type Trigonometric Functional Equation
Author(s):
Gwang Hui Kim and Young Whan Lee
Department of Mathematics, Kangnam
University Yongin, Gyeonggi, 446-702, Korea.
ghkim@kangnam.ac.kr
Department of Computer and Information Security
Daejeon University, Daejeon 300-716, Korea.
ywlee@dju.ac.kr
Abstract:
The aim of this paper is to investigate the stability
problem for
the Pexider type (hyperbolic) trigonometric functional equation
f(x+y)+f(x+σy)=λg(x)h(y) under the conditions :
|f(x+y)+f(x+σy)- λg(x)h(y)|≤φ(x),
φ(y), and min {φ(x), φ (y)}.
As a consequence, we have generalized the results of stability for
the cosine(d'Alembert), sine, and the Wilson functional equations by J.
Baker, P. Găvruta, R. Badora and R. Ger, Pl.~Kannappan, and G.
H. Kim
Paper's Title:
Approximation of an AQCQ-Functional Equation and its Applications
Author(s):
Choonkil Park and Jung Rye Lee
Department of Mathematics,
Research Institute for Natural Sciences,
Hanyang University, Seoul 133-791,
Korea;
Department of Mathematics,
Daejin University,
Kyeonggi 487-711,
Korea
baak@hanyang.ac.kr
jrlee@daejin.ac.kr
Abstract:
This paper is a survey on the generalized Hyers-Ulam stability of an AQCQ-functional equation in several spaces. Its content is divided into the following sections:
1. Introduction and preliminaries.
2. Generalized Hyers-Ulam stability of an AQCQ-functional equation in Banach spaces: direct method.
3. Generalized Hyers-Ulam stability of an AQCQ-functional equation in Banach spaces: fixed point method.
4. Generalized Hyers-Ulam stability of an AQCQ-functional equation in random Banach spaces: direct method.
5. Generalized Hyers-Ulam stability of an AQCQ-functional equation in random Banach spaces: fixed point method.
6. Generalized Hyers-Ulam stability of an AQCQ-functional equation in non-Archi-medean Banach spaces: direct method.
7. Generalized Hyers-Ulam stability of an AQCQ-functional equation in non-Archi-medean Banach spaces: fixed point method.
Paper's Title:
Finite and Infinite Order
Solutions of a Class of Higher Order Linear Differential Equations
Author(s):
Saada Hamouda
Department of Mathematics,
Laboratory of Pure and Applied Mathematics,
University of Mostaganem, B. P 227 Mostaganem,
ALGERIA
hamouda_saada@yahoo.fr
Abstract:
In this paper, we investigate the growth of solutions of higher order linear differential equations where most of the coefficients have the same order and type with each other.
Paper's Title:
Schwarz Method
for Variational Inequalities Related to Ergodic Control Problems
Author(s):
S. Saadi, H. Mécheri
Department of Mathematics, Badji Mokhtar
University, Annaba 23000,
P.O.Box. 12, Annaba 23000, Algeria
Abstract:
In this paper, we study variational inequalities related to ergodic control problems studied by M. Boulbrachène and H. Sissaoui [11], where the "discount factor" (i.e., the zero order term) is set to 0, we use an overlapping Schwarz method on nomatching grid which consists in decomposing the domain in two subdomains. For α ∈ ]0.1[ we provide the discretization on each subdomain converges in L∞ -norm.
Paper's Title:
L∞- Error Estimate of Schwarz Algorithm for Elliptic Quasi-Variational Inequalities Related to Impulse Control Problem
Author(s):
Saadi Samira and Mehri Allaoua
Lab. LANOS, Department of Mathematics,
University Badji Mokhtar Annaba,
P.O.Box 12, Annaba 23000,
Algeria.
Lab. LAIG, Department of Mathematics,
University May 8th 1945,
P.O.Box 401, Guelma 24000,
Algeria.
E-mail:
saadisamira69@yahoo.fr
allmehri@yahoo.fr
Abstract:
In this work, we study Schwarz method for a class of elliptic quasi-variational inequalities. The principal result of this investigation is to prove the error estimate in ∞-norm for two domains with overlapping nonmatching grids, using the geometrical convergence, and the uniform convergence of Cortey Dumont.
Paper's Title:
Some Grüss Type Inequalities in Inner Product Spaces
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir
Abstract:
Some inequalities in inner product spaces
that provide upper bounds for the quantities
and
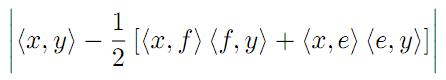
where e,f ∈ H with
and x,y are vectors in H satisfying some appropriate assumptions are
given. Applications for discrete and integral inequalities are provided as
well.
Paper's Title:
Hermite-Hadamard Type Inequalities for k-Riemann Liouville Fractional Integrals Via Two Kinds of Convexity
Author(s):
R. Hussain1, A. Ali2, G. Gulshan3, A. Latif4 and K. Rauf5
1,2,3,4Department
of Mathematics,
Mirpur University of Science and Technology, Mirpur.
Pakistan.
E-mail1:
rashida12@gmail.com
E-mail2:
unigraz2009@yahoo.com
E-mail3:
ghazalagulshan@yahoo.com
E-mail4:
asialatif87@gmail.com
5Department
of Mathematics,
University of Ilorin, Ilorin,
Nigeria.
E-mail5:
krauf@unilorin.edu.ng
Abstract:
In this article, a fundamental integral identity including the first order derivative of a given function via k-Riemann-Liouville fractional integral is established. This is used to obtain further Hermite-Hadamard type inequalities involving left-sided and right-sided k-Riemann-Liouville fractional integrals for m-convex and (s,m)-convex functions respectively.
Paper's Title:
Mapped Chebyshev Spectral Methods for Solving Second Kind Integral Equations on the Real Line
Author(s):
Ahmed Guechi and Azedine Rahmoune
Department of Mathematics, University of Bordj Bou Arréridj,
El Anasser, 34030, BBA,
Algeria.
E-mail: a.guechi2017@gmail.com
E-mail: a.rahmoune@univ-bba.dz
Abstract:
In this paper we investigate the utility of mappings to solve numerically an important class of integral equations on the real line. The main idea is to map the infinite interval to a finite one and use Chebyshev spectral-collocation method to solve the mapped integral equation in the finite interval. Numerical examples are presented to illustrate the accuracy of the method.
Paper's Title:
Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.
Paper's Title:
A Comparison Between Two Different Stochastic Epidemic Models with Respect to the Entropy
Author(s):
Farzad Fatehi and Tayebe Waezizadeh
Department of Mathematics,
University of Sussex,
Brighton BN1 9QH,
UK.
E-mail: f.fatehi@sussex.ac.uk
URL:
http://www.sussex.ac.uk/profiles/361251
Department of Pure Mathematics, Faculty
of Mathematics and Computer,
Shahid Bahonar University of Kerman,
Kerman 76169-14111,
Iran.
E-mail: waezizadeh@uk.ac.ir
URL:
http://academicstaff.uk.ac.ir/en/tavaezizadeh
Abstract:
In this paper at first a brief history of mathematical models is presented with the aim to clarify the reliability of stochastic models over deterministic models. Next, the necessary background about random variables and stochastic processes, especially Markov chains and the entropy are introduced. After that, entropy of SIR stochastic models is computed and it is proven that an epidemic will disappear after a long time. Entropy of a stochastic mathematical model determines the average uncertainty about the outcome of that random experiment. At the end, we introduce a chain binomial epidemic model and compute its entropy, which is then compared with the DTMC SIR epidemic model to show which one is nearer to reality.
Paper's Title:
Polynomial Dichotomy of C0-Quasi Semigroups in Banach Spaces
Author(s):
Sutrima1,2, Christiana Rini Indrati2, Lina Aryati2
1Department of Mathematics,
Universitas Sebelas Maret,
PO Box 57126, Surakarta,
Indonesia.
E-mail: sutrima@mipa.uns.ac.id
2Department of Mathematics,
Universitas Gadjah Mada,
PO Box 55281, Yogyakarta,
Indonesia.
E-mail: rinii@ugm.ac.id,
lina@ugm.ac.id
Abstract:
Stability of solutions of the problems is an important aspect for application purposes. Since its introduction by Datko [7], the concept of exponential stability has been developed in various types of stability by various approaches. The existing conditions use evolution operator, evolution semigroup, and quasi semigroup approach for the non-autonomous problems and a semigroup approach for the autonomous cases. However, the polynomial stability based on C0-quasi semigroups has not been discussed in the references. In this paper we propose a new stability for C0-quasi semigroups on Banach spaces i.e the polynomial stability and polynomial dichotomy. As the results, the sufficient and necessary conditions for the polynomial and uniform polynomial stability are established as well as the sufficiency for the polynomial dichotomy. The results are also confirmed by the examples.
Paper's Title:
A Multivalued Version of the
Radon-Nikodym Theorem, via the Single-valued Gould Integral
Author(s):
Domenico Candeloro1, Anca Croitoru2, Alina Gavriluţ2, Anna Rita Sambucini1
1Dept. of Mathematics and Computer
Sciences,
University of Perugia,
1, Via Vanvitelli -- 06123, Perugia,
Italy.
E-mail: domenico.candeloro@unipg.it,
anna.sambucini@unipg.it
2Faculty of Mathematics,
Al. I. Cuza University,
700506 Iaşi,
Romania.
E-mail: croitoru@uaic.ro,
gavrilut@uaic.ro
Abstract:
In this paper we consider a Gould type integral of real functions with respect to a compact and convex valued not necessarily additive measure. In particular we will introduce the concept of integrable multimeasure and, thanks to this notion, we will establish an exact Radon-Nikodym theorem relative to a fuzzy multisubmeasure which is new also in the finite dimensional case. Some results concerning the Gould integral are also obtained.
Paper's Title:
The Conservativeness of Girsanov Transformed for Symmetric Jump-diffusion Process
Author(s):
Mila Kurniawaty and Marjono
Department of Mathematics,
Universitas Brawijaya,
Malang,
Indonesia.
E-mail: mila_n12@ub.ac.id,
marjono@ub.ac.id
Abstract:
We study about the Girsanov transformed for symmetric Markov processes with jumps associated with regular Dirichlet form. We prove the conservativeness of it by dividing the regular Dirichlet form into the "small jump" part and the "big jump" part.
Paper's Title:
On a New Class of Eulerian's Type Integrals Involving Generalized Hypergeometric Functions
Author(s):
Sungtae Jun, Insuk Kim and Arjun K. Rathie
General Education Institute,
Konkuk University, Chungju 380-701,
Republic of Korea.
Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Republic of Korea.
Department of Mathematics,
Vedant College of Engineering and Technology (Rajasthan Technical University),
Bundi-323021, Rajasthan,
India.
E-mail: sjun@kku.ac.kr, iki@wku.ac.kr, arjunkumarrathie@gmail.com
Abstract:
Very recently Masjed-Jamei and Koepf established interesting and useful generalizations of various classical summation theorems for the 2F1, 3F2, 4F3, 5F4 and 6F5 generalized hypergeometric series. The main aim of this paper is to establish eleven Eulerian's type integrals involving generalized hypergeometric functions by employing these theorems. Several special cases have also been given.
Paper's Title:
Some Convergence Results for Jungck-Am Iterative Process In Hyperbolic Spaces
Author(s):
Akindele Adebayo Mebawondu and Oluwatosin Temitope Mewomo
School of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail:
216028272@stu.ukzn.ac.za,
mewomoo@ukzn.ac.za
Abstract:
In this paper, we introduce a new three steps iterative process called Jungck-AM iterative process and show that the proposed iterative process can be used to approximate fixed points of Jungck-contractive type mappings and Jungck-Suzuki type mappings. In addition, we establish some strong and Δ-convergence results for the approximation of fixed points of Jungck-Suzuki type mappings in the frame work of uniformly convex hyperbolic space. Furthermore, we show that the newly proposed iterative process has a better rate of convergence compare to the Jungck-Noor, Jungck-SP, Jungck-CR and some existing iterative processes in the literature. Finally, stability, data dependency results for Jungck-AM iterative process is established and we present an analytical proof and numerical examples to validate our claim.
Paper's Title:
A Low Order Least-Squares Nonconforming Finite Element Method for Steady Magnetohydrodynamic Equations
Author(s):
Z. Yu, D. Shi and H. Zhu
College of Science,
Zhongyuan
University of Technology,
Zhengzhou 450007,
China.
E-mail:
5772@zut.edu.cn
School of Mathematics and Statistics,
Zhengzhou University,
Zhengzhou 450001,
China.
E-mail:
shi_dy@126.com
Mathematics Department,
University of Southern Mississippi,
Hattiesburg MS, 39406,
U.S.A
E-mail:
huiqing.zhu@usm.edu
Abstract:
A low order least-squares nonconforming finite element (NFE) method is proposed for magnetohydrodynamic equations with EQ1rot element and zero-order Raviart-Thomas element. Based on the above element's typical interpolations properties, the existence and uniqueness of the approximate solutions are proved and the optimal order error estimates for the corresponding variables are derived.
Paper's Title:
Some New Mappings Related to Weighted Mean Inequalities
Author(s):
Xiu-Fen Ma
College of Mathematical and Computer,
Chongqing Normal University Foreign Trade and Business College,
No.9 of Xuefu Road, Hechuan District 401520,
Chongqing City,
The People's Republic of China.
E-mail: maxiufen86@163.com
Abstract:
In this paper, we define four mappings related to weighted mean inequalities, investigate their properties, and obtain some new refinements of weighted mean inequalities.
Paper's Title:
Generalised Models for Torsional Spine Reconnection
Author(s):
Ali Khalaf Hussain Al-Hachami
Department of Mathematics,
College of Education For Pure Sciences,
Wasit University,
Iraq.
E-mail: alhachamia@uowasit.edu.iq
Abstract:
Three-dimensional (3D) null points are available in wealth in the solar corona, and the equivalent is probably going to be valid in other astrophysical situations. On-going outcomes from sun oriented perceptions and from reproductions propose that reconnection at such 3D nulls may assume a significant job in the coronal dynamics. The properties of the torsional spine method of magnetic reconnection at 3D nulls are researched. Kinematic model are created, which incorporate the term ηJ that is spatially localised around the null, stretching out along the spine of the null. The null point is to research the impact of shifting the level of asymmetry of the null point magnetic field on the subsequent reconnection process where past examinations constantly considered a non-nonexclusive radially symmetric null. Specifically we analyse the rate of reconnection of magnetic flux at the spine of null point. Logical arrangements are determined for the enduring kinematic equation, and contrasted and the after effects of torsional spine reconnection models when the current is restricted in which the Maxwell conditions are illuminated. The geometry of the current layers inside which torsional spine reconnection happen is autonomous on the symmetry of the magnetic field. Torsional spine reconnection happens in a thin cylinder around the spine, with circular cross-segment when the fan eigenvalues are extraordinary. The short axis of the circle being along the solid field bearing. Just as it was discovered that the fundamental structure of the method of attractive reconnection considered is unaffected by changing the magnetic field symmetry, that is, the plasma flow is discovered rotational around the spine of null point. The spatiotemporal pinnacle current, and the pinnacle reconnection rate achieved, are found not to rely upon the level of asymmetry.
Paper's Title:
Analysis of a Frictional Contact Problem for Viscoelastic Piezoelectric Materials
Author(s):
Meziane Said Ameur, Tedjani Hadj Ammar and Laid Maiza
Departement of Mathematics,
El Oued University,
P.O. Box 789, 39000 El Oued,
Algeria.
E-mail:
said-ameur-meziane@univ-eloued.dz
Departement of Mathematics,
El Oued University,
P.O. Box 789, 39000 El Oued,
Algeria.
E-mail:
hadjammar-tedjani@univ-eloued.dz
Department of Mathematics,
Kasdi Merbah University,
30000 Ouargla,
Algeria.
E-mail: maiza.laid@univ-ouargla.dz
Abstract:
In this paper, we consider a mathematical model that describes the quasi-static process of contact between two thermo-electro-viscoelastic bodies with damage and adhesion. The damage of the materials caused by elastic deformations. The contact is frictional and modeled with a normal compliance condition involving adhesion effect of contact surfaces. Evolution of the bonding field is described by a first order differential equation. We derive variational formulation for the model and prove an existence and uniqueness result of the weak solution. The proof is based on arguments of evolutionary variational inequalities, parabolic inequalities, differential equations, and fixed point theorem.
Paper's Title:
Double Difference of Composition Operator on Bloch Spaces
Author(s):
Rinchen Tundup
Department of Mathematics
University of Jammu
Jammu and Kashmir
India.
E-mail: joneytun123@gmail.com
Abstract:
In this paper we characterize the compactness of double difference of three non-compact composition operators on Bloch space induced by three holomorphic self maps on the unit disc.
Paper's Title:
Numerical Approximation by the Method of Lines with Finite-volume Approach of a Solute Transport Equation in Periodic Heterogeneous Porous Medium
Author(s):
D. J. Bambi Pemba and B. Ondami
Université Marien Ngouabi,
Factuté des Sciences et Techniques,
BP 69, Brazzaville,
Congo.
E-mail: bondami@gmail.com
Abstract:
In this paper we are interested in the numerical approximation of a two-dimensional solute transport equation in heterogeneous porous media having periodic structures. It is a class of problems which has been the subject of various works in the literature, where different methods are proposed for the determination of the so-called homogenized problem. We are interested in this paper, in the direct resolution of the problem, and we use the method of lines with a finite volume approach to discretize this equation. This discretization leads to an ordinary differential equation (ODE) that we discretize by the Euler implicit scheme. Numerical experiments comparing the obtained solution and the homogenized problem solution are presented. They show that the precision and robustness of this method depend on the ratio between, the mesh size and the parameter involved in the periodic homogenization.
Paper's Title:
Solving Non-Autonomous Nonlinear Systems of Ordinary Differential Equations Using Multi-Stage Differential Transform Method
Author(s):
K. A. Ahmad, Z. Zainuddin, F. A. Abdullah
School of Mathematical Sciences
Universiti Sains Malaysia
11800 USM Penang
Malaysia.
E-mail: abumohmmadkh@hotmail.com
zarita@usm.my
farahaini@usm.my
Abstract:
Differential equations are basic tools to describe a wide variety of phenomena in nature such as, electrostatics, physics, chemistry, economics, etc. In this paper, a technique is developed to solve nonlinear and linear systems of ordinary differential equations based on the standard Differential Transform Method (DTM) and Multi-stage Differential Transform Method (MsDTM). Comparative numerical results that we are obtained by MsDTM and Runge-Kutta method are proposed. The numerical results showed that the MsDTM gives more accurate approximation as compared to the Runge-Kutta numerical method for the solutions of nonlinear and linear systems of ordinary differential equations
Paper's Title:
Generalized Von Neumann-Jordan Constant for Morrey Spaces and Small Morrey Spaces
Author(s):
H. Rahman and H. Gunawan
Department of Mathematics,
Islamic State University Maulana Malik Ibrahim Malang,
Jalan Gajayana No.50,
Indonesia.
E-mail: hairur@mat.uin-malang.ac.id
Analysis and Geometry Group,
Faculty of Mathematics and Natural Sciences,
Bandung Institute of Technology, Bandung 40132,
Indonesia.
E-mail: hgunawan@math.itb.ac.id
URL:
http://personal.fmipa.itb.ac.id/hgunawan/
Abstract:
In this paper we calculate some geometric constants for Morrey spaces and small Morrey spaces, namely generalized Von Neumann-Jordan constant, modified Von Neumann-Jordan constants, and Zbaganu constant. All these constants measure the uniformly nonsquareness of the spaces. We obtain that their values are the same as the value of Von Neumann-Jordan constant for Morrey spaces and small Morrey spaces.
Paper's Title:
Nonlinear System of Mixed Ordered Variational Inclusions Involving XOR Operation
Author(s):
Iqbal Ahmad, Abdullah and Syed Shakaib Irfan
Department of Mechanical Engineering,
College of Engineering, Qassim University
Buraidah 51452, Al-Qassim,
Saudi Arabia.
E-mail: iqbal@qec.edu.sa,
i.ahmad@qu.edu.sa
Zakir Husain Delhi College,
University of Delhi,
JLN Marg, New Delhi- 110 002,
India.
E-mail: abdullahdu@qec.edu.sa
Department of Mathematics,
Aligarh Muslim University, Aligarh,
India.
E-mail: shakaibirfan@gmail.com
Abstract:
In this work, we introduce and solve an NSMOVI frameworks system involving XOR operation with the help of a proposed iterative algorithm in real ordered positive Hilbert spaces. We discuss the existence of a solution of a considered system of inclusions involving XOR operation by applying the resolvent operator technique with XOR operation and also study the strong convergence of the sequences generated by the considered algorithm. Further, we give a numerical example in support of our considered problem which gives the grantee that all the proposed conditions of our main result are fulfilled.
Paper's Title:
On Euler's First Transformation Formula for k-hypergeometric Function
Author(s):
Sungtae Jun and Insuk Kim
General Education Institute,
Konkuk University, Chungju 380-701,
Republic of Korea.
E-mail: sjun@kku.ac.kr
Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Republic of Korea.
E-mail: iki@wku.ac.kr
Abstract:
Mubeen et al. obtained Kummer's first transformation for the k-hypergeometric function. The aim of this note is to provide the Euler-type first transformation for the k-hypergeometric function. As a limiting case, we recover the results of Mubeen et al. In addition to this, an alternate and easy derivation of Kummer's first transformation for the k-hypergeometric function is also given.
Paper's Title:
Coefficient Estimates Of Sakaguchi Kind Functions Using
Lucas Polynomials
Author(s):
H. Priya and B. Srutha Keerthi
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus,
Chennai - 600 048,
India.
E-mail:
priyaharikrishnan18@gmail.com
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus,
Chennai - 600 048,
India.
E-mail: isruthilaya06@yahoo.co.in
Abstract:
By means of (p,q) Lucas polynomials, we estimate coefficient bounds and Fekete-Szego inequalities for functions belonging to this class. Several corollaries and consequences of the main results are also obtained.
Paper's Title:
Error Bounds for Numerical Integration of Functions of Lower Smoothness and Gauss-Legendre Quadrature Rule
Author(s):
Samuel A. Surulere and Abiola O. Oladeji
Tshwane University of Technology
Department of Mathematics and Statistics
175, Nelson Mandela drive, Arcadia, Pretoria,
South Africa.
E-mail: samuel.abayomi.sas@gmail.com
Abstract:
The error bounds of the rectangular, trapezoidal and Simpson's rules which are commonly used in approximating the integral of a function (f(x)) over an interval ([a,b]) were estimated. The error bounds of the second, and third generating functions of the Gauss-Legendre quadrature rules were also estimated in this paper. It was shown that for an (f(t)) whose smoothness is increasing, the accuracy of the fourth, sixth and eighth error bound of the second, and third generating functions of the Gauss-Legendre quadrature rule does not increase. It was also shown that the accuracy of the fourth error bound of the Simpson's (1/3) and (3/8) rules does not increase.
Paper's Title:
Conservativeness Criteria of Girsanov Transformation for Non-Symmetric Jump-diffusion
Author(s):
Mila Kurniawaty
DDepartment of Mathematics,
Universitas Brawijaya, Malang,
Indonesia.
E-mail: mila_n12@ub.ac.id
Abstract:
We develop the condition in our previous paper [The Conservativeness of Girsanov transformed for symmetric jump-diffusion process (2018)] in the framework of nonsymmetric Markov process with jumps associated with regular Dirichlet form. We prove the conservativeness of it by relation in duality of Girsanov transformed process and recurrent criteria of Dirichlet form.
Paper's Title:
A Caratheodory's Approximate Solutions of Stochastic Differential Equations Under the Hölder Condition
Author(s):
Bo-Kyeong Kim and Young-Ho Kim
Department of Mathematics,
Changwon National University,
Changwon, Gyeongsangnam-do 51140,
Korea.
E-mail: claire9576@naver.com
yhkim@changwon.ac.kr
Abstract:
In this paper, based on the theorem of the uniqueness of the solution of the stochastic differential equation, the convergence possibility of the Caratheodory's approximate solution was studied by approximating the unique solution. To obtain this convergence theorem, we used a Hölder condition and a weakened linear growth condition. Furthermore, The auxiliary theorems for the existence and continuity of the Caratheodory's approximate solution were investigated as a prerequisite.
Paper's Title:
On the Class of Totally Polynomially Posinormal Operators
Author(s):
E. Shine Lal, T. Prasad, P. Ramya
Department of Mathematics,University
College,
Thiruvananthapuram, Kerala, 695034.
India.
E-mail: shinelal.e@gmail.com
Department of Mathematics,
University of Calicut,
Malapuram, Kerala 673635,
India.
E-mail: prasadvalapil@gmail.com
Department of Mathematics,
N.S.S College,
Nemmara, Kerala, 678508
India.
E-mail: ramyagcc@gmail.com
Abstract:
In this paper, we proved that if T ∈
B(H) is totally P-posinormal operator with
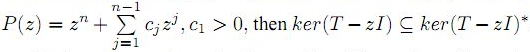 . Moreover, we study spectral continuity and range kernel orthogonality of these class of operators.
. Moreover, we study spectral continuity and range kernel orthogonality of these class of operators.
Paper's Title:
Linear System of Singularly Perturbed Initial Value Problems with Robin Initial Conditions
Author(s):
S. Dinesh, G. E. Chatzarakis, S. L. Panetsos and S. Sivamani
Department of Mathematics,
Saranathan College of Engineering,
Tiruchirappalli-620012,
Tamil Nadu,
India.
Department of Electrical and Electronic
Engineering Educators,
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail:
geaxatz@otenet.gr,
dineshselvaraj24@gmail.com,
spanetsos@aspete.gr,
winmayi2012@gmail.com
Abstract:
On the interval (0,1], this paper considers an initial value problem for a system of n singularly perturbed differential equations with Robin initial conditions. On a piecewise uniform Shishkin mesh, a computational approach based on a classical finite difference scheme is proposed. This approach is shown to be first-order convergent in the maximum norm uniformly in the perturbation parameters. The theory is illustrated by a numerical example.
Paper's Title:
Derivation of the Existence Theorem of the Solution of the Stochastic Functional Differential Equation Using Conditions Given Partial Weights
Author(s):
Young-Ho Kim
Department of Mathematics,
Changwon National University
Changwon, Gyeongsangnam 51140,
Korea.
E-mail:
yhkim@changwon.ac.kr
Abstract:
The main purpose of this note was to demonstrate the solution existence theorem for stochastic functional differential equations under sufficient conditions. As an alternative to the stochastic process theory of the stochastic functional differential equations, we impose a partial weighting condition and a weakened linear growth condition. We first show that the condition guarantees existence and uniqueness and then show some exponential estimates for the solution.
Paper's Title:
Portfolio Optimization of Sharia and Non-Sharia Stocks Using Single Index Model (Case study: Jakarta Sharia Index and Kompas 100 Index)
Author(s):
Kwardiniya Andawaningtyas, Muhammad Luthfi, Marjono, Endang Wahyu Handamari, Umu S'adah, Evi Ardiyani
Department of Mathematics,
Brawijaya University, Malang,
Indonesia.
Department of Mathematics,
IPB University, Bogor,
Indonesia.
E-mail:
dina_math@ub.ac.id
muhammadluthfi@student.ub.ac.id
marjono@ub.ac.id
ewahyu-math@ub.ac.id
u.saadah@ub.ac.id
ardiyanievi@apps.ipb.ac.id
Abstract:
Stocks are instruments with high returns but also have increased risks. One way to overcome this risk is to form a stock portfolio. This study observed 30 sharia stocks listed on the Jakarta Islamic Index (JII) and 28 non-shariah stocks listed on the Kompas 100 Index from March 2020 to September 2022. The data used is the daily closing price of stocks, the number of stock dividends, and the daily closing price of the Jakarta Composite Index (JCI) from 3rd March 2020, to 31st August 2022. In addition, interest rate of Bank Indonesia Certificate (SBI) is used as risk-free rate. This study aims to optimize the sharia and non-sharia stocks portfolio using the Single Index Model (SIM), which will then be evaluated using the Sharpe, Treynor, and Jensen ratio. The result is that the optimal portfolio of sharia stocks have better performance than the optimal portfolio of non-sharia stocks based on the Treynor ratio. Meanwhile, the optimal portfolio of non-sharia stocks have better performance than the optimal portfolio of sharia stocks based on the Sharpe and Jensen ratio.
Paper's Title:
Semicommutative and Semiprime Properties in Bi-amalgamated Rings
Author(s):
1A. Aruldoss, 2C. Selvaraj, 3G. E. Chatzarakis, 4S. L. Panetsos, 5U. Leerawat
1
Department of Mathematics,
Mepco Schlenk Engineering College,
Sivakasi-626 005, Tamilnadu,
India.
aruldossa529@gmail.com
2
Department of Mathematics,
Periyar University,
Salem - 636 011, Tamilnadu,
India.
selvavlr@yahoo.com
3,4
Department of Electrical and Electronic Engineering Educators,
School of Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
geaxatz@otenet.gr
spanetsos@aspete.gr
5
Department of Mathematics,
Faculty of Science, Kasetsart University,
Bangkok 10900,
Thailand.
fsciutl@ku.ac.th
Abstract:
Let α: A→ B and β: A→ C be two ring homomorphisms and I and I' be two ideals of B and C, respectively, such that α{-1}(I)=β{-1}(I'). In this paper, we give a characterization for the bi-amalgamation of A with (B, C) along (I, I') with respect to (α, β) (denoted by A⋈(α, β)(I, I')) to be a SIT, semiprime, semicommutative and semiregular. We also give some characterization for these rings.
Paper's Title:
Indonesia's GDP Forecast: Evidence From Fuzzy Time Series Model Using Particle Swarm Optimization Algorithm
Author(s):
Ismail Djakaria1, Djihad Wungguli2, Regina Sugi Pakadang3, Sri Endang Saleh4, Maman Abdurachman Djauhari5
1,2,3Universitas
Negeri Gorontalo,
Department of Statistics, Gorontalo,
Indonesia.
4Universitas Negeri Gorontalo,
Department of Development Economics, Gorontalo,
Indonesia.
5Indonesian Institute of Education,
Jl. Terusan Pahlawan 32, Garut 44151,
Indonesia.
E-mail: iskar@ung.ac.id
URL:
https://orcid.org/0000-0003-1358-2356
Abstract:
Gross Domestic Product (GDP) is a principal indicator used to measure the economic condition of a country. Indonesia's GDP growth from 2017 to 2019 was approximately 6 percent; however, it experienced a decline in 2020 and 2021, with rates of only -0.02 percent and 2.41 percent, respectively. In the process of economic development planning, a forecasting system is required to determine GDP in the future. The forecasting method employed in this research is fuzzy time series optimized using Particle Swarm Optimization (PSO), to enhance the accuracy and convergence of forecasted values. The dataset used comprises secondary data, specifically 54 sets of Indonesian GDP data spanning from the first quarter of 2010 to the second quarter of 2023. The analysis results indicate that the proposed method is better than the conventional fuzzy time series approach. The former method provides a predictive value for one period in the future with a Mean Absolute Percentage Error (MAPE) value of 4.40%. In contrast, the latter yields higher predictive values with a MAPE value of 7.93%.
Paper's Title:
A Multi-Stage Differential Transform Approach for Solving Differential Algebraic Systems Without Index Reduction
Author(s):
Khalil Al Ahmad, Farah Abdulla Aini, Amirah Azmi, Muhammad Abbas
School of Mathematical Sciences
Universiti Sains Malaysia
11800 USM Penang
Malaysia.
Department of Mathematics,
University of Sargodha,
40100 Sargodha,
Pakistan
E-mail:
abumohmmadkh@hotmail.com
farahaini@usm.my
amirahazmi@usm.my
muhammad.abbas@uos.edu.pk
Abstract:
This paper aims to solve differential algebraic systems without the need to reduce the index, which causes a defect in the behavior of the approximate solution. The differential transform method was developed to solve differential algebraic systems. The differential algebraic system is transferred to the algebraic system by applying the differential transform method. Then the Multi-stage differential transform method is applied to extend the interval of the convergence. The numerical results show the new technique is an efficient and flexible tool to obtain accurate results that meet the initial conditions and keep the behavior of the approximate solution consistent.
Paper's Title:
The Difference Between Two Approximate and Accurate Solutions of the Stochastic Differential Delay Equation Under Weak Conditions
Author(s):
Jin-Hyeong Kim and Young-Ho Kim
Department of Mathematics, Changwon
National University,
Changwon, Gyeongsangnam 51140,
Korea.
E-mail: ginhyung5647@changwon.ac.kr
yhkim@changwon.ac.k
Abstract:
In this paper we investigates the existence of approximate solutions derived from the Caratheodory's and the Euler-Maruyama's scheme under a uniform Lipschitz condition and a weakened linear growth condition. And by analyzing the continuity and convergence of these approximate solutions, we would like to provide reliable results to approximate the unique solutions of stochastic functional differential delay equations. In particular, we investigate how quickly the approximate solution by the Carateodori and Euler-Maruyama approximation methods approaches the accurate solution of the equation.
Paper's Title:
New Jacobi Elliptic Function Wave Solutions for Conformable Fractional Benjamin-Bona-Mahoney-Burgers Equation
Author(s):
Guechi Meriem, Guechi Fairouz
Department of Mathematics,
Faculty of Sciences,
LMFN, University Sétif1,
Algeria.
E-mail: guechi.meriem87@gmail.com
fairouz.chegaar@univ-setif.dz
Abstract:
In this paper, Jacobi elliptic function expansion method is applied to solve fractional Benjamin-Bona-Mahoney-Burgers equation with conformable derivative and power law nonlinearity. This method is straightforward, concise, effective and can be used for many other nonlinear evolution equations. Numerical solutions are given to illustrate the accuracy and validity of this method.
Search and serve lasted 0 second(s).