|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
The boundedness of Bessel-Riesz operators on generalized Morrey spaces
Author(s):
Mochammad Idris, Hendra Gunawan and Eridani
Department of Mathematics,
Bandung Institute of Technology,
Bandung 40132,
Indonesia.
E-mail:
mochidris@students.itb.ac.id
Department of Mathematics,
Bandung Institute of Technology,
Bandung 40132,
Indonesia.
E-mail: hgunawan@math.itb.ac.id
URL:
http://personal.fmipa.itb.ac.id/hgunawan/
Department of Mathematics,
Airlangga University,
Surabaya 60115,
Indonesia.
E-mail: eridani.dinadewi@gmail.com
Abstract:
In this paper, we prove the boundedness of Bessel-Riesz operators on generalized Morrey spaces. The proof uses the usual dyadic decomposition, a Hedberg-type inequality for the operators, and the boundedness of Hardy-Littlewood maximal operator. Our results reveal that the norm of the operators is dominated by the norm of the kernels.
Paper's Title:
A Note on Mixed Norm Spaces of Analytic Functions
Author(s):
K. Avetisyan
Faculty of Physics, Yerevan State
University,
Alex Manoogian st. 1, Yerevan, 375025,
Armenia
avetkaren@ysu.am
Abstract:
A direct and elementary proof of an estimate of Littlewood is given together with an application concerning the sharpness and strictness of some inclusions in mixed norm spaces of analytic functions.
Paper's Title:
Commutator For Singular Operators On Variable Exponent Sequence Spaces And Their Corresponding Ergodic Version
Author(s):
A.M. Alphonse and S.S.S. Anupindi
Department of Mathematics,
Birla Institute of Technology And Science- Pilani,
Hyderabad Campus, Jawahar Nagar, Kapra Mandal,
District.-Medchal-500 078, Telangana,
India.
E-mail:
alphonse@hyderabad.bits-pilani.ac.in
p20180442@hyderabad.bits-pilani.ac.in
URL:
https://www.bits-pilani.ac.in/hyderabad/a-michael-alphonse
https://www.bits-pilani.ac.in/research_scholars/sri-sakti-swarup-anupindi
Abstract:
In this paper, we prove strong type inequality for maximal commutator of singular operator on weighted lp spaces. Using these results we prove strong type inequality for the maximal commutator of singular operator on variable exponent sequence spaces. Using Calderon-Coifman-Weiss transference principle we prove strong type inequality for maximal ergodic commutator of singular operator on a probability space equipped with measure preserving transformation U.
Paper's Title:
A New Hardy-Hilbert's Type Inequality for Double Series and its Applications
Author(s):
Mingzhe Gao
Department of Mathematics and Computer Science, Normal College Jishou University,
Jishou Hunan, 416000,
People's Republic of China
mingzhegao1940@yahoo.com.cn
Abstract:
In this paper, it is shown that a new Hardy-Hilbert’s type
inequality for double series can be established by introducing a parameter 
and the weight function of the form 
where c is Euler
constant and 
And
the coefficient 
and 
appear simultaneously in the coefficient and the weight
function when 
In particular, for
case 
some new Hilbert’s
type inequalities are obtained. As applications, some extensions of Hardy-Littlewood’s inequality are given.
Paper's Title:
Ap Functions and Maximal Operator
Author(s):
Chunping Xie
Department of Mathematics,
Milwaukee School of Engineering,
1025 N. Broadway,
Milwaukee, Wisconsin 53202,
U. S. A.
E-mail: xie@msoe.edu
URL: http://www.msoe.edu/people/chunping.xie
Abstract:
The relationship between Ap functions and Hardy-Littlewood maximal operator on Lp,λ(w), the weighted Morrey space, has been studied. Also the extropolation theorem of Lp,λ(w) has been considered.
Paper's Title:
Maximal Singular Operators On Variable Exponent Sequence Spaces and Their Corresponding Ergodic Version
Author(s):
Sri Sakti Swarup Anupindi and Michael A. Alphonse
Department of Mathematics, Birla Institute
of Technology And Science- Pilani,
Hyderabad Campus, Jawahar Nagar, Kapra Mandal,
District.-Medchal-500 078 Telangana,
India.
E-mail:
p20180442@hyderabad.bits-pilani.ac.in
alphonse@hyderabad.bits-pilani.ac.in
URL:
https://www.bits-pilani.ac.in/hyderabad/a-michael-alphonse
https://www.bits-pilani.ac.in/research_scholars/sri-sakti-swarup-anupindi
Abstract:
In this paper, we prove strong and weak type inequalities of singular operators on weighted lwp(Z)$. Using these results, we prove strong type and weak type inequalities of the maximal singular operator of Calderon-Zygmund type on variable exponent sequence spaces lp(·)(Z). Using the Calderon-Coifman-Weiss transference principle, we prove strong type, weak type inequalities of the maximal ergodic singular operator on Lwp(X,B,μ) spaces, where (X,B,μ) is a probability space equipped with measure preserving transformation U.
Paper's Title:
Some Inequalities for the Generalized Riesz Potential on the Generalized Morrey Spaces over Hypergroups
Author(s):
I. Sihwaningrum, Renny, Y. Dasril
Jenderal Soedirman University,
Indonesia.
E-mail: idha.sihwaningrum@unsoed.ac.id
renny@unsoed.ac.id
Universiti Tun Hussein Onn,
Malaysia.
E-mail:
yosza@uthm.edu.my
Abstract:
We present in this paper some inequalities for the generalized Riesz potential on the generalized Morrey spaces over commutative hypergroups. The results can be found by employing the maximal operator.
Paper's Title:
Existence of Large Solutions to Non-Monotone Semilinear Elliptic Equations
Author(s):
Alan V. Lair, Zachary J. Proano, and Aihua W. Wood
Air Force Institute of Technology
2950 Hobson Way, AFIT/ENC
Wright-Patterson Air Force Base, OH, 45433-7765,
USA.
Aihua.Wood@afit.edu
URL: www.afit.edu
Abstract:
We study the existence of large solutions of the semilinear elliptic equation Δu=p(x)f(u) where f is not monotonic. We prove existence, on bounded and unbounded domains, under the assumption that f is Lipschitz continuous, f(0) = 0, f(s) > 0 for s > 0 and there exists a nonnegative, nondecreasing Hölder continuous function g and a constant M such that g(s) ≤ f(s) ≤ Mg(s) for large s. The nonnegative function p is allowed to be zero on much of the domain.
Paper's Title:
Fractional Integral Operators and Olsen Inequalities on
Non-Homogeneous Spaces
Author(s):
Idha Sihwaningrum, Herry P. Suryawan, Hendra Gunawan
Analysis and Geometry Group,
Faculty of Mathematics and Natural Sciences,
Bandung Institute of Technology, Bandung 40132,
Indonesia
hgunawan@math.itb.ac.id
URL:
http://personal.fmipa.itb.ac.id/hgunawan/
Abstract:
We prove the boundedness of the fractional integral operator Iα on generalized Morrey spaces of non-homogeneous type. In addition, we also present Olsen-type inequalities for a multiplication operator involving Iα. Our proof uses a result of García-Cuerva and Martell [3].
Paper's Title:
Oscillation and Boundedness of Solutions to First and Second Order Forced Dynamic Equations with Mixed Nonlinearities
Author(s):
Ravi P. Agarwal and Martin Bohner
Department of Mathematical Sciences, Florida Institute of Technology
Melbourne, FL 32901,
U.S.A.
bohner@mst.edu
URL:http://web.mst.edu/~bohner
Department of Economics and Finance, Missouri University of Science and Technology
Rolla, MO 65401,
U.S.A.
agarwal@fit.edu
Abstract:
Some oscillation and boundedness criteria for solutions to certain
first and second order forced dynamic equations
with mixed nonlinearities are established. The main tool in the proofs
is an inequality due to Hardy, Littlewood and Pólya.
The obtained results can be applied to differential equations,
difference equations and q-difference equations. The results
are illustrated with numerous examples.
Paper's Title:
Some Inequalities Concerning Derivative and Maximum Modulus of Polynomials
Author(s):
N. K. Govil, A. Liman and W. M. Shah
Department of Mathematics & Statistics,
Auburn University, Auburn,
Alabama 36849-5310,
U.S.A
Department of Mathematics,
National Institute of Technology,
Srinagar, Kashmir,
India - 190006
Department of Mathematics,
Kashmir University,
Srinagar, Kashmir,
India - 190006
govilnk@auburn.edu
abliman22@yahoo.com
wmshah@rediffmail.com
Abstract:
In this paper, we prove some compact generalizations of some well-known Bernstein type inequalities concerning the maximum modulus of a polynomial and its derivative in terms of maximum modulus of a polynomial on the unit circle. Besides, an inequality for self-inversive polynomials has also been obtained, which in particular gives some known inequalities for this class of polynomials. All the inequalities obtained are sharp.
Paper's Title:
On Generalization of Hardy-type Inequalities
Author(s):
K. Rauf, S. Ponnusamy and J. O. Omolehin
Department of Mathematics,
University of Ilorin, Ilorin,
Nigeria
krauf@unilorin.edu.ng
Department of Mathematics,
Indian Institute of Technology Madras,
Chennai- 600 036,
India
samy@iitm.ac.in
Department of Mathematics,
University of Ilorin, Ilorin,
Nigeria
omolehin_joseph@yahoo.com
Abstract:
This paper is devoted to some new generalization of Hardy-type integral inequalities and the reversed forms. The study is to determine conditions on which the generalized inequalities hold using some known hypothesis. Improvement of some inequalities are also presented.
Paper's Title:
Fractional class of analytic functions Defined Using q-Differential Operator
Author(s):
K . R. Karthikeyan, Musthafa Ibrahim and S. Srinivasan
Department of Mathematics and
Statistics,
Caledonian College of Engineering, Muscat,
Sultanate of Oman.
E-mail: kr_karthikeyan1979@yahoo.com
College of Engineering,
University of Buraimi, Al Buraimi,
Sultanate of Oman.
E-mail: musthafa.ibrahim@gmail.com
Department of Mathematics, Presidency
College (Autonomous),
Chennai-600005, Tamilnadu,
India.
Abstract:
We define a q-differential fractional operator, which generalizes Salagean and Ruscheweyh differential operators. We introduce and study a new class of analytic functions involving q-differential fractional operator. We also determine the necessary and sufficient conditions for functions to be in the class. Further, we obtain the coefficient estimates, extreme points, growth and distortion bounds.
Paper's Title:
Bounds on the Jensen Gap, and Implications for Mean-Concentrated Distributions
Author(s):
Xiang Gao, Meera Sitharam, Adrian E. Roitberg
Department of Chemistry, and Department
of Computer & Information Science & Engineering,
University of Florida,
Gainesville, FL 32611,
USA.
E-mail: qasdfgtyuiop@gmail.com
URL:
https://scholar.google.com/citations?user=t2nOdxQAAAAJ
Abstract:
This paper gives upper and lower bounds on the gap in Jensen's inequality, i.e., the difference between the expected value of a function of a random variable and the value of the function at the expected value of the random variable. The bounds depend only on growth properties of the function and specific moments of the random variable. The bounds are particularly useful for distributions that are concentrated around the mean, a commonly occurring scenario such as the average of i.i.d. samples and in statistical mechanics.
Paper's Title:
Inequalities Involving A∞ Weights by Extrapolations
Author(s):
Chunping Xie
Mathematics Department,
Milwaukee School of Engineering,
1025 N. Broadway,
Milwaukee, Wisconsin 53202,
U.S.A.
E-mail: xie@msoe.edu
URL:
https://www.msoe.edu/directory/profile/chunping.xie/
Abstract:
We generalize the extrapolation theorem from Ap weights to A∞ weights on the setting of weighted Morrey spaces by using the Rubio de Francia algorithm and ideas in a paper by D. Cruz-Uribe et al. First we have proved the classical Hardy-Littlewood maximal operator is bounded on the weighted Morrey spaces if the weight w(x) is in A∞ and then we have obtained inequalities involving the maximal operator, vector-valued maximal operator, the sharp maximal operator, and A∞ weights.
Paper's Title:
Viability
Theory And Differential Lanchester Type Models For Combat.
Differential Systems.
Author(s):
G. Isac and A. Gosselin
Department Of
Mathematics, Royal Military College Of Canada,
P.O. Box 17000, Stn Forces, Kingston,
Ontario, Canada K7k 7b4
isac-g@rmc.ca
gosselin-a@rmc.ca
URL:
http://www.rmc.ca/academic/math_cs/isac/index_e.html
URL:
http://www.rmc.ca/academic/math_cs/gosselin/index_e.html
Abstract:
In 1914, F.W. Lanchester proposed several mathematical models based on differential equations to describe combat situations [34]. Since then, his work has been extensively modified to represent a variety of competitions including entire wars. Differential Lanchester type models have been studied from many angles by many authors in hundreds of papers and reports. Lanchester type models are used in the planning of optimal strategies, supply and tactics. In this paper, we will show how these models can be studied from a viability theory stand point. We will introduce the notion of winning cone and show that it is a viable cone for these models. In the last part of our paper we will use the viability theory of differential equations to study Lanchester type models from the optimal theory point of view.
Paper's Title:
A Strengthened Hardy-Hilbert's Type Inequality
Author(s):
Weihong Wang and Bicheng Yang
Department of Mathematics, Guangdong Education Institute,
Guangzhou, Guangdong 520303,
People's Republic Of China
wwh@gdei.edu.cn
bcyang@pub.guangzhou.gd.cn
URL: http://www1.gdei.edu.cn/yangbicheng/index.html
Abstract:
By using the improved Euler-Maclaurin's summation formula and
estimating the weight coefficient, we give a new strengthened
version of the more accurate Hardy-Hilbert's type inequality. As
applications, a strengthened version of the equivalent form is
considered.
Paper's Title:
Linearly Transformable Minimal Surfaces
Author(s):
Harold R. Parks and Walter B. Woods
Department of Mathematics,
Oregon State University,
Corvallis, Oregon 97331--4605,
USA
parks@math.oregonstate.edu
URL: http://www.math.oregonstate.edu/people/view/parks/
Abstract:
We give a complete description of a nonplanar minimal surface in R3 with the surprising property that the surface remains minimal after mapping by a linear transformation that dilates by three distinct factors in three orthogonal directions. The surface is defined in closed form using Jacobi elliptic functions.
Paper's Title:
Inequalities for
the
Author(s):
S. S. Dragomir
School of Engineering and Science
Victoria University, PO 14428
Melbourne City MC,
Victoria 8001,
Australia
sever.dragomir@vu.edu.au
URL: http://www.staff.vu.edu.au/RGMIA/dragomir/
Abstract:
Some recent inequalities for the Čebyšev functional of two functions of selfadjoint linear operators in Hilbert spaces, under suitable assumptions for the involved functions and operators, are surveyed.
Paper's Title:
Hardy Type Inequalities via Convexity - The Journey so Far
Author(s):
James A.
Oguntuase and Lars-Erik Persson
Department of Mathematics,
University of Agriculture,
P. M. B. 2240, Abeokuta, Nigeria.
Department of
Mathematics, Luleĺ University of Technology,
SE-971 87, Luleĺ , Sweden.
oguntuase@yahoo.com,
larserik@sm.luth.se .
Abstract:
It is nowadays well-known that Hardy's inequality (like many other inequalities) follows directly from Jensen's inequality. Most of the development of Hardy type inequalities has not used this simple fact, which obviously was unknown by Hardy himself and many others. Here we report on some results obtained in this way mostly after 2002 by mainly using this fundamental idea.
Paper's Title:
A New Property of General Means of Order p with an Application to the Theory of Economic Growth
Author(s):
Olivier de La Grandville
Department of Management Science and Engineering,
Huang Engineering Center, Stanford University,
475 Via Ortega, Stanford, California 94305
U.S.A.
Abstract:
The purpose of this note is to demonstrate a new property of the
general mean of order p of m ordered positive numbers
.
If p < 0 and if
,
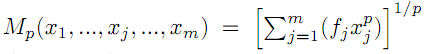
the elasticity of
with
respect to xm, defined by
,
tends towards zero, and therefore
.
This property is then applied to optimal growth theory.
Paper's Title:
Certain Compact Generalizations of Well-Known Polynomial Inequalities
Author(s):
N. A. Rather and Suhail Gulzar
Department of Mathematics,
University of Kashmir, Hazratbal Srinagar-190006,
India.
Abstract:
In this paper, certain sharp compact generalizations of well-known Bernstien-type inequalities for polynomials, from which a variety of interesting results follow as special cases, are obtained.
Paper's Title:
Weak Type Inequalities for Some Operators on Generalized Morrey Spaces Over Metric Measure Spaces
Author(s):
Idha Sihwaningrum, Ari Wardayani, Hendra Gunawan
Faculty of Mathematics and Natural
Sciences,
Jenderal Soedirman University, Purwokerto 53122,
Indonesia.
E-mail: idha.sihwaningrum@unsoed.ac.id
ariwardayani@yahoo.co.id
Faculty of Mathematics and Natural
Sciences,
Bandung Institute of Technology, Bandung 40132,
Indonesia.
E-mail: hgunawan@math.itb.ac.id
URL:
http://personal.fmipa.itb.ac.id/hgunawan/
Abstract:
We discuss weak type inequalities for maximal and fractional integral operators on generalized Morrey spaces over metric measure spaces. Here the measure satisfies the so called growth condition. By taking into account the maximal operator, we obtain a Hedberg type inequality, which leads us to the weak type inequality for the fractional integral operator on the same spaces.
Paper's Title:
A Comparison Between Two Different Stochastic Epidemic Models with Respect to the Entropy
Author(s):
Farzad Fatehi and Tayebe Waezizadeh
Department of Mathematics,
University of Sussex,
Brighton BN1 9QH,
UK.
E-mail: f.fatehi@sussex.ac.uk
URL:
http://www.sussex.ac.uk/profiles/361251
Department of Pure Mathematics, Faculty
of Mathematics and Computer,
Shahid Bahonar University of Kerman,
Kerman 76169-14111,
Iran.
E-mail: waezizadeh@uk.ac.ir
URL:
http://academicstaff.uk.ac.ir/en/tavaezizadeh
Abstract:
In this paper at first a brief history of mathematical models is presented with the aim to clarify the reliability of stochastic models over deterministic models. Next, the necessary background about random variables and stochastic processes, especially Markov chains and the entropy are introduced. After that, entropy of SIR stochastic models is computed and it is proven that an epidemic will disappear after a long time. Entropy of a stochastic mathematical model determines the average uncertainty about the outcome of that random experiment. At the end, we introduce a chain binomial epidemic model and compute its entropy, which is then compared with the DTMC SIR epidemic model to show which one is nearer to reality.
Paper's Title:
Inequalities for Functions of Selfadjoint Operators on Hilbert Spaces:
a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
College of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning inequalities for continuous functions of selfadjoint operators on complex Hilbert spaces. It is intended for use by both researchers in various fields of Linear Operator Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
A Note on Schur's Lemma in Banach Function Spaces
Author(s):
R. E. Castillo, H. Rafeiro and E. M. Rojas
Universidad Nacional de Colombia,
Departamento de Matematicas, Bogota,
Colombia.
E-mail: recastillo@unal.edu.co
United Arab Emirates University,
Department of Mathematical Sciences, Al Ain,
United Arab Emirates.
E-mail: rafeiro@uaeu.ac.ae
Universidad Nacional de Colombia,
Departamento de Matematicas, Bogota,
Colombia.
E-mail: emrojass@unal.edu.co
Abstract:
In this small note, in a self contained presentation, we show the validity of Schur's type lemma in the framework of Banach function spaces.
Paper's Title:
A Regularity of the Weak Solution Gradient of the Dirichlet Problem for Divergent Form Elliptic Equations in Morrey Spaces
Author(s):
Nicky K. Tumalun and Philotheus E. A. Tuerah
Mathematics Department, Universitas Negeri Manado,
Tondano Selatan, Minahasa Regency,
Sulawesi Utara Province,
Indonesia.
E-mail: nickytumalun@unima.ac.id,
pheatuerah@unima.ac.id
Abstract:
In this paper we prove that the gradient of the weak solution of the Dirichlet problem for divergent form elliptic equations, with the known term belongs to the Morrey spaces, is the element of the weak Morrey spaces.
Paper's Title:
Integrability of Sine and Cosine Series Having Coefficients of a New Class
Author(s):
L. Leindler Bolyai Institute,
University of Szeged, Aradi Vértanúk Tere 1, H-6720 Szeged, Hungary
leindler@math.u-szeged.hu
Abstract:
Some integrability theorems or only their sufficient part are
generalized such that the coefficients of the sine and cosine series belong to a
new class of sequences being wider than the class of sequences of rest bounded
variation, which itself is a generalization of the monotone decreasing
sequences, but a subclass of the almost monotone decreasing sequences. It is
also verified that the new class of sequences and the class of almost monotone
decreasing sequences are not comparable.
Paper's Title:
On an Extension of Hilbert’s Integral Inequality with Some Parameters
Author(s):
Bicheng Yang
Department of
Mathematics, Guangdong Education College, Guangzhou, Guangdong 510303, People’s
Republic of China.
bcyang@pub.guangzhou.gd.cn
URL:
http://www1.gdei.edu.cn/yangbicheng/index.html
Abstract:
In this paper, by introducing some parameters and estimating the
weight function, we give an extension of Hilbert’s integral inequality with a
best constant factor. As applications, we consider the equivalent form and some
particular results.
Paper's Title:
New Proofs of the Grüss Inequality
Author(s):
A.Mc.D. Mercer
and Peter R.
Mercer
Dept. Mathematics and Statistics,
University of Guelph, Guelph, Ontario,
Canada.
amercer@reach.net
Dept. Mathematics,
S.U.N.Y. College at Buffalo, Buffalo, NY,
U.S.A.
mercerpr@math.buffalostate.edu
Abstract:
We present new proofs of the Grüss inequality in its original form and in its linear functional form.
Paper's Title:
Some Approximation for the linear combinations of modified Beta operators
Author(s):
Naokant Deo
Department of Applied Mathematics
Delhi College of Engineering
Bawana Road, Delhi - 110042,
India.
dr_naokant_deo@yahoo.com
Abstract:
In this paper, we propose a sequence of new positive linear operators βn to study the ordinary approximation of unbounded functions by using some properties of the Steklov means.
Paper's Title:
Logarithmically complete monotonicity properties for the gamma functions
Author(s):
Chao-Ping Chen and Feng Qi
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University,
Jiaozuo City, Henan 454010,
China.
chenchaoping@hpu.edu.cn
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University,
Jiaozuo City, Henan 454010,
China.
qifeng@hpu.edu.cn
fengqi618@member.ams.org
Abstract:
Some logarithmically completely monotonic functions involving the gamma functions are presented. As a consequence, some known results are proved and refined.
Paper's Title:
Boundedness for Vector-Valued Multilinear Singular Integral Operators on Triebel-Lizorkin Spaces
Author(s):
Liu Lanzhe
College of Mathematics
Changsha University of Science and Technology,
Changsha 410077,
P.R. of China.
lanzheliu@263.net
Abstract:
In this paper, the boundedness for some vector-valued multilinear operators associated to certain
fractional singular integral operators on Triebel-Lizorkin space are obtained. The operators include Calderón-Zygmund
singular integral operator and fractional integral operator.
Paper's Title:
General Extension of Hardy-Hilbert's Inequality (I)
Author(s):
W. T. Sulaiman
College of Computer Science and Mathematics, University of Mosul,
Iraq.
waadsulaiman@hotmail.com
Abstract:
A generalization for Hardy-Hilbert's inequality that extends the recent
results of Yang and Debnath
[6], is given.
Paper's Title:
Boundary Value Problems for Fractional Diffusion-Wave equation
Author(s):
Varsha Daftardar-Gejji and Hossein Jafari
Department of Mathematics, University of Pune,
Ganeshkhind, Pune - 411007,
INDIA.
vsgejji@math.unipune.ernet.in
jafari_h@math.com
Abstract:
Non homogeneous fractional diffusion-wave equation has been solved under linear/nonlinear boundary conditions. As the order of time derivative changes from
0 to 2, the process changes from slow diffusion to classical diffusion to mixed diffusion-wave behaviour.
Numerical examples presented here confirm this inference. Orthogonality of eigenfunctions in case of fractional Stürm-Liouville problem has been established
Paper's Title:
On Vector Variational Inequality Problem in Terms of Bifunctions
Author(s):
C. S. Lalitha and Monika Mehta
Department of Mathematics, Rajdhani College,
Department of Mathematics, Satyawati College,
University of Delhi, Raja Garden,
Delhi 110015, India
cslalitha@rediffmail.com
University Of Delhi, Ashok Vihar,
Phase-III, Delhi 110052, India
mridul_in@yahoo.com
Abstract:
In this paper, we consider a generalized vector variational
inequality problem expressed in terms of a bifunction and establish
existence theorems for this problem by using the concepts of cone
convexity and cone strong quasiconvexity and employing the
celebrated Fan's Lemma. We also give two types of gap functions for this problem.
Paper's Title:
Komatu Integral Transforms of Analytic Functions Subordinate to Convex Functions
Author(s):
T. N. Shanmugam and C. Ramachandran
Department of Mathematics, College of Engineering,
Anna University, Chennai-600 025, Tamilnadu,
India
shan@annauniv.edu
Department of Mathematics, College of Engineering,
Anna University, Chennai-600 025, Tamilnadu,
India
crjsp2004@yahoo.com
Abstract:
In this paper, we consider the class A of the functions f(z) of the form
which are analytic in an open disk
has some property. Certain inclusion and the closure properties like convolution with convex univalent function etc. are studied.
and study certain subclass of the class A, for which
Paper's Title:
Local and Global Existence and Uniqueness Results for Second and Higher Order Impulsive Functional Differential Equations with Infinite Delay
Author(s):
Johnny Henderson and Abdelghani Ouahab
Department of Mathematics, Baylor University,
Waco, Texas 76798-7328
USA.
Johnny_Henderson@baylor.edu
Laboratoire de Mathématiques, Université de Sidi Bel Abbés
BP 89, 22000 Sidi Bel Abbées,
Algérie.
ouahab@univ-sba.dz
Abstract:
In this paper, we discuss the local and global existence and
uniqueness results for second and higher order impulsive functional
differential equations with infinite delay. We shall rely on a
nonlinear alternative of Leray-Schauder. For the global existence
and uniqueness we apply a recent Frigon and Granas nonlinear
alternative of Leray-Schauder type in Fréchet spaces.
Paper's Title:
A note on Inequalities due to Martins, Bennett and Alzer
Author(s):
József Sándor
Babeş-Bolyai University of Cluj, Department of Mathematics and Computer Sciences
Kogălniceanu Nr.1, Cluj-Napoca,
Romania.
jjsandor@hotmail.com
jsandor@member.ams.org
Abstract:
A short history of certain inequalities by Martins, Bennett as well as Alzer, is provided. It is shown that, the inequality of Alzer for negative powers [6], or Martin's reverse inequality [7] are due in fact to Alzer [2]. Some related results, as well as a conjecture, are stated.
Paper's Title:
An Approximation of Jordan Decomposable Functions for a Lipschitz Function
Author(s):
Ibraheem Alolyan
Mathematics Department,
College of Science, King Saud University
P.O.Box: 2455, Riyadh 11451,
Saudi Arabia
ialolyan05@yahoo.com
Abstract:
The well known Jordan decomposition theorem gives the useful characterization that any function of bounded variation can be written as the difference of two increasing functions. Functions which can be expressed in this way can be used to formulate an exclusion test for the recent Cellular Exclusion Algorithms for numerically computing all zero points or the global minima of functions in a given cellular domain [2,8,9]. In this paper we give an algorithm to approximate such increasing functions when only the values of the function of bounded variation can be computed. For this purpose, we are led to introduce the idea of ε-increasing functions. It is shown that for any Lipschitz continuous function, we can find two ε-increasing functions such that the Lipschitz function can be written as the difference of these functions.
Paper's Title:
Regular Variation on Time Scales and Dynamic Equations
Author(s):
Pavel Řehák
Institute of Mathematics, Academy of Sciences of the Czech Republic
Žižkova 22, CZ61662 Brno,
Czech Republic
rehak@math.muni.cz
URL:http://www.math.muni.cz/~rehak
Abstract:
The purpose of this paper is twofold. First, we want to initiate a study
of regular variation on time scales by introducing this concept in such a
way that it
unifies and extends well studied continuous and discrete cases.
Some basic properties of regularly varying functions on time scales will be
established as well.
Second, we give conditions under which certain solutions of linear second
order
dynamic equations are regularly varying.
Open problems and possible directions for a future research are discussed,
too.
Paper's Title:
A Subclass of Meromorphically Multivalent Functions with Applications to Generalized Hypergeometric Functions
Author(s):
M. K. Aouf
Mathematics Department,
Faculty of Science,
Mansoura University 35516,
Egypt
mkaouf127@yahoo.com
Abstract:
In this paper a new subclass of meromorphically multivalent functions, which
is defined by means of a Hadamard product (or convolution) involving some
suitably normalized meromorphically p-valent functions. The main object of
the present paper is to investigate the various important properties and
characteristics of this subclass of meromorphically multivalent functions.
We also derive many interesting results for the Hadamard products of
functions belonging to this subclass. Also we consider several applications
of our main results to generalized hypergeomtric functions.
Paper's Title:
A Study of the Effect of Density Dependence in a Matrix Population Model
Author(s):
N. Carter and M. Predescu
Department of Mathematical Sciences,
Bentley University,
Waltham, MA 02452,
U.S.A.
ncarter@bentley.edu
mpredescu@bentley.edu
Abstract:
We study the behavior of solutions of a three dimensional discrete time nonlinear matrix population model. We prove results concerning the existence of equilibrium points, boundedness, permanence of solutions, and global stability in special cases of interest. Moreover, numerical simulations are used to compare the dynamics of two main forms of the density dependence function (rational and exponential).
Paper's Title:
Some Remarks on a Result of Bougoffa
Author(s):
James A. Oguntuase, Lars-Erik Persson and Josip E. Pečarič
Department of
Mathematics,University of Agriculture,
P M B 2240, Abeokuta, Nigeria
Department of Mathematics,
Luleĺ University of Technology,
SE-971 87, Luleĺ , Sweden
Faculty of Textile Technology, University of Zagreb,
Pierottijeva 6, 10000 Zagreb, Croatia
oguntuase@yahoo.com,
larserik@sm.luth.se,
pecaric@hazu.hr.
Abstract:
Some new generalizations of the result of
L. Bougoffa [J. Inequal. Pure Appl. Math. 7 (2) (2006), Art. 60]
are derived and discussed.
Paper's Title:
On a Hilbert-type Inequality with the Polygamma Function
Author(s):
Bing He and Bicheng Yang
Department of Mathematics, Guangdong Education College,
Guangzhou, 510303,
China.
Department of Mathematics, Guangdong Education College,
Guangzhou, 510303,
China.
Abstract:
By applying the method of weight function and the technique of real analysis, a Hilbert-type inequality with a best constant factor is established, where the best constant factor is made of the polygamma function. Furthermore, the inverse form is given.
Paper's Title:
A New Method for Comparing Closed Intervals
Author(s):
Ibraheem Alolyan
Department of Mathematics, College of Sciences,
King Saud University, P. O. Box 2455, Riyadh 11451,
Saudi Arabia
ialolyan@ksu.edu.sa
URL:http://faculty.ksu.edu.sa/ALolyan
Abstract:
The usual ordering ``≤" on R is a total ordering, that is, for any two real numbers in R, we can determine their order without difficulty. However, for any two closed intervals in R, there is not a natural ordering among the set of all closed intervals in R. Several methods have been developed to compare two intervals. In this paper, we define the μ-ordering which is a new method for ordering closed intervals.
Paper's Title:
An Lp Inequality for `Self-Reciprocal' Polynomials. II
Author(s):
M. A. Qazi
Department of Mathematics,
Tuskegee University,
Tuskegee, Alabama 36088
U.S.A.
Abstract:
The main result of this paper is a sharp integral mean inequality for the derivative of a `self-reciprocal' polynomial.
Paper's Title:
A Note On The Global Behavior Of A Nonlinear System of Difference Equations
Author(s):
Norman H. Josephy, Mihaela Predescu and Samuel W. Woolford
Department of Mathematical Sciences,
Bentley University,
Waltham, MA 02452,
U.S.A.
mpredescu@bentley.edu
njosephy@bentley.edu
swoolford@bentley.edu
Abstract:
This paper deals with the global asymptotic stability character of solutions of a discrete time deterministic model proposed by Wikan and Eide in Bulletin of Mathematical Biology, 66, 2004, 1685-1704. A stochastic extension of this model is proposed and discussed. Computer simulations suggest that the dynamics of the stochastic model includes a mixture of the dynamics observed in the deterministic model.
Paper's Title:
On the Boundedness of Hardy's Averaging Operators
Author(s):
Dah-Chin Luor
Department of Applied Mathematics,
I-Shou University, Dashu District,
Kaohsiung City 84001,
Taiwan, R.O.C.
dclour@isu.edu.tw
Abstract:
In this paper we establish scales of sufficient conditions for the boundedness of Hardy's averaging operators on weighted Lebesgue spaces. The estimations of the operator norms are also obtained. Included in particular are the Erdélyi-Kober operators.
Paper's Title:
Szegö Limits and Haar Wavelet Basis
Author(s):
M. N. N. Namboodiri and S. Remadevi
Dept. of Mathematics, Cochin University
of Science and Technology,
Cochin-21, Kerala,
India.
Dept. of Mathematics, College of
Engineering,
Cherthala, Kerala,
India.
Abstract:
This paper deals with Szegö type limits for multiplication operators on L2 (R) with respect to Haar orthonormal basis. Similar studies have been carried out by Morrison for multiplication operators Tf using Walsh System and Legendre polynomials [14]. Unlike the Walsh and Fourier basis functions, the Haar basis functions are local in nature. It is observed that Szegö type limit exist for a class of multiplication operators Tf , f∈ L∞ (R) with respect to Haar (wavelet) system with appropriate ordering. More general classes of orderings of Haar system are identified for which the Szegö type limit exist for certain classes of multiplication operators. Some illustrative examples are also provided.
Paper's Title:
A One-Line Derivation of the Euler and Ostrogradski Equations
Author(s):
Olivier de La Grandville
Stanford University,
Department of Management Science and Engineering,
Stanford, CA 94305,
U. S. A
Abstract:
At the very heart of major results of classical physics, the Euler and Ostrogradski equations have apparently no intuitive interpretation. In this paper we show that this is not so. Relying on Euler's initial geometric approach, we show that they can be obtained through a direct reasoning that does not imply any calculation. The intuitive approach we suggest offers two benefits: it gives immediate significance to these fundamental second-order non-linear differential equations; and second, it allows to obtain a property of the calculus of variations that does not seem to have been uncovered until now: the Euler and Ostrogradski equations can be derived not necessarily by giving a variation to the optimal function -- as is always done; one could equally well start by giving a variation to their derivative(s).
Paper's Title:
Traub-Potra-Type Method for Set-Valued Maps
Author(s):
Ioannis K. Argyros and Saďd Hilout
Cameron University,
Department of Mathematics Sciences,
Lawton, OK 73505,
USA
URL: http://www.cameron.edu/~ioannisa/
Poitiers University,
Laboratoire de Mathematiques et Applications,
Bd. Pierre et Marie Curie, Teleport 2, B.P. 30179,
86962 Futuroscope Chasseneuil Cedex,
France
said.hilout@math.univ-poitiers.fr
http://www-math.univ-poitiers.fr/~hilout/
Abstract:
We introduce a new iterative method for approximating a locally unique solution of variational inclusions in Banach spaces by using generalized divided differences of the first order. This method extends a method considered by Traub (in the scalar case) and by Potra (in the Banach spaces case) for solving nonlinear equations to variational inclusions. An existence-convergence theorem and a radius of convergence are given under some conditions on divided differences operator and Lipschitz-like continuity property of set-valued mappings. The R-order of the method is equal to the unique positive root of a certain cubic equation, which is $1.839..., and as such it compares favorably to related methods such as the Secant method which is only of order $1.618....
Paper's Title:
Some New Nonlinear Integro-Differential Inequalities of Gronwall-Bellman-Pachpatte Type
Author(s):
A. ABDELDAIM
Department of Mathematics and Computer
Sciences,
Faculty of Science,
Port Said University, Port Said,
EGYPT.
Department of Mathematics,
Faculty of Science and Humanities,
Shaqra University, Dawadmi,
SAUDI ARABIA.
E-mail:
ahassen@su.edu.sa
URL:
http://faculty.ksu.edu.sa/DRABDELDAIM/Pages/Home.aspx
Abstract:
In this paper we establish some new nonlinear integro-differential inequalities of Gronwall-Bellman-Pachpatte type for function of one independent variable. The purpose of this paper is to extend certain results which proved by Pachpatte in [On some fundamental integrodifferential and integral inequalities, An. Sti. Univ. Al. I. Cuza, Iasi, Vol.23 (1977), 77-86]. The inequalities obtained here can be used in the theory of some new classes of nonlinear integro-differential equations. Some applications are also given to illustrate the usefulness of our results.
Paper's Title:
End-Point and Transversality Conditions in the Calculus of Variations: Derivations through Direct Reasoning
Author(s):
Olivier de La Grandville
Stanford University,
Department of Management Science and Engineering,
475 Via Ortega, Stanford, CA 94305,
U. S. A.
E-mail: ola@stanford.edu
Abstract:
We offer an intuitive explanation of the end-point and transversality conditions that complement the Euler equation in the calculus of variations. Our reasoning is based upon the fact that any variation given to an optimal function must entail a zero net gain to the functional, all consequences of implied changes in its derivative being fully taken into account.
Paper's Title:
Scope of the Logarithmic Mean
Author(s):
Murali Rao and Agnish Dey
Department of Mathematics,
University of Florida,
1400 Stadium Road, Gainesville,
Florida 32611,
U. S. A.
E-mail: mrao@ufl.edu
URL: http://people.clas.ufl.edu/mrao
E-mail: agnish@ufl.edu
URL: http://people.clas.ufl.edu/agnish
Abstract:
A number a is between two numbers x and y if and only if a is a convex combination of x and y, in other words, it is a "weighted mean" of x and y. Geometric mean, arithmetic mean are well known examples of these "means". Of more recent vintage is the logarithmic mean which has been considered in many articles in the literature. In this note, we first discuss some of its properties. Then we shall introduce the L function and explore the inverse of this function and its connection with the Lambert's Omega function.
Paper's Title:
Commutators of Hardy Type Operators
Author(s):
Chunping Xie
Department of Mathematics,
Milwaukee School of Engineering,
1025 N. Broadway,
Milwaukee, Wisconsin 53202,
USA.
E-mail:
xie@msoe.edu
URL:
http://www.msoe.edu/people/chunping.xie
Abstract:
The note deals with commutaors of the Hardy operator, Hardy type operators on Morrey spaces on R+. We have proved that the commutators generated by Hardy operator and Hardy type operators with a BMO function b are bounded on the Morrey spaces.
Paper's Title:
A Note on Calderon Operator
Author(s):
Chunping Xie
Department of Mathematics,
Milwaukee School of Engineering,
1025 N. Broadway,
Milwaukee, Wisconsin 53202,
U. S. A.
E-mail: xie@msoe.edu
URL: http://www.msoe.edu/people/chunping.xie
Abstract:
We have shown that the Calderon operator is bounded on Morrey Spaces on R+. Also under certain conditions on the weight, the Hardy operator, the adjoint Hardy operator, and therefore the Caldern operator are bounded on the weighted Morrey spaces.
Paper's Title:
Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.
Paper's Title:
Introducing the Dorfmanian: A Powerful Tool for the Calculus Of Variations
Author(s):
Olivier de La Grandville
Department of Management Science and Engineering,
Stanford University,
475 Via Ortega, Stanford, CA 94305,
U. S. A.
E-mail: odelagrandville@gmail.com
Abstract:
We show how a modified Hamiltonian proposed by Robert Dorfman [1] to give intuitive sense
to the Pontryagin maximum principle can be extended to easily obtain all
high-order equations of the calculus of variations. This new concept is
particularly efficient to determine the differential equations leading to
the extremals of functionals defined by n-uple integrals, while a
traditional approach would require -- in some cases repeatedly -- an
extension of Green's theorem to n-space.
Our paper is dedicated to the memory of Robert Dorfman (1916 - 2002).
Paper's Title:
On Closed Range C*-modular Operators
Author(s):
Javad Farokhi-Ostad and Ali Reza Janfada
Department of Mathematics,
Faculty of Mathematics and Statistics Sciences,
University of Birjand, Birjand,
Iran.
E-mail: j.farokhi@birjand.ac.ir
ajanfada@birjand.ac.ir
Abstract:
In this paper, for the class of the modular operators on Hilbert C*-modules, we give the conditions to closedness of their ranges. Also, the equivalence conditions for the closedness of the range of the modular projections on Hilbert C*-modules are discussed. Moreover, the mixed reverse order law for the Moore-Penrose invertible modular operators are given.
Paper's Title:
An Existence of the Solution to Neutral Stochastic Functional Differential Equations Under the Holder Condition
Author(s):
Young-Ho Kim
Department of Mathematics,
Changwon National University,
Changwon, Gyeongsangnam-do 51140,
Korea.
E-mail: iyhkim@changwon.ac.kr
Abstract:
In this paper, we show the existence and uniqueness of solution of the neutral stochastic functional differential equations under weakened H\"{o}lder condition, a weakened linear growth condition, and a contractive condition. Furthermore, in order to obtain the existence of a solution to the equation we used the Picard sequence.
Paper's Title:
On Ruled Surfaces According to Quasi-Frame in Euclidean 3-Space
Author(s):
M. Khalifa Saad and R. A. Abdel-Baky
Department of Mathematics, Faculty of
Science,
Islamic University of Madinah,
KSA.
Department of Mathematics, Faculty of Science,
Sohag University, Sohag,
EGYPT.
E-mail:
mohamed_khalifa77@science.sohag.edu.eg,
mohammed.khalifa@iu.edu.sa
Department of Mathematics, Faculty of
Science,
Assiut University, Assiut,
EGYPT.
E-mail: rbaky@live.com
Abstract:
This paper aims to study the skew ruled surfaces by using the quasi-frame of Smarandache curves in the Euclidean 3-space. Also, we reveal the relationship between Serret-Frenet and quasi-frames and give a parametric representation of a directional ruled surface using the quasi-frame. Besides, some comparative examples are given and plotted which support our method and main results.
Paper's Title:
Sweeping Surfaces with Darboux Frame in Euclidean 3-space E3
Author(s):
F. Mofarreh, R. Abdel-Baky and N. Alluhaibi
Mathematical Science Department, Faculty
of Science,
Princess Nourah bint Abdulrahman University
Riyadh 11546,
Saudi Arabia.
E-mail: fyalmofarrah@pnu.edu.sa
Department of Mathematics, Faculty of Science,
University of Assiut,
Assiut 71516,
Egypt.
E-mail: rbaky@live.com
Department of Mathematics Science and
Arts, College Rabigh Campus,
King Abdulaziz University
Jeddah,
Saudi Arabia.
E-mail: nallehaibi@kau.edu.sa
Abstract:
The curve on a regular surface has a moving frame and it is called Darboux frame. We introduce sweeping surfaces along the curve relating to the this frame and investigate their geometrical properties. Moreover, we obtain the necessary and sufficient conditions for these surfaces to be developable ruled surfaces. Finally, an example to illustrate the application of the results is introduced.
Paper's Title:
Locally Bicomplex Convex Module and Their Applications
Author(s):
Stanzin Kunga and Aditi Sharma
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: stanzinkunga19@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: aditi.sharmaro@gmail.com
Abstract:
Let X be a locally BC convex module and L(X) be the family of all continuous bicomplex linear operators on X. In this paper, we study some concepts of D-valued seminorms on locally BC convex module. Further, we study the bicomplex version of Co and (Co,1) semigroup. The work of this paper is inspired by the work in [2] and [6].
Paper's Title:
On General Class of Nonlinear Contractive Maps and their Performance Estimates
Author(s):
Olalekan Taofeek Wahab and Salaudeen Alaro Musa
Department of Mathematics and
Statistics
Kwara State University, Malete
P. M. B. 1530 Ilorin,
Nigeria.
E-mail: taofeek.wahab@kwasu.edu.ng
Abstract:
This paper considers two independent general class of nonlinear contractive maps to study the existence properties of nonlinear operators with prior degenerate. The existence properties are proved in the framework of approximate fixed points with the imposition of the general class of contractive conditions in metrical convex spaces without emphasis on completeness or compactness. For computational purposes, the performance estimates and the sensitivity dependence of these conditions are obtained for the Picard operator. Practical examples are also considered to justify the validity of the conditions. The results ensure no term is lost in the operators with prior degenerate and the conditions are strictly larger class when compare with others in the literature.
Paper's Title:
Timelike Surfaces with a Common Line of Curvature in Minkowski 3-Space
Author(s):
M.K. Saad, A.Z. Ansari, M. Akram and F. Alharbi
Department of Mathematics ,
Faculty of Science,
Islamic University of Madinah,
KSA
Abstract:
In this paper, we analyze the problem of constructing a timelike surface family from a given non-null curve line of curvature. Using the Frenet frame of the non-null curve in Minkowski space E13 we express the family of surfaces as a linear combination of the components of this frame, and derive the necessary and sufficient conditions for the coefficients to satisfy both the line of curvature and the isoparametric requirements. In addition, a necessary and sufficient condition for the given non-null curve to satisfy the line of curvature and the geodesic requirements is investigated. The extension to timelike surfaces of revolution is also outlined. Meanwhile, some representative non-null curves are chosen to construct the corresponding timelike surfaces which possessing these curves as lines of curvature. Results presented in this paper have applications in geometric modeling and the manufacturing of products. In addition, some computational examples are given and plotted.
Paper's Title:
Several New Closed-form Evaluations of the Generalized Hypergeometric Function with Argument 1/16
Author(s):
B. R. Srivatsa Kumar, Insuk Kim and Arjun K. Rathie
Department of Mathematics,
Manipal Institute of Technology,
Manipal Academy of Higher Education,
Manipal 576 104,
India.
E-mail: sri_vatsabr@yahoo.com
Department of Mathematics Education,
Wonkwang University,
Iksan, 54538,
Republic of Korea.
E-mail: iki@wku.ac.kr
Department of Mathematics,
Vedant College of Engineering and Technology,
Rajasthan Technical University,
Bundi, 323021, Rajasthan,
India.
E-mail: arjunkumarrathie@gmail.com
Abstract:
The main objective of this paper is to establish as many as thirty new closed-form evaluations of the generalized hypergeometric function q+1Fq(z) for q= 2, 3, 4. This is achieved by means of separating the generalized hypergeometric function q+1Fq(z) for q=1, 2, 3, 4, 5 into even and odd components together with the use of several known infinite series involving central binomial coefficients obtained earlier by Ji and Hei \& Ji and Zhang.
Paper's Title:
A Caratheodory's Approximate Solutions of Stochastic Differential Equations Under the Hölder Condition
Author(s):
Bo-Kyeong Kim and Young-Ho Kim
Department of Mathematics,
Changwon National University,
Changwon, Gyeongsangnam-do 51140,
Korea.
E-mail: claire9576@naver.com
yhkim@changwon.ac.kr
Abstract:
In this paper, based on the theorem of the uniqueness of the solution of the stochastic differential equation, the convergence possibility of the Caratheodory's approximate solution was studied by approximating the unique solution. To obtain this convergence theorem, we used a Hölder condition and a weakened linear growth condition. Furthermore, The auxiliary theorems for the existence and continuity of the Caratheodory's approximate solution were investigated as a prerequisite.
Paper's Title:
New Refinements for Integral and Sum Forms of Generalized Hölder Inequality For N Term
Author(s):
M. Jakfar, Manuharawati, D. Savitri
Mathematics Department,
Universitas Negeri Surabaya
Jalan Ketintang Gedung C8, Surabaya, 60321
Indonesia.
E-mail: muhammadjakfar@unesa.ac.id
manuharawati@unesa.ac.id
diansavitri@unesa.ac.id
Abstract:
We know that in the field of functional analysis, Hölder inequality is very well known, important, and very applicable. So many researchers are interested in discussing these inequalities. Many world mathematicians try to improve these inequalities. In general, the Hölder inequality has two forms, namely the integral form and the sum form. In this paper, we will introduce a new refinement of the generalization of Hölder inequalities in both integral and addition forms. Especially in the sum form, improvements will be introduced that are better than the previous improvements that have been published by Jing-feng Tian, Ming-hu Ha, and Chao Wang.
Paper's Title:
Semigroup of Linear Operator In Bicomplex Scalars
Author(s):
Stanzin Kunga, Amjad Ali and Aditi Sharma
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: stanzinkunga19@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail:
amjadladakhi687@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: aditi.sharmaro@gmail.com
Abstract:
In this paper, we have studied the generators of C0-semigroups of bicomplex linear operators on BC-Banach modules. This work is based on [5].
Paper's Title:
Approximately Dual p-Approximate Schauder Frames
Author(s):
K. Mahesh Krishna and P. Sam Johnson
Stat-Math Unit, Indian Statistical
Institute, Bangalore Centre,
Karnataka 560 059
India.
Department of Mathematical and
Computational Sciences,
National Institute of Technology Karnataka (NITK),
Surathkal, Mangaluru 575 025,
India.
E-mail: kmaheshak@gmail.com
sam@nitk.edu.in
Abstract:
Approximately dual frame in Hilbert spaces was introduced by Christensen and Laugesen to overcome difficulties in constructing dual frames for a given Hilbert space frame. It becomes even more difficult in Banach spaces to construct duals. For this purpose, we introduce approximately dual frames for a class of approximate Schauder frames for Banach spaces and develop basic theory. Approximate dual for this subclass is completely characterized and its perturbation is also studied.
Paper's Title:
Differential Equations for Indicatrices, Spacelike and Timelike Curves
Author(s):
Sameer, Pradeep Kumar Pandey
Department of Mathematics,
Jaypee University of Information Technology,
Solan, Himachal Pradesh,
India.
E-mail: sksameer08@gmail.com,
pandeypkdelhi@gmail.com
Abstract:
Motivated by the recent work of Deshmukh et al. [20], in this paper we show that Tangent, Binormal, and Principal Normal indicatrices do not form non-trivial differential equations. Finally, we obtain the 4th-order differential equations for spacelike and timelike curves.
Paper's Title:
Corrigendum for Differential Equations for Indicatrices, Spacelike and Timelike Curves
Author(s):
Sameer, Pradeep Kumar Pandey
Department of Mathematics,
Jaypee University of Information Technology,
Solan, Himachal Pradesh,
India.
E-mail: sksameer08@gmail.com,
pandeypkdelhi@gmail.com
ABSTRACT NOT FOUND. WEBSITE ERROR
Abstract:
Paper's Title:
A New Look at the Equations of the Calculus of Variations
Author(s):
Olivier de La Grandville
Faculty of Economics, Goethe University
Frankfurt,
Theodore Adorno Platz 4, 60323 Frankfurt,
Germany.
E-mail: odelagrandville@gmail.com
Abstract:
We first offer an entirely new way to derive the celebrated Euler equation of the calculus of variations. The advantage of this approach is two-fold. On the one hand, it entirely eschews the two hurdles encountered by Lagrange, which become challenging in the case of elaborate functionals: getting rid of the arbitrary character of the perturbation given to the optimal function, and demonstrating the fundamental lemma of the calculus of variations. On the other hand, it leads in a direct way to the remarkable discovery made by Robert Dorfman ( 1969) when he introduced a modified Hamiltonian, which we called a Dorfmanian (2018) to honor his memory. In turn, extending the Dorfmanian enables to obtain readily the fundamental equations of the calculus of variations for the optimization of high-order functionals, or multiple integrals.
Search and serve lasted 1 second(s).