|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Existence of Solutions for Third Order Nonlinear Boundary Value Problems
Author(s):
Yue Hu and Zuodong Yang
School of Mathematics and Computer Science, Nanjing Normal University, Jiangsu Nanjing 210097,
China.
huu3y2@163.com
College of Zhongbei, Nanjing Normal University, Jiangsu Nanjing 210046,
China.
zdyang_jin@263.net
yangzuodong@njnu.edu.cn
Abstract:
In this paper, the existence of solution for a class of third order quasilinear ordinary differential equations with nonlinear boundary value problems
(Φp(u"))'=f(t,u,u',u"), u(0)=A, u'(0)=B, R(u'(1),u"(1))=0
is established. The results are obtained by using upper and lower solution methods.
Paper's Title:
On an Extension of Hilbert’s Integral Inequality with Some Parameters
Author(s):
Bicheng Yang
Department of
Mathematics, Guangdong Education College, Guangzhou, Guangdong 510303, People’s
Republic of China.
bcyang@pub.guangzhou.gd.cn
URL:
http://www1.gdei.edu.cn/yangbicheng/index.html
Abstract:
In this paper, by introducing some parameters and estimating the
weight function, we give an extension of Hilbert’s integral inequality with a
best constant factor. As applications, we consider the equivalent form and some
particular results.
Paper's Title:
A Strengthened Hardy-Hilbert's Type Inequality
Author(s):
Weihong Wang and Bicheng Yang
Department of Mathematics, Guangdong Education Institute,
Guangzhou, Guangdong 520303,
People's Republic Of China
wwh@gdei.edu.cn
bcyang@pub.guangzhou.gd.cn
URL: http://www1.gdei.edu.cn/yangbicheng/index.html
Abstract:
By using the improved Euler-Maclaurin's summation formula and
estimating the weight coefficient, we give a new strengthened
version of the more accurate Hardy-Hilbert's type inequality. As
applications, a strengthened version of the equivalent form is
considered.
Paper's Title:
Uniqueness Problems for Difference Polynomials Sharing a Non-Zero Polynomial of Certain Degree With Finite Weight
Author(s):
V. Priyanka, S. Rajeshwari and V. Husna
Department of Mathematics,
School of Engineering,
Presidency University,
Bangalore-560064,
India.
E-mail:
priyapriyankaram1994@gmail.com
rajeshwaripreetham@gmail.com
husnav43@gmail.com
Abstract:
In this paper, we prove a result on the value distribution of difference polynomials sharing higher order derivatives of meromorphic functions which improves some earlier results. At the same time, we also prove possible uniqueness relation of entire functions when the difference polynomial generated by them sharing a non zero polynomial of certain degree. The result obtained in the paper will improve and generalize a number of recent results in a compact and convenient way.
Paper's Title:
On Positive Entire Solutions of Second Order Quasilinear Elliptic Equations
Author(s):
Zuodong Yang and Honghui Yin
Institute of Mathematics, School of Mathematics and Computer Science,
Nanjing Normal University, Jiangsu Nanjing 210097,
China;
zdyang_jin@263.net
Department of Mathematics, Huaiyin Teachers College,
Jiangsu Huaian 223001,
China;
School of Mathematics and Computer Sciences,
Nanjing Normal University, Jiangsu Nanjing 210097,
China.
yin_hh@sina.com
Abstract:
In this paper, our main purpose is to establish the existence
theorem of positive entire solutions of second order quasilinear
elliptic equations under new conditions. The main results of the
present paper are new and extend the previously known results.
Paper's Title:
Multilinear Fractional Integral Operators on Herz Spaces
Author(s):
Yasuo Komori-Furuya
School of High Technology and Human Welfare,
Tokai University,
317 Nishino Numazu Shizuoka, 410-0395
Japan
Abstract:
We prove the boundedness of the multilinear fractional integral operators of Kenig and Stein type on Herz spaces. We also show that our results are optimal.
Paper's Title:
Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
On a Hilbert-type Inequality with the Polygamma Function
Author(s):
Bing He and Bicheng Yang
Department of Mathematics, Guangdong Education College,
Guangzhou, 510303,
China.
Department of Mathematics, Guangdong Education College,
Guangzhou, 510303,
China.
Abstract:
By applying the method of weight function and the technique of real analysis, a Hilbert-type inequality with a best constant factor is established, where the best constant factor is made of the polygamma function. Furthermore, the inverse form is given.
Paper's Title:
Construction of a Frame Multiresolution Analysis on Locally Compact Abelian Groups
Author(s):
R. Kumar and Satyapriya
Department of Mathematics,
Kirori Mal College,
University of Delhi,
Delhi,
India.
E-mail: rajkmc@gmail.com
Department of Mathematics,
University of Delhi,
Delhi,
India.
E-mail: kmc.satyapriya@gmail.com
Abstract:
The frame multiresolution analysis (FMRA) on locally compact Abelian groups has been studied and the results concerning classical MRA have been worked upon to obtain new results. All the necessary conditions, which need to be imposed on the scaling function φ to construct a wavelet frame via FMRA, have been summed up. This process of construction of FMRA has aptly been illustrated by sufficient examples.
Paper's Title:
Trace Inequalities for Operators in Hilbert Spaces: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
School of Engineering
& Science
Victoria University,
PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
In this paper we survey some recent trace inequalities for operators in Hilbert spaces that are connected to Schwarz's, Buzano's and Kato's inequalities and the reverses of Schwarz inequality known in the literature as Cassels' inequality and Shisha-Mond's inequality. Applications for some functionals that are naturally associated to some of these inequalities and for functions of operators defined by power series are given. Further, various trace inequalities for convex functions are presented including refinements of Jensen inequality and several reverses of Jensen's inequality. Hermite-Hadamard type inequalities and the trace version of Slater's inequality are given. Some Lipschitz type inequalities are also surveyed. Examples for fundamental functions such as the power, logarithmic, resolvent and exponential functions are provided as well.
Paper's Title:
General Extension of Hardy-Hilbert's Inequality (I)
Author(s):
W. T. Sulaiman
College of Computer Science and Mathematics, University of Mosul,
Iraq.
waadsulaiman@hotmail.com
Abstract:
A generalization for Hardy-Hilbert's inequality that extends the recent
results of Yang and Debnath
[6], is given.
Paper's Title:
A Self Adaptive Method for Solving Split Bilevel Variational Inequalities Problem in Hilbert Spaces
Author(s):
Francis Akutsah1, Ojen Kumar Narain2, Funmilayo Abibat Kasali3 Olawale Kazeem Oyewole4 and Akindele Adebayo Mebawondu5
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 216040405@stu.ukzn.ac.za,
akutsah@gmail.com
2School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
3Mountain Top University,
Prayer City, Ogun State,
Nigeria.
E-mail: fkasali@mtu.edu.ng
4Technion-Israel
Institute of Technology.
E-mail: 217079141@stu.ukzn.ac.za,
oyewoleolawalekazeem@gmail.co
5School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
DST-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
Mountain Top University,
Prayer City, Ogun State,
Nigeria.
E-mail: dele@aims.ac.za
Abstract:
In this work, we study the split bilevel variational inequality problem in two real Hilbert spaces. We propose a new modified inertial projection and contraction method for solving the aforementioned problem when one of the operators is pseudomonotone and Lipschitz continuous while the other operator is α-strongly monotone. The use of the weakly sequential continuity condition on the Pseudomonotone operator is removed in this work. A Strong convergence theorem of the proposed method is proved under some mild conditions. In addition, some numerical experiments are presented to show the efficiency and implementation of our method in comparison with other methods in the literature in the framework of infinite dimensional Hilbert spaces. The results obtained in this paper extend, generalize and improve several.
Paper's Title:
Compactly Supported Interpolatory Orthogonal Multiwavelet Packets
Author(s):
Yang Shouzhi
Department of Mathematics,
Shantou University,
Shantou, Po Box 515063,
P.R.China.
szyang@stu.edu.cn
Abstract:
Compactly supported interpolatory orthogonal multiwavelet packets
are introduced. Precisely, if both the multiscaling function and
the corresponding multiwavelet have the same interpolatory
property, then the multiwavelet packets are also interpolatory
orthogonal. Thus, the coefficients of decomposition or synthesis
of multiwavelet packets can be realized by sampling instead of inner
products. This multiwavelet packets provide a finer decomposition
of multiwavelet packets space and give a better localization.
Paper's Title:
On Opial's Inequality for Functions of n-Independent Variables
Author(s):
S. A. A. El-Marouf and S. A. AL-Oufi
Department of Mathematics,
Faculty of Science,
Minoufiya University,
Shebin El-Koom,
Egypt
Department of Mathematics,
Faculty of Science, Taibah University,
Madenahmonwarah,
Kingdom of Saudia Arabia
Abstract:
In this paper, we introduce Opial inequalities for functions of n-independent variables. Also, we discuss some different forms of Opial inequality containing functions of n independent variables and their partial derivatives with respect to independent variables.
Paper's Title:
Properties of Certain Multivalent Functions Involving Ruscheweyh Derivatives
Author(s):
N-Eng Xu and Ding-Gong Yang
Department of Mathematics,
Changshu Institute of Technology,
Changshu, Jiangsu 215500,
China
Abstract:
Let Ap(p∈ N) be the class of functions
which are analytic
in the unit disk. By virtue of the Ruscheweyh derivatives we introduce the new
subclasses Cp(n,α,β,λ,μ) of Ap. Subordination relations, inclusion relations,
convolution properties and a sharp coefficient estimate are
obtained. We also give a sufficient condition for a function to be
in Cp(n,α,β,λ,μ)
Paper's Title:
Analysis of a Frictional Contact Problem for Viscoelastic Piezoelectric Materials
Author(s):
Meziane Said Ameur, Tedjani Hadj Ammar and Laid Maiza
Departement of Mathematics,
El Oued University,
P.O. Box 789, 39000 El Oued,
Algeria.
E-mail:
said-ameur-meziane@univ-eloued.dz
Departement of Mathematics,
El Oued University,
P.O. Box 789, 39000 El Oued,
Algeria.
E-mail:
hadjammar-tedjani@univ-eloued.dz
Department of Mathematics,
Kasdi Merbah University,
30000 Ouargla,
Algeria.
E-mail: maiza.laid@univ-ouargla.dz
Abstract:
In this paper, we consider a mathematical model that describes the quasi-static process of contact between two thermo-electro-viscoelastic bodies with damage and adhesion. The damage of the materials caused by elastic deformations. The contact is frictional and modeled with a normal compliance condition involving adhesion effect of contact surfaces. Evolution of the bonding field is described by a first order differential equation. We derive variational formulation for the model and prove an existence and uniqueness result of the weak solution. The proof is based on arguments of evolutionary variational inequalities, parabolic inequalities, differential equations, and fixed point theorem.
Paper's Title:
Growth and Approximation of Entire Solutions of Linear Partial Differential Equation in Terms of Bessel Polynomial Approximation Errors in Lp-norm, 1 ≤ p ≤ ∞
Author(s):
Devendra Kumar
Department of Mathematics, Faculty of
Sciences
Al-Baha University,
P.O.Box-7738 Alaqiq, Al-Baha-65799,
Saudi Arabia.
E-mail:
d_kumar001@rediffmail.com,
dsingh@bu.edu.sa
Abstract:
We deal with entire solutions of some special type linear homogeneous partial differential equations that are represented in convergent series of Bessel polynomials. We determine the growth orders and types of the solutions, in terms of Bessel polynomial approximation errors in both sup norm and Lp-norm, 1 ≤ p ≤ ∞.
Paper's Title:
A New Hardy-Hilbert's Type Inequality for Double Series and its Applications
Author(s):
Mingzhe Gao
Department of Mathematics and Computer Science, Normal College Jishou University,
Jishou Hunan, 416000,
People's Republic of China
mingzhegao1940@yahoo.com.cn
Abstract:
In this paper, it is shown that a new Hardy-Hilbert’s type
inequality for double series can be established by introducing a parameter 
and the weight function of the form 
where c is Euler
constant and 
And
the coefficient 
and 
appear simultaneously in the coefficient and the weight
function when 
In particular, for
case 
some new Hilbert’s
type inequalities are obtained. As applications, some extensions of Hardy-Littlewood’s inequality are given.
Paper's Title:
Analysis of the Flow Field in Stenosed Bifurcated Arteries Through a Mathematical Model
Author(s):
S. Chakravarty and S. Sen
Department of Mathematics, Visva-Bharati University,
Santiniketan 731235,
India
santabrata2004@yahoo.co.in
Abstract:
The present study is dealt with an appropriate mathematical model
of the arotic bifurcation in the presence of constrictions using which
the physiological flow field is analized. The geometry of the bifurcated
arterial segment having constrictions in both the parent and its daughter
arterial lumen frequently occurring in the diseased arteries causing
malfunction of the cardiovascular system , is formed mathematically
with the introduction of appropriate curvatures at the lateral junctions
and the flow divider. The flowing blood contained in the stenosed
bifurcated artery is treated to be Newtonian and the flow is considered
to be two dimensional. The motion of the arterial wall and its effect
on local fluid mechanics is not ruled out from the present pursuit.
The flow analysis applies the time-dependent, two-dimensional incompressible
nonlinear Navier-Stokes equations for Newtonian fluid. The flow field
can be obtained primarily following the radial coordinate transformation
and using the appropriate boundary conditions and finally adopting
a suitable finite difference scheme numerically. The influences of
the arterial wall distensibility and the presence of stenosis on the
flow field, the flow rate and the wall shear stresses are quantified
in order to indicate the susceptibility to atherosclerotic lesions
and thereby to validate the applicability of the present theoretical
model.
Paper's Title:
On Vector Variational Inequality Problem in Terms of Bifunctions
Author(s):
C. S. Lalitha and Monika Mehta
Department of Mathematics, Rajdhani College,
Department of Mathematics, Satyawati College,
University of Delhi, Raja Garden,
Delhi 110015, India
cslalitha@rediffmail.com
University Of Delhi, Ashok Vihar,
Phase-III, Delhi 110052, India
mridul_in@yahoo.com
Abstract:
In this paper, we consider a generalized vector variational
inequality problem expressed in terms of a bifunction and establish
existence theorems for this problem by using the concepts of cone
convexity and cone strong quasiconvexity and employing the
celebrated Fan's Lemma. We also give two types of gap functions for this problem.
Paper's Title:
A Subclass of Meromorphically Multivalent Functions with Applications to Generalized Hypergeometric Functions
Author(s):
M. K. Aouf
Mathematics Department,
Faculty of Science,
Mansoura University 35516,
Egypt
mkaouf127@yahoo.com
Abstract:
In this paper a new subclass of meromorphically multivalent functions, which
is defined by means of a Hadamard product (or convolution) involving some
suitably normalized meromorphically p-valent functions. The main object of
the present paper is to investigate the various important properties and
characteristics of this subclass of meromorphically multivalent functions.
We also derive many interesting results for the Hadamard products of
functions belonging to this subclass. Also we consider several applications
of our main results to generalized hypergeomtric functions.
Paper's Title:
A kind of Function Series and Its Applications
Author(s):
Yang Tianze
Mechanical Engineering,
Shandong University, Xinglongshan Campus,
Jinan, Shandong,
China.
E-mail: qdyangtianze@163.com
Abstract:
A kind of new function series is obtained in this paper. Their theorems and proofs are shown, and some applications are given. We give the expansion form of general integral and the series expansion form of function and the general expansion form of derivative. Using them in the mathematics,we get some unexpected result.
Paper's Title:
Several Applications of a Local Non-convex Young-type Inequality
Author(s):
Loredana Ciurdariu, Sorin Lugojan
Department of Mathematics,
"Politehnica" University of Timisoara,
P-ta. Victoriei, No.2, 300006-Timisoara,
Romania.
E-mail: ltirtirau87@yahoo.com
Abstract:
A local version of the Young inequality for positive numbers is used in order to deduce some inequalities about determinants and norms for real quadratic matrices and norms of positive operators on complex Hilbert spaces.
Paper's Title:
Generalized Von Neumann-Jordan Constant for Morrey Spaces and Small Morrey Spaces
Author(s):
H. Rahman and H. Gunawan
Department of Mathematics,
Islamic State University Maulana Malik Ibrahim Malang,
Jalan Gajayana No.50,
Indonesia.
E-mail: hairur@mat.uin-malang.ac.id
Analysis and Geometry Group,
Faculty of Mathematics and Natural Sciences,
Bandung Institute of Technology, Bandung 40132,
Indonesia.
E-mail: hgunawan@math.itb.ac.id
URL:
http://personal.fmipa.itb.ac.id/hgunawan/
Abstract:
In this paper we calculate some geometric constants for Morrey spaces and small Morrey spaces, namely generalized Von Neumann-Jordan constant, modified Von Neumann-Jordan constants, and Zbaganu constant. All these constants measure the uniformly nonsquareness of the spaces. We obtain that their values are the same as the value of Von Neumann-Jordan constant for Morrey spaces and small Morrey spaces.
Paper's Title:
SQIRV Model for Omicron Variant with Time Delay
Author(s):
S. Dickson, S. Padmasekaran, G. E. Chatzarakis and S. L. Panetsos
Mathematics, Periyar University, Periyar
Palkalai Nagar, Salem,
636011, Tamilnadu,
India.
E-mail:
dickson@periyaruniversity.ac.in,
padmasekarans@periyaruniversity.ac.in
Electrical and Electronic Engineering
Educators, School of
Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
spanetsos@aspete.gr
Abstract:
In order to examine the dynamics of the Omicron variant, this paper uses mathematical modelling and analysis of a SQIRV model, taking into account the delay in the conversion of susceptible individuals into infected individuals and infected individuals into recovered individuals. The pandemic was eventually controlled as a result of the massive delays. To assure the safety of the host population, this concept incorporates quarantine and the COVID-19 vaccine. Both local and global stability of the model are examined. It is found that the fundamental reproduction number affects both local and global stability conditions. Our findings show that asymptomatic cases caused by an affected population play an important role in increasing Omicron infection in the general population. The most recent data on the pandemic Omicron variant from Tamil Nadu, India, is verified.
Paper's Title:
New Fast Extragradient-like Methods for Non-Lipschitzian Pseudo-monotone Variational Inequalities
Author(s):
Morad Ali Peyvand
Department of Mathematics
Yasouj University
Yasouj,
Iran.
E-mail: peyvand@yu.ac.ir
Abstract:
An efficient double-projection method, with a new search strategy, is designed for solving variational inequalities in real Hilbert spaces with pseudo-monotone cost operator. Our proposed method uses a computationally inexpensive simple line search procedure based on local information of the operator and very weak conditions of parameters to obtain larger step sizes. A description of the algorithm along with its weak convergence is provided without assuming Lipschitz continuity. Also, a modification to the proposed method is presented, wherein the second projection onto the closed and convex subset is replaced with the one onto a subgradient half space. Numerical experiments and comparisons with related methods demonstrate the reliability and benefits of the proposed schemes.
Paper's Title:
Monotonicity Properties for Generalized Logarithmic Means
Author(s):
Chao-Ping Chen and Feng Qi
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
chenchaoping@hpu.edu.cn
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
qifeng@hpu.edu.cn,
fengqi618@member.ams.org
Url:
http://rgmia.vu.edu.au/qi.html,
http://dami.hpu.edu.cn/qifeng.html
Abstract:
In this paper, we consider the monotonicity properties for ratio of two generalized logarithmic means, and then use it to extend and complement a recently published result of F. Qi and B.-N. Guo.
Paper's Title:
Iterated Order of Fast Growth Solutions of Linear Differential Equations
Author(s):
Benharrat Belaďdi
Department of Mathematics
Laboratory of Pure and Applied Mathematics
University of Mostaganem
B. P. 227 Mostaganem,
ALGERIA.
belaidi@univ-mosta.dz
Abstract:
In this paper, we investigate the growth of solutions of the differential
equation
f(k) + Ak-1 (z) f(k-1) +...+ A1 (z) f' + A0 (z) f= F (z),
where
Ao (z), ..., Ak-1 (z)
and
F (z) 
0
are entire functions. Some estimates are given for the iterated order of solutions of the above quation when one of the coefficients As is being dominant in the sense that it has larger growth than Aj (j≠s) and F.
Paper's Title:
Positive Solutions for Systems of Three-point Nonlinear Boundary Value Problems
Author(s):
J. Henderson and S. K. Ntouyas
Department of Mathematics, Baylor University
Waco, Texas
76798-7328 USA.
Johnny_Henderson@baylor.edu
URL: http://www3.baylor.edu/~Johnny_Henderson
Department of Mathematics, University of Ioannina
451 10 Ioannina,
Greece.
sntouyas@cc.uoi.gr
URL: http://www.math.uoi.gr/~sntouyas
Abstract:
Values of λ are determined for which there exist
positive solutions of the system of three-point boundary value problems,
u''(t)+ λa(t)f(v(t))=0, v''(t)+λb(t)g(u(t))=0,
for 0 < t <1, and
satisfying, u(0) = 0, u(1)=α u(η),
v(0) = 0, v(1)=α v(η). A Guo-Krasnosel'skii fixed
point theorem is applied. Paper's Title:
Fixed Points and Stability
of the Cauchy Functional Equation Author(s):
Choonkil Park and Themistocles M. Rassias
2: Paper Source
PDF document
Department of Mathematics, Hanyang University,
Seoul 133-791,
Republic of Korea
Department of Mathematics,
National Technical University of Athens,
Zografou Campus, 15780 Athens,
Greece
baak@hanyang.ac.kr
trassias@math.ntua.gr
Abstract:
Using fixed point methods, we prove the generalized Hyers-Ulam stability of homomorphisms in Banach algebras and of derivations on Banach algebras for the Cauchy functional equation.
Paper's Title:
Generalized Efficient Solutions to One Class of Vector Optimization Problems in Banach Space
Author(s):
Peter I. Kogut, Rosanna Manzo, and Igor V. Nechay
Department of Differential Equations,
Dnipropetrovsk National University,
Naukova str., 13,
49050 Dnipropetrovsk,
Ukraine
p.kogut@i.ua
Dipartimento di Ingegneria
Dell’informazione e Matematica Applicata,
Universitŕ di Salerno,
Via
Ponte
Don Melillo,
84084 Fisciano
(Sa),
Italy
manzo@diima.unisa.it
Department of Technical Cybernetics,
Dnipropetrovsk Technical University,
Acad. Lazarjan str., 2,
49010
Dnipropetrovsk,
Ukraine
i.nechay@i.ua
Abstract:
In this paper, we study vector optimization problems in Banach spaces for essentially nonlinear operator equations with additional control and state constraints. We assume that an objective mapping possesses a weakened property of lower semicontinuity and make no assumptions on the interior of the ordering cone. Using the penalization approach we derive both sufficient and necessary conditions for the existence of efficient solutions of the above problems. We also prove the existence of the so-called generalized efficient solutions via the scalarization of some penalized vector optimization problem.
Paper's Title:
Bounds for Two Mappings Associated to
the Hermite-Hadamard Inequality
Author(s):
S. S. Dragomir1,2 and I. Gomm1
1Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428,
Melbourne City, MC 8001,
Australia.
2School of Computational & Applied Mathematics,
University of
the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
sever.dragomir@vu.edu.au
ian.gomm@vu.edu.au
URL: http://rgmia.org/dragomir
Abstract:
Some inequalities concerning two mappings associated to the celebrated Hermite-Hadamard integral inequality for convex function with applications for special means are given.
Paper's Title:
Approximation of an AQCQ-Functional Equation and its Applications
Author(s):
Choonkil Park and Jung Rye Lee
Department of Mathematics,
Research Institute for Natural Sciences,
Hanyang University, Seoul 133-791,
Korea;
Department of Mathematics,
Daejin University,
Kyeonggi 487-711,
Korea
baak@hanyang.ac.kr
jrlee@daejin.ac.kr
Abstract:
This paper is a survey on the generalized Hyers-Ulam stability of an AQCQ-functional equation in several spaces. Its content is divided into the following sections:
1. Introduction and preliminaries.
2. Generalized Hyers-Ulam stability of an AQCQ-functional equation in Banach spaces: direct method.
3. Generalized Hyers-Ulam stability of an AQCQ-functional equation in Banach spaces: fixed point method.
4. Generalized Hyers-Ulam stability of an AQCQ-functional equation in random Banach spaces: direct method.
5. Generalized Hyers-Ulam stability of an AQCQ-functional equation in random Banach spaces: fixed point method.
6. Generalized Hyers-Ulam stability of an AQCQ-functional equation in non-Archi-medean Banach spaces: direct method.
7. Generalized Hyers-Ulam stability of an AQCQ-functional equation in non-Archi-medean Banach spaces: fixed point method.
Paper's Title:
Finite and Infinite Order
Solutions of a Class of Higher Order Linear Differential Equations
Author(s):
Saada Hamouda
Department of Mathematics,
Laboratory of Pure and Applied Mathematics,
University of Mostaganem, B. P 227 Mostaganem,
ALGERIA
hamouda_saada@yahoo.fr
Abstract:
In this paper, we investigate the growth of solutions of higher order linear differential equations where most of the coefficients have the same order and type with each other.
Paper's Title:
Further Bounds for Two Mappings Related
to the Hermite-Hadamard Inequality
Author(s):
S. S. Dragomir1,2 and I. Gomm1
1Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428,
Melbourne City, MC 8001,
Australia.
2School of Computational & Applied Mathematics,
University of
the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
sever.dragomir@vu.edu.au
ian.gomm@vu.edu.au
URL: http://rgmia.org/dragomir
Abstract:
Some new results concerning two mappings associated to the celebrated Hermite-Hadamard integral inequality for twice differentiable functions with applications for special means are given.
Paper's Title:
Positive Solutions to a System of Boundary Value Problems for Higher-Dimensional Dynamic Equations on Time Scales
Author(s):
I. Y. Karaca
Department of Mathematics,
Ege University,
35100 Bornova, Izmir,
Turkey
URL:
http://ege.edu.tr
Abstract:
In this paper, we consider the system of boundary value problems for higher-dimensional dynamic equations on time scales. We establish criteria for the existence of at least one or two positive solutions. We shall also obtain criteria which lead to nonexistence of positive solutions. Examples applying our results are also given.
Paper's Title:
Some Applications of Fejér's Inequality for Convex Functions (I)
Author(s):
S.S. Dragomir1,2 and I. Gomm1
1Mathematics, School of
Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia.
URL: http://rgmia.org/dragomir
2School of Computational &
Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
Abstract:
Some applications of Fejér's inequality for convex functions are explored. Upper and lower bounds for the weighted integral
under various assumptions for f with applications to the trapezoidal quadrature rule are given. Some inequalities for special means are also provided
Paper's Title:
Inequalities for the Area Balance of Functions of Bounded Variation
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
We introduce the area balance function associated to a Lebesgue
integrable function f:[a,b] →C by
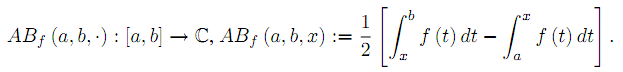
Several sharp bounds for functions of bounded variation are provided. Applications for Lipschitzian and convex functions are also given.
Paper's Title:
MSplit Equality for Monotone Inclusion Problem and Fixed Point Problem in
Real Banach Spaces
Author(s):
1,2Christian Chibueze Okeke, 3Abdumalik Usman Bello, 1Chinedu Izuchukwu, and 1Oluwatosin Temitope Mewomo
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: okekec@ukzn.ac.za
E-mail: izuchukwuc@ukzn.ac.za
E-mail: mewomoo@ukzn.ac.za
2DST-NRF
Center of Excellence in Mathematical and Statistical Sciences (CoE-Mass)
Johannesburg,
South Africa.
3Federal
University,
Dutsin-Ma, Katsina State,
Nigeria.
E-mail:
uabdulmalik@fudutsinma.edu.ng
Abstract:
In this paper a new iterative algorithm for approximating a common solution of split equality monotone inclusion problem and split equality fixed point problem is introduced. Using our algorithm, we state and prove a strong convergence theorem for approximating an element in the intersection of the set of solutions of a split equality monotone inclusion problem and the set of solutions of a split equality fixed point problem for right Bregman strongly nonexpansive mappings in the setting of p-uniformly convex Banach spaces which are also uniformly smooth. We also give some applications.
Paper's Title:
A Low Order Least-Squares Nonconforming Finite Element Method for Steady Magnetohydrodynamic Equations
Author(s):
Z. Yu, D. Shi and H. Zhu
College of Science,
Zhongyuan
University of Technology,
Zhengzhou 450007,
China.
E-mail:
5772@zut.edu.cn
School of Mathematics and Statistics,
Zhengzhou University,
Zhengzhou 450001,
China.
E-mail:
shi_dy@126.com
Mathematics Department,
University of Southern Mississippi,
Hattiesburg MS, 39406,
U.S.A
E-mail:
huiqing.zhu@usm.edu
Abstract:
A low order least-squares nonconforming finite element (NFE) method is proposed for magnetohydrodynamic equations with EQ1rot element and zero-order Raviart-Thomas element. Based on the above element's typical interpolations properties, the existence and uniqueness of the approximate solutions are proved and the optimal order error estimates for the corresponding variables are derived.
Paper's Title:
Constraint Qualifications for Multiobjective Programming Problems on Hadamard Manifolds
Author(s):
Arnav Ghosh, Balendu Bhooshan Upadhyay and I.M. Stancu-Minasian
Department of Mathematics,
Indian Institute of Technology Patna,
Patna,
India.
E-mail: arnav_2021ma09@iitp.ac.in
Department of Mathematics,
Indian Institute of Technology Patna,
Patna,
India.
E-mail: bhooshan@iitp.ac.in
"Gheorghe Mihoc-Caius Iacob" Institute of
Mathematical Statistics and Applied Mathematics of the Romanian Academy,
Bucharest,
Romania.
E-mail: stancu_minasian@yahoo.com
Abstract:
The study of optimization methods on manifolds has emerged as an immensely significant topic in mathematics due its ubiquitous applicability as well as various computational advantages associated with it. Motivated by this fact, the present article is devoted to the study of a class of constrained multiobjective programming problems (MOPP) in the framework of Hadamard manifolds. We present the generalized Guignard constraint qualification (GGCQ) in the framework of Hadamard manifolds for (MOPP). Employing (GGCQ), we derive Karush-Kuhn-Tucker type necessary optimality criteria for (MOPP). Moreover, we present several other constraint qualifications (CQs) on Hadamard manifolds, namely, Abadie's CQ, generalized Abadie's CQ, Cottle-type CQ, Slater-type CQ, linear CQ, linear objective CQ and Mangasarian-Fromovitz CQ. Further, we establish various relations between these constraint qualifications. In particular, we show that these constraint qualifications, in turn, become sufficient conditions ensuring that (GGCQ) is satisfied.
Paper's Title:
Fekete-Szegö Inequality for Certain Class of Analytic Functions
Author(s):
V. Ravichandran, Maslina Darus, M. Hussain Khan, and K. G. Subramanian
School of
Mathematical Sciences, Universiti Sains Malaysia,
11800 Usm, Penang, Malaysia
vravi@cs.usm.my
School of
Mathematical Sciences, Faculty of Sciences and Technology,
Ukm, Banki 43600, Malaysia
maslina@pkrisc.cc.ukm.my
Department of
Mathematics, Islamiah College,
Vaniambadi 635 751, India
Department of
Mathematics, Madras Christian College, Tambaram,
Chennai- 600 059, India
kgsmani@vsnl.net
Abstract:
In this present investigation, the authors obtain Fekete-Szegö inequality for a certain
class of analytic functions f(z) for which
lies in a
region starlike with respect to 1 and symmetric with respect to the real axis. Also certain application
of our main result for a class of functions defined by Hadamard product (convolution) is
given. As a special case of our result we obtain Fekete-Szegö inequality for a class of functions
defined through fractional derivatives. Also we obtain Fekete-Szegö inequality for the inverse
functions.
Paper's Title:
A Simple New Proof of Fan-Taussky-Todd Inequalities
Author(s):
Zhi-Hua Zhang and Zhen-Gang Xiao
Zixing Educational Research Section,
Chenzhou City, Hunan 423400, P. R. China.
Zhi-hua Zhang
Url: http://www.hnzxslzx.com/zzhweb/
Department Of Mathematics, Hunan Institute Of Science And Technology,
Yueyang City, Hunan 423400, P. R. China.
Zhen-gang Xiao
Abstract:
In this paper we present simple new proofs of the inequalities:
which holds for all real numbers a0 = 0, a1, · · · , an, an+1 = 0 and the coefficients
2(1 - cos(π/(n + 1))) and 2(1 + cos(π/(n + 1))) are the best possible; and
which holds for all real numbers a0 = 0, a1, · · · , an and the coefficients
2(1-cos(π/(2n + 1))) and 2(1 + cos(π/(2n + 1))) are the best possible.
Paper's Title:
Two Mappings Related to Steffensen's Inequalities
Author(s):
Liang-Cheng Wang
School of Mathematical Science,
Chongqing Institute of Technology,
Xingsheng Lu 4,
Yangjiaping 400050, Chongqing City,
China.
wangliangcheng@163.com
Abstract:
In this paper, we define two mappings closely connected with
Steffensen's inequalities, investigate their main properties,
give some refinements for Steffensen's inequalities and obtain new
inequalities.
Paper's Title:
On the Fekete-Szeg
Author(s):
T.N. Shanmugam and A. Singaravelu
Department of Mathematics,
Department of Mathematics,
College of Engineering,
Anna University, Chennai-600 025,
Tamilnadu, India
shan@annauniv.edu
Valliammai Engineering College,
Chennai-603 203,
Tamilnadu, India
sivasaisastha@rediffmail.com
Abstract:
In this present investigation, the authors obtainFekete-Szegő's inequality for certain normalized analytic functions 
defined on the open
unit disk for which 
lie in a region starlike with
respect to 1 and symmetric with respect
to the real axis. Also certain applications of the main result for a class of functions
defined by convolution are given. As a special case of this result, Fekete-Szegő's inequality for a class of functions
defined through fractional derivatives is also obtained.
Paper's Title:
A Nonlinear Proximal Alternating Directions Method for Structured Variational Inequalities
Author(s):
M. Li
Department of Management Science and Engineering, School of Economics and Management
Southeast University, Nanjing, 210096,
China.
liminnju@yahoo.com
Abstract:
In this paper, we present a nonlinear proximal alternating directions method (NPADM) for solving a class of structured variational inequalities (SVI). By choosing suitable Bregman functions, we generalize the proximal alternating directions method proposed by He, et al.. The convergence of the method is proved under quite mild assumptions and flexible parameter conditions.
Paper's Title:
Fekete-Szegö Problem for Univalent Functions with Respect to k-Symmetric
Points
Author(s):
K. Al-Shaqsi and M. Darus
School of Mathematical Sciences, Faculty of Science and Technology,
University Kebangsaan Malaysia,
Bangi 43600 Selangor D. Ehsan,
Malaysia
ommath@hotmail.com
maslina@ukm.my
Abstract:
In the present investigation, sharp upper bounds of |a3- μa22|
for functions f(z) = z + a2z2 + a2z3 + ... belonging to certain subclasses
of starlike and convex functions with respect to k-symmetric points are
obtained. Also certain applications of the main results for subclasses of
functions defined by convolution with a normalized analytic function are
given. In particular, Fekete- Szeg
Paper's Title:
Uniqueness of Meromorphic Functions and
Weighted Sharing
Author(s):
Indrajit Lahiri and Rupa Pal
Department of Mathematics, University of
Kalyani, West Bengal 741235, India
indr9431@dataone.in
Jhargram Raj College,
Jhargram, Midnapur(W),
West Bengal 721507,
India
rupa.a.pal@gmail.com
Abstract:
With the help of the notion of weighted sharing of values, we prove a result on uniqueness of meromorphic functions and as a consequence we improve a result of P. Li
Paper's Title:
Topological Aspects of Scalarization in Vector Optimization Problems.
Author(s):
Peter I. Kogut, Rosanna Manzo and Igor V. Nechay
Department of Differential Equations,
Dnipropetrovsk National University, Naukova
STR.,
13,
49010 Dnipropetrovsk,
Ukraine
p.kogut@i.ua
Universitŕ di Salerno,
Department of Technical Cybernetics,
Dipartimento di Ingegneria dell'Informazione e Matematica Applicata,
Via Ponte don Melillo, 84084 Fisciano (SA),
Italy
manzo@diima.unisa.it
Dnipropetrovsk Technical University,
Acad. Lazarjan
STR., 2,
49010 Dnipropetrovsk,
Ukraine
i.nechay@i.ua
Abstract:
In this paper, we study vector optimization problems in partially ordered Banach spaces. We suppose that the objective mapping possesses a weakened property of lower semicontinuity and make no assumptions on the interior of the ordering cone. We derive sufficient conditions for existence of efficient solutions of the above problems and discuss the role of topological properties of the objective space. We discuss the scalarization of vector optimization problems when the objective functions are vector-valued mappings with a weakened property of lower semicontinuity. We also prove the existence of the so-called generalized efficient solutions via the scalarization process. All principal notions and assertions are illustrated by numerous examples.
Paper's Title:
The Superstability of the Pexider Type Trigonometric Functional Equation
Author(s):
Gwang Hui Kim and Young Whan Lee
Department of Mathematics, Kangnam
University Yongin, Gyeonggi, 446-702, Korea.
ghkim@kangnam.ac.kr
Department of Computer and Information Security
Daejeon University, Daejeon 300-716, Korea.
ywlee@dju.ac.kr
Abstract:
The aim of this paper is to investigate the stability
problem for
the Pexider type (hyperbolic) trigonometric functional equation
f(x+y)+f(x+σy)=λg(x)h(y) under the conditions :
|f(x+y)+f(x+σy)- λg(x)h(y)|≤φ(x),
φ(y), and min {φ(x), φ (y)}.
As a consequence, we have generalized the results of stability for
the cosine(d'Alembert), sine, and the Wilson functional equations by J.
Baker, P. Găvruta, R. Badora and R. Ger, Pl.~Kannappan, and G.
H. Kim
Paper's Title:
Inclusion Properties of a Certain Subclass of Strongly Close-To-Convex Functions
Author(s):
S. M. Khairnar and M. More
Department of Mathematics,
Maharashtra Academy of Engineerring,
Alandi -412 105, Pune, Maharashtra,
INDIA.
smkhairnar2007@gmail.com,
meenamores@gmail.com.
Abstract:
The purpose of this paper is to derive some inclusion and argument properties of a new subclass of strongly close-to-convex functions in the open unit disc. We have considered an integral operator defined by convolution involving hypergeometric function in the subclass definition. The subclass also extends to the class of α-spirallike functions of complex order.
Paper's Title:
Some Distortion and Other Properties Associated with a Family of the n-Fold Symmetric Koebe Type Functions
Author(s):
H. M. Srivastava, N. Tuneski and E. Georgieva-Celakoska
Department of Mathematics and Statistics,
University of Victoria,
Victoria, British Columbia V8W 3R4,
Canada
Faculty of Mechanical Engineering, St.
Cyril and Methodius University,
Karpo'v s II b.b., MK-1000 Skopje,
Republic of Macedonia
Abstract:
In a recent work by Kamali and Srivastava [5], a certain family of the n-fold symmetric Koebe type functions was introduced and studied systematically. In an earlier investigation, Eguchi and Owa [4] had considered its special case when n=1 (see also [10]). Here, in our present sequel to these earlier works, this general family of the n-fold symmetric Koebe type functions is studied further and several distortion theorems and such other properties as the radii of spirallikeness, the radii of starlikeness and the radii of convexity, which are associated with this family of the n-fold symmetric Koebe type functions, are obtained. We also provide certain criteria that embed this family of the n-fold symmetric Koebe type functions in a function class Gλ which was introduced and studied earlier by Silverman [7].
Paper's Title:
On Some Estimates for the Logarithmic Mean
Author(s):
Shuhei Wada
Department of Information and Computer
Engineering,
Kisarazu National College of Technology,
Kisarazu, Chiba 292-0041,
Japan.
E-mail: wada@j.kisarazu.ac.jp
Abstract:
We show some estimates for the logarithmic mean that are obtained from operator inequalities between the Barbour path and the Heinz means.
Paper's Title:
Hermite-Hadamard-Fejer Type Inequalities for Harmonically s-convex Functions via Fractional Integrals
Author(s):
İmdat İşcan, Mehmet Kunt
Department of Mathematics,
Faculty of Sciences and Arts,
Giresun University, Giresun,
Turkey.
E-mail: imdat.iscan@giresun.edu.tr
Department of Mathematics,
Faculty of Sciences,
Karadeniz Technical University,
61080, Trabzon,
Turkey.
E-mail:
mkunt@ktu.edu.tr
Abstract:
In this paper, some Hermite-Hadamard-Fejer type integral inequalities for harmonically s-convex functions in fractional integral forms have been obtained.
Paper's Title:
Some New Generalizations of Jensen's Inequality with Related Results and Applications
Author(s):
Steven G. From
Department of Mathematics
University of Nebraska at Omaha
Omaha, Nebraska 68182-0243.
E-mail: sfrom@unomaha.edu
Abstract:
In this paper, some new generalizations of Jensen's inequality are presented. In particular, upper and lower bounds for the Jensen gap are given and compared analytically and numerically to previously published bounds for both the discrete and continuous Jensen's inequality cases. The new bounds compare favorably to previously proposed bounds. A new method based on a series of locally linear interpolations is given and is the basis for most of the bounds given in this paper. The wide applicability of this method will be demonstrated. As by-products of this method, we shall obtain some new Hermite-Hadamard inequalities for functions which are 3-convex or 3-concave. The new method works to obtain bounds for the Jensen gap for non-convex functions as well, provided one or two derivatives of the nonlinear function are continuous. The mean residual life function of applied probability and reliability theory plays a prominent role in construction of bounds for the Jensen gap. We also present an exact integral representation for the Jensen gap in the continuous case. We briefly discuss some inequalities for other types of convexity, such as convexity in the geometric mean, and briefly discuss applications to reliability theory.
Paper's Title:
Ostrowski Type Fractional Integral Inequalities for Generalized (s,m,
Author(s):
Artion Kashuri and Rozana Liko
University of Vlora "Ismail Qemali",
Faculty of Technical Science,
Department of Mathematics, 9400,
Albania.
E-mail:
artionkashuri@gmail.com
E-mail: rozanaliko86@gmail.com
Abstract:
In the present paper, the notion of generalized (s,m,φ)-preinvex function is introduced and some new integral inequalities for the left hand side of Gauss-Jacobi type quadrature formula involving generalized (s,m,φ)-preinvex functions along with beta function are given. Moreover, some generalizations of Ostrowski type inequalities for generalized (s,m,φ)-preinvex functions via Riemann-Liouville fractional integrals are established.
Paper's Title:
Dynamical Analysis of HIV/AIDS Epidemic Model with Two Latent Stages, Vertical Transmission and Treatment
Author(s):
Nur Shofianah, Isnani Darti, Syaiful Anam
Mathematics Department,Faculty of
Mathematics and Natural Sciences.
University of Brawijaya,
Jl. Veteran, Malang 65145,
Indonesia.
E-mail:
nur_shofianah@ub.ac.id,
isnanidarti@ub.ac.id,
syaiful@ub.ac.id
Abstract:
We discuss about dynamical analysis of HIV/AIDS epidemic model with two latent stages, vertical transmission and treatment. In this model, the spreading of HIV occurs through both horizontal and vertical transmission. There is also treatment for individual who has been HIV infected. The latent stage is divided into slow and fast latent stage based on the immune condition which varies for each individual. Dynamical analysis result shows that the model has two equilibrium points: the disease-free equilibrium point and the endemic equilibrium point. The existence and global stability of equilibrium points depend on the basic reproduction number R0. When R0 <1, only the disease-free equilibrium point exists. If R0 >1, there are two equilibrium points, which are the disease-free equilibrium point and the endemic equilibrium point. Based on the result of stability analysis, the disease-free equilibrium point is globally asymptotically stable if R0 <1, while if R0 > 1 and p=q, the endemic equilibrium point will be globally asymptotically stable. In the end, we show some numerical simulations to support the analytical result.
Paper's Title:
Composite Variational-Like Inequalities Given By Weakly Relaxed
Author(s):
Syed Shakaib Irfan, Iqbal Ahmad, Zubair Khan and Preeti Shukla
College of Engineering, Qassim University
Buraidah, Al-Qassim,
Saudi Arabia.
E-mail: shakaib@qec.edu.sa
College of Engineering, Qassim University
Buraidah, Al-Qassim,
Saudi Arabia.
E-mail: iqbal@qec.edu.sa
Department of Mathematics,
Integral University Lucknow,
India.
E-mail: zkhan@iul.ac.in
Department of Mathematics,
Integral University Lucknow,
India.
E-mail: shuklapreeti1991@gmail.com
Abstract:
In this article, we introduce a composite variational-like inequalities with weakly relaxed ζ-pseudomonotone multi-valued maping in reflexive Banach spaces. We obtain existence of solutions to the composite variational-like inequalities with weakly relaxed ζ-pseudomon -otone multi-valued maps in reflexive Banach spaces by using KKM theorem. We have also checked the solvability of the composite variational-like inequalities with weakly relaxed ζ-semi-pseudomonotone multi-valued maps in arbitrary Banach spaces using Kakutani-Fan-Glicksberg fixed point theorem.
Paper's Title:
Double Difference of Composition Operator on Bloch Spaces
Author(s):
Rinchen Tundup
Department of Mathematics
University of Jammu
Jammu and Kashmir
India.
E-mail: joneytun123@gmail.com
Abstract:
In this paper we characterize the compactness of double difference of three non-compact composition operators on Bloch space induced by three holomorphic self maps on the unit disc.
Paper's Title:
A Self-adaptive Subgradient Extragradient Algorithm for Variational Inequality Problems and Fixed Point Problems in Banach Spaces
Author(s):
F. U. Ogbuisi
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
Department of Mathematics,
University of Nigeria, Nsukka,
Nigeria.
E-mail: ferdinard.ogbuisi@unn.edu.ng
fudochukwu@yahoo.com
Abstract:
In this paper, we propose and analyze a type of subgradient extragradient algorithm for the approximation of a solution of variational inequality problem which is also a common fixed point of an infinite family of relatively nonexpansive mappings in 2-uniformly convex Banach spaces which are uniformly smooth. By using the generalized projection operator, we prove a strong convergence theorem which does not require the prior knowledge of the Lipschitz constant of cost operator. We further applied our result to constrained convex minimization problem, convex feasibility problem and infinite family of equilibrium problems. Our results improve and complement related results in 2-uniformly convex and uniformly smooth Banach spaces and Hilbert spaces.
Paper's Title:
Reduced Generalized Combination Synchronization Between Two n-Dimensional Integer-Order Hyperchaotic Systems and One m-Dimensional Fractional-Order Chaotic System
Author(s):
Smail Kaouache, Mohammed Salah Abdelouahab and Rabah Bououden
Laboratory of Mathematics and their
interactions,
Abdelhafid Boussouf University Center, Mila.
Algeria
E-mail: smailkaouache@gmail.com,
medsalah3@yahoo.fr,
rabouden@yahoo.fr
Abstract:
This paper is devoted to investigate the problem of reduced generalized combination synchronization (RGCS) between two n-dimensional integer-order hyperchaotic drive systems and one m-dimensional fractional-order chaotic response system. According to the stability theorem of fractional-order linear system, an active mode controller is proposed to accomplish this end. Moreover, the proposed synchronization scheme is applied to synchronize three different chaotic systems, which are the Danca hyperchaotic system, the modified hyperchaotic Rossler system, and the fractional-order Rabinovich-Fabrikant chaotic system. Finally, numerical results are presented to fit our theoretical analysis.
Paper's Title:
Analysis of the Dynamic Response of the Soil-pile Behavioral Model Under Lateral Load
Author(s):
Ibrahima Mbaye, Mamadou Diop, Aliou Sonko and Malick Ba
University of Thies,
Department of Mathematics, Bp 967 Thies,
Senegal.
E-mail: imbaye@univ-thies.sn
mamadou.diop@univ-thies.sn
aliousonko59@gmail.com
mmalickba@hotmail.fr
URL: https://www.univ-thies.sn
Abstract:
This work aims to extend and improve our previous study on mathematical and numerical analysis of stationary Pasternak model. In this paper a dynamic response of Pasternak model is considered. On the one hand we establish the existence and uniqueness of the solution by using the Lax-Milgram theorem and the spectral theory thus the existence of a Hilbert basis is shown and the spectral decomposition of any solution of the problem can be established and on the other hand the finite element method is used to determinate the numerical results. Furthermore, the influence of soil parameters Gp and Kp on the displacement of the pious is studied numerically at any time tn.
Paper's Title:
Coexisting Attractors and Bubbling Route to Chaos in Modified Coupled Duffing Oscillators
Author(s):
B. Deruni1, A. S. Hacinliyan1,2, E. Kandiran3, A. C. Keles2, S. Kaouache4, M.-S. Abdelouahab4, N.-E. Hamri4
1Department
of Physics,
University of Yeditepe,
Turkey.
2Department
of Information Systems and Technologies,
University of Yeditepe,
Turkey
3Department
of Software Development,
University of Yeditepe,
Turkey.
4Laboratory
of Mathematics and their interactions,
University Center of Abdelhafid Boussouf,
Mila 43000,
Algeria.
E-mail:
berc890@gmail.com
ahacinliyan@yeditepe.edu.tr
engin.kandiran@yeditepe.edu.tr
cihan.keles@yeditepe.edu.tr
s.kaouache@centr-univ-mila.dz
medsalah3@yahoo.fr
n.hamri@centre-univ-mila.dz
Abstract:
In this article dynamical behavior of coupled Duffing oscillators is analyzed under a small modification. The oscillators have cubic damping instead of linear one. Although single duffing oscillator has complex dynamics, coupled duffing systems possess a much more complex structure. The dynamical behavior of the system is investigated both numerically and analytically. Numerical results indicate that the system has double scroll attractor with suitable parameter values. On the other hand, bifurcation diagrams illustrate rich behavior of the system, and it is seen that, system enters into chaos with different routes. Beside classical bifurcations, bubbling route to chaos is observed for suitable parameter settings. On the other hand, Multistability of the system is indicated with the coexisting attractors, such that under same parameter setting the system shows different periodic and chaotic attractors. Moreover, chaotic synchronization of coupled oscillators is illustrated in final section.
Paper's Title:
Two Geometric Constants Related to Isosceles Orthogonality on Banach Space
Author(s):
Huayou Xie, Qi Liu and Yongjin Li
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P. R. China.
E-mail: xiehy33@mail2.sysu.edu.cn
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P. R. China.
E-mail: liuq325@mail2.sysu.edu.cn
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P. R. China.
E-mail: stslyj@mail.sysu.edu.cn
Abstract:
In this paper, we introduce new geometric constant C(X,ai,bi,ci,2) to measure the difference between isosceles orthogonality and special Carlsson orthogonalities. At the same time, we also present the geometric constant C(X,ai,bi,ci), which is a generalization of the rectangular constant proposed by Joly. According to the inequality on isosceles orthogonality, we give the boundary characterization of these geometric constants. Then the relationship between these geometric constants and uniformly non-square property can also be discussed. Furthermore, we show that there is a close relationship between these geometric constants and some important geometric constants.
Paper's Title:
New Refinements for Integral and Sum Forms of Generalized Hölder Inequality For N Term
Author(s):
M. Jakfar, Manuharawati, D. Savitri
Mathematics Department,
Universitas Negeri Surabaya
Jalan Ketintang Gedung C8, Surabaya, 60321
Indonesia.
E-mail: muhammadjakfar@unesa.ac.id
manuharawati@unesa.ac.id
diansavitri@unesa.ac.id
Abstract:
We know that in the field of functional analysis, Hölder inequality is very well known, important, and very applicable. So many researchers are interested in discussing these inequalities. Many world mathematicians try to improve these inequalities. In general, the Hölder inequality has two forms, namely the integral form and the sum form. In this paper, we will introduce a new refinement of the generalization of Hölder inequalities in both integral and addition forms. Especially in the sum form, improvements will be introduced that are better than the previous improvements that have been published by Jing-feng Tian, Ming-hu Ha, and Chao Wang.
Paper's Title:
Some Moduli and Inequalities Related to Birkhoff Orthogonality in Banach Spaces
Author(s):
Dandan Du and Yongjin Li
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P.R. China.
E-mail: dudd5@mail2.sysu.edu.cn
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P.R. China.
E-mail: stslyj@mail.sysu.edu.cn
Abstract:
In this paper, we shall consider two new constants δB(X) and ρB(X), which are the modulus of convexity and the modulus of smoothness related to Birkhoff orthogonality, respectively. The connections between these two constants and other well-known constants are established by some equalities and inequalities. Meanwhile, we obtain two characterizations of Hilbert spaces in terms of these two constants, study the relationships between the constants δB(X), ρB(X) and the fixed point property for nonexpansive mappings. Furthermore, we also give a characterization of the Radon plane with affine regular hexagonal unit sphere.
Paper's Title:
Higher Order Accurate Compact Schemes for Time Dependent Linear and Nonlinear Convection-Diffusion Equations
Author(s):
S. Thomas, Gopika P.B. and S. K. Nadupuri
Department of Mathematics
National Institute of Technology Calicut
Kerala
673601
India.
E-mail:
sobinputhiyaveettil@gmail.com
pbgopika@gmail.com nsk@nitc.ac.in
Abstract:
The primary objective of this work is to study higher order compact finite difference schemes for finding the numerical solution of convection-diffusion equations which are widely used in engineering applications. The first part of this work is concerned with a higher order exponential scheme for solving unsteady one dimensional linear convection-diffusion equation. The scheme is set up with a fourth order compact exponential discretization for space and cubic $C^1$-spline collocation method for time. The scheme achieves fourth order accuracy in both temporal and spatial variables and is proved to be unconditionally stable. The second part explores the utility of a sixth order compact finite difference scheme in space and Huta's improved sixth order Runge-Kutta scheme in time combined to find the numerical solution of one dimensional nonlinear convection-diffusion equations. Numerical experiments are carried out with Burgers' equation to demonstrate the accuracy of the new scheme which is sixth order in both space and time. Also a sixth order in space predictor-corrector method is proposed. A comparative study is performed of the proposed schemes with existing predictor-corrector method. The investigation of computational order of convergence is presented.
Paper's Title:
A General Fractional Control Scheme for Compound Combination Synchronization Between Different Fractional-Order Identical Chaotic Systems
Author(s):
Soumia Bensimessaoud and Smail Kaouache
Laboratory of Mathematics and their interactions, Abdelhafid Boussouf University Center, Mila, Algeria.
E-mail:
soumiabensimessaoud@gmail.com,
smailkaouache@gmail.com
Abstract:
In this paper, we aim to investigate the problem of compound combination synchronization (CCS) between four different fractional-order identical chaotic systems. Based on Laplace transformation and stability theory of linear dynamical systems, a new control law is proposed to assure the achievement of this kind of synchronization. Secondly, this control scheme is applied to realised CCS between four identical unified chaotic systems. Recall, that the proposed control scheme can be applied to wide classes of chaotic and hyperchaotic systems. Numerical simulations are given to show the effectiveness of the proposed method.
Search and serve lasted 1 second(s).