|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Generalised Models for Torsional Spine Reconnection
Author(s):
Ali Khalaf Hussain Al-Hachami
Department of Mathematics,
College of Education For Pure Sciences,
Wasit University,
Iraq.
E-mail: alhachamia@uowasit.edu.iq
Abstract:
Three-dimensional (3D) null points are available in wealth in the solar corona, and the equivalent is probably going to be valid in other astrophysical situations. On-going outcomes from sun oriented perceptions and from reproductions propose that reconnection at such 3D nulls may assume a significant job in the coronal dynamics. The properties of the torsional spine method of magnetic reconnection at 3D nulls are researched. Kinematic model are created, which incorporate the term ηJ that is spatially localised around the null, stretching out along the spine of the null. The null point is to research the impact of shifting the level of asymmetry of the null point magnetic field on the subsequent reconnection process where past examinations constantly considered a non-nonexclusive radially symmetric null. Specifically we analyse the rate of reconnection of magnetic flux at the spine of null point. Logical arrangements are determined for the enduring kinematic equation, and contrasted and the after effects of torsional spine reconnection models when the current is restricted in which the Maxwell conditions are illuminated. The geometry of the current layers inside which torsional spine reconnection happen is autonomous on the symmetry of the magnetic field. Torsional spine reconnection happens in a thin cylinder around the spine, with circular cross-segment when the fan eigenvalues are extraordinary. The short axis of the circle being along the solid field bearing. Just as it was discovered that the fundamental structure of the method of attractive reconnection considered is unaffected by changing the magnetic field symmetry, that is, the plasma flow is discovered rotational around the spine of null point. The spatiotemporal pinnacle current, and the pinnacle reconnection rate achieved, are found not to rely upon the level of asymmetry.
Paper's Title:
A Review on Minimally Supported Frequency Wavelets
Author(s):
K Pallavi1, M C Lineesh1, A Noufal2
1
Department of Mathematics,2Department of Mathematics,
Cochin University of Science and Technology,
Kerala 682022,
India.
E-mail: noufal@cusat.ac.in
Abstract:
This paper provides a review on Minimally Supported Frequency (MSF) wavelets that includes the construction and characterization of MSF wavelets. The characterization of MSF wavelets induced from an MRA is discussed and the nature of the low-pass filter associated with it is explained. The concept of wavelet set and dimension function is introduced to study this class of wavelets. Along with MSF wavelets, s-elementary wavelets and unimodular wavelets are also considered due to the similarity in definitions. Examples and illustrations are provided for more clarity.
Paper's Title:
A Simple New Proof of Fan-Taussky-Todd Inequalities
Author(s):
Zhi-Hua Zhang and Zhen-Gang Xiao
Zixing Educational Research Section,
Chenzhou City, Hunan 423400, P. R. China.
Zhi-hua Zhang
Url: http://www.hnzxslzx.com/zzhweb/
Department Of Mathematics, Hunan Institute Of Science And Technology,
Yueyang City, Hunan 423400, P. R. China.
Zhen-gang Xiao
Abstract:
In this paper we present simple new proofs of the inequalities:
which holds for all real numbers a0 = 0, a1, · · · , an, an+1 = 0 and the coefficients
2(1 - cos(π/(n + 1))) and 2(1 + cos(π/(n + 1))) are the best possible; and
which holds for all real numbers a0 = 0, a1, · · · , an and the coefficients
2(1-cos(π/(2n + 1))) and 2(1 + cos(π/(2n + 1))) are the best possible.
Paper's Title:
Composite Variational-Like Inequalities Given By Weakly Relaxed
Author(s):
Syed Shakaib Irfan, Iqbal Ahmad, Zubair Khan and Preeti Shukla
College of Engineering, Qassim University
Buraidah, Al-Qassim,
Saudi Arabia.
E-mail: shakaib@qec.edu.sa
College of Engineering, Qassim University
Buraidah, Al-Qassim,
Saudi Arabia.
E-mail: iqbal@qec.edu.sa
Department of Mathematics,
Integral University Lucknow,
India.
E-mail: zkhan@iul.ac.in
Department of Mathematics,
Integral University Lucknow,
India.
E-mail: shuklapreeti1991@gmail.com
Abstract:
In this article, we introduce a composite variational-like inequalities with weakly relaxed ζ-pseudomonotone multi-valued maping in reflexive Banach spaces. We obtain existence of solutions to the composite variational-like inequalities with weakly relaxed ζ-pseudomon -otone multi-valued maps in reflexive Banach spaces by using KKM theorem. We have also checked the solvability of the composite variational-like inequalities with weakly relaxed ζ-semi-pseudomonotone multi-valued maps in arbitrary Banach spaces using Kakutani-Fan-Glicksberg fixed point theorem.
Paper's Title:
On Zeros of Diagonally Quasiconvex Multifunctions
Author(s):
Zoran D. Mitrović
Faculty of Electrical Engineering,
University of Banja Luka,
78000 Banja Luka, Patre 5
Bosnia and Herzegovina
zmitrovic@etfbl.net
Abstract:
In this paper, we extended the notion of diagonally quasiconvexity
for multifunctions and established several existence results for
zeros of diagonally quasiconvex multifunctions. As applications we
obtain the results of fixed points, coincidence points and best
approximations for multifunctions. Using our result we also prove
the existence of solutions to the variational-like inequality
problem and generalized vector equilibrium problem. The results
of this paper generalize some known results in the literature.
Paper's Title:
On Stan Ulam and his Mathematics
Author(s):
Krzysztof Ciesielski and Themistocles M. Rassias
Mathematics Institute, Jagiellonian University,
Abstract:
In this note we give a glimpse of the curriculum vitae of Stan Ulam, his personality and some of the mathematics he was involved in.
Paper's Title:
Inequalities for Functions of Selfadjoint Operators on Hilbert Spaces:
a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
College of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning inequalities for continuous functions of selfadjoint operators on complex Hilbert spaces. It is intended for use by both researchers in various fields of Linear Operator Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
New Inequalities of Mill's Ratio and Application to The Inverse Q-function Approximation
Author(s):
Pingyi Fan
Department of Electronic Engineering,
Tsinghua University, Beijing,
China
Abstract:
In this paper, we investigate the Mill's ratio estimation problem and get two new inequalities. Compared to the well known results obtained by Gordon, they becomes tighter. Furthermore, we also discuss the inverse Q-function approximation problem and present some useful results on the inverse solution. Numerical results confirm the validness of our theoretical analysis. In addition, we also present a conjecture on the bounds of inverse solution on Q-function.
Paper's Title:
On Singular Numbers of Hankel Matrices of Markov Functions
Author(s):
Vasily A. Prokhorov
Department of Mathematics and Statistics,
University of South Alabama,
Mobile, Alabama 36688-0002,
USA.
E-mail: prokhoro@southalabama.edu
URL:
http://www.southalabama.edu/mathstat/people/prokhorov.shtml
Abstract:
Let E ⊂ (01,1) be a compact set and let μ be a positive Borel measure with support supp μ=E. Let
In the case when E=[a,b]⊂ (-1,1) and μ satisfies the condition dμ/dx>0 a.e. on E, we investigate asymptotic behavior of singular numbers σkn,n of the Hankel matrix Dn, where kn/n→θ∈[0,1] as n→∞. Moreover, we obtain asymptotics of the Kolmogorov, Gelfand and linear k-widths, k=kn, of the unit ball An,2 of Pn∩L2(Γ) in the space L2(μ,E), where Γ={z:|z|=1} and Pn is the class of all polynomials of the degree at most n.
Paper's Title:
Applications of Von Neumann Algebras to Rigidity Problems of (2-Step) Riemannian (Nil-)Manifolds
Author(s):
Atefeh Hasan-Zadeh and Hamid-Reza Fanai
DFouman Faculty of Engineering,
College of Engineering, University of Tehran,
Iran.
E-mail: hasanzadeh.a@ut.ac.ir
Department of Mathematical Sciences,
Sharif University of Technology,
Iran
E-mail: fanai@sharif.edu
Abstract:
In this paper, basic notions of von Neumann algebra and its direct analogues in the realm of groupoids and measure spaces have been considered. By recovering the action of a locally compact Lie group from a crossed product of a von Neumann algebra, other proof of one of a geometric propositions of O'Neil and an extension of it has been proposed. Also, using the advanced exploration of nilmanifolds in measure spaces and their corresponding automorphisms (Lie algebraic derivations) a different proof of an analytic theorem of Gordon and Mao has been attained. These two propositions are of the most important ones for rigidity problems of Riemannian manifolds especially 2-step nilmanifolds.
Paper's Title:
A Coincidence Theorem for Two Kakutani Maps
Author(s):
Mircea Balaj
Department of Mathematics,
University of Oradea,
410087, Oradea,
Romania.
mbalaj@uoradea.ro
Abstract:
In this paper we prove the following theorem: Let X be a nonempty compact convex set in a locally convex Hausdorff topological vector space, D be the set of its extremal points and F,T: X―◦X two Kakutani maps; if for each nonempty finite subset A of D and for any x ∈ coA, F (x) ∩ coA ≠ Ø, then F and T have a coincidence point. The proof of this theorem is given first in the case when X is a simplex, then when X is a polytope and finally in the general case. Several reformulations of this result are given in the last part of the paper.
Paper's Title:
Nonlinear System of Mixed Ordered Variational Inclusions Involving XOR Operation
Author(s):
Iqbal Ahmad, Abdullah and Syed Shakaib Irfan
Department of Mechanical Engineering,
College of Engineering, Qassim University
Buraidah 51452, Al-Qassim,
Saudi Arabia.
E-mail: iqbal@qec.edu.sa,
i.ahmad@qu.edu.sa
Zakir Husain Delhi College,
University of Delhi,
JLN Marg, New Delhi- 110 002,
India.
E-mail: abdullahdu@qec.edu.sa
Department of Mathematics,
Aligarh Muslim University, Aligarh,
India.
E-mail: shakaibirfan@gmail.com
Abstract:
In this work, we introduce and solve an NSMOVI frameworks system involving XOR operation with the help of a proposed iterative algorithm in real ordered positive Hilbert spaces. We discuss the existence of a solution of a considered system of inclusions involving XOR operation by applying the resolvent operator technique with XOR operation and also study the strong convergence of the sequences generated by the considered algorithm. Further, we give a numerical example in support of our considered problem which gives the grantee that all the proposed conditions of our main result are fulfilled.
Paper's Title:
A New Look at the Equations of the Calculus of Variations
Author(s):
Olivier de La Grandville
Faculty of Economics, Goethe University
Frankfurt,
Theodore Adorno Platz 4, 60323 Frankfurt,
Germany.
E-mail: odelagrandville@gmail.com
Abstract:
We first offer an entirely new way to derive the celebrated Euler equation of the calculus of variations. The advantage of this approach is two-fold. On the one hand, it entirely eschews the two hurdles encountered by Lagrange, which become challenging in the case of elaborate functionals: getting rid of the arbitrary character of the perturbation given to the optimal function, and demonstrating the fundamental lemma of the calculus of variations. On the other hand, it leads in a direct way to the remarkable discovery made by Robert Dorfman ( 1969) when he introduced a modified Hamiltonian, which we called a Dorfmanian (2018) to honor his memory. In turn, extending the Dorfmanian enables to obtain readily the fundamental equations of the calculus of variations for the optimization of high-order functionals, or multiple integrals.
Paper's Title:
Results Concerning Fixed Point for Soft Weakly Contraction In Soft Metric Spaces
Author(s):
Abid Khan, Santosh Kumar Sharma, Anurag Choubey, Girraj Kumar Verma, Umashankar Sharma, Ramakant Bhardwaj
Department of Mathematics,
AUMP, Gwalior,
India.
abid69304@gmail.com
Department of Mathematics,
AUMP, Gwalior,
India.
sksharma1@gwa.amity.edu
Department of Computer Science,
Technocrats Institute of Technology,
Bhopal, MP,
India.
directoracademicstit@gmail.com
Department of Mathematics,
AUMP, Gwalior,
India.
gkverma@gwa.amity.edu
Department of Physics,
RJIT BSF Tekanpur, MP,
India.
ussharma001@gmail.com
School of Applied Science
AUK, WB,
India.
rkbhardwaj100@gmail.com
Abstract:
The basic objective of the proposed research work is to make people acquainted with the concept of soft metric space by generalizing the notions of soft (ψ,φ)-weakly contractive mappings in soft metric space, as well as to look at specific fundamental and topological parts of the underlying spaces. A compatible example is given to explain the idea of said space structure. The theory is very useful in decision making problems and secure transmission as fixed point provides exact output. The fixed-point theorems on subsets of Rm that are useful in game theoretic settings.
Paper's Title:
On Vector Variational Inequality Problem in Terms of Bifunctions
Author(s):
C. S. Lalitha and Monika Mehta
Department of Mathematics, Rajdhani College,
Department of Mathematics, Satyawati College,
University of Delhi, Raja Garden,
Delhi 110015, India
cslalitha@rediffmail.com
University Of Delhi, Ashok Vihar,
Phase-III, Delhi 110052, India
mridul_in@yahoo.com
Abstract:
In this paper, we consider a generalized vector variational
inequality problem expressed in terms of a bifunction and establish
existence theorems for this problem by using the concepts of cone
convexity and cone strong quasiconvexity and employing the
celebrated Fan's Lemma. We also give two types of gap functions for this problem.
Paper's Title:
The Convergence of Modified Mann-Ishikawa Iterations when Applied to an Asymptotically Pseudocontractive Map
Author(s):
S. Soltuz
Departamento de Matematicas, Universidad de Los Andes, Carrera 1
No. 18A-10, Bogota,
Colombia
and
``T. Popoviciu" Institute of Numerical Analysis
Cluj-Napoca,
Romania
smsoltuz@gmail.com
URL:http://www.uniandes.edu.co/
Abstract:
We prove that under minimal conditions the modified Mann and Ishikawa iterations converge when dealing with an asymptotically pseudocontractive map. We give an affirmative answer to the open question from C.E. Chidume and H. Zegeye, Approximate fixed point sequences and convergence theorems for asymptotically pseudocontractive mappings, J. Math. Anal. Appl., 278 (2003), 354--366.
Paper's Title:
Ulam Stability of Functional Equations
Author(s):
Stefan Czerwik and Krzysztof Król
Institute of Mathematics
Silesian University of Technology
Kaszubska 23,
44-100 Gliwice,
Poland
Stefan.Czerwik@polsl.pl
Krzysztof.Krol@polsl.pl
Abstract:
In this survey paper we present some of the main results on Ulam-Hyers-Rassias stability for important functional equations.
Paper's Title:
Stability of Almost Multiplicative Functionals
Author(s):
Norio Niwa, Hirokazu Oka, Takeshi Miura and Sin-Ei Takahasi
Faculty of Engineering, Osaka Electro-Communication University,
Neyagawa 572-8530,
Japan
Faculty of Engineering, Ibaraki University,
Hitachi 316-8511,
Japan
Department of Applied Mathematics and Physics, Graduate School of
Science and Engineering,
Yamagata University,
Yonezawa 992-8510
Japan
oka@mx.ibaraki.ac.jp
miura@yz.yamagata-u.ac.jp
sin-ei@emperor.yz.yamagata-u.ac.jp
Abstract:
Let
δ
and p be non-negative real numbers. Let
be the
real or complex number field and
a normed algebra
over . If a mapping
satisfies
then we show that
φ
is multiplicative or
for all 
If, in
addition,
φ
satisfies
for some p≠1, then by using Hyers-Ulam-Rassias
stability of additive Cauchy equation, we show that
φ
is a ring homomorphism or
for all
In other words,
φ
is a ring homomorphism, or an approximately zero
mapping. The results of this paper are inspired by Th.M. Rassias' stability
theorem.
Paper's Title:
Real Interpolation Methods and Quasilogarithmic Operators
Author(s):
Ming Fan
School of Industrial Technology and Management,
Dalarna University, 781 88 Borlänge, Sweden
fmi@du.se
URL: http://users.du.se/~fmi
Abstract:
The purpose of this paper is to deal with nonlinear quasilogarithmic operators, which possesses the uniformly bounded commutator property on various interpolation spaces in the sense of Brudnyi-Krugljak associated with the quasi-power parameter spaces. The duality, and the domain and range spaces of these operators are under consideration. Some known inequalities for the Lebesgue integration spaces and the trace classes are carried over to the non-commutative symmetric spaces of measurable operators affiliated with a semi-finite von Neumann algebra.
Paper's Title:
Unital Compact Homomorphisms Between Extended Analytic Uniform Algebras
Author(s):
D. Alimohammadi and M. Mayghani
Department of Mathematics,
Faculty of Science, Arak University,
PO Box 38156-8-8349, Arak,
Iran.
Abstract:
Let X and K be compact plane sets with K⊆X. We denote by A(X,K) and A(X) the algebras of all continuous complex-valued functions on X which are analytic on int(K) and int(X), respectively. It is known that A(X,K) and A(X) are natural uniform algebras on X. A(X) and A(X,K) are called analytic uniform algebra and extended analytic uniform algebra on X, respectively. In this paper we study unital homomorphisms between extended analytic uniform algebras and investigate necessary and sufficient conditions for which these homomorphisms to be compact. We also determine the spectrum of unital compact endomorphisms of extended analytic uniform algebras.
Paper's Title:
Bartle Integration in Lie Algebras
Author(s):
Andreas Boukas and Philip Feinsilver
Centro Vito Volterra,
Universita di Roma Tor Vergata,
via Columbia 2, 00133 Roma,
Italy.
Department of Mathematics,
Southern Illinois University,
Carbondale, Illinois 62901,
USA.
E-mail:
andreasboukas@yahoo.com
E-mail: pfeinsil@math.siu.edu
Abstract:
Using Bartle's bilinear vector integral we define stochastic integrals of bounded operator valued functions with respect to Stieltjes measures associated with the generators of the Heisenberg and Finite Difference Lie algebras. Our definition also covers the Square of White Noise and sl/2 Lie algebras.
Paper's Title:
Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.
Paper's Title:
Introducing the Dorfmanian: A Powerful Tool for the Calculus Of Variations
Author(s):
Olivier de La Grandville
Department of Management Science and Engineering,
Stanford University,
475 Via Ortega, Stanford, CA 94305,
U. S. A.
E-mail: odelagrandville@gmail.com
Abstract:
We show how a modified Hamiltonian proposed by Robert Dorfman [1] to give intuitive sense
to the Pontryagin maximum principle can be extended to easily obtain all
high-order equations of the calculus of variations. This new concept is
particularly efficient to determine the differential equations leading to
the extremals of functionals defined by n-uple integrals, while a
traditional approach would require -- in some cases repeatedly -- an
extension of Green's theorem to n-space.
Our paper is dedicated to the memory of Robert Dorfman (1916 - 2002).
Paper's Title:
Iterative Algorithm for Split Generalized Mixed Equilibrium Problem Involving Relaxed Monotone Mappings in Real Hilbert Spaces
Author(s):
1U.A. Osisiogu, F.L. Adum, and 2C. Izuchukwu
1Department of Mathematics and
Computer Science,
Ebonyi State University, Abakaliki,
Nigeria.
E-mail: uosisiogu@gmail.com,
adumson2@yahoo.com
2School of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: izuchukwuc@ukzn.ac.za,
izuchukwu_c@yahoo.com
Abstract:
The main purpose of this paper is to introduce a certain class of split generalized mixed equilibrium problem involving relaxed monotone mappings. To solve our proposed problem, we introduce an iterative algorithm and obtain its strong convergence to a solution of the split generalized mixed equilibrium problems in Hilbert spaces. As special cases of the proposed problem, we studied the proximal split feasibility problem and variational inclusion problem.
Paper's Title:
A Generalization of Ostrowski's Inequality for Functions of Bounded
Variation via a Parameter
Author(s):
Seth Kermausuor
Department of Mathematics and Computer
Science,
Alabama State University,
Montgomery, AL 36101,
USA.
E-mail:
skermausour@alasu.edu
Abstract:
In this paper, we provide a generalization of the Ostrowski's inequality for functions of bounded variation for k points via a parameter λ∈[0,1]. As a by product, we consider some particular cases to obtained some interesting inequalities in these directions. Our results generalizes some of the results by Dragomir in [S. S. DRAGOMIR, The Ostrowski inequality for mappings of bounded variation, Bull. Austral. Math. Soc., 60 (1999), pp. 495--508.]
Paper's Title:
Extension of Factorization Theorems of Maurey to s-positively Homogeneous Operators
Author(s):
Abdelmoumen Tiaiba
Department of Physics,
University of M'sila,
Algeria.
E-mail: tiaiba05@yahoo.fr
Abstract:
In the present work, we prove that the class of s-positively homogeneous operators is a Banach space. As application, we give the generalization of some Maurey factorization theorems to T which is a s-positively homogeneous operator from X a Banach space into Lp. Where we establish necessary and sufficient conditions to proof that T factors through Lq. After this we give extend result of dual factorization theorem to same class of operators above.
Paper's Title:
Multivalued Equilibrium Problems with Trifunction
Author(s):
Muhammad Aslam Noor
Etisalat College of Engineering, P.O. Box 980, Sharjah, United Arab Emirates
noor@ece.ac.ae
Abstract:
In this paper, we use the auxiliary principle technique to
suggest some new classes of iterative algorithms for solving multivalued
equilibrium problems with trifunction. The convergence of the proposed methods
either requires partially relaxed strongly monotonicity or pseudomonotonicity.
As special cases, we obtain a number of known and new results for solving
various classes of equilibrium and variational inequality problems. Since
multivalued equilibrium problems with trifunction include equilibrium,
variational inequality and complementarity problems as specials cases, our
results continue to hold for these problems.
Paper's Title:
Positive Solutions for Systems of Three-point Nonlinear Boundary Value Problems
Author(s):
J. Henderson and S. K. Ntouyas
Department of Mathematics, Baylor University
Waco, Texas
76798-7328 USA.
Johnny_Henderson@baylor.edu
URL: http://www3.baylor.edu/~Johnny_Henderson
Department of Mathematics, University of Ioannina
451 10 Ioannina,
Greece.
sntouyas@cc.uoi.gr
URL: http://www.math.uoi.gr/~sntouyas
Abstract:
Values of λ are determined for which there exist
positive solutions of the system of three-point boundary value problems,
u''(t)+ λa(t)f(v(t))=0, v''(t)+λb(t)g(u(t))=0,
for 0 < t <1, and
satisfying, u(0) = 0, u(1)=α u(η),
v(0) = 0, v(1)=α v(η). A Guo-Krasnosel'skii fixed
point theorem is applied. Paper's Title:
Contact With Adhesion between a Deformable Body and a Foundation
Author(s):
B. Teniou and M. Sofonea
Laboratoire de Mathematiques Appliquées et Modélisation,
Laboratoire de Mathématiques et Physiques pour les Systémes, Abstract:
The aim of this work is study a dynamic contact problem between a
deformable body and a foundation where the deformations are supposed
to be small. The contact is with adhesion and normal compliance. The
behavior of this body is modeled by a nonlinear
elastic-visco-plastic law. The evolution of bonding field is
described by a nonlinear differential equation. We derive a
variational formulation of the contact problem and we prove the
existence and uniqueness of its solution. The proof is based on the
construction of three intermediate problems and then we construct a
contraction mapping whose unique fixed point will be the weak
solution of the mechanical problem. Paper's Title:
Nontrivial Solutions of Singular Superlinear Three-point
Boundary Value Problems at Resonance
Author(s):
Feng Wang, Fang Zhang
School of Mathematics and Physics,
Abstract:
The singular superlinear second order three-point boundary value
problems at resonance
are considered under some conditions concerning the first
eigenvalues corresponding to the relevant linear operators, where n ∈ (0,1) is a constant,
f is allowed to be singular at both
t=0 and t=1. The existence results of nontrivial solutions are
given by means of the topological degree theory.
Paper's Title:
Shape Diagrams for 2D Compact Sets - Part I: Analytic
Convex Sets.
Author(s):
S. Rivollier, J. Debayle and J.-C. Pinoli
Ecole Nationale Supérieure des Mines de Saint-Etienne,
CIS - LPMG, UMR CNRS
5148,
158 cours Fauriel,
42023 Saint-Etienne Cedex 2, France.
Abstract:
Shape diagrams are representations in the Euclidean plane introduced to study
3-dimensional and 2-dimensional compact convex sets. Such a set is represented by a point within a shape diagram whose coordinates are morphometrical functionals defined as normalized ratios of geometrical functionals. Classically, the geometrical functionals are the area, the perimeter, the radii of the inscribed and circumscribed circles, and the minimum and maximum Feret diameters. They allow thirty-one shape diagrams to be built. Most of these shape diagrams can also been applied to more general compact sets than compact convex sets. Starting from these six classical geometrical functionals, a detailed comparative study has been performed in order to analyze the representation relevance and discrimination power of these thirty-one shape diagrams. The purpose of this paper is to present the first part of this study, by focusing on analytic compact convex sets. A set will be called analytic if its boundary is piecewise defined by explicit functions in such a way that the six geometrical functionals can be straightforwardly calculated. The second and third part of the comparative study are published in two following papers
[19.20]. They are focused on analytic simply connected sets and convexity discrimination for analytic and discretized simply connected sets, respectively. Paper's Title:
Shape Diagrams for 2D Compact Sets - Part II: Analytic
Simply Connected Sets.
Author(s):
S. Rivollier, J. Debayle and J.-C. Pinoli
Ecole Nationale Supérieure des Mines de Saint-Etienne,
CIS - LPMG, UMR CNRS
5148,
158 cours Fauriel,
42023 Saint-Etienne Cedex 2, France.
Abstract:
Shape diagrams are representations in the Euclidean plane introduced to study 3-dimensional and 2-dimensional compact convex sets. However, they can also been applied to more general compact sets than compact convex sets. A compact set is represented by a point within a shape diagram whose coordinates are morphometrical functionals defined as normalized ratios of geometrical functionals. Classically, the geometrical functionals are the area, the perimeter, the radii of the inscribed and circumscribed circles, and the minimum and maximum Feret diameters. They allow twenty-two shape diagrams to be built. Starting from these six classical geometrical functionals, a detailed comparative study has been performed in order to analyze the representation relevance and discrimination power of these twenty-two shape diagrams. The first part of this study is published in a previous paper
16. It focused on analytic compact convex sets. A set will be called analytic if its boundary is piecewise defined by explicit functions in such a way that the six geometrical functionals can be straightforwardly calculated. The purpose of this paper is to present the second part, by focusing on analytic simply connected compact sets. The third part of the comparative study is published in a following paper
17. It is focused on convexity discrimination for analytic and discretized simply connected compact sets. Paper's Title:
Shape Diagrams for 2D Compact Sets - Part III: Convexity
Discrimination for Analytic and Discretized Simply Connected Sets.
Author(s):
S. Rivollier, J. Debayle and J.-C. Pinoli
Ecole Nationale Supérieure des Mines de Saint-Etienne,
Abstract:
Shape diagrams are representations in the Euclidean plane introduced to study 3-dimensional and 2-dimensional compact convex sets. However, they can also been applied to more general compact sets than compact convex sets. A compact set is represented by a point within a shape diagram whose coordinates are morphometrical functionals defined as normalized ratios of geometrical functionals. Classically, the geometrical functionals are the area, the perimeter, the radii of the inscribed and circumscribed circles, and the minimum and maximum Feret diameters. They allow twenty-two shape diagrams to be built. Starting from these six classical geometrical functionals, a detailed comparative study has been performed in order to analyze the representation relevance and discrimination power of these twenty-two shape diagrams. The two first parts of this study are published in previous papers
8,9. They focus on analytic compact convex sets and analytic simply connected compact sets, respectively. The purpose of this paper is to present the third part, by focusing on the convexity discrimination for analytic and discretized simply connected compact sets..
Paper's Title:
A One-Line Derivation of the Euler and Ostrogradski Equations
Author(s):
Olivier de La Grandville Stanford University, Abstract:
At the very heart of major results of
classical physics, the Euler and Ostrogradski equations have apparently no
intuitive interpretation. In this paper we show that this is not so. Relying
on Euler's initial geometric approach, we show that they can be obtained
through a direct reasoning that does not imply any calculation. The
intuitive approach we suggest offers two benefits: it gives immediate
significance to these fundamental second-order non-linear differential
equations; and second, it allows to obtain a property of the calculus of
variations that does not seem to have been uncovered until now: the Euler
and Ostrogradski equations can be derived not necessarily by giving a
variation to the optimal function -- as is always done; one could equally
well start by giving a variation to their derivative(s).
Paper's Title:
On Eigenvalues and Boundary Curvature of the C*-algebra Numerical Rang Author(s):
M. T. Heydari Department of Mathematics, E-mail:
heydari@yu.ac.ir Abstract:
Let A be a C*-algebra with unit 1 and
a∈A be a nilpotent. By Donoghue's Theorem, all corner points of
its numerical range V(a) belong to the spectrum σ(a). It is therefore natural to expect that, more
generally, the distance from a point p on the boundary ∂ V(a) of
V(a) to σ(a) should be in some sense bounded by the radius of
curvature of ∂ V(a) at p. Paper's Title:
Generalized Weighted Trapezoid and Gr
2: Paper Source
PDF document
Université Mentouri, Constantine 25000,
Algeria
tenioubou2@yahoo.fr
Univesité de Perpignan,
France.
sofonea@univ-perp.fr
2: Paper Source
PDF document
Changzou University,
Changzhou, 213164,
China.
fengwang188@163.com
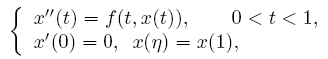
2: Paper Source
PDF document
rivollier@emse.fr;
debayle@emse.fr; pinoli@emse.fr
2: Paper Source
PDF document
rivollier@emse.fr;
debayle@emse.fr; pinoli@emse.fr
2: Paper Source
PDF document
CIS - LPMG, UMR CNRS
5148,
158 cours Fauriel,
42023 Saint-Etienne Cedex 2, France.
rivollier@emse.fr;
debayle@emse.fr; pinoli@emse.fr
2: Paper Source
PDF document
Department of Management Science and Engineering,
Stanford, CA 94305,
U. S. A
2: Paper Source
PDF document
College of Sciences,
Yasouj University,
Yasouj, 75914-74831,
Iran.
2: Paper Source
PDF document
Author(s):
Eze Raymond Nwaeze
Department of Mathematics,
Tuskegee University,
Tuskegee, AL 36088,
USA.
E-mail: enwaeze@mytu.tuskegee.edu
Abstract:
In this work, we obtain some new generalized weighted trapezoid and Grüss type inequalities on time scales for parameter functions. Our results give a broader generalization of the results due to Pachpatte in [14]. In addition, the continuous and discrete cases are also considered from which, other results are obtained.
Paper's Title:
The Concept of Convergence for 2-Dimensional Subspaces Sequence in Normed Spaces
Author(s):
M. Manuharawati, D. N. Yunianti, M. Jakfar
Mathematics Department, Universitas
Negeri Surabaya,
Jalan Ketintang Gedung C8,
Surabaya 60321,
Indonesia.
E-mail: manuharawati@unesa.ac.id,
dwiyunianti@unesa.ac.id,
muhammadjakfar@unesa.ac.id
Abstract:
In this paper, we present a concept of convergence of sequence, especially, of 2-dimensional subspaces of normed spaces. The properties of the concept are established. As consequences of our definition in an inner product space, we also obtain the continuity property of the angle between two 2-dimensional subspaces of inner product spaces.
Paper's Title:
Uniqueness Problems for Difference Polynomials Sharing a Non-Zero Polynomial of Certain Degree With Finite Weight
Author(s):
V. Priyanka, S. Rajeshwari and V. Husna
Department of Mathematics,
School of Engineering,
Presidency University,
Bangalore-560064,
India.
E-mail:
priyapriyankaram1994@gmail.com
rajeshwaripreetham@gmail.com
husnav43@gmail.com
Abstract:
In this paper, we prove a result on the value distribution of difference polynomials sharing higher order derivatives of meromorphic functions which improves some earlier results. At the same time, we also prove possible uniqueness relation of entire functions when the difference polynomial generated by them sharing a non zero polynomial of certain degree. The result obtained in the paper will improve and generalize a number of recent results in a compact and convenient way.
Paper's Title:
SQIRV Model for Omicron Variant with Time Delay
Author(s):
S. Dickson, S. Padmasekaran, G. E. Chatzarakis and S. L. Panetsos
Mathematics, Periyar University, Periyar
Palkalai Nagar, Salem,
636011, Tamilnadu,
India.
E-mail:
dickson@periyaruniversity.ac.in,
padmasekarans@periyaruniversity.ac.in
Electrical and Electronic Engineering
Educators, School of
Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
spanetsos@aspete.gr
Abstract:
In order to examine the dynamics of the Omicron variant, this paper uses mathematical modelling and analysis of a SQIRV model, taking into account the delay in the conversion of susceptible individuals into infected individuals and infected individuals into recovered individuals. The pandemic was eventually controlled as a result of the massive delays. To assure the safety of the host population, this concept incorporates quarantine and the COVID-19 vaccine. Both local and global stability of the model are examined. It is found that the fundamental reproduction number affects both local and global stability conditions. Our findings show that asymptomatic cases caused by an affected population play an important role in increasing Omicron infection in the general population. The most recent data on the pandemic Omicron variant from Tamil Nadu, India, is verified.
Paper's Title:
On the Oldest Problem in the Calculus of Variations: A New Message from Queen Dido
Author(s):
Olivier de La Grandville
Faculty of Economics,
Goethe University Frankfurt,
Theodore Adorno Platz 4, 60323 Frankfurt,
Germany.
E-mail: odelagrandville@gmail.com
Abstract:
We consider the problem of finding the optimal curve of given length linking two points in a plane such as it encloses a maximal area. We show that if the curve is not described by a single-valued function, its determination does not necessarily imply to work with a parametric representation of the curve. We show that a simpler approach is at hand -- and, who knows? -- this might well be the method Queen Dido used.
Paper's Title:
Some Nonlinear Gronwall-Bellman Type Retarded Integral Inequalities with Power and Their Applications
Author(s):
Ammar Boudeliou
Department of Mathematics, University of Constantine 1
Brothers Mentouri,
BP, 325, Ain El Bey Street, 25017,
Algeria.
E-mail: ammar_boudeliou@umc.edu.dz
Abstract:
In this paper, we investigate a certain class of nonlinear Gronwall-Bellman type integral inequalities with power in more general cases involving retarded term and more general nonlinearities. Our results generalize some known integral inequalities and other results obtained very recently. The inequalities given here can be used to estimate the bound on the solutions of retarded integral equation of Volterra type and integro-differential equations (IDE) with power. Two examples are given to show the validity of our established theorems.
Paper's Title:
Long Time Behavior for a Viscoelastic Problem with a Positive Definite Kernel
Author(s):
Nasser-eddine Tatar
King Fahd
University of Petroleum and Mineral, Department of Mathematical Sciences,
Dhahran, 31261 Saudi Arabia
tatarn@kfupm.edu.sa
Abstract:
We study the asymptotic behavior of solutions for an integro-differential problem which arises in the theory of viscoelasticity. It is proved that solutions go to rest in an exponential manner under new assumptions on the relaxation function in the memory term. In particular, we consider a new family of kernels which are not necessarily decreasing.
Paper's Title:
Essential Random Fixed Point Set of Random Operators
Author(s):
Ismat Beg
Centre for Advanced Studies in Mathematics,
Lahore University of Management Sciences (LUMS),
54792-Lahore, PAKISTAN.
ibeg@lums.edu.pk
URL: http://web.lums.edu.pk/~ibeg
Abstract:
We obtain necessary and sufficient conditions for the existence of essential random fixed point of a random operator defined on a compact metric space. The structure of the set of essential random fixed points is also studied.
Paper's Title:
Positive Periodic Time-Scale Solutions for Functional Dynamic Equations
Author(s):
Douglas R. Anderson and Joan Hoffacker
Department of Mathematics and Computer Science
Concordia College
Moorhead, MN 56562 USA
andersod@cord.edu
URL: http://www.cord.edu/faculty/andersod/
Department of Mathematical Sciences
Clemson University
Clemson, SC 29634 USA
johoff@clemson.edu
URL: http://www.math.clemson.edu/facstaff/johoff.htm
Abstract:
Using Krasnoselskii's fixed point theorem, we establish the existence of positive periodic solutions
to two pairs of related nonautonomous functional delta dynamic equations on periodic time scales, and then extend the discussion to higher-dimensional equations. Two pairs of corresponding nabla equations
are also provided in an analogous manner.
Paper's Title:
Normalized Truncated Levy models applied to the study of Financial Markets
Author(s):
M. C. Mariani, K. Martin, D. W. Dombrowski and D. Martinez
Department of Mathematical Sciences and Department of Finance,
New Mexico State University, P.O. Box 30001
Department 3MB Las Cruces, New Mexico 88003-8001
USA.
mmariani@nmsu.edu
kjmartin@nmsu.edu
Abstract:
This work is devoted to the study of the statistical properties of financial instruments from developed markets. We performed a new analysis of the behavior of companies corresponding to the DJIA index, and of the index itself, by using a normalized Truncated Levy walk model. We conclude that the Truncated Levy distribution describes perfectly the evolution of the companies and of the index near a crash.
Paper's Title:
Existence Results for Perturbed Fractional Differential
Inclusions
Author(s):
Y.-K. Chang
Department of Mathematics,
Lanzhou Jiaotong University, Lanzhou, Gansu 730070, People's
Republic of China
lzchangyk@163.com
Abstract:
This paper is mainly concerned with the following fractional differential
inclusions with boundary condition
A sufficient condition is established for the existence of solutions of the
above problem by using a fixed point theorem for multivalued maps due to
Dhage. Our result is proved under the mixed generalized Lipschitz and
Carathéodory conditions.
Paper's Title:
Regular Variation on Time Scales and Dynamic Equations
Author(s):
Pavel Řehák
Institute of Mathematics, Academy of Sciences of the Czech Republic
Žižkova 22, CZ61662 Brno,
Czech Republic
rehak@math.muni.cz
URL:http://www.math.muni.cz/~rehak
Abstract:
The purpose of this paper is twofold. First, we want to initiate a study
of regular variation on time scales by introducing this concept in such a
way that it
unifies and extends well studied continuous and discrete cases.
Some basic properties of regularly varying functions on time scales will be
established as well.
Second, we give conditions under which certain solutions of linear second
order
dynamic equations are regularly varying.
Open problems and possible directions for a future research are discussed,
too.
Paper's Title:
Inequalities for
the
Author(s):
S. S. Dragomir
School of Engineering and Science
Victoria University, PO 14428
Melbourne City MC,
Victoria 8001,
Australia
sever.dragomir@vu.edu.au
URL: http://www.staff.vu.edu.au/RGMIA/dragomir/
Abstract:
Some recent inequalities for the Čebyšev functional of two functions of selfadjoint linear operators in Hilbert spaces, under suitable assumptions for the involved functions and operators, are surveyed.
Paper's Title:
Hyperbolic Barycentric Coordinates
Author(s):
Abraham A. Ungar
Department of Mathematics, North Dakota State University,
Fargo, ND 58105,
USA
Abraham.Ungar@ndsu.edu
URL: http://math.ndsu.nodak.edu/faculty/ungar/
Abstract:
A powerful and novel way to study Einstein's special theory of relativity and its underlying geometry, the hyperbolic geometry of Bolyai and Lobachevsky, by analogies with classical mechanics and its underlying Euclidean geometry is demonstrated. The demonstration sets the stage for the extension of the notion of barycentric coordinates in Euclidean geometry, first conceived by Möbius in 1827, into hyperbolic geometry. As an example for the application of hyperbolic barycentric coordinates, the hyperbolic midpoint of any hyperbolic segment, and the centroid and orthocenter of any hyperbolic triangle are determined.
Paper's Title:
Positive Solutions to a System of Boundary Value Problems for Higher-Dimensional Dynamic Equations on Time Scales
Author(s):
I. Y. Karaca
Department of Mathematics,
Ege University,
35100 Bornova, Izmir,
Turkey
URL:
http://ege.edu.tr
Abstract:
In this paper, we consider the system of boundary value problems for higher-dimensional dynamic equations on time scales. We establish criteria for the existence of at least one or two positive solutions. We shall also obtain criteria which lead to nonexistence of positive solutions. Examples applying our results are also given.
Paper's Title:
Some Operator Order Inequalities for Continuous Functions of Selfadjoint Operators in Hilbert Spaces
Author(s):
S. S. Dragomir1,2 and Charles E. M. Pearce3
1Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428,
Melbourne City, MC 8001,
Australia.
2School of Computational & Applied Mathematics,
University of
the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
sever.dragomir@vu.edu.au
URL: http://rgmia.org/dragomir
3School
of Mathematical Sciences,
The University of Adelaide,
Adelaide,
Australia
Abstract:
Various bounds in the operator order for the following operator transform
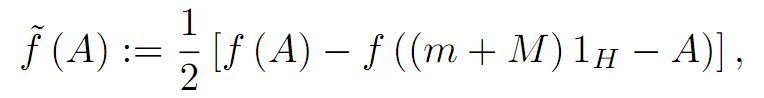
where A is a selfadjoint operator in the Hilbert space H with the
spectrum Sp( A) ⊆ [ m,M]
and f:[m,M] -> C is a continuous function on [m,M]
are given. Applications for the power and logarithmic functions are provided as
well.
Paper's Title:
End-Point and Transversality Conditions in the Calculus of Variations: Derivations through Direct Reasoning
Author(s):
Olivier de La Grandville
Stanford University,
Department of Management Science and Engineering,
475 Via Ortega, Stanford, CA 94305,
U. S. A.
E-mail: ola@stanford.edu
Abstract:
We offer an intuitive explanation of the end-point and transversality conditions that complement the Euler equation in the calculus of variations. Our reasoning is based upon the fact that any variation given to an optimal function must entail a zero net gain to the functional, all consequences of implied changes in its derivative being fully taken into account.
Paper's Title:
Some New Generalizations of Jensen's Inequality with Related Results and Applications
Author(s):
Steven G. From
Department of Mathematics
University of Nebraska at Omaha
Omaha, Nebraska 68182-0243.
E-mail: sfrom@unomaha.edu
Abstract:
In this paper, some new generalizations of Jensen's inequality are presented. In particular, upper and lower bounds for the Jensen gap are given and compared analytically and numerically to previously published bounds for both the discrete and continuous Jensen's inequality cases. The new bounds compare favorably to previously proposed bounds. A new method based on a series of locally linear interpolations is given and is the basis for most of the bounds given in this paper. The wide applicability of this method will be demonstrated. As by-products of this method, we shall obtain some new Hermite-Hadamard inequalities for functions which are 3-convex or 3-concave. The new method works to obtain bounds for the Jensen gap for non-convex functions as well, provided one or two derivatives of the nonlinear function are continuous. The mean residual life function of applied probability and reliability theory plays a prominent role in construction of bounds for the Jensen gap. We also present an exact integral representation for the Jensen gap in the continuous case. We briefly discuss some inequalities for other types of convexity, such as convexity in the geometric mean, and briefly discuss applications to reliability theory.
Paper's Title:
On operators for which T2≥-T*2
Author(s):
Messaoud Guesba1 and Mostefa Nadir2
1Department
of Mathematics,
University of El Oued 39000,
Algeria
E-mail: guesbamessaoud2@gmail.com
2Department of Mathematics,
University of Msila 28000,
Algeria
E-mail: mostefanadir@yahoo.fr
Abstract:
In this paper we introduce the new class of operators for which T2≥ -T*2 acting on a complex Hilbert space H. We give some basic properties of these operators. we study the relation between the class and some other well known classes of operators acting on H.
Paper's Title:
Euler Series Solutions for Linear Integral Equations
Author(s):
Mostefa Nadir and Mustapha Dilmi
Department of Mathematics,
University of Msila 28000,
ALGERIA.
E-mail: mostefanadir@yahoo.fr
E-mail: dilmiistapha@yahoo.fr
Abstract:
In this work, we seek the approximate solution of linear integral equations by truncation Euler series approximation. After substituting the Euler expansions for the given functions of the equation and the unknown one, the equation reduces to a linear system, the solution of this latter gives the Euler coefficients and thereafter the solution of the equation. The convergence and the error analysis of this method are discussed. Finally, we compare our numerical results by others.
Paper's Title:
MSplit Equality for Monotone Inclusion Problem and Fixed Point Problem in
Real Banach Spaces
Author(s):
1,2Christian Chibueze Okeke, 3Abdumalik Usman Bello, 1Chinedu Izuchukwu, and 1Oluwatosin Temitope Mewomo
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: okekec@ukzn.ac.za
E-mail: izuchukwuc@ukzn.ac.za
E-mail: mewomoo@ukzn.ac.za
2DST-NRF
Center of Excellence in Mathematical and Statistical Sciences (CoE-Mass)
Johannesburg,
South Africa.
3Federal
University,
Dutsin-Ma, Katsina State,
Nigeria.
E-mail:
uabdulmalik@fudutsinma.edu.ng
Abstract:
In this paper a new iterative algorithm for approximating a common solution of split equality monotone inclusion problem and split equality fixed point problem is introduced. Using our algorithm, we state and prove a strong convergence theorem for approximating an element in the intersection of the set of solutions of a split equality monotone inclusion problem and the set of solutions of a split equality fixed point problem for right Bregman strongly nonexpansive mappings in the setting of p-uniformly convex Banach spaces which are also uniformly smooth. We also give some applications.
Paper's Title:
Closedness and Skew Self-Adjointness of Nadir's Operator
Author(s):
Mostefa Nadir and Abdellatif Smati
Department of Mathematics,
University of Msila 28000,
ALGERIA.
E-mail: mostefanadir@yahoo.fr
E-mail: smatilotfi@gmail.com
Abstract:
In this paper, we present some sufficient conditions which ensure the compactness, the normality, the positivity, the closedness and the skew self-adjointness of the unbounded Nadir's operator on a Hilbert space. We get also when the measurement of its adjointness is null and other related results are also established.
Paper's Title:
Numerical Radius Isometries between Hermitian Banach Algebras
Author(s):
Mohamed Mabrouk and Ashwaq Albideewi
Department of Mathematics,
Faculty of Sciences Cite Erriadh,
University of Gabes,
6072 Zrig, Gabes,
Tunisia.
E-mail: mohamed.mabrouk@fsg.rnu.tn
Department of Mathematics,
College of Applied Sciences,
Umm Al-Qura University,
P. O. Box 715,
Makkah 21955,
Saudi Arabia.
Email: Ashwaq.F.B@hotmail.com
Abstract:
In the case of C*-algebras, the author in [2] showed that any linear unital and surjective numerical radius isometry is a Jordan *-isomorphism. In this paper, we generalize this result to the case of Hermitian Banach algebras.
Paper's Title:
The Influence of Fluid Pressure in Macromechanical Cochlear Model
Author(s):
F. E. Aboulkhouatem1, F. Kouilily1, N. Achtaich1, N. Yousfi1 and M. El Khasmi2
1Department
of Mathematics and Computer Science, Faculty of Sciences
Ben M'sik, Hassan II University, Casablanca,
Morocco.
2Department
of Biology, Faculty of Sciences
Ben M'sik, Hassan II University, Casablanca,
Morocco.
E-mail:
fatiaboulkhouatem@gemail.com
URL: http://www.fsb.univh2c.ma/
Abstract:
An increase of pressure in the structure of cochlea may cause a hearing loss. In this paper, we established the relationship between the fluid pressure and the amplitude of displacement of Basilar Membrane to clarify the mechanisms of hearing loss caused by increasing of this pressure. So, a mathematical cochlear model was formulated using finite difference method in order to explain and demonstrate this malfunction in passive model. Numerical simulations may be considered as helpful tools which may extend and complete the understanding of a cochlea dysfunction.
Paper's Title:
The Jacobson Density Theorem for Non-Commutative Ordered Banach
Algebras
Author(s):
Kelvin Muzundu
University of Zambia,
Deparment of Mathematics and Statistics,
P.O. Box 32379, Lusaka,
Zambia.
E-mail: kmzundu@gmail.com
Abstract:
The Jacobson density theorem for general non-commutative Banach algebras states as follows: Let π be a continuous, irreducible representation of a non-commutative Banach algebra A on a Banach space X. If x1,x2,...,xn are linearly independent in X and if y1,y2,...,yn are in X, then there exists an a∈ A such that π(a)xi=yi for i=1,2,...,n. By considering ordered Banach algebras A and ordered Banach spaces X, we shall establish an order-theoretic version of the Jacobson density theorem.
Paper's Title:
Several Applications of a Local Non-convex Young-type Inequality
Author(s):
Loredana Ciurdariu, Sorin Lugojan
Department of Mathematics,
"Politehnica" University of Timisoara,
P-ta. Victoriei, No.2, 300006-Timisoara,
Romania.
E-mail: ltirtirau87@yahoo.com
Abstract:
A local version of the Young inequality for positive numbers is used in order to deduce some inequalities about determinants and norms for real quadratic matrices and norms of positive operators on complex Hilbert spaces.
Paper's Title:
A Self-adaptive Subgradient Extragradient Algorithm for Variational Inequality Problems and Fixed Point Problems in Banach Spaces
Author(s):
F. U. Ogbuisi
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
Department of Mathematics,
University of Nigeria, Nsukka,
Nigeria.
E-mail: ferdinard.ogbuisi@unn.edu.ng
fudochukwu@yahoo.com
Abstract:
In this paper, we propose and analyze a type of subgradient extragradient algorithm for the approximation of a solution of variational inequality problem which is also a common fixed point of an infinite family of relatively nonexpansive mappings in 2-uniformly convex Banach spaces which are uniformly smooth. By using the generalized projection operator, we prove a strong convergence theorem which does not require the prior knowledge of the Lipschitz constant of cost operator. We further applied our result to constrained convex minimization problem, convex feasibility problem and infinite family of equilibrium problems. Our results improve and complement related results in 2-uniformly convex and uniformly smooth Banach spaces and Hilbert spaces.
Paper's Title:
Construction of a Frame Multiresolution Analysis on Locally Compact Abelian Groups
Author(s):
R. Kumar and Satyapriya
Department of Mathematics,
Kirori Mal College,
University of Delhi,
Delhi,
India.
E-mail: rajkmc@gmail.com
Department of Mathematics,
University of Delhi,
Delhi,
India.
E-mail: kmc.satyapriya@gmail.com
Abstract:
The frame multiresolution analysis (FMRA) on locally compact Abelian groups has been studied and the results concerning classical MRA have been worked upon to obtain new results. All the necessary conditions, which need to be imposed on the scaling function φ to construct a wavelet frame via FMRA, have been summed up. This process of construction of FMRA has aptly been illustrated by sufficient examples.
Paper's Title:
Coexisting Attractors and Bubbling Route to Chaos in Modified Coupled Duffing Oscillators
Author(s):
B. Deruni1, A. S. Hacinliyan1,2, E. Kandiran3, A. C. Keles2, S. Kaouache4, M.-S. Abdelouahab4, N.-E. Hamri4
1Department
of Physics,
University of Yeditepe,
Turkey.
2Department
of Information Systems and Technologies,
University of Yeditepe,
Turkey
3Department
of Software Development,
University of Yeditepe,
Turkey.
4Laboratory
of Mathematics and their interactions,
University Center of Abdelhafid Boussouf,
Mila 43000,
Algeria.
E-mail:
berc890@gmail.com
ahacinliyan@yeditepe.edu.tr
engin.kandiran@yeditepe.edu.tr
cihan.keles@yeditepe.edu.tr
s.kaouache@centr-univ-mila.dz
medsalah3@yahoo.fr
n.hamri@centre-univ-mila.dz
Abstract:
In this article dynamical behavior of coupled Duffing oscillators is analyzed under a small modification. The oscillators have cubic damping instead of linear one. Although single duffing oscillator has complex dynamics, coupled duffing systems possess a much more complex structure. The dynamical behavior of the system is investigated both numerically and analytically. Numerical results indicate that the system has double scroll attractor with suitable parameter values. On the other hand, bifurcation diagrams illustrate rich behavior of the system, and it is seen that, system enters into chaos with different routes. Beside classical bifurcations, bubbling route to chaos is observed for suitable parameter settings. On the other hand, Multistability of the system is indicated with the coexisting attractors, such that under same parameter setting the system shows different periodic and chaotic attractors. Moreover, chaotic synchronization of coupled oscillators is illustrated in final section.
Paper's Title:
Trace Inequalities for Operators in Hilbert Spaces: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
School of Engineering
& Science
Victoria University,
PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
In this paper we survey some recent trace inequalities for operators in Hilbert spaces that are connected to Schwarz's, Buzano's and Kato's inequalities and the reverses of Schwarz inequality known in the literature as Cassels' inequality and Shisha-Mond's inequality. Applications for some functionals that are naturally associated to some of these inequalities and for functions of operators defined by power series are given. Further, various trace inequalities for convex functions are presented including refinements of Jensen inequality and several reverses of Jensen's inequality. Hermite-Hadamard type inequalities and the trace version of Slater's inequality are given. Some Lipschitz type inequalities are also surveyed. Examples for fundamental functions such as the power, logarithmic, resolvent and exponential functions are provided as well.
Paper's Title:
Application of Chebyshev Polynomials to Volterra-Fredholm Integral Equations
Author(s):
Aissa Lakhal, Mostefa Nadir and Mohamed Nasseh Nadir
Department of Mathematics,
Faculty of Mathematics and
Informatics,
University of Msila,
Algeria.
E-mail:
aissa.lakhal@univ-msila.dz
mostefa.nadir@univ-msila.dz
nadir.mohamednasseh@yahoo.com
URL: https://www.mostefanadir.com
Abstract:
The goal of this work is to examine the numerical solution of linear Volterra-Fredholm integral equations of the second kind using the first, second, third and fourth Chebyshev polynomials. Noting that, the approximate solution is given in the form of series which converges to the exact one. Numerical examples are compared with other methods, in order to prove the applicability and the efficiency of this technical.
Paper's Title:
Using Direct and Fixed Point Technique of Cubic Functional Equation and its Hyers-Ulam Stability
Author(s):
Ramanuja Rao Kotti, Rajnesh Krishnan Mudaliar, Kaushal Neelam Devi, Shailendra Vikash Narayan
Fiji National University,
Department of Mathematics & Statistics,
P.O. Box 5529, Lautoka,
Fiji.
E-mail: ramanuja.kotti@fnu.ac.fj
URL: https://www.fnu.ac.fj
Abstract:
In this present work, we introduce a new type of finite dimensional cubic functional equation of the form
where Φ≥4 is an integer, and derive its general solution. The main purpose of this work is to investigate the Hyers-Ulam stability results for the above mentioned functional equation in Fuzzy Banach spaces by means of direct and fixed point methods.
Paper's Title:
The Drazin-star and Star-Drazin Solutions to Quaternion Matrix Equations
Author(s):
Ivan I. Kyrchei, Dijana Mosić, Predrag Stanimirović
Pidstryhach Institute for Applied Problems
of Mechanics and Mathematics
of NAS of Ukraine, L'viv, 79060,
Ukraine.
E-mail:
ivankyrchei26@gmail.com
Faculty of Sciences and Mathematics,
University of Niš, P.O.
Box 224, 18000, Niš, Serbia.
E-mail: dijana@pmf.ni.ac.rs
Faculty of Sciences and Mathematics,
University of Niš, P.O.
Box 224, 18000, Niš, Serbia.
E-mail: pecko@pmf.ni.ac.rs
Abstract:
The notions of the Drazin-star and star-Drazin matrices are expanded to quaternion matrices in this paper. Their determinantal representations are developed in both cases in terms of noncommutative row-column determinants of quaternion matrices and for minors of appropriate complex matrices. We study all possible two-sided quaternion matrix equations with their one-sided partial cases whose uniquely determined solutions are based on the Drazin-star and star-Drazin matrices. Solutions of these equations are represented by Cramer's rules in both cases for quaternion and complex matrix equations. A numerical example is presented to illustrate our results.
Paper's Title:
Dyadic Riesz Wavelets on Local Fields of Positive Characteristics
Author(s):
Kartik Garg, Raj Kumar, Satyapriya
Department of Mathematics,
University of Delhi,
Delhi,
India.
kartikgarg1421@gmail.com,
rajkmc@gmail.com
kmc.satyapriya@gmail.com
Abstract:
In this research paper, we introduce a novel theory for the construction of a Riesz wavelet basis in the space L2(K), where K is a local field with positive characteristics. Our approach is two fold: firstly, we derive some essential characterizations of the scaling function associated with the structure of a Riesz MRA on a local field, and secondly, we review existing methods for constructing wavelet frames in L2(K). We also present a well elaborated example for a better comprehension of our theory. Due to mathematical convenience, we limit ourselves to the case of dyadic dilations only.
Paper's Title:
New Fast Extragradient-like Methods for Non-Lipschitzian Pseudo-monotone Variational Inequalities
Author(s):
Morad Ali Peyvand
Department of Mathematics
Yasouj University
Yasouj,
Iran.
E-mail: peyvand@yu.ac.ir
Abstract:
An efficient double-projection method, with a new search strategy, is designed for solving variational inequalities in real Hilbert spaces with pseudo-monotone cost operator. Our proposed method uses a computationally inexpensive simple line search procedure based on local information of the operator and very weak conditions of parameters to obtain larger step sizes. A description of the algorithm along with its weak convergence is provided without assuming Lipschitz continuity. Also, a modification to the proposed method is presented, wherein the second projection onto the closed and convex subset is replaced with the one onto a subgradient half space. Numerical experiments and comparisons with related methods demonstrate the reliability and benefits of the proposed schemes.
Search and serve lasted 1 second(s).