|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Oscillations of First Order Linear Delay Difference Equations
Author(s):
G. E. Chatzarakis and I. P. Stavroulakis
Department of Mathematics, University of Ioannina,
451 10, Greece
ipstav@cc.uoi.gr
Abstract:
Consider the first order linear delay difference equation of
the form 
where
is
a sequence of nonnegative real numbers, k is a positive integer and 
denotes
the forward difference operator 
New
oscillation criteria are established when the well-known oscillation conditions
and
are
not satisfied. The results obtained essentially improve known results in the
literature.
Paper's Title:
Existence Results for Perturbed Fractional Differential
Inclusions
Author(s):
Y.-K. Chang
Department of Mathematics,
Lanzhou Jiaotong University, Lanzhou, Gansu 730070, People's
Republic of China
lzchangyk@163.com
Abstract:
This paper is mainly concerned with the following fractional differential
inclusions with boundary condition
A sufficient condition is established for the existence of solutions of the
above problem by using a fixed point theorem for multivalued maps due to
Dhage. Our result is proved under the mixed generalized Lipschitz and
Carathéodory conditions.
Paper's Title:
A Geometric Generalization of Busemann-Petty Problem
Author(s):
Liu Rong and Yuan Jun
Shanghai Zhangjiang Group Junior Middle School,
Huo Xiang Road, Shanghai, 201203,
China
Abstract:
The norm defined by Busemann's inequality establishes a class of star body - intersection body. This class of star body plays a key role in the solution of Busemann-Petty problem. In 2003, Giannapoulos [1] defined a norm for a new class of half-section. Based on this norm, we give a geometric generalization of Busemann-Petty problem, and get its answer as a result
Paper's Title:
On Subspace-Supercyclic Operators
Author(s):
Mansooreh Moosapoor
Assistant Professor,
Department of Mathematics,
Farhangian University, Tehran,
Iran.
E-mail: mosapor110@gmail.com
m.mosapour@cfu.ac.ir
Abstract:
In this paper, we prove that supercyclic operators are subspace-supercyclic and by this we give a positive answer to a question posed in ( L. Zhang, Z. H. Zhou, Notes about subspace-supercyclic operators, Ann. Funct. Anal., 6 (2015), pp. 60--68). We give examples of subspace-supercyclic operators that are not subspace-hypercyclic. We state that if T is an invertible supercyclic operator then Tn and T-n is subspace-supercyclic for any positive integer n. We give two subspace-supercyclicity criteria. Surprisingly, we show that subspace-supercyclic operators exist on finite-dimensional spaces.
Paper's Title:
Hermite-Hadamard Type Inequalities for MN-Convex Functions
Author(s):
Sever S. Dragomir1,2
1Mathematics,
College of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
The present work endeavours to briefly present some of the fundamental results connected to the Hermite-Hadamard inequality for special classes of convex functions such as AG, AH, GA, GG, GH, HA, HG and HH -convex functions in which the author have been involved during the last five years. For simplicity, we call these classes of functions such as MN-convex functions, where M and N stand for any of the Arithmetic (A), Geometric (G) or Harmonic (H) weighted means of positive real numbers. The survey is intended for use by both researchers in various fields of Approximation Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
An Integration Technique for Evaluating Quadratic Harmonic Sums
Author(s):
J. M. Campbell and K.-W. Chen
Department of Mathematics and Statistics,
York University, 4700 Keele St, Toronto,
ON M3J 1P3,
Canada.
E-mail: jmaxwellcampbell@gmail.com
Department of Mathematics, University of Taipei,
No. 1, Ai-Guo West Road,
Taipei 10048, Taiwan.
E-mail: kwchen@uTaipei.edu.tw
URL:
https://math.utaipei.edu.tw/p/412-1082-22.php
Abstract:
The modified Abel lemma on summation by parts has been applied in many ways recently to determine closed-form evaluations for infinite series involving generalized harmonic numbers with an upper parameter of two. We build upon such results using an integration technique that we apply to ``convert'' a given evaluation for such a series into an evaluation for a corresponding series involving squared harmonic numbers.
Paper's Title:
Existence of Positive Solutions for
Nonlinear Fractional Differential Equations
with Multi-point Boundary Conditions
Author(s):
N. Adjeroud
Khenchela University, Department of
Mathematics,
Khenchela, 40000,
Algeria.
E-mail: adjnac@gmail.com
Abstract:
This paper is devoted to the existence results of positive solutions for a nonlinear fractional differential equations with multi-point boundary conditions. By means of the Schauder fixed point theorem, some results on the existence are obtained.
Paper's Title:
Cubic Alternating Harmonic Number Sums
Author(s):
Anthony Sofo
Victoria University,
College of Engineering and Science,
Melbourne City,
Australia.
E-mail:
Anthony.Sofo@vu.edu.au
Abstract:
We develop new closed form representations of sums of cubic alternating harmonic numbers and reciprocal binomial coefficients. We also identify a new integral representation for the ζ (4) constant.
Paper's Title:
Fractional exp(-φ(ξ))- Expansion Method and its Application to Space--Time Nonlinear Fractional Equations
Author(s):
A. A. Moussa and L. A. Alhakim
Department of Management Information
System and Production Management,
College of Business and Economics, Qassim University,
P.O. BOX 6666, Buraidah: 51452,
Saudi Arabia.
E-mail: Alaamath81@gmail.com
URL:
https://scholar.google.com/citations?user=ccztZdsAAAAJ&hl=ar
Department of Management Information
System and Production Management,
College of Business and Economics, Qassim University,
P.O. BOX 6666, Buraidah: 51452,
Saudi Arabia.
E-mail: Lama2736@gmail.com
URL:
https://scholar.google.com/citations?user=OSiSh1AAAAAJ&hl=ar
Abstract:
In this paper, we mainly suggest a new method that depends on the fractional derivative proposed by Katugampola for solving nonlinear fractional partial differential equations. Using this method, we obtained numerous useful and surprising solutions for the space--time fractional nonlinear Whitham--Broer--Kaup equations and space--time fractional generalized nonlinear Hirota--Satsuma coupled KdV equations. The solutions obtained varied between hyperbolic, trigonometric, and rational functions, and we hope those interested in the real-life applications of the previous two equations will find this approach useful.
Paper's Title:
Several New Closed-form Evaluations of the Generalized Hypergeometric Function with Argument 1/16
Author(s):
B. R. Srivatsa Kumar, Insuk Kim and Arjun K. Rathie
Department of Mathematics,
Manipal Institute of Technology,
Manipal Academy of Higher Education,
Manipal 576 104,
India.
E-mail: sri_vatsabr@yahoo.com
Department of Mathematics Education,
Wonkwang University,
Iksan, 54538,
Republic of Korea.
E-mail: iki@wku.ac.kr
Department of Mathematics,
Vedant College of Engineering and Technology,
Rajasthan Technical University,
Bundi, 323021, Rajasthan,
India.
E-mail: arjunkumarrathie@gmail.com
Abstract:
The main objective of this paper is to establish as many as thirty new closed-form evaluations of the generalized hypergeometric function q+1Fq(z) for q= 2, 3, 4. This is achieved by means of separating the generalized hypergeometric function q+1Fq(z) for q=1, 2, 3, 4, 5 into even and odd components together with the use of several known infinite series involving central binomial coefficients obtained earlier by Ji and Hei \& Ji and Zhang.
Paper's Title:
A Simple New Proof of Fan-Taussky-Todd Inequalities
Author(s):
Zhi-Hua Zhang and Zhen-Gang Xiao
Zixing Educational Research Section,
Chenzhou City, Hunan 423400, P. R. China.
Zhi-hua Zhang
Url: http://www.hnzxslzx.com/zzhweb/
Department Of Mathematics, Hunan Institute Of Science And Technology,
Yueyang City, Hunan 423400, P. R. China.
Zhen-gang Xiao
Abstract:
In this paper we present simple new proofs of the inequalities:
which holds for all real numbers a0 = 0, a1, ˇ ˇ ˇ , an, an+1 = 0 and the coefficients
2(1 - cos(π/(n + 1))) and 2(1 + cos(π/(n + 1))) are the best possible; and
which holds for all real numbers a0 = 0, a1, ˇ ˇ ˇ , an and the coefficients
2(1-cos(π/(2n + 1))) and 2(1 + cos(π/(2n + 1))) are the best possible.
Paper's Title:
On Pseudo Almost
Periodic Solutions to Some Neutral Functional-Differential
Equations
Author(s):
Toka Diagana and Eduardo Hernández
Department of Mathematics, Howard University
2441 6th Street NW,
Washington DC 20059,
USA.
tdiagana@howard.edu
Departamento de Matemática, I.C.M.C. Universidade de Săo Paulo,
Caixa Postal
668, 13560-970, Săo Carlos SP,
Brazil.
lalohm@icmc.sc.usp.br
Abstract:
This paper discusses the existence and uniqueness of pseudo almost periodic solutions to a class of partial neutral functional-differential equations. Under some suitable assumptions, existence and uniqueness results are obtained. An example is given to illustrate abstract results.
Paper's Title:
On Oscillation of
Second-Order Delay Dynamic Equations on Time Scales
Author(s):
S. H. Saker
Department of Mathematics, Faculty of Science,
Mansoura University, Mansoura, 35516,
Egypt.
shsaker@mans.edu.eg
Abstract:
Some new oscillation criteria for second-order linear delay dynamic equation
on a time scale T are established. Our results improve the
recent results for delay dynamic equations and in the special case when
T=R, the results include the oscillation results established by Hille [1948,
Trans. Amer. Math. Soc. 64 (1948), 234-252] and Erbe [Canad. Math. Bull. 16
(1973), 49-56.] for differential equations. When T=Z the
results include and improve some oscillation criteria for difference
equations. When T=hZ, h>0, T=qN and T=N2, i.e., for generalized second order delay difference equations our
results are essentially new and can be applied on different types of time
scales. An example is considered to illustrate the main results.
Paper's Title:
On Some Remarkable Product of Theta-function
Author(s):
M. S. Mahadeva Naika, M. C. Maheshkumar and K. Sushan Bairy
Department of Mathematics,
Bangalore University, Central College Campus,
Bangalore-560 001,
INDIA
msmnaika@rediffmail.com
softmahe@rediffmail.com
ksbairy@gmail.com
Abstract:
On pages 338 and 339 in his first notebook, Ramanujan records
eighteen values for a certain product of theta-function. All these
have been proved by B. C. Berndt, H. H. Chan and L-C. Zhang
[4]. Recently M. S. Mahadeva Naika and B. N. Dharmendra
[7,
8] and Mahadeva Naika and M. C. Maheshkumar
[9] have obtained general theorems to establish explicit
evaluations of Ramanujan's remarkable product of theta-function.
Following Ramanujan we define a new function bM,N as
defined in (1.5). The main purpose of this paper is to
establish some new general theorems for explicit evaluations of
product of theta-function.
Paper's Title:
Positive Periodic Solutions for
Second-Order Differential Equations with Generalized Neutral Operator
Author(s):
Wing-Sum Cheung, Jingli Ren and Weiwei Han
Department of Mathematics,
The University of Hong Kong
Pokfulam
Road,
Hong Kong
Department of Mathematics, Zhengzhou University
Zhengzhou 450001,
P.R. China
wscheung@hkucc.hku.hk
renjl@zzu.edu.cn
Abstract:
By some analysis of the neutral operator
and an application of the fixed-point
index theorem, we obtain sufficient conditions for the existence,
multiplicity and nonexistence of periodic solutions to a second-order
differential equation with the prescribed neutral operator, which improve
and extend some recent results of Lu-Ge, Wu-Wang, and Zhang. An example is
given to illustrate our results. Moreover, the analysis of the generalized
neutral operator will be helpful for other types of differential equations.
Paper's Title:
New Implicit Kirk-Type Schemes for General Class of Quasi-Contractive Operators in Generalized Convex Metric Spaces
Author(s):
K. Rauf, O. T. Wahab and A. Ali
Department of Mathematics,
University of Ilorin, Ilorin,
Nigeria.
E-mail: krauf@unilorin.edu.ng
Department of Statistics and Mathematical
Sciences,
Kwara State University, Malete,
Nigeria.
Department of Mathematics,
Mirpur University of Science and Technology, Mirpur,
Pakistan.
Abstract:
In this paper, we introduce some new implicit Kirk-type iterative schemes in generalized convex metric spaces in order to approximate fixed points for general class of quasi-contractive type operators. The strong convergence, T-stability, equivalency, data dependence and convergence rate of these results were explored. The iterative schemes are faster and better, in term of speed of convergence, than their corresponding results in the literature. These results also improve and generalize several existing iterative schemes in the literature and they provide analogues of the corresponding results of other spaces, namely: normed spaces, CAT(0) spaces and so on.
Paper's Title:
Uniqueness Problems for Difference Polynomials Sharing a Non-Zero Polynomial of Certain Degree With Finite Weight
Author(s):
V. Priyanka, S. Rajeshwari and V. Husna
Department of Mathematics,
School of Engineering,
Presidency University,
Bangalore-560064,
India.
E-mail:
priyapriyankaram1994@gmail.com
rajeshwaripreetham@gmail.com
husnav43@gmail.com
Abstract:
In this paper, we prove a result on the value distribution of difference polynomials sharing higher order derivatives of meromorphic functions which improves some earlier results. At the same time, we also prove possible uniqueness relation of entire functions when the difference polynomial generated by them sharing a non zero polynomial of certain degree. The result obtained in the paper will improve and generalize a number of recent results in a compact and convenient way.
Paper's Title:
SQIRV Model for Omicron Variant with Time Delay
Author(s):
S. Dickson, S. Padmasekaran, G. E. Chatzarakis and S. L. Panetsos
Mathematics, Periyar University, Periyar
Palkalai Nagar, Salem,
636011, Tamilnadu,
India.
E-mail:
dickson@periyaruniversity.ac.in,
padmasekarans@periyaruniversity.ac.in
Electrical and Electronic Engineering
Educators, School of
Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
spanetsos@aspete.gr
Abstract:
In order to examine the dynamics of the Omicron variant, this paper uses mathematical modelling and analysis of a SQIRV model, taking into account the delay in the conversion of susceptible individuals into infected individuals and infected individuals into recovered individuals. The pandemic was eventually controlled as a result of the massive delays. To assure the safety of the host population, this concept incorporates quarantine and the COVID-19 vaccine. Both local and global stability of the model are examined. It is found that the fundamental reproduction number affects both local and global stability conditions. Our findings show that asymptomatic cases caused by an affected population play an important role in increasing Omicron infection in the general population. The most recent data on the pandemic Omicron variant from Tamil Nadu, India, is verified.
Paper's Title:
Higher Order Accurate Compact Schemes for Time Dependent Linear and Nonlinear Convection-Diffusion Equations
Author(s):
S. Thomas, Gopika P.B. and S. K. Nadupuri
Department of Mathematics
National Institute of Technology Calicut
Kerala
673601
India.
E-mail:
sobinputhiyaveettil@gmail.com
pbgopika@gmail.com nsk@nitc.ac.in
Abstract:
The primary objective of this work is to study higher order compact finite difference schemes for finding the numerical solution of convection-diffusion equations which are widely used in engineering applications. The first part of this work is concerned with a higher order exponential scheme for solving unsteady one dimensional linear convection-diffusion equation. The scheme is set up with a fourth order compact exponential discretization for space and cubic $C^1$-spline collocation method for time. The scheme achieves fourth order accuracy in both temporal and spatial variables and is proved to be unconditionally stable. The second part explores the utility of a sixth order compact finite difference scheme in space and Huta's improved sixth order Runge-Kutta scheme in time combined to find the numerical solution of one dimensional nonlinear convection-diffusion equations. Numerical experiments are carried out with Burgers' equation to demonstrate the accuracy of the new scheme which is sixth order in both space and time. Also a sixth order in space predictor-corrector method is proposed. A comparative study is performed of the proposed schemes with existing predictor-corrector method. The investigation of computational order of convergence is presented.
Paper's Title:
Positive Periodic Time-Scale Solutions for Functional Dynamic Equations
Author(s):
Douglas R. Anderson and Joan Hoffacker
Department of Mathematics and Computer Science
Concordia College
Moorhead, MN 56562 USA
andersod@cord.edu
URL: http://www.cord.edu/faculty/andersod/
Department of Mathematical Sciences
Clemson University
Clemson, SC 29634 USA
johoff@clemson.edu
URL: http://www.math.clemson.edu/facstaff/johoff.htm
Abstract:
Using Krasnoselskii's fixed point theorem, we establish the existence of positive periodic solutions
to two pairs of related nonautonomous functional delta dynamic equations on periodic time scales, and then extend the discussion to higher-dimensional equations. Two pairs of corresponding nabla equations
are also provided in an analogous manner.
Paper's Title:
Generalized Quasilinearization Method for the Forced Düffing Equation
Author(s):
Ramzi S. N. Alsaedi
Department of Mathematics, King Abdul Aziz University,
Jeddah P.O. Box 80203,
Saudi Arabia.
ramzialsaedi@yahoo.co.uk
Abstract:
A generalized quasilinearization method for the periodic
problem related to the forced D\"{u}ffing equation is developed and a
sequence of approximate solutions converging monotonically and quadratically
to the solution of the given problem is presented.
Paper's Title:
Asymptotic Distribution of Products of Weighted Sums of Dependent
Random Variables
Author(s):
Y. Miao and J. F. Li
College
of Mathematics
and Information
Science,
Henan Normal
University
Henan,
China
yumiao728@yahoo.com.cn
College
of Mathematics
and Information
Science,
Henan Normal
University, 453007
Henan,
China.
junfen_li@yahoo.com.cn
Abstract:
In this paper we establish the asymptotic distribution of products of weighted sums of dependent positive random variable, which extends the results of Rempała and Wesołowski (2002).
Paper's Title:
Nontrivial Solutions of Singular Superlinear Three-point
Boundary Value Problems at Resonance
Author(s):
Feng Wang, Fang Zhang
School of Mathematics and Physics,
Changzou University,
Changzhou, 213164,
China.
fengwang188@163.com
Abstract:
The singular superlinear second order three-point boundary value problems at resonance
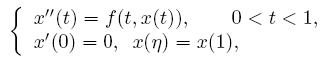
are considered under some conditions concerning the first eigenvalues corresponding to the relevant linear operators, where n ∈ (0,1) is a constant, f is allowed to be singular at both t=0 and t=1. The existence results of nontrivial solutions are given by means of the topological degree theory.
Paper's Title:
On A Conjecture of A Logarithmically Completely Monotonic Function
Author(s):
Valmir Krasniqi, Armend Sh. Shabani
Department of Mathematics,
University of Prishtina,
Republic of Kosova
E-mail:
vali.99@hotmail.com
armend_shabani@hotmail.com
Abstract:
In this short note we prove a conjecture, related to a logarithmically completely monotonic function, presented in [5]. Then, we extend by proving a more generalized theorem. At the end we pose an open problem on a logarithmically completely monotonic function involving q-Digamma function.
Paper's Title:
Credibility Based Fuzzy Entropy Measure
Author(s):
G. Yari, M. Rahimi, B. Moomivand and P. Kumar
Department of Mathematics,
Iran University
of Science and Technology,
Tehran,
Iran.
E-mail:
Yari@iust.ac.ir
E-mail:
Mt_Rahimi@iust.ac.ir
URL:
http://www.iust.ac.ir/find.php?item=30.11101.20484.en
URL:
http://webpages.iust.ac.ir/mt_rahimi/en.html
Qarzol-hasaneh
Mehr Iran Bank, Tehran,
Iran.
E-mail:
B.moomivand@qmb.ir
Department of Mathematics and Statistics,
University of Northern British Columbia,
Prince George, BC,
Canada.
E-mail:
Pranesh.Kumar@unbc.ca
Abstract:
Fuzzy entropy is the entropy of a fuzzy variable, loosely representing the information of uncertainty. This paper, first examines both previous membership and credibility based entropy measures in fuzzy environment, and then suggests an extended credibility based measure which satisfies mostly in Du Luca and Termini axioms. Furthermore, using credibility and the proposed measure, the relative entropy is defined to measure uncertainty between fuzzy numbers. Finally we provide some properties of this Credibility based fuzzy entropy measure and to clarify, give some examples.
Paper's Title:
New Refinements of Hölder's Inequality
Author(s):
Xiu-Fen Ma
College of Mathematical and Computer,
Chongqing Normal University Foreign Trade and Business College,
No.9 of Xuefu Road, Hechuan District 401520,
Chongqing City,
The People's Republic of China.
E-mail: maxiufen86@163.com
Abstract:
In this paper, we define two mappings, investigate their properties, obtain some new refinements of Hölder's inequality.
Paper's Title:
Mapped Chebyshev Spectral Methods for Solving Second Kind Integral Equations on the Real Line
Author(s):
Ahmed Guechi and Azedine Rahmoune
Department of Mathematics, University of Bordj Bou Arréridj,
El Anasser, 34030, BBA,
Algeria.
E-mail: a.guechi2017@gmail.com
E-mail: a.rahmoune@univ-bba.dz
Abstract:
In this paper we investigate the utility of mappings to solve numerically an important class of integral equations on the real line. The main idea is to map the infinite interval to a finite one and use Chebyshev spectral-collocation method to solve the mapped integral equation in the finite interval. Numerical examples are presented to illustrate the accuracy of the method.
Paper's Title:
Convergence Speed of Some Random Implicit-Kirk-type Iterations for Contractive-type Random Operators
Author(s):
H. Akewe, K.S. Eke
Department of Mathematics,
Covenant University,
Canaanland, KM 10, Idiroko Road, P. M. B. 1023, Ota, Ogun State,
Nigeria.
E-mail: hudson.akewe@covenantuniversity.edu.ng,
kanayo.eke@covenantuniversity.edu.ng
Abstract:
The main aim of this paper is to introduce a stochastic version of multistep type iterative scheme called a modified random implicit-Kirk multistep iterative scheme and prove strong convergence and stability results for a class of generalized contractive-type random operators. The rate of convergence of the random iterative schemes are also examined through an example. The results show that our new random implicit kirk multistep scheme perform better than other implicit iterative schemes in terms of convergence and thus have good potentials for further applications in equilibrium problems in computer science, physics and economics.
Paper's Title:
Global Analysis on Riemannian Manifolds
Author(s):
Louis Omenyi and Michael Uchenna
Department of Mathematics, Computer
Science, Statistics and Informatics,
Alex Ekwueme Federal University, Ndufu-Alike,
Nigeria.
E-mail: omenyi.louis@funai.edu.ng,
michael.uchenna@funai.edu.ng
URL: http://www.funai.edu.ng
Abstract:
In this paper, an exposition of the central concept of global analysis on a Riemannan manifold is given. We extend the theory of smooth vector fields from open subsets of Euclidean space to Riemannan manifolds. Specifically, we prove that a Riemannian manifold admits a unique solution for a system of ordinary differential equations generated by the flow of smooth tangent vectors. The idea of partial differential equations on Riemannian manifold is highlighted on the unit sphere.
Paper's Title:
Oscillatory Behavior of Second-Order Non-Canonical
Retarded Difference Equations
Author(s):
G.E. Chatzarakis1, N. Indrajith2, E. Thandapani3 and K.S. Vidhyaa4
1Department
of Electrical and Electronic Engineering Educators,
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail: gea.xatz@aspete.gr,
geaxatz@otenet.gr
2Department
of Mathematics,
Presidency College, Chennai - 600 005,
India.
E-mail: indrajithna@gmail.com
3Ramanujan
Institute for Advanced Study in Mathematics,
University of Madras,
Chennai - 600 005,
India.
E-mail: ethandapani@yahoo.co.in
4
Department of Mathematics,Abstract:
Using monotonic properties of nonoscillatory solutions, we obtain new oscillatory criteria for the second-order non-canonical difference equation with retarded argument
Our oscillation results improve and extend the earlier ones. Examples illustrating the results are provided.
Paper's Title:
Improved Oscillation Criteria of Second-Order Advanced Non-canonical Difference Equation
Author(s):
G. E. Chatzarakis1, N. Indrajith2, S. L. Panetsos1, E. Thandapani3
1Department
of Electrical and Electronic Engineering Educators
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail: gea.xatz@aspete.gr,
geaxatz@otenet.gr
spanetsos@aspete.gr
2Department
of Mathematics,
Presidency College, Chennai - 600 005,
India.
E-mail: indrajithna@gmail.com
3Ramanujan
Institute for Advanced Study in Mathematics,
University of Madras Chennai - 600 005,
India.
E-mail: ethandapani@yahoo.co.in
Abstract:
Employing monotonic properties of nonoscillatory solutions, we derive some new oscillation criteria for the second-order advanced non-canonical difference equation
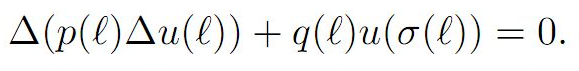
Our results extend and improve the earlier ones. The outcome is illustrated via some particular difference equations.
Paper's Title:
Conservativeness Criteria of Girsanov Transformation for Non-Symmetric Jump-diffusion
Author(s):
Mila Kurniawaty
DDepartment of Mathematics,
Universitas Brawijaya, Malang,
Indonesia.
E-mail: mila_n12@ub.ac.id
Abstract:
We develop the condition in our previous paper [The Conservativeness of Girsanov transformed for symmetric jump-diffusion process (2018)] in the framework of nonsymmetric Markov process with jumps associated with regular Dirichlet form. We prove the conservativeness of it by relation in duality of Girsanov transformed process and recurrent criteria of Dirichlet form.
Paper's Title:
Constraint Qualifications for Multiobjective Programming Problems on Hadamard Manifolds
Author(s):
Arnav Ghosh, Balendu Bhooshan Upadhyay and I.M. Stancu-Minasian
Department of Mathematics,
Indian Institute of Technology Patna,
Patna,
India.
E-mail: arnav_2021ma09@iitp.ac.in
Department of Mathematics,
Indian Institute of Technology Patna,
Patna,
India.
E-mail: bhooshan@iitp.ac.in
"Gheorghe Mihoc-Caius Iacob" Institute of
Mathematical Statistics and Applied Mathematics of the Romanian Academy,
Bucharest,
Romania.
E-mail: stancu_minasian@yahoo.com
Abstract:
The study of optimization methods on manifolds has emerged as an immensely significant topic in mathematics due its ubiquitous applicability as well as various computational advantages associated with it. Motivated by this fact, the present article is devoted to the study of a class of constrained multiobjective programming problems (MOPP) in the framework of Hadamard manifolds. We present the generalized Guignard constraint qualification (GGCQ) in the framework of Hadamard manifolds for (MOPP). Employing (GGCQ), we derive Karush-Kuhn-Tucker type necessary optimality criteria for (MOPP). Moreover, we present several other constraint qualifications (CQs) on Hadamard manifolds, namely, Abadie's CQ, generalized Abadie's CQ, Cottle-type CQ, Slater-type CQ, linear CQ, linear objective CQ and Mangasarian-Fromovitz CQ. Further, we establish various relations between these constraint qualifications. In particular, we show that these constraint qualifications, in turn, become sufficient conditions ensuring that (GGCQ) is satisfied.
Paper's Title:
A General Fractional Control Scheme for Compound Combination Synchronization Between Different Fractional-Order Identical Chaotic Systems
Author(s):
Soumia Bensimessaoud and Smail Kaouache
Laboratory of Mathematics and their interactions, Abdelhafid Boussouf University Center, Mila, Algeria.
E-mail:
soumiabensimessaoud@gmail.com,
smailkaouache@gmail.com
Abstract:
In this paper, we aim to investigate the problem of compound combination synchronization (CCS) between four different fractional-order identical chaotic systems. Based on Laplace transformation and stability theory of linear dynamical systems, a new control law is proposed to assure the achievement of this kind of synchronization. Secondly, this control scheme is applied to realised CCS between four identical unified chaotic systems. Recall, that the proposed control scheme can be applied to wide classes of chaotic and hyperchaotic systems. Numerical simulations are given to show the effectiveness of the proposed method.
Paper's Title:
The Drazin-star and Star-Drazin Solutions to Quaternion Matrix Equations
Author(s):
Ivan I. Kyrchei, Dijana Mosić, Predrag Stanimirović
Pidstryhach Institute for Applied Problems
of Mechanics and Mathematics
of NAS of Ukraine, L'viv, 79060,
Ukraine.
E-mail:
ivankyrchei26@gmail.com
Faculty of Sciences and Mathematics,
University of Ni, P.O.
Box 224, 18000, Ni, Serbia.
E-mail: dijana@pmf.ni.ac.rs
Faculty of Sciences and Mathematics,
University of Ni, P.O.
Box 224, 18000, Ni, Serbia.
E-mail: pecko@pmf.ni.ac.rs
Abstract:
The notions of the Drazin-star and star-Drazin matrices are expanded to quaternion matrices in this paper. Their determinantal representations are developed in both cases in terms of noncommutative row-column determinants of quaternion matrices and for minors of appropriate complex matrices. We study all possible two-sided quaternion matrix equations with their one-sided partial cases whose uniquely determined solutions are based on the Drazin-star and star-Drazin matrices. Solutions of these equations are represented by Cramer's rules in both cases for quaternion and complex matrix equations. A numerical example is presented to illustrate our results.
Paper's Title:
Multivalued Equilibrium Problems with Trifunction
Author(s):
Muhammad Aslam Noor
Etisalat College of Engineering, P.O. Box 980, Sharjah, United Arab Emirates
noor@ece.ac.ae
Abstract:
In this paper, we use the auxiliary principle technique to
suggest some new classes of iterative algorithms for solving multivalued
equilibrium problems with trifunction. The convergence of the proposed methods
either requires partially relaxed strongly monotonicity or pseudomonotonicity.
As special cases, we obtain a number of known and new results for solving
various classes of equilibrium and variational inequality problems. Since
multivalued equilibrium problems with trifunction include equilibrium,
variational inequality and complementarity problems as specials cases, our
results continue to hold for these problems.
Paper's Title:
Fekete-Szegö Inequality for Certain Class of Analytic Functions
Author(s):
V. Ravichandran, Maslina Darus, M. Hussain Khan, and K. G. Subramanian
School of
Mathematical Sciences, Universiti Sains Malaysia,
11800 Usm, Penang, Malaysia
vravi@cs.usm.my
School of
Mathematical Sciences, Faculty of Sciences and Technology,
Ukm, Banki 43600, Malaysia
maslina@pkrisc.cc.ukm.my
Department of
Mathematics, Islamiah College,
Vaniambadi 635 751, India
Department of
Mathematics, Madras Christian College, Tambaram,
Chennai- 600 059, India
kgsmani@vsnl.net
Abstract:
In this present investigation, the authors obtain Fekete-Szegö inequality for a certain
class of analytic functions f(z) for which
lies in a
region starlike with respect to 1 and symmetric with respect to the real axis. Also certain application
of our main result for a class of functions defined by Hadamard product (convolution) is
given. As a special case of our result we obtain Fekete-Szegö inequality for a class of functions
defined through fractional derivatives. Also we obtain Fekete-Szegö inequality for the inverse
functions.
Paper's Title:
On the Fekete-Szeg
Author(s):
T.N. Shanmugam and A. Singaravelu
Department of Mathematics,
Department of Mathematics,
College of Engineering,
Anna University, Chennai-600 025,
Tamilnadu, India
shan@annauniv.edu
Valliammai Engineering College,
Chennai-603 203,
Tamilnadu, India
sivasaisastha@rediffmail.com
Abstract:
In this present investigation, the authors obtainFekete-Szegő's inequality for certain normalized analytic functions 
defined on the open
unit disk for which 
lie in a region starlike with
respect to 1 and symmetric with respect
to the real axis. Also certain applications of the main result for a class of functions
defined by convolution are given. As a special case of this result, Fekete-Szegő's inequality for a class of functions
defined through fractional derivatives is also obtained.
Paper's Title:
A New Step Size Rule in Noor's Method for Solving General Variational Inequalities
Author(s):
Abdellah Bnouhachem
School of Management Science and Engineering, Nanjing University,
Nanjing, 210093
P.R. China.
babedallah@yahoo.com
Abstract:
In this paper, we propose a new step size rule in Noor's method
for solving general
variational inequalities. Under suitable conditions, we prove that the
new method is globally convergent. Preliminary numerical
experiments are included to illustrate the advantage and
efficiency of the proposed method.
Paper's Title:
Local and Global Existence and Uniqueness Results for Second and Higher Order Impulsive Functional Differential Equations with Infinite Delay
Author(s):
Johnny Henderson and Abdelghani Ouahab
Department of Mathematics, Baylor University,
Waco, Texas 76798-7328
USA.
Johnny_Henderson@baylor.edu
Laboratoire de Mathématiques, Université de Sidi Bel Abbés
BP 89, 22000 Sidi Bel Abbées,
Algérie.
ouahab@univ-sba.dz
Abstract:
In this paper, we discuss the local and global existence and
uniqueness results for second and higher order impulsive functional
differential equations with infinite delay. We shall rely on a
nonlinear alternative of Leray-Schauder. For the global existence
and uniqueness we apply a recent Frigon and Granas nonlinear
alternative of Leray-Schauder type in Fréchet spaces.
Paper's Title:
An Approximation of Jordan Decomposable Functions for a Lipschitz Function
Author(s):
Ibraheem Alolyan
Mathematics Department,
College of Science, King Saud University
P.O.Box: 2455, Riyadh 11451,
Saudi Arabia
ialolyan05@yahoo.com
Abstract:
The well known Jordan decomposition theorem gives the useful characterization that any function of bounded variation can be written as the difference of two increasing functions. Functions which can be expressed in this way can be used to formulate an exclusion test for the recent Cellular Exclusion Algorithms for numerically computing all zero points or the global minima of functions in a given cellular domain [2,8,9]. In this paper we give an algorithm to approximate such increasing functions when only the values of the function of bounded variation can be computed. For this purpose, we are led to introduce the idea of ε-increasing functions. It is shown that for any Lipschitz continuous function, we can find two ε-increasing functions such that the Lipschitz function can be written as the difference of these functions.
Paper's Title:
On the Asymptotic Behavior of Solutions of Third Order Nonlinear Differential Equations
Author(s):
Ivan Mojsej and Alena Tartaľová
Institute of Mathematics,
Faculty of Science, P. J. afárik University,
Jesenná 5, 041 54 Koice,
Slovak Republic
ivan.mojsej@upjs.sk
Department of Applied Mathematics and Business Informatics,
Faculty of Economics,
Technical University,
Nemcovej 32, 040 01 Koice,
Slovak Republic
alena.tartalova@tuke.sk
Abstract:
This paper is concerned with the asymptotic behavior of solutions of nonlinear differential equations of the
third order with quasiderivatives. Mainly, we present the necessary and sufficient conditions for the existence
of nonoscillatory solutions with specified asymptotic behavior as Paper's Title:
Equilibria and Periodic Solutions of Projected Dynamical Systems on Sets with Corners
Author(s):
Matthew D. Johnston and Monica-Gabriela Cojocaru
Department of Applied Mathematics, University of Waterloo,
Department of Mathematics & Statistics, University of
Guelph, Abstract:
Projected dynamical systems theory represents a bridge between the
static worlds of variational inequalities and equilibrium
problems, and the dynamic world of ordinary differential
equations. A projected dynamical system (PDS) is given by the flow
of a projected differential equation, an ordinary differential
equation whose trajectories are restricted to a constraint set
K. Projected differential equations are defined by discontinuous
vector fields and so standard differential equations theory cannot
apply. The formal study of PDS began in the 90's, although some
results existed in the literature since the 70's. In this paper we
present a novel result regarding existence of equilibria and
periodic cycles of a finite dimensional PDS on constraint sets
K, whose points satisfy a corner condition. The novelty is due
to proving existence of boundary equilibria without using a
variational inequality approach or monotonicity type conditions. Paper's Title:
Fekete-Szegö Problem for Univalent Functions with Respect to k-Symmetric
Points Author(s):
K. Al-Shaqsi and M. Darus
School of Mathematical Sciences, Faculty of Science and Technology, Abstract:
In the present investigation, sharp upper bounds of |a3- μa22|
for functions f(z) = z + a2z2 + a2z3 + ... belonging to certain subclasses
of starlike and convex functions with respect to k-symmetric points are
obtained. Also certain applications of the main results for subclasses of
functions defined by convolution with a normalized analytic function are
given. In particular, Fekete- Szeg
1: Paper Source
PDF document
Ontario, Canada
mdjohnst@math.uwaterloo.ca
Ontario, Canada
mcojocar@uoguelph.ca
1: Paper Source
PDF document
University Kebangsaan Malaysia,
Bangi 43600 Selangor D. Ehsan,
Malaysia
ommath@hotmail.com
maslina@ukm.my
Paper's Title:
On a Method of Proving the Hyers-Ulam Stability
of Functional Equations on Restricted Domains
Author(s):
Janusz Brzdęk
Department of Mathematics
Pedagogical University Podchor
Abstract:
We show that generalizations of some (classical) results on the Hyers-Ulam stability of functional equations, in several variables, can be very easily derived from a simple result on stability of a functional equation in single variable
Paper's Title:
Applications of Relations and Relators in the
Extensions of Stability Theorems for Homogeneous and Additive Functions
Author(s):
Árpád Száz
Institute of Mathematics, University of Debrecen,
H-4010 Debrecen,
Pf. 12,
Hungary
szaz@math.klte.hu
Abstract:
By working out an appropriate technique of relations and relators and extending the ideas of the direct methods of Z. Gajda and R. Ger, we prove some generalizations of the stability theorems of D. H. Hyers, T. Aoki, Th. M. Rassias and P. Găvruţă in terms of the existence and unicity of 2-homogeneous and additive approximate selections of generalized subadditive relations of semigroups to vector relator spaces. Thus, we obtain generalizations not only of the selection theorems of Z. Gajda and R. Ger, but also those of the present author.
Paper's Title:
Existence Results for Second Order Impulsive Functional Differential Equations with Infinite Delay
Author(s):
M. Lakrib, A. Oumansour and K. Yadi
Laboratoire de Mathématiques, Université Djillali
Liabées, B.P. 89 Sidi Bel Abbčs 22000, Algérie
mlakrib@univ-sba.dz
oumansour@univ-sba.dz
Laboratoire de Mathématiques, Université Abou Bekr
Belkaid, B.P. 119 Tlemcen 13000, Algérie
k_yadi@mail.univ-tlemcen.dz
Abstract:
In this paper we study the existence of solutions for second order impulsive functional differential equations with infinite delay. To obtain our results, we apply fixed point methods.
Paper's Title:
Some New Nonlinear Integro-Differential Inequalities of Gronwall-Bellman-Pachpatte Type
Author(s):
A. ABDELDAIM
Department of Mathematics and Computer
Sciences,
Faculty of Science,
Port Said University, Port Said,
EGYPT.
Department of Mathematics,
Faculty of Science and Humanities,
Shaqra University, Dawadmi,
SAUDI ARABIA.
E-mail:
ahassen@su.edu.sa
URL:
http://faculty.ksu.edu.sa/DRABDELDAIM/Pages/Home.aspx
Abstract:
In this paper we establish some new nonlinear integro-differential inequalities of Gronwall-Bellman-Pachpatte type for function of one independent variable. The purpose of this paper is to extend certain results which proved by Pachpatte in [On some fundamental integrodifferential and integral inequalities, An. Sti. Univ. Al. I. Cuza, Iasi, Vol.23 (1977), 77-86]. The inequalities obtained here can be used in the theory of some new classes of nonlinear integro-differential equations. Some applications are also given to illustrate the usefulness of our results.
Paper's Title:
Stability of an Almost Surjective epsilon-Isometry in The Dual of Real Banach Spaces
Author(s):
Minanur Rohman, Ratno Bagus Edy Wibowo, Marjono
Department of Mathematics, Faculty of
Mathematics and Natural Sciences,
Brawijaya University,
Jl. Veteran Malang 65145,
Indonesia.
E-mail:
miminanira@gmail.com
Department of Mathematics, Faculty of
Mathematics and Natural Sciences,
Brawijaya University,
Jl. Veteran Malang 65145,
Indonesia.
E-mail:
rbagus@ub.ac.id
Department of Mathematics, Faculty of
Mathematics and Natural Sciences,
Brawijaya University,
Jl. Veteran Malang 65145,
Indonesia.
E-mail:
marjono@ub.ac.id
Abstract:
In this paper, we study the stability of epsilon-isometry in the dual of real Banach spaces. We prove that the almost surjective epsilon-isometry mapping is stable in dual of each spaces. The proof uses Gâteaux differentiability space (GDS), weak-star exposed points, norm-attaining operator, and some studies about epsilon-isometry that have been done before.
Paper's Title:
Wavelet Frames in Higher Dimensional Sobolev Spaces
Author(s):
Raj Kumar, Manish Chauhan, and Reena
Department of Mathematics,
Kirori Mal College, University of Delhi,
New Delhi-110007,
India.
E-mail: rajkmc@gmail.com
Department of Mathematics,
University of Delhi,
New Delhi-110007,
India
E-mail: manish17102021@gmail.com
Department of Mathematics,
Hans Raj College, University of Delhi,
New Delhi-110007,
India
E-mail: reena.bhagwat29@gmail.com
Abstract:
In this paper, we present sufficient condition for the sequence
of vectors
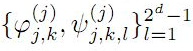to be a frame for Hs(Rd) are derived. Necessary and
sufficient conditions for the sequence of vectors
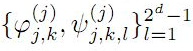to be tight wavelet frames in Hs(Rd) are obtained.
Further, as an application an example of tight wavelet frames for Hs(R2) as bivariate box spline over 3-direction are given.
Paper's Title:
A Self-adaptive Subgradient Extragradient Algorithm for Variational Inequality Problems and Fixed Point Problems in Banach Spaces
Author(s):
F. U. Ogbuisi
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
Department of Mathematics,
University of Nigeria, Nsukka,
Nigeria.
E-mail: ferdinard.ogbuisi@unn.edu.ng
fudochukwu@yahoo.com
Abstract:
In this paper, we propose and analyze a type of subgradient extragradient algorithm for the approximation of a solution of variational inequality problem which is also a common fixed point of an infinite family of relatively nonexpansive mappings in 2-uniformly convex Banach spaces which are uniformly smooth. By using the generalized projection operator, we prove a strong convergence theorem which does not require the prior knowledge of the Lipschitz constant of cost operator. We further applied our result to constrained convex minimization problem, convex feasibility problem and infinite family of equilibrium problems. Our results improve and complement related results in 2-uniformly convex and uniformly smooth Banach spaces and Hilbert spaces.
Paper's Title:
Reduced Generalized Combination Synchronization Between Two n-Dimensional Integer-Order Hyperchaotic Systems and One m-Dimensional Fractional-Order Chaotic System
Author(s):
Smail Kaouache, Mohammed Salah Abdelouahab and Rabah Bououden
Laboratory of Mathematics and their
interactions,
Abdelhafid Boussouf University Center, Mila.
Algeria
E-mail: smailkaouache@gmail.com,
medsalah3@yahoo.fr,
rabouden@yahoo.fr
Abstract:
This paper is devoted to investigate the problem of reduced generalized combination synchronization (RGCS) between two n-dimensional integer-order hyperchaotic drive systems and one m-dimensional fractional-order chaotic response system. According to the stability theorem of fractional-order linear system, an active mode controller is proposed to accomplish this end. Moreover, the proposed synchronization scheme is applied to synchronize three different chaotic systems, which are the Danca hyperchaotic system, the modified hyperchaotic Rossler system, and the fractional-order Rabinovich-Fabrikant chaotic system. Finally, numerical results are presented to fit our theoretical analysis.
Paper's Title:
Existence and Approximation of Traveling Wavefronts for the Diffusive Mackey-Glass Equation
Author(s):
C. Ramirez-Carrasco and J. Molina-Garay
Facultad de Ciencias Basicas,
Universidad Catolica del Maule, Talca,
Chile
E-mail: carloshrc1989@gmail.com
molina@imca.edu.pe
Abstract:
In this paper, we consider the diffusive Mackey-Glass model with discrete delay. This equation describes the dynamics of the blood cell production. We investigate the existence of traveling wavefronts solutions connecting the two steady states of the model. We develop an alternative proof of the existence of such solutions and we also demonstrate the existence of traveling wavefronts moving at minimum speed. The proposed approach is based on the use technique of upper-lower solutions. Finally, through an iterative procedure, we show numerical simulations that approximate the traveling wavefronts, thus confirming our theoretical results.
Paper's Title:
Coexisting Attractors and Bubbling Route to Chaos in Modified Coupled Duffing Oscillators
Author(s):
B. Deruni1, A. S. Hacinliyan1,2, E. Kandiran3, A. C. Keles2, S. Kaouache4, M.-S. Abdelouahab4, N.-E. Hamri4
1Department
of Physics,
University of Yeditepe,
Turkey.
2Department
of Information Systems and Technologies,
University of Yeditepe,
Turkey
3Department
of Software Development,
University of Yeditepe,
Turkey.
4Laboratory
of Mathematics and their interactions,
University Center of Abdelhafid Boussouf,
Mila 43000,
Algeria.
E-mail:
berc890@gmail.com
ahacinliyan@yeditepe.edu.tr
engin.kandiran@yeditepe.edu.tr
cihan.keles@yeditepe.edu.tr
s.kaouache@centr-univ-mila.dz
medsalah3@yahoo.fr
n.hamri@centre-univ-mila.dz
Abstract:
In this article dynamical behavior of coupled Duffing oscillators is analyzed under a small modification. The oscillators have cubic damping instead of linear one. Although single duffing oscillator has complex dynamics, coupled duffing systems possess a much more complex structure. The dynamical behavior of the system is investigated both numerically and analytically. Numerical results indicate that the system has double scroll attractor with suitable parameter values. On the other hand, bifurcation diagrams illustrate rich behavior of the system, and it is seen that, system enters into chaos with different routes. Beside classical bifurcations, bubbling route to chaos is observed for suitable parameter settings. On the other hand, Multistability of the system is indicated with the coexisting attractors, such that under same parameter setting the system shows different periodic and chaotic attractors. Moreover, chaotic synchronization of coupled oscillators is illustrated in final section.
Paper's Title:
Riemann-Stieltjes Integrals and Some Ostrowski Type Inequalities
Author(s):
W. G. Alshanti
Department of General Studies,
Jubail University College,
KSA.
E-mail: shantiw@ucj.edu.sa
Abstract:
In this article, we investigate new integral inequalities of Ostrowski's type of various functional aspects. For mapping's second derivative, we assume two cases, namely, L1 and L∞ spaces. Moreover, for first derivative, we investigate two different characteristics, namely, bounded variation and locally Lipchitz continuity. Applications to special means and composite quadrature rules are also carried out.
Paper's Title:
Coefficient Estimates Of Sakaguchi Kind Functions Using
Lucas Polynomials
Author(s):
H. Priya and B. Srutha Keerthi
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus,
Chennai - 600 048,
India.
E-mail:
priyaharikrishnan18@gmail.com
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus,
Chennai - 600 048,
India.
E-mail: isruthilaya06@yahoo.co.in
Abstract:
By means of (p,q) Lucas polynomials, we estimate coefficient bounds and Fekete-Szego inequalities for functions belonging to this class. Several corollaries and consequences of the main results are also obtained.
Paper's Title:
On General Class of Nonlinear Contractive Maps and their Performance Estimates
Author(s):
Olalekan Taofeek Wahab and Salaudeen Alaro Musa
Department of Mathematics and
Statistics
Kwara State University, Malete
P. M. B. 1530 Ilorin,
Nigeria.
E-mail: taofeek.wahab@kwasu.edu.ng
Abstract:
This paper considers two independent general class of nonlinear contractive maps to study the existence properties of nonlinear operators with prior degenerate. The existence properties are proved in the framework of approximate fixed points with the imposition of the general class of contractive conditions in metrical convex spaces without emphasis on completeness or compactness. For computational purposes, the performance estimates and the sensitivity dependence of these conditions are obtained for the Picard operator. Practical examples are also considered to justify the validity of the conditions. The results ensure no term is lost in the operators with prior degenerate and the conditions are strictly larger class when compare with others in the literature.
Paper's Title:
Trace Inequalities for Operators in Hilbert Spaces: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
School of Engineering
& Science
Victoria University,
PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
In this paper we survey some recent trace inequalities for operators in Hilbert spaces that are connected to Schwarz's, Buzano's and Kato's inequalities and the reverses of Schwarz inequality known in the literature as Cassels' inequality and Shisha-Mond's inequality. Applications for some functionals that are naturally associated to some of these inequalities and for functions of operators defined by power series are given. Further, various trace inequalities for convex functions are presented including refinements of Jensen inequality and several reverses of Jensen's inequality. Hermite-Hadamard type inequalities and the trace version of Slater's inequality are given. Some Lipschitz type inequalities are also surveyed. Examples for fundamental functions such as the power, logarithmic, resolvent and exponential functions are provided as well.
Paper's Title:
Timelike Surfaces with a Common Line of Curvature in Minkowski 3-Space
Author(s):
M.K. Saad, A.Z. Ansari, M. Akram and F. Alharbi
Department of Mathematics ,
Faculty of Science,
Islamic University of Madinah,
KSA
Abstract:
In this paper, we analyze the problem of constructing a timelike surface family from a given non-null curve line of curvature. Using the Frenet frame of the non-null curve in Minkowski space E13 we express the family of surfaces as a linear combination of the components of this frame, and derive the necessary and sufficient conditions for the coefficients to satisfy both the line of curvature and the isoparametric requirements. In addition, a necessary and sufficient condition for the given non-null curve to satisfy the line of curvature and the geodesic requirements is investigated. The extension to timelike surfaces of revolution is also outlined. Meanwhile, some representative non-null curves are chosen to construct the corresponding timelike surfaces which possessing these curves as lines of curvature. Results presented in this paper have applications in geometric modeling and the manufacturing of products. In addition, some computational examples are given and plotted.
Paper's Title:
Additive Mappings on Semiprime Rings Functioning as Centralizers
Author(s):
Abu Zaid Ansari and Faiza Shujat
Department of Mathematics,
Faculty of Science,
Islamic University of Madinah, Madinah
K.S.A.
E-mail: ansari.abuzaid@gmail.com,
ansari.abuzaid@iu.edu.sa
Department of Mathematics,
Faculty of Science,
Taibah University, Madinah,
K.S.A.
E-mail: faiza.shujat@gmail.com,
fullahkhan@taibahu.edu.sa
Abstract:
The objective of this research is to prove that an additive mapping T:R → R is a centralizer on R if it satisfies any one of the following identities:
for all x ∈ R, where n ≥ 1 is a fixed integer and R is any suitably torsion free semiprime ring. Some results on involution "*" are also presented as consequences of the main theorems. In addition, we will take criticism in account with examples.
Paper's Title:
Topological Aspects of Discrete Switch Dynamical Systems
Author(s):
Faiz Imam and Sharan Gopal
Department of Mathematics,
BITS - Pilani, Hyderabad Campus,
India.
E-mail: mefaizy@gmail.com
Department of Mathematics,
BITS - Pilani, Hyderabad Campus,
India.
E-mail: sharanraghu@gmail.com
ABSTRACT NOT FOUND. WEBSITE ERROR
Abstract:
Paper's Title:
On Some Nonlinear Retarded Integrodifferential Inequalities in Two and n Independent Variables and their Applications
Author(s):
Bitat Dalila and Khellaf Hassane
Department of Mathematics, Laboratory of
Applied Mathematics and Modeling,
University of Constantine,
PO Box 325, Ain El Bey Road, Constantine 25017,
Algeria.
E-mail: bitat.dalila@umc.edu.dz
khellafhassane@umc.edu.dz
URL: https://www.umc.edu.dz
Abstract:
In this paper, we establish some new nonlinear retarded integrodifferential inequalities in two and n independent variables. Some applications are given as illustration.
Paper's Title:
Portfolio Optimization of Sharia and Non-Sharia Stocks Using Single Index Model (Case study: Jakarta Sharia Index and Kompas 100 Index)
Author(s):
Kwardiniya Andawaningtyas, Muhammad Luthfi, Marjono, Endang Wahyu Handamari, Umu S'adah, Evi Ardiyani
Department of Mathematics,
Brawijaya University, Malang,
Indonesia.
Department of Mathematics,
IPB University, Bogor,
Indonesia.
E-mail:
dina_math@ub.ac.id
muhammadluthfi@student.ub.ac.id
marjono@ub.ac.id
ewahyu-math@ub.ac.id
u.saadah@ub.ac.id
ardiyanievi@apps.ipb.ac.id
Abstract:
Stocks are instruments with high returns but also have increased risks. One way to overcome this risk is to form a stock portfolio. This study observed 30 sharia stocks listed on the Jakarta Islamic Index (JII) and 28 non-shariah stocks listed on the Kompas 100 Index from March 2020 to September 2022. The data used is the daily closing price of stocks, the number of stock dividends, and the daily closing price of the Jakarta Composite Index (JCI) from 3rd March 2020, to 31st August 2022. In addition, interest rate of Bank Indonesia Certificate (SBI) is used as risk-free rate. This study aims to optimize the sharia and non-sharia stocks portfolio using the Single Index Model (SIM), which will then be evaluated using the Sharpe, Treynor, and Jensen ratio. The result is that the optimal portfolio of sharia stocks have better performance than the optimal portfolio of non-sharia stocks based on the Treynor ratio. Meanwhile, the optimal portfolio of non-sharia stocks have better performance than the optimal portfolio of sharia stocks based on the Sharpe and Jensen ratio.
Search and serve lasted 0 second(s).