|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
On Subspace-Supercyclic Operators
Author(s):
Mansooreh Moosapoor
Assistant Professor,
Department of Mathematics,
Farhangian University, Tehran,
Iran.
E-mail: mosapor110@gmail.com
m.mosapour@cfu.ac.ir
Abstract:
In this paper, we prove that supercyclic operators are subspace-supercyclic and by this we give a positive answer to a question posed in ( L. Zhang, Z. H. Zhou, Notes about subspace-supercyclic operators, Ann. Funct. Anal., 6 (2015), pp. 60--68). We give examples of subspace-supercyclic operators that are not subspace-hypercyclic. We state that if T is an invertible supercyclic operator then Tn and T-n is subspace-supercyclic for any positive integer n. We give two subspace-supercyclicity criteria. Surprisingly, we show that subspace-supercyclic operators exist on finite-dimensional spaces.
Paper's Title:
Uniform Convergence of Schwarz Method for Noncoercive Variational Inequalities Simple Proof
Author(s):
M. Haiour and E. Hadidi.
Department of mathematics, LANOS Laboratory,
Faculty of the Sciences, University Badji Mokhtar,
P.O 23000 Annaba,
Algeria.
haiourm@yahoo.fr,
ehadidi71@yahoo.fr
Abstract:
In this paper we study noncoercive variational inequalities, using the Schwarz method. The main idea of this method consists in decomposing the domain in two subdomains. We give a simple proof for the main result concerning L∞ error estimates, using the Zhou geometrical convergence and the L∞ approximation given for finite element methods by Courty-Dumont.
Paper's Title:
L∞- Error Estimate of Schwarz Algorithm for Elliptic Quasi-Variational Inequalities Related to Impulse Control Problem
Author(s):
Saadi Samira and Mehri Allaoua
Lab. LANOS, Department of Mathematics,
University Badji Mokhtar Annaba,
P.O.Box 12, Annaba 23000,
Algeria.
Lab. LAIG, Department of Mathematics,
University May 8th 1945,
P.O.Box 401, Guelma 24000,
Algeria.
E-mail:
saadisamira69@yahoo.fr
allmehri@yahoo.fr
Abstract:
In this work, we study Schwarz method for a class of elliptic quasi-variational inequalities. The principal result of this investigation is to prove the error estimate in ∞-norm for two domains with overlapping nonmatching grids, using the geometrical convergence, and the uniform convergence of Cortey Dumont.
Paper's Title:
A Low Order Least-Squares Nonconforming Finite Element Method for Steady Magnetohydrodynamic Equations
Author(s):
Z. Yu, D. Shi and H. Zhu
College of Science,
Zhongyuan
University of Technology,
Zhengzhou 450007,
China.
E-mail:
5772@zut.edu.cn
School of Mathematics and Statistics,
Zhengzhou University,
Zhengzhou 450001,
China.
E-mail:
shi_dy@126.com
Mathematics Department,
University of Southern Mississippi,
Hattiesburg MS, 39406,
U.S.A
E-mail:
huiqing.zhu@usm.edu
Abstract:
A low order least-squares nonconforming finite element (NFE) method is proposed for magnetohydrodynamic equations with EQ1rot element and zero-order Raviart-Thomas element. Based on the above element's typical interpolations properties, the existence and uniqueness of the approximate solutions are proved and the optimal order error estimates for the corresponding variables are derived.
Paper's Title:
On a Hilbert-type Inequality with the Polygamma Function
Author(s):
Bing He and Bicheng Yang
Department of Mathematics, Guangdong Education College,
Guangzhou, 510303,
China.
Department of Mathematics, Guangdong Education College,
Guangzhou, 510303,
China.
Abstract:
By applying the method of weight function and the technique of real analysis, a Hilbert-type inequality with a best constant factor is established, where the best constant factor is made of the polygamma function. Furthermore, the inverse form is given.
Paper's Title:
Two Geometric Constants Related to Isosceles Orthogonality on Banach Space
Author(s):
Huayou Xie, Qi Liu and Yongjin Li
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P. R. China.
E-mail: xiehy33@mail2.sysu.edu.cn
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P. R. China.
E-mail: liuq325@mail2.sysu.edu.cn
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P. R. China.
E-mail: stslyj@mail.sysu.edu.cn
Abstract:
In this paper, we introduce new geometric constant C(X,ai,bi,ci,2) to measure the difference between isosceles orthogonality and special Carlsson orthogonalities. At the same time, we also present the geometric constant C(X,ai,bi,ci), which is a generalization of the rectangular constant proposed by Joly. According to the inequality on isosceles orthogonality, we give the boundary characterization of these geometric constants. Then the relationship between these geometric constants and uniformly non-square property can also be discussed. Furthermore, we show that there is a close relationship between these geometric constants and some important geometric constants.
Paper's Title:
On an Extension of Hilbert’s Integral Inequality with Some Parameters
Author(s):
Bicheng Yang
Department of
Mathematics, Guangdong Education College, Guangzhou, Guangdong 510303, People’s
Republic of China.
bcyang@pub.guangzhou.gd.cn
URL:
http://www1.gdei.edu.cn/yangbicheng/index.html
Abstract:
In this paper, by introducing some parameters and estimating the
weight function, we give an extension of Hilbert’s integral inequality with a
best constant factor. As applications, we consider the equivalent form and some
particular results.
Paper's Title:
Compactly Supported Interpolatory Orthogonal Multiwavelet Packets
Author(s):
Yang Shouzhi
Department of Mathematics,
Shantou University,
Shantou, Po Box 515063,
P.R.China.
szyang@stu.edu.cn
Abstract:
Compactly supported interpolatory orthogonal multiwavelet packets
are introduced. Precisely, if both the multiscaling function and
the corresponding multiwavelet have the same interpolatory
property, then the multiwavelet packets are also interpolatory
orthogonal. Thus, the coefficients of decomposition or synthesis
of multiwavelet packets can be realized by sampling instead of inner
products. This multiwavelet packets provide a finer decomposition
of multiwavelet packets space and give a better localization.
Paper's Title:
Oscillations of First Order Linear Delay Difference Equations
Author(s):
G. E. Chatzarakis and I. P. Stavroulakis
Department of Mathematics, University of Ioannina,
451 10, Greece
ipstav@cc.uoi.gr
Abstract:
Consider the first order linear delay difference equation of
the form 
where
is
a sequence of nonnegative real numbers, k is a positive integer and 
denotes
the forward difference operator 
New
oscillation criteria are established when the well-known oscillation conditions
and
are
not satisfied. The results obtained essentially improve known results in the
literature.
Paper's Title:
A Strengthened Hardy-Hilbert's Type Inequality
Author(s):
Weihong Wang and Bicheng Yang
Department of Mathematics, Guangdong Education Institute,
Guangzhou, Guangdong 520303,
People's Republic Of China
wwh@gdei.edu.cn
bcyang@pub.guangzhou.gd.cn
URL: http://www1.gdei.edu.cn/yangbicheng/index.html
Abstract:
By using the improved Euler-Maclaurin's summation formula and
estimating the weight coefficient, we give a new strengthened
version of the more accurate Hardy-Hilbert's type inequality. As
applications, a strengthened version of the equivalent form is
considered.
Paper's Title:
Necessary and Sufficient Conditions for Uniform Convergence and Boundedness of a General Class of Sine Series
Author(s):
Laszlo Leindler
Bolyai Institute, University of Szeged,
Aradi Vértanúk tere 1,
H-6720 Szeged,
Hungary.
leindler@math.u-szeged.hu
Abstract:
For all we know theorems pertaining to sine series with coefficients from the
class γGBVS give only sufficient
conditions. Therefore we define a subclass of
Paper's Title:
Existence Results for Perturbed Fractional Differential
Inclusions
Author(s):
Y.-K. Chang
Department of Mathematics,
Lanzhou Jiaotong University, Lanzhou, Gansu 730070, People's
Republic of China
lzchangyk@163.com
Abstract:
This paper is mainly concerned with the following fractional differential
inclusions with boundary condition
A sufficient condition is established for the existence of solutions of the
above problem by using a fixed point theorem for multivalued maps due to
Dhage. Our result is proved under the mixed generalized Lipschitz and
Carathéodory conditions.
Paper's Title:
Fekete-Szegö Problem for Univalent Functions with Respect to k-Symmetric
Points
Author(s):
K. Al-Shaqsi and M. Darus
School of Mathematical Sciences, Faculty of Science and Technology,
University Kebangsaan Malaysia,
Bangi 43600 Selangor D. Ehsan,
Malaysia
ommath@hotmail.com
maslina@ukm.my
Abstract:
In the present investigation, sharp upper bounds of |a3- μa22|
for functions f(z) = z + a2z2 + a2z3 + ... belonging to certain subclasses
of starlike and convex functions with respect to k-symmetric points are
obtained. Also certain applications of the main results for subclasses of
functions defined by convolution with a normalized analytic function are
given. In particular, Fekete- Szeg
Paper's Title:
Nontrivial Solutions of Singular Superlinear Three-point
Boundary Value Problems at Resonance
Author(s):
Feng Wang, Fang Zhang
School of Mathematics and Physics,
Changzou University,
Changzhou, 213164,
China.
fengwang188@163.com
Abstract:
The singular superlinear second order three-point boundary value problems at resonance
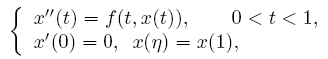
are considered under some conditions concerning the first eigenvalues corresponding to the relevant linear operators, where n ∈ (0,1) is a constant, f is allowed to be singular at both t=0 and t=1. The existence results of nontrivial solutions are given by means of the topological degree theory.
Paper's Title:
Para-chaotic Tuples of Operators
Author(s):
Bahmann Yousefi and Javad Izadi
Department of Mathematics,
Payame Noor University,
P.O. Box 19395-3697, Tehran,
Iran
b_yousefi@pnu.ac.ir
javadie2003@yahoo.com
Abstract:
In this paper, we introduce para-chaotic tuples of operators and we give some relations between para-chaoticity and Hypercyclicity Criterion for a tuple of operators.
Paper's Title:
Hermite-Hadamard-Fejer Type Inequalities for Harmonically s-convex Functions via Fractional Integrals
Author(s):
İmdat İşcan, Mehmet Kunt
Department of Mathematics,
Faculty of Sciences and Arts,
Giresun University, Giresun,
Turkey.
E-mail: imdat.iscan@giresun.edu.tr
Department of Mathematics,
Faculty of Sciences,
Karadeniz Technical University,
61080, Trabzon,
Turkey.
E-mail:
mkunt@ktu.edu.tr
Abstract:
In this paper, some Hermite-Hadamard-Fejer type integral inequalities for harmonically s-convex functions in fractional integral forms have been obtained.
Paper's Title:
On a Class of Meromorphic Functions of Janowski Type Related with a Convolution Operator
Author(s):
Abdul Rahman S. Juma, Husamaldin I. Dhayea
Department of
Mathematics,
Alanbar University, Ramadi,
Iraq.
E-mail: dr_juma@hotmail.com
Department of Mathematics,
Tikrit University, Tikrit,
Iraq.
URL: husamaddin@gmail.com
Abstract:
In this paper, we have introduced and studied new operator $Qkλ,m,γ by the Hadamard product (or convolution) of two linear operators Dkλ and Im,γ, then using this operator to study and investigate a new subclass of meromorphic functions of Janowski type, giving the coefficient bounds, a sufficient condition for a function to belong to the considered class and also a convolution property. The results presented provide generalizations of results given in earlier works.
Paper's Title:
Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
An Efficient Modification of Differential Transform Method for Solving Integral and Integro-differential Equations
Author(s):
S. Al-Ahmad, Ibrahim Mohammed Sulaiman*, and M. Mamat
Faculty of Informatics and Computing,
Universiti Sultan Zainal Abidin,
Terengganu, Besut Campus, 22200,
Malaysia.
E-mail: Alahmad.shadi@yahoo.com,
*sulaimanib@unisza.edu.my,
must@unisza.edu.my
Abstract:
In this paper, classes of integral and integro-differential equations are solved using a modified differential transform method. This proposed technique is based on differential transform method (DTM), Laplace transform (LT) procedure and Pad\'{e} approximants (PA). The proposed method which gives a good approximation for the true solution in a large region is referred to modified differential transform method (MDTM). An algorithm was developed to illustrate the flow of the proposed method. Some numerical problems are presented to check the applicability of the proposed scheme and the obtained results from the computations are compared with other existing methods to illustrates its efficiency. Numerical results have shown that the proposed MDTM method is promising compared to other existing methods for solving integral and integro-differential equations.
Paper's Title:
Multistage Analytical Approximate Solution of Quasi-Linear Differential- Algebraic System of Index Two
Author(s):
Ibrahim M. Albak, F. A. Abdullah* and Zarita Zainuddin
School of Mathematical Sciences,
Universiti Sains Malaysia,
11800 USM, Penang,
Malaysia.
E-mail: ibra13975@gmail.com,
farahaini@usm.my,
zarita@usm.my
Abstract:
In this paper, a new Multistage Transform Method (MSDTM) has been proposed by utilizing a well-known transformation technique, the Differential Transform Method (DTM), to solve Differential Algebraic Equations (DAEs) with index 2. The advantage of the proposed scheme is that it does not require an index reduction and extends the convergence domain of the solution. Some examples for various types of problems are carried out to show the ability of MSDTM in solving DAEs. The results obtained are in good agreement with the existing literature which demonstrates the effectiveness and efficiency of the proposed method.
Paper's Title:
Simple Integral Representations for the Fibonacci and Lucas Numbers
Author(s):
Seán M. Stewart
Physical Science and Engineering Division,
King Abdullah
University of Science and Technology,
Thuwal 23955-6900,
Saudi
Arabia.
E-mail: sean.stewart@kaust.edu.sa
Abstract:
Integral representations of the Fibonacci numbers Fkn + r and the Lucas numbers Lkn + r are presented. Each is established using methods that rely on nothing beyond elementary integral calculus.
Paper's Title:
Some Moduli and Inequalities Related to Birkhoff Orthogonality in Banach Spaces
Author(s):
Dandan Du and Yongjin Li
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P.R. China.
E-mail: dudd5@mail2.sysu.edu.cn
Department of Mathematics,
Sun Yat-sen University,
Guangzhou, 510275,
P.R. China.
E-mail: stslyj@mail.sysu.edu.cn
Abstract:
In this paper, we shall consider two new constants δB(X) and ρB(X), which are the modulus of convexity and the modulus of smoothness related to Birkhoff orthogonality, respectively. The connections between these two constants and other well-known constants are established by some equalities and inequalities. Meanwhile, we obtain two characterizations of Hilbert spaces in terms of these two constants, study the relationships between the constants δB(X), ρB(X) and the fixed point property for nonexpansive mappings. Furthermore, we also give a characterization of the Radon plane with affine regular hexagonal unit sphere.
Paper's Title:
A Simple New Proof of Fan-Taussky-Todd Inequalities
Author(s):
Zhi-Hua Zhang and Zhen-Gang Xiao
Zixing Educational Research Section,
Chenzhou City, Hunan 423400, P. R. China.
Zhi-hua Zhang
Url: http://www.hnzxslzx.com/zzhweb/
Department Of Mathematics, Hunan Institute Of Science And Technology,
Yueyang City, Hunan 423400, P. R. China.
Zhen-gang Xiao
Abstract:
In this paper we present simple new proofs of the inequalities:
which holds for all real numbers a0 = 0, a1, · · · , an, an+1 = 0 and the coefficients
2(1 - cos(π/(n + 1))) and 2(1 + cos(π/(n + 1))) are the best possible; and
which holds for all real numbers a0 = 0, a1, · · · , an and the coefficients
2(1-cos(π/(2n + 1))) and 2(1 + cos(π/(2n + 1))) are the best possible.
Paper's Title:
Logarithmically complete monotonicity properties for the gamma functions
Author(s):
Chao-Ping Chen and Feng Qi
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University,
Jiaozuo City, Henan 454010,
China.
chenchaoping@hpu.edu.cn
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University,
Jiaozuo City, Henan 454010,
China.
qifeng@hpu.edu.cn
fengqi618@member.ams.org
Abstract:
Some logarithmically completely monotonic functions involving the gamma functions are presented. As a consequence, some known results are proved and refined.
Paper's Title:
On Zeros of Diagonally Quasiconvex Multifunctions
Author(s):
Zoran D. Mitrović
Faculty of Electrical Engineering,
University of Banja Luka,
78000 Banja Luka, Patre 5
Bosnia and Herzegovina
zmitrovic@etfbl.net
Abstract:
In this paper, we extended the notion of diagonally quasiconvexity
for multifunctions and established several existence results for
zeros of diagonally quasiconvex multifunctions. As applications we
obtain the results of fixed points, coincidence points and best
approximations for multifunctions. Using our result we also prove
the existence of solutions to the variational-like inequality
problem and generalized vector equilibrium problem. The results
of this paper generalize some known results in the literature.
Paper's Title:
On Positive Entire Solutions of Second Order Quasilinear Elliptic Equations
Author(s):
Zuodong Yang and Honghui Yin
Institute of Mathematics, School of Mathematics and Computer Science,
Nanjing Normal University, Jiangsu Nanjing 210097,
China;
zdyang_jin@263.net
Department of Mathematics, Huaiyin Teachers College,
Jiangsu Huaian 223001,
China;
School of Mathematics and Computer Sciences,
Nanjing Normal University, Jiangsu Nanjing 210097,
China.
yin_hh@sina.com
Abstract:
In this paper, our main purpose is to establish the existence
theorem of positive entire solutions of second order quasilinear
elliptic equations under new conditions. The main results of the
present paper are new and extend the previously known results.
Paper's Title:
The Convergence of Modified Mann-Ishikawa Iterations when Applied to an Asymptotically Pseudocontractive Map
Author(s):
S. Soltuz
Departamento de Matematicas, Universidad de Los Andes, Carrera 1
No. 18A-10, Bogota,
Colombia
and
``T. Popoviciu" Institute of Numerical Analysis
Cluj-Napoca,
Romania
smsoltuz@gmail.com
URL:http://www.uniandes.edu.co/
Abstract:
We prove that under minimal conditions the modified Mann and Ishikawa iterations converge when dealing with an asymptotically pseudocontractive map. We give an affirmative answer to the open question from C.E. Chidume and H. Zegeye, Approximate fixed point sequences and convergence theorems for asymptotically pseudocontractive mappings, J. Math. Anal. Appl., 278 (2003), 354--366.
Paper's Title:
Positive Solutions for Systems of Three-point Nonlinear Boundary Value Problems
Author(s):
J. Henderson and S. K. Ntouyas
Department of Mathematics, Baylor University
Waco, Texas
76798-7328 USA.
Johnny_Henderson@baylor.edu
URL: http://www3.baylor.edu/~Johnny_Henderson
Department of Mathematics, University of Ioannina
451 10 Ioannina,
Greece.
sntouyas@cc.uoi.gr
URL: http://www.math.uoi.gr/~sntouyas
Abstract:
Values of λ are determined for which there exist
positive solutions of the system of three-point boundary value problems,
u''(t)+ λa(t)f(v(t))=0, v''(t)+λb(t)g(u(t))=0,
for 0 < t <1, and
satisfying, u(0) = 0, u(1)=α u(η),
v(0) = 0, v(1)=α v(η). A Guo-Krasnosel'skii fixed
point theorem is applied. Paper's Title:
Positive Periodic Solutions for
Second-Order Differential Equations with Generalized Neutral Operator Author(s):
Wing-Sum Cheung, Jingli Ren and Weiwei Han
1: Paper Source
PDF document
Department of Mathematics,
The University of Hong Kong
Pokfulam
Road,
Hong Kong
Department of Mathematics, Zhengzhou University
Zhengzhou 450001,
P.R. China
wscheung@hkucc.hku.hk
renjl@zzu.edu.cn
Abstract:
By some analysis of the neutral operator
and an application of the fixed-point
index theorem, we obtain sufficient conditions for the existence,
multiplicity and nonexistence of periodic solutions to a second-order
differential equation with the prescribed neutral operator, which improve
and extend some recent results of Lu-Ge, Wu-Wang, and Zhang. An example is
given to illustrate our results. Moreover, the analysis of the generalized
neutral operator will be helpful for other types of differential equations.
Paper's Title:
Approximation of Common Fixed Points of a Finite Family of Asymptotically Demicontractive Mappings in Banach Spaces
Author(s):
Yuchao Tang, Yong Cai, Liqun Hu and Liwei Liu
Department of Mathematics, NanChang University,
Nanchang 330031, P.R. China
Department of Mathematics, Xi'an Jiaotong University,
Xi'an 710049, P.R.
China
Abstract:
By virtue of new analytic techniques, we analyze and
study
several strong convergence theorems for the approximation of
common fixed points of asymptotically demicontractive mappings
via the multistep iterative sequence with errors in Banach
spaces. Our results improve and extend the corresponding ones
announced by Osilike , Osilike and Aniagbosor, Igbokwe, Cho et
al., Moore and Nnoli, Hu and all the others.
Paper's Title:
Necessary and Sufficient Conditions for Cyclic Homogeneous Polynomial Inequalities of Degree Four in Real Variables
Author(s):
Vasile Cirtoaje and Yuanzhe Zhou
Department of Automatic Control and Computers
University of Ploiesti
Romania.
vcirtoaje@upg-ploiesti.ro.
High School Affiliated to Wuhan University, China
Abstract:
In this paper, we give two sets of necessary and sufficient conditions that the inequality f4(x,y,z) ≥ 0 holds for any real numbers x,y,z, where f4(x,y,z) is a cyclic homogeneous polynomial of degree four. In addition, all equality cases of this inequality are analysed. For the particular case in which f4(1,1,1)=0, we get the main result in [3]. Several applications are given to show the effectiveness of the proposed methods.
Paper's Title:
On Convergence Theorems of an Implicit Iterative Process with Errors for a
Finite Family of Asymptotically quasi I-nonexpansive Mappings
Author(s):
Farrukh Mukhamedov and Mansoor Saburov
Department of Computational & Theoretical
Sciences,
Faculty of Sciences, International Islamic University Malaysia,
P.O. Box, 141, 25710, Kuantan,
Malaysia
Abstract:
In this paper we prove the weak and strong convergence of the implicit iterative process with errors to a common fixed point of a finite family {Tj}Ni=1 of asymptotically quasi Ij-nonexpansive mappings as well as a family of {Ij}Nj=1 of asymptotically quasi nonexpansive mappings in the framework of Banach spaces. The obtained results improve and generalize the corresponding results in the existing literature.
Paper's Title:
Properties of Certain Multivalent Functions Involving Ruscheweyh Derivatives
Author(s):
N-Eng Xu and Ding-Gong Yang
Department of Mathematics,
Changshu Institute of Technology,
Changshu, Jiangsu 215500,
China
Abstract:
Let Ap(p∈ N) be the class of functions
which are analytic
in the unit disk. By virtue of the Ruscheweyh derivatives we introduce the new
subclasses Cp(n,α,β,λ,μ) of Ap. Subordination relations, inclusion relations,
convolution properties and a sharp coefficient estimate are
obtained. We also give a sufficient condition for a function to be
in Cp(n,α,β,λ,μ)
Paper's Title:
Schwarz Method
for Variational Inequalities Related to Ergodic Control Problems
Author(s):
S. Saadi, H. Mécheri
Department of Mathematics, Badji Mokhtar
University, Annaba 23000,
P.O.Box. 12, Annaba 23000, Algeria
Abstract:
In this paper, we study variational inequalities related to ergodic control problems studied by M. Boulbrachène and H. Sissaoui [11], where the "discount factor" (i.e., the zero order term) is set to 0, we use an overlapping Schwarz method on nomatching grid which consists in decomposing the domain in two subdomains. For α ∈ ]0.1[ we provide the discretization on each subdomain converges in L∞ -norm.
Paper's Title:
Stability of an Almost Surjective epsilon-Isometry in The Dual of Real Banach Spaces
Author(s):
Minanur Rohman, Ratno Bagus Edy Wibowo, Marjono
Department of Mathematics, Faculty of
Mathematics and Natural Sciences,
Brawijaya University,
Jl. Veteran Malang 65145,
Indonesia.
E-mail:
miminanira@gmail.com
Department of Mathematics, Faculty of
Mathematics and Natural Sciences,
Brawijaya University,
Jl. Veteran Malang 65145,
Indonesia.
E-mail:
rbagus@ub.ac.id
Department of Mathematics, Faculty of
Mathematics and Natural Sciences,
Brawijaya University,
Jl. Veteran Malang 65145,
Indonesia.
E-mail:
marjono@ub.ac.id
Abstract:
In this paper, we study the stability of epsilon-isometry in the dual of real Banach spaces. We prove that the almost surjective epsilon-isometry mapping is stable in dual of each spaces. The proof uses Gâteaux differentiability space (GDS), weak-star exposed points, norm-attaining operator, and some studies about epsilon-isometry that have been done before.
Paper's Title:
Hermite-Hadamard Type Inequalities for k-Riemann Liouville Fractional Integrals Via Two Kinds of Convexity
Author(s):
R. Hussain1, A. Ali2, G. Gulshan3, A. Latif4 and K. Rauf5
1,2,3,4Department
of Mathematics,
Mirpur University of Science and Technology, Mirpur.
Pakistan.
E-mail1:
rashida12@gmail.com
E-mail2:
unigraz2009@yahoo.com
E-mail3:
ghazalagulshan@yahoo.com
E-mail4:
asialatif87@gmail.com
5Department
of Mathematics,
University of Ilorin, Ilorin,
Nigeria.
E-mail5:
krauf@unilorin.edu.ng
Abstract:
In this article, a fundamental integral identity including the first order derivative of a given function via k-Riemann-Liouville fractional integral is established. This is used to obtain further Hermite-Hadamard type inequalities involving left-sided and right-sided k-Riemann-Liouville fractional integrals for m-convex and (s,m)-convex functions respectively.
Paper's Title:
Iterative Algorithm for Split Generalized Mixed Equilibrium Problem Involving Relaxed Monotone Mappings in Real Hilbert Spaces
Author(s):
1U.A. Osisiogu, F.L. Adum, and 2C. Izuchukwu
1Department of Mathematics and
Computer Science,
Ebonyi State University, Abakaliki,
Nigeria.
E-mail: uosisiogu@gmail.com,
adumson2@yahoo.com
2School of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: izuchukwuc@ukzn.ac.za,
izuchukwu_c@yahoo.com
Abstract:
The main purpose of this paper is to introduce a certain class of split generalized mixed equilibrium problem involving relaxed monotone mappings. To solve our proposed problem, we introduce an iterative algorithm and obtain its strong convergence to a solution of the split generalized mixed equilibrium problems in Hilbert spaces. As special cases of the proposed problem, we studied the proximal split feasibility problem and variational inclusion problem.
Paper's Title:
Convergence Speed of Some Random Implicit-Kirk-type Iterations for Contractive-type Random Operators
Author(s):
H. Akewe, K.S. Eke
Department of Mathematics,
Covenant University,
Canaanland, KM 10, Idiroko Road, P. M. B. 1023, Ota, Ogun State,
Nigeria.
E-mail: hudson.akewe@covenantuniversity.edu.ng,
kanayo.eke@covenantuniversity.edu.ng
Abstract:
The main aim of this paper is to introduce a stochastic version of multistep type iterative scheme called a modified random implicit-Kirk multistep iterative scheme and prove strong convergence and stability results for a class of generalized contractive-type random operators. The rate of convergence of the random iterative schemes are also examined through an example. The results show that our new random implicit kirk multistep scheme perform better than other implicit iterative schemes in terms of convergence and thus have good potentials for further applications in equilibrium problems in computer science, physics and economics.
Paper's Title:
Some Inequalities of the Hermite-Hadamard Type for k-Fractional Conformable Integrals
Author(s):
C.-J. Huang, G. Rahman, K. S. Nisar, A. Ghaffar and F. Qi
Department of Mathematics, Ganzhou Teachers College,
Ganzhou 341000, Jiangxi,
China.
E-mail:
hcj73jx@126.com ,
huangcj1973@qq.com
Department of Mathematics, Shaheed Benazir
Bhutto University,
Sheringal, Upper Dir, Khyber Pakhtoonkhwa,
Pakistan.
E-mail: gauhar55uom@gmail.com
Department of Mathematics, College of Arts
and Science at Wadi Aldawaser, 11991,
Prince Sattam Bin Abdulaziz University, Riyadh Region,
Kingdom of Saudi Arabia.
E-mail: n.sooppy@psau.edu.sa,
ksnisar1@gmail.com
Department of Mathematical Science,
Balochistan University of Information Technology,
Engineering and Management Sciences, Quetta,
Pakistan.
E-mail: abdulghaffar.jaffar@gmail.com
School of Mathematical Sciences, Tianjin
Polytechnic University,
Tianjin 300387,
China; Institute of Mathematics,
Henan Polytechnic University, Jiaozuo 454010, Henan,
China.
E-mail: qifeng618@gmail.com,
qifeng618@qq.com
Abstract:
In the paper, the authors deal with generalized k-fractional conformable integrals, establish some inequalities of the Hermite-Hadamard type for generalized k-fractional conformable integrals for convex functions, and generalize known inequalities of the Hermite-Hadamard type for conformable fractional integrals.
Paper's Title:
An Analytical Solution of Perturbed Fisher's Equation Using Homotopy Perturbation Method (HPM), Regular Perturbation Method (RPM) and Adomian Decomposition Method (ADM)
Author(s):
Moussa Bagayogo, Youssouf Minoungou, Youssouf Pare
Departement de Mathematique,
Universite Ouaga I Pr Joseph Ki-Zerbo,
Burkina Faso.
E-mail:
moussabagayogo94@gmail.com,
m.youl@yahoo.fr,
pareyoussouf@yahoo.fr.
Abstract:
In this paper, Homotopy Perturbation Method (HPM), Regular Pertubation Method (RPM) and Adomian decomposition Method (ADM) are applied to Fisher equation. Then, the solution yielding the given initial conditions is gained. Finally, the solutions obtained by each method are compared
Paper's Title:
Dynamical Analysis of HIV/AIDS Epidemic Model with Two Latent Stages, Vertical Transmission and Treatment
Author(s):
Nur Shofianah, Isnani Darti, Syaiful Anam
Mathematics Department,Faculty of
Mathematics and Natural Sciences.
University of Brawijaya,
Jl. Veteran, Malang 65145,
Indonesia.
E-mail:
nur_shofianah@ub.ac.id,
isnanidarti@ub.ac.id,
syaiful@ub.ac.id
Abstract:
We discuss about dynamical analysis of HIV/AIDS epidemic model with two latent stages, vertical transmission and treatment. In this model, the spreading of HIV occurs through both horizontal and vertical transmission. There is also treatment for individual who has been HIV infected. The latent stage is divided into slow and fast latent stage based on the immune condition which varies for each individual. Dynamical analysis result shows that the model has two equilibrium points: the disease-free equilibrium point and the endemic equilibrium point. The existence and global stability of equilibrium points depend on the basic reproduction number R0. When R0 <1, only the disease-free equilibrium point exists. If R0 >1, there are two equilibrium points, which are the disease-free equilibrium point and the endemic equilibrium point. Based on the result of stability analysis, the disease-free equilibrium point is globally asymptotically stable if R0 <1, while if R0 > 1 and p=q, the endemic equilibrium point will be globally asymptotically stable. In the end, we show some numerical simulations to support the analytical result.
Paper's Title:
Some New Mappings Related to Weighted Mean Inequalities
Author(s):
Xiu-Fen Ma
College of Mathematical and Computer,
Chongqing Normal University Foreign Trade and Business College,
No.9 of Xuefu Road, Hechuan District 401520,
Chongqing City,
The People's Republic of China.
E-mail: maxiufen86@163.com
Abstract:
In this paper, we define four mappings related to weighted mean inequalities, investigate their properties, and obtain some new refinements of weighted mean inequalities.
Paper's Title:
Some fixed point results in partial S-metric spaces
Author(s):
M. M. Rezaee, S. Sedghi, A. Mukheimer, K. Abodayeh, and Z. D. Mitrovic
Department of Mathematics, Qaemshahr
Branch,
Islamic Azad University, Qaemshahr,
Iran.
E-mail: Rezaee.mohammad.m@gmail.com
Department of Mathematics, Qaemshahr
Branch,
Islamic Azad University, Qaemshahr,
Iran.
E-mail: sedghi.gh@qaemiau.ac.ir
Department of Mathematics and General
Sciences,
Prince Sultan University, Riyadh,
KSA.
E-mail: mukheimer@psu.edu.sa
Department of Mathematics and General
Sciences,
Prince Sultan University, Riyadh,
KSA.
E-mail: kamal@psu.edu.sa
Nonlinear Analysis Research Group,
Faculty of Mathematics and Statistics,
Ton Duc Thang University, Ho Chi Minh City,
Vietnam.
E-mail: zoran.mitrovic@tdtu.edu.vn
Abstract:
We introduce in this article a new class of generalized metric spaces, called partial S-metric spaces. In addition, we also give some interesting results on fixed points in the partial S-metric spaces and some applications.
Paper's Title:
Double Difference of Composition Operator on Bloch Spaces
Author(s):
Rinchen Tundup
Department of Mathematics
University of Jammu
Jammu and Kashmir
India.
E-mail: joneytun123@gmail.com
Abstract:
In this paper we characterize the compactness of double difference of three non-compact composition operators on Bloch space induced by three holomorphic self maps on the unit disc.
Paper's Title:
Solving Non-Autonomous Nonlinear Systems of Ordinary Differential Equations Using Multi-Stage Differential Transform Method
Author(s):
K. A. Ahmad, Z. Zainuddin, F. A. Abdullah
School of Mathematical Sciences
Universiti Sains Malaysia
11800 USM Penang
Malaysia.
E-mail: abumohmmadkh@hotmail.com
zarita@usm.my
farahaini@usm.my
Abstract:
Differential equations are basic tools to describe a wide variety of phenomena in nature such as, electrostatics, physics, chemistry, economics, etc. In this paper, a technique is developed to solve nonlinear and linear systems of ordinary differential equations based on the standard Differential Transform Method (DTM) and Multi-stage Differential Transform Method (MsDTM). Comparative numerical results that we are obtained by MsDTM and Runge-Kutta method are proposed. The numerical results showed that the MsDTM gives more accurate approximation as compared to the Runge-Kutta numerical method for the solutions of nonlinear and linear systems of ordinary differential equations
Paper's Title:
Fractional exp(-φ(ξ))- Expansion Method and its Application to Space--Time Nonlinear Fractional Equations
Author(s):
A. A. Moussa and L. A. Alhakim
Department of Management Information
System and Production Management,
College of Business and Economics, Qassim University,
P.O. BOX 6666, Buraidah: 51452,
Saudi Arabia.
E-mail: Alaamath81@gmail.com
URL:
https://scholar.google.com/citations?user=ccztZdsAAAAJ&hl=ar
Department of Management Information
System and Production Management,
College of Business and Economics, Qassim University,
P.O. BOX 6666, Buraidah: 51452,
Saudi Arabia.
E-mail: Lama2736@gmail.com
URL:
https://scholar.google.com/citations?user=OSiSh1AAAAAJ&hl=ar
Abstract:
In this paper, we mainly suggest a new method that depends on the fractional derivative proposed by Katugampola for solving nonlinear fractional partial differential equations. Using this method, we obtained numerous useful and surprising solutions for the space--time fractional nonlinear Whitham--Broer--Kaup equations and space--time fractional generalized nonlinear Hirota--Satsuma coupled KdV equations. The solutions obtained varied between hyperbolic, trigonometric, and rational functions, and we hope those interested in the real-life applications of the previous two equations will find this approach useful.
Paper's Title:
Coexisting Attractors and Bubbling Route to Chaos in Modified Coupled Duffing Oscillators
Author(s):
B. Deruni1, A. S. Hacinliyan1,2, E. Kandiran3, A. C. Keles2, S. Kaouache4, M.-S. Abdelouahab4, N.-E. Hamri4
1Department
of Physics,
University of Yeditepe,
Turkey.
2Department
of Information Systems and Technologies,
University of Yeditepe,
Turkey
3Department
of Software Development,
University of Yeditepe,
Turkey.
4Laboratory
of Mathematics and their interactions,
University Center of Abdelhafid Boussouf,
Mila 43000,
Algeria.
E-mail:
berc890@gmail.com
ahacinliyan@yeditepe.edu.tr
engin.kandiran@yeditepe.edu.tr
cihan.keles@yeditepe.edu.tr
s.kaouache@centr-univ-mila.dz
medsalah3@yahoo.fr
n.hamri@centre-univ-mila.dz
Abstract:
In this article dynamical behavior of coupled Duffing oscillators is analyzed under a small modification. The oscillators have cubic damping instead of linear one. Although single duffing oscillator has complex dynamics, coupled duffing systems possess a much more complex structure. The dynamical behavior of the system is investigated both numerically and analytically. Numerical results indicate that the system has double scroll attractor with suitable parameter values. On the other hand, bifurcation diagrams illustrate rich behavior of the system, and it is seen that, system enters into chaos with different routes. Beside classical bifurcations, bubbling route to chaos is observed for suitable parameter settings. On the other hand, Multistability of the system is indicated with the coexisting attractors, such that under same parameter setting the system shows different periodic and chaotic attractors. Moreover, chaotic synchronization of coupled oscillators is illustrated in final section.
Paper's Title:
On Euler's First Transformation Formula for k-hypergeometric Function
Author(s):
Sungtae Jun and Insuk Kim
General Education Institute,
Konkuk University, Chungju 380-701,
Republic of Korea.
E-mail: sjun@kku.ac.kr
Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Republic of Korea.
E-mail: iki@wku.ac.kr
Abstract:
Mubeen et al. obtained Kummer's first transformation for the k-hypergeometric function. The aim of this note is to provide the Euler-type first transformation for the k-hypergeometric function. As a limiting case, we recover the results of Mubeen et al. In addition to this, an alternate and easy derivation of Kummer's first transformation for the k-hypergeometric function is also given.
Paper's Title:
Algorithms for Nonlinear Problems Involving Strictly Pseudocontractive Mappings
Author(s):
Mathew Olajiire Aibinu1, Surendra Colin Thakur2, Sibusiso Moyo3
1Institute for Systems Science
& KZN E-Skill CoLab,
Durban University of Technology,
Durban 4000,
South Africa.
1DSI-NRF
Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: moaibinu@yahoo.com
mathewa@dut.ac.za
2 KZN E-Skill CoLab,
Durban University of Technology,
Durban 4000,
South Africa.
E-mail: thakur@dut.ac.za
3Institute for Systems Science & Office of the DVC Research,
Innovation & Engagement Milena Court,
Durban University of Technology,
Durban 4000,
South Africa.
E-mail: dvcrie@dut.ac.za
Abstract:
The puzzles in approximating a fixed point of nonlinear problems involving the class of strictly pseudocontractive mappings are conquered in this paper through viscosity implicit rules. Using generalized contraction mappings, a new viscosity iterative algorithm which is implicit in nature is proposed and analysed in Banach spaces for the class of strictly pseudocontractive mappings. The computations and analysis which are used in the proposed scheme are easy to follow and this gives rooms for a broad application of the scheme. It is obtained that the proposed iterative algorithm converges strongly to a fixed point of a μ-strictly pseudocontractive mapping which also solves a variational inequality problem. The result is also shown to hold for finite family of strictly pseudocontractive mappings. A numerical example is given to show the skillfulness of the proposed scheme and its implementation.
Paper's Title:
Corrigendum for Multistage Analytical Approximate Solution of Quasi-Linear Differential- Algebraic System of Index Two
Author(s):
Ibrahim M. Albak, F. A. Abdullah* and Zarita Zainuddin
School of Mathematical Sciences,
Universiti Sains Malaysia,
11800 USM, Penang,
Malaysia.
E-mail: ibra13975@gmail.com,
farahaini@usm.my,
zarita@usm.my
Abstract:
This article is a corrigendum to AJMAA Volume 18, Issue 2, Article 13, {PDF Link}.
Paper's Title:
SQIRV Model for Omicron Variant with Time Delay
Author(s):
S. Dickson, S. Padmasekaran, G. E. Chatzarakis and S. L. Panetsos
Mathematics, Periyar University, Periyar
Palkalai Nagar, Salem,
636011, Tamilnadu,
India.
E-mail:
dickson@periyaruniversity.ac.in,
padmasekarans@periyaruniversity.ac.in
Electrical and Electronic Engineering
Educators, School of
Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
spanetsos@aspete.gr
Abstract:
In order to examine the dynamics of the Omicron variant, this paper uses mathematical modelling and analysis of a SQIRV model, taking into account the delay in the conversion of susceptible individuals into infected individuals and infected individuals into recovered individuals. The pandemic was eventually controlled as a result of the massive delays. To assure the safety of the host population, this concept incorporates quarantine and the COVID-19 vaccine. Both local and global stability of the model are examined. It is found that the fundamental reproduction number affects both local and global stability conditions. Our findings show that asymptomatic cases caused by an affected population play an important role in increasing Omicron infection in the general population. The most recent data on the pandemic Omicron variant from Tamil Nadu, India, is verified.
Search and serve lasted 0 second(s).