|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Some Inequalities of the Hermite-Hadamard Type for k-Fractional Conformable Integrals
Author(s):
C.-J. Huang, G. Rahman, K. S. Nisar, A. Ghaffar and F. Qi
Department of Mathematics, Ganzhou Teachers College,
Ganzhou 341000, Jiangxi,
China.
E-mail:
hcj73jx@126.com ,
huangcj1973@qq.com
Department of Mathematics, Shaheed Benazir
Bhutto University,
Sheringal, Upper Dir, Khyber Pakhtoonkhwa,
Pakistan.
E-mail: gauhar55uom@gmail.com
Department of Mathematics, College of Arts
and Science at Wadi Aldawaser, 11991,
Prince Sattam Bin Abdulaziz University, Riyadh Region,
Kingdom of Saudi Arabia.
E-mail: n.sooppy@psau.edu.sa,
ksnisar1@gmail.com
Department of Mathematical Science,
Balochistan University of Information Technology,
Engineering and Management Sciences, Quetta,
Pakistan.
E-mail: abdulghaffar.jaffar@gmail.com
School of Mathematical Sciences, Tianjin
Polytechnic University,
Tianjin 300387,
China; Institute of Mathematics,
Henan Polytechnic University, Jiaozuo 454010, Henan,
China.
E-mail: qifeng618@gmail.com,
qifeng618@qq.com
Abstract:
In the paper, the authors deal with generalized k-fractional conformable integrals, establish some inequalities of the Hermite-Hadamard type for generalized k-fractional conformable integrals for convex functions, and generalize known inequalities of the Hermite-Hadamard type for conformable fractional integrals.
Paper's Title:
A Double Inequality for Divided Differences and Some Identities of the Psi and Polygamma Functions
Author(s):
B. N. Guo and F. Qi
School of
Mathematics and Informatics, Henan Polytechnic University, Jiaozuo City, Henan
Province, 454010, China
bai.ni.guo@gmail.com,
bai.ni.guo@hotmail.com
School of
Research Institute of Mathematical Inequality Theory, Henan Polytechnic University, Jiaozuo City, Henan Province, 454010, China
qifeng618@gmail.com,
qifeng618@hotmail.com,
qifeng618@qq.com
URL:http://qifeng618.spaces.live.com
Abstract:
In this short note, from the logarithmically completely monotonic property
of the function
, a double inequality for the divided differences and some identities of the psi and polygamma functions are presented.
Paper's Title:
On A Conjecture of A Logarithmically Completely Monotonic Function
Author(s):
Valmir Krasniqi, Armend Sh. Shabani
Department of Mathematics,
University of Prishtina,
Republic of Kosova
E-mail:
vali.99@hotmail.com
armend_shabani@hotmail.com
Abstract:
In this short note we prove a conjecture, related to a logarithmically completely monotonic function, presented in [5]. Then, we extend by proving a more generalized theorem. At the end we pose an open problem on a logarithmically completely monotonic function involving q-Digamma function.
Paper's Title:
An alternative proof of monotonicity for the extended mean values
Author(s):
Chao-Ping Chen and Feng Qi
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
chenchaoping@hpu.edu.cn
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
qifeng@hpu.edu.cn,
fengqi618@member.ams.org
Url:
http://rgmia.vu.edu.au/qi.html,
http://dami.hpu.edu.cn/qifeng.html
Abstract:
An alternative proof of monotonicity for the extended mean values is given.
Paper's Title:
Shape Diagrams for 2D Compact Sets - Part I: Analytic
Convex Sets.
Author(s):
S. Rivollier, J. Debayle and J.-C. Pinoli
Ecole Nationale Supérieure des Mines de Saint-Etienne,
CIS - LPMG, UMR CNRS 5148, 158 cours Fauriel,
42023 Saint-Etienne Cedex 2, France.
rivollier@emse.fr;
debayle@emse.fr; pinoli@emse.fr
Abstract:
Shape diagrams are representations in the Euclidean plane introduced to study 3-dimensional and 2-dimensional compact convex sets. Such a set is represented by a point within a shape diagram whose coordinates are morphometrical functionals defined as normalized ratios of geometrical functionals. Classically, the geometrical functionals are the area, the perimeter, the radii of the inscribed and circumscribed circles, and the minimum and maximum Feret diameters. They allow thirty-one shape diagrams to be built. Most of these shape diagrams can also been applied to more general compact sets than compact convex sets. Starting from these six classical geometrical functionals, a detailed comparative study has been performed in order to analyze the representation relevance and discrimination power of these thirty-one shape diagrams. The purpose of this paper is to present the first part of this study, by focusing on analytic compact convex sets. A set will be called analytic if its boundary is piecewise defined by explicit functions in such a way that the six geometrical functionals can be straightforwardly calculated. The second and third part of the comparative study are published in two following papers [19.20]. They are focused on analytic simply connected sets and convexity discrimination for analytic and discretized simply connected sets, respectively.
Paper's Title:
Numerical Solution of Certain Types of Fredholm-Volterra Integro-Fractional Differential Equations via Bernstein Polynomials
Author(s):
Alias B. Khalaf1, Azhaar H. Sallo2 and Shazad S. Ahmed3
1Department
of Mathematics, College of Science,
University of Duhok,
Kurdistan Region,
Iraq.
E-mail: aliasbkhalaf@uod.ac
2Department
of Mathematics, College of Science,
University of Duhok,
Kurdistan Region,
Iraq.
E-mail: azhaarsallo@uod.ac
3Department
of Mathematics, College of Science,
University of Sulaimani,
Kurdistan Region,
Iraq.
E-mail: shazad.ahmed@univsul.edu
Abstract:
In this article we obtain a numerical solution for a certain fractional order integro-differential equations of Fredholm-Volterra type, where the fractional derivative is defined in Caputo sense. The properties of Bernstein polynomials are applied in order to convert the fractional order integro-differential equations to the solution of algebraic equations. Some numerical examples are investigated to illustrate the method. Moreover, the results obtained by this method are compared with the exact solution and with the results of some existing methods as well.
Paper's Title:
Shape Diagrams for 2D Compact Sets - Part II: Analytic
Simply Connected Sets.
Author(s):
S. Rivollier, J. Debayle and J.-C. Pinoli
Ecole Nationale Supérieure des Mines de Saint-Etienne,
CIS - LPMG, UMR CNRS 5148, 158 cours Fauriel,
42023 Saint-Etienne Cedex 2, France.
rivollier@emse.fr;
debayle@emse.fr; pinoli@emse.fr
Abstract:
Shape diagrams are representations in the Euclidean plane introduced to study 3-dimensional and 2-dimensional compact convex sets. However, they can also been applied to more general compact sets than compact convex sets. A compact set is represented by a point within a shape diagram whose coordinates are morphometrical functionals defined as normalized ratios of geometrical functionals. Classically, the geometrical functionals are the area, the perimeter, the radii of the inscribed and circumscribed circles, and the minimum and maximum Feret diameters. They allow twenty-two shape diagrams to be built. Starting from these six classical geometrical functionals, a detailed comparative study has been performed in order to analyze the representation relevance and discrimination power of these twenty-two shape diagrams. The first part of this study is published in a previous paper 16. It focused on analytic compact convex sets. A set will be called analytic if its boundary is piecewise defined by explicit functions in such a way that the six geometrical functionals can be straightforwardly calculated. The purpose of this paper is to present the second part, by focusing on analytic simply connected compact sets. The third part of the comparative study is published in a following paper 17. It is focused on convexity discrimination for analytic and discretized simply connected compact sets.
Paper's Title:
A Study of the Effect of Density Dependence in a Matrix Population Model
Author(s):
N. Carter and M. Predescu
Department of Mathematical Sciences,
Bentley University,
Waltham, MA 02452,
U.S.A.
ncarter@bentley.edu
mpredescu@bentley.edu
Abstract:
We study the behavior of solutions of a three dimensional discrete time nonlinear matrix population model. We prove results concerning the existence of equilibrium points, boundedness, permanence of solutions, and global stability in special cases of interest. Moreover, numerical simulations are used to compare the dynamics of two main forms of the density dependence function (rational and exponential).
Paper's Title:
Numerical Solution of A System of Singularly Perturbed Convection-Diffusion Boundary-Value Problems Using Mesh Equidistribution Technique
Author(s):
Pratibhamoy Das and Srinivasan Natesan
Department of Mathematics,
Indian Institute of Technology Guwahati,
Guwahati - 781 039,
India.
pratibhamoy@gmail.com
natesan@iitg.ernet.in
URL:
http://www.iitg.ernet.in/natesan/
Abstract:
In this article, we consider a system of singularly perturbed weakly coupled convection-diffusion equations having diffusion parameters of different magnitudes. These small parameters give rise to boundary layers. An upwind finite difference scheme on adaptively generated mesh is used to obtain a suitable monitor function that gives first-order convergence which is robust with respect to the diffusion parameters. We present the results of numerical experiments for linear and semilinear system of differential equations to support the effectiveness of our preferred monitor function obtained from theoretical analysis.
Paper's Title:
Oscillations of First Order Linear Delay Difference Equations
Author(s):
G. E. Chatzarakis and I. P. Stavroulakis
Department of Mathematics, University of Ioannina,
451 10, Greece
ipstav@cc.uoi.gr
Abstract:
Consider the first order linear delay difference equation of
the form 
where
is
a sequence of nonnegative real numbers, k is a positive integer and 
denotes
the forward difference operator 
New
oscillation criteria are established when the well-known oscillation conditions
and
are
not satisfied. The results obtained essentially improve known results in the
literature.
Paper's Title:
Hyperbolic Models Arising in the Theory of Longitudinal Vibration of Elastic Bars
Author(s):
1I. Fedotov, 1J. Marais, 1,2M. Shatalov and 1H.M. Tenkam
1Department of Mathematics and Statistics,
Tshwane University
of
Technology
Private Bag X6680, Pretoria 0001
South Africa.
fedotovi@tut.ac.za,
julian.marais@gmail.com,
djouosseutenkamhm@tut.ac.za.
2Manufacturing and
Materials
Council of Scientific and Industrial
Research (CSIR)
P.O. Box 395, Pretoria, 0001
South Africa.
mshatlov@csir.co.za
Abstract:
In this paper a unified approach to the
derivation of families of one
dimensional hyperbolic differential equations and boundary conditions describing
the longitudinal vibration of elastic bars is outlined. The longitudinal and
lateral displacements are expressed in the form of a power series expansion in
the lateral coordinate. Equations of motion and boundary conditions are derived
using Hamilton's variational principle. Most of the well known models in this
field fall within the frames of the proposed theory, including the classical
model, and the more elaborated models proposed by by Rayleigh, Love, Bishop,
Mindlin, Herrmann and McNiven. The exact solution is presented for the
Mindlin-Herrmann case in terms of Green functions. Finally, deductions regarding
the accuracy of the models are made by comparison with the exact
Pochhammer-Chree solution for an isotropic cylinder.
Paper's Title:
A Wallis Type Inequality and a Double Inequality for Probability Integral
Author(s):
Jian Cao, Da-Wei Niu and Feng Qi
School of Mathematics and Informatics,
Henan Polytechnic University, Jiaozuo City,
Henan Province, 454010,
China
21caojian@163.com
School of Mathematics and Informatics,
Henan Polytechnic University, Jiaozuo City,
Henan Province, 454010,
China
nnddww@tom.com
Research Institute of Mathematical Inequality Theory,
Henan Polytechnic University, Jiaozuo City,
Henan Province, 454010,
China
qifeng@hpu.edu.cn
fengqi618@member.ams.org
qifeng618@hotmail.com
qifeng618@msn.com
qifeng618@qq.com
URL: http://rgmia.vu.edu.au/qi.html
Abstract:
In this short note, a Wallis type inequality with the best upper and lower
bounds is established. As an application, a double inequality for the
probability integral is found.
Paper's Title:
Shape Diagrams for 2D Compact Sets - Part III: Convexity
Discrimination for Analytic and Discretized Simply Connected Sets.
Author(s):
S. Rivollier, J. Debayle and J.-C. Pinoli
Ecole Nationale Supérieure des Mines de Saint-Etienne,
CIS - LPMG, UMR CNRS
5148,
158 cours Fauriel,
42023 Saint-Etienne Cedex 2, France.
rivollier@emse.fr;
debayle@emse.fr; pinoli@emse.fr
Abstract:
Shape diagrams are representations in the Euclidean plane introduced to study 3-dimensional and 2-dimensional compact convex sets. However, they can also been applied to more general compact sets than compact convex sets. A compact set is represented by a point within a shape diagram whose coordinates are morphometrical functionals defined as normalized ratios of geometrical functionals. Classically, the geometrical functionals are the area, the perimeter, the radii of the inscribed and circumscribed circles, and the minimum and maximum Feret diameters. They allow twenty-two shape diagrams to be built. Starting from these six classical geometrical functionals, a detailed comparative study has been performed in order to analyze the representation relevance and discrimination power of these twenty-two shape diagrams. The two first parts of this study are published in previous papers 8,9. They focus on analytic compact convex sets and analytic simply connected compact sets, respectively. The purpose of this paper is to present the third part, by focusing on the convexity discrimination for analytic and discretized simply connected compact sets..
Paper's Title:
Bounds on the Jensen Gap, and Implications for Mean-Concentrated Distributions
Author(s):
Xiang Gao, Meera Sitharam, Adrian E. Roitberg
Department of Chemistry, and Department
of Computer & Information Science & Engineering,
University of Florida,
Gainesville, FL 32611,
USA.
E-mail: qasdfgtyuiop@gmail.com
URL:
https://scholar.google.com/citations?user=t2nOdxQAAAAJ
Abstract:
This paper gives upper and lower bounds on the gap in Jensen's inequality, i.e., the difference between the expected value of a function of a random variable and the value of the function at the expected value of the random variable. The bounds depend only on growth properties of the function and specific moments of the random variable. The bounds are particularly useful for distributions that are concentrated around the mean, a commonly occurring scenario such as the average of i.i.d. samples and in statistical mechanics.
Paper's Title:
Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Optimal Control Analysis of HIV/AIDS Epidemic Model with an Antiretroviral Treatment
Author(s):
U. Habibah and R. A. Sari
Mathematics Department and Reseach Group
of Biomathematics,
Faculty of Mathematics and Natural Science,
Brawijaya University, Jl. Veteran Malang 65145,
Indonesia.
E-mail: ummu_habibah@ub.ac.id
Abstract:
A mathematical model of HIV/AIDS is governed by a system of ordinary differential equations in the presence of an antiretroviral treatment (ARV). The theory of optimal control is applied to an epidemic model of HIV/AIDS which an ARV is used as a control strategy in order to prevent the spread of HIV/AIDS. The optimality system is derived by applying the Pontryagin's Minimum Principle. We analyze the boundedness and positivity of solutions, and an existence of the optimal control. Numerical simulations are conducted to obtain numerical solution of the optimally system.
Paper's Title:
Orthogonal Collocation on Finite Elements Using Quintic Hermite Basis
Author(s):
P. Singh, N. Parumasur and C. Bansilal
University of KwaZulu-Natal,
School of Mathematics Statistics and Computer Sciences,
Private Bag X54001,
Durban, 4000,
South Africa.
E-mail: singhprook@gmail.com
parumasurn1@ukzn.ac.za
christelle18@gmail.com
Abstract:
In this paper we consider the orthogonal collocation on finite elements (OCFE) method using quintic Hermite (second degree smooth) basis functions and use it to solve partial differential equations (PDEs). The method is particularly tailored to solve third order BVPS and PDEs and to handle their special solutions such as travelling waves and solitons, which typically is the case in the KdV equation. The use of quintic polynomials and collocation using Gauss points yields a stable high order superconvergent method. OCFE using quintic Hermite basis is optimal since it is computationally more efficient than collocation methods using (first degree smooth) piecewise-polynomials and more accurate than the (third degree smooth) B-splines basis. Various computational simulations are presented to demonstrate the computational efficiency and versatility of the OCFE method.
Paper's Title:
Simple Integral Representations for the Fibonacci and Lucas Numbers
Author(s):
Seán M. Stewart
Physical Science and Engineering Division,
King Abdullah
University of Science and Technology,
Thuwal 23955-6900,
Saudi
Arabia.
E-mail: sean.stewart@kaust.edu.sa
Abstract:
Integral representations of the Fibonacci numbers Fkn + r and the Lucas numbers Lkn + r are presented. Each is established using methods that rely on nothing beyond elementary integral calculus.
Paper's Title:
Inequalities Relating to the Gamma Function
Author(s):
Chao-Ping Chen and Feng Qi
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
chenchaoping@hpu.edu.cn
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
qifeng@hpu.edu.cn,
fengqi618@member.ams.org
Url:
http://rgmia.vu.edu.au/qi.html,
http://dami.hpu.edu.cn/qifeng.html
Abstract:
For 
, we have
.
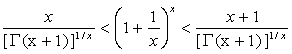For
,
,
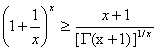And equality occurs for x=1.
Paper's Title:
Salagean-type Harmonic Univalent Functions with Respect to Symmetric Points
Author(s):
R. A. Al-Khal and H. A. Al-Kharsani
Department of Mathematics, Faculty of Science, Girls College,
P.O. Box 838,
Dammam, Saudi Arabia
ranaab@hotmail.com
hakh@hotmail.com
Abstract:
A necessary and sufficient coefficient are given for functions in a class of
complex-valued harmonic univalent functions of the form f=h+\g
using Salagean operator where h and g are analytic in the unit disk
U = {z:|z|<1}. Furthermore, distortion theorems, extreme points,
convolution condition, and convex combinations for this family of harmonic
functions are obtained.
Paper's Title:
Two Classes of Completely Monotonic Functions Involving Gamma and Polygamma Functions
Author(s):
Bai-Ni Guo, Xiao-Ai Li and Feng Qi
School of Mathematics and Informatics,
Henan Polytechnic University,
Jiaozuo City, Henan Province, 454010,
China.
bai.ni.guo@gmail.com
College of Mathematics and Information Science,
Henan Normal University, Xinxiang City,
Henan Province, 453007,
China.
lxa.hnsd@163.com
Research Institute of Mathematical Inequality Theory, Abstract:
The function Paper's Title:
Examples of Fractals Satisfying the Quasihyperbolic Boundary Condition Author(s):
Petteri Harjulehto and Riku Klén Department of Mathematics and Statistics, E-mail:
petteri.harjulehto@utu.fi E-mail:
riku.klen@utu.fi Abstract:
In this paper we give explicit examples of bounded domains that satisfy the quasihyperbolic boundary condition and calculate the values for the constants. These domains are also John domains and we calculate John constants as well. The authors do not know any other paper where exact values of parameters has been estimated. Paper's Title:
Robust Error Analysis of Solutions to Nonlinear Volterra Integral Equation in Lp Spaces Author(s):
Hamid Baghani, Javad Farokhi-Ostad and Omid Baghani Department of Mathematics, Faculty of
Mathematics, Department of Mathematics, Faculty of
Basic Sciences, Department of Mathematics and Computer
Sciences, Abstract:
In this paper, we propose a novel strategy for proving an
important inequality for a contraction integral equations. The obtained inequality allows us to express our iterative algorithm using a "for
loop" rather than a "while loop". The main tool used in this paper
is the fixed point theorem in the Lebesgue space. Also, a numerical example shows the efficiency
and the accuracy of the proposed scheme.
Paper's Title:
The RAFU remainder in Taylor's formula Author(s):
A. C. Sanchez ''Santa Eulalia'' High School, Abstract:
This work is about the remainder in Taylor's formula.
Specifically, the RAFU remainder is studied. Its mathematical expression is
given. Some examples are shown. Different ways to obtain this remainder are developed. Paper's Title:
On General Class of Nonlinear Contractive Maps and their Performance Estimates Author(s):
Olalekan Taofeek Wahab and Salaudeen Alaro Musa Department of Mathematics and
Statistics Abstract:
This paper considers two independent general class of nonlinear contractive maps to study the existence properties of nonlinear operators with prior degenerate. The existence properties are proved in the framework of approximate fixed points with the imposition of the general class of contractive conditions in metrical convex spaces without emphasis on completeness or compactness. For computational purposes, the performance estimates and the sensitivity dependence of these conditions are obtained for the Picard operator. Practical examples are also considered to justify the validity of the conditions. The results ensure no term is lost in the operators with prior degenerate and the conditions are strictly larger class when compare with others in the literature. Paper's Title:
Complete Analysis of Global Behavior of Certain System of Piecewise Linear Difference Equations Author(s):
Atiratch Laoharenoo, Ratinan Boonklurb and Watcharapol Rewlirdsirikul Department of Mathematics and Computer
Science, Department of Mathematics and Computer
Science, Abstract:
Our goal is to study the system of piecewise linear difference equations x{n+1} = |xn|-yn-b and y{n+1} = xn - |yn| + 1 where n
≥ 0 and b ≥
6. We can prove that the behavior of the solution can be divided into 2 types depending on the region of initial condition (x0,y0). That is, the solution eventually becomes the equilibrium point. Otherwise, the solution eventually becomes the periodic solution of prime period 5. All regions of initial condition for each type of solution are determined. Paper's Title:
Generalized Fuglede-Putnam Theorem and Orthogonality Author(s):
A. Bachir and A. Sagres Department of
Mathematics, Faculty of Science, King Khaled
University, Abha, P.O. Box 9004 Kingdom Saudi Arabia
Abstract:
An asymmetric Fuglede-Putnam’s theorem for dominant operators
and
Henan Polytechnic University, Jiaozuo City,
Henan Province, 454010,
China
qifeng618@gmail.com
qifeng618@hotmail.com
qifeng618@qq.com
URLhttp://rgmia.vu.edu.au/qi.html
is logarithmically completely monotonic in (0,∞) if and only if c≥1
and its reciprocal is logarithmically completely monotonic in (0,∞) if and only if
c≤0. The function
is completely monotonic in (0,∞) if and only if c≥1 and its
negative is completely monotonic in (0,∞) if and only if c≤0.
2: Paper Source
PDF document
FI-20014 University of Turku,
Finland
2: Paper Source
PDF document
University of Sistan and Baluchestan, P.O. Box 98135-674, Zahedan,
Iran.
E-mail:
h.baghani@gmail.com
Birjand University of Technology, Birjand,
Iran.
E-mail: j.farrokhi@birjandut.ac.ir
Hakim Sabzevari University, P.O. Box 397, Sabzevar,
Iran.
E-mail:
o.baghani@gmail.com
2: Paper Source
PDF document
Spain
E-mail: csanchezalicia@gmail.com
2: Paper Source
PDF document
Kwara State University, Malete
P. M. B. 1530 Ilorin,
Nigeria.
E-mail: taofeek.wahab@kwasu.edu.ng
2: Paper Source
PDF document
Kamnoetvidya Science Academy, Rayong 21210
Thailand.
E-mail: atiratch.l@kvis.ac.th
Department of Mathematics and Computer Science,
Faculty of Science, Chulalongkorn University, Bangkok 10330
Thailand.
E-mail: ratinan.b@chula.ac.th
Faculty of Science, Chulalongkorn University, Bangkok 10330
Thailand.
E-mail:
6570104323@student.chula.ac.th
1: Paper Source
PDF document
bachir_ahmed@hotmail.com
sagres@hotmail.com
Paper's Title:
Monotonicity Properties for Generalized Logarithmic Means
Author(s):
Chao-Ping Chen and Feng Qi
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
chenchaoping@hpu.edu.cn
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
qifeng@hpu.edu.cn,
fengqi618@member.ams.org
Url:
http://rgmia.vu.edu.au/qi.html,
http://dami.hpu.edu.cn/qifeng.html
Abstract:
In this paper, we consider the monotonicity properties for ratio of two generalized logarithmic means, and then use it to extend and complement a recently published result of F. Qi and B.-N. Guo.
Paper's Title:
Reverses of the Triangle Inequality in Inner Product Spaces
Author(s):
Sever S. Dragomir
School of Computer Science and Mathematics,
Victoria University Of Technology,
PO Box 14428, Mcmc 8001,
Victoria, Australia.
sever@csm.vu.edu.au
Url:
http://rgmia.vu.edu.au/SSDragomirWeb.html
Abstract:
Some new reverses for the generalised triangle inequality in inner product spaces are given. Applications in connection to the Schwarz inequality and for vector-valued integrals are provided as well.
Paper's Title:
Reverse of Martin's Inequality
Author(s):
Chao-Ping Chen, Feng Qi, and Sever S. Dragomir
Department of Applied Mathematics and Informatics,
Research Institute of Applied
Mathematics,
Henan Polytechnic University,
Jiaozuo City, Henan 454010, China
chenchaoping@sohu.com;
chenchaoping@hpu.edu.cn
Department of Applied Mathematics and Informatics,
Research Institute of Applied
Mathematics,
Henan Polytechnic University,
Jiaozuo City, Henan 454010, China
qifeng@hpu.edu.cn
Url: http://rgmia.vu.edu.au/qi.html
School of Computer Science and Mathematics,
Victoria University of Technology,
P. O. Box 14428, Melbourne City Mc,
Victoria 8001, Australia
Sever.Dragomir@vu.edu.au
Url: http://rgmia.vu.edu.au/SSDragomirWeb.html
Abstract:
In this paper, it is proved that
for all natural numbers n, and all real r < 0.
Paper's Title:
On Vector Variational Inequality Problem in Terms of Bifunctions
Author(s):
C. S. Lalitha and Monika Mehta
Department of Mathematics, Rajdhani College,
Department of Mathematics, Satyawati College,
University of Delhi, Raja Garden,
Delhi 110015, India
cslalitha@rediffmail.com
University Of Delhi, Ashok Vihar,
Phase-III, Delhi 110052, India
mridul_in@yahoo.com
Abstract:
In this paper, we consider a generalized vector variational
inequality problem expressed in terms of a bifunction and establish
existence theorems for this problem by using the concepts of cone
convexity and cone strong quasiconvexity and employing the
celebrated Fan's Lemma. We also give two types of gap functions for this problem.
Paper's Title:
On the Fekete-Szeg
Author(s):
T.N. Shanmugam and A. Singaravelu
Department of Mathematics,
Department of Mathematics,
College of Engineering,
Anna University, Chennai-600 025,
Tamilnadu, India
shan@annauniv.edu
Valliammai Engineering College,
Chennai-603 203,
Tamilnadu, India
sivasaisastha@rediffmail.com
Abstract:
In this present investigation, the authors obtainFekete-Szegő's inequality for certain normalized analytic functions 
defined on the open
unit disk for which 
lie in a region starlike with
respect to 1 and symmetric with respect
to the real axis. Also certain applications of the main result for a class of functions
defined by convolution are given. As a special case of this result, Fekete-Szegő's inequality for a class of functions
defined through fractional derivatives is also obtained.
Paper's Title:
On Positive Entire Solutions of Second Order Quasilinear Elliptic Equations
Author(s):
Zuodong Yang and Honghui Yin
Institute of Mathematics, School of Mathematics and Computer Science,
Nanjing Normal University, Jiangsu Nanjing 210097,
China;
zdyang_jin@263.net
Department of Mathematics, Huaiyin Teachers College,
Jiangsu Huaian 223001,
China;
School of Mathematics and Computer Sciences,
Nanjing Normal University, Jiangsu Nanjing 210097,
China.
yin_hh@sina.com
Abstract:
In this paper, our main purpose is to establish the existence
theorem of positive entire solutions of second order quasilinear
elliptic equations under new conditions. The main results of the
present paper are new and extend the previously known results.
Paper's Title:
A Coefficient Inequality For Certain Subclasses of Analytic
Functions Related to Complex Order
Author(s):
B. Srutha Keerthi, B. Adolf Stephen and S. Sivasubramanian
Department Of Applied Mathematics, Sri Venkateswara College Of Engineering, Anna University,
Sriperumbudur, Chennai - 602 105,
India.
laya@svce.ac.in
Department of Mathematics, Madras Christian College,
Chennai - 600059,
India
adolfmcc2003@yahoo.co.in
Department of Mathematics, College of Engineering, Anna University,
Tamilnadu, Chennai - 600 025,
India.
sivasaisastha@rediffmail.com
Abstract:
In this present investigation, the authors obtain coefficient
inequality for certain normalized analytic functions of complex order f(z) defined
on the open unit disk for which
(
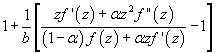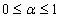and 
be a complex number) lies in a region starlike with respect to 1 and is symmetric with respect to the real axis. Also
certain applications of the main result for a class of functions of complex order
defined by convolution are given. As a special case of this result, coefficient
inequality for a class of functions defined through fractional derivatives is
obtained. The motivation of this paper is to give a generalization of the
coefficient inequalities of the subclasses of starlike and convex functions of
complex order.
Paper's Title:
Generalizations of Hermite-Hadamard's Inequalities for Log-Convex Functions
Author(s):
Ai-Jun Li
School of Mathematics and Informatics,
Henan Polytechnic University,
Jiaozuo City, Henan Province,
454010, China.
liaijun72@163.com
Abstract:
In this article, Hermite-Hadamard's inequalities are extended in
terms of the weighted power mean and log-convex
function. Several refinements, generalizations and related
inequalities are obtained.
Paper's Title:
Isoperimetric Inequalities for Dual Harmonic Quermassintegrals
Author(s):
Yuan Jun, Zao Lingzhi and Duan Xibo
School of Mathematics and Computer Science,
Nanjing Normal University, Nanjing, 210097,
China.
yuanjun_math@126.com
Department of Mathematics, Nanjing Xiaozhuang University,
Nanjing, 211171,
China.
lzhzhao@163.com
Department of Mathematics, Shandong Water Polytechnic,
Shandong, 276826,
China
dxb1111@sohu.com
Abstract:
In this paper, some isoperimetric inequalities for the dual harmonic
quermassintegrals are established.
Paper's Title:
Inequalities for
the
Author(s):
S. S. Dragomir
School of Engineering and Science
Victoria University, PO 14428
Melbourne City MC,
Victoria 8001,
Australia
sever.dragomir@vu.edu.au
URL: http://www.staff.vu.edu.au/RGMIA/dragomir/
Abstract:
Some recent inequalities for the Čebyšev functional of two functions of selfadjoint linear operators in Hilbert spaces, under suitable assumptions for the involved functions and operators, are surveyed.
Paper's Title:
Approximation of Derivatives in a Singularly Perturbed Second Order Ordinary Differential Equation with Discontinuous Terms Arising in Chemical Reactor Theory
Author(s):
R. Mythili Priyadharshini and N. Ramanujam
Department of Mathematics, Bharathidasan University,
Tiruchirappalli - 620 024, Tamilnadu, India.
matram2k3@yahoo.com
URL:
http://www.bdu.ac.in/depa/science/ramanujam.htm
Abstract:
In this paper, a singularly perturbed second order ordinary differential equation with a discontinuous convection coefficient arising in chemical reactor theory is considered. A robust-layer-resolving numerical method is suggested. An ε-uniform global error estimate for the numerical solution and also to the numerical derivative are established. Numerical results are provided to illustrate the theoretical results.
Paper's Title:
A Note On The Global Behavior Of A Nonlinear System of Difference Equations
Author(s):
Norman H. Josephy, Mihaela Predescu and Samuel W. Woolford
Department of Mathematical Sciences,
Bentley University,
Waltham, MA 02452,
U.S.A.
mpredescu@bentley.edu
njosephy@bentley.edu
swoolford@bentley.edu
Abstract:
This paper deals with the global asymptotic stability character of solutions of a discrete time deterministic model proposed by Wikan and Eide in Bulletin of Mathematical Biology, 66, 2004, 1685-1704. A stochastic extension of this model is proposed and discussed. Computer simulations suggest that the dynamics of the stochastic model includes a mixture of the dynamics observed in the deterministic model.
Paper's Title:
On the Boundedness of Hardy's Averaging Operators
Author(s):
Dah-Chin Luor
Department of Applied Mathematics,
I-Shou University, Dashu District,
Kaohsiung City 84001,
Taiwan, R.O.C.
dclour@isu.edu.tw
Abstract:
In this paper we establish scales of sufficient conditions for the boundedness of Hardy's averaging operators on weighted Lebesgue spaces. The estimations of the operator norms are also obtained. Included in particular are the Erdélyi-Kober operators.
Paper's Title:
A Geometric Generalization of Busemann-Petty Problem
Author(s):
Liu Rong and Yuan Jun
Shanghai Zhangjiang Group Junior Middle School,
Huo Xiang Road, Shanghai, 201203,
China
Abstract:
The norm defined by Busemann's inequality establishes a class of star body - intersection body. This class of star body plays a key role in the solution of Busemann-Petty problem. In 2003, Giannapoulos [1] defined a norm for a new class of half-section. Based on this norm, we give a geometric generalization of Busemann-Petty problem, and get its answer as a result
Paper's Title:
Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.
Paper's Title:
Dynamical Analysis of HIV/AIDS Epidemic Model with Two Latent Stages, Vertical Transmission and Treatment
Author(s):
Nur Shofianah, Isnani Darti, Syaiful Anam
Mathematics Department,Faculty of
Mathematics and Natural Sciences.
University of Brawijaya,
Jl. Veteran, Malang 65145,
Indonesia.
E-mail:
nur_shofianah@ub.ac.id,
isnanidarti@ub.ac.id,
syaiful@ub.ac.id
Abstract:
We discuss about dynamical analysis of HIV/AIDS epidemic model with two latent stages, vertical transmission and treatment. In this model, the spreading of HIV occurs through both horizontal and vertical transmission. There is also treatment for individual who has been HIV infected. The latent stage is divided into slow and fast latent stage based on the immune condition which varies for each individual. Dynamical analysis result shows that the model has two equilibrium points: the disease-free equilibrium point and the endemic equilibrium point. The existence and global stability of equilibrium points depend on the basic reproduction number R0. When R0 <1, only the disease-free equilibrium point exists. If R0 >1, there are two equilibrium points, which are the disease-free equilibrium point and the endemic equilibrium point. Based on the result of stability analysis, the disease-free equilibrium point is globally asymptotically stable if R0 <1, while if R0 > 1 and p=q, the endemic equilibrium point will be globally asymptotically stable. In the end, we show some numerical simulations to support the analytical result.
Paper's Title:
Kinematic Model for Magnetic Null-points in 2 Dimensions
Author(s):
Ali Khalaf Hussain Al-Hachami
Department of Mathematics,
College of Education For Pure Sciences,
Wasit University,
Iraq.
E-mail: alhachamia@uowasit.edu.iq
Abstract:
The adjacent configurations of two-dimensional magnetic null point centers are analyzed by an immediate examination about the null. The configurations are classified as either potential or non-potential. By then the non-potential cases are subdivided into three cases depending upon whether the component of current is less than, equal to or greater than a threshold current. In addition the essential structure of reconnection in 2D is examined. It unfolds that the manner by which the magnetic flux is rebuilt. In this paper, we center on the ramifications of kinematic arrangements; that is, we fathom just Maxwell's conditions and a resistive Ohm's law.
Paper's Title:
Inequalities for Functions of Selfadjoint Operators on Hilbert Spaces:
a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
College of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning inequalities for continuous functions of selfadjoint operators on complex Hilbert spaces. It is intended for use by both researchers in various fields of Linear Operator Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
The Effect of Harvesting Activities on Prey-Predator Fishery Model with Holling type II in Toxicant Aquatic Ecosystem
Author(s):
Moh Nurul Huda, Fidia Deny Tisna Amijaya, Ika Purnamasari
Department of Mathematics, Faculty of
Mathematics and Natural Science,
Mulawarman University,
Samarinda, East Kalimantan,75123
Indonesia.
E-mail: muh.nurulhuda@fmipa.unmul.ac.id
fidiadta@fmipa.unmul.ac.id
ika.purnamasari@fmipa.unmul.ac.id
Abstract:
This paper discussed prey-predator fishery models, in particular by analysing the effects of toxic substances on aquatic ecosystems. It is assumed in this model, that the prey population is plankton and the predator population is fish.\ Interaction between the two populations uses the Holling type II function. The existence of local and global critical points of the system are shown and their stability properties are analysed. Furthermore, Bionomic equilibrium and optimal control of harvesting are discussed. Finally, numerical simulations have been carried out to show in the interpretation of results.
Paper's Title:
Trace Inequalities for Operators in Hilbert Spaces: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
School of Engineering
& Science
Victoria University,
PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
In this paper we survey some recent trace inequalities for operators in Hilbert spaces that are connected to Schwarz's, Buzano's and Kato's inequalities and the reverses of Schwarz inequality known in the literature as Cassels' inequality and Shisha-Mond's inequality. Applications for some functionals that are naturally associated to some of these inequalities and for functions of operators defined by power series are given. Further, various trace inequalities for convex functions are presented including refinements of Jensen inequality and several reverses of Jensen's inequality. Hermite-Hadamard type inequalities and the trace version of Slater's inequality are given. Some Lipschitz type inequalities are also surveyed. Examples for fundamental functions such as the power, logarithmic, resolvent and exponential functions are provided as well.
Paper's Title:
A Fuzzy Soft Quotient Topology and Its Properties
Author(s):
Haripamyu, Riri Alfakhriati, Monika Rianti Helmi, Jenizon
Department of Mathematics and Data Science, Andalas University, Padang, Indonesia.
E-mail: haripamyu@sci.unand.ac.id
ririalfakhriati123@gmail.com
monikariantihelmi@sci.unand.ac.id
jenizon@gmail.com
Abstract:
This research is to construct a new topology on fuzzy soft set by using the concept of quotient topology. Then we study the concept of quotient map to define the fuzzy soft quotient map and provide some relevant properties of fuzzy soft quotient map. Furthermore, we give some examples related to fuzzy soft quotient topology and fuzzy soft quotient map to apply some properties of fuzzy soft quotient map.
Paper's Title:
Application of Chebyshev Polynomials to Volterra-Fredholm Integral Equations
Author(s):
Aissa Lakhal, Mostefa Nadir and Mohamed Nasseh Nadir
Department of Mathematics,
Faculty of Mathematics and
Informatics,
University of Msila,
Algeria.
E-mail:
aissa.lakhal@univ-msila.dz
mostefa.nadir@univ-msila.dz
nadir.mohamednasseh@yahoo.com
URL: https://www.mostefanadir.com
Abstract:
The goal of this work is to examine the numerical solution of linear Volterra-Fredholm integral equations of the second kind using the first, second, third and fourth Chebyshev polynomials. Noting that, the approximate solution is given in the form of series which converges to the exact one. Numerical examples are compared with other methods, in order to prove the applicability and the efficiency of this technical.
Paper's Title:
High Order Collocation Method for the Generalized Kuramoto-Sivashinsky Equation
Author(s):
Zanele Mkhize, Nabendra Parumasur and Pravin Singh
School of Mathematics, Statistics and
Computer Sciences,
University of KwaZulu-Natal,
Private Bag X 54001,
Durban 4000.
E-mail: mkhizez2@ukzn.ac.za
parumasurn1@ukzn.ac.za
singhp@ukzn.ac.za
URL: https://www.ukzn.ac.za
Abstract:
In this paper, we derive the heptic Hermite basis functions and use them as basis functions in the orthogonal collocation on finite elements (OCFE) method. We apply the method to solve the generalized Kuramoto-Sivashinsky equation. Various numerical simulations are presented to justify the computational efficiency of the proposed method.
Paper's Title:
Metric Functionals for the Hästö Metric
Author(s):
G. Bettencourt and S. Mendes
Departamento de Matemática,
Universidade da Beira Interior -
Covilhã Portugal,
Centro de Matemática e Aplicações
Universidade da Beira Interior -
Covilhã Portugal.
E-mail: gastao@ubi.pt
ISCTE - University Institute of Lisbon - Lisbon Portugal,
Centro de Matemática e Aplicações
Universidade da Beira Interior -
Covilhã Portugal.
E-mail: sergio.mendes@iscte-iul.pt
Abstract:
In 2002, new classes of weighted metrics on Rn were introduced by Peter Hästö. In this article we compute the metric functionals for such classes of metrics.
Paper's Title:
Fractional Integral Inequalities of Hermite-Hadamard Type for P-convex and Quasi-Convex Stochastic Process
Author(s):
Oualid Rholam, Mohammed Barmaki and Driss Gretet
National School of Applied Sciences (ENSA),
University Ibn Tofail,
B.P 242 Kenitra 14000,
phone number : +212606257757,
Morocco.
E-mail: oualid.rholam@uit.ac.ma
Science Faculty Ben M'sik,
University Hassan II,
B.P 7955 Av Driss El Harti Sidi Othmane 20700,
phone number : +212 5 22 70 46 71 ,
Morocco.
E-mail: mohammed.barmaki@uit.ac.ma
National School of Applied Sciences (ENSA),
University Ibn Tofail,
B.P 242 Kenitra 14000,
phone number : +212661403557,
Morocco.
E-mail: driss.gretete@uit.ac.ma
Abstract:
In this paper we consider the class of P-convex and Quasi-convex stochastic processes on witch we apply a general class of generalized fractional integral operator in order to establish new integral inequalities of Hermite-Hadammard type. then we obtain some results for well known types of fractional integrals. Results obtained in this paper may be starting point as well as a useful source of inspiration for further research in convex analysis.
Paper's Title:
Topological Aspects of Discrete Switch Dynamical Systems
Author(s):
Faiz Imam and Sharan Gopal
Department of Mathematics,
BITS - Pilani, Hyderabad Campus,
India.
E-mail: mefaizy@gmail.com
Department of Mathematics,
BITS - Pilani, Hyderabad Campus,
India.
E-mail: sharanraghu@gmail.com
ABSTRACT NOT FOUND. WEBSITE ERROR
Abstract:
Paper's Title:
Generalized Triangular and Symmetric Splitting Method for Steady State Probability Vector of Stochastic Matrices
Author(s):
B. Harika, D. Rajaiah, L. P. RajKumar, Malla Reddy Perati
Department of Mathematics,
Kakatiya University
E-mail: hbolledla@gmail.com
Department of Mathematics,
Kakatiya Institute of Technology and Science
E-mail: dr.mh@kitsw.ac.in
Department of Mathematics,
Kakatiya University
E-mail: ladalla@gmail.com
Department of Mathematics,
Kakatiya University
E-mail: mperati@yahoo.com
Abstract:
To find the steady state probability vector of homogenous linear system π Q=0 of stochastic rate matrix Q, generalized triangular and symmetric (GTS) splitting method is presented. Convergence analysis and choice of parameters are given when the regularized matrix A=QT+ε I of the regularized linear system Ax=b is positive definite. Analysis shows that the iterative solution of GTS method converges unconditionally to the unique solution of the regularized linear system. From the numerical results, it is clear that the solution of proposed method converges rapidly when compared to the existing methods.
Search and serve lasted 1 second(s).