|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
A Note On The Global Behavior Of A Nonlinear System of Difference Equations
Author(s):
Norman H. Josephy, Mihaela Predescu and Samuel W. Woolford
Department of Mathematical Sciences,
Bentley University,
Waltham, MA 02452,
U.S.A.
mpredescu@bentley.edu
njosephy@bentley.edu
swoolford@bentley.edu
Abstract:
This paper deals with the global asymptotic stability character of solutions of a discrete time deterministic model proposed by Wikan and Eide in Bulletin of Mathematical Biology, 66, 2004, 1685-1704. A stochastic extension of this model is proposed and discussed. Computer simulations suggest that the dynamics of the stochastic model includes a mixture of the dynamics observed in the deterministic model.
Paper's Title:
A Study of the Effect of Density Dependence in a Matrix Population Model
Author(s):
N. Carter and M. Predescu
Department of Mathematical Sciences,
Bentley University,
Waltham, MA 02452,
U.S.A.
ncarter@bentley.edu
mpredescu@bentley.edu
Abstract:
We study the behavior of solutions of a three dimensional discrete time nonlinear matrix population model. We prove results concerning the existence of equilibrium points, boundedness, permanence of solutions, and global stability in special cases of interest. Moreover, numerical simulations are used to compare the dynamics of two main forms of the density dependence function (rational and exponential).
Paper's Title:
Optimal Control Analysis of HIV/AIDS Epidemic Model with an Antiretroviral Treatment
Author(s):
U. Habibah and R. A. Sari
Mathematics Department and Reseach Group
of Biomathematics,
Faculty of Mathematics and Natural Science,
Brawijaya University, Jl. Veteran Malang 65145,
Indonesia.
E-mail: ummu_habibah@ub.ac.id
Abstract:
A mathematical model of HIV/AIDS is governed by a system of ordinary differential equations in the presence of an antiretroviral treatment (ARV). The theory of optimal control is applied to an epidemic model of HIV/AIDS which an ARV is used as a control strategy in order to prevent the spread of HIV/AIDS. The optimality system is derived by applying the Pontryagin's Minimum Principle. We analyze the boundedness and positivity of solutions, and an existence of the optimal control. Numerical simulations are conducted to obtain numerical solution of the optimally system.
Paper's Title:
The Effect of Harvesting Activities on Prey-Predator Fishery Model with Holling type II in Toxicant Aquatic Ecosystem
Author(s):
Moh Nurul Huda, Fidia Deny Tisna Amijaya, Ika Purnamasari
Department of Mathematics, Faculty of
Mathematics and Natural Science,
Mulawarman University,
Samarinda, East Kalimantan,75123
Indonesia.
E-mail: muh.nurulhuda@fmipa.unmul.ac.id
fidiadta@fmipa.unmul.ac.id
ika.purnamasari@fmipa.unmul.ac.id
Abstract:
This paper discussed prey-predator fishery models, in particular by analysing the effects of toxic substances on aquatic ecosystems. It is assumed in this model, that the prey population is plankton and the predator population is fish.\ Interaction between the two populations uses the Holling type II function. The existence of local and global critical points of the system are shown and their stability properties are analysed. Furthermore, Bionomic equilibrium and optimal control of harvesting are discussed. Finally, numerical simulations have been carried out to show in the interpretation of results.
Paper's Title:
SQIRV Model for Omicron Variant with Time Delay
Author(s):
S. Dickson, S. Padmasekaran, G. E. Chatzarakis and S. L. Panetsos
Mathematics, Periyar University, Periyar
Palkalai Nagar, Salem,
636011, Tamilnadu,
India.
E-mail:
dickson@periyaruniversity.ac.in,
padmasekarans@periyaruniversity.ac.in
Electrical and Electronic Engineering
Educators, School of
Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
spanetsos@aspete.gr
Abstract:
In order to examine the dynamics of the Omicron variant, this paper uses mathematical modelling and analysis of a SQIRV model, taking into account the delay in the conversion of susceptible individuals into infected individuals and infected individuals into recovered individuals. The pandemic was eventually controlled as a result of the massive delays. To assure the safety of the host population, this concept incorporates quarantine and the COVID-19 vaccine. Both local and global stability of the model are examined. It is found that the fundamental reproduction number affects both local and global stability conditions. Our findings show that asymptomatic cases caused by an affected population play an important role in increasing Omicron infection in the general population. The most recent data on the pandemic Omicron variant from Tamil Nadu, India, is verified.
Paper's Title:
The Dynamics of an Ebola Epidemic Model with Quarantine of Infectives
Author(s):
Eliab Horub Kweyunga
Department of Mathematics,
Kabale University,
P.O.Box 317, Kabale,
Uganda.
E-mail: hkweyunga@kab.ac.ug
Abstract:
The recurrent outbreaks of ebola in Africa present global health challenges. Ebola is a severe, very fatal disease with case fatality rates of up to 90%. In this paper, a theoretical deterministic model for ebola epidemic with quarantine of infectives is proposed and analyzed. The model exhibits two equilibria; the disease free and endemic equilibrium points. The basic reproduction number, R0, which is the main threshold, is obtained and the stability of the equilibrium points established. Using parameter values drawn from the 2014 West Africa ebola outbreak, a numerical simulation of the model is carried out. It is found that the dynamics of the model are completely determined by R0 and that a quarantine success rate of at least 70% is sufficient to contain the disease outbreak.
Paper's Title:
Jordan Canonical Form of Interval Matrices and Applications
Author(s):
S. Hema Surya, T. Nirmala and K. Ganesan
Department of Mathematics, College of
Engineering and Technology,
SRM Institute of Science and Technology,
Kattankulathur,
Chennai-603203,
India.
E-mail: nirmalat@srmist.edu.in
URL:
https://www.srmist.edu.in/faculty/dr-t-nirmala/
Abstract:
A square interval matrix over R can be converted to diagonal form if certain prerequisites are satisfied. However not all square matrices can be diagonalized. As a consequence, we strive the next simplest form to which it can be reduced while retaining important properties such as eigenvalues, rank, nullity, and so on. It turns out that any real interval matrix has a Jordan Canonical Form (JCF) over E if it has n interval eigenvalues in IR. We discuss in this paper a method for computing the Jordan canonical form of an interval matrix using a new pairing technique and a new type of interval arithmetic that will make classifying and analyzing interval matrices easier and more efficient. We conclude with a numerical example that supports the theory and application of predator-prey model.
Paper's Title:
A Comparison Between Two Different Stochastic Epidemic Models with Respect to the Entropy
Author(s):
Farzad Fatehi and Tayebe Waezizadeh
Department of Mathematics,
University of Sussex,
Brighton BN1 9QH,
UK.
E-mail: f.fatehi@sussex.ac.uk
URL:
http://www.sussex.ac.uk/profiles/361251
Department of Pure Mathematics, Faculty
of Mathematics and Computer,
Shahid Bahonar University of Kerman,
Kerman 76169-14111,
Iran.
E-mail: waezizadeh@uk.ac.ir
URL:
http://academicstaff.uk.ac.ir/en/tavaezizadeh
Abstract:
In this paper at first a brief history of mathematical models is presented with the aim to clarify the reliability of stochastic models over deterministic models. Next, the necessary background about random variables and stochastic processes, especially Markov chains and the entropy are introduced. After that, entropy of SIR stochastic models is computed and it is proven that an epidemic will disappear after a long time. Entropy of a stochastic mathematical model determines the average uncertainty about the outcome of that random experiment. At the end, we introduce a chain binomial epidemic model and compute its entropy, which is then compared with the DTMC SIR epidemic model to show which one is nearer to reality.
Paper's Title:
Invariant Subspaces Close to Almost Invariant Subspaces for Bounded Linear Operators
Author(s):
M. A. Farzaneh, A. Assadi and H. M. Mohammadinejad
Department of Mathematical and
Statistical Sciences,
University of Birjand,
PO Box 97175/615, Birjand,
Iran.
E-mail: farzaneh@birjand.ac.ir
Department of Mathematical and
Statistical Sciences,
University of Birjand,
PO Box 97175/615, Birjand,
Iran.
E-mail: assadi-aman@birjand.ac.ir
Department of Mathematical and
Statistical Sciences,
University of Birjand,
PO Box 97175/615, Birjand,
Iran.
E-mail: hmohammadin@birjand.ac.ir
Abstract:
In this paper, we consider some features of almost invariant subspace notion. At first, we restate the notion of almost invariant subspace and obtain some results. Then we try to achieve an invariant subspace completely close to an almost invariant subspace. Also, we introduce the notion of "almost equivalent subspaces" to simply the subject related to almost invariant subspaces and apply it.
Paper's Title:
Dynamical Analysis of HIV/AIDS Epidemic Model with Two Latent Stages, Vertical Transmission and Treatment
Author(s):
Nur Shofianah, Isnani Darti, Syaiful Anam
Mathematics Department,Faculty of
Mathematics and Natural Sciences.
University of Brawijaya,
Jl. Veteran, Malang 65145,
Indonesia.
E-mail:
nur_shofianah@ub.ac.id,
isnanidarti@ub.ac.id,
syaiful@ub.ac.id
Abstract:
We discuss about dynamical analysis of HIV/AIDS epidemic model with two latent stages, vertical transmission and treatment. In this model, the spreading of HIV occurs through both horizontal and vertical transmission. There is also treatment for individual who has been HIV infected. The latent stage is divided into slow and fast latent stage based on the immune condition which varies for each individual. Dynamical analysis result shows that the model has two equilibrium points: the disease-free equilibrium point and the endemic equilibrium point. The existence and global stability of equilibrium points depend on the basic reproduction number R0. When R0 <1, only the disease-free equilibrium point exists. If R0 >1, there are two equilibrium points, which are the disease-free equilibrium point and the endemic equilibrium point. Based on the result of stability analysis, the disease-free equilibrium point is globally asymptotically stable if R0 <1, while if R0 > 1 and p=q, the endemic equilibrium point will be globally asymptotically stable. In the end, we show some numerical simulations to support the analytical result.
Paper's Title:
Applications of Relations and Relators in the
Extensions of Stability Theorems for Homogeneous and Additive Functions
Author(s):
Árpád Száz
Institute of Mathematics, University of Debrecen,
H-4010 Debrecen,
Pf. 12,
Hungary
szaz@math.klte.hu
Abstract:
By working out an appropriate technique of relations and relators and extending the ideas of the direct methods of Z. Gajda and R. Ger, we prove some generalizations of the stability theorems of D. H. Hyers, T. Aoki, Th. M. Rassias and P. Găvruţă in terms of the existence and unicity of 2-homogeneous and additive approximate selections of generalized subadditive relations of semigroups to vector relator spaces. Thus, we obtain generalizations not only of the selection theorems of Z. Gajda and R. Ger, but also those of the present author.
Paper's Title:
Presentation a mathematical model for bone metastases control by using tamoxifen
Author(s):
Maryam Nikbakht, Alireza Fakharzadeh Jahromi and Aghileh Heydari
Department of Mathematics,
Payame Noor University,
P.O.Box 19395-3697, Tehran,
Iran.
.E-mail:
maryam_nikbakht@pnu.ac.ir
Department of Mathematics,
Faculty of Basic Science,
Shiraz University of Technology.
E-mail:
a_fakharzadeh@sutech.ac.ir
Department of Mathematics,
Payame Noor University,
P.O.Box 19395-3697, Tehran,
Iran.
E-mail: a-heidari@pnu.ac.ir
Abstract:
Bone is a common site for metastases (secondary tumor) because of breast and prostate cancer. According to our evaluations the mathematical aspect of the effect of drug in bone metastases has not been studied yet. Hence, this paper suggested a new mathematical model for bone metastases control by using tamoxifen. The proposed model is a system of nonlinear partial differential equations. In this paper our purpose is to present a control model for bone metastases. At end by some numerical simulations, the proposed model is examined by using physician.
Paper's Title:
The Voronovskaja Type Theorem for the Stancu Bivariate
Operators
Author(s):
Ovidiu T. Pop
National College "Mihai Eminescu",
5 Mihai Eminescu Street,
Satu Mare 440014, Romania
Vest University "Vasile Goldis" of
Arad, Branch of Satu Mare,
26 Mihai Viteazul Street
Satu Mare 440030, Romania
ovidiutiberiu@yahoo.com
Abstract:
In this paper, the Voronovskaja type theorem for the Stancu
bivariate operators is established. As particular cases, we shall
obtain the Voronovskaja type theorem for the Bernstein and Schurer
operators.
Paper's Title:
Stability Analysis Epidemic Model of SIR Type (Susceptible, Infectious, Recovered) On The Spread Dynamic of Malaria in Ambon City
Author(s):
Alwi Smith
Education Faculty, Biology Education
Programme,
University of Pattimura,
Ir. M. Putuhena Street, Poka Ambon, Moluccas, 97233,
Indonesia.
E-mail: alwi.smith1963@gmail.com
Abstract:
This research discusses the spread of malaria in Ambon city through SIR (Susceptible, Infected, Recovered) model. This research analyzes the stability of equilibrium point on deterministic model and Basic Reproduction Ratio (R0). The result shows that the epidemic model has two equilibrium points. They are disease free equilibrium, [E0=[S,I,R]=[1,0,0]], and epidemic equilibrium, Ei=[S,I,R]= [5,497808;-3,680341;-0,818288]. The Basic Reproduction Ratio of malaria disease in Ambon city is 0,181891. This result implies that malaria disease in Ambon will not be an endemic, because malaria disease in Ambon city will be eradicated slowly over time.
Paper's Title:
Hankel Operators on Copson's Spaces
Author(s):
Nicolae Popa
Institute of Mathematics of Romanian Academy,
P.O. BOX 1-764
RO-014700 Bucharest,
Romania.
E-mail: Nicolae.Popa@imar.ro, npopafoc@gmail.com
Abstract:
We give a characterization of boundedness of a Hankel matrix, generated by a pozitive decreasing sequence, acting on Copson's space cop(2).
Paper's Title:
Existence and Approximation of Traveling Wavefronts for the Diffusive Mackey-Glass Equation
Author(s):
C. Ramirez-Carrasco and J. Molina-Garay
Facultad de Ciencias Basicas,
Universidad Catolica del Maule, Talca,
Chile
E-mail: carloshrc1989@gmail.com
molina@imca.edu.pe
Abstract:
In this paper, we consider the diffusive Mackey-Glass model with discrete delay. This equation describes the dynamics of the blood cell production. We investigate the existence of traveling wavefronts solutions connecting the two steady states of the model. We develop an alternative proof of the existence of such solutions and we also demonstrate the existence of traveling wavefronts moving at minimum speed. The proposed approach is based on the use technique of upper-lower solutions. Finally, through an iterative procedure, we show numerical simulations that approximate the traveling wavefronts, thus confirming our theoretical results.
Paper's Title:
On Oscillation of
Second-Order Delay Dynamic Equations on Time Scales
Author(s):
S. H. Saker
Department of Mathematics, Faculty of Science,
Mansoura University, Mansoura, 35516,
Egypt.
shsaker@mans.edu.eg
Abstract:
Some new oscillation criteria for second-order linear delay dynamic equation
on a time scale T are established. Our results improve the
recent results for delay dynamic equations and in the special case when
T=R, the results include the oscillation results established by Hille [1948,
Trans. Amer. Math. Soc. 64 (1948), 234-252] and Erbe [Canad. Math. Bull. 16
(1973), 49-56.] for differential equations. When T=Z the
results include and improve some oscillation criteria for difference
equations. When T=hZ, h>0, T=qN and T=N2, i.e., for generalized second order delay difference equations our
results are essentially new and can be applied on different types of time
scales. An example is considered to illustrate the main results.
Paper's Title:
Some Inequalities for Gramian Normal Operators and for Gramian Self-Adjoint Operators in Pseudo-Hilbert Spaces
Author(s):
Loredana Ciurdariu
Department of Mathematics,"Politehnica" University of Timisoara,
P-ta. Victoriei, No.2, 300006-Timisoara,
ROMANIA
cloredana43@yahoo.com.
Abstract:
Several inequalities for gramian normal operators and for gramian self-adjoint operators in pseudo-Hilbert spaces are presented.
Paper's Title:
Properties of q-gamma and q-beta functions derived from the q-Gauss-Pólya inequalities
Author(s):
Sanja Varošanec
Department of Mathematics,
University of Zagreb,
Zagreb, Croatia
E-mail:
varosans@math.hr
Abstract:
We consider log-convexity and other properties of several functions related to q-gamma and q-beta functions. These properties are consequences of the general inequality, so-called q-analogue of the Gauss-Pólya inequality. Various inequalities involving these special functions are also given.
Paper's Title:
Mapped Chebyshev Spectral Methods for Solving Second Kind Integral Equations on the Real Line
Author(s):
Ahmed Guechi and Azedine Rahmoune
Department of Mathematics, University of Bordj Bou Arréridj,
El Anasser, 34030, BBA,
Algeria.
E-mail: a.guechi2017@gmail.com
E-mail: a.rahmoune@univ-bba.dz
Abstract:
In this paper we investigate the utility of mappings to solve numerically an important class of integral equations on the real line. The main idea is to map the infinite interval to a finite one and use Chebyshev spectral-collocation method to solve the mapped integral equation in the finite interval. Numerical examples are presented to illustrate the accuracy of the method.
Paper's Title:
Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.
Paper's Title:
Quantitative Estimates for Positive Linear Operators Obtained by Means of Piecewise Linear Functions
Author(s):
Vasile Mihesan
Technical University of Cluj-Napoca,
Department of Mathematics,
Str. C. Daicoviciu 15,
Cluj-Napoca,
Romania
Vasile.Mihesan@math.utcluj.ro
Abstract:
In this paper we obtain estimates for the remainder in approximating continuous
functions by positive linear operators, using piecewise linear functions.
Paper's Title:
Positive Periodic Time-Scale Solutions for Functional Dynamic Equations
Author(s):
Douglas R. Anderson and Joan Hoffacker
Department of Mathematics and Computer Science
Concordia College
Moorhead, MN 56562 USA
andersod@cord.edu
URL: http://www.cord.edu/faculty/andersod/
Department of Mathematical Sciences
Clemson University
Clemson, SC 29634 USA
johoff@clemson.edu
URL: http://www.math.clemson.edu/facstaff/johoff.htm
Abstract:
Using Krasnoselskii's fixed point theorem, we establish the existence of positive periodic solutions
to two pairs of related nonautonomous functional delta dynamic equations on periodic time scales, and then extend the discussion to higher-dimensional equations. Two pairs of corresponding nabla equations
are also provided in an analogous manner.
Paper's Title:
A general common fixed point theorem for reciprocally continuous mappings satisfying an implicit relation
Author(s):
A. Djoudi and A. Aliouche
Faculty of Science, University of Annaba,
P.O. Box 23000, Annaba,
Algeria.
adjoudi@yahoo.com
Department of Mathematics, University of Larbi Ben M'Hidi,
Oum-El-Bouaghi 04000,
Algeria.
abdmath@hotmail.com
Abstract:
A general common fixed point theorem for compatible mappings satisfying an
implicit relation is obtained by replacing the continuity of one mapping
by the reciprocal continuity of two mappings.
Paper's Title:
On a Method of Proving the Hyers-Ulam Stability
of Functional Equations on Restricted Domains
Author(s):
Janusz Brzdęk
Department of Mathematics
Pedagogical University Podchor
Abstract:
We show that generalizations of some (classical) results on the Hyers-Ulam stability of functional equations, in several variables, can be very easily derived from a simple result on stability of a functional equation in single variable
Paper's Title:
Approximation of an AQCQ-Functional Equation and its Applications
Author(s):
Choonkil Park and Jung Rye Lee
Department of Mathematics,
Research Institute for Natural Sciences,
Hanyang University, Seoul 133-791,
Korea;
Department of Mathematics,
Daejin University,
Kyeonggi 487-711,
Korea
baak@hanyang.ac.kr
jrlee@daejin.ac.kr
Abstract:
This paper is a survey on the generalized Hyers-Ulam stability of an AQCQ-functional equation in several spaces. Its content is divided into the following sections:
1. Introduction and preliminaries.
2. Generalized Hyers-Ulam stability of an AQCQ-functional equation in Banach spaces: direct method.
3. Generalized Hyers-Ulam stability of an AQCQ-functional equation in Banach spaces: fixed point method.
4. Generalized Hyers-Ulam stability of an AQCQ-functional equation in random Banach spaces: direct method.
5. Generalized Hyers-Ulam stability of an AQCQ-functional equation in random Banach spaces: fixed point method.
6. Generalized Hyers-Ulam stability of an AQCQ-functional equation in non-Archi-medean Banach spaces: direct method.
7. Generalized Hyers-Ulam stability of an AQCQ-functional equation in non-Archi-medean Banach spaces: fixed point method.
Paper's Title:
Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
A Low Order Least-Squares Nonconforming Finite Element Method for Steady Magnetohydrodynamic Equations
Author(s):
Z. Yu, D. Shi and H. Zhu
College of Science,
Zhongyuan
University of Technology,
Zhengzhou 450007,
China.
E-mail:
5772@zut.edu.cn
School of Mathematics and Statistics,
Zhengzhou University,
Zhengzhou 450001,
China.
E-mail:
shi_dy@126.com
Mathematics Department,
University of Southern Mississippi,
Hattiesburg MS, 39406,
U.S.A
E-mail:
huiqing.zhu@usm.edu
Abstract:
A low order least-squares nonconforming finite element (NFE) method is proposed for magnetohydrodynamic equations with EQ1rot element and zero-order Raviart-Thomas element. Based on the above element's typical interpolations properties, the existence and uniqueness of the approximate solutions are proved and the optimal order error estimates for the corresponding variables are derived.
Paper's Title:
On Admissible Mapping via Simulation Function
Author(s):
Anantachai Padcharoen and Pakeeta Sukprasert
Department of Mathematics,
Faculty of Science and Technology,
Rambhai Barni Rajabhat University,
Chanthaburi 22000,
Thailand.
E-mail: anantachai.p@rbru.ac.th
Department of Mathematics and Computer Science
Faculty of Science and Technology
Rajamangala University of Technology Thanyaburi (RMUTT),
Thanyaburi, Pathumthani 12110,
Thailand.
E-mail: pakeeta_s@rmutt.ac.th
Abstract:
In this paper, we present some fixed point results in complete metric spaces by using generalized admissible mapping embedded in the simulation function. Its applications, Our results used to study the existence problem of nonlinear Hammerstein integral equations.
Paper's Title:
Viability
Theory And Differential Lanchester Type Models For Combat.
Differential Systems.
Author(s):
G. Isac and A. Gosselin
Department Of
Mathematics, Royal Military College Of Canada,
P.O. Box 17000, Stn Forces, Kingston,
Ontario, Canada K7k 7b4
isac-g@rmc.ca
gosselin-a@rmc.ca
URL:
http://www.rmc.ca/academic/math_cs/isac/index_e.html
URL:
http://www.rmc.ca/academic/math_cs/gosselin/index_e.html
Abstract:
In 1914, F.W. Lanchester proposed several mathematical models based on differential equations to describe combat situations [34]. Since then, his work has been extensively modified to represent a variety of competitions including entire wars. Differential Lanchester type models have been studied from many angles by many authors in hundreds of papers and reports. Lanchester type models are used in the planning of optimal strategies, supply and tactics. In this paper, we will show how these models can be studied from a viability theory stand point. We will introduce the notion of winning cone and show that it is a viable cone for these models. In the last part of our paper we will use the viability theory of differential equations to study Lanchester type models from the optimal theory point of view.
Paper's Title:
Local and Global Existence and Uniqueness Results for Second and Higher Order Impulsive Functional Differential Equations with Infinite Delay
Author(s):
Johnny Henderson and Abdelghani Ouahab
Department of Mathematics, Baylor University,
Waco, Texas 76798-7328
USA.
Johnny_Henderson@baylor.edu
Laboratoire de Mathématiques, Université de Sidi Bel Abbés
BP 89, 22000 Sidi Bel Abbées,
Algérie.
ouahab@univ-sba.dz
Abstract:
In this paper, we discuss the local and global existence and
uniqueness results for second and higher order impulsive functional
differential equations with infinite delay. We shall rely on a
nonlinear alternative of Leray-Schauder. For the global existence
and uniqueness we apply a recent Frigon and Granas nonlinear
alternative of Leray-Schauder type in Fréchet spaces.
Paper's Title:
The Convergence of Modified Mann-Ishikawa Iterations when Applied to an Asymptotically Pseudocontractive Map
Author(s):
S. Soltuz
Departamento de Matematicas, Universidad de Los Andes, Carrera 1
No. 18A-10, Bogota,
Colombia
and
``T. Popoviciu" Institute of Numerical Analysis
Cluj-Napoca,
Romania
smsoltuz@gmail.com
URL:http://www.uniandes.edu.co/
Abstract:
We prove that under minimal conditions the modified Mann and Ishikawa iterations converge when dealing with an asymptotically pseudocontractive map. We give an affirmative answer to the open question from C.E. Chidume and H. Zegeye, Approximate fixed point sequences and convergence theorems for asymptotically pseudocontractive mappings, J. Math. Anal. Appl., 278 (2003), 354--366.
Paper's Title:
On Stan Ulam and his Mathematics
Author(s):
Krzysztof Ciesielski and Themistocles M. Rassias
Mathematics Institute, Jagiellonian University,
Abstract:
In this note we give a glimpse of the curriculum vitae of Stan Ulam, his personality and some of the mathematics he was involved in.
Paper's Title:
Ulam Stability of Functional Equations
Author(s):
Stefan Czerwik and Krzysztof Król
Institute of Mathematics
Silesian University of Technology
Kaszubska 23,
44-100 Gliwice,
Poland
Stefan.Czerwik@polsl.pl
Krzysztof.Krol@polsl.pl
Abstract:
In this survey paper we present some of the main results on Ulam-Hyers-Rassias stability for important functional equations.
Paper's Title:
An Improved Mesh Independence Principle for Solving Equations and their Discretizations using Newton's Method
Author(s):
Ioannis K. Argyros
Cameron university,
Department of Mathematics Sciences,
Lawton, OK 73505,
USA
iargyros@cameron.edu
Abstract:
We improve the mesh independence principle [1] which states that when Newton's method is applied to an equation on a Banach space as well as to their finite--dimensional discretization there is a difference of at most one between the number of steps required by the two processes to converge to within a given error tolerance. Here using a combination of Lipschitz and center Lipschitz continuity assumptions instead of just Lipschitz conditions we show that the minimum number of steps required can be at least as small as in earlier works. Some numerical examples are provided whereas our results compare favorably with earlier ones.
Paper's Title:
Hardy Type Inequalities via Convexity - The Journey so Far
Author(s):
James A.
Oguntuase and Lars-Erik Persson
Department of Mathematics,
University of Agriculture,
P. M. B. 2240, Abeokuta, Nigeria.
Department of
Mathematics, Luleå University of Technology,
SE-971 87, Luleå , Sweden.
oguntuase@yahoo.com,
larserik@sm.luth.se .
Abstract:
It is nowadays well-known that Hardy's inequality (like many other inequalities) follows directly from Jensen's inequality. Most of the development of Hardy type inequalities has not used this simple fact, which obviously was unknown by Hardy himself and many others. Here we report on some results obtained in this way mostly after 2002 by mainly using this fundamental idea.
Paper's Title:
On an Elliptic Over-Determined Problem in Dimension Two
Author(s):
Lakhdar Ragoub
Department of Mathematics and Information of Tiyadhechnology
AL Yamamah University
P.O. Box 45 180, Riyadh 11 512
Saudi Arabia.
Abstract:
We extend the method of Weinberger for a
non-linear over-determined elliptic problem
in R2.
We prove that the domain in consideration is a ball. The
tool of this investigation are maximum principles and P-functions.
Paper's Title:
Good and Special Weakly Picard Operators for the Stancu Operators with Modified Coefficients
Author(s):
Loredana-Florentina Galea and Alexandru-Mihai Bica
The Agora University of Oradea,
Piata Tineretului no. 8,
410526, Oradea,
Romania
University of Oradea,
Str. Universitatii No. 1,
410087, Oradea,
Romania
loredana.galea@univagora.ro
smbica@yahoo.com
abica@uoradea.ro
Abstract:
In this paper some properties of good and special weakly Picard operators for the Stancu operators with modified coefficients are obtained. In the study of the sequence of iterates of these operators, we obtain the property of dual monotone iteration.
Paper's Title:
Equivalence of the Nonsmooth Nonlinear Complementarity Problems to Unconstrained Minimization
Author(s):
M. A. Tawhid and J. L. Goffin
Department of Mathematics and Statistics,
School of Advanced Technologies and Mathematics,
Thompson Rivers University,
900 McGill Road, PO Box 3010, Kamloops, BC V2C 5N3
Canada
Alexandria University and Egypt Japan University of Science and Technology,
Alexandria-Egypt
mtawhid@tru.ca
Faculty of Management, McGill University,
1001 Sherbrooke Street West, Montreal, Quebec, H3A 1G5
Canada.
Jean-Louis.Goffin@McGill.ca
Abstract:
This paper deals with nonsmooth nonlinear complementarity problem, where the underlying functions are nonsmooth which admit the H-differentiability but not necessarily locally Lipschitzian or directionally differentiable. We consider a reformulation of the nonlinear complementarity problem as an unconstrained minimization problem. We describe H-differentials of the associated penalized Fischer-Burmeister and Kanzow and Kleinmichel merit functions. We show how, under appropriate P0, semimonotone (E0), P, positive definite, and strictly semimonotone (E) -conditions on an H-differential of f, finding local/global minimum of a merit function (or a `stationary point' of a merit function) leads to a solution of the given nonlinear complementarity problem. Our results not only give new results but also unify/extend various similar results proved for C1.
Paper's Title:
Some Properties of the Marshall-Olkin and Generalized Cuadras-Augé Families of Copulas
Author(s):
Edward Dobrowolski and Pranesh Kumar
Department of Mathematics and Statistics
University of Northern British Columbia
Prince George, BC,
Canada, V2N 4Z9
E-mail: Pranesh.Kumar@unbc.ca
Abstract:
We investigate some properties of the families of two parameter Marshall-Olkin and Generalized Cuadras-Augé copulas. Some new results are proved for copula parameters, dependence measure and mutual information. A numerical application is discussed.
Paper's Title:
Wavelet Frames in Higher Dimensional Sobolev Spaces
Author(s):
Raj Kumar, Manish Chauhan, and Reena
Department of Mathematics,
Kirori Mal College, University of Delhi,
New Delhi-110007,
India.
E-mail: rajkmc@gmail.com
Department of Mathematics,
University of Delhi,
New Delhi-110007,
India
E-mail: manish17102021@gmail.com
Department of Mathematics,
Hans Raj College, University of Delhi,
New Delhi-110007,
India
E-mail: reena.bhagwat29@gmail.com
Abstract:
In this paper, we present sufficient condition for the sequence
of vectors
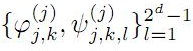to be a frame for Hs(Rd) are derived. Necessary and
sufficient conditions for the sequence of vectors
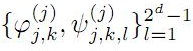to be tight wavelet frames in Hs(Rd) are obtained.
Further, as an application an example of tight wavelet frames for Hs(R2) as bivariate box spline over 3-direction are given.
Paper's Title:
Generalized k-distance-balanced Graphs
Author(s):
Amir Hosseini and Mehdi Alaeiyan
Department of mathematics, Karaj Branch,
Islamic Azad university, Karaj,
Iran.
E-mail: amir.hosseini@kiau.ac.ir,
hosseini.sam.52@gmail.com
Department of Mathematics,
Iran University of Science and Technology, Tehran,
Iran.
E-mail: alaeiyan@iust.ac.ir
Abstract:
A nonempty graph Γ is called generalized k-distance-balanced, whenever every edge ab has the following property: the number of vertices closer to a than to b, k, times of vertices closer to b than to a, or conversely, k∈ N .In this paper we determine some families of graphs that have this property, as well as to prove some other result regarding these graphs.
Paper's Title:
On a New Class of Eulerian's Type Integrals Involving Generalized Hypergeometric Functions
Author(s):
Sungtae Jun, Insuk Kim and Arjun K. Rathie
General Education Institute,
Konkuk University, Chungju 380-701,
Republic of Korea.
Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Republic of Korea.
Department of Mathematics,
Vedant College of Engineering and Technology (Rajasthan Technical University),
Bundi-323021, Rajasthan,
India.
E-mail: sjun@kku.ac.kr, iki@wku.ac.kr, arjunkumarrathie@gmail.com
Abstract:
Very recently Masjed-Jamei and Koepf established interesting and useful generalizations of various classical summation theorems for the 2F1, 3F2, 4F3, 5F4 and 6F5 generalized hypergeometric series. The main aim of this paper is to establish eleven Eulerian's type integrals involving generalized hypergeometric functions by employing these theorems. Several special cases have also been given.
Paper's Title:
An Analytical Solution of Perturbed Fisher's Equation Using Homotopy Perturbation Method (HPM), Regular Perturbation Method (RPM) and Adomian Decomposition Method (ADM)
Author(s):
Moussa Bagayogo, Youssouf Minoungou, Youssouf Pare
Departement de Mathematique,
Universite Ouaga I Pr Joseph Ki-Zerbo,
Burkina Faso.
E-mail:
moussabagayogo94@gmail.com,
m.youl@yahoo.fr,
pareyoussouf@yahoo.fr.
Abstract:
In this paper, Homotopy Perturbation Method (HPM), Regular Pertubation Method (RPM) and Adomian decomposition Method (ADM) are applied to Fisher equation. Then, the solution yielding the given initial conditions is gained. Finally, the solutions obtained by each method are compared
Paper's Title:
Formulation of Approximate Mathematical Model for Incoming Water to Some Dams on Tigris and Euphrates Rivers Using Spline Function
Author(s):
Nadia M. J. Ibrahem, Heba A. Abd Al-Razak, and Muna M. Mustafa
Mathematics Department,
College of Sciences for Women,
University of Baghdad, Baghdad,
Iraq.
E-mail:
Nadiamj_math@csw.uobaghdad.edu.iq
Abstract:
In this paper, we formulate three mathematical models using spline functions, such as linear, quadratic and cubic functions to approximate the mathematical model for incoming water to some dams. We will implement this model on dams of both rivers; dams on the Tigris are Mosul and Amara while dams on the Euphrates are Hadetha and Al-Hindya.
Paper's Title:
Solving Two Point Boundary Value Problems by Modified Sumudu Transform Homotopy Perturbation Method
Author(s):
Asem AL Nemrat and Zarita Zainuddin
School of Mathematical Sciences,
Universiti Sains Malaysia,
11800 Penang,
Malaysia.
E-mail: alnemrata@yahoo.com
zarita@usm.my
Abstract:
This paper considers a combined form of the Sumudu transform with the modified homotopy perturbation method (MHPM) to find approximate and analytical solutions for nonlinear two point boundary value problems. This method is called the modified Sumudu transform homotopy perturbation method (MSTHPM). The suggested technique avoids the round-off errors and finds the solution without any restrictive assumptions or discretization. We will introduce an appropriate initial approximation and furthermore, the residual error will be canceled in some points of the interval (RECP). Only a first order approximation of MSTHPM will be required, as compared to STHPM, which needs more iterations for the same cases of study. After comparing figures between approximate, MSTHPM, STHPM and numerical solutions, it is found through the solutions we have obtained that they are highly accurate, indicating that the MSTHPM is very effective, simple and can be used to solve other types of nonlinear boundary value problems (BVPs).
Paper's Title:
Optimization Techniques on Affine Differential Manifolds
Author(s):
Ali S Rasheed, Faik Mayah and Ahmed A H AL-Jumaili
Ministry of Higher Education and
Scientific Research,
Iraq.
E-mail: ahmedhashem@gmail.com
Department of Physics, College of
Sciences,
University of Wasit,
Iraq.
E-mail: faik.mayah@gmail.com
Abstract:
In addition to solid ground of Riemannian manifolds fundamentals, this article interviews some popular optimization methods on Riemannian manifolds. Several optimization problems can be better stated on manifolds rather than Euclidean space, such as interior point methods, which in turns based on self-concordant functions (logarithmic barrier functions). Optimization schemes like the steepest descent scheme, the Newton scheme, and others can be extended to Riemannian manifolds. This paper introduces some Riemannian and non-Riemannian schemes on manifolds.
Paper's Title:
Coexisting Attractors and Bubbling Route to Chaos in Modified Coupled Duffing Oscillators
Author(s):
B. Deruni1, A. S. Hacinliyan1,2, E. Kandiran3, A. C. Keles2, S. Kaouache4, M.-S. Abdelouahab4, N.-E. Hamri4
1Department
of Physics,
University of Yeditepe,
Turkey.
2Department
of Information Systems and Technologies,
University of Yeditepe,
Turkey
3Department
of Software Development,
University of Yeditepe,
Turkey.
4Laboratory
of Mathematics and their interactions,
University Center of Abdelhafid Boussouf,
Mila 43000,
Algeria.
E-mail:
berc890@gmail.com
ahacinliyan@yeditepe.edu.tr
engin.kandiran@yeditepe.edu.tr
cihan.keles@yeditepe.edu.tr
s.kaouache@centr-univ-mila.dz
medsalah3@yahoo.fr
n.hamri@centre-univ-mila.dz
Abstract:
In this article dynamical behavior of coupled Duffing oscillators is analyzed under a small modification. The oscillators have cubic damping instead of linear one. Although single duffing oscillator has complex dynamics, coupled duffing systems possess a much more complex structure. The dynamical behavior of the system is investigated both numerically and analytically. Numerical results indicate that the system has double scroll attractor with suitable parameter values. On the other hand, bifurcation diagrams illustrate rich behavior of the system, and it is seen that, system enters into chaos with different routes. Beside classical bifurcations, bubbling route to chaos is observed for suitable parameter settings. On the other hand, Multistability of the system is indicated with the coexisting attractors, such that under same parameter setting the system shows different periodic and chaotic attractors. Moreover, chaotic synchronization of coupled oscillators is illustrated in final section.
Paper's Title:
Semivectorial Bilevel Optimization on Affine-Finsler-Metric Manifolds
Author(s):
Faik Mayah1, Ali S Rasheed2 and Naseif J. Al- Jawari3
1Department of Physics,
College of Sciences,
University of Wasit,
Iraq.
E-mail: faik.mayah@gmail.com
2Ministry of Higher Education and Scientific Research,
Iraq.
E-mail: ali.math2018@yahoo.com
ahmedhashem@gmail.com
3Dept.
of Mathematics,
College of Science,
Mustansiriyah University, Baghdad,
Iraq.
E-mail: nsaif642014@yahoo.com
Abstract:
A Finsler manifold is a differential manifold together with a Finsler metric, in this paper we construct a new class of Finsler metric affine manifolds on bilevel semivectorial with optimization problems. The first steps for this purpose involve the study of bilevel optimization on affine manifolds. The bilevel programming problem can be viewed as a static version of the noncooperative, two-person game which was introduced in the context of unbalanced economic markets. Bilevel optimization is a special kind of optimization where one problem is embedded within another.
Paper's Title:
A New Method with Regularization for Solving Split Variational Inequality Problems in Real Hilbert Spaces
Author(s):
Francis Akutsah1 and Ojen Kumar Narain2
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 216040405@stu.ukzn.ac.za,
akutsah@gmail.com
2School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
In this paper, we introduce a new inertial extrapolation method with regularization for approximating solutions of split variational inequality problems in the frame work of real Hilbert spaces. We prove that the proposed method converges strongly to a minimum-norm solution of the problem without using the conventional two cases approach. In addition, we present some numerical experiments to show the efficiency and applicability of the proposed method. The results obtained in this paper extend, generalize and improve several results in this direction.
Paper's Title:
Li-Yorke and Expansivity for Composition Operators on Lorentz Space
Author(s):
Rajat Singh and Romesh Kumar
Department of Mathematics,
University of Jammu,
Jammu 180006,
INDIA.
E-mail: rajat.singh.rs634@gmail.com
Department of Mathematics,
University of Jammu,
Jammu 180006,
INDIA.
E-mail: romeshmath@gmail.com
Abstract:
In this paper, we investigate Li-Yorke composition operators and some of its variations on Lorentz spaces. Further, we also study expansive composition operators on these spaces. The work of the paper is essentially based on the work in [3], [6], [8] and [15].
Paper's Title:
On Automorphisms and Bi-derivations of Semiprime Rings
Author(s):
Abu Zaid Ansari, Faiza Shujat, Ahlam Fallatah
Department of Mathematics,
Faculty of Science,
Islamic University of Madinah, Madinah
K.S.A.
E-mail: ansari.abuzaid@gmail.com,
ansari.abuzaid@iu.edu.sa
Department of Mathematics
Faculty of Science
Taibah University, Madinah,
K.S.A.
E-mail: faiza.shujat@gmail.com,
fullahkhan@taibahu.edu.sa
Department of Mathematics
Faculty of Science
Taibah University, Madinah,
K.S.A.
E-mail: Afallatah@taibahu.edu.sa
Abstract:
In this article, our goal is to figure out a functional equation involving automorphisms and bi-derivations on certain semiprime ring. Also, we characterize the structure of automorphism, in case of prime rings.
Paper's Title:
ℵ0 Algebra and its Novel Application in Edge Detection
Author(s):
G. E. Chatzarakis1, S. Dickson2, S. Padmasekaran2, S. L. Panetsos1, and J. Ravi3
1Electrical
and Electronic Engineering Educators,
School of Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
spanetsos@aspete.gr
2Mathematics,
Periyar University,
Periyar Palkalai Nagar, Salem, 636011, Tamilnadu,
India.
E-mail: dix.bern@gmail.com,
padmasekarans@periyaruniversity.ac.in
3Department
of Mathematics, Amity University,
Bengaluru, Karnataka,
India.
E-mail:
jravistat@gmail.com
Abstract:
In this paper a new type of ℵ0-algebra has been defined. With its help, the fuzzy cross subalgebra and the fuzzy η-relation on the ℵ0-algebra are introduced and their respective properties are derived. Moreover, the fuzzy cross ℵ0-ideal of the ℵ0-algebra is defined with some theorems and intuitionistic fuzzy ℵ0-ideals of the ℵ0-algebra are introduced. This fuzzy algebra concept is applied in image processing to detect edges. This ℵ0-algebra is a novelty in the field of research.
Paper's Title:
Portfolio Optimization of Sharia and Non-Sharia Stocks Using Single Index Model (Case study: Jakarta Sharia Index and Kompas 100 Index)
Author(s):
Kwardiniya Andawaningtyas, Muhammad Luthfi, Marjono, Endang Wahyu Handamari, Umu S'adah, Evi Ardiyani
Department of Mathematics,
Brawijaya University, Malang,
Indonesia.
Department of Mathematics,
IPB University, Bogor,
Indonesia.
E-mail:
dina_math@ub.ac.id
muhammadluthfi@student.ub.ac.id
marjono@ub.ac.id
ewahyu-math@ub.ac.id
u.saadah@ub.ac.id
ardiyanievi@apps.ipb.ac.id
Abstract:
Stocks are instruments with high returns but also have increased risks. One way to overcome this risk is to form a stock portfolio. This study observed 30 sharia stocks listed on the Jakarta Islamic Index (JII) and 28 non-shariah stocks listed on the Kompas 100 Index from March 2020 to September 2022. The data used is the daily closing price of stocks, the number of stock dividends, and the daily closing price of the Jakarta Composite Index (JCI) from 3rd March 2020, to 31st August 2022. In addition, interest rate of Bank Indonesia Certificate (SBI) is used as risk-free rate. This study aims to optimize the sharia and non-sharia stocks portfolio using the Single Index Model (SIM), which will then be evaluated using the Sharpe, Treynor, and Jensen ratio. The result is that the optimal portfolio of sharia stocks have better performance than the optimal portfolio of non-sharia stocks based on the Treynor ratio. Meanwhile, the optimal portfolio of non-sharia stocks have better performance than the optimal portfolio of sharia stocks based on the Sharpe and Jensen ratio.
Paper's Title:
Oscillation Criteria for Second Order Delay Difference Equations via Canonical Transformations and Some New Monotonic Properties
Author(s):
R. Deepalakhmi, S. Saravanan, J. R. Graef, and E. Thandapani
Department of Interdisciplinary Studies
Tamil Nadu Dr. Ambedkar Law University
Chennai-600113,
India.
profdeepalakshmi@gmail.com
Madras School of Economics,
Chennai-600025,
India.
profsaran11@gmail.com
Department of Mathematics,
University of Tennessee at Chattanooga,
Chattanooga,TN 37403,
USA.
john-graef@utc.edu
Ramanujan Institute for Advanced Study in
Mathematics,
University of Madras,
Chennai - 600 005,
India.
ethandapani@yahoo.co.in
Abstract:
This paper is concerned with second-order linear noncanonical delay difference equations of the form
Δ(μ(t)Δ y(t))+ p(t)y(φ(t))=0.
The authors prove new oscillation criteria by first transforming the equation into canonical form and then obtaining some new monotonic properties of the positive solutions of the transformed equation. By using a comparison with first-order delay difference equations and a generalization of a technique developed by Koplatadze, they obtain their main results. Examples illustrating the improvement over known results in the literature are presented.
Search and serve lasted 1 second(s).