|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Solving Two Point Boundary Value Problems by Modified Sumudu Transform Homotopy Perturbation Method
Author(s):
Asem AL Nemrat and Zarita Zainuddin
School of Mathematical Sciences,
Universiti Sains Malaysia,
11800 Penang,
Malaysia.
E-mail: alnemrata@yahoo.com
zarita@usm.my
Abstract:
This paper considers a combined form of the Sumudu transform with the modified homotopy perturbation method (MHPM) to find approximate and analytical solutions for nonlinear two point boundary value problems. This method is called the modified Sumudu transform homotopy perturbation method (MSTHPM). The suggested technique avoids the round-off errors and finds the solution without any restrictive assumptions or discretization. We will introduce an appropriate initial approximation and furthermore, the residual error will be canceled in some points of the interval (RECP). Only a first order approximation of MSTHPM will be required, as compared to STHPM, which needs more iterations for the same cases of study. After comparing figures between approximate, MSTHPM, STHPM and numerical solutions, it is found through the solutions we have obtained that they are highly accurate, indicating that the MSTHPM is very effective, simple and can be used to solve other types of nonlinear boundary value problems (BVPs).
Paper's Title:
Recursive Bounds for the Eigenvalues of Symmetric Positive Definite Matrices
Author(s):
Pravin Singh, Shivani Singh, Virath Singh
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
University of South Africa,
Department of Decision Sciences, PO Box 392,
Pretoria,0003,
South Africa.
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
E-mail:
singhp@ukzn.ac.za,
singhs2@unisa.ac.za,
singhv@ukzn.ac.za
Abstract:
In this paper, we bound the extremal eigenvalues of a positive definite real symmetric matrix by considering a part of the characteristic equation in the region of the smallest and largest eigenvalues. An expansion around these values leads to a sequence of monotonic functions, whose zeros coincide with the extremal zeros of associated polynomials. The latter is shown to yield bounds that are fairly accurate.
Paper's Title:
New Coincidence and Fixed Point Theorems for Strictly Contractive Hybrid Maps
Author(s):
S. L. Singh and Amal M. Hashim
21, Govind Nagar, Rishikesh 249201,
Ua, India
vedicmri@sancharnet.in
Dept. of Math., College of Science,
Univ. of Basarah,
Iraq.
Abstract:
The purpose of this paper is to study the (EA)-property and noncompatible maps
of a hybrid pair of single-valued and multivalued maps in fixed point considerations. Such maps
have the remarkable property that they need not be continuous at their common fixed points. We
use this property to obtain some coincidence and fixed point theorems for strictly contractive
hybrid maps without using their continuity and completeness or compactness of the space.
Paper's Title:
Coincidences and Fixed Points of Hybrid Maps in Symmetric Spaces
Author(s):
S. L. Singh and Bhagwati Prasad
Vedic MRI, 21 Govind Nagar,
Department of Mathematics, Gurukula Kangri University,
Rishikesh 249201
India
vedicmri@gmail.com
Hardwar 249404,
India
Abstract:
The purpose of this paper is to obtain a new coincidence theorem for a
single-valued and two multivalued operators in symmetric spaces. We derive
fixed point theorems and discuss some special cases and applications.
Paper's Title:
Oblique Projectors from the Simpson Discrete Fourier Transformation Matrix
Author(s):
P. Singh and V. Singh
School of Mathematics, Computer Science
and Statistics,
University of Kwazulu-Natal,
Private Bag X54001, Durban 4001,
South Africa.
E-mail: singhp@ukzn.ac.za,
singhv@ukzn.ac.za
Abstract:
In this paper we examine the projectors of the Simpson Discrete Fourier Transform matrix of dimension two modulus four and show how they decompose the complex vector space into a direct sum of oblique eigenspaces. These projection operators are used to define a Simpson Discrete Fractional Fourier Transform (SDFRFT).
Paper's Title:
A Generalization of a Partial b-metric and Fixed Point Theorems
Author(s):
Pravin Singh and Virath Singh
Department of Mathematics, University of
KwaZulu-Natal,
Private Bag X54001, Durban,
South Africa.
E-mail: singhp@ukzn.ac.za
singhv@ukzn.ac.za
Abstract:
The purpose of this paper is to introduce the concept of a Partial α, β b-metric as a generalization of a partial b-metric and prove theorems for some contractive type mapping.
Paper's Title:
Introducing the Picard-S3 Iteration for Fixed Points
Author(s):
Pravin Singh, Virath Singh and Shivani Singh
University of KwaZulu-Natal,
School of Mathematics Statistics and Computer Sciences,
Private Bag X54001,
Durban, 4000
South Africa.
Unisa,
Department of Decision Sciences,
PO Box 392,
Pretoria, 0003
South Africa.
E-mail: singhprook@gmail.com
singhv@ukzn.ac.za
shivstarsingh@gmail.com
Abstract:
In this paper we introduce a three step iteration method and show that it can be used to approximate the fixed point of a weak contraction mapping. Furthermore, we prove that this scheme is equivalent to the Mann iterative scheme. A comparison is made with other three step iterative methods by examining the speed of convergence. Results are presented in tables to support our conclusion.
Paper's Title:
A Sum Form Functional Equation and Its Relevance in Information Theory
Author(s):
Prem Nath and Dhiraj Kumar Singh
Department of Mathematics
University of Delhi
Delhi - 110007
India
pnathmaths@gmail.com
dksingh@maths.du.ac.in
Abstract:
The general solutions of a sum form functional equation containing four unknown mappings have been investigated. The importance of these solutions in relation to various entropies in information theory has been emphasised.
Paper's Title:
A New Relaxed Complex-valued b-metric Type and Fixed Point Results
Author(s):
P. Singh, V. Singh and T. C. M. Jele
Department of Mathematics, University of
KwaZulu-Natal,
Private Bag X54001, Durban,
South Africa.
E-mail: singhp@ukzn.ac.za
singhv@ukzn.ac.za
thokozani.jele@nwu.ac.za
Abstract:
In this paper, we study the existence and uniqueness of fixed point in complex valued b-metric spaces and introduce a new relaxed α, β Complex-valued b-metric type by relaxing the triangle inequality and determine whether the fixed point theorems are applicable in these spaces.
Paper's Title:
Some Convergence Results for Jungck-Am Iterative Process In Hyperbolic Spaces
Author(s):
Akindele Adebayo Mebawondu and Oluwatosin Temitope Mewomo
School of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail:
216028272@stu.ukzn.ac.za,
mewomoo@ukzn.ac.za
Abstract:
In this paper, we introduce a new three steps iterative process called Jungck-AM iterative process and show that the proposed iterative process can be used to approximate fixed points of Jungck-contractive type mappings and Jungck-Suzuki type mappings. In addition, we establish some strong and Δ-convergence results for the approximation of fixed points of Jungck-Suzuki type mappings in the frame work of uniformly convex hyperbolic space. Furthermore, we show that the newly proposed iterative process has a better rate of convergence compare to the Jungck-Noor, Jungck-SP, Jungck-CR and some existing iterative processes in the literature. Finally, stability, data dependency results for Jungck-AM iterative process is established and we present an analytical proof and numerical examples to validate our claim.
Paper's Title:
Orthogonal Collocation on Finite Elements Using Quintic Hermite Basis
Author(s):
P. Singh, N. Parumasur and C. Bansilal
University of KwaZulu-Natal,
School of Mathematics Statistics and Computer Sciences,
Private Bag X54001,
Durban, 4000,
South Africa.
E-mail: singhprook@gmail.com
parumasurn1@ukzn.ac.za
christelle18@gmail.com
Abstract:
In this paper we consider the orthogonal collocation on finite elements (OCFE) method using quintic Hermite (second degree smooth) basis functions and use it to solve partial differential equations (PDEs). The method is particularly tailored to solve third order BVPS and PDEs and to handle their special solutions such as travelling waves and solitons, which typically is the case in the KdV equation. The use of quintic polynomials and collocation using Gauss points yields a stable high order superconvergent method. OCFE using quintic Hermite basis is optimal since it is computationally more efficient than collocation methods using (first degree smooth) piecewise-polynomials and more accurate than the (third degree smooth) B-splines basis. Various computational simulations are presented to demonstrate the computational efficiency and versatility of the OCFE method.
Paper's Title:
Bounds for the Extremal Eigenvalues of Positive Definite Matrices
Author(s):
Shivani Singh and Pravin Singh
Unisa, Department of Decision Sciences,
PO Box 392,
Pretoria,
0003,
South Africa.
E-mail: singhs2@unisa.ac.za
University of KwaZulu-Natal,
School of Mathematics Statistics and Computer Sciences
Private Bag X54001,
Durban,
4000,
South Africa.
E-mail: singhprook@gmail.com
Abstract:
We use a projection to achieve bounds for a vector function of the eigenvalues of a positive definite matrix. For various choices of the monotonic function we are able to obtain bounds for the extremal eigenvalues in terms of the traces of the matrix and its powers. These bounds are relatively simple to compute.
Paper's Title:
Results on Bounds of the Spectrum of Positive Definite Matrices by Projections
Author(s):
P. Singh, S. Singh, V. Singh
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
E-mail: singhp@ukzn.ac.za
University of South Africa, Department of
Decision Sciences,
PO Box 392, Pretoria, 0003,
South Africa.
E-mail: singhs2@unisa.ac.za
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
E-mail: singhv@ukzn.ac.za
Abstract:
In this paper, we develop further the theory of trace bounds and show that in some sense that the earlier bounds obtained by various authors on the spectrum of symmetric positive definite matrices are optimal. Our approach is by considering projection operators, from which several mathematical relationships may be derived. Also criteria for positive lower bounds are derived.
Paper's Title:
A New Relaxed b-metric Type and Fixed Point Results
Author(s):
P. Singh, V. Singh and Thokozani Cyprian Martin Jele
Department of Mathematics,
University of KwaZulu-Natal,
Private Bag X54001, Durban,
South Africa.
E-mail: singhp@ukzn.ac.za,
singhv@ukzn.ac.za,
thokozani.jele@nwu.ac.za
Abstract:
The purpose of this paper is to introduce a new relaxed α, β b-metric type by relaxing the triangle inequality. We investigate the effect that this generalization has on fixed point theorems.
Paper's Title:
Bicomplex Univalent Functions
Author(s):
Mohd Arif, Amjad Ali, Rajat Singh* and Romesh Kumar
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: azizymaths@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: amjadladakhi687@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: *rajat.singh.rs634@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: romeshmath@gmail.com
Abstract:
In this paper we introduce bicomplex univalent functions and also discuss the properties of a specific class of univalent functions.
Paper's Title:
Li-Yorke and Expansivity for Composition Operators on Lorentz Space
Author(s):
Rajat Singh and Romesh Kumar
Department of Mathematics,
University of Jammu,
Jammu 180006,
INDIA.
E-mail: rajat.singh.rs634@gmail.com
Department of Mathematics,
University of Jammu,
Jammu 180006,
INDIA.
E-mail: romeshmath@gmail.com
Abstract:
In this paper, we investigate Li-Yorke composition operators and some of its variations on Lorentz spaces. Further, we also study expansive composition operators on these spaces. The work of the paper is essentially based on the work in [3], [6], [8] and [15].
Paper's Title:
On Zeros of Diagonally Quasiconvex Multifunctions
Author(s):
Zoran D. Mitrović
Faculty of Electrical Engineering,
University of Banja Luka,
78000 Banja Luka, Patre 5
Bosnia and Herzegovina
zmitrovic@etfbl.net
Abstract:
In this paper, we extended the notion of diagonally quasiconvexity
for multifunctions and established several existence results for
zeros of diagonally quasiconvex multifunctions. As applications we
obtain the results of fixed points, coincidence points and best
approximations for multifunctions. Using our result we also prove
the existence of solutions to the variational-like inequality
problem and generalized vector equilibrium problem. The results
of this paper generalize some known results in the literature.
Paper's Title:
New Inequalities of Mill's Ratio and Application to The Inverse Q-function Approximation
Author(s):
Pingyi Fan
Department of Electronic Engineering,
Tsinghua University, Beijing,
China
Abstract:
In this paper, we investigate the Mill's ratio estimation problem and get two new inequalities. Compared to the well known results obtained by Gordon, they becomes tighter. Furthermore, we also discuss the inverse Q-function approximation problem and present some useful results on the inverse solution. Numerical results confirm the validness of our theoretical analysis. In addition, we also present a conjecture on the bounds of inverse solution on Q-function.
Paper's Title:
On a subset of Bazilevic functions
Author(s):
Marjono and D. K. Thomas
Department of Mathematics,
Faculty of Mathematics and Natural Sciences,
Brawajaya University,
Malang, Jawa Timur 65145,
Indonesia.
E-mail: marjono@ub.ac.id
Department of Mathematics,
Swansea University, Singleton Park,
Swansea, SA2 8PP,
United Kingdom.
E-mail: d.k.thomas@swansea.ac.uk
Abstract:
Let S denote the class of analytic and
univalent functions in
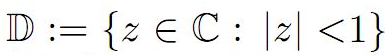of the form
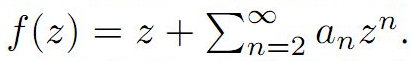For
α≥0, the subclass B1α of
S of Bazilevic functions has been extensively studied. In this paper we determine various properties of a subclass of B1α, for
α≥0 which extends early results of a class of starlike functions studied by Ram Singh.
Paper's Title:
The Higher Coefficients for Bazilevic Functions B1(α)
Author(s):
Marjono, Sa'adatul Fitri, and Krisna Adilia Daniswara
Department of Mathematics,
Faculty of Mathematics and Natural Sciences,,
Brawijaya University, Malang Jawa Timur 65145
Indonesia.
E-mail: marjono@ub.ac.id
saadatulfitri@ub.ac.id
krisnaadiliadaniswara@gmail.com
Abstract:
Let f be analytic in D{z: |z|< 1} with
, and normalized by the conditions f(0)=f'(0)-1=0. We give sharp estimates for the seventh and eighth coefficients for the class of Bazilevic functions with logarithmic growth,
B1α, defined by
for
α≥0.
Paper's Title:
High Order Collocation Method for the Generalized Kuramoto-Sivashinsky Equation
Author(s):
Zanele Mkhize, Nabendra Parumasur and Pravin Singh
School of Mathematics, Statistics and
Computer Sciences,
University of KwaZulu-Natal,
Private Bag X 54001,
Durban 4000.
E-mail: mkhizez2@ukzn.ac.za
parumasurn1@ukzn.ac.za
singhp@ukzn.ac.za
URL: https://www.ukzn.ac.za
Abstract:
In this paper, we derive the heptic Hermite basis functions and use them as basis functions in the orthogonal collocation on finite elements (OCFE) method. We apply the method to solve the generalized Kuramoto-Sivashinsky equation. Various numerical simulations are presented to justify the computational efficiency of the proposed method.
Paper's Title:
Eigenvalue Bounds based on Projections
Author(s):
Pravin Singh, Shivani Singh, Virath Singh
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
University of South Africa,
Department of Decision Sciences, PO Box 392,
Pretoria,0003,
South Africa.
University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.
E-mail:
singhp@ukzn.ac.za,
singhs2@unisa.ac.za,
singhv@ukzn.ac.za
Abstract:
In this paper, we derive expressions for the bounds of the extremal eigenvalues of positive definite matrices. Our approach is to use a symmetric projection operator onto an n-2 dimensional subspace of the real space of n tuples. These bounds are based on traces of the matrix and its powers. They are relatively easy and inexpensive to compute.
Paper's Title:
Essential Random Fixed Point Set of Random Operators
Author(s):
Ismat Beg
Centre for Advanced Studies in Mathematics,
Lahore University of Management Sciences (LUMS),
54792-Lahore, PAKISTAN.
ibeg@lums.edu.pk
URL: http://web.lums.edu.pk/~ibeg
Abstract:
We obtain necessary and sufficient conditions for the existence of essential random fixed point of a random operator defined on a compact metric space. The structure of the set of essential random fixed points is also studied.
Paper's Title:
Generalized Hypergeometric Functions Defined on the Class of Univalent Functions
Author(s):
N. Marikkannan, A. Gangadharan and C. Ganesamoorthy
Department of Applied Mathematics,
Sri Venkateswara College of Engineering,
Sriperumbudur 602105,
India.
mari@svce.ac.in
Department of Applied mathematics,
Sri Venkateswara College of Engineering,
Sriperumbudur 602105,
India.
ganga@svce.ac.in
Department of Mathematics,
Alagappa university,
Karaikudi,
India.
ganesamoorthyc@yahoo.com
Abstract:
Let A denotes the class of all analytic functions
f(z), normalized by the condition f'(0)-1=f(0)=0 defined on
the open unit disk
Paper's Title:
Salagean-type Harmonic Univalent Functions with Respect to Symmetric Points
Author(s):
R. A. Al-Khal and H. A. Al-Kharsani
Department of Mathematics, Faculty of Science, Girls College,
P.O. Box 838,
Dammam, Saudi Arabia
ranaab@hotmail.com
hakh@hotmail.com
Abstract:
A necessary and sufficient coefficient are given for functions in a class of
complex-valued harmonic univalent functions of the form f=h+\g
using Salagean operator where h and g are analytic in the unit disk
U = {z:|z|<1}. Furthermore, distortion theorems, extreme points,
convolution condition, and convex combinations for this family of harmonic
functions are obtained.
Paper's Title:
Some Inequalities for a Certain Class of Multivalent Functions
Using Multiplier Transformation
Author(s):
K. Suchithra, B. Adolf Stephen, A. Gangadharan and S. Sivasubramanian
Department Of Applied Mathematics
Sri Venkateswara College Of Engineering
Sriperumbudur, Chennai - 602105,
India.
suchithravenkat@yahoo.co.in
Department Of Mathematics,
Madras Christian College
Chennai - 600059,
India.
adolfmcc2003@yahoo.co.in
Department Of Applied Mathematics
Sri Venkateswara College Of Engineering
Sriperumbudur, Chennai - 602105,
India.
ganga@svce.ac.in
Department Of Mathematics,
Easwari Engineering College
Ramapuram, Chennai - 600089,
India.
ganga@svce.ac.in
Abstract:
The object of the present paper is to derive several inequalities
associated with differential subordinations between analytic functions
and a linear operator defined for a certain family of p-valent
functions, which is introduced here by means of a family of extended
multiplier transformations. Some special cases and consequences of
the main results are also considered.
Paper's Title:
Fekete-Szegö Problem for Univalent Functions with Respect to k-Symmetric
Points
Author(s):
K. Al-Shaqsi and M. Darus
School of Mathematical Sciences, Faculty of Science and Technology,
University Kebangsaan Malaysia,
Bangi 43600 Selangor D. Ehsan,
Malaysia
ommath@hotmail.com
maslina@ukm.my
Abstract:
In the present investigation, sharp upper bounds of |a3- μa22|
for functions f(z) = z + a2z2 + a2z3 + ... belonging to certain subclasses
of starlike and convex functions with respect to k-symmetric points are
obtained. Also certain applications of the main results for subclasses of
functions defined by convolution with a normalized analytic function are
given. In particular, Fekete- Szeg
Paper's Title:
Common Fixed Point Results for Banach Operator Pairs and Applications to Best Approximation
Author(s):
Hemant Kumar Nashine
Department of Mathematics,
Disha Institute of Management and Technology,
Satya Vihar, Vidhansabha - Chandrakhuri Marg (Baloda Bazar Road),
Mandir Hasaud,
Raipur - 492101(Chhattisgarh), India.
hemantnashine@rediffmail.com
nashine_09@rediffmail.com
Abstract:
The common fixed point results for Banach operator pair with generalized nonexpansive mappings in q-normed space have been obtained in the present work. As application, some more general best approximation results have also been determined without the assumption of linearity or affinity of mappings. These results unify and generalize various existing known results with the aid of more general class of noncommuting mappings.
Paper's Title:
Hankel Functional Connected to Lemniscate of Bernoulli
Author(s):
K. Ramanuja Rao, Rajnesh Lal and Kaushal Singh
Fiji National University,
Department of Mathematics & Statistics,
P.O. Box 5529, Lautoka,
Fiji.
E-mail: ramanuja.kotti@fnu.ac.fj
rajnesh.lal@fnu.ac.fj
kaushal.singh@fnu.ac.fj
Abstract:
The aim of present paper is to derive a higher bound (HB) of 3rd order Hankel determinant for a collection of holomorphic mappings connected with exactly to the right side of the lemniscate of Bernoulli, whose polar coordinates form is r2 = 2cos2(2θ). The method carried in this paper is more refined than the method adopted by the authors (see [1]), who worked on this problem earlier.
Paper's Title:
On Trigonometric Approximation of Continuous Functions by Deferred Matrix Means
Author(s):
Xhevat Zahir Krasniqi
Faculty of Education,
University of Prishtina "Hasan Prishtina",
Avenue "Mother Theresa " no. 5, Prishtinë
10000,
Republic of Kosovo.
E-mail: xhevat.krasniqi@uni-pr.edu
URL:
https://staff.uni-pr.edu/profile/xhevatkrasniqi
Abstract:
In this paper, for the first time, we introduce the deferred matrix means which contain the well-known generalized deferred Nörlund, deferred Nörlund, deferred Riesz, deferred Cesŕro means introduced earlier by others, and a new class of sequences (predominantly a wider class than the class of Head Bounded Variation Sequences). In addition, using the deferred matrix means of Fourier series of a continuous function, we determine the degree of approximation of such function via its modulus of continuity and a positive mediate function.
Paper's Title:
Fekete Szegö problem on the Class of Bazilevič functions B1(α) related to the Lemniscate Bernoulli
Author(s):
N. M. Asih, Marjono, Sa'adatul Fitri, Ratno Bagus Edy Wibowo
Department of Mathematics,
University of Brawijaya,
Malang 65145,
Indonesia.
Department of Mathematics,
University of Udayana,
Bali,
Indonesia.
E-mail: madeasih@unud.ac.id
Department of Mathematics,
University of Brawijaya,
Malang 65145,
Indonesia.
E-mail: marjono@ub.ac.id
Department of Mathematics,
University of Brawijaya,
Malang 65145,
Indonesia.
E-mail: saadatulfitri@ub.ac.id
Department of Mathematics,
University of Brawijaya,
Malang 65145,
Indonesia.
E-mail: rbagus@ub.ac.id
Abstract:
We provide a sharp boundaries inequalities for Fekete Szegö problem |a3-μ a22|, the coefficients of logarithmic function log~ f(z)/z, and the coefficients of the inverse function f(f'(w)) on the Bazilevič functions B1(α) related to the Lemniscate Bernoulli on the unit disk D={z: |z| < 1}. We obtained the result by using some properties of function with positive real part relates to coefficients problems.
Paper's Title:
Semigroup of Linear Operator In Bicomplex Scalars
Author(s):
Stanzin Kunga, Amjad Ali and Aditi Sharma
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: stanzinkunga19@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail:
amjadladakhi687@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: aditi.sharmaro@gmail.com
Abstract:
In this paper, we have studied the generators of C0-semigroups of bicomplex linear operators on BC-Banach modules. This work is based on [5].
Paper's Title:
Results Concerning Fixed Point for Soft Weakly Contraction In Soft Metric Spaces
Author(s):
Abid Khan, Santosh Kumar Sharma, Anurag Choubey, Girraj Kumar Verma, Umashankar Sharma, Ramakant Bhardwaj
Department of Mathematics,
AUMP, Gwalior,
India.
abid69304@gmail.com
Department of Mathematics,
AUMP, Gwalior,
India.
sksharma1@gwa.amity.edu
Department of Computer Science,
Technocrats Institute of Technology,
Bhopal, MP,
India.
directoracademicstit@gmail.com
Department of Mathematics,
AUMP, Gwalior,
India.
gkverma@gwa.amity.edu
Department of Physics,
RJIT BSF Tekanpur, MP,
India.
ussharma001@gmail.com
School of Applied Science
AUK, WB,
India.
rkbhardwaj100@gmail.com
Abstract:
The basic objective of the proposed research work is to make people acquainted with the concept of soft metric space by generalizing the notions of soft (ψ,φ)-weakly contractive mappings in soft metric space, as well as to look at specific fundamental and topological parts of the underlying spaces. A compatible example is given to explain the idea of said space structure. The theory is very useful in decision making problems and secure transmission as fixed point provides exact output. The fixed-point theorems on subsets of Rm that are useful in game theoretic settings.
Paper's Title:
Fekete-Szegö Inequality for Certain Class of Analytic Functions
Author(s):
V. Ravichandran, Maslina Darus, M. Hussain Khan, and K. G. Subramanian
School of
Mathematical Sciences, Universiti Sains Malaysia,
11800 Usm, Penang, Malaysia
vravi@cs.usm.my
School of
Mathematical Sciences, Faculty of Sciences and Technology,
Ukm, Banki 43600, Malaysia
maslina@pkrisc.cc.ukm.my
Department of
Mathematics, Islamiah College,
Vaniambadi 635 751, India
Department of
Mathematics, Madras Christian College, Tambaram,
Chennai- 600 059, India
kgsmani@vsnl.net
Abstract:
In this present investigation, the authors obtain Fekete-Szegö inequality for a certain
class of analytic functions f(z) for which
lies in a
region starlike with respect to 1 and symmetric with respect to the real axis. Also certain application
of our main result for a class of functions defined by Hadamard product (convolution) is
given. As a special case of our result we obtain Fekete-Szegö inequality for a class of functions
defined through fractional derivatives. Also we obtain Fekete-Szegö inequality for the inverse
functions.
Paper's Title:
On ε-simultaneous Approximation in Quotient Spaces
Author(s):
H. Alizadeh, Sh. Rezapour, S. M. Vaezpour
Department of
Mathematics, Aazad
Islamic University, Science and Research Branch, Tehran,
Iran
Department of Mathematics, Azarbaidjan
University of Tarbiat Moallem, Tabriz,
Iran
Department of Mathematics, Amirkabir
University of Technology, Tehran,
Iran
alizadehhossain@yahoo.com
sh.rezapour@azaruniv.edu
vaez@aut.ac.ir
URL:http://www.azaruniv.edu/~rezapour
URL:http://math-cs.aut.ac.ir/vaezpour
Abstract:
The purpose of this paper is
to develop a theory of best simultaneous approximation to
ε-simultaneous approximation. We shall introduce the
concept of ε-simultaneous pseudo Chebyshev,
ε-simultaneous quasi Chebyshev and
ε-simultaneous weakly Chebyshev subspaces of a Banach
space. Then, it will be determined under what conditions these
subspaces are transmitted to and from quotient spaces.
Paper's Title:
On the Degree of Approximation of Continuous Functions that Pertains to the Sequence-To-Sequence Transformation
Author(s):
Xhevat Z. Krasniqi
University of Prishtina,
Department of Mathematics and Computer Sciences,
5
Mother Teresa Avenue, Prishtinë, 10000,
Republic of Kosovo.
Abstract:
In this paper we prove analogous theorems like Leindler's 3 using the so-called A-transform of the B-transform of the partial sums of Fourier series. In addition, more than two such transforms are introduced and for them analogous results are showed as well.
Paper's Title:
A Subordination Theorem for Analytic Functions
Author(s):
Marjono
Department of Mathematics, Faculty of
Mathematics and Natural Sciences,
University of Brawijaya,
Jl. Veteran Malang 65145,
INDONESIA.
E-mail: marjono@ub.ac.id
URL: http://matematika.ub.ac.id
Abstract:
It is shown that if f is analytic in D={z:|z|<1}, with
f(0)=f'(0)-1=0, then for
implies
where
and that
β(γ) is the largest number such that this implication holds.
Paper's Title:
New Implicit Kirk-Type Schemes for General Class of Quasi-Contractive Operators in Generalized Convex Metric Spaces
Author(s):
K. Rauf, O. T. Wahab and A. Ali
Department of Mathematics,
University of Ilorin, Ilorin,
Nigeria.
E-mail: krauf@unilorin.edu.ng
Department of Statistics and Mathematical
Sciences,
Kwara State University, Malete,
Nigeria.
Department of Mathematics,
Mirpur University of Science and Technology, Mirpur,
Pakistan.
Abstract:
In this paper, we introduce some new implicit Kirk-type iterative schemes in generalized convex metric spaces in order to approximate fixed points for general class of quasi-contractive type operators. The strong convergence, T-stability, equivalency, data dependence and convergence rate of these results were explored. The iterative schemes are faster and better, in term of speed of convergence, than their corresponding results in the literature. These results also improve and generalize several existing iterative schemes in the literature and they provide analogues of the corresponding results of other spaces, namely: normed spaces, CAT(0) spaces and so on.
Paper's Title:
Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.
Paper's Title:
Some Inequalities of the Hermite-Hadamard Type for k-Fractional Conformable Integrals
Author(s):
C.-J. Huang, G. Rahman, K. S. Nisar, A. Ghaffar and F. Qi
Department of Mathematics, Ganzhou Teachers College,
Ganzhou 341000, Jiangxi,
China.
E-mail:
hcj73jx@126.com ,
huangcj1973@qq.com
Department of Mathematics, Shaheed Benazir
Bhutto University,
Sheringal, Upper Dir, Khyber Pakhtoonkhwa,
Pakistan.
E-mail: gauhar55uom@gmail.com
Department of Mathematics, College of Arts
and Science at Wadi Aldawaser, 11991,
Prince Sattam Bin Abdulaziz University, Riyadh Region,
Kingdom of Saudi Arabia.
E-mail: n.sooppy@psau.edu.sa,
ksnisar1@gmail.com
Department of Mathematical Science,
Balochistan University of Information Technology,
Engineering and Management Sciences, Quetta,
Pakistan.
E-mail: abdulghaffar.jaffar@gmail.com
School of Mathematical Sciences, Tianjin
Polytechnic University,
Tianjin 300387,
China; Institute of Mathematics,
Henan Polytechnic University, Jiaozuo 454010, Henan,
China.
E-mail: qifeng618@gmail.com,
qifeng618@qq.com
Abstract:
In the paper, the authors deal with generalized k-fractional conformable integrals, establish some inequalities of the Hermite-Hadamard type for generalized k-fractional conformable integrals for convex functions, and generalize known inequalities of the Hermite-Hadamard type for conformable fractional integrals.
Paper's Title:
On an extension of Edwards's double integral with applications
Author(s):
I. Kim, S. Jun, Y. Vyas and A. K. Rathie
Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Republic of Korea.
General Education Institute,
Konkuk University,
Chungju 380-701,
Republic of Korea.
Department of Mathematics, School of
Engineering,
Sir Padampat Singhania University,
Bhatewar, Udaipur, 313601, Rajasthan State,
India.
Department of Mathematics,
Vedant College of Engineering and Technology,
(Rajasthan Technical University),
Bundi-323021, Rajasthan,
India.
E-mail: iki@wku.ac.kr
sjun@kku.ac.kr
yashoverdhan.vyas@spsu.ac.in
arjunkumarrathie@gmail.com
Abstract:
The aim of this note is to provide an extension of the well known and useful Edwards's double integral. As an application, new class of twelve double integrals involving hypergeometric function have been evaluated in terms of gamma function. The results are established with the help of classical summation theorems for the series 3F2 due to Watson, Dixon and Whipple. Several new and interesting integrals have also been obtained from our main findings.
Paper's Title:
A new approach to the study of fixed point for simulation functions with application in G-metric spaces
Author(s):
Komi Afassinou and Ojen Kumar Narain
Department of Mathematical Sciences,
University of Zululand,
KwaDlangezwa,
South Africa.
E-mail: komia@aims.ac.za
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
The purpose of this work is to generalize the fixed point results of Kumar et al. [11] by introducing the concept of (α,β)-Z-contraction mapping, Suzuki generalized (α,β)-Z-contraction mapping, (α,β)-admissible mapping and triangular (α,β)-admissible mapping in the frame work of G-metric spaces. Fixed point theorems for these class of mappings are established in the frame work of a complete G-metric spaces and we establish a generalization of the fixed point result of Kumar et al. [11] and a host of others in the literature. Finally, we apply our fixed point result to solve an integral equation.
Paper's Title:
Some fixed point results in partial S-metric spaces
Author(s):
M. M. Rezaee, S. Sedghi, A. Mukheimer, K. Abodayeh, and Z. D. Mitrovic
Department of Mathematics, Qaemshahr
Branch,
Islamic Azad University, Qaemshahr,
Iran.
E-mail: Rezaee.mohammad.m@gmail.com
Department of Mathematics, Qaemshahr
Branch,
Islamic Azad University, Qaemshahr,
Iran.
E-mail: sedghi.gh@qaemiau.ac.ir
Department of Mathematics and General
Sciences,
Prince Sultan University, Riyadh,
KSA.
E-mail: mukheimer@psu.edu.sa
Department of Mathematics and General
Sciences,
Prince Sultan University, Riyadh,
KSA.
E-mail: kamal@psu.edu.sa
Nonlinear Analysis Research Group,
Faculty of Mathematics and Statistics,
Ton Duc Thang University, Ho Chi Minh City,
Vietnam.
E-mail: zoran.mitrovic@tdtu.edu.vn
Abstract:
We introduce in this article a new class of generalized metric spaces, called partial S-metric spaces. In addition, we also give some interesting results on fixed points in the partial S-metric spaces and some applications.
Paper's Title:
On The Degree of Approximation of Periodic Functions from Lipschitz and Those from Generalized Lipschitz Classes
Author(s):
Xhevat Z. Krasniqi
Faculty of Education,
University of Prishtina "Hasan Prishtina",
Avenue "Mother Theresa " no. 5, Prishtinë
10000,
Republic of Kosovo.
E-mail: xhevat.krasniqi@uni-pr.edu
Abstract:
In this paper we have introduced some new trigonometric polynomials. Using these polynomials, we have proved some theorems which determine the degree of approximation of periodic functions by a product of two special means of their Fourier series and the conjugate Fourier series. Many results proved previously by others are special case of ours.
Paper's Title:
Existence of Solution of Differential and Riemann-Liouville Equation Via Fixed Point Approach in Complex Valued b-Metric Spaces
Author(s):
K. Afassinou, A. A. Mebawondu, H. A. Abass and O. K. Narain
Department of Science Access,
University of Zululand, KwaDlangezwa,
South Africa.
E-mail: komia@aims.ac.za
DST-NRF Centre of Excellence in
Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: dele@aims.ac.za
DST-NRF Centre of Excellence in
Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: hammedabass548@gmail.com
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
In this paper, we establish some fixed point and common fixed point results for a new type of generalized contractive mapping using the notion of C-class function in the framework of complex valued b-metric spaces. As an application, we establish the existence and uniqueness of a solution for Riemann-Liouville integral and ordinary differential equation in the framework of a complete complex valued b-metric spaces. The obtained results generalize and improve some fixed point results in the literature.
Paper's Title:
Locally Bicomplex Convex Module and Their Applications
Author(s):
Stanzin Kunga and Aditi Sharma
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: stanzinkunga19@gmail.com
Department of Mathematics,
University of Jammu,
Jammu And Kashmir,
India.
E-mail: aditi.sharmaro@gmail.com
Abstract:
Let X be a locally BC convex module and L(X) be the family of all continuous bicomplex linear operators on X. In this paper, we study some concepts of D-valued seminorms on locally BC convex module. Further, we study the bicomplex version of Co and (Co,1) semigroup. The work of this paper is inspired by the work in [2] and [6].
Paper's Title:
On General Class of Nonlinear Contractive Maps and their Performance Estimates
Author(s):
Olalekan Taofeek Wahab and Salaudeen Alaro Musa
Department of Mathematics and
Statistics
Kwara State University, Malete
P. M. B. 1530 Ilorin,
Nigeria.
E-mail: taofeek.wahab@kwasu.edu.ng
Abstract:
This paper considers two independent general class of nonlinear contractive maps to study the existence properties of nonlinear operators with prior degenerate. The existence properties are proved in the framework of approximate fixed points with the imposition of the general class of contractive conditions in metrical convex spaces without emphasis on completeness or compactness. For computational purposes, the performance estimates and the sensitivity dependence of these conditions are obtained for the Picard operator. Practical examples are also considered to justify the validity of the conditions. The results ensure no term is lost in the operators with prior degenerate and the conditions are strictly larger class when compare with others in the literature.
Paper's Title:
Generalized Composition Operators On Besov Spaces
Author(s):
Vishal Sharma, Sanjay Kumar and Stanzin Dolkar
Department of Mathematics,
Central University of Jammu,
Jammu and Kashmir,
India.
E-mail: sharmavishal911@gmail.com
Department of Mathematics,
Central University of Jammu,
Jammu and Kashmir,
India.
E-mail: sanjaykmath@gmail.com
Department of Mathematics,
Central University of Jammu,
Jammu and Kashmir,
India.
E-mail: stanzin.math@cujammu.ac.in
Abstract:
In this paper, we characterize boundedness, compactness and find the essential norm estimates for generalized composition operators between Besov spaces and Sp spaces.
Paper's Title:
Growth and Approximation of Entire Solutions of Linear Partial Differential Equation in Terms of Bessel Polynomial Approximation Errors in Lp-norm, 1 ≤ p ≤ ∞
Author(s):
Devendra Kumar
Department of Mathematics, Faculty of
Sciences
Al-Baha University,
P.O.Box-7738 Alaqiq, Al-Baha-65799,
Saudi Arabia.
E-mail:
d_kumar001@rediffmail.com,
dsingh@bu.edu.sa
Abstract:
We deal with entire solutions of some special type linear homogeneous partial differential equations that are represented in convergent series of Bessel polynomials. We determine the growth orders and types of the solutions, in terms of Bessel polynomial approximation errors in both sup norm and Lp-norm, 1 ≤ p ≤ ∞.
Paper's Title:
Solving Strongly Nonlinear Fractional Fredholm Integral-Differential Equations in Caputo's Sense Using the SBA Method
Author(s):
Germain Kabore1, Bakari Abbo2, Ousseni So3 and Blaise Some1
1Laboratoire
d'Analyse Numerique, Informatique et de Biomathmathiques (L.N.I.BIO),
Universite Joseph Ki-Zerbo,
Burkina Faso.
E-mail: germainkabore982@gmail.com,
blaisesomeouaga1@gmail.com
2University
of N'Damena, Tchad.
E-mail: bakariabbo@yahoo.fr
3Laboratoire
d'Analyse Numerique, Informatique et de Biomathemathiques (L.N.I.BIO),
Ecole Normale Superieure,
Burkina Faso.
E-mail: sousseni@yahoo.fr
Abstract:
The work addressed in this article consists in constructing the exact solutions, where they exist, of fractional Fredholm-type integro-differential equations in the sense of Caputo. Our results are obtained using the SBA method. The simplification of the approach, the analysis of its convergence, and the generalization of this method to these types of highly nonlinear equations constitute our scientific contribution.
Search and serve lasted 0 second(s).