|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
On Oscillation of
Second-Order Delay Dynamic Equations on Time Scales
Author(s):
S. H. Saker
Department of Mathematics, Faculty of Science,
Mansoura University, Mansoura, 35516,
Egypt.
shsaker@mans.edu.eg
Abstract:
Some new oscillation criteria for second-order linear delay dynamic equation
on a time scale T are established. Our results improve the
recent results for delay dynamic equations and in the special case when
T=R, the results include the oscillation results established by Hille [1948,
Trans. Amer. Math. Soc. 64 (1948), 234-252] and Erbe [Canad. Math. Bull. 16
(1973), 49-56.] for differential equations. When T=Z the
results include and improve some oscillation criteria for difference
equations. When T=hZ, h>0, T=qN and T=N2, i.e., for generalized second order delay difference equations our
results are essentially new and can be applied on different types of time
scales. An example is considered to illustrate the main results.
Paper's Title:
Oscillation and Boundedness of Solutions to First and Second Order Forced Dynamic Equations with Mixed Nonlinearities
Author(s):
Ravi P. Agarwal and Martin Bohner
Department of Mathematical Sciences, Florida Institute of Technology
Melbourne, FL 32901,
U.S.A.
bohner@mst.edu
URL:http://web.mst.edu/~bohner
Department of Economics and Finance, Missouri University of Science and Technology
Rolla, MO 65401,
U.S.A.
agarwal@fit.edu
Abstract:
Some oscillation and boundedness criteria for solutions to certain
first and second order forced dynamic equations
with mixed nonlinearities are established. The main tool in the proofs
is an inequality due to Hardy, Littlewood and Pólya.
The obtained results can be applied to differential equations,
difference equations and q-difference equations. The results
are illustrated with numerous examples.
Paper's Title:
Existence of Non-spurious Solutions to Discrete Boundary Value Problems
Author(s):
Irena Rachunkova and Christopher C. Tisdell
Department of Mathematics
School of Mathematics
Palacky University
771 46 Olomouc, Czech Republic.
rachunko@risc.upol.cz
URL: http://phoenix.inf.upol.cz/~rachunekl/mathair/matha-en.htm
The University of New South Wales
Sydney 2052, Australia.
cct@unsw.edu.au
URL: http://www.maths.unsw.edu.au/~cct
Abstract:
This paper investigates discrete boundary value problems (BVPs) involving second-order difference equations and two-point boundary conditions.
General theorems guaranteeing the existence and uniqueness of solutions to the discrete BVP are established. The methods involve a sufficient growth condition to yield an a priori bound on solutions to a certain family of discrete BVPs. The em a priori bounds on solutions to the discrete BVP do not depend on the step-size and thus there are no ``spurious'' solutions. It is shown that solutions of the discrete BVP will converge to solutions of ordinary differential equations.
Paper's Title:
Oscillation Criteria for Second Order Delay Difference Equations via Canonical Transformations and Some New Monotonic Properties
Author(s):
R. Deepalakhmi, S. Saravanan, J. R. Graef, and E. Thandapani
Department of Interdisciplinary Studies
Tamil Nadu Dr. Ambedkar Law University
Chennai-600113,
India.
profdeepalakshmi@gmail.com
Madras School of Economics,
Chennai-600025,
India.
profsaran11@gmail.com
Department of Mathematics,
University of Tennessee at Chattanooga,
Chattanooga,TN 37403,
USA.
john-graef@utc.edu
Ramanujan Institute for Advanced Study in
Mathematics,
University of Madras,
Chennai - 600 005,
India.
ethandapani@yahoo.co.in
Abstract:
This paper is concerned with second-order linear noncanonical delay difference equations of the form
Δ(μ(t)Δ y(t))+ p(t)y(φ(t))=0.
The authors prove new oscillation criteria by first transforming the equation into canonical form and then obtaining some new monotonic properties of the positive solutions of the transformed equation. By using a comparison with first-order delay difference equations and a generalization of a technique developed by Koplatadze, they obtain their main results. Examples illustrating the improvement over known results in the literature are presented.
Paper's Title:
Inequalities of Gamma Function Appearing in Generalizing Probability Sampling Design
Author(s):
Mohammadkheer M. Al-Jararha And Jehad M. Al-Jararha
Department of Mathematics,
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: mohammad.ja@yu.edu.jo
Department of Statistics,
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: jehad@yu.edu.jo
Abstract:
In this paper, we investigate the complete monotonicity of some functions involving gamma function. Using the monotonic properties of these functions, we derived some inequalities involving gamma and beta functions. Such inequalities can be used to generalize different probability distribution functions. Also, they can be used to generalize some statistical designs, e.g., the probability proportional to the size without replacement design.
Paper's Title:
Fractional Integral Inequalities of Hermite-Hadamard Type for P-convex and Quasi-Convex Stochastic Process
Author(s):
Oualid Rholam, Mohammed Barmaki and Driss Gretet
National School of Applied Sciences (ENSA),
University Ibn Tofail,
B.P 242 Kenitra 14000,
phone number : +212606257757,
Morocco.
E-mail: oualid.rholam@uit.ac.ma
Science Faculty Ben M'sik,
University Hassan II,
B.P 7955 Av Driss El Harti Sidi Othmane 20700,
phone number : +212 5 22 70 46 71 ,
Morocco.
E-mail: mohammed.barmaki@uit.ac.ma
National School of Applied Sciences (ENSA),
University Ibn Tofail,
B.P 242 Kenitra 14000,
phone number : +212661403557,
Morocco.
E-mail: driss.gretete@uit.ac.ma
Abstract:
In this paper we consider the class of P-convex and Quasi-convex stochastic processes on witch we apply a general class of generalized fractional integral operator in order to establish new integral inequalities of Hermite-Hadammard type. then we obtain some results for well known types of fractional integrals. Results obtained in this paper may be starting point as well as a useful source of inspiration for further research in convex analysis.
Paper's Title:
Positive Solutions of Evolution Operator Equations
Author(s):
Radu Precup
Department of Applied Mathematics,
Babes-Bolyai University,
Cluj, Romania
Abstract:
Existence and localization results are derived from Krasnoselskii’s compressionexpansion
fixed point theorem in cones, for operator equations in spaces of continuous functions
from a compact real interval to an abstract space. The main idea, first used in [12], is to handle
two equivalent operator forms of the equation, one of fixed point type giving the operator to
which Krasnoselskii’s theorem applies and an other one of coincidence type which is used to
localize a positive solution in a shell. An application is presented for a boundary value problem
associated to a fourth order partial differential equation on a rectangular domain.
Paper's Title:
Positive Solutions for Systems of Three-point Nonlinear Boundary Value Problems
Author(s):
J. Henderson and S. K. Ntouyas
Department of Mathematics, Baylor University
Waco, Texas
76798-7328 USA.
Johnny_Henderson@baylor.edu
URL: http://www3.baylor.edu/~Johnny_Henderson
Department of Mathematics, University of Ioannina
451 10 Ioannina,
Greece.
sntouyas@cc.uoi.gr
URL: http://www.math.uoi.gr/~sntouyas
Abstract:
Values of λ are determined for which there exist
positive solutions of the system of three-point boundary value problems,
u''(t)+ λa(t)f(v(t))=0, v''(t)+λb(t)g(u(t))=0,
for 0 < t <1, and
satisfying, u(0) = 0, u(1)=α u(η),
v(0) = 0, v(1)=α v(η). A Guo-Krasnosel'skii fixed
point theorem is applied. Paper's Title:
Some New Nonlinear Integro-Differential Inequalities of Gronwall-Bellman-Pachpatte Type Author(s):
A. ABDELDAIM Department of Mathematics and Computer
Sciences, Department of Mathematics, E-mail:
ahassen@su.edu.sa
Abstract:
In this paper we establish some new nonlinear integro-differential inequalities of Gronwall-Bellman-Pachpatte type for function of one independent variable. The purpose of this paper is to extend certain results which proved by Pachpatte in [On some fundamental integrodifferential and integral inequalities, An. Sti. Univ. Al. I. Cuza, Iasi, Vol.23 (1977), 77-86]. The inequalities obtained here can be used in the theory of some new classes of nonlinear integro-differential equations. Some applications are also given to illustrate the usefulness of our results. Paper's Title:
Strong Convergence Theorem for a Common Fixed Point of an
Infinite Family of J-nonexpansive Maps with Applications Author(s):
Charlse Ejike Chidume, Otubo Emmanuel Ezzaka and Chinedu Godwin Ezea African University of Science and
Technology, Ebonyi State University, Nnamdi Azikiwe University, Abstract:
Let E be a uniformly convex and uniformly smooth real Banach space with dual space
E*. Let {Ti}∞i=1 be a family of
J-nonexpansive maps, where, for each i,~Ti maps E to 2E*.
A new class of maps, J-nonexpansive maps from E to E*, an
analogue of nonexpansive self maps of
E, is introduced. Assuming that the set of common J-fixed points
of {Ti}∞i=1 is nonempty, an iterative scheme is constructed and proved
to converge strongly to a point x* in ∩∞n=1FJTi. This result is then applied, in the case that
E is a real Hilbert space to obtain
a strong convergence theorem for approximation of a common fixed point for an infinite family of nonexpansive maps, assuming existences. The theorem
obtained is compared with some important results in the literature. Finally, the technique of proof is also of independent interest. Paper's Title:
Strong
Convergence Theorems for a Common Zero of an Infinite Family of Gamma-Inverse
Strongly Monotone Maps with Applications Author(s):
Charles Ejike Chidume, Ogonnaya Michael Romanus, and Ukamaka Victoria Nnyaba African University of Science and
Technology, Abuja, Abstract:
Let E be a uniformly convex and uniformly smooth real Banach space with
dual space E* and let Ak:E→E*,
k=1, 2, 3 , ... Paper's Title:
Convergence and Stability Results for New Three Step Iteration Process
in Modular Spaces Author(s):
Naresh Kumar and Renu Chugh Department of Mathematics, Abstract:
The aim of this paper is to introduce a new iteration process
(5) for ρ-contraction mappings in Modular spaces. We obtain some analytical proof for convergence and stability of our iteration process
(5). We show that our iteration process (5) gives faster convergence results than the leading AK iteration process
(4) for contraction mappings.
Moreover, a numerical example (using the Matlab Software) is presented to compare the rate of convergence for existing iteration processes with our new iteration process
(5). Paper's Title:
Oscillatory Behavior of Second-Order Non-Canonical
Retarded Difference Equations Author(s):
G.E. Chatzarakis1, N. Indrajith2, E. Thandapani3 and
K.S. Vidhyaa4 1Department
of Electrical and Electronic Engineering Educators,
2: Paper Source
PDF document
Faculty of Science,
Port Said University, Port Said,
EGYPT.
Faculty of Science and Humanities,
Shaqra University, Dawadmi,
SAUDI ARABIA.
URL:
http://faculty.ksu.edu.sa/DRABDELDAIM/Pages/Home.aspx
2: Paper Source
PDF document
Abuja,
Nigeria.
E-mail:
cchidume@aust.edu.ng
Abakaliki,
Nigeria.
E-mail: mrzzaka@yahoo.com
Awka,
Nigeria.
E-mail: chinedu.ezea@gmail.com
2: Paper Source
PDF document
Nigeria.
E-mail: cchidume@aust.edu.ng
E-mail: romanusogonnaya@gmail.com
E-mail: nnyabavictoriau@gmail.com
be a family of inverse strongly monotone maps such that ∩∞k=1
Ak-1(0)≠∅.
A new iterative algorithm is constructed and proved to converge strongly to a
common zero of the family.
As a consequence of this result, a strong convergence theorem for approximating
a common J-fixed point for an infinite family of
gamma-strictly J-pseudocontractive maps is proved. These results are new and
improve recent results obtained for these classes of nonlinear maps.
Furthermore, the technique of proof is of independent interest.
2: Paper Source
PDF document
M.D. University,
Rohtak-124001, Haryana,
India.
E-mail: nks280@gmail.com
E-mail: chugh.r1@gmail.com
2: Paper Source
PDF document
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail: gea.xatz@aspete.gr,
geaxatz@otenet.gr
2Department
of Mathematics,
Presidency College, Chennai - 600 005,
India.
E-mail: indrajithna@gmail.com
3Ramanujan
Institute for Advanced Study in Mathematics,
University of Madras,
Chennai - 600 005,
India.
E-mail: ethandapani@yahoo.co.in
4
Department of Mathematics,Abstract:
Using monotonic properties of nonoscillatory solutions, we obtain new oscillatory criteria for the second-order non-canonical difference equation with retarded argument
Our oscillation results improve and extend the earlier ones. Examples illustrating the results are provided.
Paper's Title:
Improved Oscillation Criteria of Second-Order Advanced Non-canonical Difference Equation
Author(s):
G. E. Chatzarakis1, N. Indrajith2, S. L. Panetsos1, E. Thandapani3
1Department
of Electrical and Electronic Engineering Educators
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail: gea.xatz@aspete.gr,
geaxatz@otenet.gr
spanetsos@aspete.gr
2Department
of Mathematics,
Presidency College, Chennai - 600 005,
India.
E-mail: indrajithna@gmail.com
3Ramanujan
Institute for Advanced Study in Mathematics,
University of Madras Chennai - 600 005,
India.
E-mail: ethandapani@yahoo.co.in
Abstract:
Employing monotonic properties of nonoscillatory solutions, we derive some new oscillation criteria for the second-order advanced non-canonical difference equation
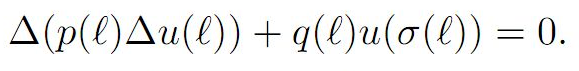
Our results extend and improve the earlier ones. The outcome is illustrated via some particular difference equations.
Paper's Title:
Solving Strongly Nonlinear Fractional Fredholm Integral-Differential Equations in Caputo's Sense Using the SBA Method
Author(s):
Germain Kabore1, Bakari Abbo2, Ousseni So3 and Blaise Some1
1Laboratoire
d'Analyse Numerique, Informatique et de Biomathmathiques (L.N.I.BIO),
Universite Joseph Ki-Zerbo,
Burkina Faso.
E-mail: germainkabore982@gmail.com,
blaisesomeouaga1@gmail.com
2University
of N'Damena, Tchad.
E-mail: bakariabbo@yahoo.fr
3Laboratoire
d'Analyse Numerique, Informatique et de Biomathemathiques (L.N.I.BIO),
Ecole Normale Superieure,
Burkina Faso.
E-mail: sousseni@yahoo.fr
Abstract:
The work addressed in this article consists in constructing the exact solutions, where they exist, of fractional Fredholm-type integro-differential equations in the sense of Caputo. Our results are obtained using the SBA method. The simplification of the approach, the analysis of its convergence, and the generalization of this method to these types of highly nonlinear equations constitute our scientific contribution.
Paper's Title:
Positive Solution For Discrete Three-Point Boundary Value
Problems
Author(s):
Wing-Sum Cheung And Jingli Ren
Department of Mathematics,
The University of Hong Kong,
Pokfulam, Hong Kong
wscheung@hku.hk
Institute of Systems Science,
Chinese Academy of Sciences,
Beijing 100080, P.R. China
renjl@mx.amss.ac.cn
Abstract:
This paper is concerned with the existence of positive solution to the discrete three-point boundary value problem
,
where
, and f is allowed to change sign. By constructing
available operators, we shall apply the method of lower solution and the method
of topology degree to obtain positive solution of the above problem for
on a suitable interval.
The associated Green’s function is first given.
Paper's Title:
Oscillations of First Order Linear Delay Difference Equations
Author(s):
G. E. Chatzarakis and I. P. Stavroulakis
Department of Mathematics, University of Ioannina,
451 10, Greece
ipstav@cc.uoi.gr
Abstract:
Consider the first order linear delay difference equation of
the form 
where
is
a sequence of nonnegative real numbers, k is a positive integer and 
denotes
the forward difference operator 
New
oscillation criteria are established when the well-known oscillation conditions
and
are
not satisfied. The results obtained essentially improve known results in the
literature.
Paper's Title:
Boundary Value Problems for Fractional Diffusion-Wave equation
Author(s):
Varsha Daftardar-Gejji and Hossein Jafari
Department of Mathematics, University of Pune,
Ganeshkhind, Pune - 411007,
INDIA.
vsgejji@math.unipune.ernet.in
jafari_h@math.com
Abstract:
Non homogeneous fractional diffusion-wave equation has been solved under linear/nonlinear boundary conditions. As the order of time derivative changes from
0 to 2, the process changes from slow diffusion to classical diffusion to mixed diffusion-wave behaviour.
Numerical examples presented here confirm this inference. Orthogonality of eigenfunctions in case of fractional Stürm-Liouville problem has been established
Paper's Title:
Some Properties of the Solution of a Second Order Elliptic Abstract Differential Equation
Author(s):
A. Aibeche and K. Laidoune
Mathematics Department, Faculty of Sciences,
University Ferhat Abbas, Setif,
Route de Scipion, 19000,
Setif,
Algeria
aibeche@univ-setif.dz
Abstract:
In this paper we study a class of non regular boundary value
problems for elliptic differential-operator equation of second order with an
operator in boundary conditions. We give conditions which guarantee the
coerciveness of the solution of the considered problem, the completeness of
system of root vectors in Banach-valued functions spaces and we establish
the Abel basis property of this system in Hilbert spaces. Finally, we apply
this abstract results to a partial differential equation in cylindrical
domain.
Paper's Title:
On a Method of Proving the Hyers-Ulam Stability
of Functional Equations on Restricted Domains
Author(s):
Janusz Brzdęk
Department of Mathematics
Pedagogical University Podchor
Abstract:
We show that generalizations of some (classical) results on the Hyers-Ulam stability of functional equations, in several variables, can be very easily derived from a simple result on stability of a functional equation in single variable
Paper's Title:
Common Fixed Point Results for Banach Operator Pairs and Applications to Best Approximation
Author(s):
Hemant Kumar Nashine
Department of Mathematics,
Disha Institute of Management and Technology,
Satya Vihar, Vidhansabha - Chandrakhuri Marg (Baloda Bazar Road),
Mandir Hasaud,
Raipur - 492101(Chhattisgarh), India.
hemantnashine@rediffmail.com
nashine_09@rediffmail.com
Abstract:
The common fixed point results for Banach operator pair with generalized nonexpansive mappings in q-normed space have been obtained in the present work. As application, some more general best approximation results have also been determined without the assumption of linearity or affinity of mappings. These results unify and generalize various existing known results with the aid of more general class of noncommuting mappings.
Paper's Title:
Bounds for Two Mappings Associated to
the Hermite-Hadamard Inequality
Author(s):
S. S. Dragomir1,2 and I. Gomm1
1Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428,
Melbourne City, MC 8001,
Australia.
2School of Computational & Applied Mathematics,
University of
the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
sever.dragomir@vu.edu.au
ian.gomm@vu.edu.au
URL: http://rgmia.org/dragomir
Abstract:
Some inequalities concerning two mappings associated to the celebrated Hermite-Hadamard integral inequality for convex function with applications for special means are given.
Paper's Title:
On Opial's Inequality for Functions of n-Independent Variables
Author(s):
S. A. A. El-Marouf and S. A. AL-Oufi
Department of Mathematics,
Faculty of Science,
Minoufiya University,
Shebin El-Koom,
Egypt
Department of Mathematics,
Faculty of Science, Taibah University,
Madenahmonwarah,
Kingdom of Saudia Arabia
Abstract:
In this paper, we introduce Opial inequalities for functions of n-independent variables. Also, we discuss some different forms of Opial inequality containing functions of n independent variables and their partial derivatives with respect to independent variables.
Paper's Title:
Further Bounds for Two Mappings Related
to the Hermite-Hadamard Inequality
Author(s):
S. S. Dragomir1,2 and I. Gomm1
1Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428,
Melbourne City, MC 8001,
Australia.
2School of Computational & Applied Mathematics,
University of
the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
sever.dragomir@vu.edu.au
ian.gomm@vu.edu.au
URL: http://rgmia.org/dragomir
Abstract:
Some new results concerning two mappings associated to the celebrated Hermite-Hadamard integral inequality for twice differentiable functions with applications for special means are given.
Paper's Title:
Some Applications of Fejér's Inequality for Convex Functions (I)
Author(s):
S.S. Dragomir1,2 and I. Gomm1
1Mathematics, School of
Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia.
URL: http://rgmia.org/dragomir
2School of Computational &
Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
Abstract:
Some applications of Fejér's inequality for convex functions are explored. Upper and lower bounds for the weighted integral
under various assumptions for f with applications to the trapezoidal quadrature rule are given. Some inequalities for special means are also provided
Paper's Title:
Some Operator Order Inequalities for Continuous Functions of Selfadjoint Operators in Hilbert Spaces
Author(s):
S. S. Dragomir1,2 and Charles E. M. Pearce3
1Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428,
Melbourne City, MC 8001,
Australia.
2School of Computational & Applied Mathematics,
University of
the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
sever.dragomir@vu.edu.au
URL: http://rgmia.org/dragomir
3School
of Mathematical Sciences,
The University of Adelaide,
Adelaide,
Australia
Abstract:
Various bounds in the operator order for the following operator transform
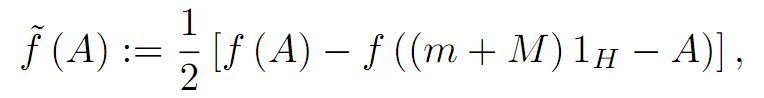
where A is a selfadjoint operator in the Hilbert space H with the
spectrum Sp( A) ⊆ [ m,M]
and f:[m,M] -> C is a continuous function on [m,M]
are given. Applications for the power and logarithmic functions are provided as
well.
Paper's Title:
Inequalities for the Area Balance of Functions of Bounded Variation
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
We introduce the area balance function associated to a Lebesgue
integrable function f:[a,b] →C by
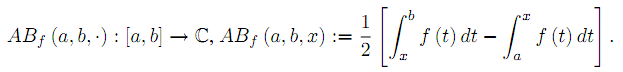
Several sharp bounds for functions of bounded variation are provided. Applications for Lipschitzian and convex functions are also given.
Paper's Title:
Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Fractional class of analytic functions Defined Using q-Differential Operator
Author(s):
K . R. Karthikeyan, Musthafa Ibrahim and S. Srinivasan
Department of Mathematics and
Statistics,
Caledonian College of Engineering, Muscat,
Sultanate of Oman.
E-mail: kr_karthikeyan1979@yahoo.com
College of Engineering,
University of Buraimi, Al Buraimi,
Sultanate of Oman.
E-mail: musthafa.ibrahim@gmail.com
Department of Mathematics, Presidency
College (Autonomous),
Chennai-600005, Tamilnadu,
India.
Abstract:
We define a q-differential fractional operator, which generalizes Salagean and Ruscheweyh differential operators. We introduce and study a new class of analytic functions involving q-differential fractional operator. We also determine the necessary and sufficient conditions for functions to be in the class. Further, we obtain the coefficient estimates, extreme points, growth and distortion bounds.
Paper's Title:
Some Inequalities of the Hermite-Hadamard Type for k-Fractional Conformable Integrals
Author(s):
C.-J. Huang, G. Rahman, K. S. Nisar, A. Ghaffar and F. Qi
Department of Mathematics, Ganzhou Teachers College,
Ganzhou 341000, Jiangxi,
China.
E-mail:
hcj73jx@126.com ,
huangcj1973@qq.com
Department of Mathematics, Shaheed Benazir
Bhutto University,
Sheringal, Upper Dir, Khyber Pakhtoonkhwa,
Pakistan.
E-mail: gauhar55uom@gmail.com
Department of Mathematics, College of Arts
and Science at Wadi Aldawaser, 11991,
Prince Sattam Bin Abdulaziz University, Riyadh Region,
Kingdom of Saudi Arabia.
E-mail: n.sooppy@psau.edu.sa,
ksnisar1@gmail.com
Department of Mathematical Science,
Balochistan University of Information Technology,
Engineering and Management Sciences, Quetta,
Pakistan.
E-mail: abdulghaffar.jaffar@gmail.com
School of Mathematical Sciences, Tianjin
Polytechnic University,
Tianjin 300387,
China; Institute of Mathematics,
Henan Polytechnic University, Jiaozuo 454010, Henan,
China.
E-mail: qifeng618@gmail.com,
qifeng618@qq.com
Abstract:
In the paper, the authors deal with generalized k-fractional conformable integrals, establish some inequalities of the Hermite-Hadamard type for generalized k-fractional conformable integrals for convex functions, and generalize known inequalities of the Hermite-Hadamard type for conformable fractional integrals.
Paper's Title:
A Self-adaptive Subgradient Extragradient Algorithm for Variational Inequality Problems and Fixed Point Problems in Banach Spaces
Author(s):
F. U. Ogbuisi
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
Department of Mathematics,
University of Nigeria, Nsukka,
Nigeria.
E-mail: ferdinard.ogbuisi@unn.edu.ng
fudochukwu@yahoo.com
Abstract:
In this paper, we propose and analyze a type of subgradient extragradient algorithm for the approximation of a solution of variational inequality problem which is also a common fixed point of an infinite family of relatively nonexpansive mappings in 2-uniformly convex Banach spaces which are uniformly smooth. By using the generalized projection operator, we prove a strong convergence theorem which does not require the prior knowledge of the Lipschitz constant of cost operator. We further applied our result to constrained convex minimization problem, convex feasibility problem and infinite family of equilibrium problems. Our results improve and complement related results in 2-uniformly convex and uniformly smooth Banach spaces and Hilbert spaces.
Paper's Title:
On Some Nonlinear Retarded Integrodifferential Inequalities in Two and n Independent Variables and their Applications
Author(s):
Bitat Dalila and Khellaf Hassane
Department of Mathematics, Laboratory of
Applied Mathematics and Modeling,
University of Constantine,
PO Box 325, Ain El Bey Road, Constantine 25017,
Algeria.
E-mail: bitat.dalila@umc.edu.dz
khellafhassane@umc.edu.dz
URL: https://www.umc.edu.dz
Abstract:
In this paper, we establish some new nonlinear retarded integrodifferential inequalities in two and n independent variables. Some applications are given as illustration.
Paper's Title:
Geometrical Properties of Subclass of Analytic Function with Odd Degree
Author(s):
K. Sivagami Sundari and B. Srutha Keerthi
Divison of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology, Chennai Campus, Chennai - 600 127,
India.
E-mail: sivagamisundari.2298@gmail.com
Divison of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology, Chennai Campus, Chennai - 600 127,
India.
E-mail: keerthivitmaths@gmail.com
Abstract:
The objective of the paper is to study the geometrical
properties of the class B(λ, t).
For which we have proved that the radius
is optimal ,(i.e)
the number
cannot be replaced by a larger one. Additionally, the graphs for various values of t and
λ are compared in order to study the sharpness of the coefficient bounds.
Paper's Title:
On the Oscillatory Behavior of Self Adjoint Fractional Extensible Beam Equations
Author(s):
S. Priyadharshini1, G.E. Chatzarakis2, S. L. Panetsos2 and V. Sadhasivam1
1Post
Graduate and Research Department of Mathematics,
Thiruvalluvar Government Arts College,
Rasipuram - 637 401, Namakkal Dt., Tamil Nadu,
India.
E-mail: s.priya25april@gmail.com,
ovsadha@gmail.com
2Department
of Electrical and Electronic Engineering Educators,
School of Pedagogical and Technological Education(ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
gea.xatz@aspete.gr,
spanetsos@aspete.gr
Abstract:
The main objective of this paper is to study the oscillatory behavior of the solutions of self adjoint fractional extensible beam equations by using integral average method. Some new sufficient conditions are established with various boundary conditions over a cylindrical domains. Examples illustrating the results are given.
Paper's Title:
New Fast Extragradient-like Methods for Non-Lipschitzian Pseudo-monotone Variational Inequalities
Author(s):
Morad Ali Peyvand
Department of Mathematics
Yasouj University
Yasouj,
Iran.
E-mail: peyvand@yu.ac.ir
Abstract:
An efficient double-projection method, with a new search strategy, is designed for solving variational inequalities in real Hilbert spaces with pseudo-monotone cost operator. Our proposed method uses a computationally inexpensive simple line search procedure based on local information of the operator and very weak conditions of parameters to obtain larger step sizes. A description of the algorithm along with its weak convergence is provided without assuming Lipschitz continuity. Also, a modification to the proposed method is presented, wherein the second projection onto the closed and convex subset is replaced with the one onto a subgradient half space. Numerical experiments and comparisons with related methods demonstrate the reliability and benefits of the proposed schemes.
Search and serve lasted 1 second(s).