|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
On the Generalized Inverse  over Integral Domains
over Integral Domains
Author(s):
Yaoming Yu and Guorong Wang
College of Education, Shanghai Normal University
Shanghai 200234
People's Republic of China.
yuyaoming@online.sh.cn
grwang@shnu.edu.cn
Abstract:
In this paper, we study further the generalized inverse
 of a matrix A over an integral domain. We give
firstly some necessary and sufficient conditions for the existence
of the generalized inverse
of a matrix A over an integral domain. We give
firstly some necessary and sufficient conditions for the existence
of the generalized inverse  , an explicit expression
for the elements of the generalized inverse
, an explicit expression
for the elements of the generalized inverse  and an
explicit expression for the generalized inverse
and an
explicit expression for the generalized inverse  ,
which reduces to the {1} inverse. Secondly, we verify that the
group inverse, the Drazin inverse, the Moore-Penrose inverse and the
weighted Moore-Penrose inverse are identical with the generalized
inverse
,
which reduces to the {1} inverse. Secondly, we verify that the
group inverse, the Drazin inverse, the Moore-Penrose inverse and the
weighted Moore-Penrose inverse are identical with the generalized
inverse 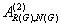 for an appropriate matrix G,
respectively, and then we unify the conditions for the existence and
the expression for the elements of the weighted Moore-Penrose
inverse, the Moore-Penrose inverse, the Drazin inverse and the group
inverse over an integral domain. Thirdly, as a simple application,
we give the relation between some rank equation and the existence of
the generalized inverse
for an appropriate matrix G,
respectively, and then we unify the conditions for the existence and
the expression for the elements of the weighted Moore-Penrose
inverse, the Moore-Penrose inverse, the Drazin inverse and the group
inverse over an integral domain. Thirdly, as a simple application,
we give the relation between some rank equation and the existence of
the generalized inverse  , and a method to compute the
generalized inverse
, and a method to compute the
generalized inverse  . Finally, we give an example of
evaluating the elements of
. Finally, we give an example of
evaluating the elements of  without calculating
without calculating
 .
.
Paper's Title:
Some fixed point results in partial S-metric spaces
Author(s):
M. M. Rezaee, S. Sedghi, A. Mukheimer, K. Abodayeh, and Z. D. Mitrovic
Department of Mathematics, Qaemshahr
Branch,
Islamic Azad University, Qaemshahr,
Iran.
E-mail: Rezaee.mohammad.m@gmail.com
Department of Mathematics, Qaemshahr
Branch,
Islamic Azad University, Qaemshahr,
Iran.
E-mail: sedghi.gh@qaemiau.ac.ir
Department of Mathematics and General
Sciences,
Prince Sultan University, Riyadh,
KSA.
E-mail: mukheimer@psu.edu.sa
Department of Mathematics and General
Sciences,
Prince Sultan University, Riyadh,
KSA.
E-mail: kamal@psu.edu.sa
Nonlinear Analysis Research Group,
Faculty of Mathematics and Statistics,
Ton Duc Thang University, Ho Chi Minh City,
Vietnam.
E-mail: zoran.mitrovic@tdtu.edu.vn
Abstract:
We introduce in this article a new class of generalized metric spaces, called partial S-metric spaces. In addition, we also give some interesting results on fixed points in the partial S-metric spaces and some applications.
Paper's Title:
A New Relaxed Complex-valued b-metric Type and Fixed Point Results
Author(s):
P. Singh, V. Singh and T. C. M. Jele
Department of Mathematics, University of
KwaZulu-Natal,
Private Bag X54001, Durban,
South Africa.
E-mail: singhp@ukzn.ac.za
singhv@ukzn.ac.za
thokozani.jele@nwu.ac.za
Abstract:
In this paper, we study the existence and uniqueness of fixed point in complex valued b-metric spaces and introduce a new relaxed α, β Complex-valued b-metric type by relaxing the triangle inequality and determine whether the fixed point theorems are applicable in these spaces.
Paper's Title:
Refinement Inequalities Among Symmetric Divergence Measures
Author(s):
Inder Jeet Taneja
Departamento de Matemática,
Universidade Federal de Santa Catarina, 88.040-900
Florianópolis, Sc, Brazil
taneja@mtm.ufsc.br
URL: http://www.mtm.ufsc.br/~taneja
Abstract:
There are three classical divergence measures in the literature
on information theory and statistics, namely, Jeffryes-Kullback-Leiber’s
J-divergence, Sibson-Burbea-Rao’s Jensen- Shannon divegernce and
Taneja’s arithemtic - geometric mean divergence. These bear an
interesting relationship among each other and are based on logarithmic
expressions. The divergence measures like Hellinger discrimination,
symmetric χ2−divergence, and triangular discrimination
are not based on logarithmic expressions. These six divergence measures are
symmetric with respect to probability distributions. In this paper some
interesting inequalities among these symmetric divergence measures are studied.
Refinements of these inequalities are also given. Some inequalities due to
Dragomir et al. [6]
are also improved.
Paper's Title:
Scope of the Logarithmic Mean
Author(s):
Murali Rao and Agnish Dey
Department of Mathematics,
University of Florida,
1400 Stadium Road, Gainesville,
Florida 32611,
U. S. A.
E-mail: mrao@ufl.edu
URL: http://people.clas.ufl.edu/mrao
E-mail: agnish@ufl.edu
URL: http://people.clas.ufl.edu/agnish
Abstract:
A number a is between two numbers x and y if and only if a is a convex combination of x and y, in other words, it is a "weighted mean" of x and y. Geometric mean, arithmetic mean are well known examples of these "means". Of more recent vintage is the logarithmic mean which has been considered in many articles in the literature. In this note, we first discuss some of its properties. Then we shall introduce the L function and explore the inverse of this function and its connection with the Lambert's Omega function.
Paper's Title:
Generalised Models for Torsional Spine Reconnection
Author(s):
Ali Khalaf Hussain Al-Hachami
Department of Mathematics,
College of Education For Pure Sciences,
Wasit University,
Iraq.
E-mail: alhachamia@uowasit.edu.iq
Abstract:
Three-dimensional (3D) null points are available in wealth in the solar corona, and the equivalent is probably going to be valid in other astrophysical situations. On-going outcomes from sun oriented perceptions and from reproductions propose that reconnection at such 3D nulls may assume a significant job in the coronal dynamics. The properties of the torsional spine method of magnetic reconnection at 3D nulls are researched. Kinematic model are created, which incorporate the term ηJ that is spatially localised around the null, stretching out along the spine of the null. The null point is to research the impact of shifting the level of asymmetry of the null point magnetic field on the subsequent reconnection process where past examinations constantly considered a non-nonexclusive radially symmetric null. Specifically we analyse the rate of reconnection of magnetic flux at the spine of null point. Logical arrangements are determined for the enduring kinematic equation, and contrasted and the after effects of torsional spine reconnection models when the current is restricted in which the Maxwell conditions are illuminated. The geometry of the current layers inside which torsional spine reconnection happen is autonomous on the symmetry of the magnetic field. Torsional spine reconnection happens in a thin cylinder around the spine, with circular cross-segment when the fan eigenvalues are extraordinary. The short axis of the circle being along the solid field bearing. Just as it was discovered that the fundamental structure of the method of attractive reconnection considered is unaffected by changing the magnetic field symmetry, that is, the plasma flow is discovered rotational around the spine of null point. The spatiotemporal pinnacle current, and the pinnacle reconnection rate achieved, are found not to rely upon the level of asymmetry.
Paper's Title:
Existence of Solution of Differential and Riemann-Liouville Equation Via Fixed Point Approach in Complex Valued b-Metric Spaces
Author(s):
K. Afassinou, A. A. Mebawondu, H. A. Abass and O. K. Narain
Department of Science Access,
University of Zululand, KwaDlangezwa,
South Africa.
E-mail: komia@aims.ac.za
DST-NRF Centre of Excellence in
Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: dele@aims.ac.za
DST-NRF Centre of Excellence in
Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: hammedabass548@gmail.com
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
In this paper, we establish some fixed point and common fixed point results for a new type of generalized contractive mapping using the notion of C-class function in the framework of complex valued b-metric spaces. As an application, we establish the existence and uniqueness of a solution for Riemann-Liouville integral and ordinary differential equation in the framework of a complete complex valued b-metric spaces. The obtained results generalize and improve some fixed point results in the literature.
Paper's Title:
Solving Strongly Nonlinear Fractional Fredholm Integral-Differential Equations in Caputo's Sense Using the SBA Method
Author(s):
Germain Kabore1, Bakari Abbo2, Ousseni So3 and Blaise Some1
1Laboratoire
d'Analyse Numerique, Informatique et de Biomathmathiques (L.N.I.BIO),
Universite Joseph Ki-Zerbo,
Burkina Faso.
E-mail: germainkabore982@gmail.com,
blaisesomeouaga1@gmail.com
2University
of N'Damena, Tchad.
E-mail: bakariabbo@yahoo.fr
3Laboratoire
d'Analyse Numerique, Informatique et de Biomathemathiques (L.N.I.BIO),
Ecole Normale Superieure,
Burkina Faso.
E-mail: sousseni@yahoo.fr
Abstract:
The work addressed in this article consists in constructing the exact solutions, where they exist, of fractional Fredholm-type integro-differential equations in the sense of Caputo. Our results are obtained using the SBA method. The simplification of the approach, the analysis of its convergence, and the generalization of this method to these types of highly nonlinear equations constitute our scientific contribution.
Paper's Title:
Contact With Adhesion between a Deformable Body and a Foundation
Author(s):
B. Teniou and M. Sofonea
Laboratoire de Mathematiques Appliquées et Modélisation,
Université Mentouri, Constantine 25000,
Algeria
tenioubou2@yahoo.fr
Laboratoire de Mathématiques et Physiques pour les Systémes,
Univesité de Perpignan,
France.
sofonea@univ-perp.fr
Abstract:
The aim of this work is study a dynamic contact problem between a
deformable body and a foundation where the deformations are supposed
to be small. The contact is with adhesion and normal compliance. The
behavior of this body is modeled by a nonlinear
elastic-visco-plastic law. The evolution of bonding field is
described by a nonlinear differential equation. We derive a
variational formulation of the contact problem and we prove the
existence and uniqueness of its solution. The proof is based on the
construction of three intermediate problems and then we construct a
contraction mapping whose unique fixed point will be the weak
solution of the mechanical problem.
Paper's Title:
Maximal Inequalities for Multidimensionally Indexed Demimartingales and the Hájek-Rényi Inequality for Associated Random Variables
Author(s):
Tasos C. Christofides and Milto Hadjikyriakou
Department of Mathematics and Statistics
University of Cyprus
P.O.Box 20537, Nicosia 1678, Cyprus
tasos@ucy.ac.cy
miltwh@gmail.com
Abstract:
Demimartingales and demisubmartingales introduced by
Newman and
Wright (1982) generalize the notion of martingales and
submartingales respectively. In this paper we define
multidimensionally indexed demimartingales and demisubmartingales
and prove a maximal inequality for this general class of random
variables. As a corollary we obtain a Hájek-Rényi inequality
for multidimensionally indexed associated random variables, the bound of which,
when reduced to the case of single index, is sharper than the bounds already
known in the literature.
Paper's Title:
On Eigenvalues and Boundary Curvature of the C*-algebra Numerical Rang
Author(s):
M. T. Heydari
Department of Mathematics,
College of Sciences,
Yasouj University,
Yasouj, 75914-74831,
Iran.
E-mail: heydari@yu.ac.ir
Abstract:
Let A be a C*-algebra with unit 1 and a∈A be a nilpotent. By Donoghue's Theorem, all corner points of its numerical range V(a) belong to the spectrum σ(a). It is therefore natural to expect that, more generally, the distance from a point p on the boundary ∂ V(a) of V(a) to σ(a) should be in some sense bounded by the radius of curvature of ∂ V(a) at p.
Paper's Title:
Some New Inequalities of Hermite-Hadamard and Fejér Type for Certain Functions with Higher Convexity
Author(s):
Steven G. From
Department of Mathematics,
University of Nebraska at Omaha,
Omaha, Nebraska 68182-0243,
U.S.A.
E-mail: sfrom@unomaha.edu
Abstract:
In this paper, we present some new inequalities of Hermite-Hadamard or Fejér
type for certain functions satisfying some higher convexity conditions on one or
more derivatives.
An open problem is given also.
Some applications to the logarithmic mean are given.
Paper's Title:
Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.
Paper's Title:
Polyanalytic Functions on Subsets of Z[i]
Author(s):
Abtin Daghighi
Linköping University,
SE-581 83,
Sweden.
E-mail: abtindaghighi@gmail.com
Abstract:
For positive integers q we consider the kernel of the powers Lq where L is one of three kinds of discrete analogues of the Cauchy-Riemann operator. The first two kinds are well-studied, but the third kind less so. We give motivations for further study of the third kind especially since its symmetry makes it more appealing for the cases q≥ 2.
From an algebraic perspective it makes sense that the chosen multiplication on the kernels is compatible with the choice of pseudo-powers. We propose such multiplications together with associated pseudo-powers. We develop a proof-tool in terms of certain sets of uniqueness.
Paper's Title:
A New Adomian Approach to Solving Integral Equations of Fredholm and Volterra Second Kind
Author(s):
Ouedraogo Seny, Nebie Abdoul Wassiha, Youssouf Pare, Blaise Some
Departement de mathematiques,
Universite Joseph Ki-Zerbo,
Burkina Faso.
E-mail: oseny@yahoo.fr,
nebwass@yahoo.fr
pareyoussouf@yahoo.fr,
some@univ-ouaga.bf
Abstract:
In order to simplify the resolution of Fredholm and Volterra's second type integral equations, we propose a new approach based on the Adomian Decompositional Method (ADM). We test the new approach on several examples with success.
Paper's Title:
Reduced Generalized Combination Synchronization Between Two n-Dimensional Integer-Order Hyperchaotic Systems and One m-Dimensional Fractional-Order Chaotic System
Author(s):
Smail Kaouache, Mohammed Salah Abdelouahab and Rabah Bououden
Laboratory of Mathematics and their
interactions,
Abdelhafid Boussouf University Center, Mila.
Algeria
E-mail: smailkaouache@gmail.com,
medsalah3@yahoo.fr,
rabouden@yahoo.fr
Abstract:
This paper is devoted to investigate the problem of reduced generalized combination synchronization (RGCS) between two n-dimensional integer-order hyperchaotic drive systems and one m-dimensional fractional-order chaotic response system. According to the stability theorem of fractional-order linear system, an active mode controller is proposed to accomplish this end. Moreover, the proposed synchronization scheme is applied to synchronize three different chaotic systems, which are the Danca hyperchaotic system, the modified hyperchaotic Rossler system, and the fractional-order Rabinovich-Fabrikant chaotic system. Finally, numerical results are presented to fit our theoretical analysis.
Paper's Title:
Hankel Functional Connected to Lemniscate of Bernoulli
Author(s):
K. Ramanuja Rao, Rajnesh Lal and Kaushal Singh
Fiji National University,
Department of Mathematics & Statistics,
P.O. Box 5529, Lautoka,
Fiji.
E-mail: ramanuja.kotti@fnu.ac.fj
rajnesh.lal@fnu.ac.fj
kaushal.singh@fnu.ac.fj
Abstract:
The aim of present paper is to derive a higher bound (HB) of 3rd order Hankel determinant for a collection of holomorphic mappings connected with exactly to the right side of the lemniscate of Bernoulli, whose polar coordinates form is r2 = 2cos2(2θ). The method carried in this paper is more refined than the method adopted by the authors (see [1]), who worked on this problem earlier.
Paper's Title:
Using Direct and Fixed Point Technique of Cubic Functional Equation and its Hyers-Ulam Stability
Author(s):
Ramanuja Rao Kotti, Rajnesh Krishnan Mudaliar, Kaushal Neelam Devi, Shailendra Vikash Narayan
Fiji National University,
Department of Mathematics & Statistics,
P.O. Box 5529, Lautoka,
Fiji.
E-mail: ramanuja.kotti@fnu.ac.fj
URL: https://www.fnu.ac.fj
Abstract:
In this present work, we introduce a new type of finite dimensional cubic functional equation of the form

where Φ≥4 is an integer, and derive its general solution. The main purpose of this work is to investigate the Hyers-Ulam stability results for the above mentioned functional equation in Fuzzy Banach spaces by means of direct and fixed point methods.
Paper's Title:
New Reverses of Schwarz, Triangle and Bessel Inequalities in Inner Product Spaces
Author(s):
S. S. Dragomir
School of Computer Science and Mathematics, Victoria
University of Technology, PO BOX
14428, MCMC 8001, VICTORIA, AUSTRALIA.
sever.dragomir@vu.edu.au
URL:
http://rgmia.vu.edu.au/SSDragomirWeb.html
Abstract:
New reverses of the Schwarz, triangle and Bessel inequalities in inner product spaces are pointed out. These results complement the recent ones obtained by the author in the earlier paper [13]. Further, they are employed to establish new Grüss type inequalities. Finally, some natural integral inequalities are stated as well.
Paper's Title:
Fixed Point Theorems for a Finite Family of Asymptotically Nonexpansive Mappings
Author(s):
E. Prempeh
Department of Mathematics,
Kwame Nkrumah University of Science and Technology,
Kumasi, Ghana
edward_prempeh2000@yahoo.com
Abstract:
Let
![]() be a real reflexive Banach space with a uniformly Gâteaux differentiable norm,
be a real reflexive Banach space with a uniformly Gâteaux differentiable norm,
![]() be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of
![]() i=1,2,...,r be a finite family of asymptotically nonexpansive mappings
such that for each
i=1,2,...,r be a finite family of asymptotically nonexpansive mappings
such that for each
![]()
![]() Let
Let
![]() be a nonempty set of common fixed points of
be a nonempty set of common fixed points of
![]() and define
and define
![]()
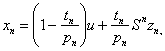
![]() associated with
associated with
![]() , converges strongly to a fixed point of
, converges strongly to a fixed point of
![]() provided
provided
![]() possesses uniform normal structure. Furthermore we prove that the iterative process:
possesses uniform normal structure. Furthermore we prove that the iterative process:
![]()
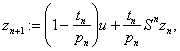
![]() , converges strongly to a fixed point of
, converges strongly to a fixed point of
![]()
Paper's Title:
Orthogonality and ε-Orthogonality in Banach Spaces
Author(s):
H. Mazaheri and S. M. Vaezpour
Faculty of Mathematics, Yazd University, Yazd, Iran
Abstract:
A concept of orthogonality on normed linear space was introduced by Brickhoff,
also the concept of ε-orthogonality was introduced by Vaezpour. In this note, we will consider the relation between these concepts and the dual of
X. Also some results on best coapproximation will be obtained.
Paper's Title:
The Invariant Subspace Problem for Linear Relations on Hilbert Spaces
Author(s):
Daniel Grixti-Cheng
Department of Mathematics and Statistics, Abstract:
We consider the invariant subspace problem for linear relations on Hilbert spaces with the aim of promoting interest in the problem as viewed from the theory of linear relations. We present an equivalence between the single valued and multivalued invariant subspace problems and give some new theorems pertaining to the invariant subspace problem for linear relations on a Hilbert space. Paper's Title:
Two Remarks on Commutators of Hardy
Operator Author(s):
Yasuo Komori-Furuya Abstract:
Fu and Lu showed that Paper's Title:
The Square Number by the Approximation Author(s):
Masaki Hisasue Abstract:
Paper's Title:
A-Normal Operators In Semi Hilbertian Spaces
Author(s):
A. Saddi Department of Mathematics, Abstract:
In this paper we study some properties and
inequalities of A-normal operators in semi-Hilbertian spaces by employing
some known results for vectors in inner product spaces. We generalize also most
of the inequalities of (α,β)-normal operators discussed in Hilbert spaces
[7]. Paper's Title:
Szegö Limits and Haar Wavelet Basis Author(s):
M. N. N. Namboodiri and S. Remadevi Dept. of Mathematics, Cochin University
of Science and Technology, Dept. of Mathematics, College of
Engineering, Abstract:
This paper deals with Szegö type limits for multiplication operators on
L2 (R) with respect to Haar orthonormal basis. Similar studies have
been carried out by Morrison for multiplication operators Tf using Walsh System and Legendre polynomials
[14]. Unlike the
Walsh and Fourier basis functions, the Haar basis functions are local in
nature. It is observed that Szegö type limit exist for a class of
multiplication operators Tf , f∈ L∞ (R) with respect to Haar
(wavelet) system with appropriate ordering. More general classes of orderings of Haar system are
identified for which the Szegö type limit exist for certain classes of
multiplication operators. Some illustrative examples are also provided.
Paper's Title:
Existence and Regularity of Minima of an Integral Functional in Unbounded Domain Author(s):
L. Aharouch, J. Bennouna and A. Bouajaja King Khalid University E-mail:
laharouch@gmail.com Université Sidi Mohammed Ben Abdellah Email:
jbennouna@hotmail.com E-mail:
kadabouajaja@hotmail.com Abstract:
We prove the existence and the regularity of minima for a functional defined on a suitable Sobolev space. Paper's Title:
Some Grüss Type Inequalities in Inner Product Spaces Author(s):
Sever S. Dragomir1,2 1Mathematics, School of Engineering
& Science URL:
http://rgmia.org/dragomir Abstract:
Some inequalities in inner product spaces
where e,f ∈ H with
Paper's Title:
Extreme Curvature of Polynomials and Level Sets Author(s):
Stephanie P. Edwards, arah J. Jensen,
Edward Niedermeyer, and Lindsay Willett Department of Mathematics, Abstract:
Let f be a real polynomial of degree n. Determining the maximum number of
zeros of kappa, the curvature of f, is an easy problem: since the zeros of kappa
are the zeros of f'', the curvature of f is 0 at most n-2 times. A much more
intriguing problem is to determine the maximum number of relative extreme values
for the function kappa. Since kappa'=0 at each extreme point of kappa, we are
interested in the maximum number of zeros of kappa'. In 2004, the first author
and R. Gordon showed that if all the zeros of f'' are real, then f has at most
n-1 points of extreme curvature. We use level curves and auxiliary functions to
study the zeros of the derivatives of these functions. We provide a partial
solution to this problem, showing that f has at most n-1 points of extreme
curvature, given certain geometrical conditions. The conjecture that f has at
most n-1 points of extreme curvature remains open. Paper's Title:
Generalized k-distance-balanced Graphs Author(s):
Amir Hosseini and Mehdi Alaeiyan Department of mathematics, Karaj Branch,
Department of Mathematics, Abstract:
A nonempty graph Γ is called
generalized k-distance-balanced, whenever every edge ab has the
following property: the number of vertices closer to a than to b, k,
times of vertices closer to b than to a, or conversely, k∈
N .In this paper we determine some families of graphs that have this property, as well as to prove some other result regarding these graphs. Paper's Title:
Analysis of a Frictional Contact Problem for Viscoelastic Piezoelectric Materials Author(s):
Meziane Said Ameur, Tedjani Hadj Ammar and Laid Maiza Departement of Mathematics, Departement of Mathematics, Department of Mathematics, Abstract:
In this paper, we consider a mathematical model that describes
the quasi-static process of contact between two thermo-electro-viscoelastic bodies with damage and adhesion. The damage of the materials caused by elastic deformations. The contact is frictional and modeled with a normal compliance condition involving adhesion effect of contact surfaces. Evolution of the
bonding field is described by a first order differential equation. We derive variational formulation for the model and prove an existence and uniqueness result of the weak solution. The proof is based on arguments of evolutionary variational inequalities, parabolic inequalities, differential equations, and fixed point theorem. Paper's Title:
Fekete-Szegö Inequality for Sakaguchi Type of functions in Petal Shaped Domain Author(s):
E. K. Nithiyanandham and B. Srutha Keerthi Division of Mathematics, School of
Advanced Sciences, Division of Mathematics, School of
Advanced Sciences, Abstract:
In this paper, we estimate coefficient bounds,|a_2|,|a_3| and |a_4|, Fekete-Szegö inequality
the function being holomorphic, we expand using Taylor series and obtain several corollaries and consequences for the main result. Paper's Title:
Toeplitz Determinant for Sakaguchi Type Functions Under Petal Shaped Domain Author(s):
B. Nandhini and B. Srutha Keerthi Division of Mathematics, School of
Advanced Sciences, Division of Mathematics, School of
Advanced Sciences, Abstract:
We introduce a new general subclass GPt,ρ of Sakaguchi kind function on a Petal shaped domain. We obtain
coefficients bounds and upper bounds for the Fekete-Szegö
functional over the class. From these functions we obtain the bounds of first four coefficients, and then we have derived the Toeplitz determinant
T2(2) and T3(1) whose diagonal entries are the coefficients of functions. Paper's Title:
On Statistically Φ-Convergence Author(s):
Supama Department of Mathematics, Abstract:
The idea of statistical convergence was introduced by Antoni Zygmund in 1935. Based on in the idea of Zygmund, Henry Fast and Hugo Steinhaus independently
introduced a concept of statistical convergence as a generalization of an ordinary convergence in the same year 1951. In this paper, by using the Orlicz function, we introduce a concept of statistical
Φ-convergence, as a generalization of the statistical convergence. Further, we observe some basic properties and some topological properties of the statistical
Φ-convergent sequences Paper's Title:
On the Oldest Problem in the Calculus of Variations: A New Message from Queen Dido Author(s):
Olivier de La Grandville Faculty of Economics, Abstract:
We consider the problem of finding the optimal
curve of given length linking two points in a plane such as it encloses a
maximal area. We show that if the curve is not described by a single-valued
function, its determination does not necessarily imply to work with a
parametric representation of the curve. We show that a simpler approach is
at hand -- and, who knows? -- this might well be the method Queen Dido used. Paper's Title:
Li-Yorke and Expansivity for Composition Operators on Lorentz Space Author(s):
Rajat Singh and Romesh Kumar Department of Mathematics, Department of Mathematics, Abstract:
In this paper, we investigate Li-Yorke composition operators and
some of its variations on Lorentz spaces. Further, we also study expansive
composition operators on these spaces. The work of the paper is essentially
based on the work in [3],
[6], [8] and [15]. Search and serve lasted 1 second(s).
vaezpour@yazduni.ac.ir
hmazaheri@yazduni.ac.ir
1: Paper Source
PDF document
The University of Melbourne,
Melbourne, VIC, 3010
Australia.
D.Grixti@ms.unimelb.edu.au
1: Paper Source
PDF document
School of High Technology for Human Welfare
Tokai University
317 Nishino Numazu, Shizuoka 410-0395 Japan
komori@wing.ncc.u-tokai.ac.jp
the commutator of multiplication operator by b and
the n-dimensional Hardy operator
is bounded on Lp if b is in some CMO space.
We shall prove the converse of this theorem
and also prove that their result is optimal by giving a counterexample
1: Paper Source
PDF document
Asahikawa Fuji Girls' High School
Asahikawa Hanasaki-cho 6-3899
Hokkaido, Japan
masaki@fuji.ed.jp
In this paper, we give square numbers by using the solutions of Pell's equation.
1: Paper Source
PDF document
College of Education for Girls in Sarat Ebeidah 61914, Abha,
King Khalid University
Saudi Arabia
adel.saddi@fsg.rnu.tn
1: Paper Source
PDF document
Cochin-21, Kerala,
India.
Cherthala, Kerala,
India.
1: Paper Source
PDF document
Faculty of Arts and Science Mha'l Asir
Saudi Arabia.
Faculté des Sciences Dhar-Mahraz
B.P 1796 Atlas Fčs,
Maroc.
1: Paper Source
PDF document
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa that provide upper bounds for the quantities
and
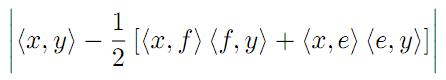
and x,y are vectors in H satisfying some appropriate assumptions are
given. Applications for discrete and integral inequalities are provided as
well.
1: Paper Source
PDF document
Hope College,
Holland, MI 49423,
U.S.A.
E-mail: sedwards@hope.edu
E-mail: tarahjaye@gmail.com
E-mail: eddie.niedermeyer@gmail.com
E-mail: willettlm1@gmail.com
WWW: http://math.hope.edu/sedwards/
1: Paper Source
PDF document
Islamic Azad university, Karaj,
Iran.
E-mail: amir.hosseini@kiau.ac.ir,
hosseini.sam.52@gmail.com
Iran University of Science and Technology, Tehran,
Iran.
E-mail: alaeiyan@iust.ac.ir
1: Paper Source
PDF document
El Oued University,
P.O. Box 789, 39000 El Oued,
Algeria.
E-mail:
said-ameur-meziane@univ-eloued.dz
El Oued University,
P.O. Box 789, 39000 El Oued,
Algeria.
E-mail:
hadjammar-tedjani@univ-eloued.dz
Kasdi Merbah University,
30000 Ouargla,
Algeria.
E-mail: maiza.laid@univ-ouargla.dz
1: Paper Source
PDF document
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: nithiyankrish@gmail.com
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com ![]() and Toeplitz determinant
T2(2) and T3(1) for functions belonging to the following class
and Toeplitz determinant
T2(2) and T3(1) for functions belonging to the following class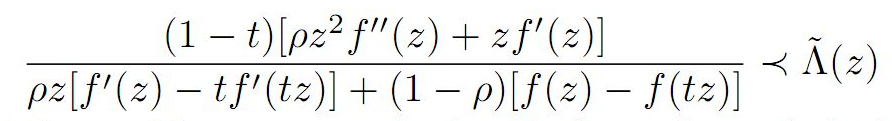
1: Paper Source
PDF document
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail:
nandhinibaskar1996@gmail.com
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com
1: Paper Source
PDF document
Gadjah Mada
University,
Yogyakarta 55281,
Indonesia.
E-mail: supama@ugm.ac.id
1: Paper Source
PDF document
Goethe University Frankfurt,
Theodore Adorno Platz 4, 60323 Frankfurt,
Germany.
E-mail: odelagrandville@gmail.com
1: Paper Source
PDF document
University of Jammu,
Jammu 180006,
INDIA.
E-mail: rajat.singh.rs634@gmail.com
University of Jammu,
Jammu 180006,
INDIA.
E-mail: romeshmath@gmail.com
© 2004-2023 Austral Internet Publishing