|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Two Further Methods for Deriving Four Results Contiguous to Kummer's Second Theorem
Author(s):
I. Kim and J. Kim
Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Korea.
E-mail: iki@wku.ac.kr
Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Korea.
E-mail: joohyung@wku.ac.kr
Abstract:
In the theory of generalized hypergeometric function, transformation and summation formulas play a key role. In particular, in one of the Kummer's transformation formulas, Kim, et al. in 2012, have obtained ten contiguous results in the form of a single result with the help of generalization of Gauss's second summation theorem obtained earlier by Lavoie, et al.. In this paper, we aim at presenting four of such results by the technique of contiguous function relations and integral method developed by MacRobert.
Paper's Title:
Two Classes of Completely Monotonic Functions Involving Gamma and Polygamma Functions
Author(s):
Bai-Ni Guo, Xiao-Ai Li and Feng Qi
School of Mathematics and Informatics,
Henan Polytechnic University,
Jiaozuo City, Henan Province, 454010,
China.
bai.ni.guo@gmail.com
College of Mathematics and Information Science,
Henan Normal University, Xinxiang City,
Henan Province, 453007,
China.
lxa.hnsd@163.com
Research Institute of Mathematical Inequality Theory, Abstract:
The function Paper's Title:
A Double Inequality for Divided Differences and Some Identities of the Psi and Polygamma Functions Author(s):
B. N. Guo and F. Qi School of
Mathematics and Informatics, Henan Polytechnic University, Jiaozuo City, Henan
Province, 454010, China School of
Research Institute of Mathematical Inequality Theory, Henan Polytechnic University, Jiaozuo City, Henan Province, 454010, China Abstract:
In this short note, from the logarithmically completely monotonic property
of the function
Paper's Title:
On A Conjecture of A Logarithmically Completely Monotonic Function Author(s):
Valmir Krasniqi, Armend Sh. Shabani Department of Mathematics, E-mail:
vali.99@hotmail.com
Abstract:
In this short note we prove a conjecture, related to a logarithmically
completely monotonic function, presented in [5].
Then, we extend by proving a more generalized theorem. At the end we pose an
open problem on a logarithmically completely monotonic function involving q-Digamma function.
Paper's Title:
Inequalities Relating to the Gamma Function Author(s):
Chao-Ping Chen and Feng Qi
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics, Abstract:
For For And
equality occurs for x=1. Paper's Title:
Local and Global Existence and Uniqueness Results for Second and Higher Order Impulsive Functional Differential Equations with Infinite Delay
Author(s):
Johnny Henderson and Abdelghani Ouahab
Department of Mathematics, Baylor University,
Laboratoire de Mathématiques, Université de Sidi Bel Abbés Abstract:
In this paper, we discuss the local and global existence and
uniqueness results for second and higher order impulsive functional
differential equations with infinite delay. We shall rely on a
nonlinear alternative of Leray-Schauder. For the global existence
and uniqueness we apply a recent Frigon and Granas nonlinear
alternative of Leray-Schauder type in Fréchet spaces. Paper's Title:
Positive Solutions for Systems of Three-point Nonlinear Boundary Value Problems Author(s):
J. Henderson and S. K. Ntouyas
Department of Mathematics, Baylor University
Department of Mathematics, University of Ioannina Abstract:
Values of λ are determined for which there exist
positive solutions of the system of three-point boundary value problems,
u''(t)+ λa(t)f(v(t))=0, v''(t)+λb(t)g(u(t))=0,
for 0 < t <1, and
satisfying, u(0) = 0, u(1)=α u(η),
v(0) = 0, v(1)=α v(η). A Guo-Krasnosel'skii fixed
point theorem is applied. Paper's Title:
Monotonicity Properties for Generalized Logarithmic Means
Author(s):
Chao-Ping Chen and Feng Qi
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics, Abstract:
In this paper, we consider the monotonicity properties for ratio of two generalized
logarithmic means, and then use it to extend and complement a recently published result of F. Qi
and B.-N. Guo.
Paper's Title:
Oscillations of First Order Linear Delay Difference Equations
Author(s):
G. E. Chatzarakis and I. P. Stavroulakis
Department of Mathematics, University of Ioannina,
Abstract:
Consider the first order linear delay difference equation of
the form Paper's Title:
Nontrivial Solutions of Singular Superlinear Three-point
Boundary Value Problems at Resonance
Author(s):
Feng Wang, Fang Zhang
School of Mathematics and Physics,
Abstract:
The singular superlinear second order three-point boundary value
problems at resonance
are considered under some conditions concerning the first
eigenvalues corresponding to the relevant linear operators, where n ∈ (0,1) is a constant,
f is allowed to be singular at both
t=0 and t=1. The existence results of nontrivial solutions are
given by means of the topological degree theory.
Paper's Title:
On Positive Entire Solutions of Second Order Quasilinear Elliptic Equations
Author(s):
Zuodong Yang and Honghui Yin
Institute of Mathematics, School of Mathematics and Computer Science, Abstract:
In this paper, our main purpose is to establish the existence
theorem of positive entire solutions of second order quasilinear
elliptic equations under new conditions. The main results of the
present paper are new and extend the previously known results. Paper's Title:
Existence of Solutions for Third Order Nonlinear Boundary Value Problems
Author(s):
Yue Hu and Zuodong Yang
School of Mathematics and Computer Science, Nanjing Normal University, Jiangsu Nanjing 210097, Abstract:
In this paper, the existence of solution for a class of third order quasilinear ordinary differential equations with nonlinear boundary value problems (Φp(u"))'=f(t,u,u',u"), u(0)=A, u'(0)=B, R(u'(1),u"(1))=0 is established. The results are obtained by using upper and lower solution methods. Paper's Title:
Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results Author(s):
Sever S. Dragomir1,2 1Mathematics, School of Engineering
& Science Abstract:
The main aim of this survey is to present recent results concerning
Ostrowski type inequalities for the Lebesgue integral of various classes of
complex and real-valued functions. The survey is intended for use by both
researchers in various fields of Classical and Modern Analysis and
Mathematical Inequalities and their Applications, domains which have grown
exponentially in the last decade, as well as by postgraduate students and
scientists applying inequalities in their specific areas. Paper's Title:
Optimal Control Analysis of HIV/AIDS Epidemic Model with an Antiretroviral Treatment Author(s):
U. Habibah and R. A. Sari Mathematics Department and Reseach Group
of Biomathematics, Abstract:
A mathematical model of HIV/AIDS is governed by a system of ordinary differential equations in the presence of an antiretroviral treatment (ARV). The theory of optimal control is applied to an epidemic model of HIV/AIDS which an ARV is used as a control strategy in order to prevent the spread of HIV/AIDS. The optimality system is derived by applying the Pontryagin's Minimum Principle. We analyze the boundedness and positivity of solutions, and an existence of the optimal control. Numerical simulations are conducted to obtain numerical solution of the optimally system. Paper's Title:
Inequalities of Gamma Function Appearing in Generalizing Probability Sampling Design Author(s):
Mohammadkheer M. Al-Jararha And Jehad M. Al-Jararha Department of Mathematics, Department of Statistics, Abstract:
In this paper, we investigate the complete monotonicity of some functions involving gamma function. Using the monotonic properties of these functions, we derived some inequalities involving gamma and beta functions. Such inequalities can be used to generalize different probability distribution functions. Also, they can be used to generalize some statistical designs, e.g., the probability proportional to the size without replacement design. Paper's Title:
An Integration Technique for Evaluating Quadratic Harmonic Sums Author(s):
J. M. Campbell and K.-W. Chen Department of Mathematics and Statistics, Department of Mathematics, University of Taipei, Abstract:
The modified Abel lemma on summation by parts has been applied in many ways recently to determine closed-form evaluations for
infinite series involving generalized harmonic numbers with an upper parameter of two.
We build upon such results using an integration technique that we apply to ``convert'' a given
evaluation for such a series
into an evaluation for a corresponding series involving squared harmonic numbers. Paper's Title:
On an Extension of Hilbert’s Integral Inequality with Some Parameters Author(s):
Bicheng Yang Department of
Mathematics, Guangdong Education College, Guangzhou, Guangdong 510303, People’s
Republic of China. Abstract:
In this paper, by introducing some parameters and estimating the
weight function, we give an extension of Hilbert’s integral inequality with a
best constant factor. As applications, we consider the equivalent form and some
particular results. Paper's Title:
Positive Solution For Discrete Three-Point Boundary Value
Problems Author(s):
Wing-Sum Cheung And Jingli Ren Institute of Systems Science,
Henan Polytechnic University, Jiaozuo City,
Henan Province, 454010,
China
qifeng618@gmail.com
qifeng618@hotmail.com
qifeng618@qq.com
URLhttp://rgmia.vu.edu.au/qi.html
is logarithmically completely monotonic in (0,∞) if and only if c≥1
and its reciprocal is logarithmically completely monotonic in (0,∞) if and only if
c≤0. The function
is completely monotonic in (0,∞) if and only if c≥1 and its
negative is completely monotonic in (0,∞) if and only if c≤0.
9: Paper Source
PDF document
bai.ni.guo@gmail.com,
bai.ni.guo@hotmail.com
qifeng618@gmail.com,
qifeng618@hotmail.com,
qifeng618@qq.com
URL:http://qifeng618.spaces.live.com
, a double inequality for the divided differences and some identities of the psi and polygamma functions are presented.
9: Paper Source
PDF document
University of Prishtina,
Republic of Kosova
armend_shabani@hotmail.com
6: Paper Source
PDF document
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
chenchaoping@hpu.edu.cn
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
qifeng@hpu.edu.cn,
fengqi618@member.ams.org
Url:
http://rgmia.vu.edu.au/qi.html,
http://dami.hpu.edu.cn/qifeng.html
, we have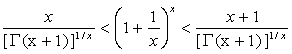
. 
, 
,
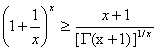4: Paper Source
PDF document
Waco, Texas 76798-7328
USA.
Johnny_Henderson@baylor.edu
BP 89, 22000 Sidi Bel Abbées,
Algérie.
ouahab@univ-sba.dz
4: Paper Source
PDF document
Waco, Texas
76798-7328 USA.
Johnny_Henderson@baylor.edu
URL: http://www3.baylor.edu/~Johnny_Henderson
451 10 Ioannina,
Greece.
sntouyas@cc.uoi.gr
URL: http://www.math.uoi.gr/~sntouyas
3: Paper Source
PDF document
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
chenchaoping@hpu.edu.cn
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
qifeng@hpu.edu.cn,
fengqi618@member.ams.org
Url:
http://rgmia.vu.edu.au/qi.html,
http://dami.hpu.edu.cn/qifeng.html
3: Paper Source
PDF document
451 10, Greece
ipstav@cc.uoi.gr
where
is
a sequence of nonnegative real numbers, k is a positive integer and 
denotes
the forward difference operator 
New
oscillation criteria are established when the well-known oscillation conditions
and
are
not satisfied. The results obtained essentially improve known results in the
literature.
3: Paper Source
PDF document
Changzou University,
Changzhou, 213164,
China.
fengwang188@163.com
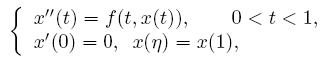
2: Paper Source
PDF document
Nanjing Normal University, Jiangsu Nanjing 210097,
China;
zdyang_jin@263.net
Department of Mathematics, Huaiyin Teachers College,
Jiangsu Huaian 223001,
China;
School of Mathematics and Computer Sciences,
Nanjing Normal University, Jiangsu Nanjing 210097,
China.
yin_hh@sina.com
2: Paper Source
PDF document
China.
huu3y2@163.com
College of Zhongbei, Nanjing Normal University, Jiangsu Nanjing 210046,
China.
zdyang_jin@263.net
yangzuodong@njnu.edu.cn
2: Paper Source
PDF document
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
2: Paper Source
PDF document
Faculty of Mathematics and Natural Science,
Brawijaya University, Jl. Veteran Malang 65145,
Indonesia.
E-mail: ummu_habibah@ub.ac.id
2: Paper Source
PDF document
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: mohammad.ja@yu.edu.jo
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: jehad@yu.edu.jo
2: Paper Source
PDF document
York University, 4700 Keele St, Toronto,
ON M3J 1P3,
Canada.
E-mail: jmaxwellcampbell@gmail.com
No. 1, Ai-Guo West Road,
Taipei 10048, Taiwan.
E-mail: kwchen@uTaipei.edu.tw
URL:
https://math.utaipei.edu.tw/p/412-1082-22.php
1: Paper Source
PDF document
bcyang@pub.guangzhou.gd.cn
URL:
http://www1.gdei.edu.cn/yangbicheng/index.html
1: Paper Source
PDF document
Department of Mathematics,
The University of Hong Kong,
Pokfulam, Hong Kong
wscheung@hku.hk
Chinese Academy of Sciences,
Beijing 100080, P.R. China
renjl@mx.amss.ac.cn
Abstract:
This paper is concerned with the existence of positive solution to the discrete three-point boundary value problem
,
where
, and f is allowed to change sign. By constructing
available operators, we shall apply the method of lower solution and the method
of topology degree to obtain positive solution of the above problem for
on a suitable interval.
The associated Green’s function is first given.
Paper's Title:
A New Hardy-Hilbert's Type Inequality for Double Series and its Applications
Author(s):
Mingzhe Gao
Department of Mathematics and Computer Science, Normal College Jishou University,
Jishou Hunan, 416000,
People's Republic of China
mingzhegao1940@yahoo.com.cn
Abstract:
In this paper, it is shown that a new Hardy-Hilbert’s type
inequality for double series can be established by introducing a parameter 
and the weight function of the form 
where c is Euler
constant and 
And
the coefficient 
and 
appear simultaneously in the coefficient and the weight
function when 
In particular, for
case 
some new Hilbert’s
type inequalities are obtained. As applications, some extensions of Hardy-Littlewood’s inequality are given.
Paper's Title:
On the Generalized Inverse 
over Integral Domains
Author(s):
Yaoming Yu and Guorong Wang
College of Education, Shanghai Normal University
Shanghai 200234
People's Republic of China.
yuyaoming@online.sh.cn
grwang@shnu.edu.cn
Abstract:
In this paper, we study further the generalized inverse
of a matrix A over an integral domain. We give
firstly some necessary and sufficient conditions for the existence
of the generalized inverse , an explicit expression
for the elements of the generalized inverse and an
explicit expression for the generalized inverse ,
which reduces to the {1} inverse. Secondly, we verify that the
group inverse, the Drazin inverse, the Moore-Penrose inverse and the
weighted Moore-Penrose inverse are identical with the generalized
inverse 
for an appropriate matrix G,
respectively, and then we unify the conditions for the existence and
the expression for the elements of the weighted Moore-Penrose
inverse, the Moore-Penrose inverse, the Drazin inverse and the group
inverse over an integral domain. Thirdly, as a simple application,
we give the relation between some rank equation and the existence of
the generalized inverse , and a method to compute the
generalized inverse . Finally, we give an example of
evaluating the elements of without calculating
.
Paper's Title:
On a Hilbert-type Inequality with the Polygamma Function
Author(s):
Bing He and Bicheng Yang
Department of Mathematics, Guangdong Education College,
Guangzhou, 510303,
China.
Department of Mathematics, Guangdong Education College,
Guangzhou, 510303,
China.
Abstract:
By applying the method of weight function and the technique of real analysis, a Hilbert-type inequality with a best constant factor is established, where the best constant factor is made of the polygamma function. Furthermore, the inverse form is given.
Paper's Title:
Positive Solutions to a System of Boundary Value Problems for Higher-Dimensional Dynamic Equations on Time Scales
Author(s):
I. Y. Karaca
Department of Mathematics,
Ege University,
35100 Bornova, Izmir,
Turkey
URL:
http://ege.edu.tr
Abstract:
In this paper, we consider the system of boundary value problems for higher-dimensional dynamic equations on time scales. We establish criteria for the existence of at least one or two positive solutions. We shall also obtain criteria which lead to nonexistence of positive solutions. Examples applying our results are also given.
Paper's Title:
Expected Utility with Subjective Events
Author(s):
Jacob Gyntelberg and Frank Hansen
Bank for International Settlements,
Basel,
Switzerland
Tohoku University, Institute for International Education,
Sendai,
Japan
Abstract:
We provide a new theory of expected utility with subjective events modeled by a lattice of projections. This approach allows us to capture the notion of a ``small world'' as a context dependent or local state space embedded into a subjective set of events, the ``grand world''. For each situation the decision makers' subjective ``small world'' reflects the events perceived to be relevant for the act under consideration. The subjective set of events need not be representable by a classical state space. Maintaining preference axioms similar in spirit to the classical axioms, we obtain an expected utility representation which is consistent across local state spaces and separates subjective probability and utility. An added benefit is that this alternative expected utility representation allows for an intuitive distinction between risk and uncertainty.
Paper's Title:
On Convergence Theorems of an Implicit Iterative Process with Errors for a
Finite Family of Asymptotically quasi I-nonexpansive Mappings
Author(s):
Farrukh Mukhamedov and Mansoor Saburov
Department of Computational & Theoretical
Sciences,
Faculty of Sciences, International Islamic University Malaysia,
P.O. Box, 141, 25710, Kuantan,
Malaysia
Abstract:
In this paper we prove the weak and strong convergence of the implicit iterative process with errors to a common fixed point of a finite family {Tj}Ni=1 of asymptotically quasi Ij-nonexpansive mappings as well as a family of {Ij}Nj=1 of asymptotically quasi nonexpansive mappings in the framework of Banach spaces. The obtained results improve and generalize the corresponding results in the existing literature.
Paper's Title:
Stability of an Almost Surjective epsilon-Isometry in The Dual of Real Banach Spaces
Author(s):
Minanur Rohman, Ratno Bagus Edy Wibowo, Marjono
Department of Mathematics, Faculty of
Mathematics and Natural Sciences,
Brawijaya University,
Jl. Veteran Malang 65145,
Indonesia.
E-mail:
miminanira@gmail.com
Department of Mathematics, Faculty of
Mathematics and Natural Sciences,
Brawijaya University,
Jl. Veteran Malang 65145,
Indonesia.
E-mail:
rbagus@ub.ac.id
Department of Mathematics, Faculty of
Mathematics and Natural Sciences,
Brawijaya University,
Jl. Veteran Malang 65145,
Indonesia.
E-mail:
marjono@ub.ac.id
Abstract:
In this paper, we study the stability of epsilon-isometry in the dual of real Banach spaces. We prove that the almost surjective epsilon-isometry mapping is stable in dual of each spaces. The proof uses Gâteaux differentiability space (GDS), weak-star exposed points, norm-attaining operator, and some studies about epsilon-isometry that have been done before.
Paper's Title:
MSplit Equality for Monotone Inclusion Problem and Fixed Point Problem in
Real Banach Spaces
Author(s):
1,2Christian Chibueze Okeke, 3Abdumalik Usman Bello, 1Chinedu Izuchukwu, and 1Oluwatosin Temitope Mewomo
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: okekec@ukzn.ac.za
E-mail: izuchukwuc@ukzn.ac.za
E-mail: mewomoo@ukzn.ac.za
2DST-NRF
Center of Excellence in Mathematical and Statistical Sciences (CoE-Mass)
Johannesburg,
South Africa.
3Federal
University,
Dutsin-Ma, Katsina State,
Nigeria.
E-mail:
uabdulmalik@fudutsinma.edu.ng
Abstract:
In this paper a new iterative algorithm for approximating a common solution of split equality monotone inclusion problem and split equality fixed point problem is introduced. Using our algorithm, we state and prove a strong convergence theorem for approximating an element in the intersection of the set of solutions of a split equality monotone inclusion problem and the set of solutions of a split equality fixed point problem for right Bregman strongly nonexpansive mappings in the setting of p-uniformly convex Banach spaces which are also uniformly smooth. We also give some applications.
Paper's Title:
Polyanalytic Functions on Subsets of Z[i]
Author(s):
Abtin Daghighi
Linköping University,
SE-581 83,
Sweden.
E-mail: abtindaghighi@gmail.com
Abstract:
For positive integers q we consider the kernel of the powers Lq where L is one of three kinds of discrete analogues of the Cauchy-Riemann operator. The first two kinds are well-studied, but the third kind less so. We give motivations for further study of the third kind especially since its symmetry makes it more appealing for the cases q≥ 2.
From an algebraic perspective it makes sense that the chosen multiplication on the kernels is compatible with the choice of pseudo-powers. We propose such multiplications together with associated pseudo-powers. We develop a proof-tool in terms of certain sets of uniqueness.
Paper's Title:
Iterative Algorithm for Split Generalized Mixed Equilibrium Problem Involving Relaxed Monotone Mappings in Real Hilbert Spaces
Author(s):
1U.A. Osisiogu, F.L. Adum, and 2C. Izuchukwu
1Department of Mathematics and
Computer Science,
Ebonyi State University, Abakaliki,
Nigeria.
E-mail: uosisiogu@gmail.com,
adumson2@yahoo.com
2School of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: izuchukwuc@ukzn.ac.za,
izuchukwu_c@yahoo.com
Abstract:
The main purpose of this paper is to introduce a certain class of split generalized mixed equilibrium problem involving relaxed monotone mappings. To solve our proposed problem, we introduce an iterative algorithm and obtain its strong convergence to a solution of the split generalized mixed equilibrium problems in Hilbert spaces. As special cases of the proposed problem, we studied the proximal split feasibility problem and variational inclusion problem.
Paper's Title:
Dynamical Analysis of HIV/AIDS Epidemic Model with Two Latent Stages, Vertical Transmission and Treatment
Author(s):
Nur Shofianah, Isnani Darti, Syaiful Anam
Mathematics Department,Faculty of
Mathematics and Natural Sciences.
University of Brawijaya,
Jl. Veteran, Malang 65145,
Indonesia.
E-mail:
nur_shofianah@ub.ac.id,
isnanidarti@ub.ac.id,
syaiful@ub.ac.id
Abstract:
We discuss about dynamical analysis of HIV/AIDS epidemic model with two latent stages, vertical transmission and treatment. In this model, the spreading of HIV occurs through both horizontal and vertical transmission. There is also treatment for individual who has been HIV infected. The latent stage is divided into slow and fast latent stage based on the immune condition which varies for each individual. Dynamical analysis result shows that the model has two equilibrium points: the disease-free equilibrium point and the endemic equilibrium point. The existence and global stability of equilibrium points depend on the basic reproduction number R0. When R0 <1, only the disease-free equilibrium point exists. If R0 >1, there are two equilibrium points, which are the disease-free equilibrium point and the endemic equilibrium point. Based on the result of stability analysis, the disease-free equilibrium point is globally asymptotically stable if R0 <1, while if R0 > 1 and p=q, the endemic equilibrium point will be globally asymptotically stable. In the end, we show some numerical simulations to support the analytical result.
Paper's Title:
Weyl's theorem for class Q and k - quasi class Q Operators
Author(s):
S. Parvatham and D. Senthilkumar
Department of Mathematics and Humanities,
Sri Ramakrishna Institute of Technology, Coimbatore-10, Tamilnadu,
India.
E-mail: parvathasathish@gmail.com
Post Graduate and Research Department of
Mathematics,
Govt. Arts College, Coimbatore-641018, Tamilnadu,
India.
E-mail: senthilsenkumhari@gmail.com
Abstract:
In this paper, we give some properties of class Q operators. It is proved that every class Q operators satisfies Weyl's theorem under the condition that T2 is isometry. Also we proved that every k quasi class Q operators is Polaroid and the spectral mapping theorem holds for this class of operator. It will be proved that single valued extension property, Weyl and generalized Weyl's theorem holds for every k quasi class Q operators.
Paper's Title:
Attempts to Define a Baum--Connes Map Via Localization of Categories for Inverse Semigroups
Author(s):
Bernhard Burgstaller
Departamento de Matematica,
Universidade Federal de Santa Catarina,
CEP 88.040-900 Florianopolis-SC,
Brasil.
E-mail:
bernhardburgstaller@yahoo.de
URL:
http://mathematik.work/bernhardburgstaller/index.html
Abstract:
An induction functor in inverse semigroup equivariant KK-theory is considered, and together with %a restriction functors certain results similar to those known from the Mackey machinery are shown. It is also verified that for any so-called E-continuous inverse semigroup its equivariant KK-theory satisfies the universal property and is a triangulated category.
Paper's Title:
Sharp Inequalities Between Hölder and Stolarsky Means of Two Positive Numbers
Author(s):
M. Bustos Gonzalez and A. I. Stan
The University of Iowa,
Department of Mathematics,
14 MacLean Hall,
Iowa City, Iowa,
USA.
E-mail:
margarita-bustosgonzalez@uiowa.edu
The Ohio State University at Marion,
Department of Mathematics,
1465 Mount Vernon Avenue,
Marion, Ohio,
USA.
E-mail: stan.7@osu.edu
Abstract:
Given any index of the Stolarsky means, we find the greatest and least indexes of the H\"older means, such that for any two positive numbers, the Stolarsky mean with the given index is bounded from below and above by the Hölder means with those indexes, of the two positive numbers. Finally, we present a geometric application of this inequality involving the Fermat-Torricelli point of a triangle.
Paper's Title:
Simple Integral Representations for the Fibonacci and Lucas Numbers
Author(s):
Seán M. Stewart
Physical Science and Engineering Division,
King Abdullah
University of Science and Technology,
Thuwal 23955-6900,
Saudi
Arabia.
E-mail: sean.stewart@kaust.edu.sa
Abstract:
Integral representations of the Fibonacci numbers Fkn + r and the Lucas numbers Lkn + r are presented. Each is established using methods that rely on nothing beyond elementary integral calculus.
Paper's Title:
Generalized Triangular and Symmetric Splitting Method for Steady State Probability Vector of Stochastic Matrices
Author(s):
B. Harika, D. Rajaiah, L. P. RajKumar, Malla Reddy Perati
Department of Mathematics,
Kakatiya University
E-mail: hbolledla@gmail.com
Department of Mathematics,
Kakatiya Institute of Technology and Science
E-mail: dr.mh@kitsw.ac.in
Department of Mathematics,
Kakatiya University
E-mail: ladalla@gmail.com
Department of Mathematics,
Kakatiya University
E-mail: mperati@yahoo.com
Abstract:
To find the steady state probability vector of homogenous linear system π Q=0 of stochastic rate matrix Q, generalized triangular and symmetric (GTS) splitting method is presented. Convergence analysis and choice of parameters are given when the regularized matrix A=QT+ε I of the regularized linear system Ax=b is positive definite. Analysis shows that the iterative solution of GTS method converges unconditionally to the unique solution of the regularized linear system. From the numerical results, it is clear that the solution of proposed method converges rapidly when compared to the existing methods.
Paper's Title:
The Drazin-star and Star-Drazin Solutions to Quaternion Matrix Equations
Author(s):
Ivan I. Kyrchei, Dijana Mosić, Predrag Stanimirović
Pidstryhach Institute for Applied Problems
of Mechanics and Mathematics
of NAS of Ukraine, L'viv, 79060,
Ukraine.
E-mail:
ivankyrchei26@gmail.com
Faculty of Sciences and Mathematics,
University of Niš, P.O.
Box 224, 18000, Niš, Serbia.
E-mail: dijana@pmf.ni.ac.rs
Faculty of Sciences and Mathematics,
University of Niš, P.O.
Box 224, 18000, Niš, Serbia.
E-mail: pecko@pmf.ni.ac.rs
Abstract:
The notions of the Drazin-star and star-Drazin matrices are expanded to quaternion matrices in this paper. Their determinantal representations are developed in both cases in terms of noncommutative row-column determinants of quaternion matrices and for minors of appropriate complex matrices. We study all possible two-sided quaternion matrix equations with their one-sided partial cases whose uniquely determined solutions are based on the Drazin-star and star-Drazin matrices. Solutions of these equations are represented by Cramer's rules in both cases for quaternion and complex matrix equations. A numerical example is presented to illustrate our results.
Search and serve lasted 1 second(s).