Paper's Title:

A Caratheodory's Approximate Solutions of Stochastic Differential Equations Under the Hölder Condition

Author(s):

Bo-Kyeong Kim and Young-Ho Kim

Department of Mathematics,
Changwon National University,
Changwon, Gyeongsangnam-do 51140,
Korea.
E-mail: claire9576@naver.com
yhkim@changwon.ac.kr

Abstract:

In this paper, based on the theorem of the uniqueness of the solution of the stochastic differential equation, the convergence possibility of the Caratheodory's approximate solution was studied by approximating the unique solution. To obtain this convergence theorem, we used a Hölder condition and a weakened linear growth condition. Furthermore, The auxiliary theorems for the existence and continuity of the Caratheodory's approximate solution were investigated as a prerequisite.

Paper's Title:

Numerical Study of a Mathematical Model of a Free-Surface Potential Flow

Author(s):

H. Serguine, F. Guechi and A. Gasmi

Department Of Mathematics, Faculty of Science,
Ferhat Abbas Universty, 19000, Setif,
Algeria.
E-mail: houria.serguine@univ-msila.dz

 
Department Of Mathematics, Faculty of Science,
Ferhat Abbas Universty, 19000, Setif,
Algeria.
E-mail:  fairouz.chegaar@univ-setif.dz

Laboratory of Pure and Applied Mathematics, Faculty of Mathematics and Computer Science,
Mohamed Boudiaf Universty, 28000, M'sila,
Algeria.
E-mail: abdelkader.gasmi@univ-msila.dz

Abstract:

In this work, the problem of a potential and two-dimensional flow with a free surface of an incompressible, irrotational and inviscid fluid of a jet in front an inclined wall is considered, where γ is the inclination angle with the horizontal. The shape of the free surface is presented by curves which are found numerically by the series truncation method. This technique is based on the conformal transformations, resulting with the surface tension effect T with the boundary conditions on the free surfaces given by Bernoulli's equation. The found results are dependant on parameters which are: the Weber's number α and the angle γ. For each Weber's number value, only one solution is specified and some shapes of free surfaces of the jet are illustrated.

Paper's Title:

Using Direct and Fixed Point Technique of Cubic Functional Equation and its Hyers-Ulam Stability

Author(s):

Ramanuja Rao Kotti, Rajnesh Krishnan Mudaliar, Kaushal Neelam Devi, Shailendra Vikash Narayan

Fiji National University,
Department of Mathematics & Statistics,
P.O. Box 5529, Lautoka,
Fiji.
E-mail: ramanuja.kotti@fnu.ac.fj
URL: https://www.fnu.ac.fj

Abstract:

In this present work, we introduce a new type of finite dimensional cubic functional equation of the form

where Φ≥4 is an integer, and derive its general solution. The main purpose of this work is to investigate the Hyers-Ulam stability results for the above mentioned functional equation in Fuzzy Banach spaces by means of direct and fixed point methods.

Paper's Title:

On a Generalized Biharmonic Equation in Plane Polars with Applications to Functionally Graded Materials

Author(s):

Ciro D'Apice

Department of Information Engineering and Applied Mathematics (DIIMA),
University of Salerno, 84084 Fisciano (SA),
Salerno, Italy.
dapice@diima.unisa.it

Abstract:

In this paper we consider a generalized biharmonic equation modelling a two-dimensional inhomogeneous elastic state in the curvilinear rectangle where denote plane polar coordinates. Such an arch--like region is maintained in equilibrium under self--equilibrated traction applied on the edge while the other three edges and are traction free. Our aim is to derive some explicit spatial exponential decay bounds for the specific Airy stress function and its derivatives. Two types of smoothly varying inhomogeneity are considered: (i) the elastic moduli vary smoothly with the polar angle, (ii) they vary smoothly with the polar distance. Such types of smoothly varying inhomogeneous elastic materials provide a model for technological important functionally graded materials. The results of the present paper prove how the spatial decay rate varies with the constitutive profile.

Paper's Title:

Reconstruction of Discontinuities of Functions Given Noisy Data

Author(s):

Eric D. Mbakop

67A Beaver Park Rd,
Framingham, MA, 01702,
U. S. A.
ericsteve86@yahoo.fr

Abstract:

Suppose one is given noisy data of a discontinuous piecewise-smooth function along with a bound on its second derivative. The locations of the points of discontinuity of f and their jump sizes are not assumed known, but are instead retrieved stably from the noisy data. The novelty of this paper is a numerical method that allows one to locate some of these points of discontinuity with an accuracy that can be made arbitrarily small.

Paper's Title:

On the Generalized Stability and Asymptotic Behavior of Quadratic Mappings

Author(s):

Hark-Mahn Kim, Sang-Baek Lee and Eunyoung Son

Abstract:

We extend the stability of quadratic mappings to the stability of general quadratic mappings with several variables, and then obtain an improved asymptotic property of quadratic mappings on restricted domains.

Paper's Title:

Stability of Almost Multiplicative Functionals

Author(s):

Norio Niwa, Hirokazu Oka, Takeshi Miura and Sin-Ei Takahasi

Abstract:

Let δ and p be non-negative real numbers. Let be the real or complex number field and a normed algebra over . If a mapping satisfies

then we show that φ is multiplicative or for all If, in addition, φ satisfies

for some p≠1, then by using Hyers-Ulam-Rassias stability of additive Cauchy equation, we show that φ is a ring homomorphism or for all In other words, φ is a ring homomorphism, or an approximately zero mapping. The results of this paper are inspired by Th.M. Rassias' stability theorem.

Paper's Title:

A Coincidence Theorem for Two Kakutani Maps

Author(s):

Mircea Balaj

Department of Mathematics,
University of Oradea,
410087, Oradea,
Romania.
 mbalaj@uoradea.ro

Abstract:

In this paper we prove the following theorem: Let X be a nonempty compact convex set in a locally convex Hausdorff topological vector space, D be the set of its extremal points and F,T: X―◦X two Kakutani maps; if for each nonempty finite subset A of D and for any x ∈ coA, F (x) ∩ coA ≠ Ø, then F and T have a coincidence point. The proof of this theorem is given first in the case when X is a simplex, then when X is a polytope and finally in the general case. Several reformulations of this result are given in the last part of the paper.

Paper's Title:

Some New Generalizations of Jensen's Inequality with Related Results and Applications

Author(s):

Steven G. From

Department of Mathematics
University of Nebraska at Omaha
Omaha, Nebraska 68182-0243.

E-mail: sfrom@unomaha.edu

Abstract:

In this paper, some new generalizations of Jensen's inequality are presented. In particular, upper and lower bounds for the Jensen gap are given and compared analytically and numerically to previously published bounds for both the discrete and continuous Jensen's inequality cases. The new bounds compare favorably to previously proposed bounds. A new method based on a series of locally linear interpolations is given and is the basis for most of the bounds given in this paper. The wide applicability of this method will be demonstrated. As by-products of this method, we shall obtain some new Hermite-Hadamard inequalities for functions which are 3-convex or 3-concave. The new method works to obtain bounds for the Jensen gap for non-convex functions as well, provided one or two derivatives of the nonlinear function are continuous. The mean residual life function of applied probability and reliability theory plays a prominent role in construction of bounds for the Jensen gap. We also present an exact integral representation for the Jensen gap in the continuous case. We briefly discuss some inequalities for other types of convexity, such as convexity in the geometric mean, and briefly discuss applications to reliability theory.

Paper's Title:

A Note on Divergent Fourier Series and λ-Permutations

Author(s):

A. Castillo, J. Chavez and H. Kim

Tufts University,
Department of Mathematics,
Medford, MA 02155,
USA
E-mail: angel.castillo@tufts.edu

Texas Tech University,
Department of Mathematics and Statistics,
Lubbock, TX 79409,
USA
E-mail: josechavez5@my.unt.edu

University of Michigan-Dearborn,
Department of Mathematics and Statistics,
Dearborn, MI 48128,
USA.
E-mail: khyejin@umich.edu

Abstract:

We present a continuous function on [-π,π] whose Fourier series diverges and it cannot be rearranged to converge by a λ-permutation.

Paper's Title:

Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.

Paper's Title:

A Low Order Least-Squares Nonconforming Finite Element Method for Steady Magnetohydrodynamic Equations

Author(s):

Z. Yu, D. Shi and H. Zhu

College of Science,
Zhongyuan University of Technology,
Zhengzhou 450007,
China.
E-mail: 5772@zut.edu.cn

School of Mathematics and Statistics,
Zhengzhou University,
Zhengzhou 450001,
China.
E-mail: shi_dy@126.com

Mathematics Department,
University of Southern Mississippi,
Hattiesburg MS, 39406,
U.S.A
E-mail: huiqing.zhu@usm.edu

Abstract:

A low order least-squares nonconforming finite element (NFE) method is proposed for magnetohydrodynamic equations with EQ₁^rot element and zero-order Raviart-Thomas element. Based on the above element's typical interpolations properties, the existence and uniqueness of the approximate solutions are proved and the optimal order error estimates for the corresponding variables are derived.

Paper's Title:

On a subset of Bazilevic functions

Author(s):

Marjono and D. K. Thomas

Department of Mathematics,
Faculty of Mathematics and Natural Sciences,
Brawajaya University,
Malang, Jawa Timur 65145,
Indonesia.
E-mail: marjono@ub.ac.id

Department of Mathematics,
Swansea University, Singleton Park,
Swansea, SA2 8PP,
United Kingdom.
E-mail: d.k.thomas@swansea.ac.uk

Abstract:

Let S denote the class of analytic and univalent functions in 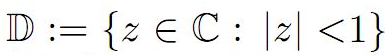of the form 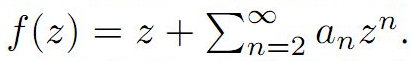For α≥0, the subclass B₁α of S of Bazilevic functions has been extensively studied. In this paper we determine various properties of a subclass of B₁α, for α≥0 which extends early results of a class of starlike functions studied by Ram Singh.

Paper's Title:

An Existence of the Solution to Neutral Stochastic Functional Differential Equations Under the Holder Condition

Author(s):

Young-Ho Kim

Department of Mathematics,
Changwon National University,
Changwon, Gyeongsangnam-do 51140,
Korea.

E-mail: iyhkim@changwon.ac.kr

Abstract:

In this paper, we show the existence and uniqueness of solution of the neutral stochastic functional differential equations under weakened H\"{o}lder condition, a weakened linear growth condition, and a contractive condition. Furthermore, in order to obtain the existence of a solution to the equation we used the Picard sequence.

Paper's Title:

Analysis of a Frictional Contact Problem for Viscoelastic Piezoelectric Materials

Author(s):

Meziane Said Ameur, Tedjani Hadj Ammar and Laid Maiza

Departement of Mathematics,
El Oued University,
P.O. Box 789, 39000 El Oued,
Algeria.
E-mail: said-ameur-meziane@univ-eloued.dz

Departement of Mathematics,
El Oued University,
P.O. Box 789, 39000 El Oued,
Algeria.
E-mail: hadjammar-tedjani@univ-eloued.dz

Department of Mathematics,
Kasdi Merbah University,
30000 Ouargla,
Algeria.
E-mail: maiza.laid@univ-ouargla.dz

Abstract:

In this paper, we consider a mathematical model that describes the quasi-static process of contact between two thermo-electro-viscoelastic bodies with damage and adhesion. The damage of the materials caused by elastic deformations. The contact is frictional and modeled with a normal compliance condition involving adhesion effect of contact surfaces. Evolution of the bonding field is described by a first order differential equation. We derive variational formulation for the model and prove an existence and uniqueness result of the weak solution. The proof is based on arguments of evolutionary variational inequalities, parabolic inequalities, differential equations, and fixed point theorem.

Paper's Title:

Riemann-Stieltjes Integrals and Some Ostrowski Type Inequalities

Author(s):

W. G. Alshanti

Department of General Studies,
Jubail University College,
KSA.
E-mail: shantiw@ucj.edu.sa

Abstract:

In this article, we investigate new integral inequalities of Ostrowski's type of various functional aspects. For mapping's second derivative, we assume two cases, namely, L₁ and L_∞ spaces. Moreover, for first derivative, we investigate two different characteristics, namely, bounded variation and locally Lipchitz continuity. Applications to special means and composite quadrature rules are also carried out.

Paper's Title:

A Review on Minimally Supported Frequency Wavelets

Author(s):

K Pallavi¹, M C Lineesh¹, A Noufal²

¹Department of Mathematics,
National Institute of Technology Calicut,
Kerala 673601,
India.
E-mail:  pavikrishnakumar@gmail.com
lineesh@nitc.ac.in