|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Some Convergence Results for Jungck-Am Iterative Process In Hyperbolic Spaces
Author(s):
Akindele Adebayo Mebawondu and Oluwatosin Temitope Mewomo
School of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail:
216028272@stu.ukzn.ac.za,
mewomoo@ukzn.ac.za
Abstract:
In this paper, we introduce a new three steps iterative process called Jungck-AM iterative process and show that the proposed iterative process can be used to approximate fixed points of Jungck-contractive type mappings and Jungck-Suzuki type mappings. In addition, we establish some strong and Δ-convergence results for the approximation of fixed points of Jungck-Suzuki type mappings in the frame work of uniformly convex hyperbolic space. Furthermore, we show that the newly proposed iterative process has a better rate of convergence compare to the Jungck-Noor, Jungck-SP, Jungck-CR and some existing iterative processes in the literature. Finally, stability, data dependency results for Jungck-AM iterative process is established and we present an analytical proof and numerical examples to validate our claim.
Paper's Title:
Asymptotic Behavior of Mixed Type Functional Equations
Author(s):
J. M. Rassias
Pedagogical Department, E.E., National and
Capodistrian University of Athens, Section of Mathematics And Informatics, 4, Agamemnonos
Str., Aghia Paraskevi, Athens 15342,Greece
jrassias@primedu.uoa.gr
URL:
http://www.primedu.uoa.gr/~jrassias/
Abstract:
In 1983 Skof [24] was the first author to solve the Ulam problem for additive mappings on a restricted domain. In 1998 Jung [14] investigated the Hyers-Ulam stability of additive and quadratic mappings on restricted domains. In this paper we improve the bounds and thus the results obtained by Jung [14], in 1998 and by the author [21], in 2002. Besides we establish new theorems about the Ulam stability of mixed type functional equations on restricted domains. Finally, we apply our recent results to the asymptotic behavior of functional equations of different types.
Paper's Title:
A Fixed Point Approach to
the Stability of the Equation
![]()
Author(s):
Soon-Mo Jung
Mathematics Section, College of Science and Technology
Hong-Ik
University, 339-701 Chochiwon
Republic of Korea.
smjung@hongik.ac.kr
Abstract:
We will apply a fixed point method for proving the Hyers--Ulam stability of
the functional equation
![]() .
.
Paper's Title:
New Coincidence and Fixed Point Theorems for Strictly Contractive Hybrid Maps
Author(s):
S. L. Singh and Amal M. Hashim
21, Govind Nagar, Rishikesh 249201,
Ua, India
vedicmri@sancharnet.in
Dept. of Math., College of Science,
Univ. of Basarah,
Iraq.
Abstract:
The purpose of this paper is to study the (EA)-property and noncompatible maps
of a hybrid pair of single-valued and multivalued maps in fixed point considerations. Such maps
have the remarkable property that they need not be continuous at their common fixed points. We
use this property to obtain some coincidence and fixed point theorems for strictly contractive
hybrid maps without using their continuity and completeness or compactness of the space.
Paper's Title:
Ulam Stability of Functional Equations
Author(s):
Stefan Czerwik and Krzysztof Król
Institute of Mathematics
Silesian University of Technology
Kaszubska 23,
44-100 Gliwice,
Poland
Stefan.Czerwik@polsl.pl
Krzysztof.Krol@polsl.pl
Abstract:
In this survey paper we present some of the main results on Ulam-Hyers-Rassias stability for important functional equations.
Paper's Title:
Common Fixed Point Results for Banach Operator Pairs and Applications to Best Approximation
Author(s):
Hemant Kumar Nashine
Department of Mathematics,
Disha Institute of Management and Technology,
Satya Vihar, Vidhansabha - Chandrakhuri Marg (Baloda Bazar Road),
Mandir Hasaud,
Raipur - 492101(Chhattisgarh), India.
hemantnashine@rediffmail.com
nashine_09@rediffmail.com
Abstract:
The common fixed point results for Banach operator pair with generalized nonexpansive mappings in q-normed space have been obtained in the present work. As application, some more general best approximation results have also been determined without the assumption of linearity or affinity of mappings. These results unify and generalize various existing known results with the aid of more general class of noncommuting mappings.
Paper's Title:
Ulam Stability of Reciprocal Difference and Adjoint Functional Equations
Author(s):
K. Ravi, J. M. Rassias and B. V. Senthil Kumar
Department of Mathematics,
Sacred Heart College, Tirupattur - 635601,
India
Pedagogical Department E. E.,
Section of Mathematics and Informatics,
National and Capodistrian University of Athens,
4, Agamemnonos Str., Aghia Paraskevi,
Athens, Attikis 15342,
GREECE
Department of Mathematics,
C.Abdul Hakeem College of Engineering and
Technology, Melvisharam - 632 509, India
shckavi@yahoo.co.in
jrassias@primedu.uoa.gr
bvssree@yahoo.co.in
Abstract:
In this paper, the reciprocal difference functional equation (or RDF equation) and the reciprocal adjoint functional equation (or RAF equation) are introduced. Then the pertinent Ulam stability problem for these functional equations is solved, together with the extended Ulam (or Rassias) stability problem and the generalized Ulam (or Ulam-Gavruta-Rassias) stability problem for the same equations.
Paper's Title:
Applications of Relations and Relators in the
Extensions of Stability Theorems for Homogeneous and Additive Functions
Author(s):
Árpád Száz
Institute of Mathematics, University of Debrecen,
H-4010 Debrecen,
Pf. 12,
Hungary
szaz@math.klte.hu
Abstract:
By working out an appropriate technique of relations and relators and extending the ideas of the direct methods of Z. Gajda and R. Ger, we prove some generalizations of the stability theorems of D. H. Hyers, T. Aoki, Th. M. Rassias and P. Găvruţă in terms of the existence and unicity of 2-homogeneous and additive approximate selections of generalized subadditive relations of semigroups to vector relator spaces. Thus, we obtain generalizations not only of the selection theorems of Z. Gajda and R. Ger, but also those of the present author.
Paper's Title:
A Generalization of a Trace Inequality for Positive Definite Matrices
Author(s):
E. V. Belmega, M. Jungers, and S. Lasaulce
Université Paris-Sud Xi, SUPELEC,
Laboratoire Des Signaux Et Systèmes,
Gif-Sur-Yvette,
France.
belmega@lss.supelec.fr
http://veronica.belmega.lss.supelec.fr
CNRS, ENSEM, CRAN, Vandoeuvre,
France.
marc.jungers@cran.uhp-nancy.fr
http://perso.ensem.inpl-nancy.fr/Marc.Jungers/
CNRS, SUPELEC, Laboratoire des Signaux et
Systèmes,
Gif-Sur-Yvette,
France.
lasaulce@lss.supelec.fr
http://samson.lasaulce.lss.supelec.fr
Abstract:
In this note, we provide a generalization of the trace inequality derived in [Belmega].
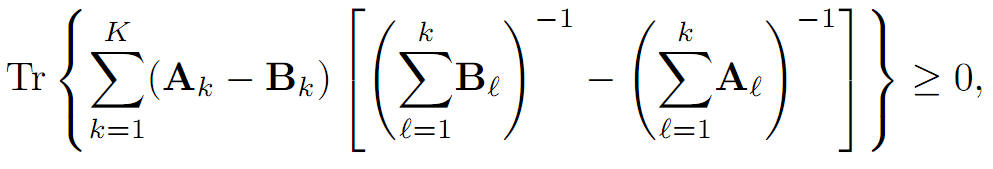
More precisely, we prove that for arbitrary K ≥ 1 where Tr(∙) denotes the matrix trace operator, A1, B1 are any positive definite matrices and Ak, Bk for all k∈{2,...,k}, are any positive semidefinite matrices.
Paper's Title:
Komatu Integral Transforms of Analytic Functions Subordinate to Convex Functions
Author(s):
T. N. Shanmugam and C. Ramachandran
Department of Mathematics, College of Engineering,
Anna University, Chennai-600 025, Tamilnadu,
India
shan@annauniv.edu
Department of Mathematics, College of Engineering,
Anna University, Chennai-600 025, Tamilnadu,
India
crjsp2004@yahoo.com
Abstract:
In this paper, we consider the class A of the functions f(z) of the form
which are analytic in an open disk
has some property. Certain inclusion and the closure properties like convolution with convex univalent function etc. are studied.

 and study certain subclass of the class A, for which
and study certain subclass of the class A, for which
Paper's Title:
On the Generalized Stability and
Asymptotic Behavior of Quadratic Mappings
Author(s):
Hark-Mahn Kim, Sang-Baek Lee and Eunyoung Son
Department of Mathematics
Chungnam National University
Daejeon,
305-764,
Republic of Korea
hmkim@cnu.ac.kr
Abstract:
We extend the stability of quadratic mappings to the stability of general quadratic mappings with several variables, and then obtain an improved asymptotic property of quadratic mappings on restricted domains.
Paper's Title:
Hyers-Ulam-Rassias Stability
of a Generalized Jensen Functional Equation
Author(s):
A. Charifi, B. Bouikhalene, E. Elqorachi and A. Redouani
Department of
Mathematics, Faculty of Sciences,
Ibn Tofail University,
Kenitra, Morocco
charifi2000@yahoo.fr
bbouikhalene@yahoo.fr
Department of
Mathematics, Faculty of Sciences,
Ibn Zohr University,
Agadir, Morocco
elqorachi@hotmail.com
Redouani-ahmed@yahoo.fr
Abstract:
In this paper we obtain the Hyers-Ulam-Rassias stability for the generalized Jensen's functional equation in abelian group (G,+). Furthermore we discuss the case where G is amenable and we give a note on the Hyers-Ulam-stability of the K-spherical (n × n)-matrix functional equation.
Paper's Title:
Approximation of an AQCQ-Functional Equation and its Applications
Author(s):
Choonkil Park and Jung Rye Lee
Department of Mathematics,
Research Institute for Natural Sciences,
Hanyang University, Seoul 133-791,
Korea;
Department of Mathematics,
Daejin University,
Kyeonggi 487-711,
Korea
baak@hanyang.ac.kr
jrlee@daejin.ac.kr
Abstract:
This paper is a survey on the generalized Hyers-Ulam stability of an AQCQ-functional equation in several spaces. Its content is divided into the following sections:
1. Introduction and preliminaries.
2. Generalized Hyers-Ulam stability of an AQCQ-functional equation in Banach spaces: direct method.
3. Generalized Hyers-Ulam stability of an AQCQ-functional equation in Banach spaces: fixed point method.
4. Generalized Hyers-Ulam stability of an AQCQ-functional equation in random Banach spaces: direct method.
5. Generalized Hyers-Ulam stability of an AQCQ-functional equation in random Banach spaces: fixed point method.
6. Generalized Hyers-Ulam stability of an AQCQ-functional equation in non-Archi-medean Banach spaces: direct method.
7. Generalized Hyers-Ulam stability of an AQCQ-functional equation in non-Archi-medean Banach spaces: fixed point method.
Paper's Title:
Characterization of Caristi Type Mapping Through its Absolute Derivative
Author(s):
M. Muslikh1, A. Kilicman2,3, S. H. Sapar4 and N. Bacho5
1Department of Mathematics,
University of Brawijaya,
Malang 65143, East Java,
Indonesia.
E-mail: mslk@ub.ac.id
2Department of Mathematics,
Universiti Putra Malaysia,
43400 UPM, Serdang, Selangor,
Malaysia
E-mail: akilic@upm.edu.my
3Department of Electrical and Electronic Engineering,
Istanbul Gelisim University,
Avcilar, Istanbul,
Turkey
4Department of Mathematics,
Universiti Putra Malaysia,
43400 UPM, Serdang, Selangor,
Malaysia
E-mail: sitihas@upm.edu.my
5Department of Mathematics,
Universiti Putra Malaysia,
43400 UPM, Serdang, Selangor,
Malaysia
E-mail: norfifah@upm.edu.my
Abstract:
The purpose of this article to characterize the Caristi type mapping by the absolute derivative. The equivalences of the Caristi mapping with contraction mapping is discussed too. In addition, it was shown that the contraction mapping can be tested through its absolute derivative.
Paper's Title:
Pointwise Convergence of Fourier-type Series with Exponential Weights
Author(s):
Hee Sun Jung and Ryozi Sakai
Department of Mathematics Education,
Sungkyunkwan University,
Seoul 110-745,
Republic of Korea.
E-mail: hsun90@skku.edu
Department of Mathematics,
Meijo University, Nagoya 468-8502,
Japan.
E-mail: ryozi@hm.aitai.ne.jp
Abstract:
Let R = ( - ∞,∞), and let Q∈C1(R):R→[0,∞) be an even function. We consider the exponential weights w(x)=e-Q(x), x∈R. In this paper we obtain a pointwise convergence theorem for the Fourier-type series with respect to the orthonormal polynomials {pn(w2;x)}.
Paper's Title:
Fixed Point Theorems for a Finite Family of Asymptotically Nonexpansive Mappings
Author(s):
E. Prempeh
Department of Mathematics,
Kwame Nkrumah University of Science and Technology,
Kumasi, Ghana
edward_prempeh2000@yahoo.com
Abstract:
Let
![]() be a real reflexive Banach space with a uniformly Gâteaux differentiable norm,
be a real reflexive Banach space with a uniformly Gâteaux differentiable norm,
![]() be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of
![]() i=1,2,...,r be a finite family of asymptotically nonexpansive mappings
such that for each
i=1,2,...,r be a finite family of asymptotically nonexpansive mappings
such that for each
![]()
![]() Let
Let
![]() be a nonempty set of common fixed points of
be a nonempty set of common fixed points of
![]() and define
and define
![]()
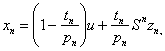
![]() associated with
associated with
![]() , converges strongly to a fixed point of
, converges strongly to a fixed point of
![]() provided
provided
![]() possesses uniform normal structure. Furthermore we prove that the iterative process:
possesses uniform normal structure. Furthermore we prove that the iterative process:
![]()
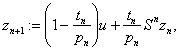
![]() , converges strongly to a fixed point of
, converges strongly to a fixed point of
![]()
Paper's Title:
A general common fixed point theorem for reciprocally continuous mappings satisfying an implicit relation
Author(s):
A. Djoudi and A. Aliouche
Faculty of Science, University of Annaba,
P.O. Box 23000, Annaba,
Algeria.
adjoudi@yahoo.com
Department of Mathematics, University of Larbi Ben M'Hidi,
Oum-El-Bouaghi 04000,
Algeria.
abdmath@hotmail.com
Abstract:
A general common fixed point theorem for compatible mappings satisfying an
implicit relation is obtained by replacing the continuity of one mapping
by the reciprocal continuity of two mappings.
Paper's Title:
On the Ulam Stability for Euler-Lagrange Type Quadratic Functional Equations
Author(s):
Matina John Rassias and John Michael Rassias
Statistics and Modelling Science,
University of Strathclyde,
Livingstone Tower,
26 Richmond Str,
Glasgow, Uk, G1 1xh
Pedagogical Department, E. E., National and Capodistrian University of Athens,
Section of Mathematics and Informatics,
4, Agamemnonos Str, Aghia Paraskevi,
Athens 15342, Greece
Abstract:
In 1940 (and 1968) S. M. Ulam proposed the well-known Ulam stability problem.
In 1941 D.H. Hyers solved the Hyers-Ulam problem for linear mappings. In 1951 D. G. Bourgin
has been the second author treating the Ulam problem for additive mappings. In 1978 according
to P.M. Gruber this kind of stability problems is of particular interest in probability theory and in
the case of functional equations of different types. In 1982-2004 we established the Hyers-Ulam
stability for the Ulam problem for different mappings. In 1992-2000 J.M. Rassias investigated
the Ulam stability for Euler-Lagrange mappings. In this article we solve the Ulam problem
for Euler-Lagrange type quadratic functional equations. These stability results can be applied
in mathematical statistics, stochastic analysis, algebra, geometry, as well as in psychology and
sociology.
Paper's Title:
Solution of the Hyers-Ulam Stability Problem for Quadratic Type Functional Equations in Several Variables
Author(s):
John Michael Rassias
Pedagogical Department, E.E., National and Capodistrian University of Athens,
Section of Mathematics and Informatics,
4, Agamemnonos Str., Aghia Paraskevi,
Athens 15342,
Greece
jrassias@primedu.uoa.gr
URL: http://www.primedu.uoa.gr/~jrassias/
Abstract:
In 1940 (and 1968) S. M. Ulam proposed the well-known Ulam stability problem. In 1941 D. H. Hyers solved the Hyers-Ulam problem for linear mappings. In 1951 D. G. Bourgin has been the second author treating the Ulam problem for additive mappings. In 1978 according to P. M. Gruber this kind of stability problems is of particular interest in probability theory and in the case of functional equations of different types. In 1982-2004 we established the Hyers-Ulam stability for the Ulam problem for different mappings. In this article we solve the Hyers-Ulam problem for quadratic type functional equations in several variables. These stability results can be applied in stochastic analysis, financial and actuarial mathematics, as well as in psychology and sociology.
Paper's Title:
A Stability of the G-type Functional Equation
Author(s):
Gwang Hui Kim
Department of Mathematics, Kangnam University
Suwon 449-702, Korea.
ghkim@kangnam.ac.kr
Abstract:
We will investigate the stability in the sense of G
Paper's Title:
Iterative Approximation of Zeros of Accretive Type Maps, with Applications
Author(s):
Charles Ejike Chidume, Chinedu Godwin Ezea, and Emmanuel Ezzaka Otubo
African University of Science and
Technology, Abuja,
Nigeria.
E-mail: cchidume@aust.edu.ng
E-mail: chinedu.ezea@gmail.com
E-mail: mrzzaka@yahoo.com
Department of Mathematics,
Nnamdi Azikiwe University,
Awka,
Nigeria
E-mail: chinedu.ezea@gmail.com
Ebonyi State University,
Abakaliki,
Nigeria
E-mail: mrzzaka@yahoo.com
Abstract:
Let E be a reflexive real Banach space with uniformly Gâteaux differentiable norm. Let J:E→ E* be the normalized duality map on E and let A:E*→ E be a map such that AJ is an accretive and uniformly continuous map. Suppose that (AJ)-1(0) in nonempty. Then, an iterative sequence is constructed and proved to converge strongly to some u* in (AJ)-1(0). Application of our theorem in the case that E is a real Hilbert space yields a sequence which converges strongly to a zero of A. Finally, non-trivial examples of maps A for which AJ is accretive are presented..
Paper's Title:
Iterative Algorithm for Split Generalized Mixed Equilibrium Problem Involving Relaxed Monotone Mappings in Real Hilbert Spaces
Author(s):
1U.A. Osisiogu, F.L. Adum, and 2C. Izuchukwu
1Department of Mathematics and
Computer Science,
Ebonyi State University, Abakaliki,
Nigeria.
E-mail: uosisiogu@gmail.com,
adumson2@yahoo.com
2School of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: izuchukwuc@ukzn.ac.za,
izuchukwu_c@yahoo.com
Abstract:
The main purpose of this paper is to introduce a certain class of split generalized mixed equilibrium problem involving relaxed monotone mappings. To solve our proposed problem, we introduce an iterative algorithm and obtain its strong convergence to a solution of the split generalized mixed equilibrium problems in Hilbert spaces. As special cases of the proposed problem, we studied the proximal split feasibility problem and variational inclusion problem.
Paper's Title:
Existence of Solution of Differential and Riemann-Liouville Equation Via Fixed Point Approach in Complex Valued b-Metric Spaces
Author(s):
K. Afassinou, A. A. Mebawondu, H. A. Abass and O. K. Narain
Department of Science Access,
University of Zululand, KwaDlangezwa,
South Africa.
E-mail: komia@aims.ac.za
DST-NRF Centre of Excellence in
Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: dele@aims.ac.za
DST-NRF Centre of Excellence in
Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: hammedabass548@gmail.com
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
In this paper, we establish some fixed point and common fixed point results for a new type of generalized contractive mapping using the notion of C-class function in the framework of complex valued b-metric spaces. As an application, we establish the existence and uniqueness of a solution for Riemann-Liouville integral and ordinary differential equation in the framework of a complete complex valued b-metric spaces. The obtained results generalize and improve some fixed point results in the literature.
Paper's Title:
D-Iterative Method for Solving a Delay Differential Equation and a Two-Point Second-Order Boundary Value Problems in Banach Spaces
Author(s):
Francis Akutsah1, Akindele Adebayo Mebawondu2, Oluwatosin Babasola3, Paranjothi Pillay4 and Ojen Kumar Narain5
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 216040405@stu.ukzn.ac.za,
akutsah@gmail.com
2School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
DST-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
Mountain Top University,
Prayer City, Ogun State,
Nigeria.
E-mail: dele@aims.ac.za
3Department
of Mathematical Sciences,
University of Bath,
Claverton Down,
Bath, BA2 7AY
UK.
E-mail: ob377@bath.ac.uk
4School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: pillaypi@ukzn.ac.za
5School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
The purpose of this paper is to re-establish the convergence, stability and data dependence results established by [2] and [3] by removing the strong assumptions imposed on the sequences which were used to obtain their results. In addition, we introduced a modified approach using the D-iterative method to solve a two-point second-order boundary value problem, and also obtain the solution of a delay differential equations using the obtained results in this paper. The results presented in this paper do not only extend and improve the results obtained in [2, 3], it further extends and improve some existing results in the literature.
Paper's Title:
A Self Adaptive Method for Solving Split Bilevel Variational Inequalities Problem in Hilbert Spaces
Author(s):
Francis Akutsah1, Ojen Kumar Narain2, Funmilayo Abibat Kasali3 Olawale Kazeem Oyewole4 and Akindele Adebayo Mebawondu5
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 216040405@stu.ukzn.ac.za,
akutsah@gmail.com
2School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
3Mountain Top University,
Prayer City, Ogun State,
Nigeria.
E-mail: fkasali@mtu.edu.ng
4Technion-Israel
Institute of Technology.
E-mail: 217079141@stu.ukzn.ac.za,
oyewoleolawalekazeem@gmail.co
5School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
DST-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
Mountain Top University,
Prayer City, Ogun State,
Nigeria.
E-mail: dele@aims.ac.za
Abstract:
In this work, we study the split bilevel variational inequality problem in two real Hilbert spaces. We propose a new modified inertial projection and contraction method for solving the aforementioned problem when one of the operators is pseudomonotone and Lipschitz continuous while the other operator is α-strongly monotone. The use of the weakly sequential continuity condition on the Pseudomonotone operator is removed in this work. A Strong convergence theorem of the proposed method is proved under some mild conditions. In addition, some numerical experiments are presented to show the efficiency and implementation of our method in comparison with other methods in the literature in the framework of infinite dimensional Hilbert spaces. The results obtained in this paper extend, generalize and improve several.
Paper's Title:
On Stan Ulam and his Mathematics
Author(s):
Krzysztof Ciesielski and Themistocles M. Rassias
Mathematics Institute, Jagiellonian University,
Abstract:
In this note we give a glimpse of the curriculum vitae of Stan Ulam, his personality and some of the mathematics he was involved in.
Paper's Title:
On a Method of Proving the Hyers-Ulam Stability
of Functional Equations on Restricted Domains
Author(s):
Janusz Brzdęk
Department of Mathematics
Pedagogical University Podchor
Abstract:
We show that generalizations of some (classical) results on the Hyers-Ulam stability of functional equations, in several variables, can be very easily derived from a simple result on stability of a functional equation in single variable
Paper's Title:
Fixed Points and Stability
of the Cauchy Functional Equation
Author(s):
Choonkil Park and Themistocles M. Rassias
Department of Mathematics, Hanyang University,
Seoul 133-791,
Republic of Korea
Department of Mathematics,
National Technical University of Athens,
Zografou Campus, 15780 Athens,
Greece
baak@hanyang.ac.kr
trassias@math.ntua.gr
Abstract:
Using fixed point methods, we prove the generalized Hyers-Ulam stability of homomorphisms in Banach algebras and of derivations on Banach algebras for the Cauchy functional equation.
Paper's Title:
An Efficient Modification of Differential Transform Method for Solving Integral and Integro-differential Equations
Author(s):
S. Al-Ahmad, Ibrahim Mohammed Sulaiman*, and M. Mamat
Faculty of Informatics and Computing,
Universiti Sultan Zainal Abidin,
Terengganu, Besut Campus, 22200,
Malaysia.
E-mail: Alahmad.shadi@yahoo.com,
*sulaimanib@unisza.edu.my,
must@unisza.edu.my
Abstract:
In this paper, classes of integral and integro-differential equations are solved using a modified differential transform method. This proposed technique is based on differential transform method (DTM), Laplace transform (LT) procedure and Pad\'{e} approximants (PA). The proposed method which gives a good approximation for the true solution in a large region is referred to modified differential transform method (MDTM). An algorithm was developed to illustrate the flow of the proposed method. Some numerical problems are presented to check the applicability of the proposed scheme and the obtained results from the computations are compared with other existing methods to illustrates its efficiency. Numerical results have shown that the proposed MDTM method is promising compared to other existing methods for solving integral and integro-differential equations.
Paper's Title:
A Self-adaptive Subgradient Extragradient Algorithm for Variational Inequality Problems and Fixed Point Problems in Banach Spaces
Author(s):
F. U. Ogbuisi
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
Department of Mathematics,
University of Nigeria, Nsukka,
Nigeria.
E-mail: ferdinard.ogbuisi@unn.edu.ng
fudochukwu@yahoo.com
Abstract:
In this paper, we propose and analyze a type of subgradient extragradient algorithm for the approximation of a solution of variational inequality problem which is also a common fixed point of an infinite family of relatively nonexpansive mappings in 2-uniformly convex Banach spaces which are uniformly smooth. By using the generalized projection operator, we prove a strong convergence theorem which does not require the prior knowledge of the Lipschitz constant of cost operator. We further applied our result to constrained convex minimization problem, convex feasibility problem and infinite family of equilibrium problems. Our results improve and complement related results in 2-uniformly convex and uniformly smooth Banach spaces and Hilbert spaces.
Paper's Title:
ψ(m,q)-Isometric Mappings on Metric Spaces
Author(s):
Sid Ahmed Ould Beinane, Sidi Hamidou Jah and Sid Ahmed Ould Ahmed Mahmoud
Mathematical Analysis and Applications,
Mathematics Department, College of Science,
Jouf University,
Sakaka P.O.Box 2014,
Saudi Arabia.
E-mail: beinane06@gmail.com
Department of Mathematics, College of
Science Qassim University,
P.O. Box 6640, Buraydah 51452,
Saudi Arabia.
E-mail: jahsiidi@yahoo.fr
Mathematical Analysis and Applications,
Mathematics Department, College of Science, Jouf University,
Sakaka P.O.Box 2014,
Saudi Arabia.
E-mail: sidahmed@ju.edu.sa,
sidahmed.sidha@gmail.com
Abstract:
The concept of (m,p)-isometric operators on Banach space was extended to
(m,q)-isometric mappings on general metric spaces in [6].
This paper is devoted to define the concept of
ψ(m, q)-isometric, which is the
extension of A(m, p)-isometric operators on Banach spaces introduced in [10].
Let T,ψ: (E,d) -> (E, d) be two mappings.
For some positive integer m and q ∈ (0,∞).
T is said to be an ψ(m,q)-isometry,
if for all y,z ∈ E,

Paper's Title:
A New Method with Regularization for Solving Split Variational Inequality Problems in Real Hilbert Spaces
Author(s):
Francis Akutsah1 and Ojen Kumar Narain2
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 216040405@stu.ukzn.ac.za,
akutsah@gmail.com
2School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
In this paper, we introduce a new inertial extrapolation method with regularization for approximating solutions of split variational inequality problems in the frame work of real Hilbert spaces. We prove that the proposed method converges strongly to a minimum-norm solution of the problem without using the conventional two cases approach. In addition, we present some numerical experiments to show the efficiency and applicability of the proposed method. The results obtained in this paper extend, generalize and improve several results in this direction.
Paper's Title:
Trace Inequalities for Operators in Hilbert Spaces: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
School of Engineering
& Science
Victoria University,
PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
In this paper we survey some recent trace inequalities for operators in Hilbert spaces that are connected to Schwarz's, Buzano's and Kato's inequalities and the reverses of Schwarz inequality known in the literature as Cassels' inequality and Shisha-Mond's inequality. Applications for some functionals that are naturally associated to some of these inequalities and for functions of operators defined by power series are given. Further, various trace inequalities for convex functions are presented including refinements of Jensen inequality and several reverses of Jensen's inequality. Hermite-Hadamard type inequalities and the trace version of Slater's inequality are given. Some Lipschitz type inequalities are also surveyed. Examples for fundamental functions such as the power, logarithmic, resolvent and exponential functions are provided as well.
Paper's Title:
Using Direct and Fixed Point Technique of Cubic Functional Equation and its Hyers-Ulam Stability
Author(s):
Ramanuja Rao Kotti, Rajnesh Krishnan Mudaliar, Kaushal Neelam Devi, Shailendra Vikash Narayan
Fiji National University,
Department of Mathematics & Statistics,
P.O. Box 5529, Lautoka,
Fiji.
E-mail: ramanuja.kotti@fnu.ac.fj
URL: https://www.fnu.ac.fj
Abstract:
In this present work, we introduce a new type of finite dimensional cubic functional equation of the form

where Φ≥4 is an integer, and derive its general solution. The main purpose of this work is to investigate the Hyers-Ulam stability results for the above mentioned functional equation in Fuzzy Banach spaces by means of direct and fixed point methods.
Paper's Title:
A New Iterative Approximation of a Split Fixed Point Constraint Equilibrium Problem
Author(s):
Musa Adewale Olona1, Adhir Maharaj2 and Ojen Kumar Narain3
1School
of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 219095783@stu.ukzn.ac.za
2Department
of Mathematics,
Durban University of Technology, Durban,
South Africa.
E-mail: adhirm@dut.ac.za
3School
of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
The purpose of this paper is to introduce an iterative algorithm for approximating an element in the solution set of the common split feasibility problem for fixed points of demimetric mappings and equilibrium problem for monotone mapping in real Hilbert spaces. Motivated by self-adaptive step size method, we incorporate the inertial technique to accelerate the convergence of the proposed method and establish a strong convergence of the sequence generated by the proposed algorithm. Finally, we present a numerical example to illustrate the significant performance of our method. Our results extend and improve some existing results in the literature.
Search and serve lasted 0 second(s).