|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Solving Two Point Boundary Value Problems by Modified Sumudu Transform Homotopy Perturbation Method
Author(s):
Asem AL Nemrat and Zarita Zainuddin
School of Mathematical Sciences,
Universiti Sains Malaysia,
11800 Penang,
Malaysia.
E-mail: alnemrata@yahoo.com
zarita@usm.my
Abstract:
This paper considers a combined form of the Sumudu transform with the modified homotopy perturbation method (MHPM) to find approximate and analytical solutions for nonlinear two point boundary value problems. This method is called the modified Sumudu transform homotopy perturbation method (MSTHPM). The suggested technique avoids the round-off errors and finds the solution without any restrictive assumptions or discretization. We will introduce an appropriate initial approximation and furthermore, the residual error will be canceled in some points of the interval (RECP). Only a first order approximation of MSTHPM will be required, as compared to STHPM, which needs more iterations for the same cases of study. After comparing figures between approximate, MSTHPM, STHPM and numerical solutions, it is found through the solutions we have obtained that they are highly accurate, indicating that the MSTHPM is very effective, simple and can be used to solve other types of nonlinear boundary value problems (BVPs).
Paper's Title:
Composite Variational-Like Inequalities Given By Weakly Relaxed
Author(s):
Syed Shakaib Irfan, Iqbal Ahmad, Zubair Khan and Preeti Shukla
College of Engineering, Qassim University
Buraidah, Al-Qassim,
Saudi Arabia.
E-mail: shakaib@qec.edu.sa
College of Engineering, Qassim University
Buraidah, Al-Qassim,
Saudi Arabia.
E-mail: iqbal@qec.edu.sa
Department of Mathematics,
Integral University Lucknow,
India.
E-mail: zkhan@iul.ac.in
Department of Mathematics,
Integral University Lucknow,
India.
E-mail: shuklapreeti1991@gmail.com
Abstract:
In this article, we introduce a composite variational-like inequalities with weakly relaxed ζ-pseudomonotone multi-valued maping in reflexive Banach spaces. We obtain existence of solutions to the composite variational-like inequalities with weakly relaxed ζ-pseudomon -otone multi-valued maps in reflexive Banach spaces by using KKM theorem. We have also checked the solvability of the composite variational-like inequalities with weakly relaxed ζ-semi-pseudomonotone multi-valued maps in arbitrary Banach spaces using Kakutani-Fan-Glicksberg fixed point theorem.
Paper's Title:
Some Convergence Results for Jungck-Am Iterative Process In Hyperbolic Spaces
Author(s):
Akindele Adebayo Mebawondu and Oluwatosin Temitope Mewomo
School of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail:
216028272@stu.ukzn.ac.za,
mewomoo@ukzn.ac.za
Abstract:
In this paper, we introduce a new three steps iterative process called Jungck-AM iterative process and show that the proposed iterative process can be used to approximate fixed points of Jungck-contractive type mappings and Jungck-Suzuki type mappings. In addition, we establish some strong and Δ-convergence results for the approximation of fixed points of Jungck-Suzuki type mappings in the frame work of uniformly convex hyperbolic space. Furthermore, we show that the newly proposed iterative process has a better rate of convergence compare to the Jungck-Noor, Jungck-SP, Jungck-CR and some existing iterative processes in the literature. Finally, stability, data dependency results for Jungck-AM iterative process is established and we present an analytical proof and numerical examples to validate our claim.
Paper's Title:
Additive Mappings on Semiprime Rings Functioning as Centralizers
Author(s):
Abu Zaid Ansari and Faiza Shujat
Department of Mathematics,
Faculty of Science,
Islamic University of Madinah, Madinah
K.S.A.
E-mail: ansari.abuzaid@gmail.com,
ansari.abuzaid@iu.edu.sa
Department of Mathematics,
Faculty of Science,
Taibah University, Madinah,
K.S.A.
E-mail: faiza.shujat@gmail.com,
fullahkhan@taibahu.edu.sa
Abstract:
The objective of this research is to prove that an additive mapping T:R → R is a centralizer on R if it satisfies any one of the following identities:
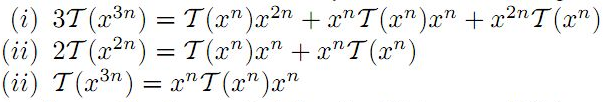
for all x ∈ R, where n ≥ 1 is a fixed integer and R is any suitably torsion free semiprime ring. Some results on involution "*" are also presented as consequences of the main theorems. In addition, we will take criticism in account with examples.
Paper's Title:
Coefficient Bounds for Sakaguchi Kind of Functions Associated with Sine Function
Author(s):
Serap Bulut, H. Priya and B. Srutha Keerth
Kocaeli University,
Faculty of Aviation and Space Sciences,
Arslanbey Campus, 41285 Kartepe-Kocaeli,
Turkey.
E-mail: serap.bulut@kocaeli.edu.tr
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus, Chennai - 600 048,
India.
E-mail: priyaharikrishnan18@gmail.com,
priya.h2020@vitstudent.ac.in
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus, Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com,
sruthakeerthi.b@vit.ac.in
Abstract:
In this paper, we introduce a new general subclass of analytic functions with respect to symmetric points in the domain of sine function. We obtain sharp coefficient bounds and upper bounds for the Fekete-Szegö functional. Also we get sharp bounds for the logarithmic coefficients of functions belonging to this new class.
Paper's Title:
Common Fixed Point Results for Banach Operator Pairs and Applications to Best Approximation
Author(s):
Hemant Kumar Nashine
Department of Mathematics,
Disha Institute of Management and Technology,
Satya Vihar, Vidhansabha - Chandrakhuri Marg (Baloda Bazar Road),
Mandir Hasaud,
Raipur - 492101(Chhattisgarh), India.
hemantnashine@rediffmail.com
nashine_09@rediffmail.com
Abstract:
The common fixed point results for Banach operator pair with generalized nonexpansive mappings in q-normed space have been obtained in the present work. As application, some more general best approximation results have also been determined without the assumption of linearity or affinity of mappings. These results unify and generalize various existing known results with the aid of more general class of noncommuting mappings.
Paper's Title:
On Sufficient Conditions for Strong Starlikeness
Author(s):
V. Ravichandran, M. H. Khan, M. Darus, And
K. G. Subramanian School of Mathematical Sciences, Universiti Sains Malaysia,
11800 Usm Penang, Malaysia
vravi@cs.usm.my
Url: http://cs.usm.my/~vravi/index.html
Department of Mathematics, Islamiah College, Vaniambadi 635 751, India
khanhussaff@yahoo.co.in
School of Mathematical Sciences, Faculty of Science and Technology, UKM, Bangi
43600,
Malaysia
maslina@pkrisc.cc.ukm.my
Url:
http://www.webspawner.com/users/maslinadarus
Department of Mathematics, Madras Christian College, Tambaram, Chennai 600 059,
India
kgsmani@vsnl.net
Abstract:
In the present investigation, we obtain some sufficient
conditions for a normalized analytic function f(z) defined on the unit disk to
satisfy the condition
![]()
![]()
Paper's Title:
Existence Results for Perturbed Fractional Differential
Inclusions
Author(s):
Y.-K. Chang
Department of Mathematics,
Lanzhou Jiaotong University, Lanzhou, Gansu 730070, People's
Republic of China
lzchangyk@163.com
Abstract:
This paper is mainly concerned with the following fractional differential
inclusions with boundary condition
A sufficient condition is established for the existence of solutions of the
above problem by using a fixed point theorem for multivalued maps due to
Dhage. Our result is proved under the mixed generalized Lipschitz and
Carathéodory conditions.
Paper's Title:
The Dynamics of an Ebola Epidemic Model with Quarantine of Infectives
Author(s):
Eliab Horub Kweyunga
Department of Mathematics,
Kabale University,
P.O.Box 317, Kabale,
Uganda.
E-mail: hkweyunga@kab.ac.ug
Abstract:
The recurrent outbreaks of ebola in Africa present global health challenges. Ebola is a severe, very fatal disease with case fatality rates of up to 90%. In this paper, a theoretical deterministic model for ebola epidemic with quarantine of infectives is proposed and analyzed. The model exhibits two equilibria; the disease free and endemic equilibrium points. The basic reproduction number, R0, which is the main threshold, is obtained and the stability of the equilibrium points established. Using parameter values drawn from the 2014 West Africa ebola outbreak, a numerical simulation of the model is carried out. It is found that the dynamics of the model are completely determined by R0 and that a quarantine success rate of at least 70% is sufficient to contain the disease outbreak.
Paper's Title:
Convergence Speed of Some Random Implicit-Kirk-type Iterations for Contractive-type Random Operators
Author(s):
H. Akewe, K.S. Eke
Department of Mathematics,
Covenant University,
Canaanland, KM 10, Idiroko Road, P. M. B. 1023, Ota, Ogun State,
Nigeria.
E-mail: hudson.akewe@covenantuniversity.edu.ng,
kanayo.eke@covenantuniversity.edu.ng
Abstract:
The main aim of this paper is to introduce a stochastic version of multistep type iterative scheme called a modified random implicit-Kirk multistep iterative scheme and prove strong convergence and stability results for a class of generalized contractive-type random operators. The rate of convergence of the random iterative schemes are also examined through an example. The results show that our new random implicit kirk multistep scheme perform better than other implicit iterative schemes in terms of convergence and thus have good potentials for further applications in equilibrium problems in computer science, physics and economics.
Paper's Title:
A New Relaxed Complex-valued b-metric Type and Fixed Point Results
Author(s):
P. Singh, V. Singh and T. C. M. Jele
Department of Mathematics, University of
KwaZulu-Natal,
Private Bag X54001, Durban,
South Africa.
E-mail: singhp@ukzn.ac.za
singhv@ukzn.ac.za
thokozani.jele@nwu.ac.za
Abstract:
In this paper, we study the existence and uniqueness of fixed point in complex valued b-metric spaces and introduce a new relaxed α, β Complex-valued b-metric type by relaxing the triangle inequality and determine whether the fixed point theorems are applicable in these spaces.
Paper's Title:
Fekete-Szegö Inequality for Sakaguchi Type of functions in Petal Shaped Domain
Author(s):
E. K. Nithiyanandham and B. Srutha Keerthi
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: nithiyankrish@gmail.com
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com
Abstract:
In this paper, we estimate coefficient bounds,|a_2|,|a_3| and |a_4|, Fekete-Szegö inequality
![]() and Toeplitz determinant
T2(2) and T3(1) for functions belonging to the following class
and Toeplitz determinant
T2(2) and T3(1) for functions belonging to the following class
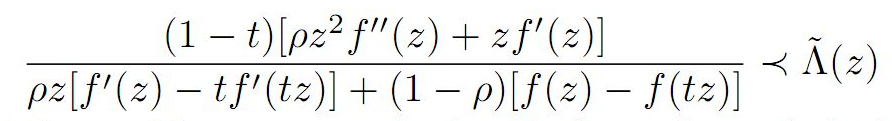
the function being holomorphic, we expand using Taylor series and obtain several corollaries and consequences for the main result.
Paper's Title:
Toeplitz Determinant for Sakaguchi Type Functions Under Petal Shaped Domain
Author(s):
B. Nandhini and B. Srutha Keerthi
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail:
nandhinibaskar1996@gmail.com
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com
Abstract:
We introduce a new general subclass GPt,ρ of Sakaguchi kind function on a Petal shaped domain. We obtain coefficients bounds and upper bounds for the Fekete-Szegö functional over the class. From these functions we obtain the bounds of first four coefficients, and then we have derived the Toeplitz determinant T2(2) and T3(1) whose diagonal entries are the coefficients of functions.
Paper's Title:
Some Nonlinear Gronwall-Bellman Type Retarded Integral Inequalities with Power and Their Applications
Author(s):
Ammar Boudeliou
Department of Mathematics, University of Constantine 1
Brothers Mentouri,
BP, 325, Ain El Bey Street, 25017,
Algeria.
E-mail: ammar_boudeliou@umc.edu.dz
Abstract:
In this paper, we investigate a certain class of nonlinear Gronwall-Bellman type integral inequalities with power in more general cases involving retarded term and more general nonlinearities. Our results generalize some known integral inequalities and other results obtained very recently. The inequalities given here can be used to estimate the bound on the solutions of retarded integral equation of Volterra type and integro-differential equations (IDE) with power. Two examples are given to show the validity of our established theorems.
Paper's Title:
Fekete-Szegö Inequality for Certain Class of Analytic Functions
Author(s):
V. Ravichandran, Maslina Darus, M. Hussain Khan, and K. G. Subramanian
School of
Mathematical Sciences, Universiti Sains Malaysia,
11800 Usm, Penang, Malaysia
vravi@cs.usm.my
School of
Mathematical Sciences, Faculty of Sciences and Technology,
Ukm, Banki 43600, Malaysia
maslina@pkrisc.cc.ukm.my
Department of
Mathematics, Islamiah College,
Vaniambadi 635 751, India
Department of
Mathematics, Madras Christian College, Tambaram,
Chennai- 600 059, India
kgsmani@vsnl.net
Abstract:
In this present investigation, the authors obtain Fekete-Szegö inequality for a certain
class of analytic functions f(z) for which
 lies in a
region starlike with respect to 1 and symmetric with respect to the real axis. Also certain application
of our main result for a class of functions defined by Hadamard product (convolution) is
given. As a special case of our result we obtain Fekete-Szegö inequality for a class of functions
defined through fractional derivatives. Also we obtain Fekete-Szegö inequality for the inverse
functions.
lies in a
region starlike with respect to 1 and symmetric with respect to the real axis. Also certain application
of our main result for a class of functions defined by Hadamard product (convolution) is
given. As a special case of our result we obtain Fekete-Szegö inequality for a class of functions
defined through fractional derivatives. Also we obtain Fekete-Szegö inequality for the inverse
functions.
Paper's Title:
Differential Sandwich Theorems for Some Subclasses of Analytic Functions
Author(s):
T. N. Shanmugam, V. Ravichandran and S. Sivasubramanian
Department of Mathematics, College of Engineering,
Anna university, Chennai 600 025,
India
shan@annauniv.edu
URL: http://www.annauniv.edu/shan
School of Mathematical Sciences,
Universiti Sains Malaysia,
11800 USM Penang,
Malaysia
vravi@cs.usm.my
URL: http://cs.usm.my/~vravi
Department of Mathematics, Easwari Engineering college,
Ramapuram, Chennai 600 089,
India
sivasaisastha@rediffmail.com
Abstract:
Let ![]() and
and ![]() be univalent in
be univalent in ![]() with
with ![]() We give some applications of first order differential subordination and superordination to obtain sufficient conditions for normalized analytic function
We give some applications of first order differential subordination and superordination to obtain sufficient conditions for normalized analytic function ![]() with
with ![]() to satisfy
to satisfy ![]()
Paper's Title:
On the Fekete-Szeg
Author(s):
T.N. Shanmugam and A. Singaravelu
Department of Mathematics,
Department of Mathematics,
College of Engineering,
Anna University, Chennai-600 025,
Tamilnadu, India
shan@annauniv.edu
Valliammai Engineering College,
Chennai-603 203,
Tamilnadu, India
sivasaisastha@rediffmail.com
Abstract:
In this present investigation, the authors obtainFekete-Szegő's inequality for certain normalized analytic functions ![]() defined on the open
unit disk for which
defined on the open
unit disk for which ![]() lie in a region starlike with
respect to 1 and symmetric with respect
to the real axis. Also certain applications of the main result for a class of functions
defined by convolution are given. As a special case of this result, Fekete-Szegő's inequality for a class of functions
defined through fractional derivatives is also obtained.
lie in a region starlike with
respect to 1 and symmetric with respect
to the real axis. Also certain applications of the main result for a class of functions
defined by convolution are given. As a special case of this result, Fekete-Szegő's inequality for a class of functions
defined through fractional derivatives is also obtained.
Paper's Title:
Coincidences and Fixed Points of Hybrid Maps in Symmetric Spaces
Author(s):
S. L. Singh and Bhagwati Prasad
Vedic MRI, 21 Govind Nagar,
Department of Mathematics, Gurukula Kangri University,
Rishikesh 249201
India
vedicmri@gmail.com
Hardwar 249404,
India
Abstract:
The purpose of this paper is to obtain a new coincidence theorem for a
single-valued and two multivalued operators in symmetric spaces. We derive
fixed point theorems and discuss some special cases and applications.
Paper's Title:
On Sandwich Theorems for Certain Subclass of Analytic Functions Involving Dziok-Srivastava Operator
Author(s):
T. N. Shanmugam, M. P. Jeyarama and A. Singaravelu
Department of Mathematics
College of Engineering, Anna University
Chennai - 600 025,
India
drtns2001@yahoo.com
Department of Mathematics
Easwari Engineering College
Ramapuram, Chennai - 600089
Tamilnadu, India
jeyaraman-mp@yahoo.co.i
Department of Mathematics
Valliammai Engineering College
Chennai - 603203
Tamilnadu, India.
asing-59@yahoo.com
Abstract:
The purpose of this present paper is to derive some subordination and superordination results for certain normalized analytic functions in the open unit disk, acted upon by Dziok-Srivastava operator. Relevant connections of the results, which are presented in this paper, with various known results are also considered.
Paper's Title:
Inclusion and Neighborhood
Properties for Certain Subclasses of Analytic Functions Associated with
Convolution Structure
Author(s):
M. K. Aouf
Mathematics Department,
Faculty of Science,
Mansoura University 35516,
Egypt.
mkaouf127@yahoo.com
Abstract:
In this paper we introduce and investigate two new subclasses of multivalently analytic functions of complex order defined by using the familiar convolution structure of analytic functions. In this paper we obtain the coefficient estimates and the consequent inclusion relationships involving the neighborhoods of the p-valently analytic functions.
Paper's Title:
On Convergence Theorems of an Implicit Iterative Process with Errors for a
Finite Family of Asymptotically quasi I-nonexpansive Mappings
Author(s):
Farrukh Mukhamedov and Mansoor Saburov
Department of Computational & Theoretical
Sciences,
Faculty of Sciences, International Islamic University Malaysia,
P.O. Box, 141, 25710, Kuantan,
Malaysia
Abstract:
In this paper we prove the weak and strong convergence of the implicit iterative process with errors to a common fixed point of a finite family {Tj}Ni=1 of asymptotically quasi Ij-nonexpansive mappings as well as a family of {Ij}Nj=1 of asymptotically quasi nonexpansive mappings in the framework of Banach spaces. The obtained results improve and generalize the corresponding results in the existing literature.
Paper's Title:
On Reformations of 2--Hilbert Spaces
Author(s):
M. Eshaghi Gordji, A. Divandari, M. R. Safi and Y. J. Cho
Department of Mathematics, Semnan
University,
P.O. Box 35195--363, Semnan,
Iran
meshaghi@semnan.ac.ir, madjid.eshaghi@gmail.com
Department of Mathematics, Semnan
University,
Iran
Department of Mathematics, Semnan
University,
Iran
safi@semnan.ac.ir, SafiMohammadReza@yahoo.com
Department of Mathematics Education and
the RINS,
Gyeongsang National University
Chinju 660-701,
Korea
Abstract:
In this paper, first, we introduce the new concept of (complex) 2--Hilbert spaces, that is, we define the concept of 2--inner product spaces with a complex valued 2--inner product by using the 2--norm. Next, we prove some theorems on Schwartz's inequality, the polarization identity, the parallelogram laws and related important properties. Finally, we give some open problems related to 2--Hilbert spaces.
Paper's Title:
A Comparison Between Two Different Stochastic Epidemic Models with Respect to the Entropy
Author(s):
Farzad Fatehi and Tayebe Waezizadeh
Department of Mathematics,
University of Sussex,
Brighton BN1 9QH,
UK.
E-mail: f.fatehi@sussex.ac.uk
URL:
http://www.sussex.ac.uk/profiles/361251
Department of Pure Mathematics, Faculty
of Mathematics and Computer,
Shahid Bahonar University of Kerman,
Kerman 76169-14111,
Iran.
E-mail: waezizadeh@uk.ac.ir
URL:
http://academicstaff.uk.ac.ir/en/tavaezizadeh
Abstract:
In this paper at first a brief history of mathematical models is presented with the aim to clarify the reliability of stochastic models over deterministic models. Next, the necessary background about random variables and stochastic processes, especially Markov chains and the entropy are introduced. After that, entropy of SIR stochastic models is computed and it is proven that an epidemic will disappear after a long time. Entropy of a stochastic mathematical model determines the average uncertainty about the outcome of that random experiment. At the end, we introduce a chain binomial epidemic model and compute its entropy, which is then compared with the DTMC SIR epidemic model to show which one is nearer to reality.
Paper's Title:
A Self-adaptive Subgradient Extragradient Algorithm for Variational Inequality Problems and Fixed Point Problems in Banach Spaces
Author(s):
F. U. Ogbuisi
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
Department of Mathematics,
University of Nigeria, Nsukka,
Nigeria.
E-mail: ferdinard.ogbuisi@unn.edu.ng
fudochukwu@yahoo.com
Abstract:
In this paper, we propose and analyze a type of subgradient extragradient algorithm for the approximation of a solution of variational inequality problem which is also a common fixed point of an infinite family of relatively nonexpansive mappings in 2-uniformly convex Banach spaces which are uniformly smooth. By using the generalized projection operator, we prove a strong convergence theorem which does not require the prior knowledge of the Lipschitz constant of cost operator. We further applied our result to constrained convex minimization problem, convex feasibility problem and infinite family of equilibrium problems. Our results improve and complement related results in 2-uniformly convex and uniformly smooth Banach spaces and Hilbert spaces.
Paper's Title:
Coexisting Attractors and Bubbling Route to Chaos in Modified Coupled Duffing Oscillators
Author(s):
B. Deruni1, A. S. Hacinliyan1,2, E. Kandiran3, A. C. Keles2, S. Kaouache4, M.-S. Abdelouahab4, N.-E. Hamri4
1Department
of Physics,
University of Yeditepe,
Turkey.
2Department
of Information Systems and Technologies,
University of Yeditepe,
Turkey
3Department
of Software Development,
University of Yeditepe,
Turkey.
4Laboratory
of Mathematics and their interactions,
University Center of Abdelhafid Boussouf,
Mila 43000,
Algeria.
E-mail:
berc890@gmail.com
ahacinliyan@yeditepe.edu.tr
engin.kandiran@yeditepe.edu.tr
cihan.keles@yeditepe.edu.tr
s.kaouache@centr-univ-mila.dz
medsalah3@yahoo.fr
n.hamri@centre-univ-mila.dz
Abstract:
In this article dynamical behavior of coupled Duffing oscillators is analyzed under a small modification. The oscillators have cubic damping instead of linear one. Although single duffing oscillator has complex dynamics, coupled duffing systems possess a much more complex structure. The dynamical behavior of the system is investigated both numerically and analytically. Numerical results indicate that the system has double scroll attractor with suitable parameter values. On the other hand, bifurcation diagrams illustrate rich behavior of the system, and it is seen that, system enters into chaos with different routes. Beside classical bifurcations, bubbling route to chaos is observed for suitable parameter settings. On the other hand, Multistability of the system is indicated with the coexisting attractors, such that under same parameter setting the system shows different periodic and chaotic attractors. Moreover, chaotic synchronization of coupled oscillators is illustrated in final section.
Paper's Title:
Existence of Solution of Differential and Riemann-Liouville Equation Via Fixed Point Approach in Complex Valued b-Metric Spaces
Author(s):
K. Afassinou, A. A. Mebawondu, H. A. Abass and O. K. Narain
Department of Science Access,
University of Zululand, KwaDlangezwa,
South Africa.
E-mail: komia@aims.ac.za
DST-NRF Centre of Excellence in
Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: dele@aims.ac.za
DST-NRF Centre of Excellence in
Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: hammedabass548@gmail.com
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
In this paper, we establish some fixed point and common fixed point results for a new type of generalized contractive mapping using the notion of C-class function in the framework of complex valued b-metric spaces. As an application, we establish the existence and uniqueness of a solution for Riemann-Liouville integral and ordinary differential equation in the framework of a complete complex valued b-metric spaces. The obtained results generalize and improve some fixed point results in the literature.
Paper's Title:
Nonlinear System of Mixed Ordered Variational Inclusions Involving XOR Operation
Author(s):
Iqbal Ahmad, Abdullah and Syed Shakaib Irfan
Department of Mechanical Engineering,
College of Engineering, Qassim University
Buraidah 51452, Al-Qassim,
Saudi Arabia.
E-mail: iqbal@qec.edu.sa,
i.ahmad@qu.edu.sa
Zakir Husain Delhi College,
University of Delhi,
JLN Marg, New Delhi- 110 002,
India.
E-mail: abdullahdu@qec.edu.sa
Department of Mathematics,
Aligarh Muslim University, Aligarh,
India.
E-mail: shakaibirfan@gmail.com
Abstract:
In this work, we introduce and solve an NSMOVI frameworks system involving XOR operation with the help of a proposed iterative algorithm in real ordered positive Hilbert spaces. We discuss the existence of a solution of a considered system of inclusions involving XOR operation by applying the resolvent operator technique with XOR operation and also study the strong convergence of the sequences generated by the considered algorithm. Further, we give a numerical example in support of our considered problem which gives the grantee that all the proposed conditions of our main result are fulfilled.
Paper's Title:
Preserver of Local Spectrum of Skew-product Operators
Author(s):
Rohollah Parvinianzadeh1,*, Meysam Asadipour2 and Jumakhan Pazhman3
1Department
of Mathematics,
College of Sciences,
University of Yasouj,
Yasouj, 75918-74934,
Iran.
E-mail: r.parvinian@yu.ac.ir
2Department
of Mathematics,
College of Sciences,
University of Yasouj,
Yasouj, 75918-74934,
Iran.
E-mail: Asadipour@yu.ac.ir
3Department
of Mathematics,
Ghor Institute of higher education,
Afghanistan.
E-mail: jumapazhman@gmail.com
Abstract:
Let H and K be infinite-dimensional complex Hilbert spaces, and B(H) (resp. B(K)) be the algebra of all bounded linear operators on H (resp. on K). For an operator T∈ B(H) and a vector h∈ H, let σT(h) denote the local spectrum of T at h. For two nonzero vectors h0∈ H and k0∈ K, we show that if two maps φ1 and φ2 from B(H) into B(K) satisfy
σφ1(T)φ2(S)*(k0)= σTS*(h0})
for all T, S ∈ B(H), and their range containing all operators of rank at most two, then there exist bijective linear maps P : H→ K and Q : K→ H such that φ1(T) = PTQ and φ2(T)* =Q-1T*P-1 for all T ∈ B(H). Also, we obtain some interesting results in this direction.
Paper's Title:
On Statistically Φ-Convergence
Author(s):
Supama
Department of Mathematics,
Gadjah Mada
University,
Yogyakarta 55281,
Indonesia.
E-mail: supama@ugm.ac.id
Abstract:
The idea of statistical convergence was introduced by Antoni Zygmund in 1935. Based on in the idea of Zygmund, Henry Fast and Hugo Steinhaus independently introduced a concept of statistical convergence as a generalization of an ordinary convergence in the same year 1951. In this paper, by using the Orlicz function, we introduce a concept of statistical Φ-convergence, as a generalization of the statistical convergence. Further, we observe some basic properties and some topological properties of the statistical Φ-convergent sequences
Paper's Title:
SQIRV Model for Omicron Variant with Time Delay
Author(s):
S. Dickson, S. Padmasekaran, G. E. Chatzarakis and S. L. Panetsos
Mathematics, Periyar University, Periyar
Palkalai Nagar, Salem,
636011, Tamilnadu,
India.
E-mail:
dickson@periyaruniversity.ac.in,
padmasekarans@periyaruniversity.ac.in
Electrical and Electronic Engineering
Educators, School of
Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr,
spanetsos@aspete.gr
Abstract:
In order to examine the dynamics of the Omicron variant, this paper uses mathematical modelling and analysis of a SQIRV model, taking into account the delay in the conversion of susceptible individuals into infected individuals and infected individuals into recovered individuals. The pandemic was eventually controlled as a result of the massive delays. To assure the safety of the host population, this concept incorporates quarantine and the COVID-19 vaccine. Both local and global stability of the model are examined. It is found that the fundamental reproduction number affects both local and global stability conditions. Our findings show that asymptomatic cases caused by an affected population play an important role in increasing Omicron infection in the general population. The most recent data on the pandemic Omicron variant from Tamil Nadu, India, is verified.
Paper's Title:
On Some Nonlinear Retarded Integrodifferential Inequalities in Two and n Independent Variables and their Applications
Author(s):
Bitat Dalila and Khellaf Hassane
Department of Mathematics, Laboratory of
Applied Mathematics and Modeling,
University of Constantine,
PO Box 325, Ain El Bey Road, Constantine 25017,
Algeria.
E-mail: bitat.dalila@umc.edu.dz
khellafhassane@umc.edu.dz
URL: https://www.umc.edu.dz
Abstract:
In this paper, we establish some new nonlinear retarded integrodifferential inequalities in two and n independent variables. Some applications are given as illustration.
Paper's Title:
Higher Order Accurate Compact Schemes for Time Dependent Linear and Nonlinear Convection-Diffusion Equations
Author(s):
S. Thomas, Gopika P.B. and S. K. Nadupuri
Department of Mathematics
National Institute of Technology Calicut
Kerala
673601
India.
E-mail:
sobinputhiyaveettil@gmail.com
pbgopika@gmail.com nsk@nitc.ac.in
Abstract:
The primary objective of this work is to study higher order compact finite difference schemes for finding the numerical solution of convection-diffusion equations which are widely used in engineering applications. The first part of this work is concerned with a higher order exponential scheme for solving unsteady one dimensional linear convection-diffusion equation. The scheme is set up with a fourth order compact exponential discretization for space and cubic $C^1$-spline collocation method for time. The scheme achieves fourth order accuracy in both temporal and spatial variables and is proved to be unconditionally stable. The second part explores the utility of a sixth order compact finite difference scheme in space and Huta's improved sixth order Runge-Kutta scheme in time combined to find the numerical solution of one dimensional nonlinear convection-diffusion equations. Numerical experiments are carried out with Burgers' equation to demonstrate the accuracy of the new scheme which is sixth order in both space and time. Also a sixth order in space predictor-corrector method is proposed. A comparative study is performed of the proposed schemes with existing predictor-corrector method. The investigation of computational order of convergence is presented.
Paper's Title:
A General Fractional Control Scheme for Compound Combination Synchronization Between Different Fractional-Order Identical Chaotic Systems
Author(s):
Soumia Bensimessaoud and Smail Kaouache
Laboratory of Mathematics and their interactions, Abdelhafid Boussouf University Center, Mila, Algeria.
E-mail:
soumiabensimessaoud@gmail.com,
smailkaouache@gmail.com
Abstract:
In this paper, we aim to investigate the problem of compound combination synchronization (CCS) between four different fractional-order identical chaotic systems. Based on Laplace transformation and stability theory of linear dynamical systems, a new control law is proposed to assure the achievement of this kind of synchronization. Secondly, this control scheme is applied to realised CCS between four identical unified chaotic systems. Recall, that the proposed control scheme can be applied to wide classes of chaotic and hyperchaotic systems. Numerical simulations are given to show the effectiveness of the proposed method.
Paper's Title:
On Automorphisms and Bi-derivations of Semiprime Rings
Author(s):
Abu Zaid Ansari, Faiza Shujat, Ahlam Fallatah
Department of Mathematics,
Faculty of Science,
Islamic University of Madinah, Madinah
K.S.A.
E-mail: ansari.abuzaid@gmail.com,
ansari.abuzaid@iu.edu.sa
Department of Mathematics
Faculty of Science
Taibah University, Madinah,
K.S.A.
E-mail: faiza.shujat@gmail.com,
fullahkhan@taibahu.edu.sa
Department of Mathematics
Faculty of Science
Taibah University, Madinah,
K.S.A.
E-mail: Afallatah@taibahu.edu.sa
Abstract:
In this article, our goal is to figure out a functional equation involving automorphisms and bi-derivations on certain semiprime ring. Also, we characterize the structure of automorphism, in case of prime rings.
Paper's Title:
A New Iterative Approximation of a Split Fixed Point Constraint Equilibrium Problem
Author(s):
Musa Adewale Olona1, Adhir Maharaj2 and Ojen Kumar Narain3
1School
of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 219095783@stu.ukzn.ac.za
2Department
of Mathematics,
Durban University of Technology, Durban,
South Africa.
E-mail: adhirm@dut.ac.za
3School
of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
The purpose of this paper is to introduce an iterative algorithm for approximating an element in the solution set of the common split feasibility problem for fixed points of demimetric mappings and equilibrium problem for monotone mapping in real Hilbert spaces. Motivated by self-adaptive step size method, we incorporate the inertial technique to accelerate the convergence of the proposed method and establish a strong convergence of the sequence generated by the proposed algorithm. Finally, we present a numerical example to illustrate the significant performance of our method. Our results extend and improve some existing results in the literature.
Search and serve lasted 1 second(s).