Paper's Title:

Hyperbolic Barycentric Coordinates

Author(s):

Abraham A. Ungar

Abstract:

A powerful and novel way to study Einstein's special theory of relativity and its underlying geometry, the hyperbolic geometry of Bolyai and Lobachevsky, by analogies with classical mechanics and its underlying Euclidean geometry is demonstrated. The demonstration sets the stage for the extension of the notion of barycentric coordinates in Euclidean geometry, first conceived by Möbius in 1827, into hyperbolic geometry. As an example for the application of hyperbolic barycentric coordinates, the hyperbolic midpoint of any hyperbolic segment, and the centroid and orthocenter of any hyperbolic triangle are determined.

Paper's Title:

Applications of Relations and Relators in the Extensions of Stability Theorems for Homogeneous and Additive Functions

Author(s):

Árpád Száz

Abstract:

By working out an appropriate technique of relations and relators and extending the ideas of the direct methods of Z. Gajda and R. Ger, we prove some generalizations of the stability theorems of D. H. Hyers, T. Aoki, Th. M. Rassias and P. Găvruţă in terms of the existence and unicity of 2-homogeneous and additive approximate selections of generalized subadditive relations of semigroups to vector relator spaces. Thus, we obtain generalizations not only of the selection theorems of Z. Gajda and R. Ger, but also those of the present author.

Paper's Title:

Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.

Paper's Title:

On Trigonometric Approximation of Continuous Functions by Deferred Matrix Means

Author(s):

Xhevat Zahir Krasniqi

Faculty of Education,
University of Prishtina "Hasan Prishtina",
Avenue "Mother Theresa " no. 5, Prishtinë 10000,
Republic of Kosovo.
E-mail: xhevat.krasniqi@uni-pr.edu
URL: https://staff.uni-pr.edu/profile/xhevatkrasniqi

Abstract:

In this paper, for the first time, we introduce the deferred matrix means which contain the well-known generalized deferred Nörlund, deferred Nörlund, deferred Riesz, deferred Cesàro means introduced earlier by others, and a new class of sequences (predominantly a wider class than the class of Head Bounded Variation Sequences). In addition, using the deferred matrix means of Fourier series of a continuous function, we determine the degree of approximation of such function via its modulus of continuity and a positive mediate function.

Paper's Title:

Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.

Paper's Title:

Necessary and Sufficient Conditions for Uniform Convergence and Boundedness of a General Class of Sine Series

Author(s):

Laszlo Leindler

Bolyai Institute, University of Szeged,
Aradi Vértanúk tere 1,
H-6720 Szeged,
Hungary.
leindler@math.u-szeged.hu

Abstract:

For all we know theorems pertaining to sine series with coefficients from the class γGBVS give only sufficient conditions. Therefore we define a subclass of γGBVS in order to produce necessary and sufficient conditions for the uniform convergence and boundedness if the coefficients of the sine series belong to this subclass; and prove two theorems of this type.

Paper's Title:

On the Degree of Approximation of Continuous Functions that Pertains to the Sequence-To-Sequence Transformation

Author(s):

Xhevat Z. Krasniqi

University of Prishtina,
Department of Mathematics and Computer Sciences,
5 Mother Teresa Avenue, Prishtinë, 10000,
Republic of Kosovo.
 

xheki00@hotmail.com

Abstract:

In this paper we prove analogous theorems like Leindler's 3 using the so-called A-transform of the B-transform of the partial sums of Fourier series. In addition, more than two such transforms are introduced and for them analogous results are showed as well.

Paper's Title:

Sharp L^p Improving Results for Singular Measures on Cⁿ⁺¹

Author(s):

E. Ferreyra, M. Urciuolo

FaMAF-CIEM,
Universidad Nacional de Córdoba-Conicet,
Ciudad Universitaria, 5000 Córdoba,
Argentina

eferrey@famaf.unc.edu.ar
urciuolo@famaf.unc.edu.ar

Abstract:

For j=1,...,n, let Ω_j be open sets of the complex plane and let φ_j be holomorphic functions on Ω_j such that φ_j^'' does not vanish identically on Ω_j. We consider φ(z₁,...,z_n) =φ₁(z₁) +...+φ_n(z_n). We characterize the pairs (p,q) such that the convolution operator with the surface measure supported on a compact subset of the graph of φ is p-q bounded.

Paper's Title:

New Reverses of Schwarz, Triangle and Bessel Inequalities in Inner Product Spaces

Author(s):

S. S. Dragomir

Abstract:

New reverses of the Schwarz, triangle and Bessel inequalities in inner product spaces are pointed out. These results complement the recent ones obtained by the author in the earlier paper [13]. Further, they are employed to establish new Grüss type inequalities. Finally, some natural integral inequalities are stated as well.

Paper's Title:

Integrability of Sine and Cosine Series Having Coefficients of a New Class

Author(s):

L. Leindler

Abstract:

Some integrability theorems or only their sufficient part are generalized such that the coefficients of the sine and cosine series belong to a new class of sequences being wider than the class of sequences of rest bounded variation, which itself is a generalization of the monotone decreasing sequences, but a subclass of the almost monotone decreasing sequences. It is also verified that the new class of sequences and the class of almost monotone decreasing sequences are not comparable.

Paper's Title:

Refinement Inequalities Among Symmetric Divergence Measures

Author(s):

Inder Jeet Taneja

Departamento de Matemática,
Universidade Federal de Santa Catarina, 88.040-900
Florianópolis, Sc, Brazil
taneja@mtm.ufsc.br
URL: http://www.mtm.ufsc.br/~taneja

Abstract:

There are three classical divergence measures in the literature on information theory and statistics, namely, Jeffryes-Kullback-Leiber’s J-divergence, Sibson-Burbea-Rao’s Jensen- Shannon divegernce and Taneja’s arithemtic - geometric mean divergence. These bear an interesting relationship among each other and are based on logarithmic expressions. The divergence measures like Hellinger discrimination, symmetric χ²−divergence, and triangular discrimination are not based on logarithmic expressions. These six divergence measures are symmetric with respect to probability distributions. In this paper some interesting inequalities among these symmetric divergence measures are studied. Refinements of these inequalities are also given. Some inequalities due to Dragomir et al. [6] are also improved.

Paper's Title:

On a Method of Proving the Hyers-Ulam Stability of Functional Equations on Restricted Domains

Author(s):

Janusz Brzdęk

Department of Mathematics
 Pedagogical University Podchorąźych 2,
30-084 Kraków,
Poland
jbrzdek@ap.krakow.pl

Abstract:

We show that generalizations of some (classical) results on the Hyers-Ulam stability of functional equations, in several variables, can be very easily derived from a simple result on stability of a functional equation in single variable

Paper's Title:

On a Subclass of Uniformly Convex Functions Defined by the Dziok-Srivastava Operator

Author(s):

M. K. Aouf and G. Murugusundaramoorthy

Mathematics Department, Faculty of Science,
Mansoura University 35516,
Egypt.
mkaouf127@yahoo.com

School of Science and Humanities, VIT University
Vellore - 632014,
India.
gmsmoorthy@yahoo.com

Abstract:

Making use of the Dziok-Srivastava operator, we define a new subclass T^l_m([α₁];α,β) of uniformly convex function with negative coefficients. In this paper, we obtain coefficient estimates, distortion theorems, locate extreme points and obtain radii of close-to-convexity, starlikeness and convexity for functions belonging to the class T^l_m([α₁];α,β) . We consider integral operators associated with functions belonging to the class H^l_m([α₁];α,β) defined via the Dziok-Srivastava operator. We also obtain several results for the modified Hadamard products of functions belonging to the class T^l_m([α₁];α,β) and we obtain properties associated with generalized fractional calculus operators.

Paper's Title:

A Sum Form Functional Equation and Its Relevance in Information Theory

Author(s):

Prem Nath and Dhiraj Kumar Singh

Department of Mathematics
University of Delhi
Delhi - 110007
India
pnathmaths@gmail.com
dksingh@maths.du.ac.in

Abstract:

The general solutions of a sum form functional equation containing four unknown mappings have been investigated. The importance of these solutions in relation to various entropies in information theory has been emphasised.

Paper's Title:

Inequalities for the Čebyšev Functional of Two Functions of Selfadjoint Operators in Hilbert Spaces

Author(s):

S. S. Dragomir

Abstract:

Some recent inequalities for the Čebyšev functional of two functions of selfadjoint linear operators in Hilbert spaces, under suitable assumptions for the involved functions and operators, are surveyed.

Paper's Title:

Stability of Almost Multiplicative Functionals

Author(s):

Norio Niwa, Hirokazu Oka, Takeshi Miura and Sin-Ei Takahasi

Abstract:

Let δ and p be non-negative real numbers. Let be the real or complex number field and a normed algebra over . If a mapping satisfies

then we show that φ is multiplicative or for all If, in addition, φ satisfies

for some p≠1, then by using Hyers-Ulam-Rassias stability of additive Cauchy equation, we show that φ is a ring homomorphism or for all In other words, φ is a ring homomorphism, or an approximately zero mapping. The results of this paper are inspired by Th.M. Rassias' stability theorem.

Paper's Title:

Fejér-type Inequalities

Author(s):

Nicuşor Minculete and Flavia-Corina Mitroi

"Dimitrie Cantemir" University,
107 Bisericii Române Street, Braşov, 500068,
România
minculeten@yahoo.com 

University of Craiova, Department of Mathematics,
Street A. I. Cuza 13, Craiova, RO-200585,
Romania
fcmitroi@yahoo.com 
 

Abstract:

The aim of this paper is to present some new Fejér-type results for convex functions. Improvements of Young's inequality (the arithmetic-geometric mean inequality) and other applications to special means are pointed as well.

Paper's Title:

On Convergence Theorems of an Implicit Iterative Process with Errors for a Finite Family of Asymptotically quasi I-nonexpansive Mappings

Author(s):

Farrukh Mukhamedov and Mansoor Saburov

Department of Computational & Theoretical Sciences,
Faculty of Sciences, International Islamic University Malaysia,
P.O. Box, 141, 25710, Kuantan,
Malaysia

farrukh_m@iiu.edu.my

msaburov@gmail.com

http://www.iium.edu.my

Abstract:

In this paper we prove the weak and strong convergence of the implicit iterative process with errors to a common fixed point of a finite family {T_j}^N_i=1 of asymptotically quasi I_j-nonexpansive mappings as well as a family of {Ij}^N_j=1 of asymptotically quasi nonexpansive mappings in the framework of Banach spaces. The obtained results improve and generalize the corresponding results in the existing literature.

Paper's Title:

Some Double λ-Convergent Sequence Spaces Over n-Normed Spaces

Author(s):

Kuldip Raj, Renu Anand and Seema Jamwal

School of Mathematics,
Shri Mata Vaishno Devi University Katra-182320,
Jammu and Kashmir,
India.

E-mail: kuldipraj68@gmail.com,  renuanand71@gmail.com, seemajamwal8@gmail.com

Abstract:

In this paper we introduce some double generalized λ-convergent sequence spaces over n-normed spaces defined by Musielak-Orlicz function M = (M_k,l). We also made an attempt to study some topological and algebraic properties of these sequence spaces.

Paper's Title:

Hermite-Hadamard-Fejer Type Inequalities for Harmonically s-convex Functions via Fractional Integrals

Author(s):

İmdat İşcan, Mehmet Kunt

Department of Mathematics,
Faculty of Sciences and Arts,
Giresun University, Giresun,
Turkey.
E-mail: imdat.iscan@giresun.edu.tr

Department of Mathematics,
Faculty of Sciences,
Karadeniz Technical University,
61080, Trabzon,
Turkey.
E-mail: mkunt@ktu.edu.tr

Abstract:

In this paper, some Hermite-Hadamard-Fejer type integral inequalities for harmonically s-convex functions in fractional integral forms have been obtained.

Paper's Title:

Some Grüss Type Inequalities in Inner Product Spaces

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa

URL: http://rgmia.org/dragomir 

Abstract:

Some inequalities in inner product spaces that provide upper bounds for the quantities

and  ,

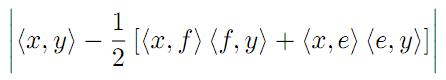
where e,f ∈ H with and x,y are vectors in H satisfying some appropriate assumptions are given. Applications for discrete and integral inequalities are provided as well.

Paper's Title:

C*-valued metric projection and Moore-Penrose inverse on Hilbert C*-modules

Author(s):

M. Eshaghi Gordji, H. Fathi and S.A.R. Hosseinioun

Department of Mathematics,
Semnan University, P.O. Box 35195-363, Semnan,
Iran.
Center of Excellence in Nonlinear Analysis and Applications (CENAA),
Semnan University,
Iran.
E-mail: Madjid.Eshaghi@gmail.com

Department of Mathematics,
Shahid Beheshti University, Tehran,
Iran.
E-mail: Hedayat.fathi@yahoo.com

Department of Mathematical Sciences,
University of Arkansas, Fayetteville, Arkansas 72701,
USA.
E-mail: shossein@uark.net

Abstract:

Let t be a regular operator between Hilbert C^*-modules and t^† be its Moore-Penrose inverse. We give some characterizations for t^† based on C^*-valued metric projection. Moore-Penrose inverse of bounded operators and elements of a C^*-algebra is studied as a special case.

Paper's Title:

Relation Between The Set Of Non-decreasing Functions And The Set Of Convex Functions

Author(s):

Qefsere Doko Gjonbalaj and Luigj Gjoka

Department of Mathematics, Faculty of Electrical and Computer Engineering,
University of Prishtina "Hasan Prishtina",
Prishtine 10000,
Kosova

E-mail: qefsere.gjonbalaj@uni-pr.edu
 

Department of Engineering Mathematics,
Polytechnic University of Tirana, Tirana,
Albania.

E-mail: luigjgjoka@ymail.com

Abstract:

In this article we address the problem of integral presentation of a convex function. Let I be an interval in R. Here, using the Riemann or Lebesgue’s integration theory, we find the necessary and sufficient condition for a function f: I→ R to be convex in I.

Paper's Title:

Cubic Alternating Harmonic Number Sums

Author(s):

Anthony Sofo

Victoria University,
College of Engineering and Science,
Melbourne City,
Australia.
E-mail: Anthony.Sofo@vu.edu.au

Abstract:

We develop new closed form representations of sums of cubic alternating harmonic numbers and reciprocal binomial coefficients. We also identify a new integral representation for the ζ (4)  constant.

Paper's Title:

Inequalities for Functions of Selfadjoint Operators on Hilbert Spaces:
a Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, College of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: https://rgmia.org/dragomir 

Abstract:

The main aim of this survey is to present recent results concerning inequalities for continuous functions of selfadjoint operators on complex Hilbert spaces. It is intended for use by both researchers in various fields of Linear Operator Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.

Paper's Title:

Estimates of Norms on Krein Spaces

Author(s):

Satheesh K. Athira, P. Sam Johnson and K. Kamaraj

Department of Mathematical and Computational Sciences,
National Institute of Technology Karnataka,
Surathkal, Mangaluru 575 025,
India.
E-mail: athirachandri@gmail.com

Department of Mathematical and Computational Sciences,
National Institute of Technology Karnataka,
Surathkal, Mangaluru 575 025,
India.
E-mail:sam@nitk.edu.in

Department of Mathematics,
University College of Engineering Arni,
Anna University, Arni 632 326,
India.
E-mail: krajkj@yahoo.com

Abstract:

Various norms can be defined on a Krein space by choosing different underlying fundamental decompositions. Some estimates of norms on Krein spaces are discussed and a few results in Bognar's paper are generalized.

Paper's Title:

Trace Inequalities for Operators in Hilbert Spaces: a Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University,
PO Box 14428 Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: https://rgmia.org/dragomir 

Abstract:

In this paper we survey some recent trace inequalities for operators in Hilbert spaces that are connected to Schwarz's, Buzano's and Kato's inequalities and the reverses of Schwarz inequality known in the literature as Cassels' inequality and Shisha-Mond's inequality. Applications for some functionals that are naturally associated to some of these inequalities and for functions of operators defined by power series are given. Further, various trace inequalities for convex functions are presented including refinements of Jensen inequality and several reverses of Jensen's inequality. Hermite-Hadamard type inequalities and the trace version of Slater's inequality are given. Some Lipschitz type inequalities are also surveyed. Examples for fundamental functions such as the power, logarithmic, resolvent and exponential functions are provided as well.

Search and serve lasted 0 second(s).