Abstract:

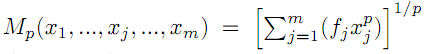
The purpose of this note is to demonstrate a new property of the general mean of order p of m ordered positive numbers . If p < 0 and if , the elasticity of with respect to x_m, defined by , tends towards zero, and therefore . This property is then applied to optimal growth theory.

Paper's Title:

Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.

Paper's Title:

Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.

Paper's Title:

The Conservativeness of Girsanov Transformed for Symmetric Jump-diffusion Process

Author(s):

Mila Kurniawaty and Marjono

Department of Mathematics,
Universitas Brawijaya,
Malang,
Indonesia.
E-mail: mila_n12@ub.ac.id, marjono@ub.ac.id

Abstract:

We study about the Girsanov transformed for symmetric Markov processes with jumps associated with regular Dirichlet form. We prove the conservativeness of it by dividing the regular Dirichlet form  into the "small jump" part and the "big jump" part.

Paper's Title:

Numerical Approximation by the Method of Lines with Finite-volume Approach of a Solute Transport Equation in Periodic Heterogeneous Porous Medium

Author(s):

D. J. Bambi Pemba and B. Ondami

Université Marien Ngouabi,
Factuté des Sciences et Techniques,
BP 69, Brazzaville,
Congo.
E-mail: bondami@gmail.com

Abstract:

In this paper we are interested in the numerical approximation of a two-dimensional solute transport equation in heterogeneous porous media having periodic structures. It is a class of problems which has been the subject of various works in the literature, where different methods are proposed for the determination of the so-called homogenized problem. We are interested in this paper, in the direct resolution of the problem, and we use the method of lines with a finite volume approach to discretize this equation. This discretization leads to an ordinary differential equation (ODE) that we discretize by the Euler implicit scheme. Numerical experiments comparing the obtained solution and the homogenized problem solution are presented. They show that the precision and robustness of this method depend on the ratio between, the mesh size and the parameter involved in the periodic homogenization.

Paper's Title:

Reduced Generalized Combination Synchronization Between Two n-Dimensional Integer-Order Hyperchaotic Systems and One m-Dimensional Fractional-Order Chaotic System

Author(s):

Smail Kaouache, Mohammed Salah Abdelouahab and Rabah Bououden

Laboratory of Mathematics and their interactions,
Abdelhafid Boussouf University Center, Mila.
Algeria
E-mail: smailkaouache@gmail.com, medsalah3@yahoo.fr, rabouden@yahoo.fr

Abstract:

This paper is devoted to investigate the problem of reduced generalized combination synchronization (RGCS) between two n-dimensional integer-order hyperchaotic drive systems and one m-dimensional fractional-order chaotic response system. According to the stability theorem of fractional-order linear system, an active mode controller is proposed to accomplish this end. Moreover, the proposed synchronization scheme is applied to synchronize three different chaotic systems, which are the Danca hyperchaotic system, the modified hyperchaotic Rossler system, and the fractional-order Rabinovich-Fabrikant chaotic system. Finally, numerical results are presented to fit our theoretical analysis.

Paper's Title:

Coexisting Attractors and Bubbling Route to Chaos in Modified Coupled Duffing Oscillators

Author(s):

B. Deruni¹, A. S. Hacinliyan^1,2, E. Kandiran³, A. C. Keles², S. Kaouache⁴, M.-S. Abdelouahab⁴, N.-E. Hamri⁴

¹Department of Physics,
University of Yeditepe,
Turkey.

²Department of Information Systems and Technologies,
University of Yeditepe,
Turkey

³Department of Software Development,
University of Yeditepe,
Turkey.

⁴Laboratory of Mathematics and their interactions,
University Center of Abdelhafid Boussouf,
Mila 43000,
Algeria.

E-mail: berc890@gmail.com
ahacinliyan@yeditepe.edu.tr
engin.kandiran@yeditepe.edu.tr
cihan.keles@yeditepe.edu.tr
s.kaouache@centr-univ-mila.dz
medsalah3@yahoo.fr
n.hamri@centre-univ-mila.dz

Abstract:

In this article dynamical behavior of coupled Duffing oscillators is analyzed under a small modification. The oscillators have cubic damping instead of linear one. Although single duffing oscillator has complex dynamics, coupled duffing systems possess a much more complex structure. The dynamical behavior of the system is investigated both numerically and analytically. Numerical results indicate that the system has double scroll attractor with suitable parameter values. On the other hand, bifurcation diagrams illustrate rich behavior of the system, and it is seen that, system enters into chaos with different routes. Beside classical bifurcations, bubbling route to chaos is observed for suitable parameter settings. On the other hand, Multistability of the system is indicated with the coexisting attractors, such that under same parameter setting the system shows different periodic and chaotic attractors. Moreover, chaotic synchronization of coupled oscillators is illustrated in final section.

Paper's Title:

Generalized Von Neumann-Jordan Constant for Morrey Spaces and Small Morrey Spaces

Author(s):

H. Rahman and H. Gunawan

Department of Mathematics,
Islamic State University Maulana Malik Ibrahim Malang,
Jalan Gajayana No.50,
Indonesia.
E-mail: hairur@mat.uin-malang.ac.id

Analysis and Geometry Group,
Faculty of Mathematics and Natural Sciences,
Bandung Institute of Technology, Bandung 40132,
Indonesia.
E-mail: hgunawan@math.itb.ac.id
URL:  http://personal.fmipa.itb.ac.id/hgunawan/

Abstract:

In this paper we calculate some geometric constants for Morrey spaces and small Morrey spaces, namely generalized Von Neumann-Jordan constant, modified Von Neumann-Jordan constants, and Zbaganu constant. All these constants measure the uniformly nonsquareness of the spaces. We obtain that their values are the same as the value of Von Neumann-Jordan constant for Morrey spaces and small Morrey spaces.

Paper's Title:

Conservativeness Criteria of Girsanov Transformation for Non-Symmetric Jump-diffusion

Author(s):

Mila Kurniawaty

DDepartment of Mathematics,
Universitas Brawijaya, Malang,
Indonesia.
E-mail: mila_n12@ub.ac.id

Abstract:

We develop the condition in our previous paper [The Conservativeness of Girsanov transformed for symmetric jump-diffusion process (2018)] in the framework of nonsymmetric Markov process with jumps associated with regular Dirichlet form. We prove the conservativeness of it by relation in duality of Girsanov transformed process and recurrent criteria of Dirichlet form.

Paper's Title:

Estimation for Bounded Solutions of Some Nonlinear Integral Inequalities with Delay in Several Variables

Author(s):

Smakdji Mohamed Elhadi, Denche Mouhamed and Khellaf Hassane

Department of Mathematics
University of Frères Mentouri
PO Box 25000, Ain Elbay,
Constantine,
Algeria.
E-mail: khellafhassane@umc.edu.dz

Abstract:

In this paper, some new nonlinear retarded integral inequalities of Gronwall-Bellman type for functions of two and n-independents variables are investigated. The derived results can be applied in the study of differential-integral equations with time delay. An example is given to illustrate the application of our results.

Paper's Title:

SQIRV Model for Omicron Variant with Time Delay

Author(s):

S. Dickson, S. Padmasekaran, G. E. Chatzarakis and S. L. Panetsos

Mathematics, Periyar University, Periyar Palkalai Nagar, Salem,
636011, Tamilnadu,
India.
E-mail: dickson@periyaruniversity.ac.in, padmasekarans@periyaruniversity.ac.in

Electrical and Electronic Engineering Educators, School of
Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr, spanetsos@aspete.gr

Abstract:

In order to examine the dynamics of the Omicron variant, this paper uses mathematical modelling and analysis of a SQIRV model, taking into account the delay in the conversion of susceptible individuals into infected individuals and infected individuals into recovered individuals. The pandemic was eventually controlled as a result of the massive delays. To assure the safety of the host population, this concept incorporates quarantine and the COVID-19 vaccine. Both local and global stability of the model are examined. It is found that the fundamental reproduction number affects both local and global stability conditions. Our findings show that asymptomatic cases caused by an affected population play an important role in increasing Omicron infection in the general population. The most recent data on the pandemic Omicron variant from Tamil Nadu, India, is verified.

Paper's Title:

Topological Aspects of Discrete Switch Dynamical Systems

Author(s):

Faiz Imam and Sharan Gopal

Department of Mathematics,
BITS - Pilani, Hyderabad Campus,
India.
E-mail: mefaizy@gmail.com

Department of Mathematics,
BITS - Pilani, Hyderabad Campus,
India.
E-mail: sharanraghu@gmail.com

ABSTRACT NOT FOUND. WEBSITE ERROR

Abstract:

Paper's Title:

Numerical Study of a Mathematical Model of a Free-Surface Potential Flow

Author(s):

H. Serguine, F. Guechi and A. Gasmi

Department Of Mathematics, Faculty of Science,
Ferhat Abbas Universty, 19000, Setif,
Algeria.
E-mail: houria.serguine@univ-msila.dz

 
Department Of Mathematics, Faculty of Science,
Ferhat Abbas Universty, 19000, Setif,
Algeria.
E-mail:  fairouz.chegaar@univ-setif.dz

Laboratory of Pure and Applied Mathematics, Faculty of Mathematics and Computer Science,
Mohamed Boudiaf Universty, 28000, M'sila,
Algeria.
E-mail: abdelkader.gasmi@univ-msila.dz

Abstract:

In this work, the problem of a potential and two-dimensional flow with a free surface of an incompressible, irrotational and inviscid fluid of a jet in front an inclined wall is considered, where γ is the inclination angle with the horizontal. The shape of the free surface is presented by curves which are found numerically by the series truncation method. This technique is based on the conformal transformations, resulting with the surface tension effect T with the boundary conditions on the free surfaces given by Bernoulli's equation. The found results are dependant on parameters which are: the Weber's number α and the angle γ. For each Weber's number value, only one solution is specified and some shapes of free surfaces of the jet are illustrated.

Paper's Title:

A General Fractional Control Scheme for Compound Combination Synchronization Between Different Fractional-Order Identical Chaotic Systems

Author(s):

Soumia Bensimessaoud and Smail Kaouache

Laboratory of Mathematics and their interactions, Abdelhafid Boussouf University Center, Mila, Algeria.
E-mail: soumiabensimessaoud@gmail.com, smailkaouache@gmail.com

Abstract:

In this paper, we aim to investigate the problem of compound combination synchronization (CCS) between four different fractional-order identical chaotic systems. Based on Laplace transformation and stability theory of linear dynamical systems, a new control law is proposed to assure the achievement of this kind of synchronization. Secondly, this control scheme is applied to realised CCS between four identical unified chaotic systems. Recall, that the proposed control scheme can be applied to wide classes of chaotic and hyperchaotic systems. Numerical simulations are given to show the effectiveness of the proposed method.

Paper's Title:

Eigenvalue Bounds based on Projections

Author(s):

Pravin Singh, Shivani Singh, Virath Singh

University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.

University of South Africa,
Department of Decision Sciences, PO Box 392,
 Pretoria,0003,
South Africa.

University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.

E-mail: singhp@ukzn.ac.za, singhs2@unisa.ac.za, singhv@ukzn.ac.za
 

Abstract:

In this paper, we derive expressions for the bounds of the extremal eigenvalues of positive definite matrices. Our approach is to use a symmetric projection operator onto an n-2 dimensional subspace of the real space of n tuples. These bounds are based on traces of the matrix and its powers. They are relatively easy and inexpensive to compute.

Paper's Title:

Solving Strongly Nonlinear Fractional Fredholm Integral-Differential Equations in Caputo's Sense Using the SBA Method

Author(s):

Germain Kabore¹, Bakari Abbo², Ousseni So³ and Blaise Some¹

¹Laboratoire d'Analyse Numerique, Informatique et de Biomathmathiques (L.N.I.BIO),
Universite Joseph Ki-Zerbo,
Burkina Faso.
E-mail: germainkabore982@gmail.com, blaisesomeouaga1@gmail.com

²University of N'Damena, Tchad.
E-mail: bakariabbo@yahoo.fr

³Laboratoire d'Analyse Numerique, Informatique et de Biomathemathiques (L.N.I.BIO),
Ecole Normale Superieure,
Burkina Faso.
E-mail: sousseni@yahoo.fr

Abstract:

The work addressed in this article consists in constructing the exact solutions, where they exist, of fractional Fredholm-type integro-differential equations in the sense of Caputo. Our results are obtained using the SBA method. The simplification of the approach, the analysis of its convergence, and the generalization of this method to these types of highly nonlinear equations constitute our scientific contribution.

Paper's Title:

Recursive Bounds for the Eigenvalues of Symmetric Positive Definite Matrices

Author(s):

Pravin Singh, Shivani Singh, Virath Singh

University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.

University of South Africa,
Department of Decision Sciences, PO Box 392,
 Pretoria,0003,
South Africa.

University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.

E-mail: singhp@ukzn.ac.za, singhs2@unisa.ac.za, singhv@ukzn.ac.za
 

Abstract:

In this paper, we bound the extremal eigenvalues of a positive definite real symmetric matrix by considering a part of the characteristic equation in the region of the smallest and largest eigenvalues. An expansion around these values leads to a sequence of monotonic functions, whose zeros coincide with the extremal zeros of associated polynomials. The latter is shown to yield bounds that are fairly accurate.

Search and serve lasted 0 second(s).