|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
On the Hohov Convolution Of The Class Sp(α,β)
Author(s):
T. N. Shanmugam and S. Sivasubramanian
Department of Mathematics,
Anna University,
Chennai 600025,
Tamilnadu, India.
shan@annauniv.edu
Department of Mathematics,
Easwari Engineering College,
Chennai-600089,
Tamilnadu, India,
sivasaisastha@rediffmail.com
Abstract:
Let F(a,b;c;z) be the Gaussian hypergeometric function and Ia,b;c(f)=zF(a,b;c;z)*f(z) be the Hohlov operator defined on the class A of all normalized analytic functions. We determine conditions on the parameters a,b,c such that Ia,b;c(f) will be in the class of parabolic starlike functions Sp(α,β). Our results extend several earlier results.
Paper's Title:
General Extension of Hardy-Hilbert's Inequality (I)
Author(s):
W. T. Sulaiman
College of Computer Science and Mathematics, University of Mosul,
Iraq.
waadsulaiman@hotmail.com
Abstract:
A generalization for Hardy-Hilbert's inequality that extends the recent
results of Yang and Debnath
[6], is given.
Paper's Title:
A Sum Form Functional Equation and Its Relevance in Information Theory
Author(s):
Prem Nath and Dhiraj Kumar Singh
Department of Mathematics
University of Delhi
Delhi - 110007
India
pnathmaths@gmail.com
dksingh@maths.du.ac.in
Abstract:
The general solutions of a sum form functional equation containing four unknown mappings have been investigated. The importance of these solutions in relation to various entropies in information theory has been emphasised.
Paper's Title:
On Some Ramanujan's Schläfli Type Modular Equations
Author(s):
K. R. Vasuki
Department of Mathematics, Acharya Institute of Technology, Soldevanahalli,
Chikkabanavara (Post), Hesaragatta Main Road, Bangalore-560 090,
INDIA.
vasuki_kr@hotmail.com
Abstract:
In this paper, we give new proof of
certain Ramanujan-Schläfli modular equations. We also obtain a new modular
equation of degree 23.
Paper's Title:
On the Generalized Inverse  over Integral Domains
over Integral Domains
Author(s):
Yaoming Yu and Guorong Wang
College of Education, Shanghai Normal University
Shanghai 200234
People's Republic of China.
yuyaoming@online.sh.cn
grwang@shnu.edu.cn
Abstract:
In this paper, we study further the generalized inverse
 of a matrix A over an integral domain. We give
firstly some necessary and sufficient conditions for the existence
of the generalized inverse
of a matrix A over an integral domain. We give
firstly some necessary and sufficient conditions for the existence
of the generalized inverse  , an explicit expression
for the elements of the generalized inverse
, an explicit expression
for the elements of the generalized inverse  and an
explicit expression for the generalized inverse
and an
explicit expression for the generalized inverse  ,
which reduces to the {1} inverse. Secondly, we verify that the
group inverse, the Drazin inverse, the Moore-Penrose inverse and the
weighted Moore-Penrose inverse are identical with the generalized
inverse
,
which reduces to the {1} inverse. Secondly, we verify that the
group inverse, the Drazin inverse, the Moore-Penrose inverse and the
weighted Moore-Penrose inverse are identical with the generalized
inverse 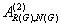 for an appropriate matrix G,
respectively, and then we unify the conditions for the existence and
the expression for the elements of the weighted Moore-Penrose
inverse, the Moore-Penrose inverse, the Drazin inverse and the group
inverse over an integral domain. Thirdly, as a simple application,
we give the relation between some rank equation and the existence of
the generalized inverse
for an appropriate matrix G,
respectively, and then we unify the conditions for the existence and
the expression for the elements of the weighted Moore-Penrose
inverse, the Moore-Penrose inverse, the Drazin inverse and the group
inverse over an integral domain. Thirdly, as a simple application,
we give the relation between some rank equation and the existence of
the generalized inverse  , and a method to compute the
generalized inverse
, and a method to compute the
generalized inverse  . Finally, we give an example of
evaluating the elements of
. Finally, we give an example of
evaluating the elements of  without calculating
without calculating
 .
.
Paper's Title:
On Convergence Theorems of an Implicit Iterative Process with Errors for a
Finite Family of Asymptotically quasi I-nonexpansive Mappings
Author(s):
Farrukh Mukhamedov and Mansoor Saburov
Department of Computational & Theoretical
Sciences,
Faculty of Sciences, International Islamic University Malaysia,
P.O. Box, 141, 25710, Kuantan,
Malaysia
Abstract:
In this paper we prove the weak and strong convergence of the implicit iterative process with errors to a common fixed point of a finite family {Tj}Ni=1 of asymptotically quasi Ij-nonexpansive mappings as well as a family of {Ij}Nj=1 of asymptotically quasi nonexpansive mappings in the framework of Banach spaces. The obtained results improve and generalize the corresponding results in the existing literature.
Paper's Title:
Komatu Integral Transforms of Analytic Functions Subordinate to Convex Functions
Author(s):
T. N. Shanmugam and C. Ramachandran
Department of Mathematics, College of Engineering,
Anna University, Chennai-600 025, Tamilnadu,
India
shan@annauniv.edu
Department of Mathematics, College of Engineering,
Anna University, Chennai-600 025, Tamilnadu,
India
crjsp2004@yahoo.com
Abstract:
In this paper, we consider the class A of the functions f(z) of the form
which are analytic in an open disk
has some property. Certain inclusion and the closure properties like convolution with convex univalent function etc. are studied.

 and study certain subclass of the class A, for which
and study certain subclass of the class A, for which
Paper's Title:
On Sandwich Theorems for Certain Subclass of Analytic Functions Involving Dziok-Srivastava Operator
Author(s):
T. N. Shanmugam, M. P. Jeyarama and A. Singaravelu
Department of Mathematics
College of Engineering, Anna University
Chennai - 600 025,
India
drtns2001@yahoo.com
Department of Mathematics
Easwari Engineering College
Ramapuram, Chennai - 600089
Tamilnadu, India
jeyaraman-mp@yahoo.co.i
Department of Mathematics
Valliammai Engineering College
Chennai - 603203
Tamilnadu, India.
asing-59@yahoo.com
Abstract:
The purpose of this present paper is to derive some subordination and superordination results for certain normalized analytic functions in the open unit disk, acted upon by Dziok-Srivastava operator. Relevant connections of the results, which are presented in this paper, with various known results are also considered.
Paper's Title:
Some Inequalities for a Certain Class of Multivalent Functions
Using Multiplier Transformation
Author(s):
K. Suchithra, B. Adolf Stephen, A. Gangadharan and S. Sivasubramanian
Department Of Applied Mathematics
Sri Venkateswara College Of Engineering
Sriperumbudur, Chennai - 602105,
India.
suchithravenkat@yahoo.co.in
Department Of Mathematics,
Madras Christian College
Chennai - 600059,
India.
adolfmcc2003@yahoo.co.in
Department Of Applied Mathematics
Sri Venkateswara College Of Engineering
Sriperumbudur, Chennai - 602105,
India.
ganga@svce.ac.in
Department Of Mathematics,
Easwari Engineering College
Ramapuram, Chennai - 600089,
India.
ganga@svce.ac.in
Abstract:
The object of the present paper is to derive several inequalities
associated with differential subordinations between analytic functions
and a linear operator defined for a certain family of p-valent
functions, which is introduced here by means of a family of extended
multiplier transformations. Some special cases and consequences of
the main results are also considered.
Paper's Title:
A Subclass of Meromorphically Multivalent Functions with Applications to Generalized Hypergeometric Functions
Author(s):
M. K. Aouf
Mathematics Department,
Faculty of Science,
Mansoura University 35516,
Egypt
mkaouf127@yahoo.com
Abstract:
In this paper a new subclass of meromorphically multivalent functions, which
is defined by means of a Hadamard product (or convolution) involving some
suitably normalized meromorphically p-valent functions. The main object of
the present paper is to investigate the various important properties and
characteristics of this subclass of meromorphically multivalent functions.
We also derive many interesting results for the Hadamard products of
functions belonging to this subclass. Also we consider several applications
of our main results to generalized hypergeomtric functions.
Paper's Title:
Some Identities for Ramanujan - Göllnitz - Gordon Continued fraction
Author(s):
M. S. Mahadeva Naika, B. N. Dharmendra and S. Chandan Kumar
Department of Mathematics,
Bangalore University,
Central College Campus,
Bangalore-560 001,
INDIA
Department of Mathematics,
Maharani's Science College for Women,
J. L. B. Road, Mysore-570 001,
INDIA
Abstract:
In this paper, we obtain certain P--Q eta--function identities, using which we establish identities providing modular relations between Ramanujan-Göllnitz-Gordon continued fraction H(q) and H(q^n) for n= 2, 3, 4, 5, 7, 8, 9, 11, 13, 15, 17, 19, 23, 25, 29 and 55.
Paper's Title:
Linear System of Singularly Perturbed Initial Value Problems with Robin Initial Conditions
Author(s):
S. Dinesh, G. E. Chatzarakis, S. L. Panetsos and S. Sivamani
Department of Mathematics,
Saranathan College of Engineering,
Tiruchirappalli-620012,
Tamil Nadu,
India.
Department of Electrical and Electronic
Engineering Educators,
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail:
geaxatz@otenet.gr,
dineshselvaraj24@gmail.com,
spanetsos@aspete.gr,
winmayi2012@gmail.com
Abstract:
On the interval (0,1], this paper considers an initial value problem for a system of n singularly perturbed differential equations with Robin initial conditions. On a piecewise uniform Shishkin mesh, a computational approach based on a classical finite difference scheme is proposed. This approach is shown to be first-order convergent in the maximum norm uniformly in the perturbation parameters. The theory is illustrated by a numerical example.
Paper's Title:
An alternative proof of monotonicity for the extended mean values
Author(s):
Chao-Ping Chen and Feng Qi
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
chenchaoping@hpu.edu.cn
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
qifeng@hpu.edu.cn,
fengqi618@member.ams.org
Url:
http://rgmia.vu.edu.au/qi.html,
http://dami.hpu.edu.cn/qifeng.html
Abstract:
An alternative proof of monotonicity for the extended mean values is given.
Paper's Title:
Classes of Meromorphic p-valent Parabolic Starlike Functions with Positive Coefficients
Author(s):
S. Sivaprasad Kumar, V. Ravichandran, and G. Murugusundaramoorthy
Department of Applied Mathematics
Delhi College of Engineering,
Delhi 110042, India
sivpk71@yahoo.com
School of Mathematical Sciences
Universiti Sains Malaysia
11800 USM Penang
Malaysia
vravi@cs.usm.my
URL: http://cs.usm.my/~vravi
Department of Mathematics
Vellore Institute of Technology (Deemed University)
Vellore 632 014, India
gmsmoorthy@yahoo.com
Abstract:
In the present paper, we consider two general subclasses of meromorphic p-valent starlike functions with positive coefficients and obtain a necessary and sufficient condition for functions to be in these classes. Also we obtain certain other related results as a consequences of our main results.
Paper's Title:
A New Hardy-Hilbert's Type Inequality for Double Series and its Applications
Author(s):
Mingzhe Gao
Department of Mathematics and Computer Science, Normal College Jishou University,
Jishou Hunan, 416000,
People's Republic of China
mingzhegao1940@yahoo.com.cn
Abstract:
In this paper, it is shown that a new Hardy-Hilberts type
inequality for double series can be established by introducing a parameter ![]() and the weight function of the form
and the weight function of the form ![]() where c is Euler
constant and
where c is Euler
constant and ![]() And
the coefficient
And
the coefficient ![]() and
and ![]() appear simultaneously in the coefficient and the weight
function when
appear simultaneously in the coefficient and the weight
function when ![]() In particular, for
case
In particular, for
case ![]() some new Hilberts
type inequalities are obtained. As applications, some extensions of Hardy-Littlewoods inequality are given.
some new Hilberts
type inequalities are obtained. As applications, some extensions of Hardy-Littlewoods inequality are given.
Paper's Title:
On Vector Variational Inequality Problem in Terms of Bifunctions
Author(s):
C. S. Lalitha and Monika Mehta
Department of Mathematics, Rajdhani College,
Department of Mathematics, Satyawati College,
University of Delhi, Raja Garden,
Delhi 110015, India
cslalitha@rediffmail.com
University Of Delhi, Ashok Vihar,
Phase-III, Delhi 110052, India
mridul_in@yahoo.com
Abstract:
In this paper, we consider a generalized vector variational
inequality problem expressed in terms of a bifunction and establish
existence theorems for this problem by using the concepts of cone
convexity and cone strong quasiconvexity and employing the
celebrated Fan's Lemma. We also give two types of gap functions for this problem.
Paper's Title:
Normalized Truncated Levy models applied to the study of Financial Markets
Author(s):
M. C. Mariani, K. Martin, D. W. Dombrowski and D. Martinez
Department of Mathematical Sciences and Department of Finance,
New Mexico State University, P.O. Box 30001
Department 3MB Las Cruces, New Mexico 88003-8001
USA.
mmariani@nmsu.edu
kjmartin@nmsu.edu
Abstract:
This work is devoted to the study of the statistical properties of financial instruments from developed markets. We performed a new analysis of the behavior of companies corresponding to the DJIA index, and of the index itself, by using a normalized Truncated Levy walk model. We conclude that the Truncated Levy distribution describes perfectly the evolution of the companies and of the index near a crash.
Paper's Title:
On a Subclass of Uniformly Convex Functions Defined by the Dziok-Srivastava Operator
Author(s):
M. K. Aouf and G. Murugusundaramoorthy
Mathematics Department, Faculty of Science,
Mansoura University 35516,
Egypt.
mkaouf127@yahoo.com
School of Science and Humanities, VIT University
Vellore - 632014,
India.
gmsmoorthy@yahoo.com
Abstract:
Making use of the Dziok-Srivastava operator, we define a new subclass Tlm([α1];α,β) of uniformly convex function with
negative coefficients. In this paper, we obtain coefficient estimates,
distortion theorems, locate extreme points and obtain radii of
close-to-convexity, starlikeness and convexity for functions belonging to the
class Tlm([α1];α,β) . We
consider integral operators associated with functions belonging to the class
Hlm([α1];α,β) defined via the Dziok-Srivastava
operator. We also obtain several results for the modified Hadamard products of
functions belonging to the class Tlm([α1];α,β)
and we obtain properties associated with generalized fractional calculus
operators.
Paper's Title:
On a Hilbert-type Inequality with the Polygamma Function
Author(s):
Bing He and Bicheng Yang
Department of Mathematics, Guangdong Education College,
Guangzhou, 510303,
China.
Department of Mathematics, Guangdong Education College,
Guangzhou, 510303,
China.
Abstract:
By applying the method of weight function and the technique of real analysis, a Hilbert-type inequality with a best constant factor is established, where the best constant factor is made of the polygamma function. Furthermore, the inverse form is given.
Paper's Title:
On Generalization of Hardy-type Inequalities
Author(s):
K. Rauf, S. Ponnusamy and J. O. Omolehin
Department of Mathematics,
University of Ilorin, Ilorin,
Nigeria
krauf@unilorin.edu.ng
Department of Mathematics,
Indian Institute of Technology Madras,
Chennai- 600 036,
India
samy@iitm.ac.in
Department of Mathematics,
University of Ilorin, Ilorin,
Nigeria
omolehin_joseph@yahoo.com
Abstract:
This paper is devoted to some new generalization of Hardy-type integral inequalities and the reversed forms. The study is to determine conditions on which the generalized inequalities hold using some known hypothesis. Improvement of some inequalities are also presented.
Paper's Title:
Solving Non-Autonomous Nonlinear Systems of Ordinary Differential Equations Using Multi-Stage Differential Transform Method
Author(s):
K. A. Ahmad, Z. Zainuddin, F. A. Abdullah
School of Mathematical Sciences
Universiti Sains Malaysia
11800 USM Penang
Malaysia.
E-mail: abumohmmadkh@hotmail.com
zarita@usm.my
farahaini@usm.my
Abstract:
Differential equations are basic tools to describe a wide variety of phenomena in nature such as, electrostatics, physics, chemistry, economics, etc. In this paper, a technique is developed to solve nonlinear and linear systems of ordinary differential equations based on the standard Differential Transform Method (DTM) and Multi-stage Differential Transform Method (MsDTM). Comparative numerical results that we are obtained by MsDTM and Runge-Kutta method are proposed. The numerical results showed that the MsDTM gives more accurate approximation as compared to the Runge-Kutta numerical method for the solutions of nonlinear and linear systems of ordinary differential equations
Paper's Title:
A Determinantal Representation of Core EP Inverse
Author(s):
Divya Shenoy Purushothama
Department of Mathematics,
Manipal Institute of Technology,
Manipal Academy of Higher Education,
Manipal -576104, Karnataka,
India.
E-mail: divya.shenoy@manipal.edu
URL:
https://manipal.edu/mit/department-faculty/faculty-list/divya-shenoy-p.html
Abstract:
The notion of Core EP inverse is introduced by Prasad in the article "Core - EP inverse" and proved its existence and uniqueness. Also, a formula for computing the Core EP inverse is obtained from particular linear combination of minors of a given matrix. Here a determinantal representation for Core EP inverse of a matrix A with the help of rank factorization of A is obtained.
Paper's Title:
The Drazin-star and Star-Drazin Solutions to Quaternion Matrix Equations
Author(s):
Ivan I. Kyrchei, Dijana Mosić, Predrag Stanimirović
Pidstryhach Institute for Applied Problems
of Mechanics and Mathematics
of NAS of Ukraine, L'viv, 79060,
Ukraine.
E-mail:
ivankyrchei26@gmail.com
Faculty of Sciences and Mathematics,
University of Ni, P.O.
Box 224, 18000, Ni, Serbia.
E-mail: dijana@pmf.ni.ac.rs
Faculty of Sciences and Mathematics,
University of Ni, P.O.
Box 224, 18000, Ni, Serbia.
E-mail: pecko@pmf.ni.ac.rs
Abstract:
The notions of the Drazin-star and star-Drazin matrices are expanded to quaternion matrices in this paper. Their determinantal representations are developed in both cases in terms of noncommutative row-column determinants of quaternion matrices and for minors of appropriate complex matrices. We study all possible two-sided quaternion matrix equations with their one-sided partial cases whose uniquely determined solutions are based on the Drazin-star and star-Drazin matrices. Solutions of these equations are represented by Cramer's rules in both cases for quaternion and complex matrix equations. A numerical example is presented to illustrate our results.
Search and serve lasted 1 second(s).