Paper's Title:

On the Equiform Geometry of the Involute-evolute Curve Couple in Hyperbolic and de Sitter Spaces

Author(s):

M. Khalifa Saad, H. S. Abdel-Aziz and A. A. Abdel-Salam

Department of Mathematics,
Faculty of Science,
Islamic University of Madinah,
KSA.
E-mail: mohammed.khalifa@iu.edu.sa

Department of Mathematics,
Faculty of Science,
Sohag University, Sohag,
EGYPT.
E-mail: habdelaziz2005@yahoo.com

Department of Mathematics,
Faculty of Science,
Sohag University, Sohag,
EGYPT.
E-mail: asem2e@yahoo.com

Abstract:

In this paper, we aim to investigate the equiform differential geometric properties of the involute-evolute curve couple with constant equiform curvatures in three-dimensional hyperbolic and de Sitter spaces. Also, we obtain some relations between the curvature functions of these curves and investigate some special curves with respect to their equiform curvatures. Finally, we defray two computational examples to support our main findings.

Paper's Title:

Hyers-Ulam-Rassias Stability of a Generalized Jensen Functional Equation

Author(s):

A. Charifi, B. Bouikhalene, E. Elqorachi and A. Redouani

Abstract:

In this paper we obtain the Hyers-Ulam-Rassias stability for the generalized Jensen's functional equation in abelian group (G,+). Furthermore we discuss the case where G is amenable and we give a note on the Hyers-Ulam-stability of the K-spherical (n × n)-matrix functional equation.

Paper's Title:

On Ruled Surfaces According to Quasi-Frame in Euclidean 3-Space

Author(s):

M. Khalifa Saad and R. A. Abdel-Baky

Department of Mathematics, Faculty of Science,
Islamic University of Madinah,
KSA.
Department of Mathematics, Faculty of Science,
Sohag University, Sohag,
EGYPT.
E-mail: mohamed_khalifa77@science.sohag.edu.eg, mohammed.khalifa@iu.edu.sa

Department of Mathematics, Faculty of Science,
Assiut University, Assiut,
EGYPT.
E-mail: rbaky@live.com

Abstract:

This paper aims to study the skew ruled surfaces by using the quasi-frame of Smarandache curves in the Euclidean 3-space. Also, we reveal the relationship between Serret-Frenet and quasi-frames and give a parametric representation of a directional ruled surface using the quasi-frame. Besides, some comparative examples are given and plotted which support our method and main results.

Paper's Title:

Ulam Stability of Reciprocal Difference and Adjoint Functional Equations

Author(s):

K. Ravi, J. M. Rassias and B. V. Senthil Kumar

Department of Mathematics,
Sacred Heart College, Tirupattur - 635601,
India

Pedagogical Department E. E.,
Section of Mathematics and Informatics,
National and Capodistrian University of Athens,
4, Agamemnonos Str., Aghia Paraskevi,
Athens, Attikis 15342,
GREECE

Department of Mathematics,
C.Abdul Hakeem College of Engineering and
Technology, Melvisharam - 632 509, India

shckavi@yahoo.co.in
jrassias@primedu.uoa.gr
bvssree@yahoo.co.in
 

Abstract:

In this paper, the reciprocal difference functional equation (or RDF equation) and the reciprocal adjoint functional equation (or RAF equation) are introduced. Then the pertinent Ulam stability problem for these functional equations is solved, together with the extended Ulam (or Rassias) stability problem and the generalized Ulam (or Ulam-Gavruta-Rassias) stability problem for the same equations.

Paper's Title:

Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.

Paper's Title:

Solving Non-Autonomous Nonlinear Systems of Ordinary Differential Equations Using Multi-Stage Differential Transform Method

Author(s):

K. A. Ahmad, Z. Zainuddin, F. A. Abdullah

School of Mathematical Sciences Universiti Sains Malaysia
11800 USM Penang
Malaysia.
E-mail: abumohmmadkh@hotmail.com
zarita@usm.my
farahaini@usm.my

Abstract:

Differential equations are basic tools to describe a wide variety of phenomena in nature such as, electrostatics, physics, chemistry, economics, etc. In this paper, a technique is developed to solve nonlinear and linear systems of ordinary differential equations based on the standard Differential Transform Method (DTM) and Multi-stage Differential Transform Method (MsDTM). Comparative numerical results that we are obtained by MsDTM and Runge-Kutta method are proposed. The numerical results showed that the MsDTM gives more accurate approximation as compared to the Runge-Kutta numerical method for the solutions of nonlinear and linear systems of ordinary differential equations

Paper's Title:

Numerical Solution of Certain Types of Fredholm-Volterra Integro-Fractional Differential Equations via Bernstein Polynomials

Author(s):

Alias B. Khalaf¹, Azhaar H. Sallo² and Shazad S. Ahmed³

¹Department of Mathematics, College of Science,
University of Duhok,
Kurdistan Region,
Iraq.
E-mail:  aliasbkhalaf@uod.ac

²Department of Mathematics, College of Science,
University of Duhok,
Kurdistan Region,
Iraq.
E-mail:  azhaarsallo@uod.ac

³Department of Mathematics, College of Science,
University of Sulaimani,
Kurdistan Region,
Iraq.
E-mail: shazad.ahmed@univsul.edu

Abstract:

In this article we obtain a numerical solution for a certain fractional order integro-differential equations of Fredholm-Volterra type, where the fractional derivative is defined in Caputo sense. The properties of Bernstein polynomials are applied in order to convert the fractional order integro-differential equations to the solution of algebraic equations. Some numerical examples are investigated to illustrate the method. Moreover, the results obtained by this method are compared with the exact solution and with the results of some existing methods as well.

Paper's Title:

Timelike Surfaces with a Common Line of Curvature in Minkowski 3-Space

Author(s):

M.K. Saad, A.Z. Ansari, M. Akram and F. Alharbi

Department of Mathematics ,
Faculty of Science,
Islamic University of Madinah,
KSA

Abstract:

In this paper, we analyze the problem of constructing a timelike surface family from a given non-null curve line of curvature. Using the Frenet frame of the non-null curve in Minkowski space E₁³  we express the family of surfaces as a linear combination of the components of this frame, and derive the necessary and sufficient conditions for the coefficients to satisfy both the line of curvature and the isoparametric requirements. In addition, a necessary and sufficient condition for the given non-null curve to satisfy the line of curvature and the geodesic requirements is investigated. The extension to timelike surfaces of revolution is also outlined. Meanwhile, some representative non-null curves are chosen to construct the corresponding timelike surfaces which possessing these curves as lines of curvature. Results presented in this paper have applications in geometric modeling and the manufacturing of products. In addition, some computational examples are given and plotted.

Paper's Title:

Weak Solution for Hyperbolic Equations with a Non-Local Condition

Author(s):

Lazhar Bougoffa

King Khalid University, Faculty of Science, Department of Mathematics,
P.O.Box 9004, Abha, Saudi Arabia
abogafah@kku.edu.sa

Abstract:

In this paper, we study hyperbolic equations with a non-local condition. We prove the existence and uniqueness of weak solutions, using energy inequality and the density of the range of the operator generated by the problem.

Paper's Title:

Kinematic Model for Magnetic Null-points in 2 Dimensions

Author(s):

Ali Khalaf Hussain Al-Hachami

Department of Mathematics,
College of Education For Pure Sciences,
Wasit University,
Iraq.
E-mail: alhachamia@uowasit.edu.iq

Abstract:

The adjacent configurations of two-dimensional magnetic null point centers are analyzed by an immediate examination about the null. The configurations are classified as either potential or non-potential. By then the non-potential cases are subdivided into three cases depending upon whether the component of current is less than, equal to or greater than a threshold current. In addition the essential structure of reconnection in 2D is examined. It unfolds that the manner by which the magnetic flux is rebuilt. In this paper, we center on the ramifications of kinematic arrangements; that is, we fathom just Maxwell's conditions and a resistive Ohm's law.

Paper's Title:

Generalised Models for Torsional Spine Reconnection

Author(s):

Ali Khalaf Hussain Al-Hachami

Department of Mathematics,
College of Education For Pure Sciences,
Wasit University,
Iraq.
E-mail: alhachamia@uowasit.edu.iq

Abstract:

Three-dimensional (3D) null points are available in wealth in the solar corona, and the equivalent is probably going to be valid in other astrophysical situations. On-going outcomes from sun oriented perceptions and from reproductions propose that reconnection at such 3D nulls may assume a significant job in the coronal dynamics. The properties of the torsional spine method of magnetic reconnection at 3D nulls are researched. Kinematic model are created, which incorporate the term ηJ that is spatially localised around the null, stretching out along the spine of the null. The null point is to research the impact of shifting the level of asymmetry of the null point magnetic field on the subsequent reconnection process where past examinations constantly considered a non-nonexclusive radially symmetric null. Specifically we analyse the rate of reconnection of magnetic flux at the spine of null point. Logical arrangements are determined for the enduring kinematic equation, and contrasted and the after effects of torsional spine reconnection models when the current is restricted in which the Maxwell conditions are illuminated. The geometry of the current layers inside which torsional spine reconnection happen is autonomous on the symmetry of the magnetic field. Torsional spine reconnection happens in a thin cylinder around the spine, with circular cross-segment when the fan eigenvalues are extraordinary. The short axis of the circle being along the solid field bearing. Just as it was discovered that the fundamental structure of the method of attractive reconnection considered is unaffected by changing the magnetic field symmetry, that is, the plasma flow is discovered rotational around the spine of null point. The spatiotemporal pinnacle current, and the pinnacle reconnection rate achieved, are found not to rely upon the level of asymmetry.

Paper's Title:

Fractional exp(-φ(ξ))- Expansion Method and its Application to Space--Time Nonlinear Fractional Equations

Author(s):

A. A. Moussa and L. A. Alhakim

Department of Management Information System and Production Management,
College of Business and Economics, Qassim University,
P.O. BOX 6666, Buraidah: 51452,
Saudi Arabia.
E-mail: Alaamath81@gmail.com
URL: https://scholar.google.com/citations?user=ccztZdsAAAAJ&hl=ar

Department of Management Information System and Production Management,
College of Business and Economics, Qassim University,
P.O. BOX 6666, Buraidah: 51452,
Saudi Arabia.
E-mail: Lama2736@gmail.com
URL: https://scholar.google.com/citations?user=OSiSh1AAAAAJ&hl=ar

Abstract:

In this paper, we mainly suggest a new method that depends on the fractional derivative proposed by Katugampola for solving nonlinear fractional partial differential equations. Using this method, we obtained numerous useful and surprising solutions for the space--time fractional nonlinear Whitham--Broer--Kaup equations and space--time fractional generalized nonlinear Hirota--Satsuma coupled KdV equations. The solutions obtained varied between hyperbolic, trigonometric, and rational functions, and we hope those interested in the real-life applications of the previous two equations will find this approach useful.

Paper's Title:

Application of Chebyshev Polynomials to Volterra-Fredholm Integral Equations

Author(s):

Aissa Lakhal, Mostefa Nadir and Mohamed Nasseh Nadir

Department of Mathematics,
Faculty of Mathematics and
Informatics,
University of Msila,
Algeria.

E-mail: aissa.lakhal@univ-msila.dz
mostefa.nadir@univ-msila.dz
nadir.mohamednasseh@yahoo.com

URL: https://www.mostefanadir.com

Abstract:

The goal of this work is to examine the numerical solution of linear Volterra-Fredholm integral equations of the second kind using the first, second, third and fourth Chebyshev polynomials. Noting that, the approximate solution is given in the form of series which converges to the exact one. Numerical examples are compared with other methods, in order to prove the applicability and the efficiency of this technical.

Paper's Title:

Fractional Integral Inequalities of Hermite-Hadamard Type for P-convex and Quasi-Convex Stochastic Process

Author(s):

Oualid Rholam, Mohammed Barmaki and Driss Gretet

National School of Applied Sciences (ENSA),
University Ibn Tofail,
B.P 242 Kenitra 14000,
phone number : +212606257757,
Morocco.
E-mail: oualid.rholam@uit.ac.ma

 
Science Faculty Ben M'sik,
University Hassan II,
B.P 7955 Av Driss El Harti Sidi Othmane 20700,
phone number : +212 5 22 70 46 71 ,
Morocco.
E-mail:  mohammed.barmaki@uit.ac.ma

National School of Applied Sciences (ENSA),
University Ibn Tofail,
B.P 242 Kenitra 14000,
phone number : +212661403557,
Morocco.
E-mail: driss.gretete@uit.ac.ma 

Abstract:

In this paper we consider the class of P-convex and Quasi-convex stochastic processes on witch we apply a general class of generalized fractional integral operator in order to establish new integral inequalities of Hermite-Hadammard type. then we obtain some results for well known types of fractional integrals. Results obtained in this paper may be starting point as well as a useful source of inspiration for further research in convex analysis.

Paper's Title:

New Reverses of Schwarz, Triangle and Bessel Inequalities in Inner Product Spaces

Author(s):

S. S. Dragomir

Abstract:

New reverses of the Schwarz, triangle and Bessel inequalities in inner product spaces are pointed out. These results complement the recent ones obtained by the author in the earlier paper [13]. Further, they are employed to establish new Grüss type inequalities. Finally, some natural integral inequalities are stated as well.

Paper's Title:

Generalized Fuglede-Putnam Theorem and Orthogonality

Author(s):

A. Bachir and A. Sagres

Department of Mathematics, Faculty of Science, King Khaled University, Abha, P.O. Box 9004 Kingdom Saudi Arabia
bachir_ahmed@hotmail.com
sagres@hotmail.com

Abstract:

An asymmetric Fuglede-Putnam’s theorem for dominant operators and p-hyponormal operators is proved, as a consequence of this result, we obtain that the range of the generalized derivation induced by the above classes of operators is orthogonal to its kernel.

Paper's Title:

Reverses of the Triangle Inequality in Inner Product Spaces

Author(s):

Sever S. Dragomir

School of Computer Science and Mathematics,
Victoria University Of Technology,
PO Box 14428, Mcmc 8001,
Victoria, Australia.
sever@csm.vu.edu.au
Url: http://rgmia.vu.edu.au/SSDragomirWeb.html

Abstract:

Some new reverses for the generalised triangle inequality in inner product spaces are given. Applications in connection to the Schwarz inequality and for vector-valued integrals are provided as well.

Paper's Title:

Boundary Value Problems for Fractional Diffusion-Wave equation

Author(s):

Varsha Daftardar-Gejji and Hossein Jafari

Department of Mathematics, University of Pune,
Ganeshkhind, Pune - 411007,
INDIA.
vsgejji@math.unipune.ernet.in
jafari_h@math.com

Abstract:

Non homogeneous fractional diffusion-wave equation has been solved under linear/nonlinear boundary conditions. As the order of time derivative changes from 0 to 2, the process changes from slow diffusion to classical diffusion to mixed diffusion-wave behaviour.
Numerical examples presented here confirm this inference. Orthogonality of eigenfunctions in case of fractional Stürm-Liouville problem has been established

Paper's Title:

A Reverse of the Triangle Inequality in Inner Product Spaces and Applications for Polynomials

Author(s):

I. Brnetić, S. S. Dragomir, R. Hoxha and J. Pečarić

Department of Applied Mathematics, Faculty of Electrical Engineering and Computing,
University of Zagreb, Unska 3, 10 000 Zagreb,
Croatia
andrea@zpm.fer.hr

School of Computer Science & Mathematics, Victoria University
Po Box 14428, Melbourne Vic 8001
Australia
sever.dragomir@vu.edu.au
URL:http://rgmia.vu.edu.au/dragomir

Faculty of Applied Technical Sciences, University of Prishtina,
Mother Theresa 5, 38 000 Prishtina
Kosova
razimhoxha@yahoo.com

Faculty of Textile Technology, University of Zagreb,
Pierottijeva 6, 10000 Zagreb,
Croatia
pecaric@hazu.hr

Abstract:

A reverse of the triangle inequality in inner product spaces related to the celebrated Diaz-Metcalf inequality with applications for complex polynomials is given.

Paper's Title:

On Vector Variational Inequality Problem in Terms of Bifunctions

Author(s):

C. S. Lalitha and Monika Mehta

Department of Mathematics, Rajdhani College,
University of Delhi, Raja Garden,
Delhi 110015, India
cslalitha@rediffmail.com

Department of Mathematics, Satyawati College,
University Of Delhi, Ashok Vihar,
Phase-III, Delhi 110052, India
mridul_in@yahoo.com

Abstract:

In this paper, we consider a generalized vector variational inequality problem expressed in terms of a bifunction and establish existence theorems for this problem by using the concepts of cone convexity and cone strong quasiconvexity and employing the celebrated Fan's Lemma. We also give two types of gap functions for this problem.

Paper's Title:

Salagean-type Harmonic Univalent Functions with Respect to Symmetric Points

Author(s):

R. A. Al-Khal and H. A. Al-Kharsani

Department of Mathematics, Faculty of Science, Girls College,
P.O. Box 838,
Dammam, Saudi Arabia
ranaab@hotmail.com
hakh@hotmail.com

Abstract:

A necessary and sufficient coefficient are given for functions in a class of complex-valued harmonic univalent functions of the form f=h+\g using Salagean operator where h and g are analytic in the unit disk U = {z:|z|<1}. Furthermore, distortion theorems, extreme points, convolution condition, and convex combinations for this family of harmonic functions are obtained.

Paper's Title:

A-Normal Operators In Semi Hilbertian Spaces

Author(s):

A. Saddi

Department of Mathematics,
College of Education for Girls in Sarat Ebeidah 61914, Abha,
King Khalid University
Saudi Arabia
adel.saddi@fsg.rnu.tn
 

Abstract:

In this paper we study some properties and inequalities of A-normal operators in semi-Hilbertian spaces by employing some known results for vectors in inner product spaces. We generalize also most of the inequalities of (α,β)-normal operators discussed in Hilbert spaces [7].

Paper's Title:

Existence and Regularity of Minima of an Integral Functional in Unbounded Domain

Author(s):

L. Aharouch, J. Bennouna and A. Bouajaja

King Khalid University
Faculty of Arts and Science Mha'l Asir
Saudi Arabia.

E-mail: laharouch@gmail.com

Université Sidi Mohammed Ben Abdellah
Faculté des Sciences Dhar-Mahraz
B.P 1796 Atlas Fès,
Maroc.

Email: jbennouna@hotmail.com

E-mail: kadabouajaja@hotmail.com

Abstract:

We prove the existence and the regularity of minima for a functional defined on a suitable Sobolev space.

Paper's Title:

Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.

Paper's Title:

Coexisting Attractors and Bubbling Route to Chaos in Modified Coupled Duffing Oscillators

Author(s):

B. Deruni¹, A. S. Hacinliyan^1,2, E. Kandiran³, A. C. Keles², S. Kaouache⁴, M.-S. Abdelouahab⁴, N.-E. Hamri⁴

¹Department of Physics,
University of Yeditepe,
Turkey.

²Department of Information Systems and Technologies,
University of Yeditepe,
Turkey

³Department of Software Development,
University of Yeditepe,
Turkey.

⁴Laboratory of Mathematics and their interactions,
University Center of Abdelhafid Boussouf,
Mila 43000,
Algeria.

E-mail: berc890@gmail.com
ahacinliyan@yeditepe.edu.tr
engin.kandiran@yeditepe.edu.tr
cihan.keles@yeditepe.edu.tr
s.kaouache@centr-univ-mila.dz
medsalah3@yahoo.fr
n.hamri@centre-univ-mila.dz

Abstract:

In this article dynamical behavior of coupled Duffing oscillators is analyzed under a small modification. The oscillators have cubic damping instead of linear one. Although single duffing oscillator has complex dynamics, coupled duffing systems possess a much more complex structure. The dynamical behavior of the system is investigated both numerically and analytically. Numerical results indicate that the system has double scroll attractor with suitable parameter values. On the other hand, bifurcation diagrams illustrate rich behavior of the system, and it is seen that, system enters into chaos with different routes. Beside classical bifurcations, bubbling route to chaos is observed for suitable parameter settings. On the other hand, Multistability of the system is indicated with the coexisting attractors, such that under same parameter setting the system shows different periodic and chaotic attractors. Moreover, chaotic synchronization of coupled oscillators is illustrated in final section.

Paper's Title:

Additive Mappings on Semiprime Rings Functioning as Centralizers

Author(s):

Abu Zaid Ansari and Faiza Shujat

Department of Mathematics,
Faculty of Science,
Islamic University of Madinah, Madinah
K.S.A.
E-mail: ansari.abuzaid@gmail.com, ansari.abuzaid@iu.edu.sa

Department of Mathematics,
Faculty of Science,
Taibah University, Madinah,
K.S.A.
E-mail: faiza.shujat@gmail.com, fullahkhan@taibahu.edu.sa

Abstract:

The objective of this research is to prove that an additive mapping T:R → R is a centralizer on R if it satisfies any one of the following identities:

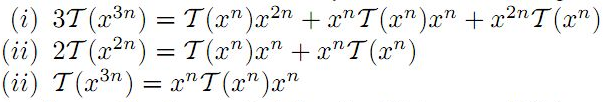
for all x ∈ R, where n ≥ 1 is a fixed integer and R is any suitably torsion free semiprime ring. Some results on involution "*" are also presented as consequences of the main theorems. In addition, we will take criticism in account with examples.

Search and serve lasted 0 second(s).