|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Power and Euler-Lagrange Norms
Author(s):
Mohammad Sal Moslehian and John Michael Rassias
Department of Mathematics,
Ferdowsi University,
P. O. Box 1159, Mashhad 91775,
Iran;
Department of Pure Mathematics,
University of Leeds,
Leeds LS2 9JT,
United Kingdom.
moslehian@ferdowsi.um.ac.ir
URL: http://www.um.ac.ir/~moslehian/
Pedagogical Department, E.E., Section of Mathematics and Informatics
National and Capodistrian University of Athens,
4, Agamemnonos str., Aghia Paraskevi, Attikis 15342, Athens,
Greece.
jrassias@primedu.uoa.gr
URL: http://www.primedu.uoa.gr/~jrassias/
Abstract:
We introduce the notions of power and Euler-Lagrange norms by
replacing the triangle inequality, in the definition of norm, by
appropriate inequalities. We prove that every usual norm is a power
norm and vice versa. We also show that every norm is an
Euler-Lagrange norm and that the converse is true under certain
condition.
Paper's Title:
q-Norms are Really Norms
Author(s):
H. Belbachir, M. Mirzavaziri and M. S. Moslehian
USTHB, Faculté de Mathématiques,
B.P. 32, El Alia, 16111,
Bab Ezzouar, Alger,
Algérie.
hbelbachir@usthb.dz
Department of Mathematics,
Ferdowsi University, P. O. Box 1159,
Mashhad 91775, Iran.
mirzavaziri@math.um.ac.ir
URL: http://www.mirzavaziri.com
Department of Mathematics,
Ferdowsi University,
P. O. Box 1159,
Mashhad 91775, Iran.
moslehian@ferdowsi.um.ac.ir
URL: http://www.um.ac.ir/~moslehian/
Abstract:
Replacing the triangle inequality, in the definition of a
norm, by ![]() , we introduce the notion of a q-norm. We establish that
every q-norm is a norm in the usual sense, and that the converse is true as
well.
, we introduce the notion of a q-norm. We establish that
every q-norm is a norm in the usual sense, and that the converse is true as
well.
Paper's Title:
Differentiability of
Distance Functions in p-Normed Spaces
Author(s):
M. S. Moslehian, A. Niknam, S. Shadkam Torbati
Department of Pure Mathematics,
Centre of Excellence in Analysis on Algebraic Structures (CEAAS),,
Ferdowsi University of Mashhad,
P. O. Box
1159, Mashhad,
Iran
moslehian@ferdowsi.um.ac.ir
niknam@math.um.ac.ir
shadkam.s@wali.um.ac.ir
Abstract:
The farthest point mapping in a p-normed space X is studied in virtue of the Gateaux derivative and the Frechet derivative. Let M be a closed bounded subset of X having the uniformly p-Gateaux differentiable norm. Under certain conditions, it is shown that every maximizing sequence is convergent, moreover, if M is a uniquely remotal set then the farthest point mapping is continuous and so M is singleton. In addition, a Hahn--Banach type theorem in $p$-normed spaces is proved.
Paper's Title:
Trace Inequalities for Operators in Hilbert Spaces: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
School of Engineering
& Science
Victoria University,
PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
In this paper we survey some recent trace inequalities for operators in Hilbert spaces that are connected to Schwarz's, Buzano's and Kato's inequalities and the reverses of Schwarz inequality known in the literature as Cassels' inequality and Shisha-Mond's inequality. Applications for some functionals that are naturally associated to some of these inequalities and for functions of operators defined by power series are given. Further, various trace inequalities for convex functions are presented including refinements of Jensen inequality and several reverses of Jensen's inequality. Hermite-Hadamard type inequalities and the trace version of Slater's inequality are given. Some Lipschitz type inequalities are also surveyed. Examples for fundamental functions such as the power, logarithmic, resolvent and exponential functions are provided as well.
Paper's Title:
Stability of a Pexiderized Equation
Author(s):
Maryam Amyar
Department of Mathematics,
Islamic Azad University, Rahnamaei Ave,
Mashhad 91735, Iran,
and Banach Mathematical Research Group (BMRG)
amyari@mshdiau.ac.ir
URL: http://amyari.mshdiau.ac.ir
Abstract:
The aim of the paper is to prove the
stability of the Pexiderized equation f(x)=g(y+x)-h(y-x), for any
amenable abelian group.
Paper's Title:
A Reverse
of the Triangle Inequality in Inner Product Spaces and Applications for
Polynomials
Author(s):
I. Brnetić, S. S. Dragomir, R. Hoxha and J. Pečarić
Department of Applied Mathematics, Faculty of Electrical
Engineering and Computing,
University of Zagreb, Unska 3, 10 000 Zagreb,
Croatia
andrea@zpm.fer.hr
School of Computer Science & Mathematics, Victoria University
Po Box 14428, Melbourne Vic 8001
Australia
sever.dragomir@vu.edu.au
URL:http://rgmia.vu.edu.au/dragomir
Faculty of Applied Technical Sciences, University of Prishtina,
Mother
Theresa 5, 38 000 Prishtina
Kosova
razimhoxha@yahoo.com
Faculty of Textile Technology, University of Zagreb,
Pierottijeva 6, 10000
Zagreb,
Croatia
pecaric@hazu.hr
Abstract:
A reverse of the triangle inequality in inner product spaces related to the
celebrated Diaz-Metcalf inequality with applications for complex polynomials
is given.
Paper's Title:
On Stan Ulam and his Mathematics
Author(s):
Krzysztof Ciesielski and Themistocles M. Rassias
Mathematics Institute, Jagiellonian University,
Abstract:
In this note we give a glimpse of the curriculum vitae of Stan Ulam, his personality and some of the mathematics he was involved in.
Paper's Title:
Applications of Relations and Relators in the
Extensions of Stability Theorems for Homogeneous and Additive Functions
Author(s):
Árpád Száz
Institute of Mathematics, University of Debrecen,
H-4010 Debrecen,
Pf. 12,
Hungary
szaz@math.klte.hu
Abstract:
By working out an appropriate technique of relations and relators and extending the ideas of the direct methods of Z. Gajda and R. Ger, we prove some generalizations of the stability theorems of D. H. Hyers, T. Aoki, Th. M. Rassias and P. Găvruţă in terms of the existence and unicity of 2-homogeneous and additive approximate selections of generalized subadditive relations of semigroups to vector relator spaces. Thus, we obtain generalizations not only of the selection theorems of Z. Gajda and R. Ger, but also those of the present author.
Paper's Title:
Approximation of an AQCQ-Functional Equation and its Applications
Author(s):
Choonkil Park and Jung Rye Lee
Department of Mathematics,
Research Institute for Natural Sciences,
Hanyang University, Seoul 133-791,
Korea;
Department of Mathematics,
Daejin University,
Kyeonggi 487-711,
Korea
baak@hanyang.ac.kr
jrlee@daejin.ac.kr
Abstract:
This paper is a survey on the generalized Hyers-Ulam stability of an AQCQ-functional equation in several spaces. Its content is divided into the following sections:
1. Introduction and preliminaries.
2. Generalized Hyers-Ulam stability of an AQCQ-functional equation in Banach spaces: direct method.
3. Generalized Hyers-Ulam stability of an AQCQ-functional equation in Banach spaces: fixed point method.
4. Generalized Hyers-Ulam stability of an AQCQ-functional equation in random Banach spaces: direct method.
5. Generalized Hyers-Ulam stability of an AQCQ-functional equation in random Banach spaces: fixed point method.
6. Generalized Hyers-Ulam stability of an AQCQ-functional equation in non-Archi-medean Banach spaces: direct method.
7. Generalized Hyers-Ulam stability of an AQCQ-functional equation in non-Archi-medean Banach spaces: fixed point method.
Paper's Title:
On Commutator of Aluthge Transforms and Fuglede-Putnam Property
Author(s):
(Manzar Maleki, Ali Reza Janfada and Seyed Mohammad Sadegh Nabavi Sales
International Campus, Faculty of
Mathematical Sciences,
Ferdowsi University of Mashhad, Mashhad,
Iran.
E-mail: manzar.maleki@gmail.com
Faculty of Mathematics and Statistics,
Department of Mathematics,
University of Birjand,
P. O. Box 414, Birjand 9717851367,
Iran.
E-mail: ajanfada@birjand.ac.ir
Department of Pure Mathematics, Hakim
Sabzevari University,
P.O. Box 397, Sabzevar,
Iran.
E-mail: sadegh.nabavi@hsu.ac.ir
Abstract:
We deal with the well-known Fuglede-Putnam theorem and related FP-property. We show that if
(A,B) has the FP-property, then so has
![]() where 0≤
t1,t2≤1 are arbitrary.
We first prove that
where 0≤
t1,t2≤1 are arbitrary.
We first prove that
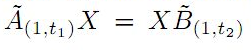 if and only if
AX=XB for all X, whenever (A,B) has the FP-property. We
prove some similar results for
if and only if
AX=XB for all X, whenever (A,B) has the FP-property. We
prove some similar results for
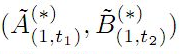 instead of $
instead of $![]() as well. Also we introduce the sequence of generalized iterations of Aluthge transform of operators and express some results for this notion associated to the FP-property.
as well. Also we introduce the sequence of generalized iterations of Aluthge transform of operators and express some results for this notion associated to the FP-property.
Paper's Title:
Using Direct and Fixed Point Technique of Cubic Functional Equation and its Hyers-Ulam Stability
Author(s):
Ramanuja Rao Kotti, Rajnesh Krishnan Mudaliar, Kaushal Neelam Devi, Shailendra Vikash Narayan
Fiji National University,
Department of Mathematics & Statistics,
P.O. Box 5529, Lautoka,
Fiji.
E-mail: ramanuja.kotti@fnu.ac.fj
URL: https://www.fnu.ac.fj
Abstract:
In this present work, we introduce a new type of finite dimensional cubic functional equation of the form

where Φ≥4 is an integer, and derive its general solution. The main purpose of this work is to investigate the Hyers-Ulam stability results for the above mentioned functional equation in Fuzzy Banach spaces by means of direct and fixed point methods.
Paper's Title:
Some New Inequalities for Hypo-q-Norms on a Cartesian Product of Normed Linear Spaces
Author(s):
Sever S. Dragomir1,2
1Applied
Mathematics Research Group, ISILC,
Victoria University,
PO Box 14428, Melbourne City, MC 8001,
Australia.
E-mail: sever.dragomir@vu.edu.au
URL:
http://rgmia.org/dragomir
2School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
Abstract:
Let ( E,|| · ||) be a normed
linear space over the real or complex number field K. If by
Sn,p with p∈[ 1,∞]
we denote the spheres generated by the $p$-norms ||
· ||n,p on Kn, then we consider
the following hypo-q-norms on
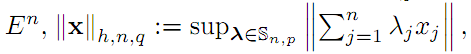 with q>1 and
with q>1 and
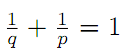 if p>1, q=1 if
p=∞
and q=∞ if p=1. For p=2, we also consider the hypo-Euclidean norm on En, i.e.,
if p>1, q=1 if
p=∞
and q=∞ if p=1. For p=2, we also consider the hypo-Euclidean norm on En, i.e.,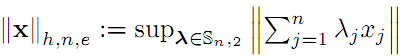
In this paper we have obtained among others the following inequalities
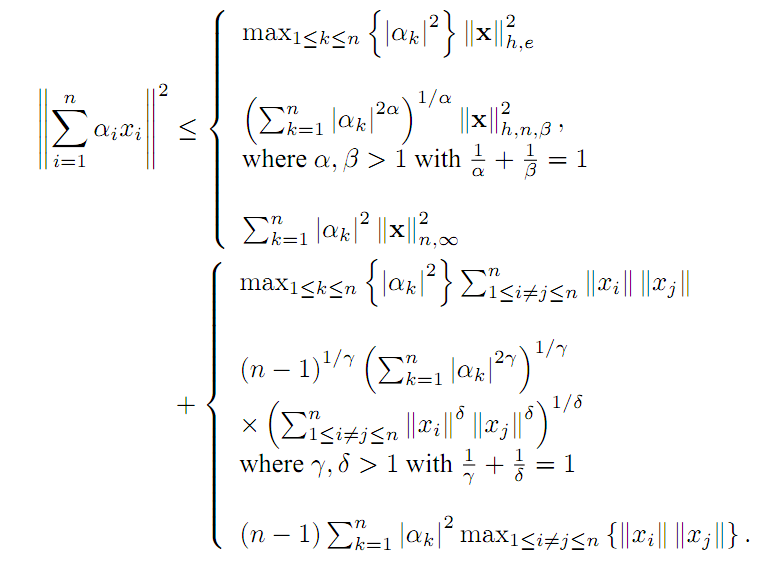
The case for n=2 and the connection with the following new norms
![]() and
and
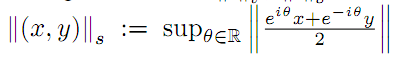
are also investigated. When the norm || · || is generated by an inner product, further bounds are given as well.
Paper's Title:
On Pseudo Almost
Periodic Solutions to Some Neutral Functional-Differential
Equations
Author(s):
Toka Diagana and Eduardo Hernández
Department of Mathematics, Howard University
2441 6th Street NW,
Washington DC 20059,
USA.
tdiagana@howard.edu
Departamento de Matemática, I.C.M.C. Universidade de São Paulo,
Caixa Postal
668, 13560-970, São Carlos SP,
Brazil.
lalohm@icmc.sc.usp.br
Abstract:
This paper discusses the existence and uniqueness of pseudo almost periodic solutions to a class of partial neutral functional-differential equations. Under some suitable assumptions, existence and uniqueness results are obtained. An example is given to illustrate abstract results.
Paper's Title:
On a Method of Proving the Hyers-Ulam Stability
of Functional Equations on Restricted Domains
Author(s):
Janusz Brzdęk
Department of Mathematics
Pedagogical University Podchor
Abstract:
We show that generalizations of some (classical) results on the Hyers-Ulam stability of functional equations, in several variables, can be very easily derived from a simple result on stability of a functional equation in single variable
Paper's Title:
A Fixed Point Approach to
the Stability of the Equation
![]()
Author(s):
Soon-Mo Jung
Mathematics Section, College of Science and Technology
Hong-Ik
University, 339-701 Chochiwon
Republic of Korea.
smjung@hongik.ac.kr
Abstract:
We will apply a fixed point method for proving the Hyers--Ulam stability of
the functional equation
![]() .
.
Paper's Title:
Fixed Points and Stability
of the Cauchy Functional Equation
Author(s):
Choonkil Park and Themistocles M. Rassias
Department of Mathematics, Hanyang University,
Seoul 133-791,
Republic of Korea
Department of Mathematics,
National Technical University of Athens,
Zografou Campus, 15780 Athens,
Greece
baak@hanyang.ac.kr
trassias@math.ntua.gr
Abstract:
Using fixed point methods, we prove the generalized Hyers-Ulam stability of homomorphisms in Banach algebras and of derivations on Banach algebras for the Cauchy functional equation.
Paper's Title:
Hyperbolic Barycentric Coordinates
Author(s):
Abraham A. Ungar
Department of Mathematics, North Dakota State University,
Fargo, ND 58105,
USA
Abraham.Ungar@ndsu.edu
URL: http://math.ndsu.nodak.edu/faculty/ungar/
Abstract:
A powerful and novel way to study Einstein's special theory of relativity and its underlying geometry, the hyperbolic geometry of Bolyai and Lobachevsky, by analogies with classical mechanics and its underlying Euclidean geometry is demonstrated. The demonstration sets the stage for the extension of the notion of barycentric coordinates in Euclidean geometry, first conceived by Möbius in 1827, into hyperbolic geometry. As an example for the application of hyperbolic barycentric coordinates, the hyperbolic midpoint of any hyperbolic segment, and the centroid and orthocenter of any hyperbolic triangle are determined.
Paper's Title:
Hyers-Ulam-Rassias Stability
of a Generalized Jensen Functional Equation
Author(s):
A. Charifi, B. Bouikhalene, E. Elqorachi and A. Redouani
Department of
Mathematics, Faculty of Sciences,
Ibn Tofail University,
Kenitra, Morocco
charifi2000@yahoo.fr
bbouikhalene@yahoo.fr
Department of
Mathematics, Faculty of Sciences,
Ibn Zohr University,
Agadir, Morocco
elqorachi@hotmail.com
Redouani-ahmed@yahoo.fr
Abstract:
In this paper we obtain the Hyers-Ulam-Rassias stability for the generalized Jensen's functional equation in abelian group (G,+). Furthermore we discuss the case where G is amenable and we give a note on the Hyers-Ulam-stability of the K-spherical (n × n)-matrix functional equation.
Paper's Title:
A-Normal Operators In Semi Hilbertian Spaces
Author(s):
A. Saddi
Department of Mathematics,
College of Education for Girls in Sarat Ebeidah 61914, Abha,
King Khalid University
Saudi Arabia
adel.saddi@fsg.rnu.tn
Abstract:
In this paper we study some properties and inequalities of A-normal operators in semi-Hilbertian spaces by employing some known results for vectors in inner product spaces. We generalize also most of the inequalities of (α,β)-normal operators discussed in Hilbert spaces [7].
Paper's Title:
C*-valued metric projection and Moore-Penrose inverse on Hilbert C*-modules
Author(s):
M. Eshaghi Gordji, H. Fathi and S.A.R. Hosseinioun
Department of Mathematics,
Semnan University, P.O. Box 35195-363, Semnan,
Iran.
Center of Excellence in Nonlinear Analysis and Applications (CENAA),
Semnan University,
Iran.
E-mail: Madjid.Eshaghi@gmail.com
Department of Mathematics,
Shahid Beheshti University, Tehran,
Iran.
E-mail: Hedayat.fathi@yahoo.com
Department of Mathematical Sciences,
University of Arkansas, Fayetteville, Arkansas 72701,
USA.
E-mail: shossein@uark.net
Abstract:
Let t be a regular operator between Hilbert C*-modules and t be its Moore-Penrose inverse. We give some characterizations for t based on C*-valued metric projection. Moore-Penrose inverse of bounded operators and elements of a C*-algebra is studied as a special case.
Paper's Title:
On the Hyers-Ulam Stability of Homomorphisms and Lie Derivations
Author(s):
Javad Izadi and Bahmann Yousefi
Department of Mathematics, Payame Noor
University,
P.O. Box: 19395-3697, Tehran,
Iran.
E-mail: javadie2003@yahoo.com,
b_yousefi@pnu.ac.ir
Abstract:
Let A be a Lie Banach*-algebra. For each elements (a, b) and (c, d) in A2:= A * A, by definitions
(a, b) (c, d)= (ac, bd),
|(a, b)|= |a|+ |b|,
(a, b)*= (a*, b*),
A2 can be considered as a Banach*-algebra. This Banach*-algebra is called a Lie Banach*-algebra whenever it is equipped with the following definitions of Lie product:
for all a, b, c, d in A. Also, if A is a Lie Banach*-algebra, then D: A2→A2 satisfying
D ([ (a, b), (c, d)])= [ D (a, b), (c, d)]+ [(a, b), D (c, d)]
for all $a, b, c, d∈A, is a Lie derivation on A2. Furthermore, if A is a Lie Banach*-algebra, then D is called a Lie* derivation on A2 whenever D is a Lie derivation with D (a, b)*= D (a*, b*) for all a, b∈A. In this paper, we investigate the Hyers-Ulam stability of Lie Banach*-algebra homomorphisms and Lie* derivations on the Banach*-algebra A2.
Paper's Title:
Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.
Paper's Title:
The Automatic Continuity of N-Homomorphisms in Certain *-Banach Algebras
Author(s):
M. Aboulekhlef, Y. Tidli
Laboratory of Applied Mathematics and
Information and Communication Technology
Polydisciplinary Faculty of Khouribga
University of Sultan Moulay Slimane
Morocco.
E-mail: aboulekhlef@gmail.com
y.tidli@gmail.com
Abstract:
In this study, we prove the automatic continuity of surjective n-homomorphism between complete p-normed algebras. We show also that if Α and Β are complete *-p-normed algebras, Β is *simple and ψ: Α → Β is a surjective n-homomorphism under certain conditions, then ψ is continuous.
Paper's Title:
The Drazin-star and Star-Drazin Solutions to Quaternion Matrix Equations
Author(s):
Ivan I. Kyrchei, Dijana Mosić, Predrag Stanimirović
Pidstryhach Institute for Applied Problems
of Mechanics and Mathematics
of NAS of Ukraine, L'viv, 79060,
Ukraine.
E-mail:
ivankyrchei26@gmail.com
Faculty of Sciences and Mathematics,
University of Ni, P.O.
Box 224, 18000, Ni, Serbia.
E-mail: dijana@pmf.ni.ac.rs
Faculty of Sciences and Mathematics,
University of Ni, P.O.
Box 224, 18000, Ni, Serbia.
E-mail: pecko@pmf.ni.ac.rs
Abstract:
The notions of the Drazin-star and star-Drazin matrices are expanded to quaternion matrices in this paper. Their determinantal representations are developed in both cases in terms of noncommutative row-column determinants of quaternion matrices and for minors of appropriate complex matrices. We study all possible two-sided quaternion matrix equations with their one-sided partial cases whose uniquely determined solutions are based on the Drazin-star and star-Drazin matrices. Solutions of these equations are represented by Cramer's rules in both cases for quaternion and complex matrix equations. A numerical example is presented to illustrate our results.
Search and serve lasted 1 second(s).