|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
On Vector Variational Inequality Problem in Terms of Bifunctions
Author(s):
C. S. Lalitha and Monika Mehta
Department of Mathematics, Rajdhani College,
Department of Mathematics, Satyawati College,
University of Delhi, Raja Garden,
Delhi 110015, India
cslalitha@rediffmail.com
University Of Delhi, Ashok Vihar,
Phase-III, Delhi 110052, India
mridul_in@yahoo.com
Abstract:
In this paper, we consider a generalized vector variational
inequality problem expressed in terms of a bifunction and establish
existence theorems for this problem by using the concepts of cone
convexity and cone strong quasiconvexity and employing the
celebrated Fan's Lemma. We also give two types of gap functions for this problem.
Paper's Title:
The Iterated Variational Method for the Eigenelements of a Class of Two-Point Boundary Value Problems
Author(s):
Muhammed I. Syam and Qasem M. Al-Mdallal
Department of Mathematical Sciences, College of Science, UAE University,
P. O. Box 17551, Al-Ain,
United Arab Emirates
Q.Almdallal@uaeu.ac.ae
M.Syam@uaeu.ac.ae
Abstract:
The iterated variational method is considered in the approximation
of eigenvalues and eigenfunctions for a class of two point boundary
value problems. The implementation of this method is easy and
competes well with other methods. Numerical examples are presented
to show the efficiency of the method proposed. Comparison with the
work of others is also illustrated.
Paper's Title:
Preserver of Local Spectrum of Skew-product Operators
Author(s):
Rohollah Parvinianzadeh1,*, Meysam Asadipour2 and Jumakhan Pazhman3
1Department
of Mathematics,
College of Sciences,
University of Yasouj,
Yasouj, 75918-74934,
Iran.
E-mail: r.parvinian@yu.ac.ir
2Department
of Mathematics,
College of Sciences,
University of Yasouj,
Yasouj, 75918-74934,
Iran.
E-mail: Asadipour@yu.ac.ir
3Department
of Mathematics,
Ghor Institute of higher education,
Afghanistan.
E-mail: jumapazhman@gmail.com
Abstract:
Let H and K be infinite-dimensional complex Hilbert spaces, and B(H) (resp. B(K)) be the algebra of all bounded linear operators on H (resp. on K). For an operator T∈ B(H) and a vector h∈ H, let σT(h) denote the local spectrum of T at h. For two nonzero vectors h0∈ H and k0∈ K, we show that if two maps φ1 and φ2 from B(H) into B(K) satisfy
σφ1(T)φ2(S)*(k0)= σTS*(h0})
for all T, S ∈ B(H), and their range containing all operators of rank at most two, then there exist bijective linear maps P : H→ K and Q : K→ H such that φ1(T) = PTQ and φ2(T)* =Q-1T*P-1 for all T ∈ B(H). Also, we obtain some interesting results in this direction.
Paper's Title:
On the Class of Totally Polynomially Posinormal Operators
Author(s):
E. Shine Lal, T. Prasad, P. Ramya
Department of Mathematics,University
College,
Thiruvananthapuram, Kerala, 695034.
India.
E-mail: shinelal.e@gmail.com
Department of Mathematics,
University of Calicut,
Malapuram, Kerala 673635,
India.
E-mail: prasadvalapil@gmail.com
Department of Mathematics,
N.S.S College,
Nemmara, Kerala, 678508
India.
E-mail: ramyagcc@gmail.com
Abstract:
In this paper, we proved that if T ∈
B(H) is totally P-posinormal operator with
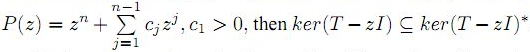. Moreover, we study spectral continuity and range kernel orthogonality of these class of operators.
Paper's Title:
Complete Analysis of Global Behavior of Certain System of Piecewise Linear Difference Equations
Author(s):
Atiratch Laoharenoo, Ratinan Boonklurb and Watcharapol Rewlirdsirikul
Department of Mathematics and Computer
Science,
Kamnoetvidya Science Academy, Rayong 21210
Thailand.
E-mail: atiratch.l@kvis.ac.th
Department of Mathematics and Computer Science,
Faculty of Science, Chulalongkorn University, Bangkok 10330
Thailand.
E-mail: ratinan.b@chula.ac.th
Department of Mathematics and Computer
Science,
Faculty of Science, Chulalongkorn University, Bangkok 10330
Thailand.
E-mail:
6570104323@student.chula.ac.th
Abstract:
Our goal is to study the system of piecewise linear difference equations x{n+1} = |xn|-yn-b and y{n+1} = xn - |yn| + 1 where n ≥ 0 and b ≥ 6. We can prove that the behavior of the solution can be divided into 2 types depending on the region of initial condition (x0,y0). That is, the solution eventually becomes the equilibrium point. Otherwise, the solution eventually becomes the periodic solution of prime period 5. All regions of initial condition for each type of solution are determined.
Paper's Title:
An Algorithm to Compute Gaussian-Type Quadrature Formulae
that Integrate Polynomials and Some Spline Functions Exactly
Author(s):
Allal Guessab
Laboratoire de Mathématiques Appliquées,
Université de Pau, 64000, Pau,
France.
allal.guessab@univ-pau.fr
URL: http://www.univ-pau.fr/~aguessab/
Abstract:
It is well-known that for sufficiently smooth integrands on an interval, numerical integration can be performed stably and efficiently via the classical (polynomial) Gauss quadrature formulae. However, for many other sets of integrands these quadrature formulae do not perform well. A very natural way of avoiding this problem is to include a wide class among arbitrary functions (not necessary polynomials) to be integrated exactly. The spline functions are natural candidates for such problems. In this paper, after studying Gaussian type quadrature formulae which are exact for spline functions and which contain boundary terms involving derivatives at both end points, we present a fast algorithm for computing their nodes and weights. It is also shown, taking advantage of the close connection with ordinary Gauss quadrature formula, that the latter are computed, via eigenvalues and eigenvectors of real symmetric tridiagonal matrices. Hence a new class of quadrature formulae can then be computed directly by standard software for ordinary Gauss quadrature formula. Comparative results with classical Gauss quadrature formulae are given to illustrate the numerical performance of the approach.
Paper's Title:
Oscillations of First Order Linear Delay Difference Equations
Author(s):
G. E. Chatzarakis and I. P. Stavroulakis
Department of Mathematics, University of Ioannina,
451 10, Greece
ipstav@cc.uoi.gr
Abstract:
Consider the first order linear delay difference equation of
the form 
where
is
a sequence of nonnegative real numbers, k is a positive integer and 
denotes
the forward difference operator 
New
oscillation criteria are established when the well-known oscillation conditions
and
are
not satisfied. The results obtained essentially improve known results in the
literature.
Paper's Title:
1-type Pseudo-Chebyshev Subspaces in Generalized 2-normed Spaces
Author(s):
Sh. Rezapour
Department of Mathematics, Azarbaijan University of Tarbiat Moallem,
Azarshahr, Tabriz,
Iran
sh.rezapour@azaruniv.edu
Abstract:
We construct a generalized 2-normed space from every normed space.
We introduce 1-type pseudo-Chebyshev subspaces in generalized
2-normed spaces and give some results in this field.
Paper's Title:
On Interaction of Discontinuous Waves in a Gas with Dust Particles
Author(s):
J. Jena
Department of Mathematics, Netaji Subhas institute of technology,
Sector-3, Dwarka, New Delhi - 110 075,
India.
jjena67@rediffmail.com
jjena@nsit.ac.in
Abstract:
In this paper, the interaction of the strong shock with the weak discontinuity has been investigated for the system of partial differential equations describing one dimensional unsteady plane flow of an inviscid gas with large number of dust particles. The amplitudes of the reflected and transmitted waves after interaction of the weak discontinuity through a strong shock are evaluated by exploiting the results of general theory of wave interaction.
Paper's Title:
Trapping of Water Waves By Underwater Ridges
Author(s):
1A. M. Marin, 1R. D. Ortiz and 2J. A. Rodriguez-Ceballos.
1Facultad de Ciencias Exactas y Naturales
Universidad de Cartagena
Sede Piedra de Bolivar, Avenida del Consulado
Cartagena de Indias, Bolivar,
Colombia.
2Instituto Tecnológico de
Morelia Facultad de Ciencias Fisico Matematicas
Universidad Michoacana
Tecnológico
1500, Col. Lomas de Santiaguito Edificio Be ,
Ciudad Universitaria,
58120 Morelia, Michoacan,
Mexico.
amarinr@unicartagena.edu.co,
ortizo@unicartagena.edu.co.
URL: www.unicartagena.edu.co.
Abstract:
As is well-known, underwater ridges and
submerged horizontal cylinders can serve as waveguides for surface water waves.
For large values of the wavenumber in the direction of the ridge, there is only
one trapped wave (this was proved in Bonnet & Joly (1993, SIAM J. Appl. Math.
53, pp 1507-1550)).
We construct the asymptotics of these trapped waves and their frequencies at
high frequency by means of reducing the initial problem to a pair of boundary
integral equations and then by applying the method of Zhevandrov & Merzon (2003,
AMS Transl. (2) 208, pp 235-284), in order to solve
them.
Paper's Title:
A Nonhomogeneous Subdiffusion Heat Equation
Author(s):
Joel-Arturo Rodriguez-Ceballos, Ana-Magnolia Marin, Ruben-Dario Ortiz
Instituto Tecnológico de Morelia,
Morelia, Michoacan,
Mexico
E-mail: joel@ifm.umich.mx
Universidad de Cartagena,
Campus San Pablo,
Cartagena de Indias, Bolivar,
Colombia
E-mail: amarinr@unicartagena.edu.co
E-mail: joel@ifm.umich.mx
Abstract:
In this paper we consider a nonhomogeneous subdiffusion heat equation of fractional order with Dirichlet boundary conditions.
Paper's Title:
Orthogonal Collocation on Finite Elements Using Quintic Hermite Basis
Author(s):
P. Singh, N. Parumasur and C. Bansilal
University of KwaZulu-Natal,
School of Mathematics Statistics and Computer Sciences,
Private Bag X54001,
Durban, 4000,
South Africa.
E-mail: singhprook@gmail.com
parumasurn1@ukzn.ac.za
christelle18@gmail.com
Abstract:
In this paper we consider the orthogonal collocation on finite elements (OCFE) method using quintic Hermite (second degree smooth) basis functions and use it to solve partial differential equations (PDEs). The method is particularly tailored to solve third order BVPS and PDEs and to handle their special solutions such as travelling waves and solitons, which typically is the case in the KdV equation. The use of quintic polynomials and collocation using Gauss points yields a stable high order superconvergent method. OCFE using quintic Hermite basis is optimal since it is computationally more efficient than collocation methods using (first degree smooth) piecewise-polynomials and more accurate than the (third degree smooth) B-splines basis. Various computational simulations are presented to demonstrate the computational efficiency and versatility of the OCFE method.
Paper's Title:
Hankel Functional Connected to Lemniscate of Bernoulli
Author(s):
K. Ramanuja Rao, Rajnesh Lal and Kaushal Singh
Fiji National University,
Department of Mathematics & Statistics,
P.O. Box 5529, Lautoka,
Fiji.
E-mail: ramanuja.kotti@fnu.ac.fj
rajnesh.lal@fnu.ac.fj
kaushal.singh@fnu.ac.fj
Abstract:
The aim of present paper is to derive a higher bound (HB) of 3rd order Hankel determinant for a collection of holomorphic mappings connected with exactly to the right side of the lemniscate of Bernoulli, whose polar coordinates form is r2 = 2cos2(2θ). The method carried in this paper is more refined than the method adopted by the authors (see [1]), who worked on this problem earlier.
Paper's Title:
On General Class of Nonlinear Contractive Maps and their Performance Estimates
Author(s):
Olalekan Taofeek Wahab and Salaudeen Alaro Musa
Department of Mathematics and
Statistics
Kwara State University, Malete
P. M. B. 1530 Ilorin,
Nigeria.
E-mail: taofeek.wahab@kwasu.edu.ng
Abstract:
This paper considers two independent general class of nonlinear contractive maps to study the existence properties of nonlinear operators with prior degenerate. The existence properties are proved in the framework of approximate fixed points with the imposition of the general class of contractive conditions in metrical convex spaces without emphasis on completeness or compactness. For computational purposes, the performance estimates and the sensitivity dependence of these conditions are obtained for the Picard operator. Practical examples are also considered to justify the validity of the conditions. The results ensure no term is lost in the operators with prior degenerate and the conditions are strictly larger class when compare with others in the literature.
Paper's Title:
Generalized Triangular and Symmetric Splitting Method for Steady State Probability Vector of Stochastic Matrices
Author(s):
B. Harika, D. Rajaiah, L. P. RajKumar, Malla Reddy Perati
Department of Mathematics,
Kakatiya University
E-mail: hbolledla@gmail.com
Department of Mathematics,
Kakatiya Institute of Technology and Science
E-mail: dr.mh@kitsw.ac.in
Department of Mathematics,
Kakatiya University
E-mail: ladalla@gmail.com
Department of Mathematics,
Kakatiya University
E-mail: mperati@yahoo.com
Abstract:
To find the steady state probability vector of homogenous linear system π Q=0 of stochastic rate matrix Q, generalized triangular and symmetric (GTS) splitting method is presented. Convergence analysis and choice of parameters are given when the regularized matrix A=QT+ε I of the regularized linear system Ax=b is positive definite. Analysis shows that the iterative solution of GTS method converges unconditionally to the unique solution of the regularized linear system. From the numerical results, it is clear that the solution of proposed method converges rapidly when compared to the existing methods.
Paper's Title:
A note on Inequalities due to Martins, Bennett and Alzer
Author(s):
József Sándor
Babeş-Bolyai University of Cluj, Department of Mathematics and Computer Sciences
Kogălniceanu Nr.1, Cluj-Napoca,
Romania.
jjsandor@hotmail.com
jsandor@member.ams.org
Abstract:
A short history of certain inequalities by Martins, Bennett as well as Alzer, is provided. It is shown that, the inequality of Alzer for negative powers [6], or Martin's reverse inequality [7] are due in fact to Alzer [2]. Some related results, as well as a conjecture, are stated.
Paper's Title:
On Pseudo Almost
Periodic Solutions to Some Neutral Functional-Differential
Equations
Author(s):
Toka Diagana and Eduardo Hernández
Department of Mathematics, Howard University
2441 6th Street NW,
Washington DC 20059,
USA.
tdiagana@howard.edu
Departamento de Matemática, I.C.M.C. Universidade de São Paulo,
Caixa Postal
668, 13560-970, São Carlos SP,
Brazil.
lalohm@icmc.sc.usp.br
Abstract:
This paper discusses the existence and uniqueness of pseudo almost periodic solutions to a class of partial neutral functional-differential equations. Under some suitable assumptions, existence and uniqueness results are obtained. An example is given to illustrate abstract results.
Paper's Title:
On Weighted Toeplitz Operators
Author(s):
S. C. Arora and Ritu Kathuria
Department of Mathematics,
University of Delhi,
Delhi 110007,
India.
Department of Mathematics,
Motilal Nehru College, University of Delhi,
Delhi 110021,
India.
Abstract:
A weighted Toeplitz operator on H2(β) is defined as Tφf=P(φf) where P is the projection from L2(β) onto H2(β) and the symbol φ ∈ L2(β) for a given sequence β=‹βn›n∈ Z of positive numbers. In this paper, a matrix characterization of a weighted multiplication operator on L2β is given and it is used to deduce the same for a weighted Toeplitz operator. The eigenvalues of some weighted Toeplitz operators are also determined.
Paper's Title:
Existence Results for Second Order Impulsive Functional Differential Equations with Infinite Delay
Author(s):
M. Lakrib, A. Oumansour and K. Yadi
Laboratoire de Mathématiques, Université Djillali
Liabées, B.P. 89 Sidi Bel Abbès 22000, Algérie
mlakrib@univ-sba.dz
oumansour@univ-sba.dz
Laboratoire de Mathématiques, Université Abou Bekr
Belkaid, B.P. 119 Tlemcen 13000, Algérie
k_yadi@mail.univ-tlemcen.dz
Abstract:
In this paper we study the existence of solutions for second order impulsive functional differential equations with infinite delay. To obtain our results, we apply fixed point methods.
Paper's Title:
A Comparison Between Two Different Stochastic Epidemic Models with Respect to the Entropy
Author(s):
Farzad Fatehi and Tayebe Waezizadeh
Department of Mathematics,
University of Sussex,
Brighton BN1 9QH,
UK.
E-mail: f.fatehi@sussex.ac.uk
URL:
http://www.sussex.ac.uk/profiles/361251
Department of Pure Mathematics, Faculty
of Mathematics and Computer,
Shahid Bahonar University of Kerman,
Kerman 76169-14111,
Iran.
E-mail: waezizadeh@uk.ac.ir
URL:
http://academicstaff.uk.ac.ir/en/tavaezizadeh
Abstract:
In this paper at first a brief history of mathematical models is presented with the aim to clarify the reliability of stochastic models over deterministic models. Next, the necessary background about random variables and stochastic processes, especially Markov chains and the entropy are introduced. After that, entropy of SIR stochastic models is computed and it is proven that an epidemic will disappear after a long time. Entropy of a stochastic mathematical model determines the average uncertainty about the outcome of that random experiment. At the end, we introduce a chain binomial epidemic model and compute its entropy, which is then compared with the DTMC SIR epidemic model to show which one is nearer to reality.
Paper's Title:
A Note on Taylor Expansions Without the Differentiability Assumption
Author(s):
Moawia Alghalith
Economics Dept.,
University of the West Indies,
St Augustine,
Trinidad and Tobago.
E-mail: malghalith@gmail.com
Abstract:
We introduce new Taylor expansions when the function is not differentiable.
Retraction
This article has been retracted under the authority of the Editor on Chief on 1 April, 2021. The PDF file is no longer available, but can be obtained from the editorial office upon request.
Paper's Title:
Solving Two Point Boundary Value Problems by Modified Sumudu Transform Homotopy Perturbation Method
Author(s):
Asem AL Nemrat and Zarita Zainuddin
School of Mathematical Sciences,
Universiti Sains Malaysia,
11800 Penang,
Malaysia.
E-mail: alnemrata@yahoo.com
zarita@usm.my
Abstract:
This paper considers a combined form of the Sumudu transform with the modified homotopy perturbation method (MHPM) to find approximate and analytical solutions for nonlinear two point boundary value problems. This method is called the modified Sumudu transform homotopy perturbation method (MSTHPM). The suggested technique avoids the round-off errors and finds the solution without any restrictive assumptions or discretization. We will introduce an appropriate initial approximation and furthermore, the residual error will be canceled in some points of the interval (RECP). Only a first order approximation of MSTHPM will be required, as compared to STHPM, which needs more iterations for the same cases of study. After comparing figures between approximate, MSTHPM, STHPM and numerical solutions, it is found through the solutions we have obtained that they are highly accurate, indicating that the MSTHPM is very effective, simple and can be used to solve other types of nonlinear boundary value problems (BVPs).
Paper's Title:
On The Degree of Approximation of Periodic Functions from Lipschitz and Those from Generalized Lipschitz Classes
Author(s):
Xhevat Z. Krasniqi
Faculty of Education,
University of Prishtina "Hasan Prishtina",
Avenue "Mother Theresa " no. 5, Prishtinë
10000,
Republic of Kosovo.
E-mail: xhevat.krasniqi@uni-pr.edu
Abstract:
In this paper we have introduced some new trigonometric polynomials. Using these polynomials, we have proved some theorems which determine the degree of approximation of periodic functions by a product of two special means of their Fourier series and the conjugate Fourier series. Many results proved previously by others are special case of ours.
Paper's Title:
Fractional exp(-φ(ξ))- Expansion Method and its Application to Space--Time Nonlinear Fractional Equations
Author(s):
A. A. Moussa and L. A. Alhakim
Department of Management Information
System and Production Management,
College of Business and Economics, Qassim University,
P.O. BOX 6666, Buraidah: 51452,
Saudi Arabia.
E-mail: Alaamath81@gmail.com
URL:
https://scholar.google.com/citations?user=ccztZdsAAAAJ&hl=ar
Department of Management Information
System and Production Management,
College of Business and Economics, Qassim University,
P.O. BOX 6666, Buraidah: 51452,
Saudi Arabia.
E-mail: Lama2736@gmail.com
URL:
https://scholar.google.com/citations?user=OSiSh1AAAAAJ&hl=ar
Abstract:
In this paper, we mainly suggest a new method that depends on the fractional derivative proposed by Katugampola for solving nonlinear fractional partial differential equations. Using this method, we obtained numerous useful and surprising solutions for the space--time fractional nonlinear Whitham--Broer--Kaup equations and space--time fractional generalized nonlinear Hirota--Satsuma coupled KdV equations. The solutions obtained varied between hyperbolic, trigonometric, and rational functions, and we hope those interested in the real-life applications of the previous two equations will find this approach useful.
Paper's Title:
Some Properties on a Class of p-valent Functions Involving Generalized Differential Operator
Author(s):
A. T. Yousef, Z. Salleh and T. Al-Hawary
Department of Mathematics,
Faculty of Ocean Engineering Technology and Informatics, Universiti Malaysia
Terengganu,
21030 Kuala Nerus, Terengganu,
Malaysia.
E-mail: abduljabaryousef@gmail.com,
zabidin@umt.edu.my
Department of Applied Science,
Ajloun College, Al-Balqa Applied University,
Ajloun 26816,
Jordan.
E-mail: tariq_amh@yahoo.com
Abstract:
This paper aiming to introduce a new differential operator
in the open unit disc
We then, introduce a new subclass of analytic function
Moreover, we discuss coefficient estimates, growth and distortion theorems, and
inclusion properties for the functions belonging to the class
Paper's Title:
The RAFU remainder in Taylor's formula
Author(s):
A. C. Sanchez
''Santa Eulalia'' High School,
Spain
E-mail: csanchezalicia@gmail.com
Abstract:
This work is about the remainder in Taylor's formula. Specifically, the RAFU remainder is studied. Its mathematical expression is given. Some examples are shown. Different ways to obtain this remainder are developed.
Paper's Title:
Oscillatory Behavior of Second-Order Non-Canonical
Retarded Difference Equations
Author(s):
G.E. Chatzarakis1, N. Indrajith2, E. Thandapani3 and K.S. Vidhyaa4
1Department
of Electrical and Electronic Engineering Educators,
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail: gea.xatz@aspete.gr,
geaxatz@otenet.gr
2Department
of Mathematics,
Presidency College, Chennai - 600 005,
India.
E-mail: indrajithna@gmail.com
3Ramanujan
Institute for Advanced Study in Mathematics,
University of Madras,
Chennai - 600 005,
India.
E-mail: ethandapani@yahoo.co.in
4
Department of Mathematics,Abstract:
Using monotonic properties of nonoscillatory solutions, we obtain new oscillatory criteria for the second-order non-canonical difference equation with retarded argument
Our oscillation results improve and extend the earlier ones. Examples illustrating the results are provided.
Paper's Title:
On Statistically Φ-Convergence
Author(s):
Supama
Department of Mathematics,
Gadjah Mada
University,
Yogyakarta 55281,
Indonesia.
E-mail: supama@ugm.ac.id
Abstract:
The idea of statistical convergence was introduced by Antoni Zygmund in 1935. Based on in the idea of Zygmund, Henry Fast and Hugo Steinhaus independently introduced a concept of statistical convergence as a generalization of an ordinary convergence in the same year 1951. In this paper, by using the Orlicz function, we introduce a concept of statistical Φ-convergence, as a generalization of the statistical convergence. Further, we observe some basic properties and some topological properties of the statistical Φ-convergent sequences
Search and serve lasted 0 second(s).