|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.
Paper's Title:
Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Robust Error Analysis of Solutions to Nonlinear Volterra Integral Equation in Lp Spaces
Author(s):
Hamid Baghani, Javad Farokhi-Ostad and Omid Baghani
Department of Mathematics, Faculty of
Mathematics,
University of Sistan and Baluchestan, P.O. Box 98135-674, Zahedan,
Iran.
E-mail:
h.baghani@gmail.com
Department of Mathematics, Faculty of
Basic Sciences,
Birjand University of Technology, Birjand,
Iran.
E-mail: j.farrokhi@birjandut.ac.ir
Department of Mathematics and Computer
Sciences,
Hakim Sabzevari University, P.O. Box 397, Sabzevar,
Iran.
E-mail:
o.baghani@gmail.com
Abstract:
In this paper, we propose a novel strategy for proving an important inequality for a contraction integral equations. The obtained inequality allows us to express our iterative algorithm using a "for loop" rather than a "while loop". The main tool used in this paper is the fixed point theorem in the Lebesgue space. Also, a numerical example shows the efficiency and the accuracy of the proposed scheme.
Paper's Title:
Dynamical Analysis of HIV/AIDS Epidemic Model with Two Latent Stages, Vertical Transmission and Treatment
Author(s):
Nur Shofianah, Isnani Darti, Syaiful Anam
Mathematics Department,Faculty of
Mathematics and Natural Sciences.
University of Brawijaya,
Jl. Veteran, Malang 65145,
Indonesia.
E-mail:
nur_shofianah@ub.ac.id,
isnanidarti@ub.ac.id,
syaiful@ub.ac.id
Abstract:
We discuss about dynamical analysis of HIV/AIDS epidemic model with two latent stages, vertical transmission and treatment. In this model, the spreading of HIV occurs through both horizontal and vertical transmission. There is also treatment for individual who has been HIV infected. The latent stage is divided into slow and fast latent stage based on the immune condition which varies for each individual. Dynamical analysis result shows that the model has two equilibrium points: the disease-free equilibrium point and the endemic equilibrium point. The existence and global stability of equilibrium points depend on the basic reproduction number R0. When R0 <1, only the disease-free equilibrium point exists. If R0 >1, there are two equilibrium points, which are the disease-free equilibrium point and the endemic equilibrium point. Based on the result of stability analysis, the disease-free equilibrium point is globally asymptotically stable if R0 <1, while if R0 > 1 and p=q, the endemic equilibrium point will be globally asymptotically stable. In the end, we show some numerical simulations to support the analytical result.
Paper's Title:
Inequalities Relating to the Gamma Function
Author(s):
Chao-Ping Chen and Feng Qi
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
chenchaoping@hpu.edu.cn
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
qifeng@hpu.edu.cn,
fengqi618@member.ams.org
Url:
http://rgmia.vu.edu.au/qi.html,
http://dami.hpu.edu.cn/qifeng.html
Abstract:
For 
, we have
.
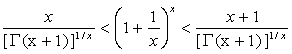For
,
,
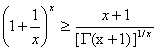And equality occurs for x=1.
Paper's Title:
Long Time Behavior for a Viscoelastic Problem with a Positive Definite Kernel
Author(s):
Nasser-eddine Tatar
King Fahd
University of Petroleum and Mineral, Department of Mathematical Sciences,
Dhahran, 31261 Saudi Arabia
tatarn@kfupm.edu.sa
Abstract:
We study the asymptotic behavior of solutions for an integro-differential problem which arises in the theory of viscoelasticity. It is proved that solutions go to rest in an exponential manner under new assumptions on the relaxation function in the memory term. In particular, we consider a new family of kernels which are not necessarily decreasing.
Paper's Title:
Stability of a Pexiderized Equation
Author(s):
Maryam Amyar
Department of Mathematics,
Islamic Azad University, Rahnamaei Ave,
Mashhad 91735, Iran,
and Banach Mathematical Research Group (BMRG)
amyari@mshdiau.ac.ir
URL: http://amyari.mshdiau.ac.ir
Abstract:
The aim of the paper is to prove the
stability of the Pexiderized equation f(x)=g(y+x)-h(y-x), for any
amenable abelian group.
Paper's Title:
A Wallis Type Inequality and a Double Inequality for Probability Integral
Author(s):
Jian Cao, Da-Wei Niu and Feng Qi
School of Mathematics and Informatics,
Henan Polytechnic University, Jiaozuo City,
Henan Province, 454010,
China
21caojian@163.com
School of Mathematics and Informatics,
Henan Polytechnic University, Jiaozuo City,
Henan Province, 454010,
China
nnddww@tom.com
Research Institute of Mathematical Inequality Theory,
Henan Polytechnic University, Jiaozuo City,
Henan Province, 454010,
China
qifeng@hpu.edu.cn
fengqi618@member.ams.org
qifeng618@hotmail.com
qifeng618@msn.com
qifeng618@qq.com
URL: http://rgmia.vu.edu.au/qi.html
Abstract:
In this short note, a Wallis type inequality with the best upper and lower
bounds is established. As an application, a double inequality for the
probability integral is found.
Paper's Title:
The Convergence of Modified Mann-Ishikawa Iterations when Applied to an Asymptotically Pseudocontractive Map
Author(s):
S. Soltuz
Departamento de Matematicas, Universidad de Los Andes, Carrera 1
No. 18A-10, Bogota,
Colombia
and
``T. Popoviciu" Institute of Numerical Analysis
Cluj-Napoca,
Romania
smsoltuz@gmail.com
URL:http://www.uniandes.edu.co/
Abstract:
We prove that under minimal conditions the modified Mann and Ishikawa iterations converge when dealing with an asymptotically pseudocontractive map. We give an affirmative answer to the open question from C.E. Chidume and H. Zegeye, Approximate fixed point sequences and convergence theorems for asymptotically pseudocontractive mappings, J. Math. Anal. Appl., 278 (2003), 354--366.
Paper's Title:
A Subclass of Meromorphically Multivalent Functions with Applications to Generalized Hypergeometric Functions
Author(s):
M. K. Aouf
Mathematics Department,
Faculty of Science,
Mansoura University 35516,
Egypt
mkaouf127@yahoo.com
Abstract:
In this paper a new subclass of meromorphically multivalent functions, which
is defined by means of a Hadamard product (or convolution) involving some
suitably normalized meromorphically p-valent functions. The main object of
the present paper is to investigate the various important properties and
characteristics of this subclass of meromorphically multivalent functions.
We also derive many interesting results for the Hadamard products of
functions belonging to this subclass. Also we consider several applications
of our main results to generalized hypergeomtric functions.
Paper's Title:
Inequalities for
the
Author(s):
S. S. Dragomir
School of Engineering and Science
Victoria University, PO 14428
Melbourne City MC,
Victoria 8001,
Australia
sever.dragomir@vu.edu.au
URL: http://www.staff.vu.edu.au/RGMIA/dragomir/
Abstract:
Some recent inequalities for the Čebyšev functional of two functions of selfadjoint linear operators in Hilbert spaces, under suitable assumptions for the involved functions and operators, are surveyed.
Paper's Title:
Ellipses of Minimal Area and of Minimal Eccentricity Circumscribed About a Convex Quadrilateral
Author(s):
Alan Horwitz
Penn State University,
25 Yearsley Mill Rd.,
Media, PA 19063,
U.S.A
alh4@psu.edu
Abstract:
First, we fill in key gaps in Steiner's nice characterization of
the most nearly circular ellipse which passes through the vertices of a convex
quadrilateral,
. Steiner proved that there is only one pair of conjugate
directions, M1 and M2, that belong to all ellipses of circumscription.
Then he proves that if there is an ellipse, E, whose equal
conjugate diameters possess the directional constants M1 and M2,
then E must be an ellipse of circumscription which has minimal eccentricity.
However, Steiner does not show the existence or uniqueness of such an ellipse.
We prove that there is a unique ellipse of minimal eccentricity which passes
through the vertices of
. We also show that there exists an ellipse which passes through the vertices of
and whose
equal conjugate diameters
possess the directional constants M1 and M2. We also show
that there exists a unique ellipse of minimal area which passes through the
vertices of
. Finally, we call a convex quadrilateral,
, bielliptic if the unique
inscribed and circumscribed ellipses of minimal eccentricity have the same
eccentricity. This generalizes the notion of bicentric quadrilaterals. In
particular, we show the existence of a bielliptic convex quadrilateral which is
not bicentric.
Paper's Title:
The Riemann-Stieltjes Integral on Time Scales
Author(s):
D. Mozyrska, E. Pawłuszewicz, D. Torres
Faculty Of Computer Science,
Białystok University Of Technology,
15-351 Białystok,
Poland
d.mozyrska@pb.edu.pl
Department Of Mathematics,
University Of Aveiro,
3810-193 Aveiro,
Portugal
ewa@ua.pt
Department Of Mathematics,
University Of Aveiro,
3810-193 Aveiro,
Portugal
delfim@ua.pt
Abstract:
We study the process of integration on time scales in the sense of Riemann-Stieltjes. Analogues of the classical properties are proved for a generic time scale, and examples are given
Paper's Title:
On a Class of Uniformly Convex Functions Defined by Convolution with Fixed Coefficient
Author(s):
T. N. Shanmugam, S. Sivasubramanian, and G. Murugusundaramoorthy
Department of Mathematics,
College of Engineering,
Anna University,
Chennai - 600 025,
India.
drtns2001@yahoo.com
Department of Mathematics,
University College of Engineering,
Tindivanam
Anna University-Chennai,
Saram-604 703,
India.
sivasaisastha@rediffmail.com
School of Sciences and Humanities,
VIT University, Vellore-632 014,
India.
gmsmoorthy@yahoo.com
Abstract:
We define a new subclass of uniformly convex functions with negative and fixed second coefficients defined by convolution. The main object of this paper is to obtain coefficient estimates distortion bounds, closure theorems and extreme points for functions belong to this new class . The results are generalized to families with fixed finitely many coefficients.
Paper's Title:
Strong Convergence Theorems for a Common Zero of an Infinite Family of Gamma-Inverse Strongly Monotone Maps with Applications
Author(s):
Charles Ejike Chidume, Ogonnaya Michael Romanus, and Ukamaka Victoria Nnyaba
African University of Science and
Technology, Abuja,
Nigeria.
E-mail: cchidume@aust.edu.ng
E-mail: romanusogonnaya@gmail.com
E-mail: nnyabavictoriau@gmail.com
Abstract:
Let E be a uniformly convex and uniformly smooth real Banach space with
dual space E* and let Ak:E→E*,
k=1, 2, 3 , ...
be a family of inverse strongly monotone maps such that ∩∞k=1
Ak-1(0)≠∅.
A new iterative algorithm is constructed and proved to converge strongly to a
common zero of the family.
As a consequence of this result, a strong convergence theorem for approximating
a common J-fixed point for an infinite family of
gamma-strictly J-pseudocontractive maps is proved. These results are new and
improve recent results obtained for these classes of nonlinear maps.
Furthermore, the technique of proof is of independent interest.
Paper's Title:
Iterative Approximation of Zeros of Accretive Type Maps, with Applications
Author(s):
Charles Ejike Chidume, Chinedu Godwin Ezea, and Emmanuel Ezzaka Otubo
African University of Science and
Technology, Abuja,
Nigeria.
E-mail: cchidume@aust.edu.ng
E-mail: chinedu.ezea@gmail.com
E-mail: mrzzaka@yahoo.com
Department of Mathematics,
Nnamdi Azikiwe University,
Awka,
Nigeria
E-mail: chinedu.ezea@gmail.com
Ebonyi State University,
Abakaliki,
Nigeria
E-mail: mrzzaka@yahoo.com
Abstract:
Let E be a reflexive real Banach space with uniformly Gâteaux differentiable norm. Let J:E→ E* be the normalized duality map on E and let A:E*→ E be a map such that AJ is an accretive and uniformly continuous map. Suppose that (AJ)-1(0) in nonempty. Then, an iterative sequence is constructed and proved to converge strongly to some u* in (AJ)-1(0). Application of our theorem in the case that E is a real Hilbert space yields a sequence which converges strongly to a zero of A. Finally, non-trivial examples of maps A for which AJ is accretive are presented..
Paper's Title:
Coefficient Estimates for Certain Subclasses of Bi-univalent Sakaguchi
Type Functions by using Faber Polynomial
Author(s):
P. Murugabharathi, B. Srutha Keerthi
Mathematics Division,
School of Advanced Sciences,
VIT Chennai, Vandaloor, Kelambakkam Road,
Chennai - 600 127, India.
E-mail: bharathi.muhi@gmail.com
E-mail: sruthilaya06@yahoo.co.in
Abstract:
In this work, considering a general subclass of bi-univalent Sakaguchi type functions, we determine estimates for the general Taylor-Maclaurin coefficients of the functions in these classes. For this purpose, we use the Faber polynomial expansions. In certain cases, our estimates improve some of those existing coefficient bounds.
Paper's Title:
A Multivalued Version of the
Radon-Nikodym Theorem, via the Single-valued Gould Integral
Author(s):
Domenico Candeloro1, Anca Croitoru2, Alina Gavriluţ2, Anna Rita Sambucini1
1Dept. of Mathematics and Computer
Sciences,
University of Perugia,
1, Via Vanvitelli -- 06123, Perugia,
Italy.
E-mail: domenico.candeloro@unipg.it,
anna.sambucini@unipg.it
2Faculty of Mathematics,
Al. I. Cuza University,
700506 Iaşi,
Romania.
E-mail: croitoru@uaic.ro,
gavrilut@uaic.ro
Abstract:
In this paper we consider a Gould type integral of real functions with respect to a compact and convex valued not necessarily additive measure. In particular we will introduce the concept of integrable multimeasure and, thanks to this notion, we will establish an exact Radon-Nikodym theorem relative to a fuzzy multisubmeasure which is new also in the finite dimensional case. Some results concerning the Gould integral are also obtained.
Paper's Title:
Inequalities for Functions of Selfadjoint Operators on Hilbert Spaces:
a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
College of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning inequalities for continuous functions of selfadjoint operators on complex Hilbert spaces. It is intended for use by both researchers in various fields of Linear Operator Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Hermite-Hadamard Type Inequalities for MN-Convex Functions
Author(s):
Sever S. Dragomir1,2
1Mathematics,
College of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
The present work endeavours to briefly present some of the fundamental results connected to the Hermite-Hadamard inequality for special classes of convex functions such as AG, AH, GA, GG, GH, HA, HG and HH -convex functions in which the author have been involved during the last five years. For simplicity, we call these classes of functions such as MN-convex functions, where M and N stand for any of the Arithmetic (A), Geometric (G) or Harmonic (H) weighted means of positive real numbers. The survey is intended for use by both researchers in various fields of Approximation Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Trace Inequalities for Operators in Hilbert Spaces: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
School of Engineering
& Science
Victoria University,
PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
In this paper we survey some recent trace inequalities for operators in Hilbert spaces that are connected to Schwarz's, Buzano's and Kato's inequalities and the reverses of Schwarz inequality known in the literature as Cassels' inequality and Shisha-Mond's inequality. Applications for some functionals that are naturally associated to some of these inequalities and for functions of operators defined by power series are given. Further, various trace inequalities for convex functions are presented including refinements of Jensen inequality and several reverses of Jensen's inequality. Hermite-Hadamard type inequalities and the trace version of Slater's inequality are given. Some Lipschitz type inequalities are also surveyed. Examples for fundamental functions such as the power, logarithmic, resolvent and exponential functions are provided as well.
Search and serve lasted 0 second(s).