|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Common Fixed Point Results for Banach Operator Pairs and Applications to Best Approximation
Author(s):
Hemant Kumar Nashine
Department of Mathematics,
Disha Institute of Management and Technology,
Satya Vihar, Vidhansabha - Chandrakhuri Marg (Baloda Bazar Road),
Mandir Hasaud,
Raipur - 492101(Chhattisgarh), India.
hemantnashine@rediffmail.com
nashine_09@rediffmail.com
Abstract:
The common fixed point results for Banach operator pair with generalized nonexpansive mappings in q-normed space have been obtained in the present work. As application, some more general best approximation results have also been determined without the assumption of linearity or affinity of mappings. These results unify and generalize various existing known results with the aid of more general class of noncommuting mappings.
Paper's Title:
Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Some Convergence Results for Jungck-Am Iterative Process In Hyperbolic Spaces
Author(s):
Akindele Adebayo Mebawondu and Oluwatosin Temitope Mewomo
School of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail:
216028272@stu.ukzn.ac.za,
mewomoo@ukzn.ac.za
Abstract:
In this paper, we introduce a new three steps iterative process called Jungck-AM iterative process and show that the proposed iterative process can be used to approximate fixed points of Jungck-contractive type mappings and Jungck-Suzuki type mappings. In addition, we establish some strong and Δ-convergence results for the approximation of fixed points of Jungck-Suzuki type mappings in the frame work of uniformly convex hyperbolic space. Furthermore, we show that the newly proposed iterative process has a better rate of convergence compare to the Jungck-Noor, Jungck-SP, Jungck-CR and some existing iterative processes in the literature. Finally, stability, data dependency results for Jungck-AM iterative process is established and we present an analytical proof and numerical examples to validate our claim.
Paper's Title:
D-Iterative Method for Solving a Delay Differential Equation and a Two-Point Second-Order Boundary Value Problems in Banach Spaces
Author(s):
Francis Akutsah1, Akindele Adebayo Mebawondu2, Oluwatosin Babasola3, Paranjothi Pillay4 and Ojen Kumar Narain5
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 216040405@stu.ukzn.ac.za,
akutsah@gmail.com
2School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
DST-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
Mountain Top University,
Prayer City, Ogun State,
Nigeria.
E-mail: dele@aims.ac.za
3Department
of Mathematical Sciences,
University of Bath,
Claverton Down,
Bath, BA2 7AY
UK.
E-mail: ob377@bath.ac.uk
4School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: pillaypi@ukzn.ac.za
5School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
The purpose of this paper is to re-establish the convergence, stability and data dependence results established by [2] and [3] by removing the strong assumptions imposed on the sequences which were used to obtain their results. In addition, we introduced a modified approach using the D-iterative method to solve a two-point second-order boundary value problem, and also obtain the solution of a delay differential equations using the obtained results in this paper. The results presented in this paper do not only extend and improve the results obtained in [2, 3], it further extends and improve some existing results in the literature.
Paper's Title:
New Implicit Kirk-Type Schemes for General Class of Quasi-Contractive Operators in Generalized Convex Metric Spaces
Author(s):
K. Rauf, O. T. Wahab and A. Ali
Department of Mathematics,
University of Ilorin, Ilorin,
Nigeria.
E-mail: krauf@unilorin.edu.ng
Department of Statistics and Mathematical
Sciences,
Kwara State University, Malete,
Nigeria.
Department of Mathematics,
Mirpur University of Science and Technology, Mirpur,
Pakistan.
Abstract:
In this paper, we introduce some new implicit Kirk-type iterative schemes in generalized convex metric spaces in order to approximate fixed points for general class of quasi-contractive type operators. The strong convergence, T-stability, equivalency, data dependence and convergence rate of these results were explored. The iterative schemes are faster and better, in term of speed of convergence, than their corresponding results in the literature. These results also improve and generalize several existing iterative schemes in the literature and they provide analogues of the corresponding results of other spaces, namely: normed spaces, CAT(0) spaces and so on.
Paper's Title:
Existence of Solution of Differential and Riemann-Liouville Equation Via Fixed Point Approach in Complex Valued b-Metric Spaces
Author(s):
K. Afassinou, A. A. Mebawondu, H. A. Abass and O. K. Narain
Department of Science Access,
University of Zululand, KwaDlangezwa,
South Africa.
E-mail: komia@aims.ac.za
DST-NRF Centre of Excellence in
Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: dele@aims.ac.za
DST-NRF Centre of Excellence in
Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: hammedabass548@gmail.com
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
In this paper, we establish some fixed point and common fixed point results for a new type of generalized contractive mapping using the notion of C-class function in the framework of complex valued b-metric spaces. As an application, we establish the existence and uniqueness of a solution for Riemann-Liouville integral and ordinary differential equation in the framework of a complete complex valued b-metric spaces. The obtained results generalize and improve some fixed point results in the literature.
Paper's Title:
Robust Error Analysis of Solutions to Nonlinear Volterra Integral Equation in Lp Spaces
Author(s):
Hamid Baghani, Javad Farokhi-Ostad and Omid Baghani
Department of Mathematics, Faculty of
Mathematics,
University of Sistan and Baluchestan, P.O. Box 98135-674, Zahedan,
Iran.
E-mail:
h.baghani@gmail.com
Department of Mathematics, Faculty of
Basic Sciences,
Birjand University of Technology, Birjand,
Iran.
E-mail: j.farrokhi@birjandut.ac.ir
Department of Mathematics and Computer
Sciences,
Hakim Sabzevari University, P.O. Box 397, Sabzevar,
Iran.
E-mail:
o.baghani@gmail.com
Abstract:
In this paper, we propose a novel strategy for proving an important inequality for a contraction integral equations. The obtained inequality allows us to express our iterative algorithm using a "for loop" rather than a "while loop". The main tool used in this paper is the fixed point theorem in the Lebesgue space. Also, a numerical example shows the efficiency and the accuracy of the proposed scheme.
Paper's Title:
Hermite-Hadamard Type Inequalities for k-Riemann Liouville Fractional Integrals Via Two Kinds of Convexity
Author(s):
R. Hussain1, A. Ali2, G. Gulshan3, A. Latif4 and K. Rauf5
1,2,3,4Department
of Mathematics,
Mirpur University of Science and Technology, Mirpur.
Pakistan.
E-mail1:
rashida12@gmail.com
E-mail2:
unigraz2009@yahoo.com
E-mail3:
ghazalagulshan@yahoo.com
E-mail4:
asialatif87@gmail.com
5Department
of Mathematics,
University of Ilorin, Ilorin,
Nigeria.
E-mail5:
krauf@unilorin.edu.ng
Abstract:
In this article, a fundamental integral identity including the first order derivative of a given function via k-Riemann-Liouville fractional integral is established. This is used to obtain further Hermite-Hadamard type inequalities involving left-sided and right-sided k-Riemann-Liouville fractional integrals for m-convex and (s,m)-convex functions respectively.
Paper's Title:
Kinematic Model for Magnetic Null-points in 2 Dimensions
Author(s):
Ali Khalaf Hussain Al-Hachami
Department of Mathematics,
College of Education For Pure Sciences,
Wasit University,
Iraq.
E-mail: alhachamia@uowasit.edu.iq
Abstract:
The adjacent configurations of two-dimensional magnetic null point centers are analyzed by an immediate examination about the null. The configurations are classified as either potential or non-potential. By then the non-potential cases are subdivided into three cases depending upon whether the component of current is less than, equal to or greater than a threshold current. In addition the essential structure of reconnection in 2D is examined. It unfolds that the manner by which the magnetic flux is rebuilt. In this paper, we center on the ramifications of kinematic arrangements; that is, we fathom just Maxwell's conditions and a resistive Ohm's law.
Paper's Title:
Generalised Models for Torsional Spine Reconnection
Author(s):
Ali Khalaf Hussain Al-Hachami
Department of Mathematics,
College of Education For Pure Sciences,
Wasit University,
Iraq.
E-mail: alhachamia@uowasit.edu.iq
Abstract:
Three-dimensional (3D) null points are available in wealth in the solar corona, and the equivalent is probably going to be valid in other astrophysical situations. On-going outcomes from sun oriented perceptions and from reproductions propose that reconnection at such 3D nulls may assume a significant job in the coronal dynamics. The properties of the torsional spine method of magnetic reconnection at 3D nulls are researched. Kinematic model are created, which incorporate the term ηJ that is spatially localised around the null, stretching out along the spine of the null. The null point is to research the impact of shifting the level of asymmetry of the null point magnetic field on the subsequent reconnection process where past examinations constantly considered a non-nonexclusive radially symmetric null. Specifically we analyse the rate of reconnection of magnetic flux at the spine of null point. Logical arrangements are determined for the enduring kinematic equation, and contrasted and the after effects of torsional spine reconnection models when the current is restricted in which the Maxwell conditions are illuminated. The geometry of the current layers inside which torsional spine reconnection happen is autonomous on the symmetry of the magnetic field. Torsional spine reconnection happens in a thin cylinder around the spine, with circular cross-segment when the fan eigenvalues are extraordinary. The short axis of the circle being along the solid field bearing. Just as it was discovered that the fundamental structure of the method of attractive reconnection considered is unaffected by changing the magnetic field symmetry, that is, the plasma flow is discovered rotational around the spine of null point. The spatiotemporal pinnacle current, and the pinnacle reconnection rate achieved, are found not to rely upon the level of asymmetry.
Paper's Title:
Fractional Integral Inequalities of Hermite-Hadamard Type for P-convex and Quasi-Convex Stochastic Process
Author(s):
Oualid Rholam, Mohammed Barmaki and Driss Gretet
National School of Applied Sciences (ENSA),
University Ibn Tofail,
B.P 242 Kenitra 14000,
phone number : +212606257757,
Morocco.
E-mail: oualid.rholam@uit.ac.ma
Science Faculty Ben M'sik,
University Hassan II,
B.P 7955 Av Driss El Harti Sidi Othmane 20700,
phone number : +212 5 22 70 46 71 ,
Morocco.
E-mail: mohammed.barmaki@uit.ac.ma
National School of Applied Sciences (ENSA),
University Ibn Tofail,
B.P 242 Kenitra 14000,
phone number : +212661403557,
Morocco.
E-mail: driss.gretete@uit.ac.ma
Abstract:
In this paper we consider the class of P-convex and Quasi-convex stochastic processes on witch we apply a general class of generalized fractional integral operator in order to establish new integral inequalities of Hermite-Hadammard type. then we obtain some results for well known types of fractional integrals. Results obtained in this paper may be starting point as well as a useful source of inspiration for further research in convex analysis.
Paper's Title:
Fekete-Szegö Inequality for Certain Class of Analytic Functions
Author(s):
V. Ravichandran, Maslina Darus, M. Hussain Khan, and K. G. Subramanian
School of
Mathematical Sciences, Universiti Sains Malaysia,
11800 Usm, Penang, Malaysia
vravi@cs.usm.my
School of
Mathematical Sciences, Faculty of Sciences and Technology,
Ukm, Banki 43600, Malaysia
maslina@pkrisc.cc.ukm.my
Department of
Mathematics, Islamiah College,
Vaniambadi 635 751, India
Department of
Mathematics, Madras Christian College, Tambaram,
Chennai- 600 059, India
kgsmani@vsnl.net
Abstract:
In this present investigation, the authors obtain Fekete-Szegö inequality for a certain
class of analytic functions f(z) for which
 lies in a
region starlike with respect to 1 and symmetric with respect to the real axis. Also certain application
of our main result for a class of functions defined by Hadamard product (convolution) is
given. As a special case of our result we obtain Fekete-Szegö inequality for a class of functions
defined through fractional derivatives. Also we obtain Fekete-Szegö inequality for the inverse
functions.
lies in a
region starlike with respect to 1 and symmetric with respect to the real axis. Also certain application
of our main result for a class of functions defined by Hadamard product (convolution) is
given. As a special case of our result we obtain Fekete-Szegö inequality for a class of functions
defined through fractional derivatives. Also we obtain Fekete-Szegö inequality for the inverse
functions.
Paper's Title:
Differential Sandwich Theorems for Some Subclasses of Analytic Functions
Author(s):
T. N. Shanmugam, V. Ravichandran and S. Sivasubramanian
Department of Mathematics, College of Engineering,
Anna university, Chennai 600 025,
India
shan@annauniv.edu
URL: http://www.annauniv.edu/shan
School of Mathematical Sciences,
Universiti Sains Malaysia,
11800 USM Penang,
Malaysia
vravi@cs.usm.my
URL: http://cs.usm.my/~vravi
Department of Mathematics, Easwari Engineering college,
Ramapuram, Chennai 600 089,
India
sivasaisastha@rediffmail.com
Abstract:
Let ![]() and
and ![]() be univalent in
be univalent in ![]() with
with ![]() We give some applications of first order differential subordination and superordination to obtain sufficient conditions for normalized analytic function
We give some applications of first order differential subordination and superordination to obtain sufficient conditions for normalized analytic function ![]() with
with ![]() to satisfy
to satisfy ![]()
Paper's Title:
On Sandwich Theorems for Certain Subclass of Analytic Functions Involving Dziok-Srivastava Operator
Author(s):
T. N. Shanmugam, M. P. Jeyarama and A. Singaravelu
Department of Mathematics
College of Engineering, Anna University
Chennai - 600 025,
India
drtns2001@yahoo.com
Department of Mathematics
Easwari Engineering College
Ramapuram, Chennai - 600089
Tamilnadu, India
jeyaraman-mp@yahoo.co.i
Department of Mathematics
Valliammai Engineering College
Chennai - 603203
Tamilnadu, India.
asing-59@yahoo.com
Abstract:
The purpose of this present paper is to derive some subordination and superordination results for certain normalized analytic functions in the open unit disk, acted upon by Dziok-Srivastava operator. Relevant connections of the results, which are presented in this paper, with various known results are also considered.
Paper's Title:
Solving Fractional Transport Equation via Walsh Function
Author(s):
A. Kadem
L. M. F. N., Mathematics Department,
University of Setif,
Algeria
abdelouahak@yahoo.fr
Abstract:
In this paper we give a complete proof of A method for the solution of fractional transport equation in three-dimensional case by using Walsh function is presented. The main characteristic of this technique is that it reduces these problems to those of solving a system of algebraic equations, thus greatly simplifying the problem.
Paper's Title:
Mapped Chebyshev Spectral Methods for Solving Second Kind Integral Equations on the Real Line
Author(s):
Ahmed Guechi and Azedine Rahmoune
Department of Mathematics, University of Bordj Bou Arréridj,
El Anasser, 34030, BBA,
Algeria.
E-mail: a.guechi2017@gmail.com
E-mail: a.rahmoune@univ-bba.dz
Abstract:
In this paper we investigate the utility of mappings to solve numerically an important class of integral equations on the real line. The main idea is to map the infinite interval to a finite one and use Chebyshev spectral-collocation method to solve the mapped integral equation in the finite interval. Numerical examples are presented to illustrate the accuracy of the method.
Paper's Title:
Convergence Speed of Some Random Implicit-Kirk-type Iterations for Contractive-type Random Operators
Author(s):
H. Akewe, K.S. Eke
Department of Mathematics,
Covenant University,
Canaanland, KM 10, Idiroko Road, P. M. B. 1023, Ota, Ogun State,
Nigeria.
E-mail: hudson.akewe@covenantuniversity.edu.ng,
kanayo.eke@covenantuniversity.edu.ng
Abstract:
The main aim of this paper is to introduce a stochastic version of multistep type iterative scheme called a modified random implicit-Kirk multistep iterative scheme and prove strong convergence and stability results for a class of generalized contractive-type random operators. The rate of convergence of the random iterative schemes are also examined through an example. The results show that our new random implicit kirk multistep scheme perform better than other implicit iterative schemes in terms of convergence and thus have good potentials for further applications in equilibrium problems in computer science, physics and economics.
Paper's Title:
Some Inequalities of the Hermite-Hadamard Type for k-Fractional Conformable Integrals
Author(s):
C.-J. Huang, G. Rahman, K. S. Nisar, A. Ghaffar and F. Qi
Department of Mathematics, Ganzhou Teachers College,
Ganzhou 341000, Jiangxi,
China.
E-mail:
hcj73jx@126.com ,
huangcj1973@qq.com
Department of Mathematics, Shaheed Benazir
Bhutto University,
Sheringal, Upper Dir, Khyber Pakhtoonkhwa,
Pakistan.
E-mail: gauhar55uom@gmail.com
Department of Mathematics, College of Arts
and Science at Wadi Aldawaser, 11991,
Prince Sattam Bin Abdulaziz University, Riyadh Region,
Kingdom of Saudi Arabia.
E-mail: n.sooppy@psau.edu.sa,
ksnisar1@gmail.com
Department of Mathematical Science,
Balochistan University of Information Technology,
Engineering and Management Sciences, Quetta,
Pakistan.
E-mail: abdulghaffar.jaffar@gmail.com
School of Mathematical Sciences, Tianjin
Polytechnic University,
Tianjin 300387,
China; Institute of Mathematics,
Henan Polytechnic University, Jiaozuo 454010, Henan,
China.
E-mail: qifeng618@gmail.com,
qifeng618@qq.com
Abstract:
In the paper, the authors deal with generalized k-fractional conformable integrals, establish some inequalities of the Hermite-Hadamard type for generalized k-fractional conformable integrals for convex functions, and generalize known inequalities of the Hermite-Hadamard type for conformable fractional integrals.
Paper's Title:
A new approach to the study of fixed point for simulation functions with application in G-metric spaces
Author(s):
Komi Afassinou and Ojen Kumar Narain
Department of Mathematical Sciences,
University of Zululand,
KwaDlangezwa,
South Africa.
E-mail: komia@aims.ac.za
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
The purpose of this work is to generalize the fixed point results of Kumar et al. [11] by introducing the concept of (α,β)-Z-contraction mapping, Suzuki generalized (α,β)-Z-contraction mapping, (α,β)-admissible mapping and triangular (α,β)-admissible mapping in the frame work of G-metric spaces. Fixed point theorems for these class of mappings are established in the frame work of a complete G-metric spaces and we establish a generalization of the fixed point result of Kumar et al. [11] and a host of others in the literature. Finally, we apply our fixed point result to solve an integral equation.
Paper's Title:
Fekete-Szegö Inequality for Sakaguchi Type of functions in Petal Shaped Domain
Author(s):
E. K. Nithiyanandham and B. Srutha Keerthi
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: nithiyankrish@gmail.com
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com
Abstract:
In this paper, we estimate coefficient bounds,|a_2|,|a_3| and |a_4|, Fekete-Szegö inequality
![]() and Toeplitz determinant
T2(2) and T3(1) for functions belonging to the following class
and Toeplitz determinant
T2(2) and T3(1) for functions belonging to the following class
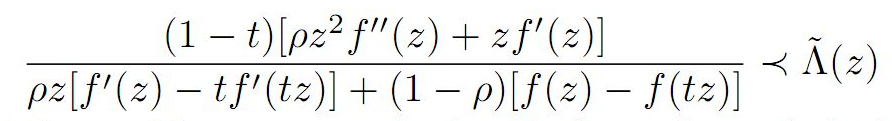
the function being holomorphic, we expand using Taylor series and obtain several corollaries and consequences for the main result.
Paper's Title:
Toeplitz Determinant for Sakaguchi Type Functions Under Petal Shaped Domain
Author(s):
B. Nandhini and B. Srutha Keerthi
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail:
nandhinibaskar1996@gmail.com
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com
Abstract:
We introduce a new general subclass GPt,ρ of Sakaguchi kind function on a Petal shaped domain. We obtain coefficients bounds and upper bounds for the Fekete-Szegö functional over the class. From these functions we obtain the bounds of first four coefficients, and then we have derived the Toeplitz determinant T2(2) and T3(1) whose diagonal entries are the coefficients of functions.
Paper's Title:
Coefficient Bounds for Sakaguchi Kind of Functions Associated with Sine Function
Author(s):
Serap Bulut, H. Priya and B. Srutha Keerth
Kocaeli University,
Faculty of Aviation and Space Sciences,
Arslanbey Campus, 41285 Kartepe-Kocaeli,
Turkey.
E-mail: serap.bulut@kocaeli.edu.tr
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus, Chennai - 600 048,
India.
E-mail: priyaharikrishnan18@gmail.com,
priya.h2020@vitstudent.ac.in
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus, Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com,
sruthakeerthi.b@vit.ac.in
Abstract:
In this paper, we introduce a new general subclass of analytic functions with respect to symmetric points in the domain of sine function. We obtain sharp coefficient bounds and upper bounds for the Fekete-Szegö functional. Also we get sharp bounds for the logarithmic coefficients of functions belonging to this new class.
Search and serve lasted 1 second(s).