Paper's Title:

Hyperbolic Barycentric Coordinates

Author(s):

Abraham A. Ungar

Abstract:

A powerful and novel way to study Einstein's special theory of relativity and its underlying geometry, the hyperbolic geometry of Bolyai and Lobachevsky, by analogies with classical mechanics and its underlying Euclidean geometry is demonstrated. The demonstration sets the stage for the extension of the notion of barycentric coordinates in Euclidean geometry, first conceived by Möbius in 1827, into hyperbolic geometry. As an example for the application of hyperbolic barycentric coordinates, the hyperbolic midpoint of any hyperbolic segment, and the centroid and orthocenter of any hyperbolic triangle are determined.

Paper's Title:

On a subset of Bazilevic functions

Author(s):

Marjono and D. K. Thomas

Department of Mathematics,
Faculty of Mathematics and Natural Sciences,
Brawajaya University,
Malang, Jawa Timur 65145,
Indonesia.
E-mail: marjono@ub.ac.id

Department of Mathematics,
Swansea University, Singleton Park,
Swansea, SA2 8PP,
United Kingdom.
E-mail: d.k.thomas@swansea.ac.uk

Abstract:

Let S denote the class of analytic and univalent functions in 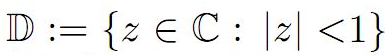of the form 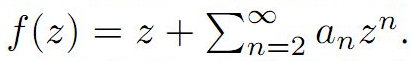For α≥0, the subclass B₁α of S of Bazilevic functions has been extensively studied. In this paper we determine various properties of a subclass of B₁α, for α≥0 which extends early results of a class of starlike functions studied by Ram Singh.

Paper's Title:

The Higher Coefficients for Bazilevic Functions B₁(α)

Author(s):

Marjono, Sa'adatul Fitri, and Krisna Adilia Daniswara

Department of Mathematics,
Faculty of Mathematics and Natural Sciences,,
Brawijaya University, Malang Jawa Timur 65145
Indonesia.
E-mail: marjono@ub.ac.id
saadatulfitri@ub.ac.id
krisnaadiliadaniswara@gmail.com
 

Abstract:

Let f be analytic in D{z: |z|< 1} with , and normalized by the conditions f(0)=f'(0)-1=0. We give sharp estimates for the seventh and eighth coefficients for the class of Bazilevic functions with logarithmic growth, B₁α, defined by for α≥0.

Paper's Title:

Fekete Szegö problem on the Class of Bazilevič functions B₁(α) related to the Lemniscate Bernoulli

Author(s):

N. M. Asih, Marjono, Sa'adatul Fitri, Ratno Bagus Edy Wibowo

Department of Mathematics,
University of Brawijaya,
Malang 65145,
Indonesia.
Department of Mathematics,
University of Udayana,
Bali,
Indonesia.
E-mail: madeasih@unud.ac.id

Department of Mathematics,
University of Brawijaya,
Malang 65145,
Indonesia.
E-mail: marjono@ub.ac.id

Department of Mathematics,
University of Brawijaya,
Malang 65145,
Indonesia.
E-mail: saadatulfitri@ub.ac.id

Department of Mathematics,
University of Brawijaya,
Malang 65145,
Indonesia.
E-mail: rbagus@ub.ac.id

Abstract:

We provide a sharp boundaries inequalities for Fekete Szegö problem |a₃-μ a₂²|, the coefficients of logarithmic function log~ f(z)/z, and the coefficients of the inverse function f(f'(w)) on the Bazilevič functions B₁(α) related to the Lemniscate Bernoulli on the unit disk D={z: |z| < 1}. We obtained the result by using some properties of function with positive real part relates to coefficients problems.

Paper's Title:

On Sufficient Conditions for Strong Starlikeness

Author(s):

V. Ravichandran, M. H. Khan, M. Darus, And K. G. Subramanian

School of Mathematical Sciences, Universiti Sains Malaysia, 11800 Usm Penang, Malaysia
vravi@cs.usm.my
Url: http://cs.usm.my/~vravi/index.html

Department of Mathematics, Islamiah College, Vaniambadi 635 751, India
khanhussaff@yahoo.co.in

School of Mathematical Sciences, Faculty of Science and Technology, UKM, Bangi 43600,
Malaysia
maslina@pkrisc.cc.ukm.my
Url: http://www.webspawner.com/users/maslinadarus

Department of Mathematics, Madras Christian College, Tambaram, Chennai 600 059, India
kgsmani@vsnl.net

Abstract:

In the present investigation, we obtain some sufficient conditions for a normalized analytic function f(z) defined on the unit disk to satisfy the condition

Paper's Title:

Asymptotic Analysis of Positive Decreasing Solutions of a Class of Systems of Second Order Nonlinear Differential Equations in the Framework of Regular Variation

Author(s):

Jaroslav Jaroš, Kusano Takaŝi, Tomoyuki Tanigawa

Department of Mathematical Analysis and Numerical Mathematics,
Faculty of Mathematics, Physics and Informatics,
Comenius Universiy, 842 48 Bratislava,
Slovakia.

E-mail: ksntksjm4@gmail.com

Professor Emeritus at: Hiroshima University,
Department of Mathematics, Faculty of Science,
Higashi-Hiroshima 739-8526,
Japan.

E-mail: jaros@fmph.uniba.sk

Department of Mathematics, Faculty of Education,
Kumamoto University, Kumamoto 860-8555,
Japan.

E-mail: tanigawa@educ.kumamoto-u.ac.jp
 

Abstract:

The system of nonlinear differential equations

is under consideration, where α_i and β_i are positive constants and p_i(t) and q_i(t) are continuous regularly varying functions on [a,∞). Two kinds of criteria are established for the existence of strongly decreasing regularly varying solutions with negative indices of (A) with precise asymptotic behavior at infinity. Fixed point techniques and basic theory of regular variation are utilized for this purpose.

Paper's Title:

A Subordination Theorem for Analytic Functions

Author(s):

Marjono

Department of Mathematics, Faculty of Mathematics and Natural Sciences,
University of Brawijaya,
Jl. Veteran Malang 65145,
INDONESIA.
E-mail: marjono@ub.ac.id
URL: http://matematika.ub.ac.id

Abstract:

It is shown that if f is analytic in D={z:|z|<1}, with f(0)=f'(0)-1=0, then for implies where and that β(γ) is the largest number such that this implication holds.

Paper's Title:

Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.

Paper's Title:

Approximately Dual p-Approximate Schauder Frames

Author(s):

K. Mahesh Krishna and P. Sam Johnson

Stat-Math Unit, Indian Statistical Institute, Bangalore Centre,
Karnataka 560 059
India.

Department of Mathematical and Computational Sciences,
National Institute of Technology Karnataka (NITK),
Surathkal, Mangaluru 575 025,
India.

E-mail: kmaheshak@gmail.com sam@nitk.edu.in
 

Abstract:

Approximately dual frame in Hilbert spaces was introduced by Christensen and Laugesen to overcome difficulties in constructing dual frames for a given Hilbert space frame. It becomes even more difficult in Banach spaces to construct duals. For this purpose, we introduce approximately dual frames for a class of approximate Schauder frames for Banach spaces and develop basic theory. Approximate dual for this subclass is completely characterized and its perturbation is also studied.

Paper's Title:

On Certain Classes of Harmonic Univalent Functions Based on Salagean Operator

Author(s):

G. Murugusundaramoorthy, Thomas Rosy, and B. A. Stephen

Department of Applied Mathematics and Informatics,
Department of Mathematics, Vellore Institute of Technology,
Deemed University, Vellore - 632014, India.
gmsmoorthy@yahoo.com 

Department of Applied Mathematics and Informatics,
Department of Mathematics, Madras Christian College,
Chennai - 600059, India.
drthomasrosy@rediffmail.com 

Abstract:

We define and investigate a class of complex-valued harmonic univalent functions of the form f = h + g using Salagean operator where h and g are analytic in the unit disc U = { z : |z| < 1 }. A necessary and sufficient coefficient conditions are given for functions in these classes. Furthermore, distortion theorems, inclusion relations, extreme points, convolution conditions and convex combinations for this family of harmonic functions are obtained.

Paper's Title:

On the Fekete-Szegő Inequality for Some Subclasses of Analytic Functions

Author(s):

T.N. Shanmugam and A. Singaravelu

Department of Mathematics,
College of Engineering,
Anna University, Chennai-600 025,
Tamilnadu, India
shan@annauniv.edu

Department of Mathematics,
Valliammai Engineering College,
Chennai-603 203,
Tamilnadu, India
sivasaisastha@rediffmail.com

Abstract:

In this present investigation, the authors obtainFekete-Szegő's inequality for certain normalized analytic functions defined on the open unit disk for which lie in a region starlike with respect to 1 and symmetric with respect to the real axis. Also certain applications of the main result for a class of functions defined by convolution are given. As a special case of this result, Fekete-Szegő's inequality for a class of functions defined through fractional derivatives is also obtained.

Paper's Title:

Fractional class of analytic functions Defined Using q-Differential Operator

Author(s):

K . R. Karthikeyan, Musthafa Ibrahim and S. Srinivasan

Department of Mathematics and Statistics,
Caledonian College of Engineering, Muscat,
Sultanate of Oman.
E-mail: kr_karthikeyan1979@yahoo.com

College of Engineering,
University of Buraimi, Al Buraimi,
Sultanate of Oman.
E-mail: musthafa.ibrahim@gmail.com

Department of Mathematics, Presidency College (Autonomous),
Chennai-600005, Tamilnadu,
India.
 

Abstract:

We define a q-differential fractional operator, which generalizes Salagean and Ruscheweyh differential operators. We introduce and study a new class of analytic functions involving q-differential fractional operator. We also determine the necessary and sufficient conditions for functions to be in the class. Further, we obtain the coefficient estimates, extreme points, growth and distortion bounds.

Paper's Title:

A Low Order Least-Squares Nonconforming Finite Element Method for Steady Magnetohydrodynamic Equations

Author(s):

Z. Yu, D. Shi and H. Zhu

College of Science,
Zhongyuan University of Technology,
Zhengzhou 450007,
China.
E-mail: 5772@zut.edu.cn

School of Mathematics and Statistics,
Zhengzhou University,
Zhengzhou 450001,
China.
E-mail: shi_dy@126.com

Mathematics Department,
University of Southern Mississippi,
Hattiesburg MS, 39406,
U.S.A
E-mail: huiqing.zhu@usm.edu

Abstract:

A low order least-squares nonconforming finite element (NFE) method is proposed for magnetohydrodynamic equations with EQ₁^rot element and zero-order Raviart-Thomas element. Based on the above element's typical interpolations properties, the existence and uniqueness of the approximate solutions are proved and the optimal order error estimates for the corresponding variables are derived.

Paper's Title:

Higher Order Accurate Compact Schemes for Time Dependent Linear and Nonlinear Convection-Diffusion Equations

Author(s):

S. Thomas, Gopika P.B. and S. K. Nadupuri

Department of Mathematics
National Institute of Technology Calicut
Kerala
673601
India.
E-mail: sobinputhiyaveettil@gmail.com pbgopika@gmail.com nsk@nitc.ac.in
 

Abstract:

The primary objective of this work is to study higher order compact finite difference schemes for finding the numerical solution of convection-diffusion equations which are widely used in engineering applications. The first part of this work is concerned with a higher order exponential scheme for solving unsteady one dimensional linear convection-diffusion equation. The scheme is set up with a fourth order compact exponential discretization for space and cubic $C^1$-spline collocation method for time. The scheme achieves fourth order accuracy in both temporal and spatial variables and is proved to be unconditionally stable. The second part explores the utility of a sixth order compact finite difference scheme in space and Huta's improved sixth order Runge-Kutta scheme in time combined to find the numerical solution of one dimensional nonlinear convection-diffusion equations. Numerical experiments are carried out with Burgers' equation to demonstrate the accuracy of the new scheme which is sixth order in both space and time. Also a sixth order in space predictor-corrector method is proposed. A comparative study is performed of the proposed schemes with existing predictor-corrector method. The investigation of computational order of convergence is presented.

Paper's Title:

Viability Theory And Differential Lanchester Type Models For Combat.
Differential Systems.

Author(s):

G. Isac and A. Gosselin

Department Of Mathematics, Royal Military College Of Canada,
P.O. Box 17000, Stn Forces, Kingston, Ontario, Canada K7k 7b4
isac-g@rmc.ca
gosselin-a@rmc.ca
URL: http://www.rmc.ca/academic/math_cs/isac/index_e.html
URL: http://www.rmc.ca/academic/math_cs/gosselin/index_e.html

Abstract:

In 1914, F.W. Lanchester proposed several mathematical models based on differential equations to describe combat situations [34]. Since then, his work has been extensively modified to represent a variety of competitions including entire wars. Differential Lanchester type models have been studied from many angles by many authors in hundreds of papers and reports. Lanchester type models are used in the planning of optimal strategies, supply and tactics. In this paper, we will show how these models can be studied from a viability theory stand point. We will introduce the notion of winning cone and show that it is a viable cone for these models. In the last part of our paper we will use the viability theory of differential equations to study Lanchester type models from the optimal theory point of view.

Paper's Title:

An Easy and Efficient Way for Solving A class of Singular Two Point Boundary Value Problems

Author(s):

Muhammed I. Syam, Muhammed N. Anwar and Basem S. Attili

Mathematical Sciences Department
United Arab Emirates University, P. O. Box 17551
Al-Ain, United Arab Emirates
b.attili@uaeu.ac.ae

Abstract:

We will consider an efficient and easy way for solving a certain class of singular two point boundary value problems. We will employ the least squares method which proved to be efficient for this type of problems. Enough examples that were considered by others will be solved with comparison with the results presented there.

Paper's Title:

Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.

Paper's Title:

A Comparison Between Two Different Stochastic Epidemic Models with Respect to the Entropy

Author(s):

Farzad Fatehi and Tayebe Waezizadeh

Department of Mathematics,
University of Sussex,
Brighton BN1 9QH,
UK.
E-mail: f.fatehi@sussex.ac.uk
URL: http://www.sussex.ac.uk/profiles/361251

Department of Pure Mathematics, Faculty of Mathematics and Computer,
Shahid Bahonar University of Kerman,
Kerman 76169-14111,
Iran.
E-mail: waezizadeh@uk.ac.ir
URL: http://academicstaff.uk.ac.ir/en/tavaezizadeh

Abstract:

In this paper at first a brief history of mathematical models is presented with the aim to clarify the reliability of stochastic models over deterministic models. Next, the necessary background about random variables and stochastic processes, especially Markov chains and the entropy are introduced. After that, entropy of SIR stochastic models is computed and it is proven that an epidemic will disappear after a long time. Entropy of a stochastic mathematical model determines the average uncertainty about the outcome of that random experiment. At the end, we introduce a chain binomial epidemic model and compute its entropy, which is then compared with the DTMC SIR epidemic model to show which one is nearer to reality.

Paper's Title:

Bounds on the Jensen Gap, and Implications for Mean-Concentrated Distributions

Author(s):

Xiang Gao, Meera Sitharam, Adrian E. Roitberg

Department of Chemistry, and Department of Computer & Information Science & Engineering,
University of Florida,
Gainesville, FL 32611,
USA.
E-mail: qasdfgtyuiop@gmail.com
URL: https://scholar.google.com/citations?user=t2nOdxQAAAAJ

Abstract:

This paper gives upper and lower bounds on the gap in Jensen's inequality, i.e., the difference between the expected value of a function of a random variable and the value of the function at the expected value of the random variable. The bounds depend only on growth properties of the function and specific moments of the random variable. The bounds are particularly useful for distributions that are concentrated around the mean, a commonly occurring scenario such as the average of i.i.d. samples and in statistical mechanics.

Paper's Title:

Hankel Functional Connected to Lemniscate of Bernoulli

Author(s):

K. Ramanuja Rao, Rajnesh Lal and Kaushal Singh

Fiji National University,
Department of Mathematics & Statistics,
P.O. Box 5529, Lautoka,
Fiji.
E-mail: ramanuja.kotti@fnu.ac.fj
 rajnesh.lal@fnu.ac.fj
kaushal.singh@fnu.ac.fj

Abstract:

The aim of present paper is to derive a higher bound (HB) of 3^rd order Hankel determinant for a collection of holomorphic mappings connected with exactly to the right side of the lemniscate of Bernoulli, whose polar coordinates form is r² = 2cos²(2θ). The method carried in this paper is more refined than the method adopted by the authors (see [1]), who worked on this problem earlier.

Paper's Title:

Fekete-Szegö Inequality for Sakaguchi Type of functions in Petal Shaped Domain

Author(s):

E. K. Nithiyanandham and B. Srutha Keerthi

Division of Mathematics, School of Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: nithiyankrish@gmail.com

Division of Mathematics, School of Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com

Abstract:

In this paper, we estimate coefficient bounds,|a_2|,|a_3| and |a_4|, Fekete-Szegö inequality and Toeplitz determinant T₂(2) and T₃(1) for functions belonging to the following class

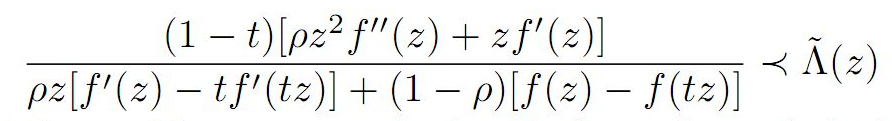
the function being holomorphic, we expand using Taylor series and obtain several corollaries and consequences for the main result.

Paper's Title:

Toeplitz Determinant for Sakaguchi Type Functions Under Petal Shaped Domain

Author(s):

B. Nandhini and B. Srutha Keerthi

Division of Mathematics, School of Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: nandhinibaskar1996@gmail.com

Division of Mathematics, School of Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com

Abstract:

We introduce a new general subclass GP^t,ρ of Sakaguchi kind function on a Petal shaped domain. We obtain coefficients bounds and upper bounds for the Fekete-Szegö functional over the class. From these functions we obtain the bounds of first four coefficients, and then we have derived the Toeplitz determinant T₂(2) and T₃(1) whose diagonal entries are the coefficients of functions.

Search and serve lasted 0 second(s).