Paper's Title:

Approximately Dual p-Approximate Schauder Frames

Author(s):

K. Mahesh Krishna and P. Sam Johnson

Stat-Math Unit, Indian Statistical Institute, Bangalore Centre,
Karnataka 560 059
India.

Department of Mathematical and Computational Sciences,
National Institute of Technology Karnataka (NITK),
Surathkal, Mangaluru 575 025,
India.

E-mail: kmaheshak@gmail.com sam@nitk.edu.in
 

Abstract:

Approximately dual frame in Hilbert spaces was introduced by Christensen and Laugesen to overcome difficulties in constructing dual frames for a given Hilbert space frame. It becomes even more difficult in Banach spaces to construct duals. For this purpose, we introduce approximately dual frames for a class of approximate Schauder frames for Banach spaces and develop basic theory. Approximate dual for this subclass is completely characterized and its perturbation is also studied.

Paper's Title:

Additive Mappings on Semiprime Rings Functioning as Centralizers

Author(s):

Abu Zaid Ansari and Faiza Shujat

Department of Mathematics,
Faculty of Science,
Islamic University of Madinah, Madinah
K.S.A.
E-mail: ansari.abuzaid@gmail.com, ansari.abuzaid@iu.edu.sa

Department of Mathematics,
Faculty of Science,
Taibah University, Madinah,
K.S.A.
E-mail: faiza.shujat@gmail.com, fullahkhan@taibahu.edu.sa

Abstract:

The objective of this research is to prove that an additive mapping T:R → R is a centralizer on R if it satisfies any one of the following identities:

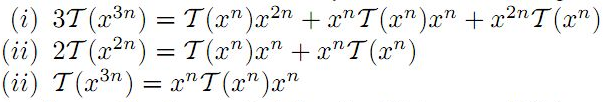
for all x ∈ R, where n ≥ 1 is a fixed integer and R is any suitably torsion free semiprime ring. Some results on involution "*" are also presented as consequences of the main theorems. In addition, we will take criticism in account with examples.

Paper's Title:

A Unifying View of Some Banach Algebras

Author(s):

R. Kantrowitz

Mathematics & Statistics Department,
Hamilton College,
198 College Hill Road,
Clinton, NY 13323, USA.
E-mail: rkantrow@hamilton.edu

Abstract:

The purpose of this article is to shed light on a unifying framework for some normed algebras and, in particular, for some Banach algebras. The focus is on linear operators T between normed algebras X and Y and specified subalgebras A of Y. When the action of T on products in X satisfies a certain operative equation, the subspace T^-1(A) is stable under the multiplication of X and is readily equipped with a family of canonical submultiplicative norms. It turns out that many familiar and important spaces are encompassed under this versatile perspective, and we offer a sampling of several such. In this sense, the article presents an alternative lens through which to view a host of normed algebras. Moreover, recognition that a normed linear space conforms to this general structure provides another avenue to confirming that it is at once stable under multiplication and also outfitted with an abundance of equivalent submultiplicative norms.

Paper's Title:

Estimates of Norms on Krein Spaces

Author(s):

Satheesh K. Athira, P. Sam Johnson and K. Kamaraj

Department of Mathematical and Computational Sciences,
National Institute of Technology Karnataka,
Surathkal, Mangaluru 575 025,
India.
E-mail: athirachandri@gmail.com

Department of Mathematical and Computational Sciences,
National Institute of Technology Karnataka,
Surathkal, Mangaluru 575 025,
India.
E-mail:sam@nitk.edu.in

Department of Mathematics,
University College of Engineering Arni,
Anna University, Arni 632 326,
India.
E-mail: krajkj@yahoo.com

Abstract:

Various norms can be defined on a Krein space by choosing different underlying fundamental decompositions. Some estimates of norms on Krein spaces are discussed and a few results in Bognar's paper are generalized.

Paper's Title:

q-Norms are Really Norms

Author(s):

H. Belbachir, M. Mirzavaziri and M. S. Moslehian

USTHB, Faculté de Mathématiques,
B.P. 32, El Alia, 16111,
Bab Ezzouar, Alger,
Algérie.
hbelbachir@usthb.dz

Department of Mathematics,
Ferdowsi University, P. O. Box 1159,
Mashhad 91775, Iran.
mirzavaziri@math.um.ac.ir
URL: http://www.mirzavaziri.com

Department of Mathematics,
Ferdowsi University,
P. O. Box 1159,
Mashhad 91775, Iran.
moslehian@ferdowsi.um.ac.ir
URL: http://www.um.ac.ir/~moslehian/

Abstract:

Replacing the triangle inequality, in the definition of a norm, by , we introduce the notion of a q-norm. We establish that every q-norm is a norm in the usual sense, and that the converse is true as well.

Paper's Title:

A New Family of Periodic Functions as Explicit Roots of a Class of Polynomial Equations

Author(s):

M. Artzrouni

Department of Mathematics, University of Pau
64013 Pau Cedex
Pau, France
marc.artzrouni@univ-pau.fr
URL: http://www.univ-pau.fr/~artzroun

Abstract:

For any positive integer n a new family of periodic functions in power series form and of period n is used to solve in closed form a class of polynomial equations of order n. The n roots are the values of the appropriate function from that family taken at 0, 1, ... , n-1.

Paper's Title:

Note on the Rank of Birkhoff Interpolation

Author(s):

J. Rubió-Massegú

Applied Mathematics III, Universitat Politècnica de Catalunya,
Colom 1, 08222, Terrassa,
Spain
josep.rubio@upc.edu

Abstract:

The relationship between a variant of the rank of a univariate Birkhoff interpolation problem, called normal rank, and other numbers of interest associated to the interpolation problem is studied.

Paper's Title:

Power and Euler-Lagrange Norms

Author(s):

Mohammad Sal Moslehian and John Michael Rassias

Department of Mathematics,
Ferdowsi University,
P. O. Box 1159, Mashhad 91775,
Iran;
Department of Pure Mathematics,
University of Leeds,
Leeds LS2 9JT,
United Kingdom.
moslehian@ferdowsi.um.ac.ir
URL: http://www.um.ac.ir/~moslehian/

Pedagogical Department, E.E., Section of Mathematics and Informatics
National and Capodistrian University of Athens,
4, Agamemnonos str., Aghia Paraskevi, Attikis 15342, Athens,
Greece.
jrassias@primedu.uoa.gr
URL: http://www.primedu.uoa.gr/~jrassias/

Abstract:

We introduce the notions of power and Euler-Lagrange norms by replacing the triangle inequality, in the definition of norm, by appropriate inequalities. We prove that every usual norm is a power norm and vice versa. We also show that every norm is an Euler-Lagrange norm and that the converse is true under certain condition.

Paper's Title:

Stability of Almost Multiplicative Functionals

Author(s):

Norio Niwa, Hirokazu Oka, Takeshi Miura and Sin-Ei Takahasi

Abstract:

Let δ and p be non-negative real numbers. Let be the real or complex number field and a normed algebra over . If a mapping satisfies

then we show that φ is multiplicative or for all If, in addition, φ satisfies

for some p≠1, then by using Hyers-Ulam-Rassias stability of additive Cauchy equation, we show that φ is a ring homomorphism or for all In other words, φ is a ring homomorphism, or an approximately zero mapping. The results of this paper are inspired by Th.M. Rassias' stability theorem.

Paper's Title:

Some Properties of the Marshall-Olkin and Generalized Cuadras-Augé Families of Copulas

Author(s):

Edward Dobrowolski and Pranesh Kumar

Department of Mathematics and Statistics
University of Northern British Columbia
Prince George, BC,
Canada, V2N 4Z9

E-mail: Pranesh.Kumar@unbc.ca  

Abstract:

We investigate some properties of the families of two parameter Marshall-Olkin and Generalized Cuadras-Augé copulas. Some new results are proved for copula parameters, dependence measure and mutual information. A numerical application is discussed.

Paper's Title:

On Some Constructive Method of Rational Approximation

Author(s):

Vasiliy A. Prokhorov

Department of Mathematics and Statistics
University of South Alabama
Mobile, Alabama 36688-0002,
USA.

E-mail: prokhoro@southalabama.edu
URL: http://www.southalabama.edu/mathstat/people/prokhorov.shtml

Abstract:

We study a constructive method of rational approximation of analytic functions based on ideas of the theory of Hankel operators. Some properties of the corresponding Hankel operator are investigated. We also consider questions related to the convergence of rational approximants. Analogues of Montessus de Ballore's and Gonchars's theorems on the convergence of rows of Padé approximants are proved.

Paper's Title:

The Dynamics of an Ebola Epidemic Model with Quarantine of Infectives

Author(s):

Eliab Horub Kweyunga

Department of Mathematics,
Kabale University,
P.O.Box 317, Kabale,
Uganda.

E-mail: hkweyunga@kab.ac.ug

Abstract:

The recurrent outbreaks of ebola in Africa present global health challenges. Ebola is a severe, very fatal disease with case fatality rates of up to 90%. In this paper, a theoretical deterministic model for ebola epidemic with quarantine of infectives is proposed and analyzed. The model exhibits two equilibria; the disease free and endemic equilibrium points. The basic reproduction number, R₀, which is the main threshold, is obtained and the stability of the equilibrium points established. Using parameter values drawn from the 2014 West Africa ebola outbreak, a numerical simulation of the model is carried out. It is found that the dynamics of the model are completely determined by R₀ and that a quarantine success rate of at least 70% is sufficient to contain the disease outbreak.

Paper's Title:

Simplicial (co)-homology of Band Semigroup

Author(s):

Yasser Farhat

Academic Support Department,
Abu Dhabi Polytechnic,
P.O. Box 111499, Abu Dhabi,
UAE.

E-mail: yasser.farhat@adpoly.ac.ae, farhat.yasser.1@gmail.com

Abstract:

We consider the Banach algebra l¹(S), with convolution, where S is a band semigroup. We prove directly, without using the cyclic cohomology, that the simplicial cohomology groups Hⁿ(l¹(S), l¹(S)^*) vanish for all n≥1. This proceeds in three steps. In each step, we introduce a bounded linear map. By iteration in each step, we achieve our goal.

Paper's Title:

Several Applications of a Local Non-convex Young-type Inequality

Author(s):

Loredana Ciurdariu, Sorin Lugojan

Department of Mathematics,
"Politehnica" University of Timisoara,
P-ta. Victoriei, No.2, 300006-Timisoara,
Romania.

E-mail: ltirtirau87@yahoo.com

Abstract:

A local version of the Young inequality for positive numbers is used in order to deduce some inequalities about determinants and norms for real quadratic matrices and norms of positive operators on complex Hilbert spaces.

Paper's Title:

Bounds for the Extremal Eigenvalues of Positive Definite Matrices

Author(s):

Shivani Singh and Pravin Singh

Unisa, Department of Decision Sciences,
PO Box 392,
Pretoria,
0003,
South Africa.
E-mail: singhs2@unisa.ac.za

University of KwaZulu-Natal,
School of Mathematics Statistics and Computer Sciences
Private Bag X54001,
Durban,
4000,
South Africa.
E-mail: singhprook@gmail.com

Abstract:

We use a projection to achieve bounds for a vector function of the eigenvalues of a positive definite matrix. For various choices of the monotonic function we are able to obtain bounds for the extremal eigenvalues in terms of the traces of the matrix and its powers. These bounds are relatively simple to compute.

Paper's Title:

Jordan Canonical Form of Interval Matrices and Applications

Author(s):

S. Hema Surya, T. Nirmala and K. Ganesan

Department of Mathematics, College of Engineering and Technology,
SRM Institute of Science and Technology,
Kattankulathur,
Chennai-603203,
India.
E-mail: nirmalat@srmist.edu.in
URL: https://www.srmist.edu.in/faculty/dr-t-nirmala/

Abstract:

A square interval matrix over R can be converted to diagonal form if certain prerequisites are satisfied. However not all square matrices can be diagonalized. As a consequence, we strive the next simplest form to which it can be reduced while retaining important properties such as eigenvalues, rank, nullity, and so on. It turns out that any real interval matrix has a Jordan Canonical Form (JCF) over E if it has n interval eigenvalues in IR. We discuss in this paper a method for computing the Jordan canonical form of an interval matrix using a new pairing technique and a new type of interval arithmetic that will make classifying and analyzing interval matrices easier and more efficient. We conclude with a numerical example that supports the theory and application of predator-prey model.

Paper's Title:

The Automatic Continuity of N-Homomorphisms in Certain *-Banach Algebras

Author(s):

M. Aboulekhlef, Y. Tidli

Laboratory of Applied Mathematics and Information and Communication Technology
Polydisciplinary Faculty of Khouribga
University of Sultan Moulay Slimane
Morocco.
E-mail: aboulekhlef@gmail.com y.tidli@gmail.com

Abstract:

In this study, we prove the automatic continuity of surjective n-homomorphism between complete p-normed algebras. We show also that if Α and Β are complete *-p-normed algebras, Β is *simple and ψ: Α → Β is a surjective n-homomorphism under certain conditions, then ψ is continuous.

Paper's Title:

Eigenvalue Bounds based on Projections

Author(s):

Pravin Singh, Shivani Singh, Virath Singh

University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.

University of South Africa,
Department of Decision Sciences, PO Box 392,
 Pretoria,0003,
South Africa.

University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.

E-mail: singhp@ukzn.ac.za, singhs2@unisa.ac.za, singhv@ukzn.ac.za
 

Abstract:

In this paper, we derive expressions for the bounds of the extremal eigenvalues of positive definite matrices. Our approach is to use a symmetric projection operator onto an n-2 dimensional subspace of the real space of n tuples. These bounds are based on traces of the matrix and its powers. They are relatively easy and inexpensive to compute.

Paper's Title:

Recursive Bounds for the Eigenvalues of Symmetric Positive Definite Matrices

Author(s):

Pravin Singh, Shivani Singh, Virath Singh

University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.

University of South Africa,
Department of Decision Sciences, PO Box 392,
 Pretoria,0003,
South Africa.

University of KwaZulu-Natal,
Private Bag X54001,
Durban, 4001,
South Africa.

E-mail: singhp@ukzn.ac.za, singhs2@unisa.ac.za, singhv@ukzn.ac.za
 

Abstract:

In this paper, we bound the extremal eigenvalues of a positive definite real symmetric matrix by considering a part of the characteristic equation in the region of the smallest and largest eigenvalues. An expansion around these values leads to a sequence of monotonic functions, whose zeros coincide with the extremal zeros of associated polynomials. The latter is shown to yield bounds that are fairly accurate.

Paper's Title:

Automatic Continuity of Generalized Derivations in Certain *-Banach Algebras

Author(s):

M. Aboulekhlef, Y. Tidli and M. Belam

Laboratory of Applied Mathematics and Information and Communication Technology Polydisciplinary
Faculty of Khouribga University of Sultan Moulay Slimane
Morocco.
E-mail: aboulekhlef@gmail.com y.tidli@gmail.com m.belam@gmail.com

Abstract:

Consider the map φ of the Banach algebra Β in Β, if there exists a derivation δ of Β in Β so that for every  x, y ∈ Β , φ(xy) =φ(x)y+xδ(y) . φ is called a generalized derivation of Β. In [9], Bresar introduced the concept of generalized derivations. We prove several results about the automatic continuity of generalized derivations on certain Banach algebras.

Search and serve lasted 1 second(s).