Paper's Title:

Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.

Paper's Title:

An Efficient Modification of Differential Transform Method for Solving Integral and Integro-differential Equations

Author(s):

S. Al-Ahmad, Ibrahim Mohammed Sulaiman^*, and M. Mamat

Faculty of Informatics and Computing,
Universiti Sultan Zainal Abidin,
Terengganu, Besut Campus, 22200,
Malaysia.
E-mail: Alahmad.shadi@yahoo.com, ^*sulaimanib@unisza.edu.my, must@unisza.edu.my
 

Abstract:

In this paper, classes of integral and integro-differential equations are solved using a modified differential transform method. This proposed technique is based on differential transform method (DTM), Laplace transform (LT) procedure and Pad\'{e} approximants (PA). The proposed method which gives a good approximation for the true solution in a large region is referred to modified differential transform method (MDTM). An algorithm was developed to illustrate the flow of the proposed method. Some numerical problems are presented to check the applicability of the proposed scheme and the obtained results from the computations are compared with other existing methods to illustrates its efficiency. Numerical results have shown that the proposed MDTM method is promising compared to other existing methods for solving integral and integro-differential equations.

Paper's Title:

Nonlinear System of Mixed Ordered Variational Inclusions Involving XOR Operation

Author(s):

Iqbal Ahmad, Abdullah and Syed Shakaib Irfan

Department of Mechanical Engineering,
College of Engineering, Qassim University
Buraidah 51452, Al-Qassim,
Saudi Arabia.
E-mail: iqbal@qec.edu.sa, i.ahmad@qu.edu.sa

Zakir Husain Delhi College,
University of Delhi,
JLN Marg, New Delhi- 110 002,
India.
E-mail: abdullahdu@qec.edu.sa

Department of Mathematics,
Aligarh Muslim University, Aligarh,
India.
E-mail: shakaibirfan@gmail.com

Abstract:

In this work, we introduce and solve an NSMOVI frameworks system involving XOR operation with the help of a proposed iterative algorithm in real ordered positive Hilbert spaces. We discuss the existence of a solution of a considered system of inclusions involving XOR operation by applying the resolvent operator technique with XOR operation and also study the strong convergence of the sequences generated by the considered algorithm. Further, we give a numerical example in support of our considered problem which gives the grantee that all the proposed conditions of our main result are fulfilled.

Paper's Title:

Antiderivatives and Integrals Involving Incomplete Beta Functions with Applications

Author(s):

R. AlAhmad^1,2 and H. Almefleh¹

Mathematics Department,
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: rami_thenat@yu.edu.jo

Faculty of Engineering,
Higher Colleges of Technology,
Ras Alkhaimah,
UAE.

Abstract:

In this paper, we prove that incomplete beta functions are antiderivatives of several products and powers of trigonometric functions, we give formulas for antiderivatives for products and powers of trigonometric functions in term of incomplete beta functions, and we evaluate integrals involving trigonometric functions using incomplete beta functions. Also, we extend some properties of the beta functions to the incomplete beta functions. As an application for the above results, we find the moments for certain probability distributions.

Paper's Title:

Solving Non-Autonomous Nonlinear Systems of Ordinary Differential Equations Using Multi-Stage Differential Transform Method

Author(s):

K. A. Ahmad, Z. Zainuddin, F. A. Abdullah

School of Mathematical Sciences Universiti Sains Malaysia
11800 USM Penang
Malaysia.
E-mail: abumohmmadkh@hotmail.com
zarita@usm.my
farahaini@usm.my

Abstract:

Differential equations are basic tools to describe a wide variety of phenomena in nature such as, electrostatics, physics, chemistry, economics, etc. In this paper, a technique is developed to solve nonlinear and linear systems of ordinary differential equations based on the standard Differential Transform Method (DTM) and Multi-stage Differential Transform Method (MsDTM). Comparative numerical results that we are obtained by MsDTM and Runge-Kutta method are proposed. The numerical results showed that the MsDTM gives more accurate approximation as compared to the Runge-Kutta numerical method for the solutions of nonlinear and linear systems of ordinary differential equations

Paper's Title:

Composite Variational-Like Inequalities Given By Weakly Relaxed ζ-Semi-Pseudomonotone Multi-Valued Mapping

Author(s):

Syed Shakaib Irfan, Iqbal Ahmad, Zubair Khan and Preeti Shukla

College of Engineering, Qassim University
Buraidah, Al-Qassim,
Saudi Arabia.
E-mail: shakaib@qec.edu.sa

College of Engineering, Qassim University
Buraidah, Al-Qassim,
Saudi Arabia.
E-mail: iqbal@qec.edu.sa

Department of Mathematics,
Integral University Lucknow,
India.
E-mail: zkhan@iul.ac.in

Department of Mathematics,
Integral University Lucknow,
India.
E-mail: shuklapreeti1991@gmail.com

Abstract:

In this article, we introduce a composite variational-like inequalities with weakly relaxed ζ-pseudomonotone multi-valued maping in reflexive Banach spaces. We obtain existence of solutions to the composite variational-like inequalities with weakly relaxed ζ-pseudomon -otone multi-valued maps in reflexive Banach spaces by using KKM theorem. We have also checked the solvability of the composite variational-like inequalities with weakly relaxed ζ-semi-pseudomonotone multi-valued maps in arbitrary Banach spaces using Kakutani-Fan-Glicksberg fixed point theorem.

Paper's Title:

Some Approximation for the linear combinations of modified Beta operators

Author(s):

Naokant Deo

Department of Applied Mathematics
Delhi College of Engineering
Bawana Road, Delhi - 110042,
India.
dr_naokant_deo@yahoo.com

Abstract:

In this paper, we propose a sequence of new positive linear operators β_n to study the ordinary approximation of unbounded functions by using some properties of the Steklov means.

Paper's Title:

Some Generalized Difference Sequence Spaces Defined by Orlicz Functions

Author(s):

Ramzi S. N. Alsaedi and Ahmad H. A. Bataineh

Department of Mathematics, King Abdul Aziz University,
Jeddah P.O.Box 80203,
Saudia Arabia
ramzialsaedi@yahoo.co.uk

Department of Mathematics, Al al-Bayt University,
Mafraq 25113,
Jordan
ahabf2003@yahoo.ca

Abstract:

In this paper, we define the sequence spaces: [V,M,p,u,Δ ],[V,M,p,u,Δ]₀ and [V,M,p,u,Δ]_∞, where for any sequence x=(x_n), the difference sequence Δx is given by Δx=(Δx_n) = (x_n-x_n-1) . We also study some properties and theorems of these spaces. These are generalizations of those defined and studied by Savas and Savas and some others before.

Paper's Title:

Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.

Paper's Title:

Integrating Factors and First Integrals of a Class of Third Order Differential Equations

Author(s):

Mohammadkheer Al-Jararha

Department of Mathematics,
Yarmouk University,
Irbid 21163,
Jordan.

E-mail: mohammad.ja@yu.edu.jo

Abstract:

The principle of finding an integrating factor for a none exact differential equations is extended to a class of third order differential equations. If the third order equation is not exact, under certain conditions, an integrating factor exists which transforms it to an exact one. Hence, it can be reduced into a second order differential equation. In this paper, we give explicit forms for certain integrating factors of a class of the third order differential equations.

Paper's Title:

On Finding Integrating Factors and First Integrals for a Class of Higher Order Differential Equations

Author(s):

Mohammadkheer M. Al-Jararha

Department of Mathematics,
Yarmouk University,
Irbid, 21163,
Jordan.
E-mail: mohammad.ja@yu.edu.jo

Abstract:

If the $n-th$ order differential equation is not exact, under certain conditions, an integrating factor exists which transforms the differential equation into an exact one. Thus, the order of differential equation can be reduced to the lower order. In this paper, we present a technique for finding integrating factors of the following class of differential equations:
 

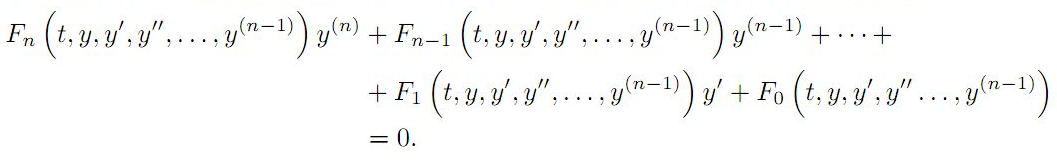
Here, the functions F₀,F₁,F₂, …,F_n are assumed to be continuous functions with their first partial derivatives on some simply connected domain Ω ⊂ Rⁿ⁺¹. We also presented some demonstrative examples

Paper's Title:

Formulation of Approximate Mathematical Model for Incoming Water to Some Dams on Tigris and Euphrates Rivers Using Spline Function

Author(s):

Nadia M. J. Ibrahem, Heba A. Abd Al-Razak, and Muna M. Mustafa

Mathematics Department,
College of Sciences for Women,
University of Baghdad, Baghdad,
Iraq.
E-mail: Nadiamj_math@csw.uobaghdad.edu.iq

Abstract:

In this paper, we formulate three mathematical models using spline functions, such as linear, quadratic and cubic functions to approximate the mathematical model for incoming water to some dams. We will implement this model on dams of both rivers; dams on the Tigris are Mosul and Amara while dams on the Euphrates are Hadetha and Al-Hindya.

Paper's Title:

Coefficient Bounds for Sakaguchi Kind of Functions Associated with Sine Function

Author(s):

Serap Bulut, H. Priya and B. Srutha Keerth

Kocaeli University,
Faculty of Aviation and Space Sciences,
Arslanbey Campus, 41285 Kartepe-Kocaeli,
Turkey.
E-mail: serap.bulut@kocaeli.edu.tr

 
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus, Chennai - 600 048,
India.
E-mail: priyaharikrishnan18@gmail.com, priya.h2020@vitstudent.ac.in

Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus, Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com, sruthakeerthi.b@vit.ac.in

Abstract:

In this paper, we introduce a new general subclass of analytic functions with respect to symmetric points in the domain of sine function. We obtain sharp coefficient bounds and upper bounds for the Fekete-Szegö functional. Also we get sharp bounds for the logarithmic coefficients of functions belonging to this new class.

Paper's Title:

Coincidences and Fixed Points of Hybrid Maps in Symmetric Spaces

Author(s):

S. L. Singh and Bhagwati Prasad

Vedic MRI, 21 Govind Nagar,
Rishikesh 249201
India
vedicmri@gmail.com

Department of Mathematics, Gurukula Kangri University,
Hardwar 249404,
India

Abstract:

The purpose of this paper is to obtain a new coincidence theorem for a single-valued and two multivalued operators in symmetric spaces. We derive fixed point theorems and discuss some special cases and applications.

Paper's Title:

Positive Solutions to a System of Boundary Value Problems for Higher-Dimensional Dynamic Equations on Time Scales

Author(s):

I. Y. Karaca

Department of Mathematics,
Ege University,
35100 Bornova, Izmir,
Turkey

ilkay.karaca@ege.edu.tr

URL: http://ege.edu.tr
 

Abstract:

In this paper, we consider the system of boundary value problems for higher-dimensional dynamic equations on time scales. We establish criteria for the existence of at least one or two positive solutions. We shall also obtain criteria which lead to nonexistence of positive solutions. Examples applying our results are also given.

Paper's Title:

Hyponormal and K-Quasi-Hyponormal Operators On Semi-Hilbertian Spaces

Author(s):

Ould Ahmed Mahmoud Sid Ahmed and Abdelkader Benali

Mathematics Department,
College of Science,
Aljouf University,
Aljouf 2014,
Saudi Arabia.
E-mail: sididahmed@ju.edu.sa

Mathematics Department, Faculty of Science,
Hassiba Benbouali, University of Chlef,
B.P. 151 Hay Essalem, Chlef 02000,
Algeria.
E-mail: benali4848@gmail.com

Abstract:

Let H be a Hilbert space and let A be a positive bounded operator on H. The semi-inner product < u|v>_A:=<Au|v>, u,v ∈ H induces a semi-norm || .||_A on H. This makes H into a semi-Hilbertian space. In this paper we introduce the notions of hyponormalities and k-quasi-hyponormalities for operators on semi Hilbertian space (H,||.||_A), based on the works that studied normal, isometry, unitary and partial isometries operators in these spaces. Also, we generalize some results which are already known for hyponormal and quasi-hyponormal operators. An operator T ∈ B_A (H) is said to be (A, k)-quasi-hyponormal if

Paper's Title:

A Fuzzy Soft Quotient Topology and Its Properties

Author(s):

Haripamyu, Riri Alfakhriati, Monika Rianti Helmi, Jenizon

Department of Mathematics and Data Science, Andalas University, Padang, Indonesia.
E-mail: haripamyu@sci.unand.ac.id
ririalfakhriati123@gmail.com
monikariantihelmi@sci.unand.ac.id
jenizon@gmail.com

Abstract:

This research is to construct a new topology on fuzzy soft set by using the concept of quotient topology. Then we study the concept of quotient map to define the fuzzy soft quotient map and provide some relevant properties of fuzzy soft quotient map. Furthermore, we give some examples related to fuzzy soft quotient topology and fuzzy soft quotient map to apply some properties of fuzzy soft quotient map.

Paper's Title:

A New Iterative Approximation of a Split Fixed Point Constraint Equilibrium Problem

Author(s):

Musa Adewale Olona¹, Adhir Maharaj² and Ojen Kumar Narain³

¹School of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 219095783@stu.ukzn.ac.za

²Department of Mathematics,
Durban University of Technology, Durban,
South Africa.
E-mail: adhirm@dut.ac.za

³School of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za

Abstract:

The purpose of this paper is to introduce an iterative algorithm for approximating an element in the solution set of the common split feasibility problem for fixed points of demimetric mappings and equilibrium problem for monotone mapping in real Hilbert spaces. Motivated by self-adaptive step size method, we incorporate the inertial technique to accelerate the convergence of the proposed method and establish a strong convergence of the sequence generated by the proposed algorithm. Finally, we present a numerical example to illustrate the significant performance of our method. Our results extend and improve some existing results in the literature.

Paper's Title:

Solving Strongly Nonlinear Fractional Fredholm Integral-Differential Equations in Caputo's Sense Using the SBA Method

Author(s):

Germain Kabore¹, Bakari Abbo², Ousseni So³ and Blaise Some¹

¹Laboratoire d'Analyse Numerique, Informatique et de Biomathmathiques (L.N.I.BIO),
Universite Joseph Ki-Zerbo,
Burkina Faso.
E-mail: germainkabore982@gmail.com, blaisesomeouaga1@gmail.com

²University of N'Damena, Tchad.
E-mail: bakariabbo@yahoo.fr

³Laboratoire d'Analyse Numerique, Informatique et de Biomathemathiques (L.N.I.BIO),
Ecole Normale Superieure,
Burkina Faso.
E-mail: sousseni@yahoo.fr

Abstract:

The work addressed in this article consists in constructing the exact solutions, where they exist, of fractional Fredholm-type integro-differential equations in the sense of Caputo. Our results are obtained using the SBA method. The simplification of the approach, the analysis of its convergence, and the generalization of this method to these types of highly nonlinear equations constitute our scientific contribution.

Paper's Title:

Dyadic Riesz Wavelets on Local Fields of Positive Characteristics

Author(s):

Kartik Garg, Raj Kumar, Satyapriya

Department of Mathematics,
University of Delhi,
Delhi,
India.
kartikgarg1421@gmail.com,
rajkmc@gmail.com
kmc.satyapriya@gmail.com

 

Abstract:

In this research paper, we introduce a novel theory for the construction of a Riesz wavelet basis in the space L²(K), where K is a local field with positive characteristics. Our approach is two fold: firstly, we derive some essential characterizations of the scaling function associated with the structure of a Riesz MRA on a local field, and secondly, we review existing methods for constructing wavelet frames in L²(K). We also present a well elaborated example for a better comprehension of our theory. Due to mathematical convenience, we limit ourselves to the case of dyadic dilations only.

Search and serve lasted 0 second(s).