Paper's Title:

Convergence and Stability Results for New Three Step Iteration Process in Modular Spaces

Author(s):

Naresh Kumar and Renu Chugh

Department of Mathematics,
M.D. University,
Rohtak-124001, Haryana,
India.
E-mail: nks280@gmail.com
E-mail: chugh.r1@gmail.com

Abstract:

The aim of this paper is to introduce a new iteration process (5) for ρ-contraction mappings in Modular spaces. We obtain some analytical proof for convergence and stability of our iteration process (5). We show that our iteration process (5) gives faster convergence results than the leading AK iteration process (4) for contraction mappings. Moreover, a numerical example (using the Matlab Software) is presented to compare the rate of convergence for existing iteration processes with our new iteration process (5).

Paper's Title:

Solving Fixed Point Problems and Variational Inclusions Using Viscosity Approximations

Author(s):

P. Patel, R. Shukla

Department of Mathematics, School of Advanced Sciences, VIT-AP University\\
Amaravati, 522237, Andhra Pradesh,
India.
E-mail: prashant.patel9999@gmail.com, prashant.p@vitap.ac.in

Department of Mathematical Sciences & Computing, Walter Sisulu University,
Mthatha 5117,
South Africa.
E-mail: rshukla@wsu.ac.za

Abstract:

This paper proposes a new algorithm to find a common element of the fixed point set of a finite family of demimetric mappings and the set of solutions of a general split variational inclusion problem in Hilbert spaces. The algorithm is based on the viscosity approximation method, which is a powerful tool for solving fixed point problems and variational inclusion problems. Under some conditions, we prove that the sequence generated by the algorithm converges strongly to this common solution.

Paper's Title:

Viscosity Approximation Methods for Split Monotone Variational Inclusions and Fixed Point Problems of a Finite Family of ξ-Demimetric Mappings

Author(s):

Prashant Patel and Rahul Shukla

Department of Mathematics,
School of Advanced Sciences,
VIT-AP University, Inavolu,
Beside AP Secretariat,
Amaravati, 522237,
Andhra Pradesh,
India.
E-mail: prashant.patel9999@gmail.com, prashant.p@vitap.ac.in  

 
Department of Mathematical Sciences & Computing,
Walter Sisulu University,
Mthatha 5117,
South Africa.
E-mail: rshukla@wsu.ac.za
 

Abstract:

In this paper, we study viscosity approximation methods and present a new algorithm to find a common element of the fixed point of a finite family of ξ-demimetric mappings and the set of solutions of split monotone variational inclusion problem in Hilbert spaces. Under some conditions, we prove a strong convergence theorem which converges to this common solution.

Paper's Title:

A Multi-Stage Differential Transform Approach for Solving Differential Algebraic Systems Without Index Reduction

Author(s):

Khalil Al Ahmad, Farah Abdulla Aini, Amirah Azmi, Muhammad Abbas

School of Mathematical Sciences Universiti Sains Malaysia
11800 USM Penang
Malaysia.
 
Department of Mathematics,
University of Sargodha,
40100 Sargodha,
Pakistan

E-mail: abumohmmadkh@hotmail.com
farahaini@usm.my
amirahazmi@usm.my
muhammad.abbas@uos.edu.pk
 

Abstract:

This paper aims to solve differential algebraic systems without the need to reduce the index, which causes a defect in the behavior of the approximate solution. The differential transform method was developed to solve differential algebraic systems. The differential algebraic system is transferred to the algebraic system by applying the differential transform method. Then the Multi-stage differential transform method is applied to extend the interval of the convergence. The numerical results show the new technique is an efficient and flexible tool to obtain accurate results that meet the initial conditions and keep the behavior of the approximate solution consistent.

Paper's Title:

Stability of a Mixed Additive, Quadratic and Cubic Functional Equation In Quasi-Banach Spaces

Author(s):

A. Najati and F. Moradlou

Department of Mathematics, Faculty of Sciences,
University of Mohaghegh Ardabili, Ardabil,
Iran
a.nejati@yahoo.com

Faculty of Mathematical Sciences,
University of Tabriz, Tabriz,
Iran
moradlou@tabrizu.ac.ir
 

Abstract:

In this paper we establish the general solution of a mixed additive, quadratic and cubic functional equation and investigate the Hyers--Ulam--Rassias stability of this equation in quasi-Banach spaces. The concept of Hyers-Ulam-Rassias stability originated from Th. M. Rassias' stability theorem that appeared in his paper: On the stability of the linear mapping in Banach spaces, Proc. Amer. Math. Soc. 72 (1978), 297--300.

Paper's Title:

Convergence Speed of Some Random Implicit-Kirk-type Iterations for Contractive-type Random Operators

Author(s):

H. Akewe, K.S. Eke

Department of Mathematics,
Covenant University, 
Canaanland, KM 10, Idiroko Road, P. M. B. 1023, Ota, Ogun State,
Nigeria.
E-mail: hudson.akewe@covenantuniversity.edu.ng, kanayo.eke@covenantuniversity.edu.ng

Abstract:

The main aim of this paper is to introduce a stochastic version of multistep type iterative scheme called a modified random implicit-Kirk multistep iterative scheme and prove strong convergence and stability results for a class of generalized contractive-type random operators. The rate of convergence of the random iterative schemes are also examined through an example. The results show that our new random implicit kirk multistep scheme perform better than other implicit iterative schemes in terms of convergence and thus have good potentials for further applications in equilibrium problems in computer science, physics and economics.

Paper's Title:

Numerical Study of a Mathematical Model of a Free-Surface Potential Flow

Author(s):

H. Serguine, F. Guechi and A. Gasmi

Department Of Mathematics, Faculty of Science,
Ferhat Abbas Universty, 19000, Setif,
Algeria.
E-mail: houria.serguine@univ-msila.dz

 
Department Of Mathematics, Faculty of Science,
Ferhat Abbas Universty, 19000, Setif,
Algeria.
E-mail:  fairouz.chegaar@univ-setif.dz

Laboratory of Pure and Applied Mathematics, Faculty of Mathematics and Computer Science,
Mohamed Boudiaf Universty, 28000, M'sila,
Algeria.
E-mail: abdelkader.gasmi@univ-msila.dz

Abstract:

In this work, the problem of a potential and two-dimensional flow with a free surface of an incompressible, irrotational and inviscid fluid of a jet in front an inclined wall is considered, where γ is the inclination angle with the horizontal. The shape of the free surface is presented by curves which are found numerically by the series truncation method. This technique is based on the conformal transformations, resulting with the surface tension effect T with the boundary conditions on the free surfaces given by Bernoulli's equation. The found results are dependant on parameters which are: the Weber's number α and the angle γ. For each Weber's number value, only one solution is specified and some shapes of free surfaces of the jet are illustrated.

Paper's Title:

Essential Random Fixed Point Set of Random Operators

Author(s):

Ismat Beg

Centre for Advanced Studies in Mathematics,
Lahore University of Management Sciences (LUMS),
54792-Lahore, PAKISTAN. ibeg@lums.edu.pk
URL: http://web.lums.edu.pk/~ibeg

Abstract:

We obtain necessary and sufficient conditions for the existence of essential random fixed point of a random operator defined on a compact metric space. The structure of the set of essential random fixed points is also studied.

Paper's Title:

Some Properties of the Solution of a Second Order Elliptic Abstract Differential Equation

Author(s):

A. Aibeche and K. Laidoune

Mathematics Department, Faculty of Sciences, University Ferhat Abbas, Setif,
Route de Scipion, 19000, Setif,
Algeria
aibeche@univ-setif.dz

Abstract:

In this paper we study a class of non regular boundary value problems for elliptic differential-operator equation of second order with an operator in boundary conditions. We give conditions which guarantee the coerciveness of the solution of the considered problem, the completeness of system of root vectors in Banach-valued functions spaces and we establish the Abel basis property of this system in Hilbert spaces. Finally, we apply this abstract results to a partial differential equation in cylindrical domain.

Paper's Title:

Approximation of an AQCQ-Functional Equation and its Applications

Author(s):

Choonkil Park and Jung Rye Lee

Department of Mathematics,
Research Institute for Natural Sciences,
Hanyang University, Seoul 133-791,
Korea;

Department of Mathematics,
Daejin University,
Kyeonggi 487-711,
Korea

baak@hanyang.ac.kr
jrlee@daejin.ac.kr

Abstract:

This paper is a survey on the generalized Hyers-Ulam stability of an AQCQ-functional equation in several spaces. Its content is divided into the following sections:

1. Introduction and preliminaries.

2. Generalized Hyers-Ulam stability of an AQCQ-functional equation in Banach spaces: direct method.

3. Generalized Hyers-Ulam stability of an AQCQ-functional equation in Banach spaces: fixed point method.

4. Generalized Hyers-Ulam stability of an AQCQ-functional equation in random Banach spaces: direct method.

5. Generalized Hyers-Ulam stability of an AQCQ-functional equation in random Banach spaces: fixed point method.

6. Generalized Hyers-Ulam stability of an AQCQ-functional equation in non-Archi-medean Banach spaces: direct method.

7. Generalized Hyers-Ulam stability of an AQCQ-functional equation in non-Archi-medean Banach spaces: fixed point method.

Paper's Title:

Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.

Paper's Title:

Euler Series Solutions for Linear Integral Equations

Author(s):

Mostefa Nadir and Mustapha Dilmi

Department of Mathematics,
University of Msila 28000,
ALGERIA.
E-mail: mostefanadir@yahoo.fr
E-mail: dilmiistapha@yahoo.fr

Abstract:

In this work, we seek the approximate solution of linear integral equations by truncation Euler series approximation. After substituting the Euler expansions for the given functions of the equation and the unknown one, the equation reduces to a linear system, the solution of this latter gives the Euler coefficients and thereafter the solution of the equation. The convergence and the error analysis of this method are discussed. Finally, we compare our numerical results by others.

Paper's Title:

Some Convergence Results for  Jungck-Am Iterative Process In Hyperbolic Spaces

Author(s):

Akindele Adebayo Mebawondu and Oluwatosin Temitope Mewomo

School of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 216028272@stu.ukzn.ac.za, mewomoo@ukzn.ac.za

Abstract:

In this paper, we introduce a new three steps iterative process called Jungck-AM iterative process and show that the proposed iterative process can be used to approximate fixed points of Jungck-contractive type mappings and Jungck-Suzuki type mappings. In addition, we establish some strong and Δ-convergence results for the approximation of fixed points of Jungck-Suzuki type mappings in the frame work of uniformly convex hyperbolic space. Furthermore, we show that the newly proposed iterative process has a better rate of convergence compare to the Jungck-Noor, Jungck-SP, Jungck-CR and some existing iterative processes in the literature. Finally, stability, data dependency results for Jungck-AM iterative process is established and we present an analytical proof and numerical examples to validate our claim.

Paper's Title:

A new approach to the study of fixed point for simulation functions with application in G-metric spaces

Author(s):

Komi Afassinou and Ojen Kumar Narain

Department of Mathematical Sciences, University of Zululand,
KwaDlangezwa,
South Africa.
E-mail: komia@aims.ac.za

School of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za

Abstract:

The purpose of this work is to generalize the fixed point results of Kumar et al. [11] by introducing the concept of (α,β)-Z-contraction mapping, Suzuki generalized (α,β)-Z-contraction mapping, (α,β)-admissible mapping and triangular (α,β)-admissible mapping in the frame work of G-metric spaces. Fixed point theorems for these class of mappings are established in the frame work of a complete G-metric spaces and we establish a generalization of the fixed point result of Kumar et al. [11] and a host of others in the literature. Finally, we apply our fixed point result to solve an integral equation.

Paper's Title:

Analysis of a Dynamic Elasto-viscoplastic Frictionless Antiplan Contact Problem with Normal Compliance

Author(s):

A. Ourahmoun¹, B. Bouderah², T. Serrar³

^1,2Applied Mathematics Laboratory,
M'sila University, 28000,
Algeria.
E-mail: ourahmounabbes@yahoo.fr

³Applied Mathematics Laboratory,
Setif 1 University, 19000,
Algeria.

Abstract:

We consider a mathematical model which describes the dynamic evolution of a thermo elasto viscoplastic contact problem between a body and a rigid foundation. The mechanical and thermal properties of the obstacle coating material near its surface. A variational formulation of this dynamic contact phenomenon is derived in the context of general models of thermo elasto viscoplastic materials. The displacements and temperatures of the bodies in contact are governed by the coupled system consisting of a variational inequality and a parabolic differential equation. The proof is based on a classical existence and uniqueness result on parabolic inequalities,differential equations and fixed point arguments.

Paper's Title:

Existence of Solution of Differential and Riemann-Liouville Equation Via Fixed Point Approach in Complex Valued b-Metric Spaces

Author(s):

K. Afassinou, A. A. Mebawondu, H. A. Abass and O. K. Narain

Department of Science Access,
University of Zululand, KwaDlangezwa,
South Africa.
E-mail: komia@aims.ac.za

DST-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: dele@aims.ac.za

DST-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: hammedabass548@gmail.com

School of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za

Abstract:

In this paper, we establish some fixed point and common fixed point results for a new type of generalized contractive mapping using the notion of C-class function in the framework of complex valued b-metric spaces. As an application, we establish the existence and uniqueness of a solution for Riemann-Liouville integral and ordinary differential equation in the framework of a complete complex valued b-metric spaces. The obtained results generalize and improve some fixed point results in the literature.

Paper's Title:

Numerical Solution of Certain Types of Fredholm-Volterra Integro-Fractional Differential Equations via Bernstein Polynomials

Author(s):

Alias B. Khalaf¹, Azhaar H. Sallo² and Shazad S. Ahmed³

¹Department of Mathematics, College of Science,
University of Duhok,
Kurdistan Region,
Iraq.
E-mail:  aliasbkhalaf@uod.ac

²Department of Mathematics, College of Science,
University of Duhok,
Kurdistan Region,
Iraq.
E-mail:  azhaarsallo@uod.ac

³Department of Mathematics, College of Science,
University of Sulaimani,
Kurdistan Region,
Iraq.
E-mail: shazad.ahmed@univsul.edu

Abstract:

In this article we obtain a numerical solution for a certain fractional order integro-differential equations of Fredholm-Volterra type, where the fractional derivative is defined in Caputo sense. The properties of Bernstein polynomials are applied in order to convert the fractional order integro-differential equations to the solution of algebraic equations. Some numerical examples are investigated to illustrate the method. Moreover, the results obtained by this method are compared with the exact solution and with the results of some existing methods as well.

Paper's Title:

Fekete-Szegö Inequality for Sakaguchi Type of functions in Petal Shaped Domain

Author(s):

E. K. Nithiyanandham and B. Srutha Keerthi

Division of Mathematics, School of Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: nithiyankrish@gmail.com

Division of Mathematics, School of Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com

Abstract:

In this paper, we estimate coefficient bounds,|a_2|,|a_3| and |a_4|, Fekete-Szegö inequality and Toeplitz determinant T₂(2) and T₃(1) for functions belonging to the following class

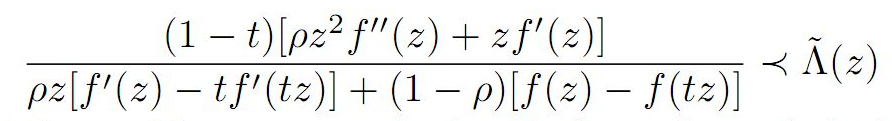
the function being holomorphic, we expand using Taylor series and obtain several corollaries and consequences for the main result.

Paper's Title:

Toeplitz Determinant for Sakaguchi Type Functions Under Petal Shaped Domain

Author(s):

B. Nandhini and B. Srutha Keerthi

Division of Mathematics, School of Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: nandhinibaskar1996@gmail.com

Division of Mathematics, School of Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com

Abstract:

We introduce a new general subclass GP^t,ρ of Sakaguchi kind function on a Petal shaped domain. We obtain coefficients bounds and upper bounds for the Fekete-Szegö functional over the class. From these functions we obtain the bounds of first four coefficients, and then we have derived the Toeplitz determinant T₂(2) and T₃(1) whose diagonal entries are the coefficients of functions.

Paper's Title:

D-Iterative Method for Solving a Delay Differential Equation and a Two-Point Second-Order Boundary Value Problems in Banach Spaces

Author(s):

Francis Akutsah¹, Akindele Adebayo Mebawondu², Oluwatosin Babasola³, Paranjothi Pillay⁴ and Ojen Kumar Narain⁵

¹School of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: 216040405@stu.ukzn.ac.za, akutsah@gmail.com

²School of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa. 
DST-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
Mountain Top University,
Prayer City, Ogun State,
Nigeria.
E-mail: dele@aims.ac.za

³Department of Mathematical Sciences,
University of Bath,
Claverton Down,
Bath, BA2 7AY
UK.
E-mail: ob377@bath.ac.uk

⁴School of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: pillaypi@ukzn.ac.za

⁵School of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za

Abstract:

The purpose of this paper is to re-establish the convergence, stability and data dependence results established by [2] and [3] by removing the strong assumptions imposed on the sequences which were used to obtain their results. In addition, we introduced a modified approach using the D-iterative method to solve a two-point second-order boundary value problem, and also obtain the solution of a delay differential equations using the obtained results in this paper. The results presented in this paper do not only extend and improve the results obtained in [2, 3], it further extends and improve some existing results in the literature.

Search and serve lasted 0 second(s).