Paper's Title:

Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.

Paper's Title:

Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.

Paper's Title:

Some Operator Order Inequalities for Continuous Functions of Selfadjoint Operators in Hilbert Spaces

Author(s):

S. S. Dragomir^1,2 and Charles E. M. Pearce³

¹Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428, Melbourne City, MC 8001,
Australia.

²School of Computational & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.

sever.dragomir@vu.edu.au 
URL: http://rgmia.org/dragomir

³School of Mathematical Sciences,
The University of Adelaide,
Adelaide,
Australia
 

Abstract:

Various bounds in the operator order for the following operator transform

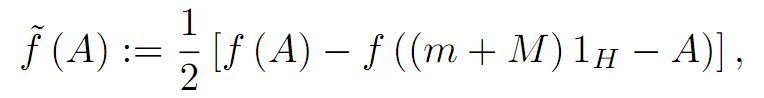
where A is a selfadjoint operator in the Hilbert space H with the spectrum Sp( A) ⊆ [ m,M] and f:[m,M] ->  C is a continuous function on [m,M]  are given. Applications for the power and logarithmic functions are provided as well.

Paper's Title:

Inequalities for Functions of Selfadjoint Operators on Hilbert Spaces:
a Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, College of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: https://rgmia.org/dragomir 

Abstract:

The main aim of this survey is to present recent results concerning inequalities for continuous functions of selfadjoint operators on complex Hilbert spaces. It is intended for use by both researchers in various fields of Linear Operator Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.

Paper's Title:

Hermite-Hadamard Type Inequalities for MN-Convex Functions

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, College of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: https://rgmia.org/dragomir 

Abstract:

The present work endeavours to briefly present some of the fundamental results connected to the Hermite-Hadamard inequality for special classes of convex functions such as AG, AH, GA, GG, GH, HA, HG and HH -convex functions in which the author have been involved during the last five years. For simplicity, we call these classes of functions such as MN-convex functions, where M and N stand for any of the Arithmetic (A), Geometric (G) or Harmonic (H) weighted means of positive real numbers. The survey is intended for use by both researchers in various fields of Approximation Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.

Paper's Title:

Bounds for Two Mappings Associated to the Hermite-Hadamard Inequality

Author(s):

S. S. Dragomir^1,2 and I. Gomm¹

¹Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428, Melbourne City, MC 8001,
Australia.

²School of Computational & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.

sever.dragomir@vu.edu.au
ian.gomm@vu.edu.au
URL: http://rgmia.org/dragomir  
 

Abstract:

Some inequalities concerning two mappings associated to the celebrated Hermite-Hadamard integral inequality for convex function with applications for special means are given.

Paper's Title:

Further Bounds for Two Mappings Related to the Hermite-Hadamard Inequality

Author(s):

S. S. Dragomir^1,2 and I. Gomm¹

¹Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428, Melbourne City, MC 8001,
Australia.

²School of Computational & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.

sever.dragomir@vu.edu.au
ian.gomm@vu.edu.au
URL: http://rgmia.org/dragomir  
 

Abstract:

Some new results concerning two mappings associated to the celebrated Hermite-Hadamard integral inequality for twice differentiable functions with applications for special means are given.

Paper's Title:

Some Applications of Fejér's Inequality for Convex Functions (I)

Author(s):

S.S. Dragomir^1,2 and I. Gomm¹

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia.

sever.dragomir@vu.edu.au

URL: http://rgmia.org/dragomir

²School of Computational & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.

Abstract:

Some applications of Fejér's inequality for convex functions are explored. Upper and lower bounds for the weighted integral

under various assumptions for f with applications to the trapezoidal quadrature rule are given. Some inequalities for special means are also provided

Paper's Title:

Scope of the Logarithmic Mean

Author(s):

Murali Rao and Agnish Dey

Department of Mathematics,
University of Florida,
1400 Stadium Road, Gainesville,
Florida 32611,
U. S. A.

E-mail: mrao@ufl.edu

URL: http://people.clas.ufl.edu/mrao

E-mail: agnish@ufl.edu

URL: http://people.clas.ufl.edu/agnish 

Abstract:

A number a is between two numbers x and y if and only if a is a convex combination of x and y, in other words, it is a "weighted mean" of x and y. Geometric mean, arithmetic mean are well known examples of these "means". Of more recent vintage is the logarithmic mean which has been considered in many articles in the literature. In this note, we first discuss some of its properties. Then we shall introduce the L function and explore the inverse of this function and its connection with the Lambert's Omega function.

Paper's Title:

Inequalities for the Area Balance of Functions of Bounded Variation

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

We introduce the area balance function associated to a Lebesgue integrable function f:[a,b] →C by

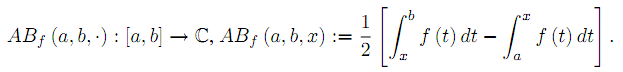
Several sharp bounds for functions of bounded variation are provided. Applications for Lipschitzian and convex functions are also given.

Paper's Title:

Generalizations of Hermite-Hadamard's Inequalities for Log-Convex Functions

Author(s):

Ai-Jun Li

School of Mathematics and Informatics, Henan Polytechnic University,
Jiaozuo City, Henan Province,
454010, China.
liaijun72@163.com

Abstract:

In this article, Hermite-Hadamard's inequalities are extended in terms of the weighted power mean and log-convex function. Several refinements, generalizations and related inequalities are obtained.

Paper's Title:

Some New Generalizations of Jensen's Inequality with Related Results and Applications

Author(s):

Steven G. From

Department of Mathematics
University of Nebraska at Omaha
Omaha, Nebraska 68182-0243.

E-mail: sfrom@unomaha.edu

Abstract:

In this paper, some new generalizations of Jensen's inequality are presented. In particular, upper and lower bounds for the Jensen gap are given and compared analytically and numerically to previously published bounds for both the discrete and continuous Jensen's inequality cases. The new bounds compare favorably to previously proposed bounds. A new method based on a series of locally linear interpolations is given and is the basis for most of the bounds given in this paper. The wide applicability of this method will be demonstrated. As by-products of this method, we shall obtain some new Hermite-Hadamard inequalities for functions which are 3-convex or 3-concave. The new method works to obtain bounds for the Jensen gap for non-convex functions as well, provided one or two derivatives of the nonlinear function are continuous. The mean residual life function of applied probability and reliability theory plays a prominent role in construction of bounds for the Jensen gap. We also present an exact integral representation for the Jensen gap in the continuous case. We briefly discuss some inequalities for other types of convexity, such as convexity in the geometric mean, and briefly discuss applications to reliability theory.

Paper's Title:

Some Inequalities of the Hermite-Hadamard Type for k-Fractional Conformable Integrals

Author(s):

C.-J. Huang, G. Rahman, K. S. Nisar, A. Ghaffar and F. Qi

Department of Mathematics, Ganzhou Teachers College,
Ganzhou 341000, Jiangxi,
China.
E-mail: hcj73jx@126.com , huangcj1973@qq.com

Department of Mathematics, Shaheed Benazir Bhutto University,
Sheringal, Upper Dir, Khyber Pakhtoonkhwa,
Pakistan.
E-mail: gauhar55uom@gmail.com

Department of Mathematics, College of Arts and Science at Wadi Aldawaser, 11991,
Prince Sattam Bin Abdulaziz University, Riyadh Region,
Kingdom of Saudi Arabia.
E-mail: n.sooppy@psau.edu.sa, ksnisar1@gmail.com

Department of Mathematical Science, Balochistan University of Information Technology,
Engineering and Management Sciences, Quetta,
Pakistan.
E-mail: abdulghaffar.jaffar@gmail.com

School of Mathematical Sciences, Tianjin Polytechnic University,
Tianjin 300387,
China; Institute of Mathematics,
Henan Polytechnic University, Jiaozuo 454010, Henan,
China.
E-mail: qifeng618@gmail.com, qifeng618@qq.com

Abstract:

In the paper, the authors deal with generalized k-fractional conformable integrals, establish some inequalities of the Hermite-Hadamard type for generalized k-fractional conformable integrals for convex functions, and generalize known inequalities of the Hermite-Hadamard type for conformable fractional integrals.

Paper's Title:

Sharp Inequalities Between Hölder and Stolarsky Means of Two Positive Numbers

Author(s):

M. Bustos Gonzalez and A. I. Stan

The University of Iowa,
Department of Mathematics,
14 MacLean Hall,
Iowa City, Iowa,
USA.
E-mail: margarita-bustosgonzalez@uiowa.edu
 
The Ohio State University at Marion,
Department of Mathematics,
1465 Mount Vernon Avenue,
Marion, Ohio,
USA.
E-mail: stan.7@osu.edu

Abstract:

Given any index of the Stolarsky means, we find the greatest and least indexes of the H\"older means, such that for any two positive numbers, the Stolarsky mean with the given index is bounded from below and above by the Hölder means with those indexes, of the two positive numbers. Finally, we present a geometric application of this inequality involving the Fermat-Torricelli point of a triangle.

Paper's Title:

Trace Inequalities for Operators in Hilbert Spaces: a Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University,
PO Box 14428 Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: https://rgmia.org/dragomir 

Abstract:

In this paper we survey some recent trace inequalities for operators in Hilbert spaces that are connected to Schwarz's, Buzano's and Kato's inequalities and the reverses of Schwarz inequality known in the literature as Cassels' inequality and Shisha-Mond's inequality. Applications for some functionals that are naturally associated to some of these inequalities and for functions of operators defined by power series are given. Further, various trace inequalities for convex functions are presented including refinements of Jensen inequality and several reverses of Jensen's inequality. Hermite-Hadamard type inequalities and the trace version of Slater's inequality are given. Some Lipschitz type inequalities are also surveyed. Examples for fundamental functions such as the power, logarithmic, resolvent and exponential functions are provided as well.

Paper's Title:

Refinement of Jensen's Inequality for Analytical Convex (Concave) Functions

Author(s):

P. Kórus, Z. Retkes

Institute of Applied Pedagogy,
Juhász Gyula Faculty of Education,
University of Szeged,
Hattyas utca 10, H-6725 Szeged,
Hungary.
E-mail: korus.peter@szte.hu

65 Manor Road, Desford, LE9 9JQ,
United Kingdom.
E-mail: tigris35711@gmail.com

Abstract:

The well-known Jensen inequality and Hermite--Hadamard inequality were extended using iterated integrals by Z. Retkes in 2008 and then by P. Kórus in 2019. In this paper, we consider analytical convex (concave) functions in order to obtain new refinements of Jensen's inequality. We apply the main result to the classical HM--GM--AM, AM--RMS, triangle inequalities and present an application to the geometric series. We also give Mercer type variants of Jensen's inequality.

Search and serve lasted 0 second(s).