Paper's Title:

On the Generalized Inverse over Integral Domains

Author(s):

Yaoming Yu and Guorong Wang

College of Education, Shanghai Normal University
Shanghai 200234
People's Republic of China.
yuyaoming@online.sh.cn
grwang@shnu.edu.cn

Abstract:

In this paper, we study further the generalized inverse of a matrix A over an integral domain. We give firstly some necessary and sufficient conditions for the existence of the generalized inverse , an explicit expression for the elements of the generalized inverse and an explicit expression for the generalized inverse , which reduces to the {1} inverse. Secondly, we verify that the group inverse, the Drazin inverse, the Moore-Penrose inverse and the weighted Moore-Penrose inverse are identical with the generalized inverse for an appropriate matrix G, respectively, and then we unify the conditions for the existence and the expression for the elements of the weighted Moore-Penrose inverse, the Moore-Penrose inverse, the Drazin inverse and the group inverse over an integral domain. Thirdly, as a simple application, we give the relation between some rank equation and the existence of the generalized inverse , and a method to compute the generalized inverse . Finally, we give an example of evaluating the elements of without calculating .

Paper's Title:

A Determinantal Representation of Core EP Inverse

Author(s):

Divya Shenoy Purushothama

Department of Mathematics,
Manipal Institute of Technology,
Manipal Academy of Higher Education,
Manipal -576104, Karnataka,
India.
E-mail:  divya.shenoy@manipal.edu
URL: https://manipal.edu/mit/department-faculty/faculty-list/divya-shenoy-p.html

Abstract:

The notion of Core EP inverse is introduced by Prasad in the article "Core - EP inverse" and proved its existence and uniqueness. Also, a formula for computing the Core EP inverse is obtained from particular linear combination of minors of a given matrix. Here a determinantal representation for Core EP inverse of a matrix A with the help of rank factorization of A is obtained.

Paper's Title:

A Note on Evaluation of a New Class of Integrals Involving Generalized Hypergeometric Function

Author(s):

Madhav Prasad Poudel, Dongkyu Lim^*, Narayan Prasad Pahari, Arjun K. Rathie

School of Engineering,
Pokhara University, Pokhara-30, Kaski,
Nepal.
E-mail: pdmadav@gmail.com

Department of Mathematics Education,
Andong National University, Andong 36729,
Republic of Korea.
E-mail: dklim@anu.ac.kr

Central Department of Mathematics,
Tribhuvan University, Kirtipur, Kathmandu,
Nepal.
E-mail: nppahari@gmail.com

Department of Mathematics,
Vedant College of Engineering & Technology (Rajasthan Technical University), Village: Tulsi,
Jakhamund, Dist. Bundi, Rajasthan State,
India.
E-mail: arjunkumarrathie@gmail.com

Abstract:

In the theory of hypergeometric and generalized hypergeometric series, classical summation theorems such as those of Gauss, Gauss second, Bailey and Kummer for the series ₂F₁; Watson, Dixon, Whipple and Saalshutz play a key role. Applications of the above mentioned summation theorems are well known for the series ₃F₂. In our present investigation, we aim to evaluate twenty five new class of integrals involving generalized hypergeometric function in the form of a single integral of the form:

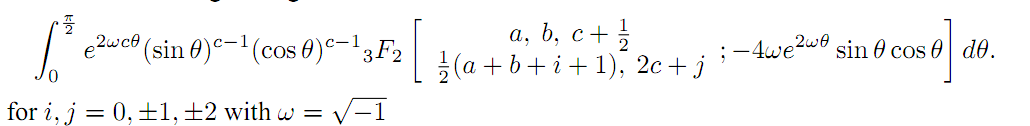
The results are established with the help of the generalizations of the classical Watson's summation theorem obtained earlier by Lavoie et al.. Fifty interesting integrals in the form of two integrals (twenty five each) have also been given as special cases of our main findings.

Paper's Title:

On the Three Variable Reciprocity Theorem and Its Applications

Author(s):

D. D. Somashekara and D. Mamta

Department of Studies in Mathematics,
University of Mysore,
Manasagangotri, Mysore-570 006
India
dsomashekara@yahoo.com 

Department of Mathematics,
The National Institute of Engineering,
Mysore-570 008,
India
mathsmamta@yahoo.com  
 

Abstract:

In this paper we show how the three variable reciprocity theorem can be easily derived from the well known two variable reciprocity theorem of Ramanujan by parameter augmentation. Further we derive some q-gamma, q-beta and eta-function identities from the three variable reciprocity theorem.

Paper's Title:

On the Class of Totally Polynomially Posinormal Operators

Author(s):

E. Shine Lal, T. Prasad, P. Ramya

Department of Mathematics,University College,
Thiruvananthapuram, Kerala, 695034.
India.
E-mail: shinelal.e@gmail.com

 
Department of Mathematics,
University of Calicut,
Malapuram, Kerala 673635,
India.
E-mail: prasadvalapil@gmail.com

Department of Mathematics,
N.S.S College,
Nemmara, Kerala, 678508
India.
E-mail: ramyagcc@gmail.com

Abstract:

In this paper, we proved that if  T ∈ B(H)  is totally P-posinormal operator with . Moreover, we study spectral continuity and range kernel orthogonality of these class of operators.

Paper's Title:

Classes of Meromorphic p-valent Parabolic Starlike Functions with Positive Coefficients

Author(s):

S. Sivaprasad Kumar, V. Ravichandran, and G. Murugusundaramoorthy

Department of Applied Mathematics
Delhi College of Engineering,
Delhi 110042, India
sivpk71@yahoo.com

School of Mathematical Sciences
Universiti Sains Malaysia
11800 USM Penang
Malaysia
vravi@cs.usm.my
URL: http://cs.usm.my/~vravi

Department of Mathematics
Vellore Institute of Technology (Deemed University)
Vellore 632 014, India
gmsmoorthy@yahoo.com

Abstract:

In the present paper, we consider two general subclasses of meromorphic p-valent starlike functions with positive coefficients and obtain a necessary and sufficient condition for functions to be in these classes. Also we obtain certain other related results as a consequences of our main results.

Paper's Title:

Coincidences and Fixed Points of Hybrid Maps in Symmetric Spaces

Author(s):

S. L. Singh and Bhagwati Prasad

Vedic MRI, 21 Govind Nagar,
Rishikesh 249201
India
vedicmri@gmail.com

Department of Mathematics, Gurukula Kangri University,
Hardwar 249404,
India

Abstract:

The purpose of this paper is to obtain a new coincidence theorem for a single-valued and two multivalued operators in symmetric spaces. We derive fixed point theorems and discuss some special cases and applications.

Paper's Title:

Some Inequalities for a Certain Class of Multivalent Functions Using Multiplier Transformation

Author(s):

K. Suchithra, B. Adolf Stephen, A. Gangadharan and S. Sivasubramanian

Department Of Applied Mathematics
Sri Venkateswara College Of Engineering
Sriperumbudur, Chennai - 602105,
India.
suchithravenkat@yahoo.co.in

Department Of Mathematics,
Madras Christian College
Chennai - 600059,
India.
adolfmcc2003@yahoo.co.in

Department Of Applied Mathematics
Sri Venkateswara College Of Engineering
Sriperumbudur, Chennai - 602105,
India.
ganga@svce.ac.in

Department Of Mathematics,
Easwari Engineering College
Ramapuram, Chennai - 600089,
India.
ganga@svce.ac.in

Abstract:

The object of the present paper is to derive several inequalities associated with differential subordinations between analytic functions and a linear operator defined for a certain family of p-valent functions, which is introduced here by means of a family of extended multiplier transformations. Some special cases and consequences of the main results are also considered.

Paper's Title:

Some properties of k-quasi class Q* operators

Author(s):

Shqipe Lohaj and Valdete Rexhëbeqaj Hamiti

Department of Mathematics,
Faculty of Electrical and Computer Engineering,
University of Prishtina "Hasan Prishtina",
Prishtine 10000,
Kosova.
E-mail: shqipe.lohaj@uni-pr.edu

Department of Mathematics,
Faculty of Electrical and Computer Engineering,
University of Prishtina "Hasan Prishtina",
Prishtine 10000,
Kosova.
E-mail: valdete.rexhebeqaj@uni-pr.edu

Abstract:

In this paper, we give some results of k-quasi class Q^* operators. We proved that if T is an invertible operator and N be an operator such that N commutes with T^*T, then N is k-quasi class Q^* if and only if TNT^-1 is of k-quasi class Q^*. With example we proved that exist an operator k-quasi class Q^* which is quasi nilpotent but it is not quasi hyponormal.

Paper's Title:

Existence of Solution of Differential and Riemann-Liouville Equation Via Fixed Point Approach in Complex Valued b-Metric Spaces

Author(s):

K. Afassinou, A. A. Mebawondu, H. A. Abass and O. K. Narain

Department of Science Access,
University of Zululand, KwaDlangezwa,
South Africa.
E-mail: komia@aims.ac.za

DST-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: dele@aims.ac.za

DST-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: hammedabass548@gmail.com

School of Mathematics, Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za

Abstract:

In this paper, we establish some fixed point and common fixed point results for a new type of generalized contractive mapping using the notion of C-class function in the framework of complex valued b-metric spaces. As an application, we establish the existence and uniqueness of a solution for Riemann-Liouville integral and ordinary differential equation in the framework of a complete complex valued b-metric spaces. The obtained results generalize and improve some fixed point results in the literature.

Paper's Title:

A New Relaxed Complex-valued b-metric Type and Fixed Point Results

Author(s):

P. Singh, V. Singh and T. C. M. Jele

Department of Mathematics, University of KwaZulu-Natal,
Private Bag X54001, Durban,
South Africa.
E-mail: singhp@ukzn.ac.za
singhv@ukzn.ac.za
thokozani.jele@nwu.ac.za

Abstract:

In this paper, we study the existence and uniqueness of fixed point in complex valued b-metric spaces and introduce a new relaxed α, β Complex-valued b-metric type by relaxing the triangle inequality and determine whether the fixed point theorems are applicable in these spaces.

Paper's Title:

Higher Order Accurate Compact Schemes for Time Dependent Linear and Nonlinear Convection-Diffusion Equations

Author(s):

S. Thomas, Gopika P.B. and S. K. Nadupuri

Department of Mathematics
National Institute of Technology Calicut
Kerala
673601
India.
E-mail: sobinputhiyaveettil@gmail.com pbgopika@gmail.com nsk@nitc.ac.in
 

Abstract:

The primary objective of this work is to study higher order compact finite difference schemes for finding the numerical solution of convection-diffusion equations which are widely used in engineering applications. The first part of this work is concerned with a higher order exponential scheme for solving unsteady one dimensional linear convection-diffusion equation. The scheme is set up with a fourth order compact exponential discretization for space and cubic $C^1$-spline collocation method for time. The scheme achieves fourth order accuracy in both temporal and spatial variables and is proved to be unconditionally stable. The second part explores the utility of a sixth order compact finite difference scheme in space and Huta's improved sixth order Runge-Kutta scheme in time combined to find the numerical solution of one dimensional nonlinear convection-diffusion equations. Numerical experiments are carried out with Burgers' equation to demonstrate the accuracy of the new scheme which is sixth order in both space and time. Also a sixth order in space predictor-corrector method is proposed. A comparative study is performed of the proposed schemes with existing predictor-corrector method. The investigation of computational order of convergence is presented.

Search and serve lasted 0 second(s).