|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Inequalities Relating to the Gamma Function
Author(s):
Chao-Ping Chen and Feng Qi
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
chenchaoping@hpu.edu.cn
Department of Applied Mathematics and Informatics,
Research Institute of Applied Mathematics,
Henan Polytechnic University, Jiaozuo
City, Henan 454000, China
qifeng@hpu.edu.cn,
fengqi618@member.ams.org
Url:
http://rgmia.vu.edu.au/qi.html,
http://dami.hpu.edu.cn/qifeng.html
Abstract:
For ![]() , we have
, we have
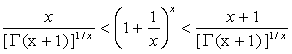 .
.
For![]() ,
,
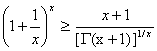 ,
,
And equality occurs for x=1.
Paper's Title:
Positive Periodic Time-Scale Solutions for Functional Dynamic Equations
Author(s):
Douglas R. Anderson and Joan Hoffacker
Department of Mathematics and Computer Science
Concordia College
Moorhead, MN 56562 USA
andersod@cord.edu
URL: http://www.cord.edu/faculty/andersod/
Department of Mathematical Sciences
Clemson University
Clemson, SC 29634 USA
johoff@clemson.edu
URL: http://www.math.clemson.edu/facstaff/johoff.htm
Abstract:
Using Krasnoselskii's fixed point theorem, we establish the existence of positive periodic solutions
to two pairs of related nonautonomous functional delta dynamic equations on periodic time scales, and then extend the discussion to higher-dimensional equations. Two pairs of corresponding nabla equations
are also provided in an analogous manner.
Paper's Title:
Generalized Fuglede-Putnam Theorem and Orthogonality
Author(s):
A. Bachir and A. Sagres
Department of
Mathematics, Faculty of Science, King Khaled
University, Abha, P.O. Box 9004 Kingdom Saudi Arabia
bachir_ahmed@hotmail.com
sagres@hotmail.com
Abstract:
An asymmetric Fuglede-Putnam’s theorem for dominant operators
and
Paper's Title:
A Wallis Type Inequality and a Double Inequality for Probability Integral
Author(s):
Jian Cao, Da-Wei Niu and Feng Qi
School of Mathematics and Informatics,
Henan Polytechnic University, Jiaozuo City,
Henan Province, 454010,
China
21caojian@163.com
School of Mathematics and Informatics,
Henan Polytechnic University, Jiaozuo City,
Henan Province, 454010,
China
nnddww@tom.com
Research Institute of Mathematical Inequality Theory,
Henan Polytechnic University, Jiaozuo City,
Henan Province, 454010,
China
qifeng@hpu.edu.cn
fengqi618@member.ams.org
qifeng618@hotmail.com
qifeng618@msn.com
qifeng618@qq.com
URL: http://rgmia.vu.edu.au/qi.html
Abstract:
In this short note, a Wallis type inequality with the best upper and lower
bounds is established. As an application, a double inequality for the
probability integral is found.
Paper's Title:
Positive Solutions to a System of Boundary Value Problems for Higher-Dimensional Dynamic Equations on Time Scales
Author(s):
I. Y. Karaca
Department of Mathematics,
Ege University,
35100 Bornova, Izmir,
Turkey
URL:
http://ege.edu.tr
Abstract:
In this paper, we consider the system of boundary value problems for higher-dimensional dynamic equations on time scales. We establish criteria for the existence of at least one or two positive solutions. We shall also obtain criteria which lead to nonexistence of positive solutions. Examples applying our results are also given.
Paper's Title:
Dynamical Analysis of HIV/AIDS Epidemic Model with Two Latent Stages, Vertical Transmission and Treatment
Author(s):
Nur Shofianah, Isnani Darti, Syaiful Anam
Mathematics Department,Faculty of
Mathematics and Natural Sciences.
University of Brawijaya,
Jl. Veteran, Malang 65145,
Indonesia.
E-mail:
nur_shofianah@ub.ac.id,
isnanidarti@ub.ac.id,
syaiful@ub.ac.id
Abstract:
We discuss about dynamical analysis of HIV/AIDS epidemic model with two latent stages, vertical transmission and treatment. In this model, the spreading of HIV occurs through both horizontal and vertical transmission. There is also treatment for individual who has been HIV infected. The latent stage is divided into slow and fast latent stage based on the immune condition which varies for each individual. Dynamical analysis result shows that the model has two equilibrium points: the disease-free equilibrium point and the endemic equilibrium point. The existence and global stability of equilibrium points depend on the basic reproduction number R0. When R0 <1, only the disease-free equilibrium point exists. If R0 >1, there are two equilibrium points, which are the disease-free equilibrium point and the endemic equilibrium point. Based on the result of stability analysis, the disease-free equilibrium point is globally asymptotically stable if R0 <1, while if R0 > 1 and p=q, the endemic equilibrium point will be globally asymptotically stable. In the end, we show some numerical simulations to support the analytical result.
Paper's Title:
The Concept of Convergence for 2-Dimensional Subspaces Sequence in Normed Spaces
Author(s):
M. Manuharawati, D. N. Yunianti, M. Jakfar
Mathematics Department, Universitas
Negeri Surabaya,
Jalan Ketintang Gedung C8,
Surabaya 60321,
Indonesia.
E-mail: manuharawati@unesa.ac.id,
dwiyunianti@unesa.ac.id,
muhammadjakfar@unesa.ac.id
Abstract:
In this paper, we present a concept of convergence of sequence, especially, of 2-dimensional subspaces of normed spaces. The properties of the concept are established. As consequences of our definition in an inner product space, we also obtain the continuity property of the angle between two 2-dimensional subspaces of inner product spaces.
Paper's Title:
On the Generalized Inverse  over Integral Domains
over Integral Domains
Author(s):
Yaoming Yu and Guorong Wang
College of Education, Shanghai Normal University
Shanghai 200234
People's Republic of China.
yuyaoming@online.sh.cn
grwang@shnu.edu.cn
Abstract:
In this paper, we study further the generalized inverse
 of a matrix A over an integral domain. We give
firstly some necessary and sufficient conditions for the existence
of the generalized inverse
of a matrix A over an integral domain. We give
firstly some necessary and sufficient conditions for the existence
of the generalized inverse  , an explicit expression
for the elements of the generalized inverse
, an explicit expression
for the elements of the generalized inverse  and an
explicit expression for the generalized inverse
and an
explicit expression for the generalized inverse  ,
which reduces to the {1} inverse. Secondly, we verify that the
group inverse, the Drazin inverse, the Moore-Penrose inverse and the
weighted Moore-Penrose inverse are identical with the generalized
inverse
,
which reduces to the {1} inverse. Secondly, we verify that the
group inverse, the Drazin inverse, the Moore-Penrose inverse and the
weighted Moore-Penrose inverse are identical with the generalized
inverse 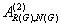 for an appropriate matrix G,
respectively, and then we unify the conditions for the existence and
the expression for the elements of the weighted Moore-Penrose
inverse, the Moore-Penrose inverse, the Drazin inverse and the group
inverse over an integral domain. Thirdly, as a simple application,
we give the relation between some rank equation and the existence of
the generalized inverse
for an appropriate matrix G,
respectively, and then we unify the conditions for the existence and
the expression for the elements of the weighted Moore-Penrose
inverse, the Moore-Penrose inverse, the Drazin inverse and the group
inverse over an integral domain. Thirdly, as a simple application,
we give the relation between some rank equation and the existence of
the generalized inverse  , and a method to compute the
generalized inverse
, and a method to compute the
generalized inverse  . Finally, we give an example of
evaluating the elements of
. Finally, we give an example of
evaluating the elements of  without calculating
without calculating
 .
.
Paper's Title:
Local and Global Existence and Uniqueness Results for Second and Higher Order Impulsive Functional Differential Equations with Infinite Delay
Author(s):
Johnny Henderson and Abdelghani Ouahab
Department of Mathematics, Baylor University,
Waco, Texas 76798-7328
USA.
Johnny_Henderson@baylor.edu
Laboratoire de Mathématiques, Université de Sidi Bel Abbés
BP 89, 22000 Sidi Bel Abbées,
Algérie.
ouahab@univ-sba.dz
Abstract:
In this paper, we discuss the local and global existence and
uniqueness results for second and higher order impulsive functional
differential equations with infinite delay. We shall rely on a
nonlinear alternative of Leray-Schauder. For the global existence
and uniqueness we apply a recent Frigon and Granas nonlinear
alternative of Leray-Schauder type in Fréchet spaces.
Paper's Title:
Oscillation and Boundedness of Solutions to First and Second Order Forced Dynamic Equations with Mixed Nonlinearities
Author(s):
Ravi P. Agarwal and Martin Bohner
Department of Mathematical Sciences, Florida Institute of Technology
Melbourne, FL 32901,
U.S.A.
bohner@mst.edu
URL:http://web.mst.edu/~bohner
Department of Economics and Finance, Missouri University of Science and Technology
Rolla, MO 65401,
U.S.A.
agarwal@fit.edu
Abstract:
Some oscillation and boundedness criteria for solutions to certain
first and second order forced dynamic equations
with mixed nonlinearities are established. The main tool in the proofs
is an inequality due to Hardy, Littlewood and Pólya.
The obtained results can be applied to differential equations,
difference equations and q-difference equations. The results
are illustrated with numerous examples.
Paper's Title:
Long Correlations Applied to the Study of Agricultural Indices in Comparison with the S&P500 index
Author(s):
M. C. Mariani, J. Libbin, M.P. Beccar Varela,
V. Kumar Mani, C. Erickson, D.J. Valles Rosales
Department of Mathematical Sciences,
Science Hall 236, New Mexico State University,
Las Cruces, NM 88003-8001,
USA.
mmariani@nmsu.edu
Abstract:
Long-time correlations in agricultural indices are studied and their behavior is compared to the well-established S&P500 index. Hurst exponent and Detrended Fluctuation Analysis (DFA) techniques are used in this analysis. We detected long-correlations in the agricultural indices and briefly discussed some features specific in comparison to the S&P500 index.
Paper's Title:
The Dynamics of an Ebola Epidemic Model with Quarantine of Infectives
Author(s):
Eliab Horub Kweyunga
Department of Mathematics,
Kabale University,
P.O.Box 317, Kabale,
Uganda.
E-mail: hkweyunga@kab.ac.ug
Abstract:
The recurrent outbreaks of ebola in Africa present global health challenges. Ebola is a severe, very fatal disease with case fatality rates of up to 90%. In this paper, a theoretical deterministic model for ebola epidemic with quarantine of infectives is proposed and analyzed. The model exhibits two equilibria; the disease free and endemic equilibrium points. The basic reproduction number, R0, which is the main threshold, is obtained and the stability of the equilibrium points established. Using parameter values drawn from the 2014 West Africa ebola outbreak, a numerical simulation of the model is carried out. It is found that the dynamics of the model are completely determined by R0 and that a quarantine success rate of at least 70% is sufficient to contain the disease outbreak.
Paper's Title:
Birkhoff-James orthogonality and Best Approximant in L1(X)
Author(s):
Mecheri Hacene and Rebiai Belgacem
Department of Mathematics and
Informatics,
LAMIS laboratory, University of Tebessa,
Algeria.
E-mail: mecherih2000@yahoo.fr
Department of Mathematics and
Informatics,
LAMIS laboratory, University of Tebessa,
Algeria.
E-mail: brebiai@gmail.com
Abstract:
Let X be a complex Banach space and let (X,ρ) be a positive measure space. The Birkhoff-James orthogonality is a generalization of Hilbert space orthogonality to Banach spaces. We use this notion of orthogonality to establish a new characterization of Birkhoff-James orthogonality of bounded linear operators in L1(X,ρ) also implies best approximation has been proved.
Paper's Title:
Hermite-Hadamard Type Inequalities for MN-Convex Functions
Author(s):
Sever S. Dragomir1,2
1Mathematics,
College of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
The present work endeavours to briefly present some of the fundamental results connected to the Hermite-Hadamard inequality for special classes of convex functions such as AG, AH, GA, GG, GH, HA, HG and HH -convex functions in which the author have been involved during the last five years. For simplicity, we call these classes of functions such as MN-convex functions, where M and N stand for any of the Arithmetic (A), Geometric (G) or Harmonic (H) weighted means of positive real numbers. The survey is intended for use by both researchers in various fields of Approximation Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Semicommutative and Semiprime Properties in Bi-amalgamated Rings
Author(s):
1A. Aruldoss, 2C. Selvaraj, 3G. E. Chatzarakis, 4S. L. Panetsos, 5U. Leerawat
1
Department of Mathematics,
Mepco Schlenk Engineering College,
Sivakasi-626 005, Tamilnadu,
India.
aruldossa529@gmail.com
2
Department of Mathematics,
Periyar University,
Salem - 636 011, Tamilnadu,
India.
selvavlr@yahoo.com
3,4
Department of Electrical and Electronic Engineering Educators,
School of Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
geaxatz@otenet.gr
spanetsos@aspete.gr
5
Department of Mathematics,
Faculty of Science, Kasetsart University,
Bangkok 10900,
Thailand.
fsciutl@ku.ac.th
Abstract:
Let α: A→ B and β: A→ C be two ring homomorphisms and I and I' be two ideals of B and C, respectively, such that α{-1}(I)=β{-1}(I'). In this paper, we give a characterization for the bi-amalgamation of A with (B, C) along (I, I') with respect to (α, β) (denoted by A⋈(α, β)(I, I')) to be a SIT, semiprime, semicommutative and semiregular. We also give some characterization for these rings.
Paper's Title:
Indonesia's GDP Forecast: Evidence From Fuzzy Time Series Model Using Particle Swarm Optimization Algorithm
Author(s):
Ismail Djakaria1, Djihad Wungguli2, Regina Sugi Pakadang3, Sri Endang Saleh4, Maman Abdurachman Djauhari5
1,2,3Universitas
Negeri Gorontalo,
Department of Statistics, Gorontalo,
Indonesia.
4Universitas Negeri Gorontalo,
Department of Development Economics, Gorontalo,
Indonesia.
5Indonesian Institute of Education,
Jl. Terusan Pahlawan 32, Garut 44151,
Indonesia.
E-mail: iskar@ung.ac.id
URL:
https://orcid.org/0000-0003-1358-2356
Abstract:
Gross Domestic Product (GDP) is a principal indicator used to measure the economic condition of a country. Indonesia's GDP growth from 2017 to 2019 was approximately 6 percent; however, it experienced a decline in 2020 and 2021, with rates of only -0.02 percent and 2.41 percent, respectively. In the process of economic development planning, a forecasting system is required to determine GDP in the future. The forecasting method employed in this research is fuzzy time series optimized using Particle Swarm Optimization (PSO), to enhance the accuracy and convergence of forecasted values. The dataset used comprises secondary data, specifically 54 sets of Indonesian GDP data spanning from the first quarter of 2010 to the second quarter of 2023. The analysis results indicate that the proposed method is better than the conventional fuzzy time series approach. The former method provides a predictive value for one period in the future with a Mean Absolute Percentage Error (MAPE) value of 4.40%. In contrast, the latter yields higher predictive values with a MAPE value of 7.93%.
Search and serve lasted 1 second(s).