Department of Mathematics,
Birla Institute of Technology And Science- Pilani,
Hyderabad Campus, Jawahar Nagar, Kapra Mandal,
District.-Medchal-500 078, Telangana,
India.
E-mail: alphonse@hyderabad.bits-pilani.ac.in
p20180442@hyderabad.bits-pilani.ac.in
URL: https://www.bits-pilani.ac.in/hyderabad/a-michael-alphonse
https://www.bits-pilani.ac.in/research_scholars/sri-sakti-swarup-anupindi

Abstract:

In this paper, we prove strong type inequality for maximal commutator of singular operator on weighted lp spaces. Using these results we prove strong type inequality for the maximal commutator of singular operator on variable exponent sequence spaces. Using Calderon-Coifman-Weiss transference principle we prove strong type inequality for maximal ergodic commutator of singular operator on a probability space equipped with measure preserving transformation U.

Paper's Title:

Note on the Rank of Birkhoff Interpolation

Author(s):

J. Rubió-Massegú

Applied Mathematics III, Universitat Politècnica de Catalunya,
Colom 1, 08222, Terrassa,
Spain
josep.rubio@upc.edu

Abstract:

The relationship between a variant of the rank of a univariate Birkhoff interpolation problem, called normal rank, and other numbers of interest associated to the interpolation problem is studied.

Paper's Title:

A Geometric Generalization of Busemann-Petty Problem

Author(s):

Liu Rong and Yuan Jun

Shanghai Zhangjiang Group Junior Middle School,
Huo Xiang Road, Shanghai, 201203,
China

yuanjun_math@126.com

liurong@shu.edu.cn

Abstract:

The norm defined by Busemann's inequality establishes a class of star body - intersection body. This class of star body plays a key role in the solution of Busemann-Petty problem. In 2003, Giannapoulos [1] defined a norm for a new class of half-section. Based on this norm, we give a geometric generalization of Busemann-Petty problem, and get its answer as a result

Paper's Title:

A_p Functions and Maximal Operator

Author(s):

Chunping Xie

Department of Mathematics,
Milwaukee School of Engineering,
1025 N. Broadway,
Milwaukee, Wisconsin 53202,
U. S. A.

E-mail: xie@msoe.edu

URL: http://www.msoe.edu/people/chunping.xie

Abstract:

The relationship between A_p functions and Hardy-Littlewood maximal operator on L^p,λ(w), the weighted Morrey space, has been studied. Also the extropolation theorem of L^p,λ(w) has been considered.

Paper's Title:

Bounds for Two Mappings Associated to the Hermite-Hadamard Inequality

Author(s):

S. S. Dragomir^1,2 and I. Gomm¹

¹Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428, Melbourne City, MC 8001,
Australia.

²School of Computational & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.

sever.dragomir@vu.edu.au
ian.gomm@vu.edu.au
URL: http://rgmia.org/dragomir  
 

Abstract:

Some inequalities concerning two mappings associated to the celebrated Hermite-Hadamard integral inequality for convex function with applications for special means are given.

Paper's Title:

Further Bounds for Two Mappings Related to the Hermite-Hadamard Inequality

Author(s):

S. S. Dragomir^1,2 and I. Gomm¹

¹Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428, Melbourne City, MC 8001,
Australia.

²School of Computational & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.

sever.dragomir@vu.edu.au
ian.gomm@vu.edu.au
URL: http://rgmia.org/dragomir  
 

Abstract:

Some new results concerning two mappings associated to the celebrated Hermite-Hadamard integral inequality for twice differentiable functions with applications for special means are given.

Paper's Title:

Some Applications of Fejér's Inequality for Convex Functions (I)

Author(s):

S.S. Dragomir^1,2 and I. Gomm¹

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia.

sever.dragomir@vu.edu.au

URL: http://rgmia.org/dragomir

²School of Computational & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.

Abstract:

Some applications of Fejér's inequality for convex functions are explored. Upper and lower bounds for the weighted integral

under various assumptions for f with applications to the trapezoidal quadrature rule are given. Some inequalities for special means are also provided

Paper's Title:

Inequalities for the Area Balance of Functions of Bounded Variation

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

We introduce the area balance function associated to a Lebesgue integrable function f:[a,b] →C by

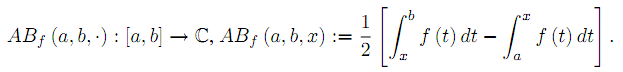
Several sharp bounds for functions of bounded variation are provided. Applications for Lipschitzian and convex functions are also given.

Paper's Title:

Presentation a mathematical model for bone metastases control by using tamoxifen

Author(s):

Maryam Nikbakht, Alireza Fakharzadeh Jahromi and Aghileh Heydari

Department of Mathematics,
Payame Noor University,
P.O.Box 19395-3697, Tehran,
Iran.
.E-mail: maryam_nikbakht@pnu.ac.ir

Department of Mathematics,
Faculty of Basic Science,
Shiraz University of Technology.
E-mail: a_fakharzadeh@sutech.ac.ir

Department of Mathematics,
Payame Noor University,
P.O.Box 19395-3697, Tehran,
Iran.
E-mail: a-heidari@pnu.ac.ir

Abstract:

Bone is a common site for metastases (secondary tumor) because of breast and prostate cancer. According to our evaluations the mathematical aspect of the effect of drug in bone metastases has not been studied yet. Hence, this paper suggested a new mathematical model for bone metastases control by using tamoxifen. The proposed model is a system of nonlinear partial differential equations. In this paper our purpose is to present a control model for bone metastases. At end by some numerical simulations, the proposed model is examined by using physician.

Paper's Title:

Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.

Paper's Title:

A Note on Calderon Operator

Author(s):

Chunping Xie

Department of Mathematics,
Milwaukee School of Engineering,
1025 N. Broadway,
Milwaukee, Wisconsin 53202,
U. S. A.

E-mail: xie@msoe.edu

URL: http://www.msoe.edu/people/chunping.xie

Abstract:

We have shown that the Calderon operator is bounded on Morrey Spaces on R⁺. Also under certain conditions on the weight, the Hardy operator, the adjoint Hardy operator, and therefore the Caldern operator are bounded on the weighted Morrey spaces.

Paper's Title:

Bounds on the Jensen Gap, and Implications for Mean-Concentrated Distributions

Author(s):

Xiang Gao, Meera Sitharam, Adrian E. Roitberg

Department of Chemistry, and Department of Computer & Information Science & Engineering,
University of Florida,
Gainesville, FL 32611,
USA.
E-mail: qasdfgtyuiop@gmail.com
URL: https://scholar.google.com/citations?user=t2nOdxQAAAAJ

Abstract:

This paper gives upper and lower bounds on the gap in Jensen's inequality, i.e., the difference between the expected value of a function of a random variable and the value of the function at the expected value of the random variable. The bounds depend only on growth properties of the function and specific moments of the random variable. The bounds are particularly useful for distributions that are concentrated around the mean, a commonly occurring scenario such as the average of i.i.d. samples and in statistical mechanics.

Paper's Title:

High Order Collocation Method for the Generalized Kuramoto-Sivashinsky Equation

Author(s):

Zanele Mkhize, Nabendra Parumasur and Pravin Singh

School of Mathematics, Statistics and Computer Sciences,
University of KwaZulu-Natal,
Private Bag X 54001,
Durban 4000.
E-mail: mkhizez2@ukzn.ac.za
parumasurn1@ukzn.ac.za
 singhp@ukzn.ac.za
URL: https://www.ukzn.ac.za

Abstract:

In this paper, we derive the heptic Hermite basis functions and use them as basis functions in the orthogonal collocation on finite elements (OCFE) method. We apply the method to solve the generalized Kuramoto-Sivashinsky equation. Various numerical simulations are presented to justify the computational efficiency of the proposed method.

Search and serve lasted 1 second(s).