|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
On A Conjecture of A Logarithmically Completely Monotonic Function
Author(s):
Valmir Krasniqi, Armend Sh. Shabani
Department of Mathematics,
University of Prishtina,
Republic of Kosova
E-mail:
vali.99@hotmail.com
armend_shabani@hotmail.com
Abstract:
In this short note we prove a conjecture, related to a logarithmically completely monotonic function, presented in [5]. Then, we extend by proving a more generalized theorem. At the end we pose an open problem on a logarithmically completely monotonic function involving q-Digamma function.
Paper's Title:
Existence Results for Second Order Impulsive Functional Differential Equations with Infinite Delay
Author(s):
M. Lakrib, A. Oumansour and K. Yadi
Laboratoire de Mathématiques, Université Djillali
Liabées, B.P. 89 Sidi Bel Abbès 22000, Algérie
mlakrib@univ-sba.dz
oumansour@univ-sba.dz
Laboratoire de Mathématiques, Université Abou Bekr
Belkaid, B.P. 119 Tlemcen 13000, Algérie
k_yadi@mail.univ-tlemcen.dz
Abstract:
In this paper we study the existence of solutions for second order impulsive functional differential equations with infinite delay. To obtain our results, we apply fixed point methods.
Paper's Title:
Some interesting properties of finite continuous Cesàro operators
Author(s):
Abdelouahab Mansour and Abderrazak Hechifa
Operator theory laboratory (LABTHOP),
Eloued University,
Algeria.
E-mail:
amansour@math.univ-lyon1.fr
Mathematics Department,
Faculty of Science,
Badji Mokhtar University, -Annaba,
Algeria.
E-mail:
abderrazak02@gmail.com
Abstract:
A complex scalar λ is called an extended eigenvalue of a bounded linear operator T on a complex Banach space if there is a nonzero operator X such that TX = λ XT, the operator X is called extended eigenoperator of T corresponding to the extended eigenvalue λ.
In this paper we prove some properties of extended eigenvalue and extended eigenoperator for
C1 on Lp([0,1]), where C1 is the Cesàro operator defined on the complex Banach spaces Lp([0 , 1]) for
1<p<∞ by the expression
Paper's Title:
Some Remarks On Quasinearly Subharmonic Functions Author(s):
Mansour Kalantar Universite Toulouse III-Paul Sabatier,
Abstract:
We prove some basic properties of quasi-nearly subharmonic functions and quasi-nearly subharmonic functions in the narrow sense. Paper's Title:
On Oscillation of
Second-Order Delay Dynamic Equations on Time Scales
Author(s):
S. H. Saker
Department of Mathematics, Faculty of Science, Abstract:
Some new oscillation criteria for second-order linear delay dynamic equation
on a time scale T are established. Our results improve the
recent results for delay dynamic equations and in the special case when
T=R, the results include the oscillation results established by Hille [1948,
Trans. Amer. Math. Soc. 64 (1948), 234-252] and Erbe [Canad. Math. Bull. 16
(1973), 49-56.] for differential equations. When T=Z the
results include and improve some oscillation criteria for difference
equations. When T=hZ, h>0, T=qN and T=N2, i.e., for generalized second order delay difference equations our
results are essentially new and can be applied on different types of time
scales. An example is considered to illustrate the main results. Paper's Title:
Topological Aspects of Scalarization in Vector Optimization Problems.
Author(s):
Peter I. Kogut, Rosanna Manzo
and Igor V. Nechay
Department of Differential Equations,
Università di Salerno,
Department of Technical Cybernetics, 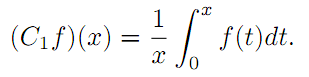
3: Paper Source
PDF document
118 Route de Narbonne, 31062 Toulouse,
France.
E-mail:
mansour.kalantar@math.univ-toulouse.fr,
mankalantar12@yahoo.com
2: Paper Source
PDF document
Mansoura University, Mansoura, 35516,
Egypt.
shsaker@mans.edu.eg
2: Paper Source
PDF document
Dnipropetrovsk National University, Naukova
STR.,
13,
49010 Dnipropetrovsk,
Ukraine
p.kogut@i.ua
Dipartimento di Ingegneria dell'Informazione e Matematica Applicata,
Via Ponte don Melillo, 84084 Fisciano (SA),
Italy
manzo@diima.unisa.it
Dnipropetrovsk Technical University,
Acad. Lazarjan
STR., 2,
49010 Dnipropetrovsk,
Ukraine
i.nechay@i.ua
Abstract:
In this paper, we study vector optimization problems in partially ordered Banach spaces. We suppose that the objective mapping possesses a weakened property of lower semicontinuity and make no assumptions on the interior of the ordering cone. We derive sufficient conditions for existence of efficient solutions of the above problems and discuss the role of topological properties of the objective space. We discuss the scalarization of vector optimization problems when the objective functions are vector-valued mappings with a weakened property of lower semicontinuity. We also prove the existence of the so-called generalized efficient solutions via the scalarization process. All principal notions and assertions are illustrated by numerous examples.
Paper's Title:
On Euler's First Transformation Formula for k-hypergeometric Function
Author(s):
Sungtae Jun and Insuk Kim
General Education Institute,
Konkuk University, Chungju 380-701,
Republic of Korea.
E-mail: sjun@kku.ac.kr
Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Republic of Korea.
E-mail: iki@wku.ac.kr
Abstract:
Mubeen et al. obtained Kummer's first transformation for the k-hypergeometric function. The aim of this note is to provide the Euler-type first transformation for the k-hypergeometric function. As a limiting case, we recover the results of Mubeen et al. In addition to this, an alternate and easy derivation of Kummer's first transformation for the k-hypergeometric function is also given.
Paper's Title:
Several New Closed-form Evaluations of the Generalized Hypergeometric Function with Argument 1/16
Author(s):
B. R. Srivatsa Kumar, Insuk Kim and Arjun K. Rathie
Department of Mathematics,
Manipal Institute of Technology,
Manipal Academy of Higher Education,
Manipal 576 104,
India.
E-mail: sri_vatsabr@yahoo.com
Department of Mathematics Education,
Wonkwang University,
Iksan, 54538,
Republic of Korea.
E-mail: iki@wku.ac.kr
Department of Mathematics,
Vedant College of Engineering and Technology,
Rajasthan Technical University,
Bundi, 323021, Rajasthan,
India.
E-mail: arjunkumarrathie@gmail.com
Abstract:
The main objective of this paper is to establish as many as thirty new closed-form evaluations of the generalized hypergeometric function q+1Fq(z) for q= 2, 3, 4. This is achieved by means of separating the generalized hypergeometric function q+1Fq(z) for q=1, 2, 3, 4, 5 into even and odd components together with the use of several known infinite series involving central binomial coefficients obtained earlier by Ji and Hei \& Ji and Zhang.
Paper's Title:
On Perturbed Reflection Coefficients
Author(s):
J. L. Díaz-Barrero and J. J. Egozcue
Applied Mathematics III,
Universidad Politécnica de Cataluña,
Barcelona, Spain
jose.luis.diaz@upc.edu
juan.jose.egozcue@upc.edu
Abstract:
Many control and signal processing applications require testing
stability of polynomials. Classical tests for locating zeros of
polynomials are recursive, but they must be stopped whenever the so
called "singular polynomials" appear. These ``singular cases'' are
often avoided by perturbing the "singular polynomial".
Perturbation techniques although always successful are not proven to
be well-founded. Our aim is to give a mathematical foundation to a
perturbation method in order to overcome "singular cases" when
using Levinson recursion as a testing method. The non-singular
polynomials are proven to be dense in the set of all polynomials
respect the L²-norm on the unit circle . The proof is
constructive and can be used algorithmically.
Paper's Title:
On a Subclass of Uniformly Convex Functions Defined by the Dziok-Srivastava Operator
Author(s):
M. K. Aouf and G. Murugusundaramoorthy
Mathematics Department, Faculty of Science,
Mansoura University 35516,
Egypt.
mkaouf127@yahoo.com
School of Science and Humanities, VIT University
Vellore - 632014,
India.
gmsmoorthy@yahoo.com
Abstract:
Making use of the Dziok-Srivastava operator, we define a new subclass Tlm([α1];α,β) of uniformly convex function with
negative coefficients. In this paper, we obtain coefficient estimates,
distortion theorems, locate extreme points and obtain radii of
close-to-convexity, starlikeness and convexity for functions belonging to the
class Tlm([α1];α,β) . We
consider integral operators associated with functions belonging to the class
Hlm([α1];α,β) defined via the Dziok-Srivastava
operator. We also obtain several results for the modified Hadamard products of
functions belonging to the class Tlm([α1];α,β)
and we obtain properties associated with generalized fractional calculus
operators.
Paper's Title:
A Subclass of Meromorphically Multivalent Functions with Applications to Generalized Hypergeometric Functions
Author(s):
M. K. Aouf
Mathematics Department,
Faculty of Science,
Mansoura University 35516,
Egypt
mkaouf127@yahoo.com
Abstract:
In this paper a new subclass of meromorphically multivalent functions, which
is defined by means of a Hadamard product (or convolution) involving some
suitably normalized meromorphically p-valent functions. The main object of
the present paper is to investigate the various important properties and
characteristics of this subclass of meromorphically multivalent functions.
We also derive many interesting results for the Hadamard products of
functions belonging to this subclass. Also we consider several applications
of our main results to generalized hypergeomtric functions.
Paper's Title:
Inclusion and Neighborhood
Properties for Certain Subclasses of Analytic Functions Associated with
Convolution Structure
Author(s):
M. K. Aouf
Mathematics Department,
Faculty of Science,
Mansoura University 35516,
Egypt.
mkaouf127@yahoo.com
Abstract:
In this paper we introduce and investigate two new subclasses of multivalently analytic functions of complex order defined by using the familiar convolution structure of analytic functions. In this paper we obtain the coefficient estimates and the consequent inclusion relationships involving the neighborhoods of the p-valently analytic functions.
Paper's Title:
Generalized Efficient Solutions to One Class of Vector Optimization Problems in Banach Space
Author(s):
Peter I. Kogut, Rosanna Manzo, and Igor V. Nechay
Department of Differential Equations,
Dnipropetrovsk National University,
Naukova str., 13,
49050 Dnipropetrovsk,
Ukraine
p.kogut@i.ua
Dipartimento di Ingegneria
Dell’informazione e Matematica Applicata,
Università di Salerno,
Via
Ponte
Don Melillo,
84084 Fisciano
(Sa),
Italy
manzo@diima.unisa.it
Department of Technical Cybernetics,
Dnipropetrovsk Technical University,
Acad. Lazarjan str., 2,
49010
Dnipropetrovsk,
Ukraine
i.nechay@i.ua
Abstract:
In this paper, we study vector optimization problems in Banach spaces for essentially nonlinear operator equations with additional control and state constraints. We assume that an objective mapping possesses a weakened property of lower semicontinuity and make no assumptions on the interior of the ordering cone. Using the penalization approach we derive both sufficient and necessary conditions for the existence of efficient solutions of the above problems. We also prove the existence of the so-called generalized efficient solutions via the scalarization of some penalized vector optimization problem.
Paper's Title:
A Dynamic Contact Problem for an Electro Viscoelastic Body
Author(s):
Denche M. and Ait Kaki L.
Laboratoire Equations Differentielles,
Departement de Mathematiques,
Universite Constantine 1,
Algeria.
Ecole Normale Superieure,
Departement des Sciences Exactes et Informatique,
Plateau Mansourah, Constantine.
Algeria.
E-mail:
m.denche@umc.edu.dz
leilaitkaki@yahoo.fr
Abstract:
We consider a dynamic problem which describes a contact between a piezoelectric body and a conductive foundation. The frictionless contact is modelled with the normal compliance, the electric conditions are supposed almost perfect. We prove the existence of a unique weak solution for almost perfect electric contact.
Search and serve lasted 1 second(s).