|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
The boundedness of Bessel-Riesz operators on generalized Morrey spaces
Author(s):
Mochammad Idris, Hendra Gunawan and Eridani
Department of Mathematics,
Bandung Institute of Technology,
Bandung 40132,
Indonesia.
E-mail:
mochidris@students.itb.ac.id
Department of Mathematics,
Bandung Institute of Technology,
Bandung 40132,
Indonesia.
E-mail: hgunawan@math.itb.ac.id
URL:
http://personal.fmipa.itb.ac.id/hgunawan/
Department of Mathematics,
Airlangga University,
Surabaya 60115,
Indonesia.
E-mail: eridani.dinadewi@gmail.com
Abstract:
In this paper, we prove the boundedness of Bessel-Riesz operators on generalized Morrey spaces. The proof uses the usual dyadic decomposition, a Hedberg-type inequality for the operators, and the boundedness of Hardy-Littlewood maximal operator. Our results reveal that the norm of the operators is dominated by the norm of the kernels.
Paper's Title:
Generalized Von Neumann-Jordan Constant for Morrey Spaces and Small Morrey Spaces
Author(s):
H. Rahman and H. Gunawan
Department of Mathematics,
Islamic State University Maulana Malik Ibrahim Malang,
Jalan Gajayana No.50,
Indonesia.
E-mail: hairur@mat.uin-malang.ac.id
Analysis and Geometry Group,
Faculty of Mathematics and Natural Sciences,
Bandung Institute of Technology, Bandung 40132,
Indonesia.
E-mail: hgunawan@math.itb.ac.id
URL:
http://personal.fmipa.itb.ac.id/hgunawan/
Abstract:
In this paper we calculate some geometric constants for Morrey spaces and small Morrey spaces, namely generalized Von Neumann-Jordan constant, modified Von Neumann-Jordan constants, and Zbaganu constant. All these constants measure the uniformly nonsquareness of the spaces. We obtain that their values are the same as the value of Von Neumann-Jordan constant for Morrey spaces and small Morrey spaces.
Paper's Title:
Fractional Integral Operators and Olsen Inequalities on
Non-Homogeneous Spaces
Author(s):
Idha Sihwaningrum, Herry P. Suryawan, Hendra Gunawan
Analysis and Geometry Group,
Faculty of Mathematics and Natural Sciences,
Bandung Institute of Technology, Bandung 40132,
Indonesia
hgunawan@math.itb.ac.id
URL:
http://personal.fmipa.itb.ac.id/hgunawan/
Abstract:
We prove the boundedness of the fractional integral operator Iα on generalized Morrey spaces of non-homogeneous type. In addition, we also present Olsen-type inequalities for a multiplication operator involving Iα. Our proof uses a result of García-Cuerva and Martell [3].
Paper's Title:
Weak Type Inequalities for Some Operators on Generalized Morrey Spaces Over Metric Measure Spaces
Author(s):
Idha Sihwaningrum, Ari Wardayani, Hendra Gunawan
Faculty of Mathematics and Natural
Sciences,
Jenderal Soedirman University, Purwokerto 53122,
Indonesia.
E-mail: idha.sihwaningrum@unsoed.ac.id
ariwardayani@yahoo.co.id
Faculty of Mathematics and Natural
Sciences,
Bandung Institute of Technology, Bandung 40132,
Indonesia.
E-mail: hgunawan@math.itb.ac.id
URL:
http://personal.fmipa.itb.ac.id/hgunawan/
Abstract:
We discuss weak type inequalities for maximal and fractional integral operators on generalized Morrey spaces over metric measure spaces. Here the measure satisfies the so called growth condition. By taking into account the maximal operator, we obtain a Hedberg type inequality, which leads us to the weak type inequality for the fractional integral operator on the same spaces.
Paper's Title:
Some Inequalities for the Generalized Riesz Potential on the Generalized Morrey Spaces over Hypergroups
Author(s):
I. Sihwaningrum, Renny, Y. Dasril
Jenderal Soedirman University,
Indonesia.
E-mail: idha.sihwaningrum@unsoed.ac.id
renny@unsoed.ac.id
Universiti Tun Hussein Onn,
Malaysia.
E-mail:
yosza@uthm.edu.my
Abstract:
We present in this paper some inequalities for the generalized Riesz potential on the generalized Morrey spaces over commutative hypergroups. The results can be found by employing the maximal operator.
Paper's Title:
The Concept of Convergence for 2-Dimensional Subspaces Sequence in Normed Spaces
Author(s):
M. Manuharawati, D. N. Yunianti, M. Jakfar
Mathematics Department, Universitas
Negeri Surabaya,
Jalan Ketintang Gedung C8,
Surabaya 60321,
Indonesia.
E-mail: manuharawati@unesa.ac.id,
dwiyunianti@unesa.ac.id,
muhammadjakfar@unesa.ac.id
Abstract:
In this paper, we present a concept of convergence of sequence, especially, of 2-dimensional subspaces of normed spaces. The properties of the concept are established. As consequences of our definition in an inner product space, we also obtain the continuity property of the angle between two 2-dimensional subspaces of inner product spaces.
Paper's Title:
On Reformations of 2--Hilbert Spaces
Author(s):
M. Eshaghi Gordji, A. Divandari, M. R. Safi and Y. J. Cho
Department of Mathematics, Semnan
University,
P.O. Box 35195--363, Semnan,
Iran
meshaghi@semnan.ac.ir, madjid.eshaghi@gmail.com
Department of Mathematics, Semnan
University,
Iran
Department of Mathematics, Semnan
University,
Iran
safi@semnan.ac.ir, SafiMohammadReza@yahoo.com
Department of Mathematics Education and
the RINS,
Gyeongsang National University
Chinju 660-701,
Korea
Abstract:
In this paper, first, we introduce the new concept of (complex) 2--Hilbert spaces, that is, we define the concept of 2--inner product spaces with a complex valued 2--inner product by using the 2--norm. Next, we prove some theorems on Schwartz's inequality, the polarization identity, the parallelogram laws and related important properties. Finally, we give some open problems related to 2--Hilbert spaces.
Paper's Title:
Some Double λ-Convergent Sequence Spaces Over n-Normed Spaces
Author(s):
Kuldip Raj, Renu Anand and Seema Jamwal
School of Mathematics,
Shri Mata Vaishno Devi University Katra-182320,
Jammu and Kashmir,
India.
E-mail: kuldipraj68@gmail.com, renuanand71@gmail.com, seemajamwal8@gmail.com
Abstract:
In this paper we introduce some double generalized λ-convergent sequence spaces over n-normed spaces defined by Musielak-Orlicz function M = (Mk,l). We also made an attempt to study some topological and algebraic properties of these sequence spaces.
Paper's Title:
New Reverses of Schwarz, Triangle and Bessel Inequalities in Inner Product Spaces
Author(s):
S. S. Dragomir
School of Computer Science and Mathematics, Victoria
University of Technology, PO BOX
14428, MCMC 8001, VICTORIA, AUSTRALIA.
sever.dragomir@vu.edu.au
URL:
http://rgmia.vu.edu.au/SSDragomirWeb.html
Abstract:
New reverses of the Schwarz, triangle and Bessel inequalities in inner product spaces are pointed out. These results complement the recent ones obtained by the author in the earlier paper [13]. Further, they are employed to establish new Grüss type inequalities. Finally, some natural integral inequalities are stated as well.
Paper's Title:
Necessary and Sufficient Conditions for the Boundedness of Fractional Integral Operators on Hypergroups
Author(s):
Ari Wardayani, Mutia Nur Estri, Wihantoro, Idha Sihwaningrum
Faculty of Mathematics and Natural
Sciences,
Jenderal Soedirman University,
Indonesia.
E-mail: ari.wardayani@unsoed.ac.id
mutia.estri@unsoed.ac.id
wihantoro@unsoed.ac.id
idha.sihwaningrum@unsoed.ac.id
Abstract:
We prove in this paper the necessary and sufficient conditions for the boundedness of the fractional integral operators on Lebesgue spaces over commutative hypergroups. The necessity proofs take into account the Haar measure, meanwhile the sufficiency proofs employ the maximal operators.
Paper's Title:
Some Grüss Type Inequalities in Inner Product Spaces
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir
Abstract:
Some inequalities in inner product spaces
that provide upper bounds for the quantities
and
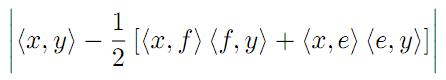
where e,f ∈ H with
and x,y are vectors in H satisfying some appropriate assumptions are
given. Applications for discrete and integral inequalities are provided as
well.
Search and serve lasted 0 second(s).