|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Certain Coefficient Estimates for Bi-univalent Sakaguchi Type Functions
Author(s):
B. Srutha Keerthi, S. Chinthamani
Department of Applied Mathematics,
Sri Venkateswara College of Engineering,
Sriperumbudur, Chennai - 602105,
India
Abstract:
Estimates on the initial coefficients are obtained for normalized analytic functions f in the open unit disk with f and its inverse g = f-1 satisfying the conditions that zf'(z) / f(z) and zg'(z) / g(z) are both subordinate to a starlike univalent function whose range is symmetric with respect to the real axis. Several related classes of functions are also considered, and connections to earlier known results are made.
Paper's Title:
Coefficient Estimates for Certain Subclasses of Bi-univalent Sakaguchi
Type Functions by using Faber Polynomial
Author(s):
P. Murugabharathi, B. Srutha Keerthi
Mathematics Division,
School of Advanced Sciences,
VIT Chennai, Vandaloor, Kelambakkam Road,
Chennai - 600 127, India.
E-mail: bharathi.muhi@gmail.com
E-mail: sruthilaya06@yahoo.co.in
Abstract:
In this work, considering a general subclass of bi-univalent Sakaguchi type functions, we determine estimates for the general Taylor-Maclaurin coefficients of the functions in these classes. For this purpose, we use the Faber polynomial expansions. In certain cases, our estimates improve some of those existing coefficient bounds.
Paper's Title:
Geometrical Properties of Subclass of Analytic Function with Odd Degree
Author(s):
K. Sivagami Sundari and B. Srutha Keerthi
Divison of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology, Chennai Campus, Chennai - 600 127,
India.
E-mail: sivagamisundari.2298@gmail.com
Divison of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology, Chennai Campus, Chennai - 600 127,
India.
E-mail: keerthivitmaths@gmail.com
Abstract:
The objective of the paper is to study the geometrical
properties of the class B(λ, t).
For which we have proved that the radius
 is optimal ,(i.e)
the number
is optimal ,(i.e)
the number
 cannot be replaced by a larger one. Additionally, the graphs for various values of t and
λ are compared in order to study the sharpness of the coefficient bounds.
cannot be replaced by a larger one. Additionally, the graphs for various values of t and
λ are compared in order to study the sharpness of the coefficient bounds.
Paper's Title:
Neighborhoods of Certain Subclasses of Analytic Functions of Complex Order with Negative Coefficients
Author(s):
B. Srutha Keerthi, B. Adolf Stephen, A. Gangadharan, and S. Sivasubramanian
Department of Applied Mathematics,
Sri Venkateswara College of Engineering,
Sriperumbudur, Chennai - 602105,
India.
sruthilaya06@yahoo.co.in
Department of Mathematics,
Madras Christian College,
Chennai - 600059,
India
adolfmcc2003@yahoo.co.in
Department of Applied Mathematics,
Sri Venkateswara College of Engineering,
Sriperumbudur, Chennai - 602105,
India.
ganga@svce.ac.in
Department of Mathematics,
Easwari Engineering College,
Ramapuram, Chennai - 600089,
India
sivasaisastha@rediffmail.com
Abstract:
The main object of this paper is to prove several inclusion relations associated with the (n, δ) neighborhoods of various subclasses of convex functions of complex order by making use of the known concept of neighborhoods of analytic functions.
Paper's Title:
Coefficient Estimates Of Sakaguchi Kind Functions Using
Lucas Polynomials
Author(s):
H. Priya and B. Srutha Keerthi
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus,
Chennai - 600 048,
India.
E-mail:
priyaharikrishnan18@gmail.com
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus,
Chennai - 600 048,
India.
E-mail: isruthilaya06@yahoo.co.in
Abstract:
By means of (p,q) Lucas polynomials, we estimate coefficient bounds and Fekete-Szego inequalities for functions belonging to this class. Several corollaries and consequences of the main results are also obtained.
Paper's Title:
Fekete-Szeg÷ Inequality for Sakaguchi Type of functions in Petal Shaped Domain
Author(s):
E. K. Nithiyanandham and B. Srutha Keerthi
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: nithiyankrish@gmail.com
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com
Abstract:
In this paper, we estimate coefficient bounds,|a_2|,|a_3| and |a_4|, Fekete-Szeg÷ inequality
![]() and Toeplitz determinant
T2(2) and T3(1) for functions belonging to the following class
and Toeplitz determinant
T2(2) and T3(1) for functions belonging to the following class

the function being holomorphic, we expand using Taylor series and obtain several corollaries and consequences for the main result.
Paper's Title:
Toeplitz Determinant for Sakaguchi Type Functions Under Petal Shaped Domain
Author(s):
B. Nandhini and B. Srutha Keerthi
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail:
nandhinibaskar1996@gmail.com
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com
Abstract:
We introduce a new general subclass GPt,ρ of Sakaguchi kind function on a Petal shaped domain. We obtain coefficients bounds and upper bounds for the Fekete-Szeg÷ functional over the class. From these functions we obtain the bounds of first four coefficients, and then we have derived the Toeplitz determinant T2(2) and T3(1) whose diagonal entries are the coefficients of functions.
Paper's Title:
Coefficient Bounds for Sakaguchi Kind of Functions Associated with Sine Function
Author(s):
Serap Bulut, H. Priya and B. Srutha Keerth
Kocaeli University,
Faculty of Aviation and Space Sciences,
Arslanbey Campus, 41285 Kartepe-Kocaeli,
Turkey.
E-mail: serap.bulut@kocaeli.edu.tr
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus, Chennai - 600 048,
India.
E-mail: priyaharikrishnan18@gmail.com,
priya.h2020@vitstudent.ac.in
Department of Mathematics,
School of Advanced Sciences,
VIT Chennai Campus, Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com,
sruthakeerthi.b@vit.ac.in
Abstract:
In this paper, we introduce a new general subclass of analytic functions with respect to symmetric points in the domain of sine function. We obtain sharp coefficient bounds and upper bounds for the Fekete-Szeg÷ functional. Also we get sharp bounds for the logarithmic coefficients of functions belonging to this new class.
Paper's Title:
A Coefficient Inequality For Certain Subclasses of Analytic
Functions Related to Complex Order
Author(s):
B. Srutha Keerthi, B. Adolf Stephen and S. Sivasubramanian
Department Of Applied Mathematics, Sri Venkateswara College Of Engineering, Anna University,
Sriperumbudur, Chennai - 602 105,
India.
laya@svce.ac.in
Department of Mathematics, Madras Christian College,
Chennai - 600059,
India
adolfmcc2003@yahoo.co.in
Department of Mathematics, College of Engineering, Anna University,
Tamilnadu, Chennai - 600 025,
India.
sivasaisastha@rediffmail.com
Abstract:
In this present investigation, the authors obtain coefficient
inequality for certain normalized analytic functions of complex order f(z) defined
on the open unit disk for which
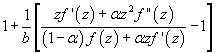 (
( and
and  be a complex number) lies in a region starlike with respect to 1 and is symmetric with respect to the real axis. Also
certain applications of the main result for a class of functions of complex order
defined by convolution are given. As a special case of this result, coefficient
inequality for a class of functions defined through fractional derivatives is
obtained. The motivation of this paper is to give a generalization of the
coefficient inequalities of the subclasses of starlike and convex functions of
complex order.
be a complex number) lies in a region starlike with respect to 1 and is symmetric with respect to the real axis. Also
certain applications of the main result for a class of functions of complex order
defined by convolution are given. As a special case of this result, coefficient
inequality for a class of functions defined through fractional derivatives is
obtained. The motivation of this paper is to give a generalization of the
coefficient inequalities of the subclasses of starlike and convex functions of
complex order.
Search and serve lasted 1 second(s).