|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Orthogonal Collocation on Finite Elements Using Quintic Hermite Basis
Author(s):
P. Singh, N. Parumasur and C. Bansilal
University of KwaZulu-Natal,
School of Mathematics Statistics and Computer Sciences,
Private Bag X54001,
Durban, 4000,
South Africa.
E-mail: singhprook@gmail.com
parumasurn1@ukzn.ac.za
christelle18@gmail.com
Abstract:
In this paper we consider the orthogonal collocation on finite elements (OCFE) method using quintic Hermite (second degree smooth) basis functions and use it to solve partial differential equations (PDEs). The method is particularly tailored to solve third order BVPS and PDEs and to handle their special solutions such as travelling waves and solitons, which typically is the case in the KdV equation. The use of quintic polynomials and collocation using Gauss points yields a stable high order superconvergent method. OCFE using quintic Hermite basis is optimal since it is computationally more efficient than collocation methods using (first degree smooth) piecewise-polynomials and more accurate than the (third degree smooth) B-splines basis. Various computational simulations are presented to demonstrate the computational efficiency and versatility of the OCFE method.
Paper's Title:
High Order Collocation Method for the Generalized Kuramoto-Sivashinsky Equation
Author(s):
Zanele Mkhize, Nabendra Parumasur and Pravin Singh
School of Mathematics, Statistics and
Computer Sciences,
University of KwaZulu-Natal,
Private Bag X 54001,
Durban 4000.
E-mail: mkhizez2@ukzn.ac.za
parumasurn1@ukzn.ac.za
singhp@ukzn.ac.za
URL: https://www.ukzn.ac.za
Abstract:
In this paper, we derive the heptic Hermite basis functions and use them as basis functions in the orthogonal collocation on finite elements (OCFE) method. We apply the method to solve the generalized Kuramoto-Sivashinsky equation. Various numerical simulations are presented to justify the computational efficiency of the proposed method.
Paper's Title:
On Weighted Toeplitz Operators
Author(s):
S. C. Arora and Ritu Kathuria
Department of Mathematics,
University of Delhi,
Delhi 110007,
India.
Department of Mathematics,
Motilal Nehru College, University of Delhi,
Delhi 110021,
India.
Abstract:
A weighted Toeplitz operator on H2(β) is defined as Tφf=P(φf) where P is the projection from L2(β) onto H2(β) and the symbol φ ∈ L2(β) for a given sequence β=‹βn›n∈ Z of positive numbers. In this paper, a matrix characterization of a weighted multiplication operator on L2β is given and it is used to deduce the same for a weighted Toeplitz operator. The eigenvalues of some weighted Toeplitz operators are also determined.
Paper's Title:
Fekete-Szegö Inequality for Sakaguchi Type of functions in Petal Shaped Domain
Author(s):
E. K. Nithiyanandham and B. Srutha Keerthi
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: nithiyankrish@gmail.com
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com
Abstract:
In this paper, we estimate coefficient bounds,|a_2|,|a_3| and |a_4|, Fekete-Szegö inequality
![]() and Toeplitz determinant
T2(2) and T3(1) for functions belonging to the following class
and Toeplitz determinant
T2(2) and T3(1) for functions belonging to the following class

the function being holomorphic, we expand using Taylor series and obtain several corollaries and consequences for the main result.
Paper's Title:
Toeplitz Determinant for Sakaguchi Type Functions Under Petal Shaped Domain
Author(s):
B. Nandhini and B. Srutha Keerthi
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail:
nandhinibaskar1996@gmail.com
Division of Mathematics, School of
Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com
Abstract:
We introduce a new general subclass GPt,ρ of Sakaguchi kind function on a Petal shaped domain. We obtain coefficients bounds and upper bounds for the Fekete-Szegö functional over the class. From these functions we obtain the bounds of first four coefficients, and then we have derived the Toeplitz determinant T2(2) and T3(1) whose diagonal entries are the coefficients of functions.
Paper's Title:
Hyponormal and K-Quasi-Hyponormal Operators On Semi-Hilbertian Spaces
Author(s):
Ould Ahmed Mahmoud Sid Ahmed and Abdelkader Benali
Mathematics Department,
College of Science,
Aljouf University,
Aljouf 2014,
Saudi Arabia.
E-mail:
sididahmed@ju.edu.sa
Mathematics Department, Faculty of
Science,
Hassiba Benbouali, University of Chlef,
B.P. 151 Hay Essalem, Chlef 02000,
Algeria.
E-mail:
benali4848@gmail.com
Abstract:
Let H be a Hilbert space and let A be a positive bounded operator on H. The semi-inner product < u|v>A:=<Au|v>, u,v ∈ H induces a semi-norm || .||A on H. This makes H into a semi-Hilbertian space. In this paper we introduce the notions of hyponormalities and k-quasi-hyponormalities for operators on semi Hilbertian space (H,||.||A), based on the works that studied normal, isometry, unitary and partial isometries operators in these spaces. Also, we generalize some results which are already known for hyponormal and quasi-hyponormal operators. An operator T ∈ BA (H) is said to be (A, k)-quasi-hyponormal if
![]()
Paper's Title:
Some properties of k-quasi class Q* operators
Author(s):
Shqipe Lohaj and Valdete Rexhëbeqaj Hamiti
Department of Mathematics,
Faculty of Electrical and Computer Engineering,
University of Prishtina "Hasan Prishtina",
Prishtine 10000,
Kosova.
E-mail: shqipe.lohaj@uni-pr.edu
Department of Mathematics,
Faculty of Electrical and Computer Engineering,
University of Prishtina "Hasan Prishtina",
Prishtine 10000,
Kosova.
E-mail: valdete.rexhebeqaj@uni-pr.edu
Abstract:
In this paper, we give some results of k-quasi class Q* operators. We proved that if T is an invertible operator and N be an operator such that N commutes with T*T, then N is k-quasi class Q* if and only if TNT-1 is of k-quasi class Q*. With example we proved that exist an operator k-quasi class Q* which is quasi nilpotent but it is not quasi hyponormal.
Paper's Title:
Some properties of quasinormal, paranormal and 2-k* paranormal operators
Author(s):
Shqipe Lohaj
Department of Mathematics,
University of Prishtina,
10000,
Kosova.
E-mail: shqipe.lohaj@uni-pr.edu
Abstract:
In the beginning of this paper some conditions under which an operator is partial isometry are given. Further, the class of 2-k* paranormal operators is defined and some properties of this class in Hilbert space are shown. It has been proved that an unitarily operator equivalent with an operator of a 2-k* paranormal operator is a 2-k* paranormal operator, and if is a 2-k* paranormal operator, that commutes with an isometric operator, then their product also is a $2-k^*$ paranormal operator.
Paper's Title:
On a New Class of Eulerian's Type Integrals Involving Generalized Hypergeometric Functions
Author(s):
Sungtae Jun, Insuk Kim and Arjun K. Rathie
General Education Institute,
Konkuk University, Chungju 380-701,
Republic of Korea.
Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Republic of Korea.
Department of Mathematics,
Vedant College of Engineering and Technology (Rajasthan Technical University),
Bundi-323021, Rajasthan,
India.
E-mail: sjun@kku.ac.kr, iki@wku.ac.kr, arjunkumarrathie@gmail.com
Abstract:
Very recently Masjed-Jamei and Koepf established interesting and useful generalizations of various classical summation theorems for the 2F1, 3F2, 4F3, 5F4 and 6F5 generalized hypergeometric series. The main aim of this paper is to establish eleven Eulerian's type integrals involving generalized hypergeometric functions by employing these theorems. Several special cases have also been given.
Paper's Title:
Two Further Methods for Deriving Four Results Contiguous to Kummer's Second Theorem
Author(s):
I. Kim and J. Kim
Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Korea.
E-mail: iki@wku.ac.kr
Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Korea.
E-mail: joohyung@wku.ac.kr
Abstract:
In the theory of generalized hypergeometric function, transformation and summation formulas play a key role. In particular, in one of the Kummer's transformation formulas, Kim, et al. in 2012, have obtained ten contiguous results in the form of a single result with the help of generalization of Gauss's second summation theorem obtained earlier by Lavoie, et al.. In this paper, we aim at presenting four of such results by the technique of contiguous function relations and integral method developed by MacRobert.
Paper's Title:
A Note on Evaluation of a New Class of Integrals Involving Generalized Hypergeometric Function
Author(s):
Madhav Prasad Poudel, Dongkyu Lim*, Narayan Prasad Pahari, Arjun K. Rathie
School of Engineering,
Pokhara University, Pokhara-30, Kaski,
Nepal.
E-mail: pdmadav@gmail.com
Department of Mathematics Education,
Andong National University, Andong 36729,
Republic of Korea.
E-mail: dklim@anu.ac.kr
Central Department of Mathematics,
Tribhuvan University, Kirtipur, Kathmandu,
Nepal.
E-mail: nppahari@gmail.com
Department of Mathematics,
Vedant College of Engineering & Technology (Rajasthan Technical University),
Village: Tulsi,
Jakhamund, Dist. Bundi, Rajasthan State,
India.
E-mail:
arjunkumarrathie@gmail.com
Abstract:
In the theory of hypergeometric and generalized hypergeometric series, classical summation theorems such as those of Gauss, Gauss second, Bailey and Kummer for the series
2F1; Watson, Dixon, Whipple and Saalshutz play a key role. Applications of the above mentioned summation theorems are well known for the series
3F2. In our present investigation, we aim to evaluate twenty five new class of integrals involving generalized hypergeometric function in the form of a single integral of the form:
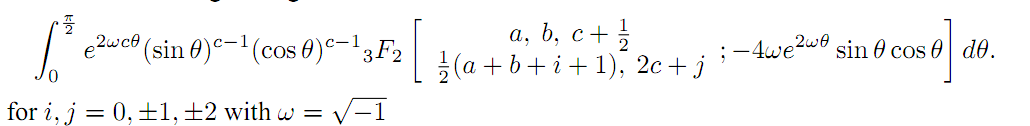
The results are established with the help of the generalizations of the classical Watson's summation theorem obtained earlier by Lavoie et al.. Fifty interesting integrals in the form of two integrals (twenty five each) have also been given as special cases of our main findings.
Search and serve lasted 0 second(s).