Paper's Title:

New Proofs of the Grüss Inequality

Author(s):

A.Mc.D. Mercer and Peter R. Mercer

Abstract:

We present new proofs of the Grüss inequality in its original form and in its linear functional form.

Paper's Title:

On a Subclass of Uniformly Convex Functions Defined by the Dziok-Srivastava Operator

Author(s):

M. K. Aouf and G. Murugusundaramoorthy

Mathematics Department, Faculty of Science,
Mansoura University 35516,
Egypt.
mkaouf127@yahoo.com

School of Science and Humanities, VIT University
Vellore - 632014,
India.
gmsmoorthy@yahoo.com

Abstract:

Making use of the Dziok-Srivastava operator, we define a new subclass T^l_m([α₁];α,β) of uniformly convex function with negative coefficients. In this paper, we obtain coefficient estimates, distortion theorems, locate extreme points and obtain radii of close-to-convexity, starlikeness and convexity for functions belonging to the class T^l_m([α₁];α,β) . We consider integral operators associated with functions belonging to the class H^l_m([α₁];α,β) defined via the Dziok-Srivastava operator. We also obtain several results for the modified Hadamard products of functions belonging to the class T^l_m([α₁];α,β) and we obtain properties associated with generalized fractional calculus operators.

Paper's Title:

Inequalities for the Čebyšev Functional of Two Functions of Selfadjoint Operators in Hilbert Spaces

Author(s):

S. S. Dragomir

Abstract:

Some recent inequalities for the Čebyšev functional of two functions of selfadjoint linear operators in Hilbert spaces, under suitable assumptions for the involved functions and operators, are surveyed.

Paper's Title:

Some Operator Order Inequalities for Continuous Functions of Selfadjoint Operators in Hilbert Spaces

Author(s):

S. S. Dragomir^1,2 and Charles E. M. Pearce³

¹Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428, Melbourne City, MC 8001,
Australia.

²School of Computational & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.

sever.dragomir@vu.edu.au 
URL: http://rgmia.org/dragomir

³School of Mathematical Sciences,
The University of Adelaide,
Adelaide,
Australia
 

Abstract:

Various bounds in the operator order for the following operator transform

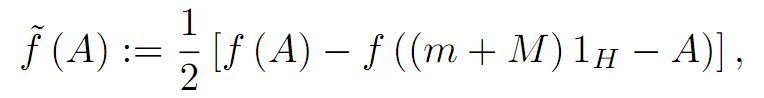
where A is a selfadjoint operator in the Hilbert space H with the spectrum Sp( A) ⊆ [ m,M] and f:[m,M] ->  C is a continuous function on [m,M]  are given. Applications for the power and logarithmic functions are provided as well.

Paper's Title:

Some Grüss Type Inequalities in Inner Product Spaces

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa

URL: http://rgmia.org/dragomir 

Abstract:

Some inequalities in inner product spaces that provide upper bounds for the quantities

and  ,

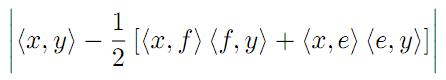
where e,f ∈ H with and x,y are vectors in H satisfying some appropriate assumptions are given. Applications for discrete and integral inequalities are provided as well.

Paper's Title:

Inequalities for Functions of Selfadjoint Operators on Hilbert Spaces:
a Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, College of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: https://rgmia.org/dragomir 

Abstract:

The main aim of this survey is to present recent results concerning inequalities for continuous functions of selfadjoint operators on complex Hilbert spaces. It is intended for use by both researchers in various fields of Linear Operator Theory and Mathematical Inequalities, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.

Paper's Title:

Trace Inequalities for Operators in Hilbert Spaces: a Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University,
PO Box 14428 Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: https://rgmia.org/dragomir 

Abstract:

In this paper we survey some recent trace inequalities for operators in Hilbert spaces that are connected to Schwarz's, Buzano's and Kato's inequalities and the reverses of Schwarz inequality known in the literature as Cassels' inequality and Shisha-Mond's inequality. Applications for some functionals that are naturally associated to some of these inequalities and for functions of operators defined by power series are given. Further, various trace inequalities for convex functions are presented including refinements of Jensen inequality and several reverses of Jensen's inequality. Hermite-Hadamard type inequalities and the trace version of Slater's inequality are given. Some Lipschitz type inequalities are also surveyed. Examples for fundamental functions such as the power, logarithmic, resolvent and exponential functions are provided as well.

Search and serve lasted 0 second(s).