|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Strong Convergence Theorems for a Common Zero of an Infinite Family of Gamma-Inverse Strongly Monotone Maps with Applications
Author(s):
Charles Ejike Chidume, Ogonnaya Michael Romanus, and Ukamaka Victoria Nnyaba
African University of Science and
Technology, Abuja,
Nigeria.
E-mail: cchidume@aust.edu.ng
E-mail: romanusogonnaya@gmail.com
E-mail: nnyabavictoriau@gmail.com
Abstract:
Let E be a uniformly convex and uniformly smooth real Banach space with
dual space E* and let Ak:E→E*,
k=1, 2, 3 , ...
be a family of inverse strongly monotone maps such that ∩∞k=1
Ak-1(0)≠∅.
A new iterative algorithm is constructed and proved to converge strongly to a
common zero of the family.
As a consequence of this result, a strong convergence theorem for approximating
a common J-fixed point for an infinite family of
gamma-strictly J-pseudocontractive maps is proved. These results are new and
improve recent results obtained for these classes of nonlinear maps.
Furthermore, the technique of proof is of independent interest.
Paper's Title:
Strong Convergence Theorem for a Common Fixed Point of an
Infinite Family of J-nonexpansive Maps with Applications
Author(s):
Charlse Ejike Chidume, Otubo Emmanuel Ezzaka and Chinedu Godwin Ezea
African University of Science and
Technology,
Abuja,
Nigeria.
E-mail:
cchidume@aust.edu.ng
Ebonyi State University,
Abakaliki,
Nigeria.
E-mail: mrzzaka@yahoo.com
Nnamdi Azikiwe University,
Awka,
Nigeria.
E-mail: chinedu.ezea@gmail.com
Abstract:
Let E be a uniformly convex and uniformly smooth real Banach space with dual space E*. Let {Ti}∞i=1 be a family of J-nonexpansive maps, where, for each i,~Ti maps E to 2E*. A new class of maps, J-nonexpansive maps from E to E*, an analogue of nonexpansive self maps of E, is introduced. Assuming that the set of common J-fixed points of {Ti}∞i=1 is nonempty, an iterative scheme is constructed and proved to converge strongly to a point x* in ∩∞n=1FJTi. This result is then applied, in the case that E is a real Hilbert space to obtain a strong convergence theorem for approximation of a common fixed point for an infinite family of nonexpansive maps, assuming existences. The theorem obtained is compared with some important results in the literature. Finally, the technique of proof is also of independent interest.
Paper's Title:
Iterative Approximation of Zeros of Accretive Type Maps, with Applications
Author(s):
Charles Ejike Chidume, Chinedu Godwin Ezea, and Emmanuel Ezzaka Otubo
African University of Science and
Technology, Abuja,
Nigeria.
E-mail: cchidume@aust.edu.ng
E-mail: chinedu.ezea@gmail.com
E-mail: mrzzaka@yahoo.com
Department of Mathematics,
Nnamdi Azikiwe University,
Awka,
Nigeria
E-mail: chinedu.ezea@gmail.com
Ebonyi State University,
Abakaliki,
Nigeria
E-mail: mrzzaka@yahoo.com
Abstract:
Let E be a reflexive real Banach space with uniformly Gâteaux differentiable norm. Let J:E→ E* be the normalized duality map on E and let A:E*→ E be a map such that AJ is an accretive and uniformly continuous map. Suppose that (AJ)-1(0) in nonempty. Then, an iterative sequence is constructed and proved to converge strongly to some u* in (AJ)-1(0). Application of our theorem in the case that E is a real Hilbert space yields a sequence which converges strongly to a zero of A. Finally, non-trivial examples of maps A for which AJ is accretive are presented..
Paper's Title:
The Convergence of Modified Mann-Ishikawa Iterations when Applied to an Asymptotically Pseudocontractive Map
Author(s):
S. Soltuz
Departamento de Matematicas, Universidad de Los Andes, Carrera 1
No. 18A-10, Bogota,
Colombia
and
``T. Popoviciu" Institute of Numerical Analysis
Cluj-Napoca,
Romania
smsoltuz@gmail.com
URL:http://www.uniandes.edu.co/
Abstract:
We prove that under minimal conditions the modified Mann and Ishikawa iterations converge when dealing with an asymptotically pseudocontractive map. We give an affirmative answer to the open question from C.E. Chidume and H. Zegeye, Approximate fixed point sequences and convergence theorems for asymptotically pseudocontractive mappings, J. Math. Anal. Appl., 278 (2003), 354--366.
Paper's Title:
Fixed Point Theorems for a Finite Family of Asymptotically Nonexpansive Mappings
Author(s):
E. Prempeh
Department of Mathematics,
Kwame Nkrumah University of Science and Technology,
Kumasi, Ghana
edward_prempeh2000@yahoo.com
Abstract:
Let
be a real reflexive Banach space with a uniformly Gâteaux differentiable norm,
be a nonempty bounded closed convex subset of
i=1,2,...,r be a finite family of asymptotically nonexpansive mappings
such that for each
Let
be a nonempty set of common fixed points of
and define
. Let
be fixed and let
be such that
as
. We can prove that the sequence
satisfying the relation
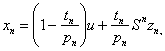
associated with
, converges strongly to a fixed point of
provided
possesses uniform normal structure. Furthermore we prove that the iterative process:
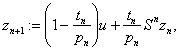
, converges strongly to a fixed point of
Paper's Title:
On Convergence Theorems of an Implicit Iterative Process with Errors for a
Finite Family of Asymptotically quasi I-nonexpansive Mappings
Author(s):
Farrukh Mukhamedov and Mansoor Saburov
Department of Computational & Theoretical
Sciences,
Faculty of Sciences, International Islamic University Malaysia,
P.O. Box, 141, 25710, Kuantan,
Malaysia
Abstract:
In this paper we prove the weak and strong convergence of the implicit iterative process with errors to a common fixed point of a finite family {Tj}Ni=1 of asymptotically quasi Ij-nonexpansive mappings as well as a family of {Ij}Nj=1 of asymptotically quasi nonexpansive mappings in the framework of Banach spaces. The obtained results improve and generalize the corresponding results in the existing literature.
Paper's Title:
Robust Error Analysis of Solutions to Nonlinear Volterra Integral Equation in Lp Spaces
Author(s):
Hamid Baghani, Javad Farokhi-Ostad and Omid Baghani
Department of Mathematics, Faculty of
Mathematics,
University of Sistan and Baluchestan, P.O. Box 98135-674, Zahedan,
Iran.
E-mail:
h.baghani@gmail.com
Department of Mathematics, Faculty of
Basic Sciences,
Birjand University of Technology, Birjand,
Iran.
E-mail: j.farrokhi@birjandut.ac.ir
Department of Mathematics and Computer
Sciences,
Hakim Sabzevari University, P.O. Box 397, Sabzevar,
Iran.
E-mail:
o.baghani@gmail.com
Abstract:
In this paper, we propose a novel strategy for proving an important inequality for a contraction integral equations. The obtained inequality allows us to express our iterative algorithm using a "for loop" rather than a "while loop". The main tool used in this paper is the fixed point theorem in the Lebesgue space. Also, a numerical example shows the efficiency and the accuracy of the proposed scheme.
Paper's Title:
MSplit Equality for Monotone Inclusion Problem and Fixed Point Problem in
Real Banach Spaces
Author(s):
1,2Christian Chibueze Okeke, 3Abdumalik Usman Bello, 1Chinedu Izuchukwu, and 1Oluwatosin Temitope Mewomo
1School
of Mathematics,
Statistics and Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: okekec@ukzn.ac.za
E-mail: izuchukwuc@ukzn.ac.za
E-mail: mewomoo@ukzn.ac.za
2DST-NRF
Center of Excellence in Mathematical and Statistical Sciences (CoE-Mass)
Johannesburg,
South Africa.
3Federal
University,
Dutsin-Ma, Katsina State,
Nigeria.
E-mail:
uabdulmalik@fudutsinma.edu.ng
Abstract:
In this paper a new iterative algorithm for approximating a common solution of split equality monotone inclusion problem and split equality fixed point problem is introduced. Using our algorithm, we state and prove a strong convergence theorem for approximating an element in the intersection of the set of solutions of a split equality monotone inclusion problem and the set of solutions of a split equality fixed point problem for right Bregman strongly nonexpansive mappings in the setting of p-uniformly convex Banach spaces which are also uniformly smooth. We also give some applications.
Paper's Title:
Iterative Approximation of Common Fixed Points of a Finite Family of Asymptotically Hemi-contractive Type Mappings
Author(s):
Jui-Chi Huang
Center for General Education,
Northern Taiwan Institute of Science and Technology,
Peito, Taipei,
Taiwan, 11202, R.O.C.
juichi@ntist.edu.tw
Abstract:
In this paper, we prove that the sequence of
the modified Ishikawa-Xu,
Ishikawa-Liu, Mann-Xu and Mann-Liu iterative types of a finite family of
asymptotically hemi-contractive type mappings converges strongly to a common
fixed point of the family in a real p-uniformly convex Banach space with
p>1. Our results improve and extend some recent results.
Search and serve lasted 0 second(s).