Paper's Title:

Two Further Methods for Deriving Four Results Contiguous to Kummer's Second Theorem

Author(s):

I. Kim and J. Kim

Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Korea.
E-mail: iki@wku.ac.kr  

Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Korea.
E-mail: joohyung@wku.ac.kr
 

Abstract:

In the theory of generalized hypergeometric function, transformation and summation formulas play a key role. In particular, in one of the Kummer's transformation formulas, Kim, et al. in 2012, have obtained ten contiguous results in the form of a single result with the help of generalization of Gauss's second summation theorem obtained earlier by Lavoie, et al.. In this paper, we aim at presenting four of such results by the technique of contiguous function relations and integral method developed by MacRobert.

Paper's Title:

On a New Class of Eulerian's Type Integrals Involving Generalized Hypergeometric Functions

Author(s):

Sungtae Jun, Insuk Kim and Arjun K. Rathie

General Education Institute,
Konkuk University, Chungju 380-701,
Republic of Korea.

Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Republic of Korea.

Department of Mathematics,
Vedant College of Engineering and Technology (Rajasthan Technical University),
Bundi-323021, Rajasthan,
India.

E-mail: sjun@kku.ac.kr, iki@wku.ac.kr, arjunkumarrathie@gmail.com

Abstract:

Very recently Masjed-Jamei and Koepf established interesting and useful generalizations of various classical summation theorems for the ₂F₁, ₃F₂, ₄F₃, ₅F₄ and ₆F₅ generalized hypergeometric series. The main aim of this paper is to establish eleven Eulerian's type integrals involving generalized hypergeometric functions by employing these theorems. Several special cases have also been given.

Paper's Title:

On an extension of Edwards's double integral with applications

Author(s):

I. Kim, S. Jun, Y. Vyas and A. K. Rathie

Department of Mathematics Education,
Wonkwang University,
Iksan, 570-749,
Republic of Korea.

General Education Institute,
Konkuk University,
Chungju 380-701,
Republic of Korea.

Department of Mathematics, School of Engineering,
Sir Padampat Singhania University,
Bhatewar, Udaipur, 313601, Rajasthan State,
India.

Department of Mathematics,
Vedant College of Engineering and Technology,
(Rajasthan Technical University),
Bundi-323021, Rajasthan,
India.

E-mail: iki@wku.ac.kr sjun@kku.ac.kr
yashoverdhan.vyas@spsu.ac.in arjunkumarrathie@gmail.com

Abstract:

The aim of this note is to provide an extension of the well known and useful Edwards's double integral. As an application, new class of twelve double integrals involving hypergeometric function have been evaluated in terms of gamma function. The results are established with the help of classical summation theorems for the series ₃F₂ due to Watson, Dixon and Whipple. Several new and interesting integrals have also been obtained from our main findings.

Paper's Title:

A Note on Evaluation of a New Class of Integrals Involving Generalized Hypergeometric Function

Author(s):

Madhav Prasad Poudel, Dongkyu Lim^*, Narayan Prasad Pahari, Arjun K. Rathie

School of Engineering,
Pokhara University, Pokhara-30, Kaski,
Nepal.
E-mail: pdmadav@gmail.com

Department of Mathematics Education,
Andong National University, Andong 36729,
Republic of Korea.
E-mail: dklim@anu.ac.kr

Central Department of Mathematics,
Tribhuvan University, Kirtipur, Kathmandu,
Nepal.
E-mail: nppahari@gmail.com

Department of Mathematics,
Vedant College of Engineering & Technology (Rajasthan Technical University), Village: Tulsi,
Jakhamund, Dist. Bundi, Rajasthan State,
India.
E-mail: arjunkumarrathie@gmail.com

Abstract:

In the theory of hypergeometric and generalized hypergeometric series, classical summation theorems such as those of Gauss, Gauss second, Bailey and Kummer for the series ₂F₁; Watson, Dixon, Whipple and Saalshutz play a key role. Applications of the above mentioned summation theorems are well known for the series ₃F₂. In our present investigation, we aim to evaluate twenty five new class of integrals involving generalized hypergeometric function in the form of a single integral of the form:

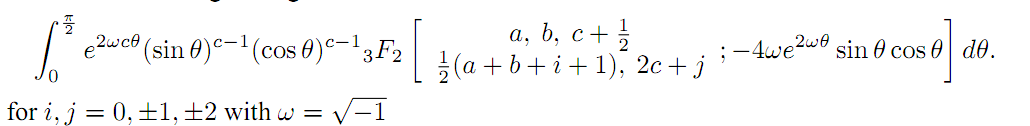
The results are established with the help of the generalizations of the classical Watson's summation theorem obtained earlier by Lavoie et al.. Fifty interesting integrals in the form of two integrals (twenty five each) have also been given as special cases of our main findings.

Paper's Title:

Evaluation of a New Class of Double Integrals Involving Generalized Hypergeometric Function ₄F₃

Author(s):

Joohyung Kim, Insuk Kim and Harsh V. Harsh

Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Korea.
E-mail: joohyung@wku.ac.kr
 
Department of Mathematics Education,
Wonkwang University, Iksan, 570-749,
Korea.
E-mail: iki@wku.ac.kr

Department of Mathematics, Amity School of Eng. and Tech.,
Amity University Rajasthan
NH-11C, Jaipur-303002, Rajasthan,
India.
E-mail: harshvardhanharsh@gmail.com

Abstract:

Very recently, Kim evaluated some double integrals involving a generalized hypergeometric function ₃F₂ with the help of generalization of Edwards's well-known double integral due to Kim,  et al. and generalized classical Watson's summation theorem obtained earlier by Lavoie,  et al. In this research paper we evaluate one hundred double integrals involving generalized hypergeometric function ₄F₃ in the form of four master formulas (25 each) viz. in the most general form for any integer. Some interesting results have also be obtained as special cases of our main findings.

Paper's Title:

Several New Closed-form Evaluations of the Generalized Hypergeometric Function with Argument 1/16

Author(s):

B. R. Srivatsa Kumar, Insuk Kim and Arjun K. Rathie

Department of Mathematics,
Manipal Institute of Technology,
Manipal Academy of Higher Education,
Manipal 576 104,
India.
E-mail: sri_vatsabr@yahoo.com

Department of Mathematics Education,
Wonkwang University,
Iksan, 54538,
Republic of Korea.
E-mail: iki@wku.ac.kr

Department of Mathematics,
Vedant College of Engineering and Technology,
Rajasthan Technical University,
Bundi, 323021, Rajasthan,
India.
E-mail: arjunkumarrathie@gmail.com 

Abstract:

The main objective of this paper is to establish as many as thirty new closed-form evaluations of the generalized hypergeometric function _q+1F_q(z) for q= 2, 3, 4. This is achieved by means of separating the generalized hypergeometric function _q+1F_q(z) for q=1, 2, 3, 4, 5 into even and odd components together with the use of several known infinite series involving central binomial coefficients obtained earlier by Ji and Hei \& Ji and Zhang.

Search and serve lasted 0 second(s).