²Department of Mathematics,
Cochin University of Science and Technology,
Kerala 682022,
India.
E-mail: noufal@cusat.ac.in

Abstract:

This paper provides a review on Minimally Supported Frequency (MSF) wavelets that includes the construction and characterization of MSF wavelets. The characterization of MSF wavelets induced from an MRA is discussed and the nature of the low-pass filter associated with it is explained. The concept of wavelet set and dimension function is introduced to study this class of wavelets. Along with MSF wavelets, s-elementary wavelets and unimodular wavelets are also considered due to the similarity in definitions. Examples and illustrations are provided for more clarity.

Paper's Title:

Construction of a Frame Multiresolution Analysis on Locally Compact Abelian Groups

Author(s):

R. Kumar and Satyapriya

Department of Mathematics,
Kirori Mal College,
University of Delhi,
Delhi,
India.
E-mail: rajkmc@gmail.com

 
Department of Mathematics,
University of Delhi,
Delhi,
India.
E-mail: kmc.satyapriya@gmail.com

Abstract:

The frame multiresolution analysis (FMRA) on locally compact Abelian groups has been studied and the results concerning classical MRA have been worked upon to obtain new results. All the necessary conditions, which need to be imposed on the scaling function φ to construct a wavelet frame via FMRA, have been summed up. This process of construction of FMRA has aptly been illustrated by sufficient examples.

Paper's Title:

Existence of solutions for Neutral Stochastic Functional Differential Systems with Infinite Delay in Abstract Space

Author(s):

P. Balasubramaniam, A. V. A. Kumar and S. K. Ntouyas

Department of Mathematics, Gandhigram Rural Institute,
Deemed University, Gandhigram - 624 302, Tamil Nadu, India.
pbalgri@rediffmail.com

Department of Mathematics, Gandhigram Rural Institute,
Deemed University, Gandhigram - 624 302, Tamil Nadu, India.
nnddww@tom.com

Department of Mathematics, University of Ioannina,
451 10 Ioannina,
Greece.
sntouyas@cc.uoi.gr
URL: http://www.math.uoi.gr/~sntouyas

Abstract:

In this paper we prove existence results for semilinear stochastic neutral functional differential systems with unbounded delay in abstract space. Our theory makes use of analytic semigroups and fractional power of closed operators and Sadovskii fixed point theorem.

Paper's Title:

Existence Results for Second Order Impulsive Functional Differential Equations with Infinite Delay

Author(s):

M. Lakrib, A. Oumansour and K. Yadi  

Laboratoire de Mathématiques, Université Djillali
Liabées, B.P. 89 Sidi Bel Abbès 22000, Algérie
mlakrib@univ-sba.dz
oumansour@univ-sba.dz

Laboratoire de Mathématiques, Université Abou Bekr
Belkaid, B.P. 119 Tlemcen 13000, Algérie
k_yadi@mail.univ-tlemcen.dz

Abstract:

In this paper we study the existence of solutions for second order impulsive functional differential equations with infinite delay. To obtain our results, we apply fixed point methods.

Paper's Title:

Wavelet Frames in Higher Dimensional Sobolev Spaces

Author(s):

Raj Kumar, Manish Chauhan, and Reena

Department of Mathematics,
Kirori Mal College, University of Delhi,
New Delhi-110007,
India.
E-mail: rajkmc@gmail.com

Department of Mathematics,
University of Delhi,
New Delhi-110007,
India
E-mail: manish17102021@gmail.com

Department of Mathematics,
Hans Raj College, University of Delhi,
New Delhi-110007,
India
E-mail: reena.bhagwat29@gmail.com

Abstract:

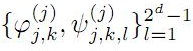In this paper, we present sufficient condition for the sequence of vectors to be a frame for H^s(R^d) are derived. Necessary and sufficient conditions for the sequence of vectors 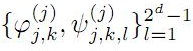to be tight wavelet frames in H^s(R^d) are obtained. Further, as an application an example of tight wavelet frames for H^s(R²) as bivariate box spline over 3-direction are given.

Paper's Title:

New Exact Taylor's Expansions without the Remainder: Application to Finance

Author(s):

Moawia Alghalith

Economics Dept.,
University of the West Indies,
St Augustine,
Trinidad and Tobago.

E-mail: malghalith@gmail.com

Abstract:

We present new exact Taylor's expansions with fixed coefficients and without the remainder. We apply the method to the portfolio model.

Corrigendum.
A corrigendum for this article has been published. To view the corrigendum, please click here.

Paper's Title:

Solving Two Point Boundary Value Problems by Modified Sumudu Transform Homotopy Perturbation Method

Author(s):

Asem AL Nemrat and Zarita Zainuddin

School of Mathematical Sciences,
Universiti Sains Malaysia,
11800 Penang,
Malaysia.
E-mail: alnemrata@yahoo.com
zarita@usm.my

Abstract:

This paper considers a combined form of the Sumudu transform with the modified homotopy perturbation method (MHPM) to find approximate and analytical solutions for nonlinear two point boundary value problems. This method is called the modified Sumudu transform homotopy perturbation method (MSTHPM). The suggested technique avoids the round-off errors and finds the solution without any restrictive assumptions or discretization. We will introduce an appropriate initial approximation and furthermore, the residual error will be canceled in some points of the interval (RECP). Only a first order approximation of MSTHPM will be required, as compared to STHPM, which needs more iterations for the same cases of study. After comparing figures between approximate, MSTHPM, STHPM and numerical solutions, it is found through the solutions we have obtained that they are highly accurate, indicating that the MSTHPM is very effective, simple and can be used to solve other types of nonlinear boundary value problems (BVPs).

Paper's Title:

Multistage Analytical Approximate Solution of Quasi-Linear Differential- Algebraic System of Index Two

Author(s):

Ibrahim M. Albak, F. A. Abdullah^* and Zarita Zainuddin