|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Some Inequalities for a Certain Class of Multivalent Functions
Using Multiplier Transformation
Author(s):
K. Suchithra, B. Adolf Stephen, A. Gangadharan and S. Sivasubramanian
Department Of Applied Mathematics
Sri Venkateswara College Of Engineering
Sriperumbudur, Chennai - 602105,
India.
suchithravenkat@yahoo.co.in
Department Of Mathematics,
Madras Christian College
Chennai - 600059,
India.
adolfmcc2003@yahoo.co.in
Department Of Applied Mathematics
Sri Venkateswara College Of Engineering
Sriperumbudur, Chennai - 602105,
India.
ganga@svce.ac.in
Department Of Mathematics,
Easwari Engineering College
Ramapuram, Chennai - 600089,
India.
ganga@svce.ac.in
Abstract:
The object of the present paper is to derive several inequalities
associated with differential subordinations between analytic functions
and a linear operator defined for a certain family of p-valent
functions, which is introduced here by means of a family of extended
multiplier transformations. Some special cases and consequences of
the main results are also considered.
Paper's Title:
Neighborhoods of Certain Subclasses of Analytic Functions of Complex Order with Negative Coefficients
Author(s):
B. Srutha Keerthi, B. Adolf Stephen, A. Gangadharan, and S. Sivasubramanian
Department of Applied Mathematics,
Sri Venkateswara College of Engineering,
Sriperumbudur, Chennai - 602105,
India.
sruthilaya06@yahoo.co.in
Department of Mathematics,
Madras Christian College,
Chennai - 600059,
India
adolfmcc2003@yahoo.co.in
Department of Applied Mathematics,
Sri Venkateswara College of Engineering,
Sriperumbudur, Chennai - 602105,
India.
ganga@svce.ac.in
Department of Mathematics,
Easwari Engineering College,
Ramapuram, Chennai - 600089,
India
sivasaisastha@rediffmail.com
Abstract:
The main object of this paper is to prove several inclusion relations associated with the (n, δ) neighborhoods of various subclasses of convex functions of complex order by making use of the known concept of neighborhoods of analytic functions.
Paper's Title:
On Certain Classes of Harmonic Univalent Functions Based on Salagean Operator
Author(s):
G. Murugusundaramoorthy, Thomas Rosy, and B. A. Stephen
Department of Applied Mathematics and Informatics,
Department of Mathematics, Vellore Institute of Technology,
Deemed University, Vellore - 632014, India.
gmsmoorthy@yahoo.com
Department of Applied Mathematics and Informatics,
Department of Mathematics, Madras Christian College,
Chennai - 600059, India.
drthomasrosy@rediffmail.com
Abstract:
We define and investigate a class of complex-valued harmonic univalent functions of the form f = h + g using Salagean operator where h and g are analytic in the unit disc U = { z : |z| < 1 }. A necessary and sufficient coefficient conditions are given for functions in these classes. Furthermore, distortion theorems, inclusion relations, extreme points, convolution conditions and convex combinations for this family of harmonic functions are obtained.
Paper's Title:
A Coefficient Inequality For Certain Subclasses of Analytic
Functions Related to Complex Order
Author(s):
B. Srutha Keerthi, B. Adolf Stephen and S. Sivasubramanian
Department Of Applied Mathematics, Sri Venkateswara College Of Engineering, Anna University,
Sriperumbudur, Chennai - 602 105,
India.
laya@svce.ac.in
Department of Mathematics, Madras Christian College,
Chennai - 600059,
India
adolfmcc2003@yahoo.co.in
Department of Mathematics, College of Engineering, Anna University,
Tamilnadu, Chennai - 600 025,
India.
sivasaisastha@rediffmail.com
Abstract:
In this present investigation, the authors obtain coefficient
inequality for certain normalized analytic functions of complex order f(z) defined
on the open unit disk for which
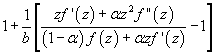 (
( and
and  be a complex number) lies in a region starlike with respect to 1 and is symmetric with respect to the real axis. Also
certain applications of the main result for a class of functions of complex order
defined by convolution are given. As a special case of this result, coefficient
inequality for a class of functions defined through fractional derivatives is
obtained. The motivation of this paper is to give a generalization of the
coefficient inequalities of the subclasses of starlike and convex functions of
complex order.
be a complex number) lies in a region starlike with respect to 1 and is symmetric with respect to the real axis. Also
certain applications of the main result for a class of functions of complex order
defined by convolution are given. As a special case of this result, coefficient
inequality for a class of functions defined through fractional derivatives is
obtained. The motivation of this paper is to give a generalization of the
coefficient inequalities of the subclasses of starlike and convex functions of
complex order.
Paper's Title:
On Stan Ulam and his Mathematics
Author(s):
Krzysztof Ciesielski and Themistocles M. Rassias
Mathematics Institute, Jagiellonian University,
Abstract:
In this note we give a glimpse of the curriculum vitae of Stan Ulam, his personality and some of the mathematics he was involved in.
Paper's Title:
Properties of Certain Multivalent Functions Involving Ruscheweyh Derivatives
Author(s):
N-Eng Xu and Ding-Gong Yang
Department of Mathematics,
Changshu Institute of Technology,
Changshu, Jiangsu 215500,
China
Abstract:
Let Ap(p∈ N) be the class of functions
which are analytic
in the unit disk. By virtue of the Ruscheweyh derivatives we introduce the new
subclasses Cp(n,α,β,λ,μ) of Ap. Subordination relations, inclusion relations,
convolution properties and a sharp coefficient estimate are
obtained. We also give a sufficient condition for a function to be
in Cp(n,α,β,λ,μ)
Paper's Title:
Bounds on the Jensen Gap, and Implications for Mean-Concentrated Distributions
Author(s):
Xiang Gao, Meera Sitharam, Adrian E. Roitberg
Department of Chemistry, and Department
of Computer & Information Science & Engineering,
University of Florida,
Gainesville, FL 32611,
USA.
E-mail: qasdfgtyuiop@gmail.com
URL:
https://scholar.google.com/citations?user=t2nOdxQAAAAJ
Abstract:
This paper gives upper and lower bounds on the gap in Jensen's inequality, i.e., the difference between the expected value of a function of a random variable and the value of the function at the expected value of the random variable. The bounds depend only on growth properties of the function and specific moments of the random variable. The bounds are particularly useful for distributions that are concentrated around the mean, a commonly occurring scenario such as the average of i.i.d. samples and in statistical mechanics.
Paper's Title:
Hankel Functional Connected to Lemniscate of Bernoulli
Author(s):
K. Ramanuja Rao, Rajnesh Lal and Kaushal Singh
Fiji National University,
Department of Mathematics & Statistics,
P.O. Box 5529, Lautoka,
Fiji.
E-mail: ramanuja.kotti@fnu.ac.fj
rajnesh.lal@fnu.ac.fj
kaushal.singh@fnu.ac.fj
Abstract:
The aim of present paper is to derive a higher bound (HB) of 3rd order Hankel determinant for a collection of holomorphic mappings connected with exactly to the right side of the lemniscate of Bernoulli, whose polar coordinates form is r2 = 2cos2(2θ). The method carried in this paper is more refined than the method adopted by the authors (see [1]), who worked on this problem earlier.
Search and serve lasted 0 second(s).