Paper's Title:

On the Oscillatory Behavior of Self Adjoint Fractional Extensible Beam Equations

Author(s):

S. Priyadharshini¹, G.E. Chatzarakis², S. L. Panetsos² and V. Sadhasivam¹

¹Post Graduate and Research Department of Mathematics,
Thiruvalluvar Government Arts College,
Rasipuram - 637 401, Namakkal Dt., Tamil Nadu,
India.
E-mail: s.priya25april@gmail.com, ovsadha@gmail.com

²Department of Electrical and Electronic Engineering Educators,
School of Pedagogical and Technological Education(ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr, gea.xatz@aspete.gr, spanetsos@aspete.gr

Abstract:

The main objective of this paper is to study the oscillatory behavior of the solutions of self adjoint fractional extensible beam equations by using integral average method. Some new sufficient conditions are established with various boundary conditions over a cylindrical domains. Examples illustrating the results are given.

Paper's Title:

Improved Oscillation Criteria of Second-Order Advanced Non-canonical Difference Equation

Author(s):

G. E. Chatzarakis¹, N. Indrajith², S. L. Panetsos¹, E. Thandapani³

¹Department of Electrical and Electronic Engineering Educators
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail: gea.xatz@aspete.gr, geaxatz@otenet.gr
spanetsos@aspete.gr

²Department of Mathematics,
Presidency College, Chennai - 600 005,
India.
E-mail: indrajithna@gmail.com

³Ramanujan Institute for Advanced Study in Mathematics,
University of Madras Chennai - 600 005,
India.
E-mail: ethandapani@yahoo.co.in

Abstract:

Employing monotonic properties of nonoscillatory solutions, we derive some new oscillation criteria for the second-order advanced non-canonical difference equation

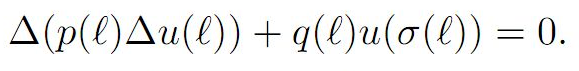
Our results extend and improve the earlier ones. The outcome is illustrated via some particular difference equations.

Paper's Title:

SQIRV Model for Omicron Variant with Time Delay

Author(s):

S. Dickson, S. Padmasekaran, G. E. Chatzarakis and S. L. Panetsos

Mathematics, Periyar University, Periyar Palkalai Nagar, Salem,
636011, Tamilnadu,
India.
E-mail: dickson@periyaruniversity.ac.in, padmasekarans@periyaruniversity.ac.in

Electrical and Electronic Engineering Educators, School of
Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr, spanetsos@aspete.gr

Abstract:

In order to examine the dynamics of the Omicron variant, this paper uses mathematical modelling and analysis of a SQIRV model, taking into account the delay in the conversion of susceptible individuals into infected individuals and infected individuals into recovered individuals. The pandemic was eventually controlled as a result of the massive delays. To assure the safety of the host population, this concept incorporates quarantine and the COVID-19 vaccine. Both local and global stability of the model are examined. It is found that the fundamental reproduction number affects both local and global stability conditions. Our findings show that asymptomatic cases caused by an affected population play an important role in increasing Omicron infection in the general population. The most recent data on the pandemic Omicron variant from Tamil Nadu, India, is verified.

Paper's Title:

Linear System of Singularly Perturbed Initial Value Problems with Robin Initial Conditions

Author(s):

S. Dinesh, G. E. Chatzarakis, S. L. Panetsos and S. Sivamani

Department of Mathematics,
Saranathan College of Engineering,
Tiruchirappalli-620012,
Tamil Nadu,
India.

Department of Electrical and Electronic Engineering Educators,
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.

E-mail: geaxatz@otenet.gr, dineshselvaraj24@gmail.com,
spanetsos@aspete.gr, winmayi2012@gmail.com

Abstract:

On the interval (0,1], this paper considers an initial value problem for a system of n singularly perturbed differential equations with Robin initial conditions. On a piecewise uniform Shishkin mesh, a computational approach based on a classical finite difference scheme is proposed. This approach is shown to be first-order convergent in the maximum norm uniformly in the perturbation parameters. The theory is illustrated by a numerical example.

Paper's Title:

ℵ0 Algebra and its Novel Application in Edge Detection

Author(s):

G. E. Chatzarakis¹, S. Dickson², S. Padmasekaran², S. L. Panetsos¹, and J. Ravi³

¹Electrical and Electronic Engineering Educators,
School of Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
E-mail: geaxatz@otenet.gr, spanetsos@aspete.gr

²Mathematics, Periyar University,
Periyar Palkalai Nagar, Salem, 636011, Tamilnadu,
India.
E-mail: dix.bern@gmail.com, padmasekarans@periyaruniversity.ac.in

³Department of Mathematics, Amity University,
Bengaluru, Karnataka,
India.
E-mail: jravistat@gmail.com
 

Abstract:

In this paper a new type of ℵ₀-algebra has been defined. With its help, the fuzzy cross subalgebra and the fuzzy η-relation on the ℵ₀-algebra are introduced and their respective properties are derived. Moreover, the fuzzy cross ℵ₀-ideal of the ℵ₀-algebra is defined with some theorems and intuitionistic fuzzy ℵ₀-ideals of the ℵ₀-algebra are introduced. This fuzzy algebra concept is applied in image processing to detect edges. This ℵ₀-algebra is a novelty in the field of research.

Paper's Title:

Semicommutative and Semiprime Properties in Bi-amalgamated Rings

Author(s):

¹A. Aruldoss, ²C. Selvaraj, ³G. E. Chatzarakis, ⁴S. L. Panetsos, ⁵U. Leerawat

¹ Department of Mathematics,
Mepco Schlenk Engineering College,
Sivakasi-626 005, Tamilnadu,
India.
aruldossa529@gmail.com

² Department of Mathematics,
Periyar University,
Salem - 636 011, Tamilnadu,
India.
selvavlr@yahoo.com

 ^3,4 Department of Electrical and Electronic Engineering Educators,
School of Pedagogical and Technological Education (ASPETE),
Marousi 15122, Athens,
Greece.
geaxatz@otenet.gr spanetsos@aspete.gr

⁵ Department of Mathematics,
Faculty of Science, Kasetsart University,
Bangkok 10900,
Thailand.
fsciutl@ku.ac.th

Abstract:

Let α: A→ B and β: A→ C be two ring homomorphisms and I and I' be two ideals of B and C, respectively, such that α^{-1}(I)=β^{-1}(I'). In this paper, we give a characterization for the bi-amalgamation of A with (B, C) along (I, I') with respect to (α, β) (denoted by A⋈^{(α, β)}(I, I')) to be a SIT, semiprime, semicommutative and semiregular. We also give some characterization for these rings.

Search and serve lasted 1 second(s).