|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
A New Property of General Means of Order p with an Application to the Theory of Economic Growth
Author(s):
Olivier de La Grandville
Department of Management Science and Engineering,
Huang Engineering Center, Stanford University,
475 Via Ortega, Stanford, California 94305
U.S.A.
Abstract:
The purpose of this note is to demonstrate a new property of the
general mean of order p of m ordered positive numbers
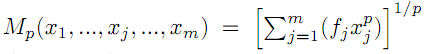
,
the elasticity of
with
respect to xm, defined by
,
tends towards zero, and therefore
.
This property is then applied to optimal growth theory.
Paper's Title:
A New Look at the Equations of the Calculus of Variations
Author(s):
Olivier de La Grandville
Faculty of Economics, Goethe University
Frankfurt,
Theodore Adorno Platz 4, 60323 Frankfurt,
Germany.
E-mail: odelagrandville@gmail.com
Abstract:
We first offer an entirely new way to derive the celebrated Euler equation of the calculus of variations. The advantage of this approach is two-fold. On the one hand, it entirely eschews the two hurdles encountered by Lagrange, which become challenging in the case of elaborate functionals: getting rid of the arbitrary character of the perturbation given to the optimal function, and demonstrating the fundamental lemma of the calculus of variations. On the other hand, it leads in a direct way to the remarkable discovery made by Robert Dorfman ( 1969) when he introduced a modified Hamiltonian, which we called a Dorfmanian (2018) to honor his memory. In turn, extending the Dorfmanian enables to obtain readily the fundamental equations of the calculus of variations for the optimization of high-order functionals, or multiple integrals.
Paper's Title:
End-Point and Transversality Conditions in the Calculus of Variations: Derivations through Direct Reasoning
Author(s):
Olivier de La Grandville
Stanford University,
Department of Management Science and Engineering,
475 Via Ortega, Stanford, CA 94305,
U. S. A.
E-mail: ola@stanford.edu
Abstract:
We offer an intuitive explanation of the end-point and transversality conditions that complement the Euler equation in the calculus of variations. Our reasoning is based upon the fact that any variation given to an optimal function must entail a zero net gain to the functional, all consequences of implied changes in its derivative being fully taken into account.
Paper's Title:
Introducing the Dorfmanian: A Powerful Tool for the Calculus Of Variations
Author(s):
Olivier de La Grandville
Department of Management Science and Engineering,
Stanford University,
475 Via Ortega, Stanford, CA 94305,
U. S. A.
E-mail: odelagrandville@gmail.com
Abstract:
We show how a modified Hamiltonian proposed by Robert Dorfman [1] to give intuitive sense
to the Pontryagin maximum principle can be extended to easily obtain all
high-order equations of the calculus of variations. This new concept is
particularly efficient to determine the differential equations leading to
the extremals of functionals defined by n-uple integrals, while a
traditional approach would require -- in some cases repeatedly -- an
extension of Green's theorem to n-space.
Our paper is dedicated to the memory of Robert Dorfman (1916 - 2002).
Paper's Title:
A New Interpretation of the Number e
Author(s):
Olivier de La Grandville
Faculty of Economics, Goethe University,
Frankfurt, Theodor-Adorno Platz 4,
60323 Frankfurt am Main,
Germany.
E-mail:
odelagrandville@gmail.com
Abstract:
We show that e is the amount that 1 becomes when it is invested during an arbitrary time span of length T, at any continuously compounded interest rates as long as their average is equal to 1/T . A purely mathematical interpretation of e is the amount a unit quantity becomes after any duration T when the average of its instantaneous growth rates is 1/T. This property can be shown to remain valid if T tends to infinity as long as the integral of the growth rates converges to unity.
Paper's Title:
On the Oldest Problem in the Calculus of Variations: A New Message from Queen Dido
Author(s):
Olivier de La Grandville
Faculty of Economics,
Goethe University Frankfurt,
Theodore Adorno Platz 4, 60323 Frankfurt,
Germany.
E-mail: odelagrandville@gmail.com
Abstract:
We consider the problem of finding the optimal curve of given length linking two points in a plane such as it encloses a maximal area. We show that if the curve is not described by a single-valued function, its determination does not necessarily imply to work with a parametric representation of the curve. We show that a simpler approach is at hand -- and, who knows? -- this might well be the method Queen Dido used.
Paper's Title:
The Degree of Homogeneity: Definition, Geometric Interpretation and New, Direct Proofs of Euler's Theorem
Author(s):
Olivier de La Grandville
Faculty of Economics, Goethe University
Frankfurt,
Theodore Adorno Platz 4, 60323 Frankfurt,
Germany.
E-mail: odelagrandville@gmail.com
Abstract:
We show how the degree of homogeneity of a function is a highly useful, precise measure of the sensitivity of a function to a change in its variables. This measure can be evaluated directly thanks to a simple geometric construct, entirely independently of measurement units. The usefulness of this concept is also illustrated by the fact that it leads to new, direct proofs, geometric as well as algebraic, of Euler's theorem; this is in contrast to the traditional approach that requires a limiting process.
Paper's Title:
A One-Line Derivation of the Euler and Ostrogradski Equations
Author(s):
Olivier de La Grandville
Stanford University,
Department of Management Science and Engineering,
Stanford, CA 94305,
U. S. A
Abstract:
At the very heart of major results of classical physics, the Euler and Ostrogradski equations have apparently no intuitive interpretation. In this paper we show that this is not so. Relying on Euler's initial geometric approach, we show that they can be obtained through a direct reasoning that does not imply any calculation. The intuitive approach we suggest offers two benefits: it gives immediate significance to these fundamental second-order non-linear differential equations; and second, it allows to obtain a property of the calculus of variations that does not seem to have been uncovered until now: the Euler and Ostrogradski equations can be derived not necessarily by giving a variation to the optimal function -- as is always done; one could equally well start by giving a variation to their derivative(s).
Search and serve lasted 0 second(s).